A Terahertz Identification Method for Internal Interface Structures of Polymers Based on the Long Short-Term Memory Classification Network
Abstract
:1. Introduction
2. Theory and Methodology
2.1. Terahertz Detection Theory
2.2. LSTM Theory
3. Experiment Setup
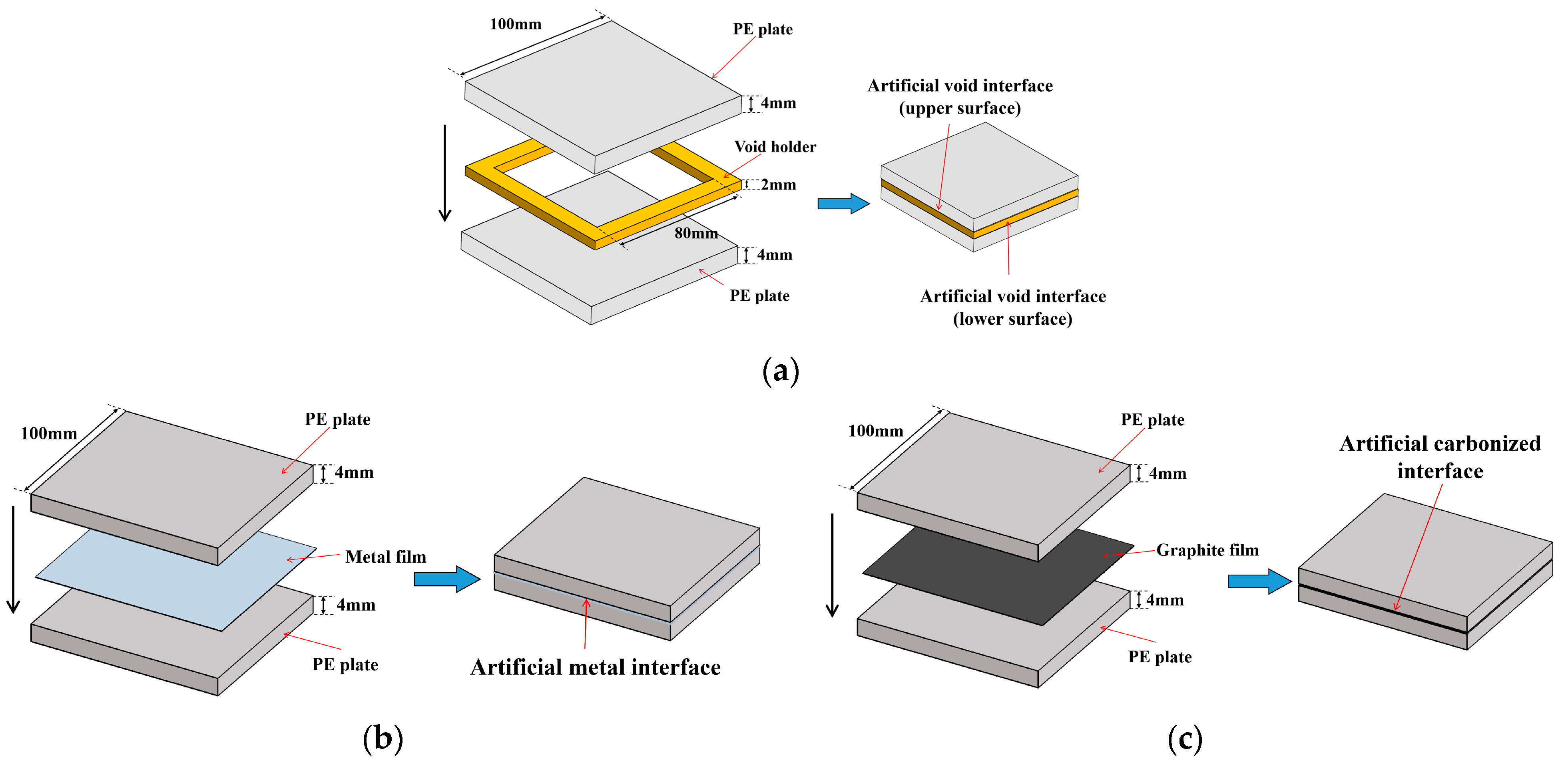
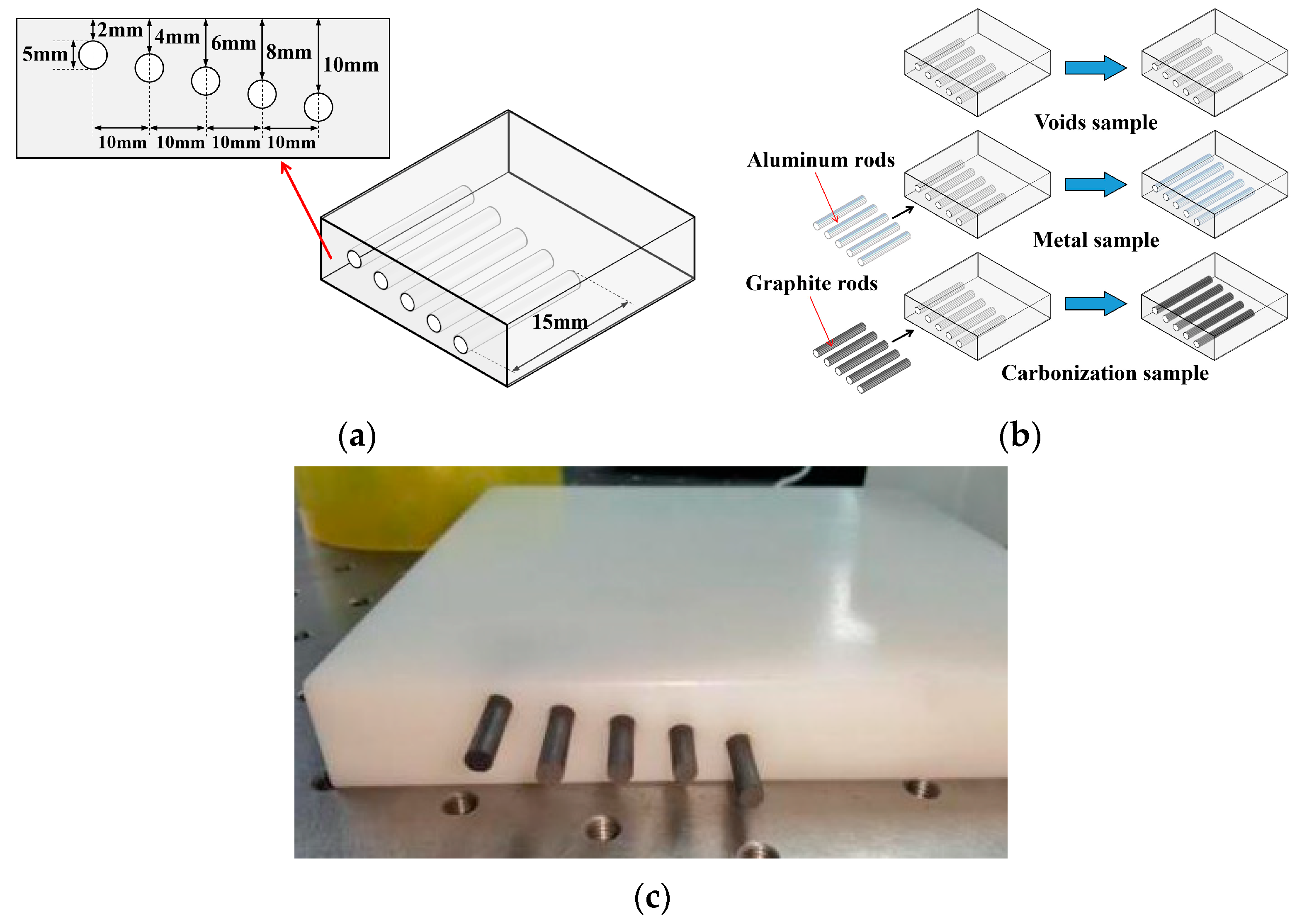
3.1. Experimental Samples
3.2. THz System
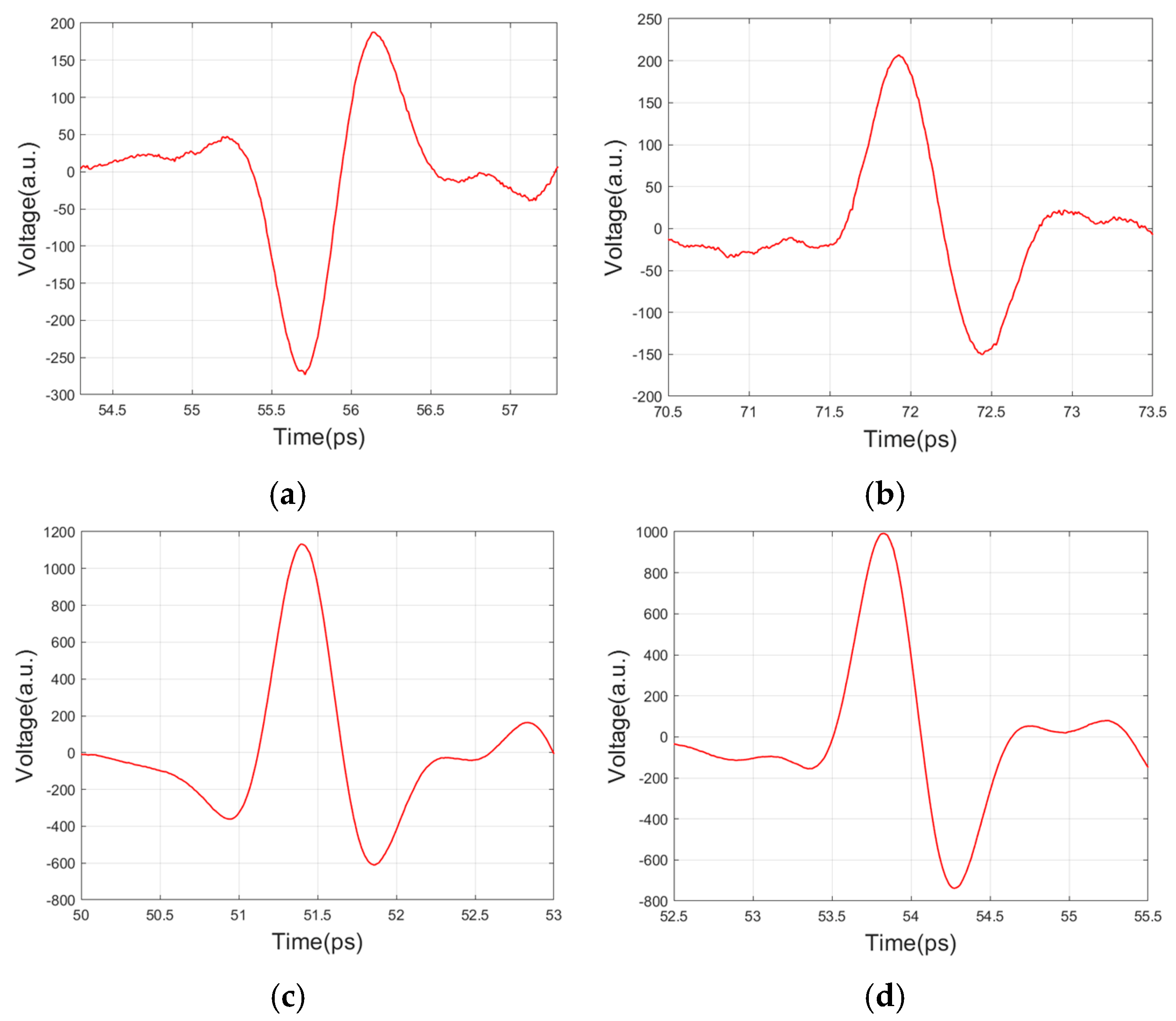
4. Experiments and Discussion
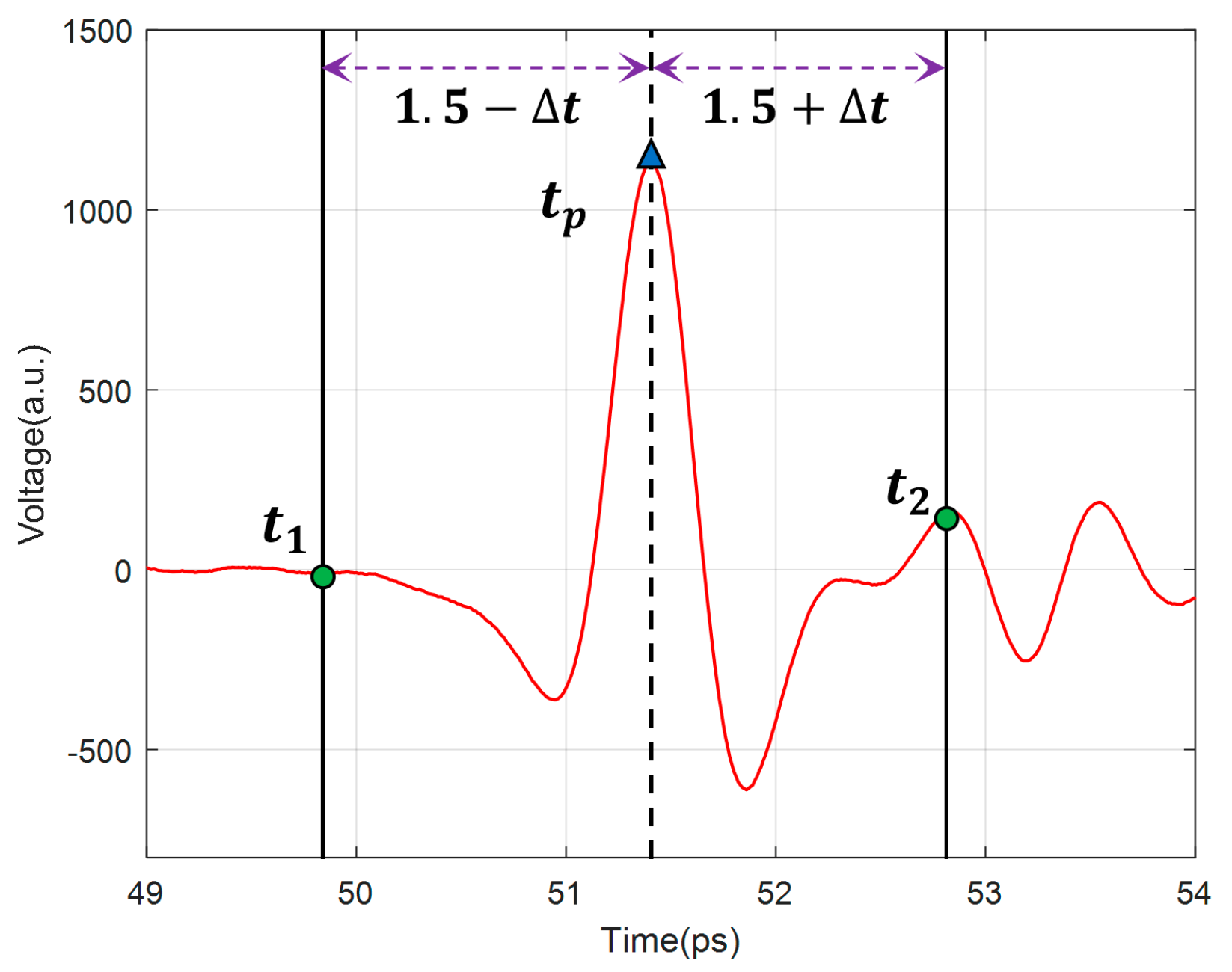
4.1. LSTM Training
4.2. 3D Identification Imaging Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guan, Z.; Liu, Y.; Zhou, Y.; Jiang, Z.; Wang, L.; Shi, W. External Insulation of Insulators and Transmission and Transformation Equipment; Tsinghua University Press: Beijing, China, 2006; pp. 65–86. [Google Scholar]
- Wang, L.; Fu, K.; Mei, H.; Zhang, F.; Guo, C.; Zhang, Z. Influence of environmental humidity on infrared measurement temperature of composite insulators. High Voltage Eng. 2019, 45, 1951–1961. [Google Scholar]
- Wang, S.; Hou, M.; Ma, K.; Li, Z.; Geng, H.; Zhang, W.; Li, N. Research on the Influence of Extremely Cold Environment on the Performance of Silicone Rubber and Fluorinated Silicone Rubber. Polymers 2022, 14, 1898. [Google Scholar] [CrossRef] [PubMed]
- Lennartz-Sassinek, S.; Main, I.G.; Zaiser, M.; Graham, C.C. Acceleration and localization of subcritical crack growth in a natural composite material. Phys. Rev. E 2014, 90, 052401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, L.; Li, T.; Zhou, X.; Guan, W.; Wang, Z.; Wang, S. Statistical Analysis of String Fracture and Core Breakdown of Composite Insulators in Zhejiang Province. In Proceedings of the IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019. [Google Scholar]
- Su, C.Q. Failure analysis of three 230 kV XLPE cables. In Proceedings of the Transmission and Distribution Conference and Exposition: Latin America, São Paulo, Brazil, 8–10 November 2010. [Google Scholar]
- Yuan, C.; Xie, C.; Li, L.; Zhang, F.; Gubanski, S.M. Ultrasonic phased array detection of internal defects in composite insulators. IEEE Trans. Dielectrics Electr. Insul. 2016, 23, 525–531. [Google Scholar] [CrossRef]
- Cheng, L.; Liao, R.; Yang, L.; Zhang, F. An Optimized Infrared Detection Strategy for Defective Composite Insulators According to the Law of Heat Flux Propagation Considering the Environmental Factors. IEEE Access 2018, 6, 38137–38146. [Google Scholar] [CrossRef]
- Contin, A.; Schena, G.; Stanic, G.L.; Peruzzi, G. In Inspection of ground-wall insulation for AC rotating machines using X-ray tomography. In Proceedings of the IEEE Electrical Insulation Conference (EIC), Montreal, QC, Canada, 2–5 June 2013. [Google Scholar]
- Qaddoumi, N.N.; El-Hag, A.H.; Saker, Y. Outdoor Insulators Testing Using Artificial Neural Network-Based Near-Field Microwave Technique. IEEE Trans. Instrum. Meas. 2014, 63, 260–266. [Google Scholar] [CrossRef]
- Tzydynzhapov, G.; Gusikhin, P.; Muravev, V.; Dremin, A.; Nefyodov, Y.; Kukushkin, I. New Real-Time Sub-Terahertz Security Body Scanner. J. Infrared Millim. Terahertz Waves 2020, 41, 632–641. [Google Scholar] [CrossRef]
- Tan, X.; Huang, S.; Zhong, Y.; Yuan, H.; Zhou, Y.; Xiao, Q.; Guo, L.; Tang, S.; Yang, Z.; Qi, C. In Detection and identification of flammable and explosive liquids using THz time-domain spectroscopy with principal component analysis algorithm. In Proceedings of the UK-Europe-China Workshop on Millimetre Waves and Terahertz Technologies (UCMMT), Liverpool, UK, 11–13 September 2017. [Google Scholar]
- AlNabooda, M.O.; Shubair, R.M.; Rishani, N.R.; Aldabbagh, G. In Terahertz spectroscopy and imaging for the detection and identification of Illicit drugs. In Proceedings of the Sensors Networks Smart and Emerging Technologies (SENSET), Beirut, Lebanon, 12–14 September 2017. [Google Scholar]
- Geng, Z.; Zhang, X.; Fan, Z.; Lv, X.; Chen, H. A Route to Terahertz Metamaterial Biosensor Integrated with Microfluidics for Liver Cancer Biomarker Testing in Early Stage. Sci. Rep. 2017, 7, 16378. [Google Scholar] [CrossRef] [Green Version]
- Lian, F.; Xu, D.; Fu, M.; Ge, H.; Jiang, Y.; Zhang, Y. Identification of Transgenic Ingredients in Maize Using Terahertz Spectra. IEEE Trans. Terahertz Sci. Technol. 2017, 7, 378–384. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, X.; Yang, K.; Liu, Y.; Liu, Y.; Fu, W.; Luo, Y. Biomedical Applications of Terahertz Spectroscopy and Imaging. Trends Biotechnol. 2016, 34, 810–824. [Google Scholar] [CrossRef]
- Ellrich, F.; Bauer, M.; Schreiner, N.; Keil, A.; Pfeiffer, T.; Klier, J.; Weber, S.; Jonuscheit, J.; Friederich, F.; Molter, D. Terahertz Quality Inspection for Automotive and Aviation Industries. J. Infrared Millim. Terahertz Waves 2020, 41, 470–489. [Google Scholar] [CrossRef] [Green Version]
- Zimdars, D.; Valdmanis, J.A.; White, J.S.; Stuk, G.; Winfree, W.P.; Madaras, E.I. In Time domain terahertz detection of flaws within space shuttle sprayed on foam insulation. In Proceedings of the Conference on Lasers and Electro-Optics/International Quantum Electronics Conference and Photonic Applications Systems Technologies, San Francisco, CA, USA, 16 May 2004. [Google Scholar]
- Mei, H.; Jiang, H.; Yin, F.; Wang, L.; Farzaneh, M. Terahertz Imaging Method for Composite Insulator Defects Based on Edge Detection Algorithm. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Jiang, H.; Mei, H.; Bian, X.; Li, L.; Wang, L.; Wang, L. In Detection of Double-layer Air Gap Defects Based on Terahertz Imaging Method. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, Scotland, 17–20 May 2021. [Google Scholar]
- Zhang, Z.; Peng, G.; Tan, Y.; Pu, T.; Wang, L. THz wave detection of gap defects based on convolutional neural network improved by residual shrinkage network. CSEE J. Power Energy Syst. 2020, 1–10. [Google Scholar] [CrossRef]
- Lai, C.F.; Chien, W.C.; Yang, L.T.; Qiang, W. LSTM and Edge Computing for Big Data Feature Recognition of Industrial Electrical Equipment. IEEE Trans. Ind. Inform. 2019, 15, 2469–2477. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Z.; Liu, P.; Wang, Z.; Zhang, L. Battery Fault Diagnosis for Electric Vehicles Based on Voltage Abnormality by Combining the Long Short-Term Memory Neural Network and the Equivalent Circuit Model. IEEE Trans. Power. Electron. 2021, 36, 1303–1315. [Google Scholar] [CrossRef]
- Sun, F.; Fan, M.; Cao, B.; Zheng, D.; Liu, H.; Liu, L. Terahertz Based Thickness Measurement of Thermal Barrier Coatings Using Long Short-Term Memory Networks and Local Extrema. IEEE Trans. Ind. Inform. 2022, 18, 2508–2517. [Google Scholar] [CrossRef]
- Kniffin, G.P.; Zurk, L.M. Model-Based Material Parameter Estimation for Terahertz Reflection Spectroscopy. IEEE Trans. Terahertz Sci. Technol. 2012, 2, 231–241. [Google Scholar] [CrossRef] [Green Version]
- Dhillon, S.S.; Vitiello, M.S.; Linfield, E.H.; Davies, A.G.; Hoffmann, M.C.; Booske, J.; Paoloni, C.; Gensch, M.; Weightman, P.; Williams, G.P. The 2017 terahertz science and technology roadmap. J. Phys. D Appl. Phys. 2017, 50, 043001. [Google Scholar] [CrossRef]
- Duvillaret, L.; Garet, F.; Coutaz, J. A reliable method for extraction of material parameters in terahertz time-domain spectroscopy. IEEE J. Sel. Top. Quantum Electron. 1996, 2, 739–746. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Su, Z.; Li, H.; Zhang, Y. In An LSTM based classification method for time series trend forecasting. In Proceedings of the IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China,, 19–21 June 2019. [Google Scholar]
- Ueta, G.; Wada, J.; Okabe, S.; Miyashita, M.; Nishida, C.; Kamei, M. Insulation characteristics of epoxy insulator with internal void-shaped micro-defects. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 535–543. [Google Scholar] [CrossRef]
- Chen, X.; Xu, Y.; Cao, X.; Gubanski, S.M. On the conducting and non-conducting electrical trees in XLPE cable insulation specimens. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 95–103. [Google Scholar] [CrossRef]
- Li, S.; Wang, W.; Yu, S.; Li, J. Degradation of cross linked polystyrene by repetitive impulse surface flashovers in vacuum. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 1934–1941. [Google Scholar] [CrossRef]
- Tang, J.; Wang, L. In Research on the Discharge between High—Voltage Cable Metal Sheath and Insulation Shield. In Proceedings of the IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019. [Google Scholar]
- Florkowski, M.; Florkowska, B.; Rybak, A.; Zydron, P. Metal migration at conductor / XLPE interface subjected to partial discharges at different electrical stresses. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 456–462. [Google Scholar] [CrossRef]
- Zhang, T. Research and Application of High and Extra High Voltage Super-Clean Cable Material. Master Thesis, Harbin University of Science and Technology, Heilongjiang, China, 2016. [Google Scholar]
- Wietzke, S.; Jansen, C.; Reuter, M.; Jung, T.; Kraft, D.; Chatterjee, S.; Fischer, B.M.; Koch, M. Terahertz spectroscopy on polymers: A review of morphological studies. J. Mol. Struct. 2011, 1006, 41–51. [Google Scholar] [CrossRef]



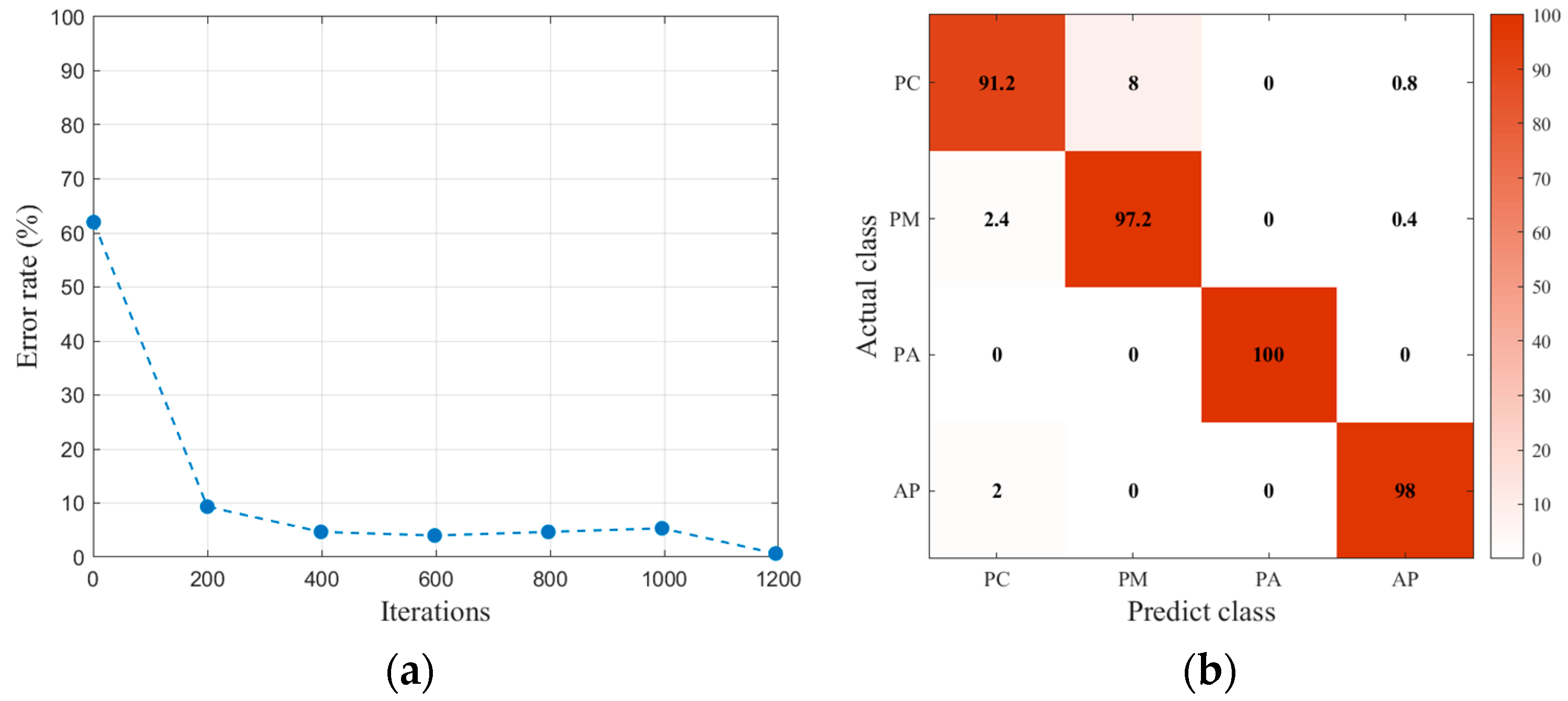



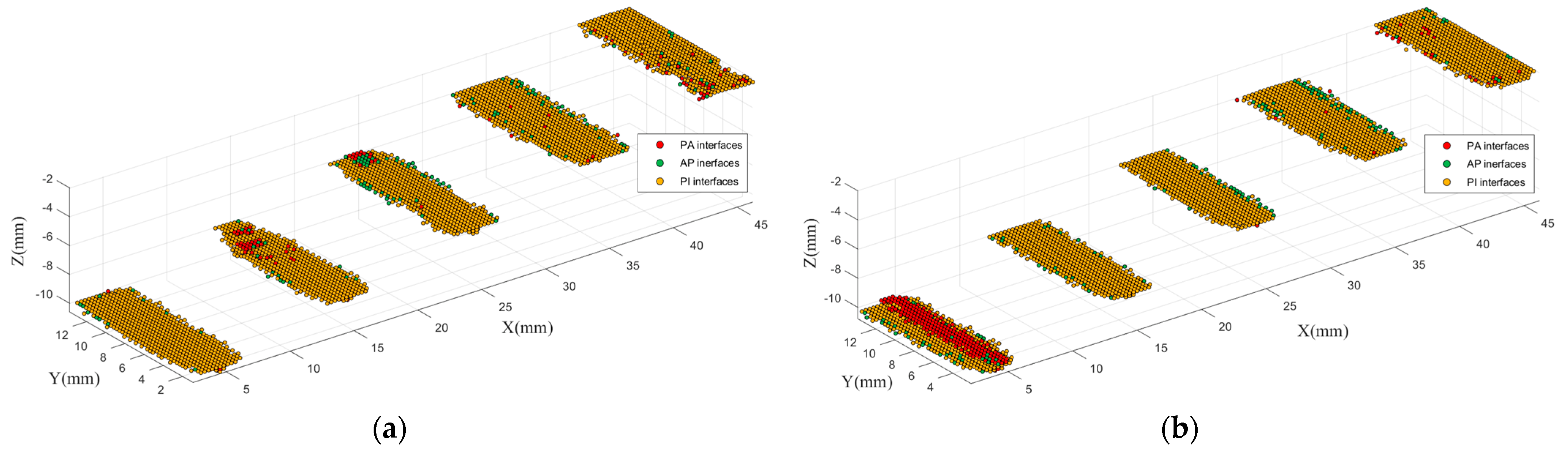
| Actual Interface | Number of PA Points | Number of AP Points | Number of PM Points | Number of PC Points | Correct Identification Rate |
|---|---|---|---|---|---|
| PA interface I | 57 | 0 | 5 | 3 | 87.69% |
| AP interface I | 5 | 89 | 8 | 26 | 69.53% |
| PA interface II | 118 | 3 | 2 | 15 | 85.51% |
| AP interface II | 12 | 102 | 46 | 22 | 56.04% |
| PA interface III | 161 | 13 | 21 | 6 | 80.10% |
| AP interface III | 15 | 75 | 38 | 69 | 38.07% |
| PA interface IV | 244 | 0 | 9 | 1 | 96.06% |
| AP interface IV | 6 | 85 | 48 | 60 | 42.71% |
| PA interface V | 230 | 0 | 6 | 5 | 95.44% |
| AP interface V | 66 | 17 | 37 | 21 | 12.06% |
| Actual Interface | Number of PA Points | Number of AP Points | Number of PM Points | Number of PC Points | Correct Identification Rate |
|---|---|---|---|---|---|
| PM interface I | 33 | 16 | 423 | 163 | 66.61% |
| PM interface II | 11 | 41 | 459 | 262 | 59.38% |
| PM interface III | 48 | 50 | 415 | 304 | 50.80% |
| PM interface IV | 80 | 19 | 478 | 237 | 58.72% |
| PM interface V | 51 | 12 | 533 | 357 | 55.93% |
| Actual Interface | Number of PA Points | Number of AP Points | Number of PM Points | Number of PC Points | Correct Identification Rate |
|---|---|---|---|---|---|
| PC interface I | 23 | 15 | 353 | 158 | 28.78% |
| PC interface II | 5 | 58 | 240 | 293 | 49.16% |
| PC interface III | 16 | 28 | 416 | 115 | 20.00% |
| PC interface IV | 55 | 21 | 533 | 154 | 20.18% |
| PC interface V | 231 | 38 | 348 | 328 | 34.71% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Mei, H.; Liu, J.; Chen, D.; Wang, L. A Terahertz Identification Method for Internal Interface Structures of Polymers Based on the Long Short-Term Memory Classification Network. Polymers 2022, 14, 2611. https://doi.org/10.3390/polym14132611
Wang S, Mei H, Liu J, Chen D, Wang L. A Terahertz Identification Method for Internal Interface Structures of Polymers Based on the Long Short-Term Memory Classification Network. Polymers. 2022; 14(13):2611. https://doi.org/10.3390/polym14132611
Chicago/Turabian StyleWang, Shushan, Hongwei Mei, Jianjun Liu, Dabing Chen, and Liming Wang. 2022. "A Terahertz Identification Method for Internal Interface Structures of Polymers Based on the Long Short-Term Memory Classification Network" Polymers 14, no. 13: 2611. https://doi.org/10.3390/polym14132611
APA StyleWang, S., Mei, H., Liu, J., Chen, D., & Wang, L. (2022). A Terahertz Identification Method for Internal Interface Structures of Polymers Based on the Long Short-Term Memory Classification Network. Polymers, 14(13), 2611. https://doi.org/10.3390/polym14132611







