Thermal Diffusivity and Conductivity of Polyolefins by Thermal Lens Technique
Abstract
:1. Introduction
2. Materials and Methods
2.1. Samples
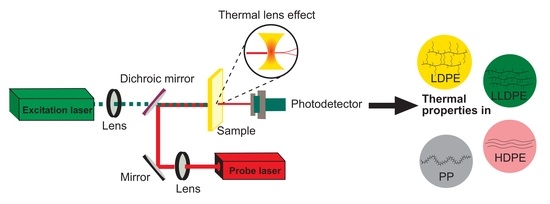
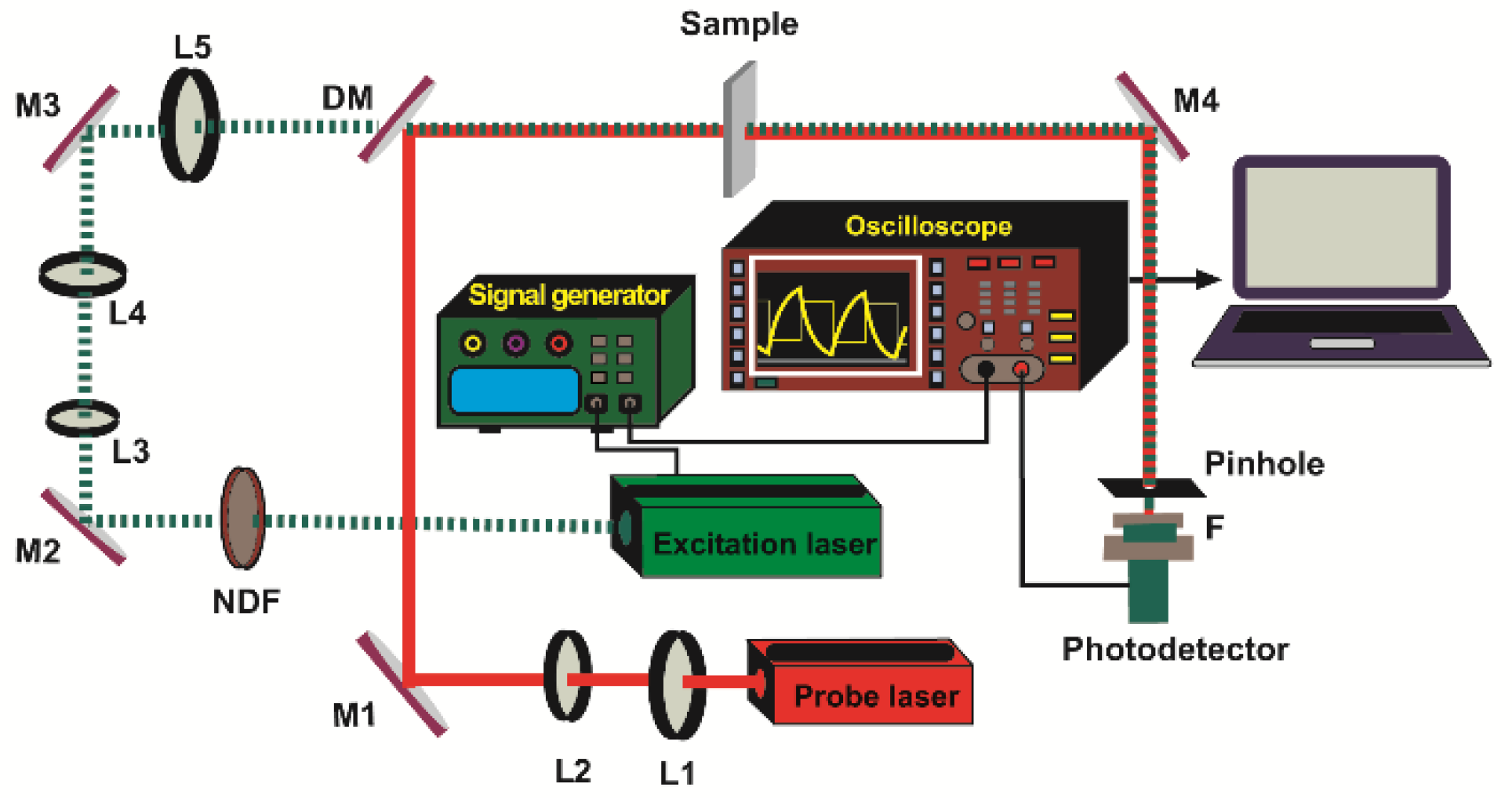
2.2. TLS Setup
2.3. Characterization of Samples
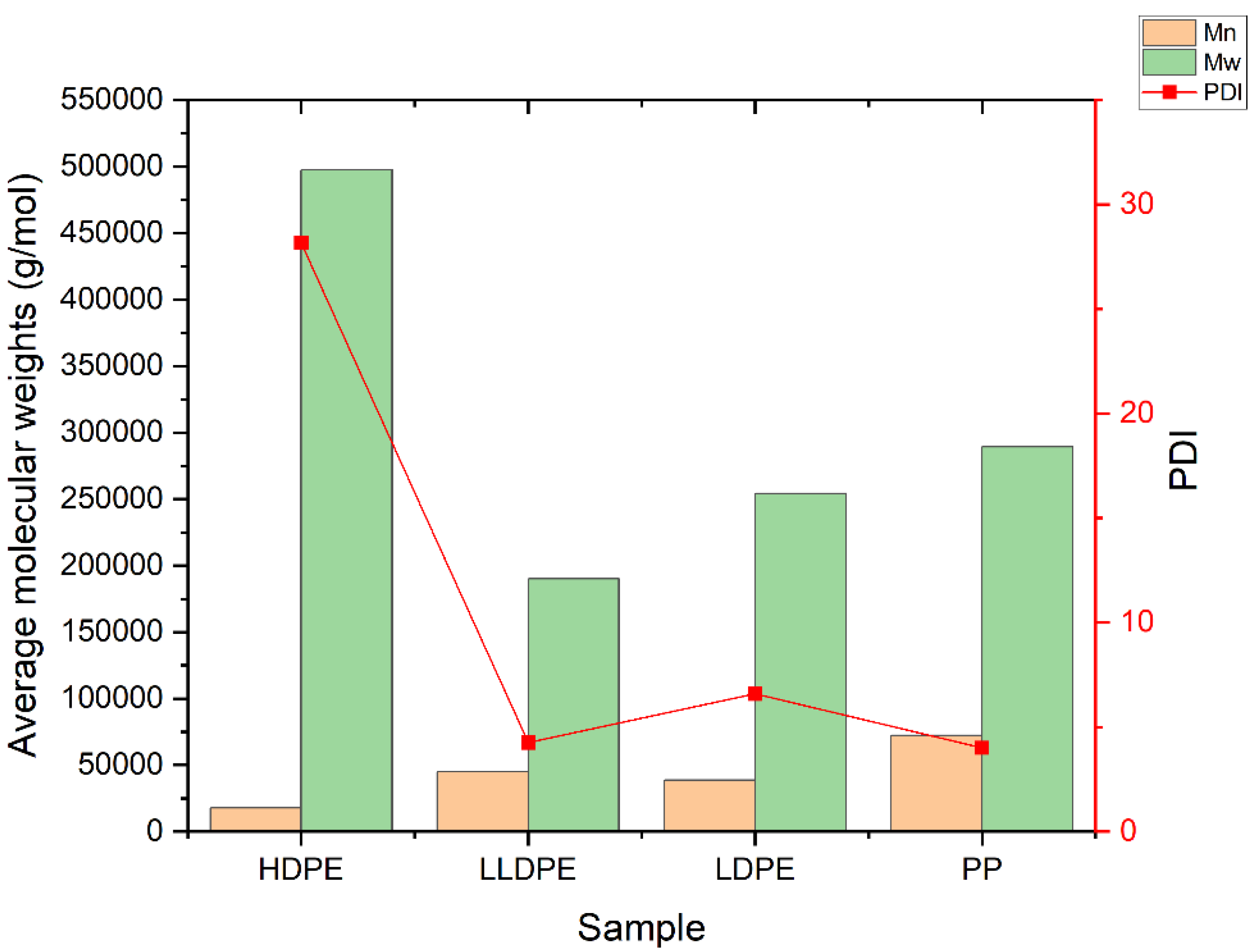
2.3.1. Molecular Characterization
2.3.2. Rheological Characterization
2.3.3. Density
2.3.4. Thermal Properties
3. Results
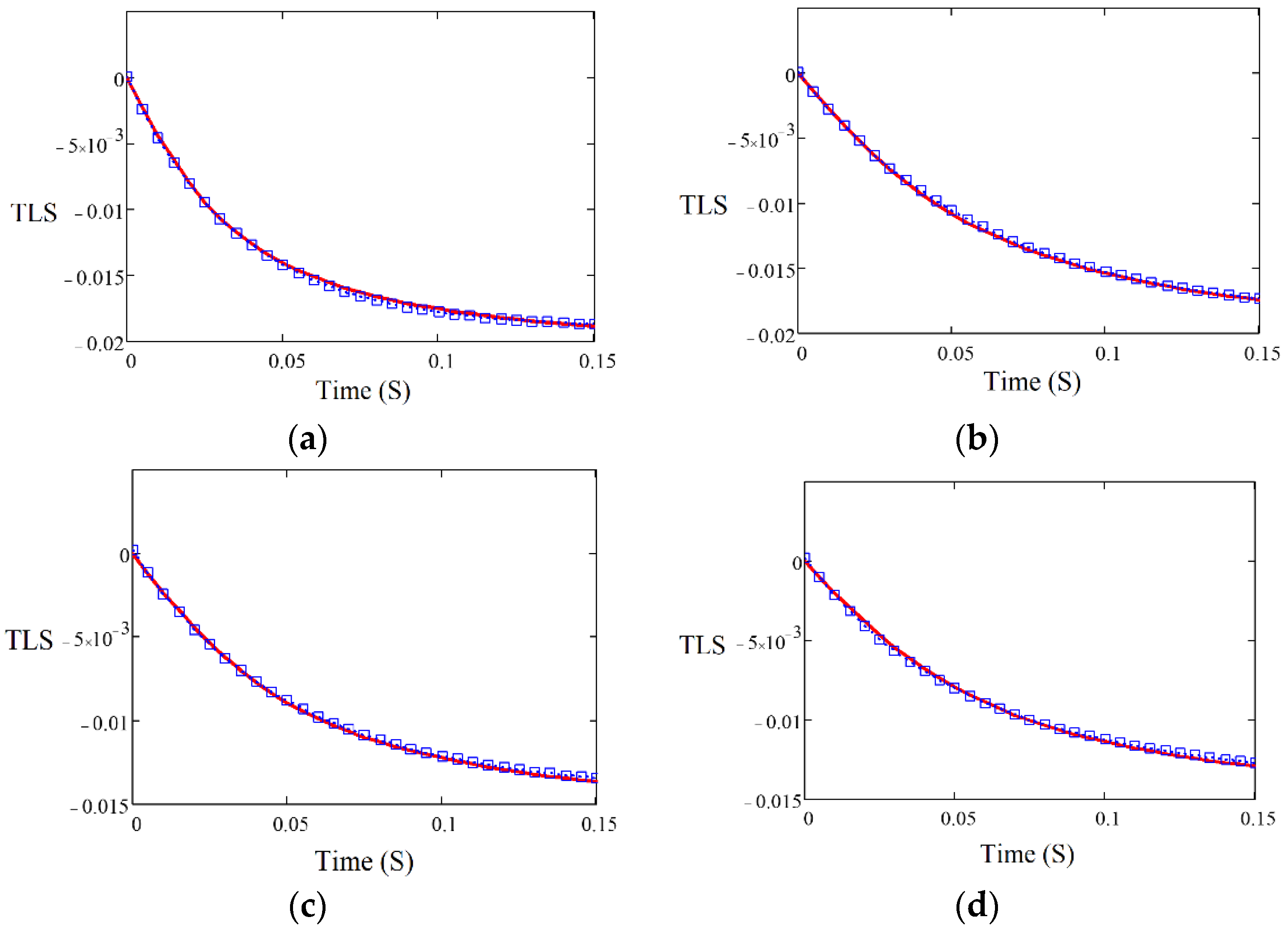
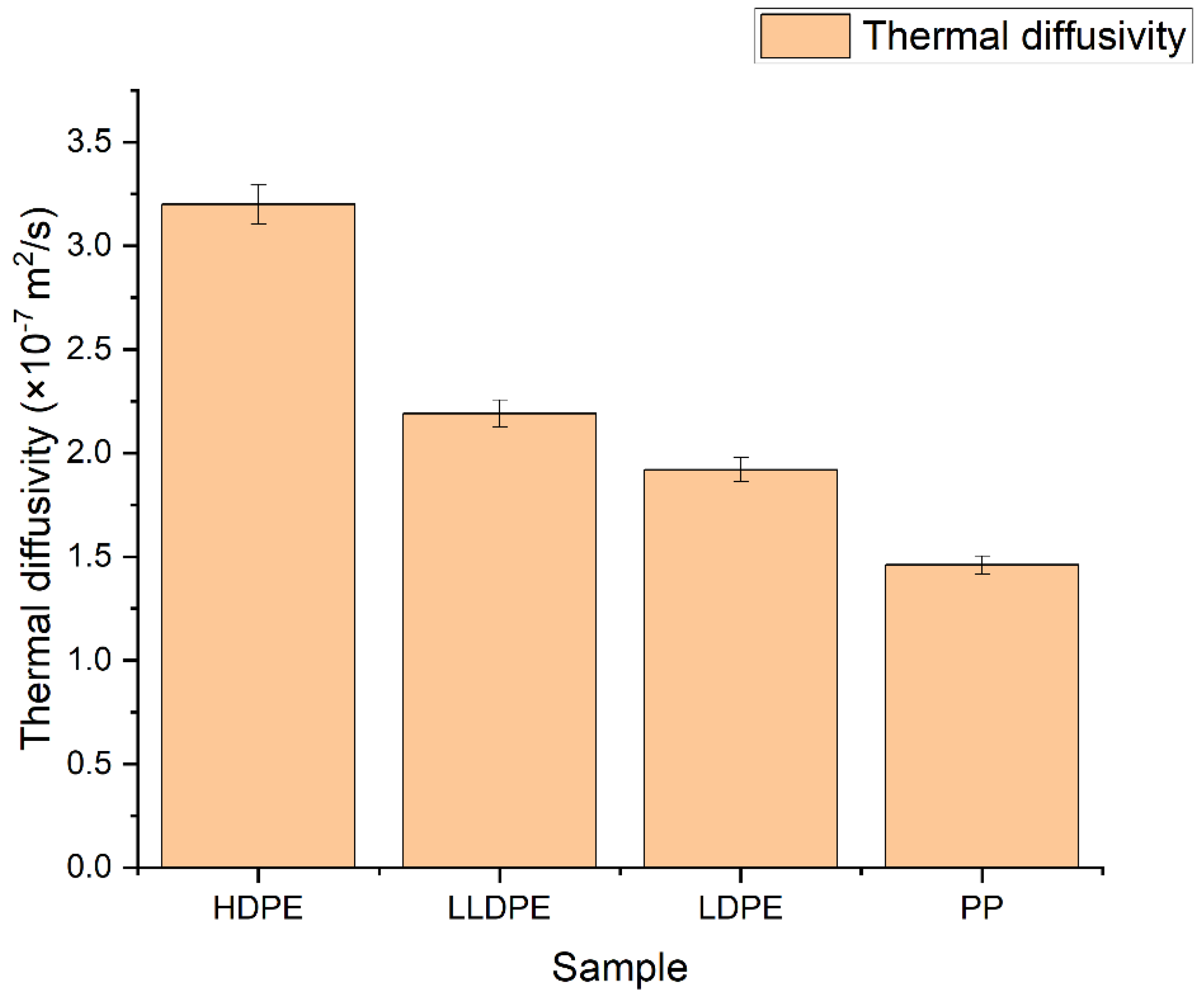
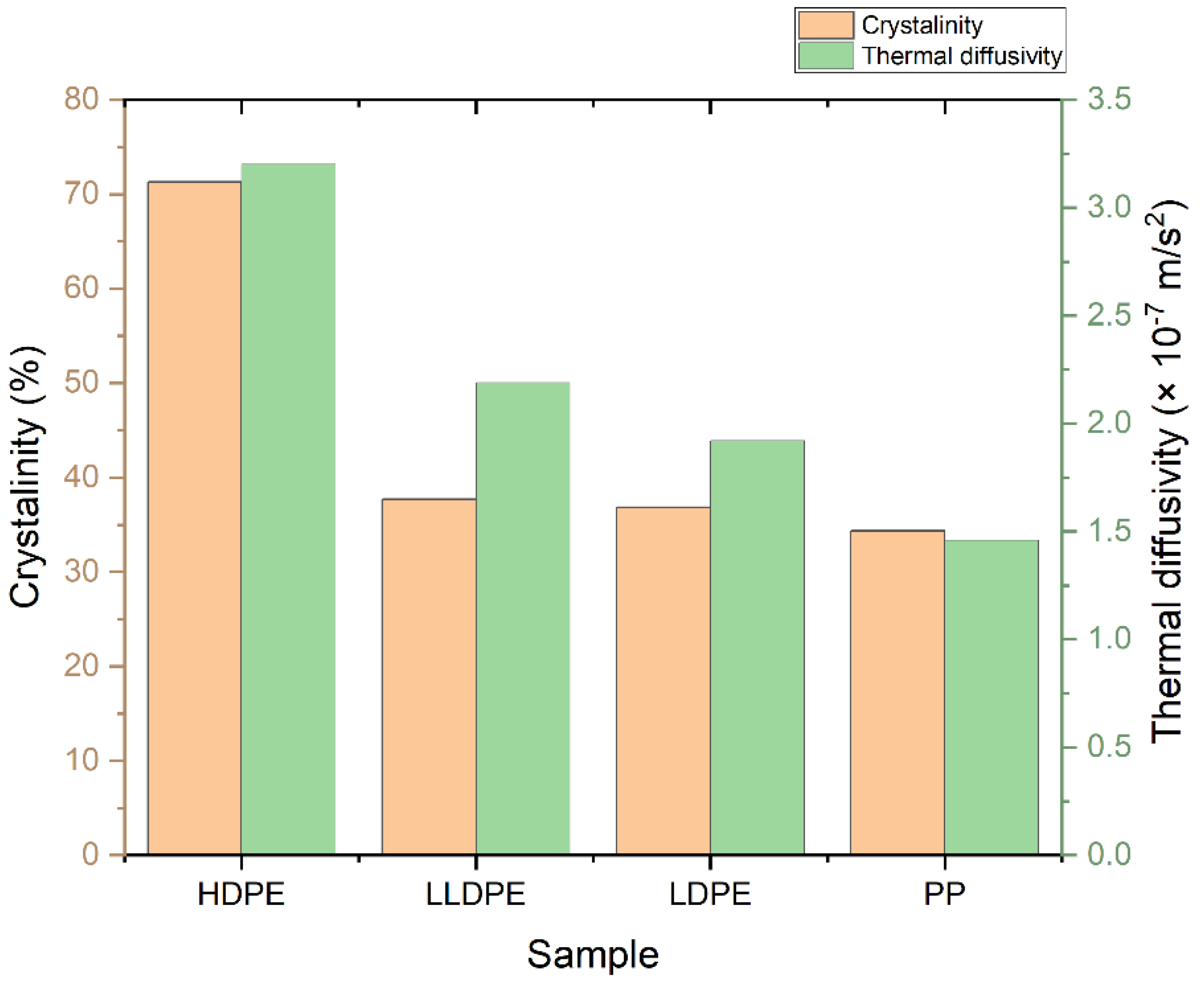
3.1. Thermal Diffusivity
3.2. Thermal Conductivity
3.3. Molecular Structure
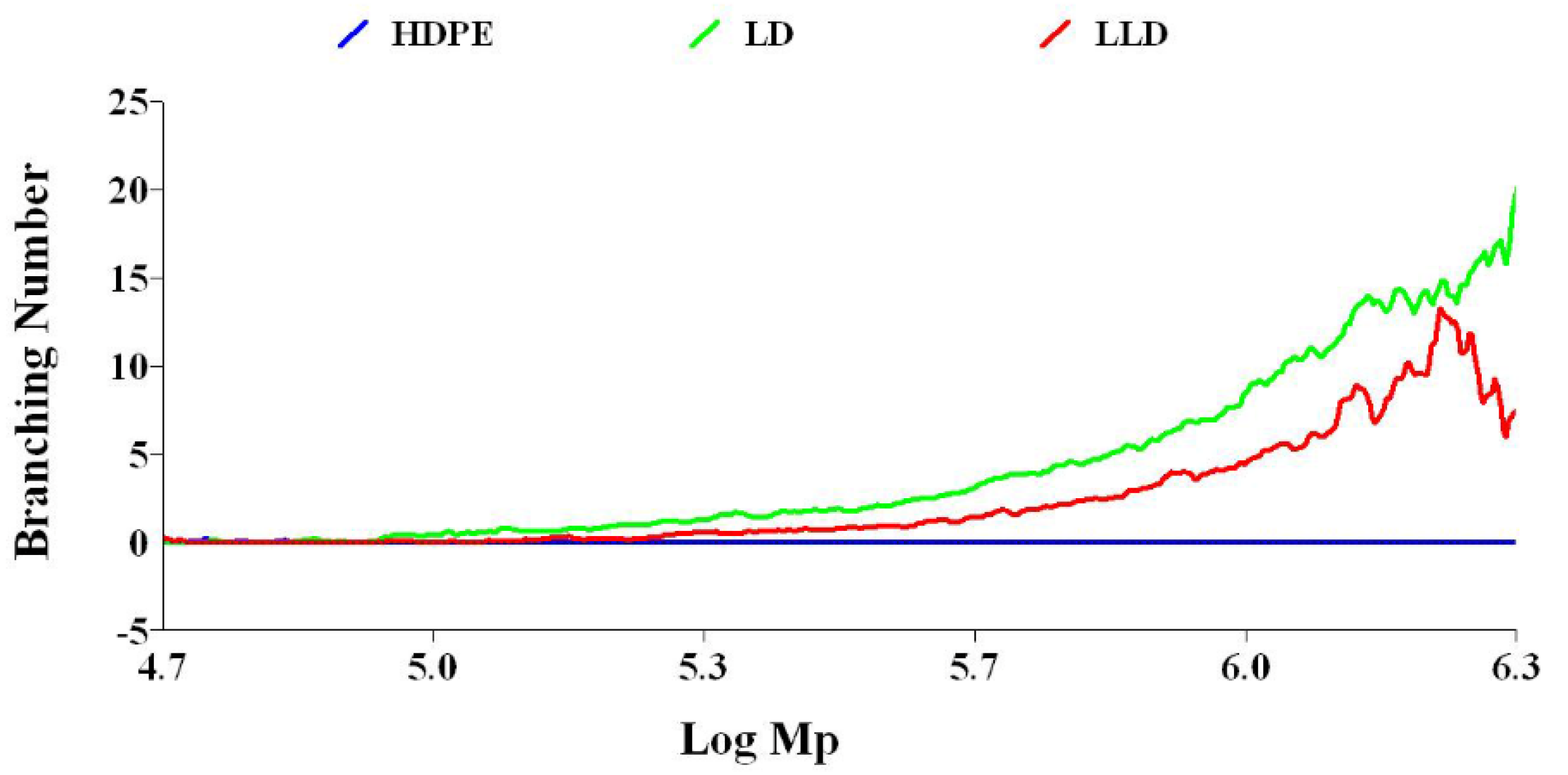
3.3.1. Branching Number
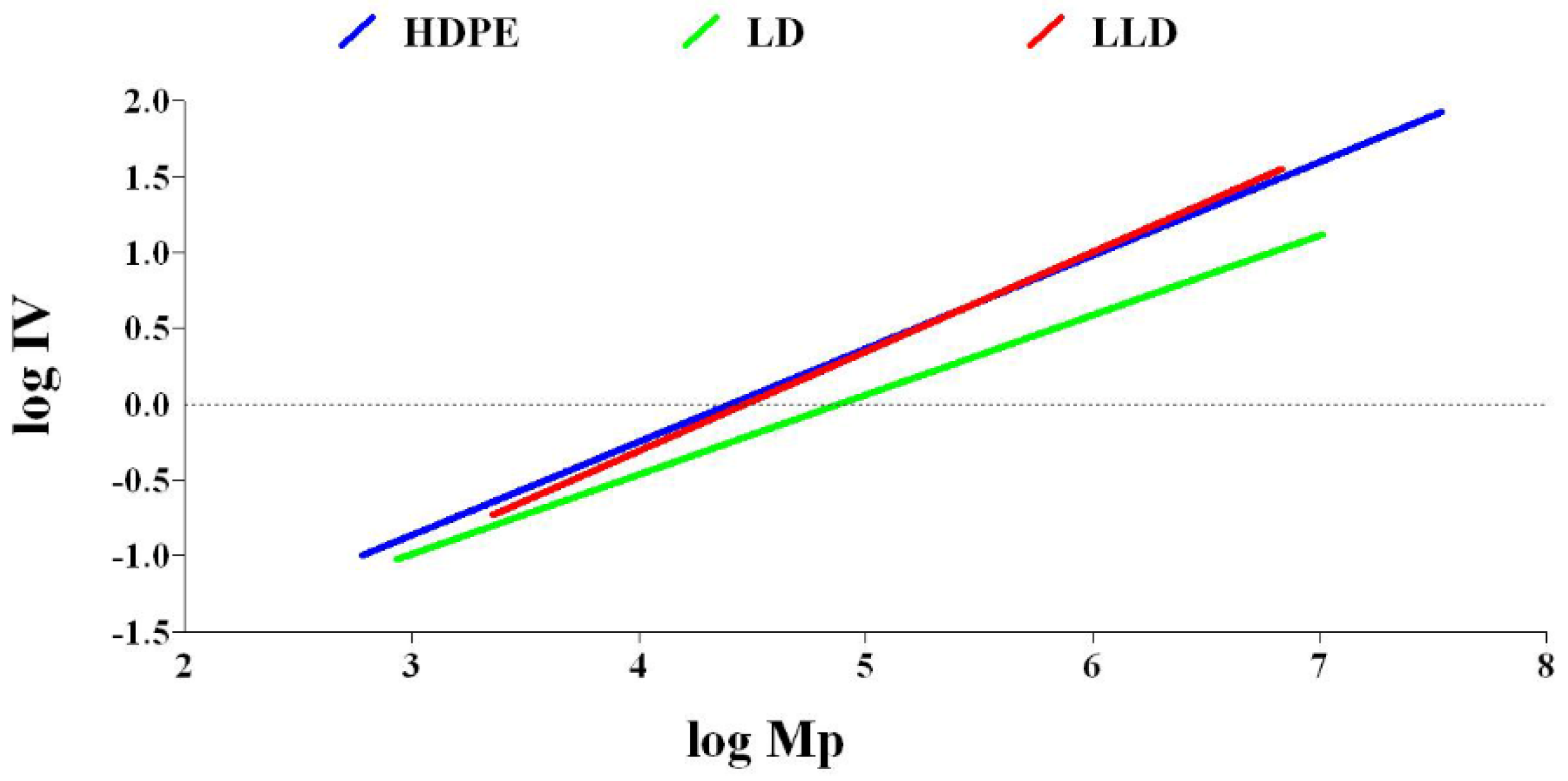
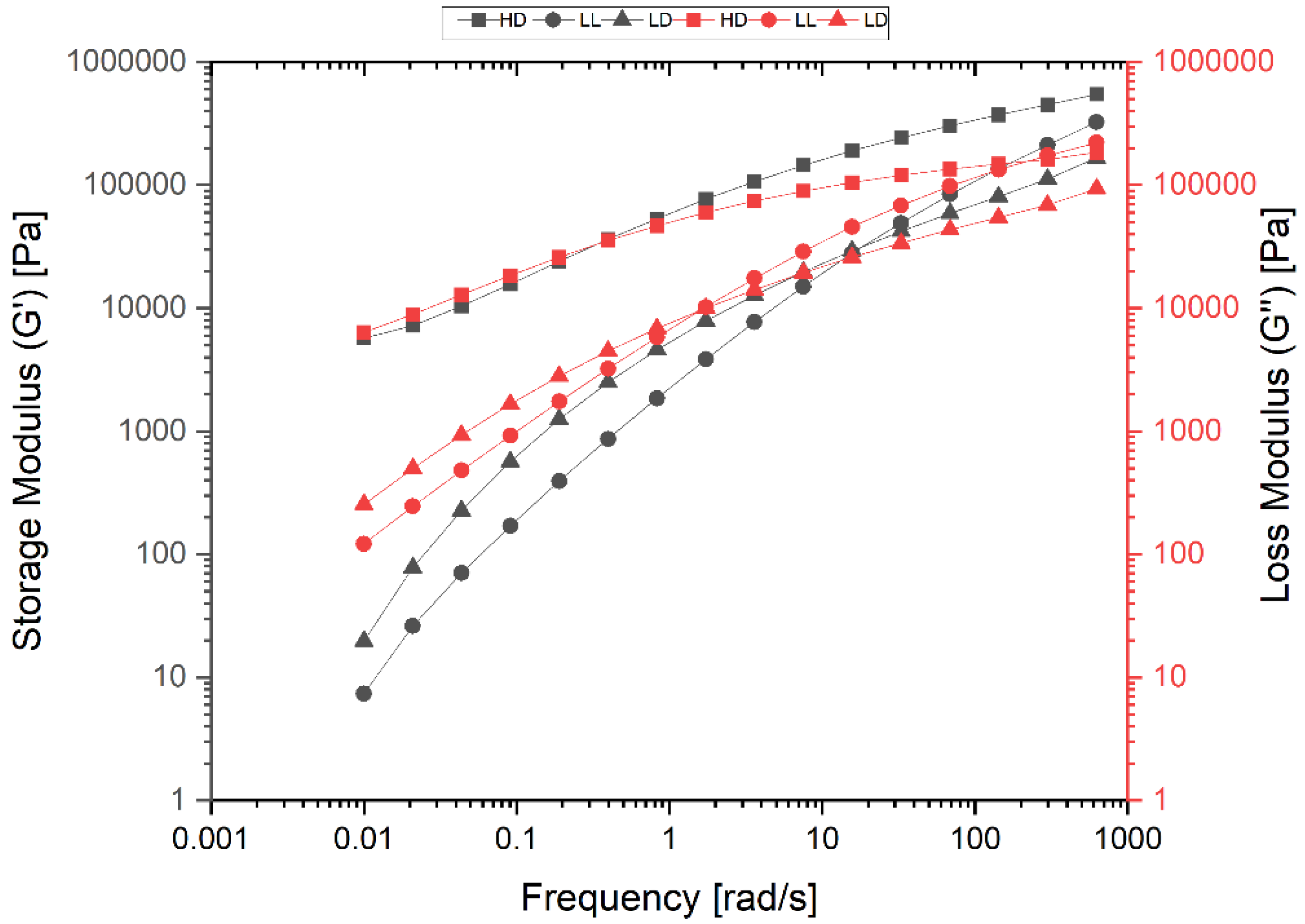
3.3.2. Rheology
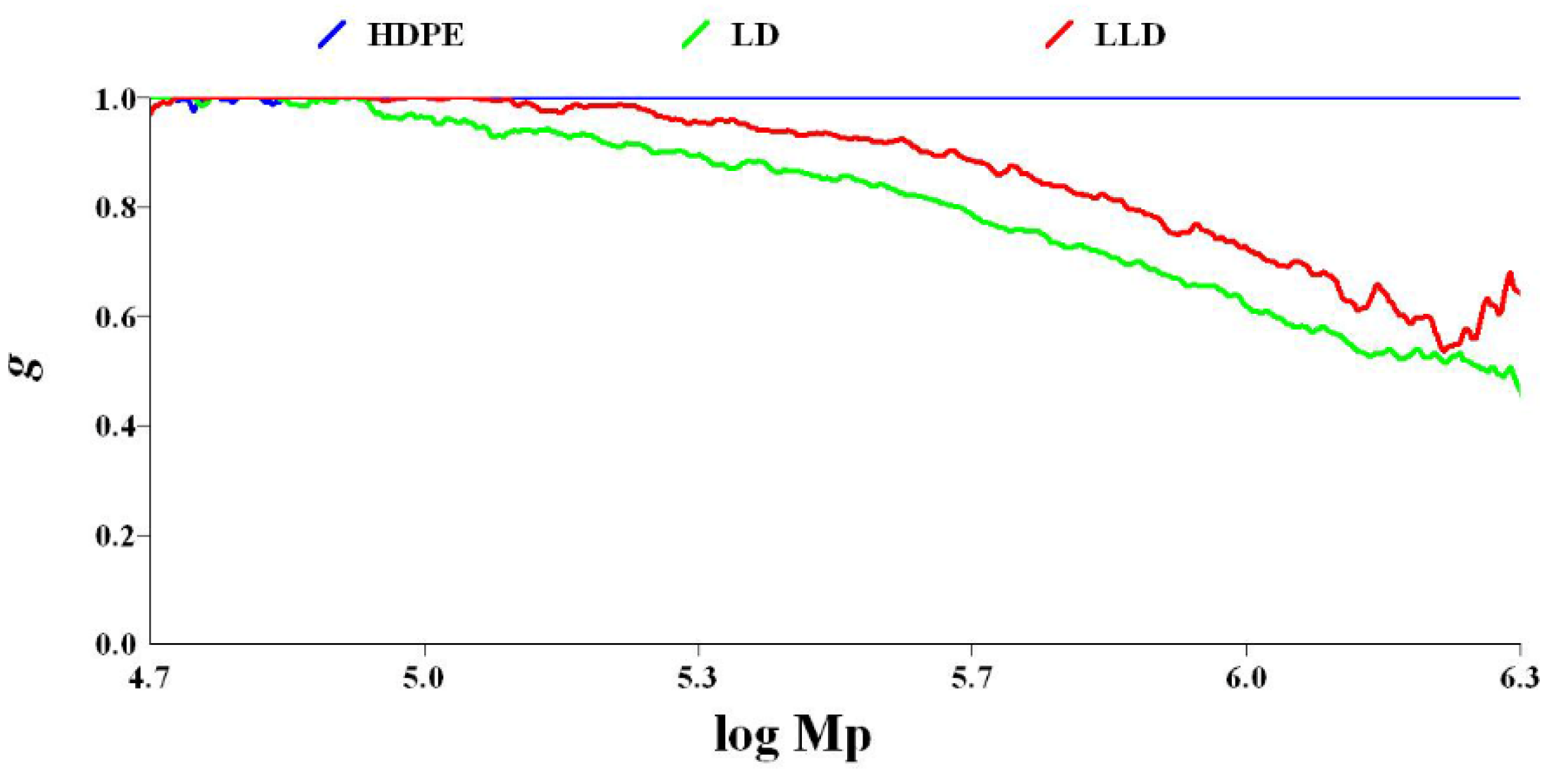
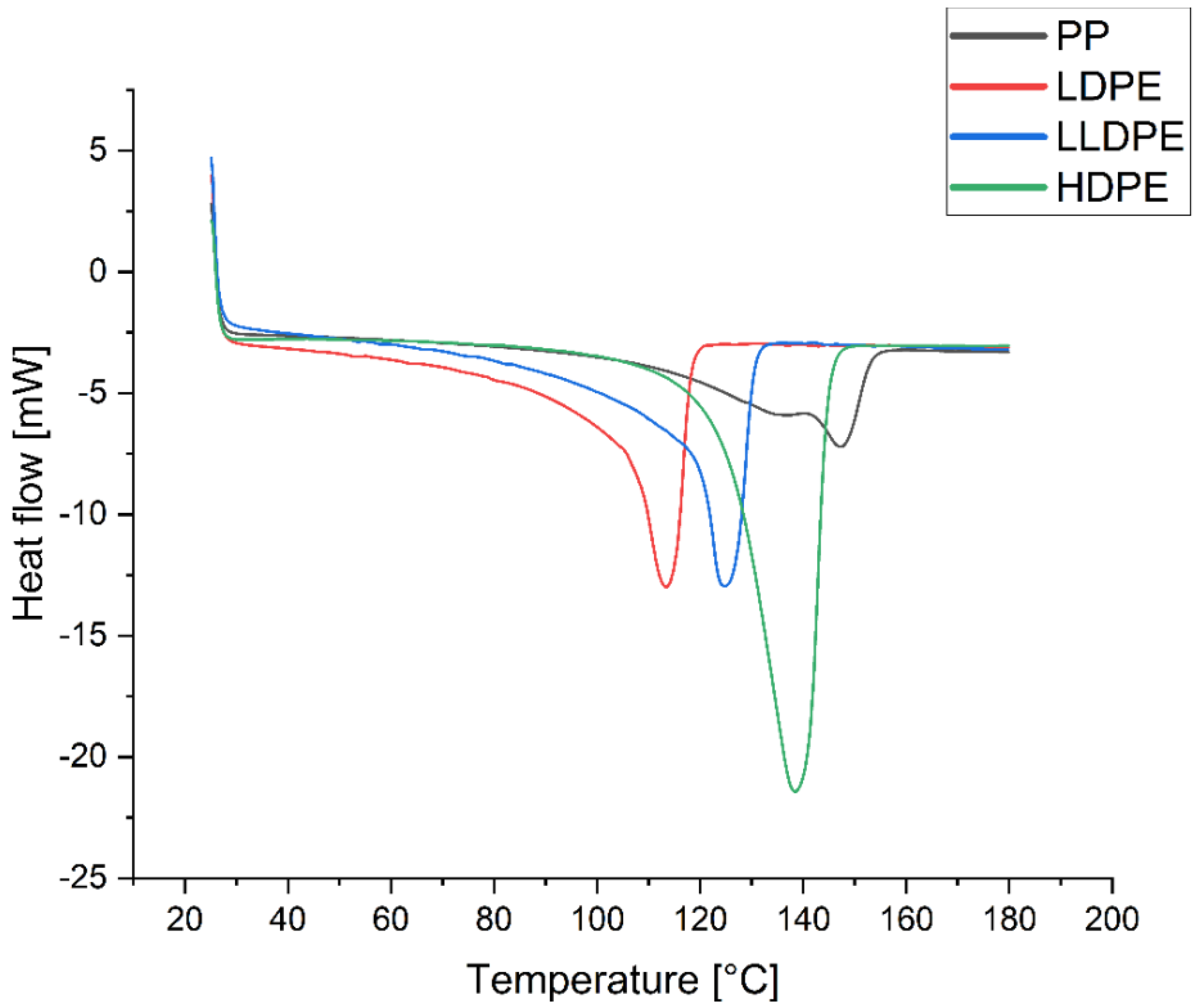
3.3.3. Crystallinity
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Palacios, A.; Cong, L.; Navarro, M.; Ding, Y.; Barreneche, C. Thermal conductivity measurement techniques for characterizing thermal energy storage materials—A review. Renew. Sustain. Energy Rev. 2019, 108, 32–52. [Google Scholar] [CrossRef]
- Guo, Y.; Ruan, K.; Shi, X.; Yang, X.; Gu, J. Factors affecting thermal conductivities of the polymers and polymer composites: A review. Compos. Sci. Technol. 2020, 193, 108134. [Google Scholar] [CrossRef]
- Weingrill, H.; Hohenauer, W.; Resch-Fauster, K.; Zauner, C. Analyzing Thermal Conductivity of Polyethylene-Based Compounds Filled with Copper. Macromol. Mater. Eng. 2019, 304, 1800644. [Google Scholar] [CrossRef] [Green Version]
- Hosier, I.L.; Andritsch, T.; Vaughan, A.S.; Stevens, G.C.; McAllister, N.; Basu, S.; German, I. Enhanced Boron Nitride/Polyolefin Blends for High Voltage Applications. IEEE Trans. Nanotechnol. 2021, 20, 794–802. [Google Scholar] [CrossRef]
- Chaudhry, A.; Mabrouk, A.; Abdala, A. Thermally enhanced pristine polyolefins: Fundamentals, progress and prospective. J. Mater. Res. Technol. 2020, 9, 10796–10806. [Google Scholar] [CrossRef]
- Leite, N.; Cella, N.; Vargas, H.; Miranda, L. Photoacoustic measurement of thermal diffusivity of polymer foils. J. Appl. Phys. 1987, 61, 3025–3027. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Fujii, M. Measurements of the thermal conductivity and thermal diffusivity of polymers. Polym. Eng. Sci. 2003, 43, 1755–1764. [Google Scholar] [CrossRef]
- dos Santos, W.N.; Mummery, P.; Wallwork, A. Thermal diffusivity of polymers by the laser flash technique. Polym. Test. 2005, 24, 628–634. [Google Scholar] [CrossRef]
- Subhani, S.; Ghali, V. Measurement of thermal diffusivity of fiber reinforced polymers using quadratic frequency modulated thermal wave imaging. Infrared Phys. Technol. 2019, 99, 187–192. [Google Scholar] [CrossRef]
- Venerus, D.; Schieber, J.; Iddir, H.; Guzman, J.; Broerman, A. Measurement of thermal diffusivity in polymer melts using forced Rayleigh light scattering. J. Polym. Sci. Part B Polym. Phys. 1999, 37, 1069–1078. [Google Scholar] [CrossRef]
- dos Santos, W.N.; dos Santos, J.N.; Mummery, P.; Wallwork, A. Thermal diffusivity of polymers by modified angström method. Polym. Test. 2010, 29, 107–112. [Google Scholar] [CrossRef]
- Boué, C.; Holé, S. Infrared thermography protocol for simple measurements of thermal diffusivity and conductivity. Infrared Phys. Technol. 2012, 55, 376–379. [Google Scholar] [CrossRef]
- Lang, S. Technique for the measurement of thermal diffusivity based on the Laser Intensity Modulation Method (LIMM). Ferroelectrics 1989, 93, 87–93. [Google Scholar] [CrossRef]
- Hashimoto, T.; Matsui, Y.; Hagihara, A.; Miyamoto, A. Thermal diffusivity measurement of polymer films by the temperature wave method using joule-heating. Thermochim. Acta 1990, 163, 317–324. [Google Scholar] [CrossRef]
- Choy, C.; Yang, G.; Wong, Y. Thermal diffusivity of polymer films by pulsed photothermal radiometry. J. Polym. Sci. Part B Polym. Phys. 1997, 35, 1621–1631. [Google Scholar] [CrossRef]
- Wong, P.; Fung, P.; Tam, H. Low thermal diffusivity measurements of thin films using mirage technique. J. Appl. Phys. 1998, 84, 6623–6627. [Google Scholar] [CrossRef]
- Bauer, S.; De Reggi, A.S. Pulsed electrothermal technique for measuring the thermal diffusivity of dielectric films on conducting substrates. J. Appl. Phys. 1996, 80, 6124–6128. [Google Scholar] [CrossRef]
- Cabrera, H.; Mendoza, D.; Benítez, J.; Flores, C.B.; Alvarado, S.; Marín, E. Thermal diffusivity of few-layers graphene measured by an all-optical method. J. Phys. D Appl. Phys. 2015, 48, 465501. [Google Scholar] [CrossRef]
- Cabrera, H.; Matroodi, F.; Cabrera-Díaz, H.D.; Ramírez-Miquet, E.E. Frequency-resolved photothermal lens: An alternative approach for thermal diffusivity measurements in weak absorbing thin samples. Int. J. Heat Mass Transf. 2020, 158, 120036. [Google Scholar] [CrossRef]
- Hansen, D.; Ho, C.C. Thermal conductivity of high polymers. J. Polym. Sci. Part A Gen. Pap. 1965, 3, 659–670. [Google Scholar] [CrossRef]
- Washo, B.D.; Hansen, D. Heat conduction in linear amorphous high polymers: Orientation anisotropy. J. Appl. Phys. 1969, 40, 2423–2427. [Google Scholar] [CrossRef]
- Bai, L.; Zhao, X.; Bao, R.-Y.; Liu, Z.-Y.; Yang, M.-B.; Yang, W. Effect of temperature, crystallinity and molecular chain orientation on the thermal conductivity of polymers: A case study of PLLA. J. Mater. Sci. 2018, 53, 10543–10553. [Google Scholar] [CrossRef]
- Marcano, A.; Cabrera, H.; Guerra, M.; Cruz, R.A.; Jacinto, C.; Catunda, T. Optimizing and calibrating a mode-mismatched thermal lens experiment for low absorption measurement. JOSA B 2006, 23, 1408–1413. [Google Scholar] [CrossRef]
- Polymer Handbook, 3rd ed.; Bandrup, J.; Immergut, E.H. (Eds.) Wiley: New York, NY, USA, 1989; p. V/61. [Google Scholar]

| Sample | Grade | MFI (g/10 min) |
|---|---|---|
| HDPE | DR-720 | 0.2 ± 0.02 1 |
| LLDPE | 22B02 | 2 ± 0.02 1 |
| LDPE | 2420E02 | 1.9 ± 0.02 1 |
| PP | ZR340R | 25 ± 3 2 |
| Sample | D(×10−7), m2/s | ρ, g/cm3 | Cp 1, J/gK | κ, W/mK |
|---|---|---|---|---|
| HDPE | 3.20 | 0.958 | 1.76 | 0.54 |
| LLDPE | 2.19 | 0.922 | 2.03 | 0.41 |
| LDPE | 1.92 | 0.921 | 2.09 | 0.37 |
| PP | 1.46 | 0.903 | 1.67 | 0.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbasgholi-NA, B.; Nokhbeh, S.R.; Aldaghri, O.A.; Ibnaouf, K.H.; Madkhali, N.; Cabrera, H. Thermal Diffusivity and Conductivity of Polyolefins by Thermal Lens Technique. Polymers 2022, 14, 2707. https://doi.org/10.3390/polym14132707
Abbasgholi-NA B, Nokhbeh SR, Aldaghri OA, Ibnaouf KH, Madkhali N, Cabrera H. Thermal Diffusivity and Conductivity of Polyolefins by Thermal Lens Technique. Polymers. 2022; 14(13):2707. https://doi.org/10.3390/polym14132707
Chicago/Turabian StyleAbbasgholi-NA, Behnaz, Seyed Reza Nokhbeh, Osamah A. Aldaghri, Khalid Hassan Ibnaouf, Nawal Madkhali, and Humberto Cabrera. 2022. "Thermal Diffusivity and Conductivity of Polyolefins by Thermal Lens Technique" Polymers 14, no. 13: 2707. https://doi.org/10.3390/polym14132707
APA StyleAbbasgholi-NA, B., Nokhbeh, S. R., Aldaghri, O. A., Ibnaouf, K. H., Madkhali, N., & Cabrera, H. (2022). Thermal Diffusivity and Conductivity of Polyolefins by Thermal Lens Technique. Polymers, 14(13), 2707. https://doi.org/10.3390/polym14132707