Synchronization of a Passive Oscillator and a Liquid Crystal Elastomer Self-Oscillator Powered by Steady Illumination
Abstract
:1. Introduction
2. Model and Formulation
2.1. Dynamics of Two Coupled Oscillators
2.2. Dynamic LCE Model of the LCE Fiber
2.3. Nondimensionalization
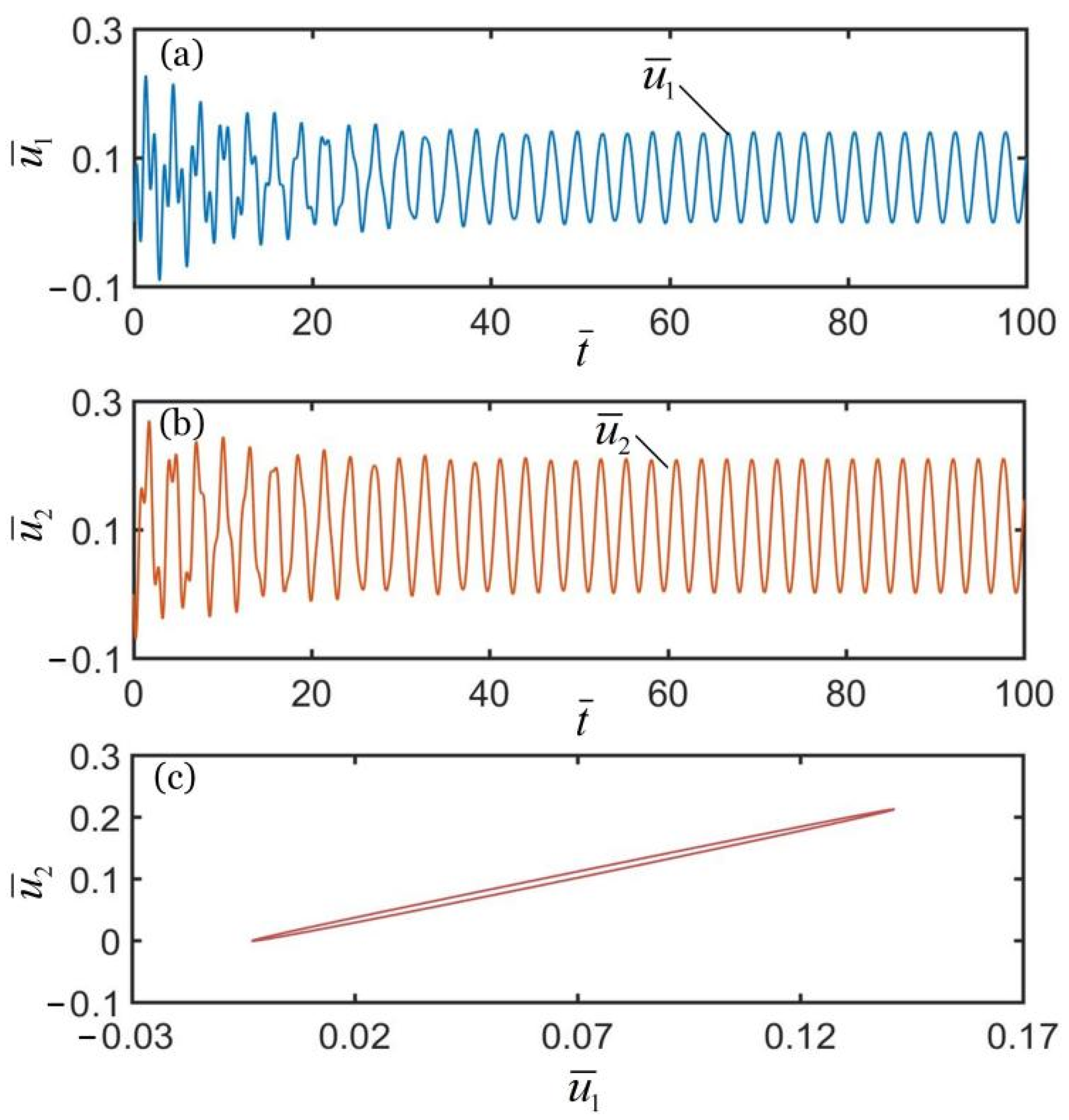
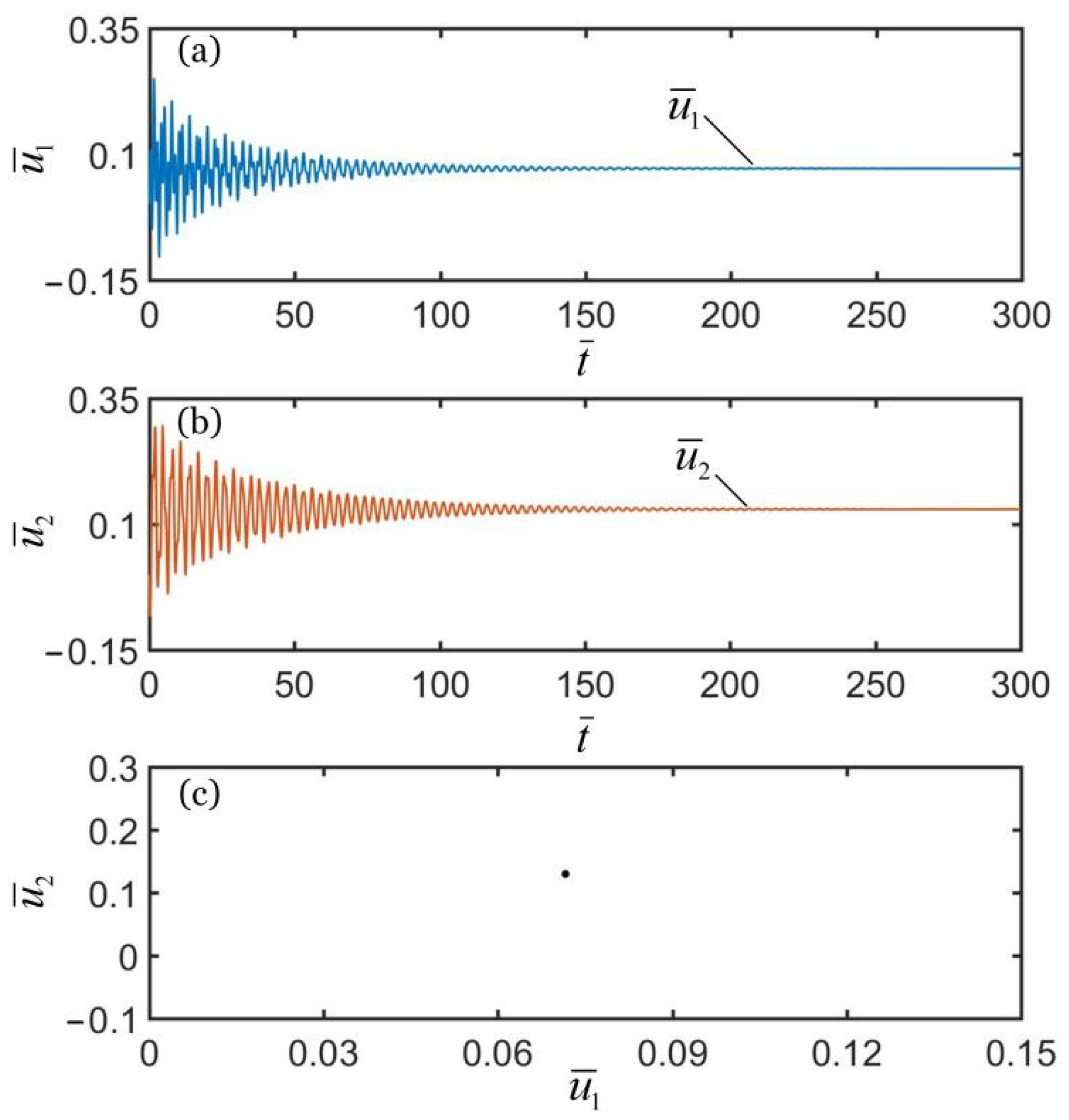
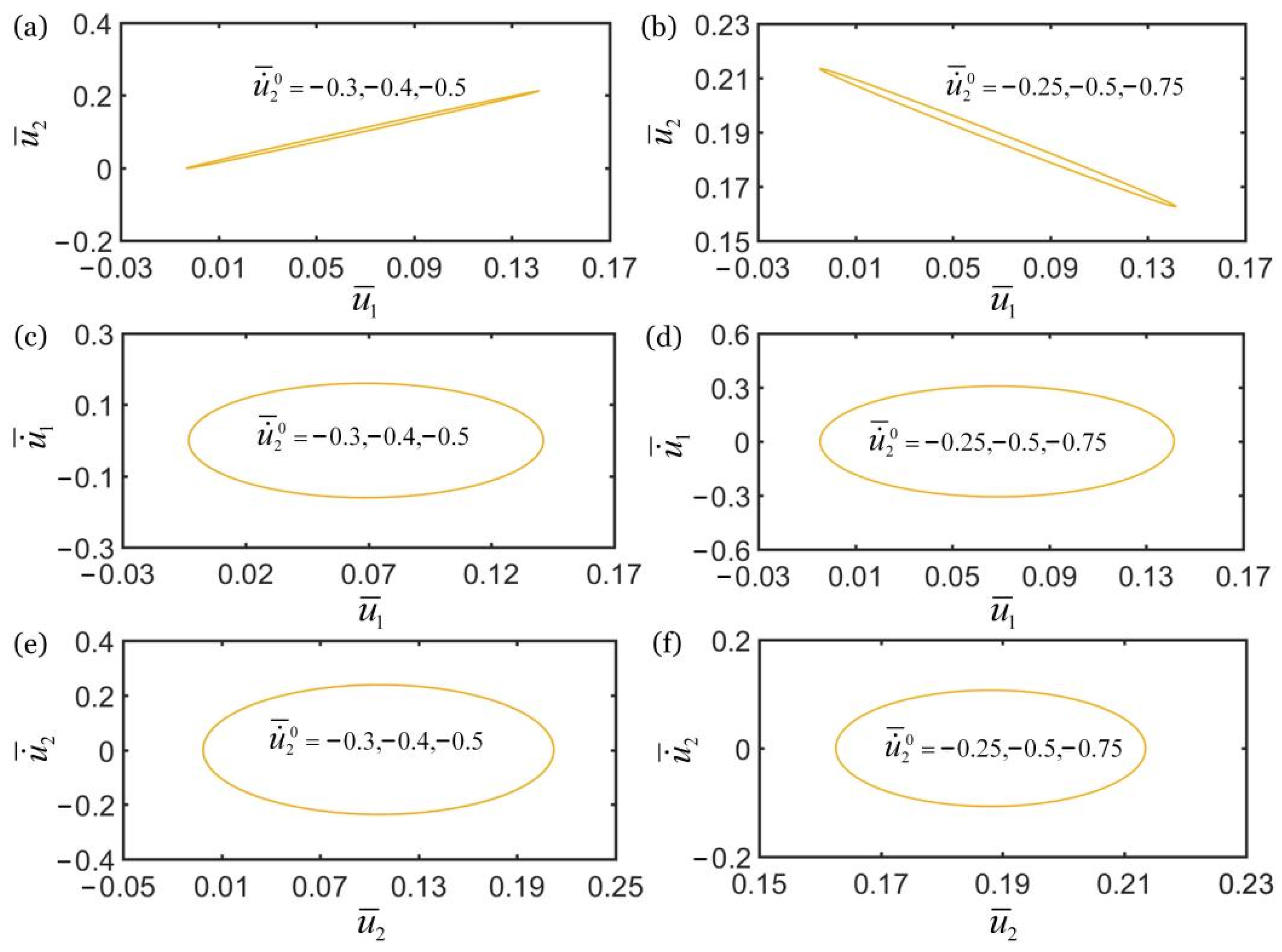
3. Three Synchronization Regimes and Their Mechanisms
3.1. Three Synchronous Regimes
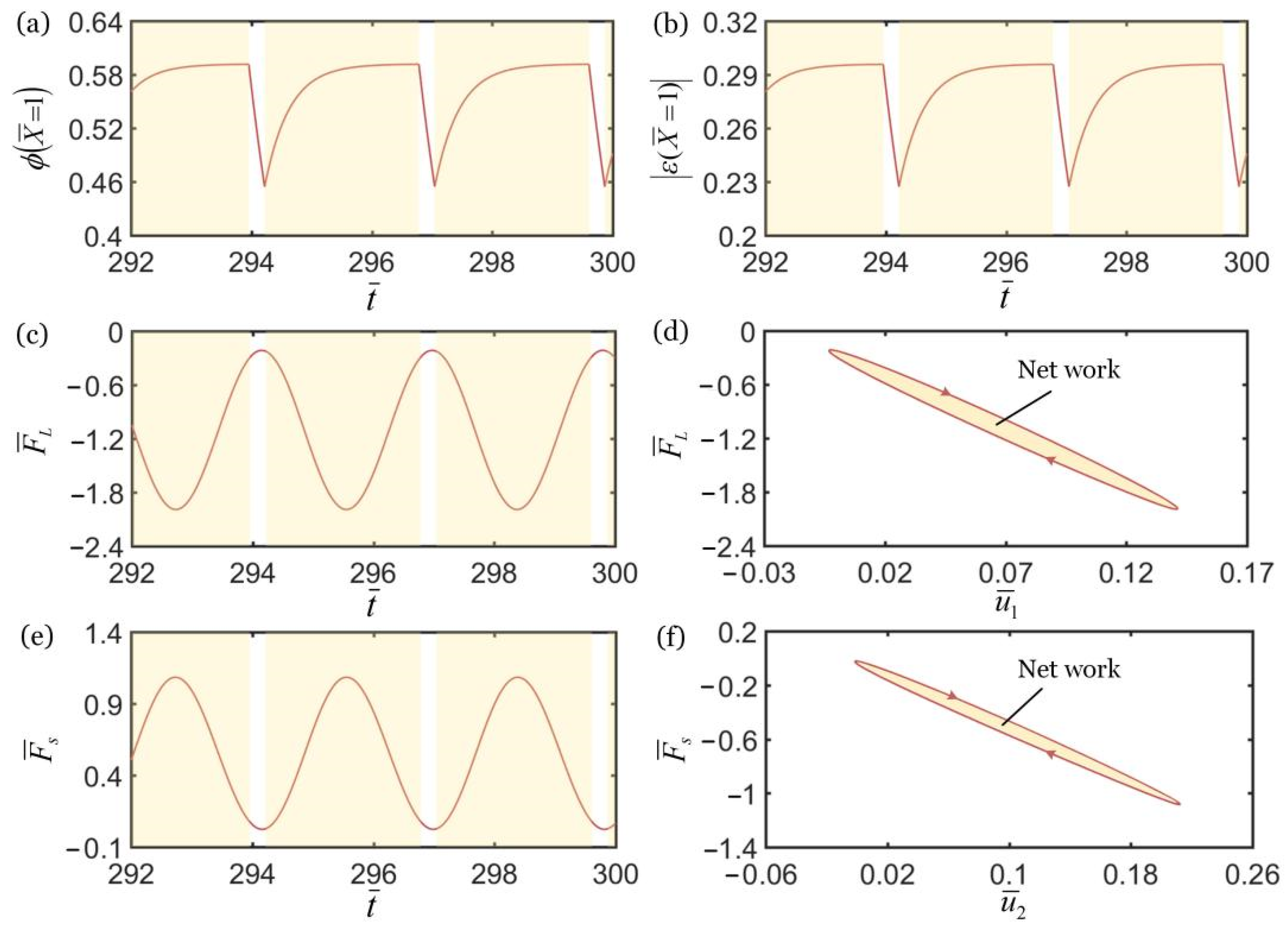
3.2. Mechanisms of Self-Oscillation in the in-Phase Regime
3.3. Mechanisms of Self-Oscillation in the Anti-Phase Regime
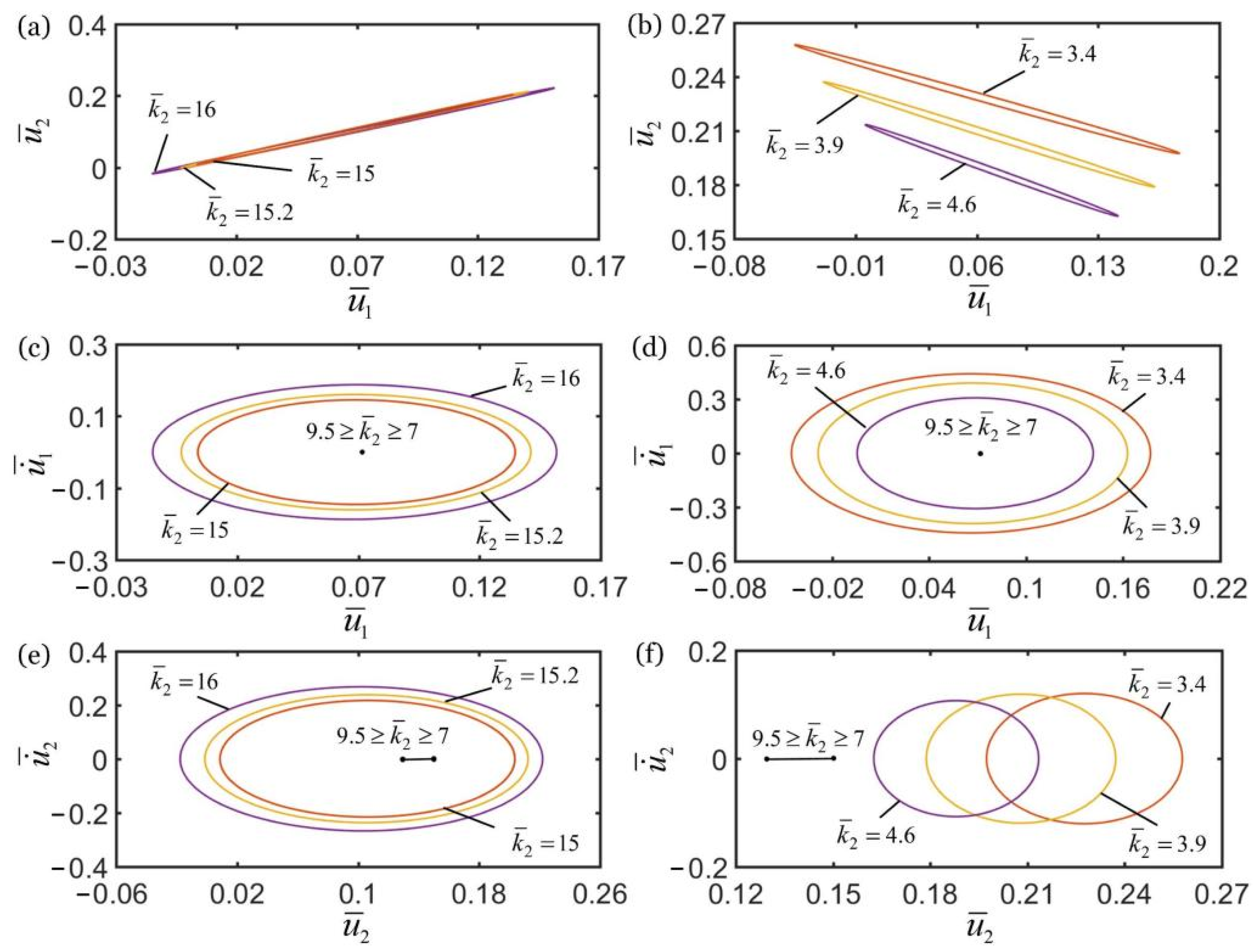
4. Parametric Study
4.1. Effect of Spring Constant of Spring
4.2. Effect of Damping Coefficient
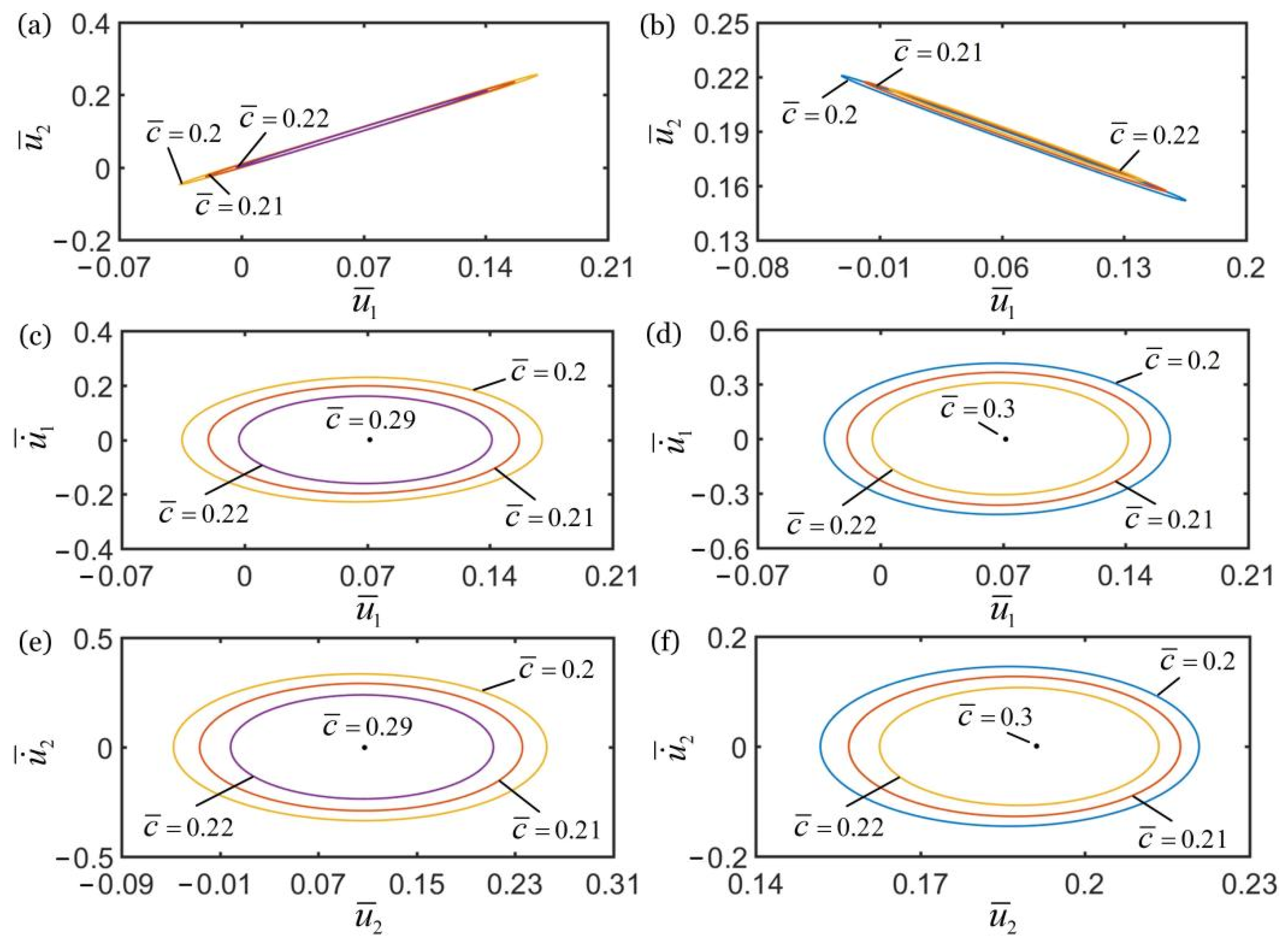
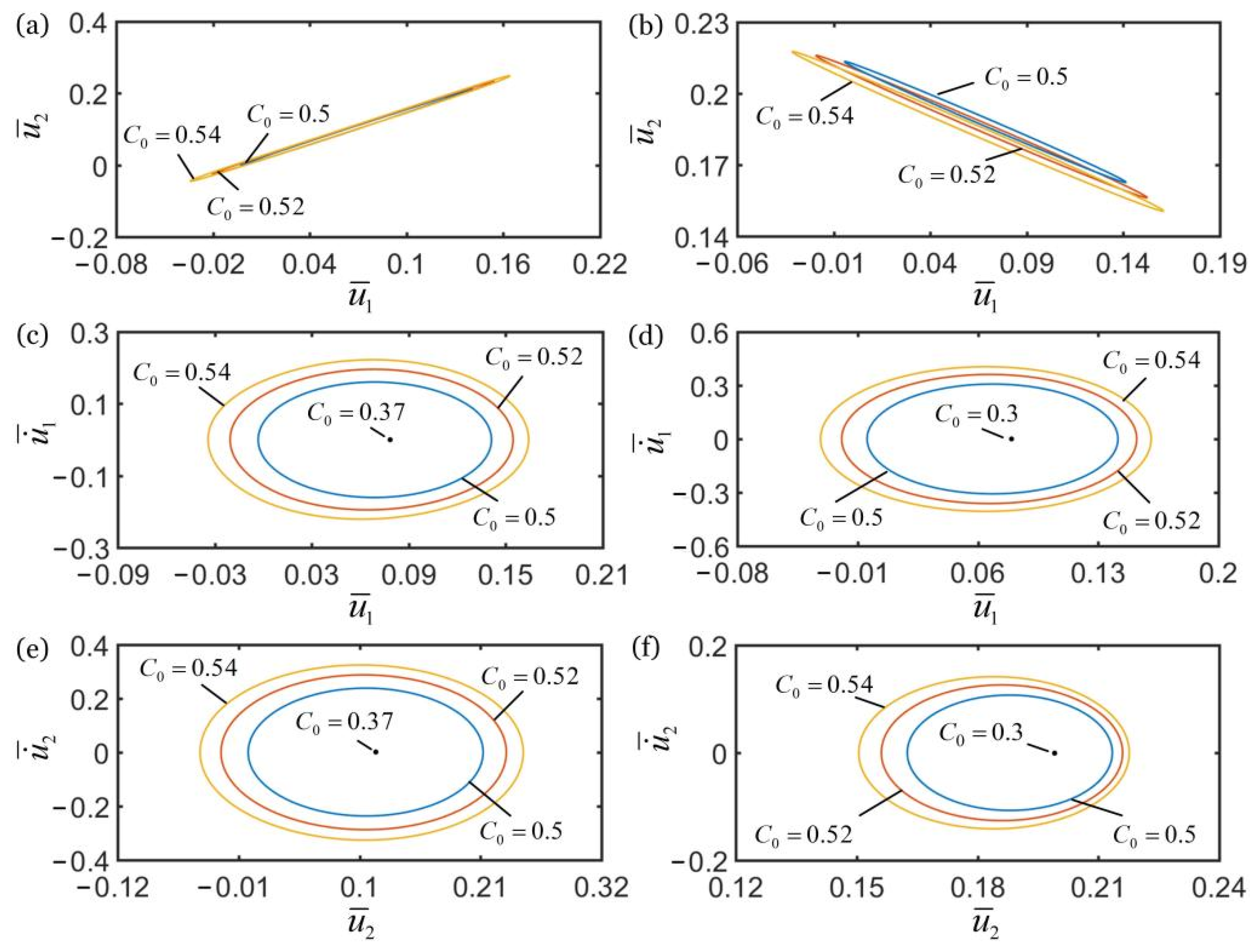
4.3. Effect of Contraction Coefficient
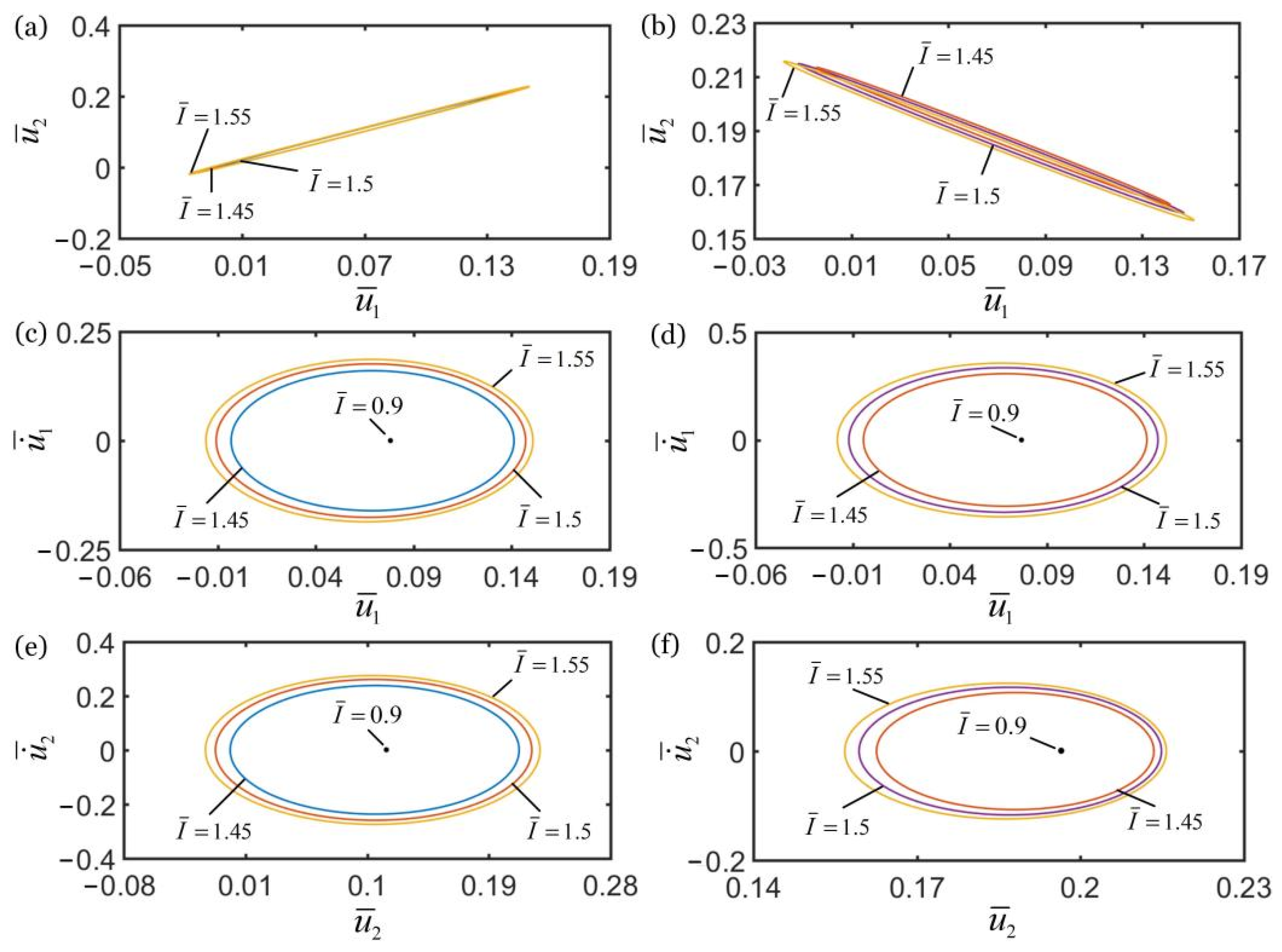
4.4. Effect of Light Intensity
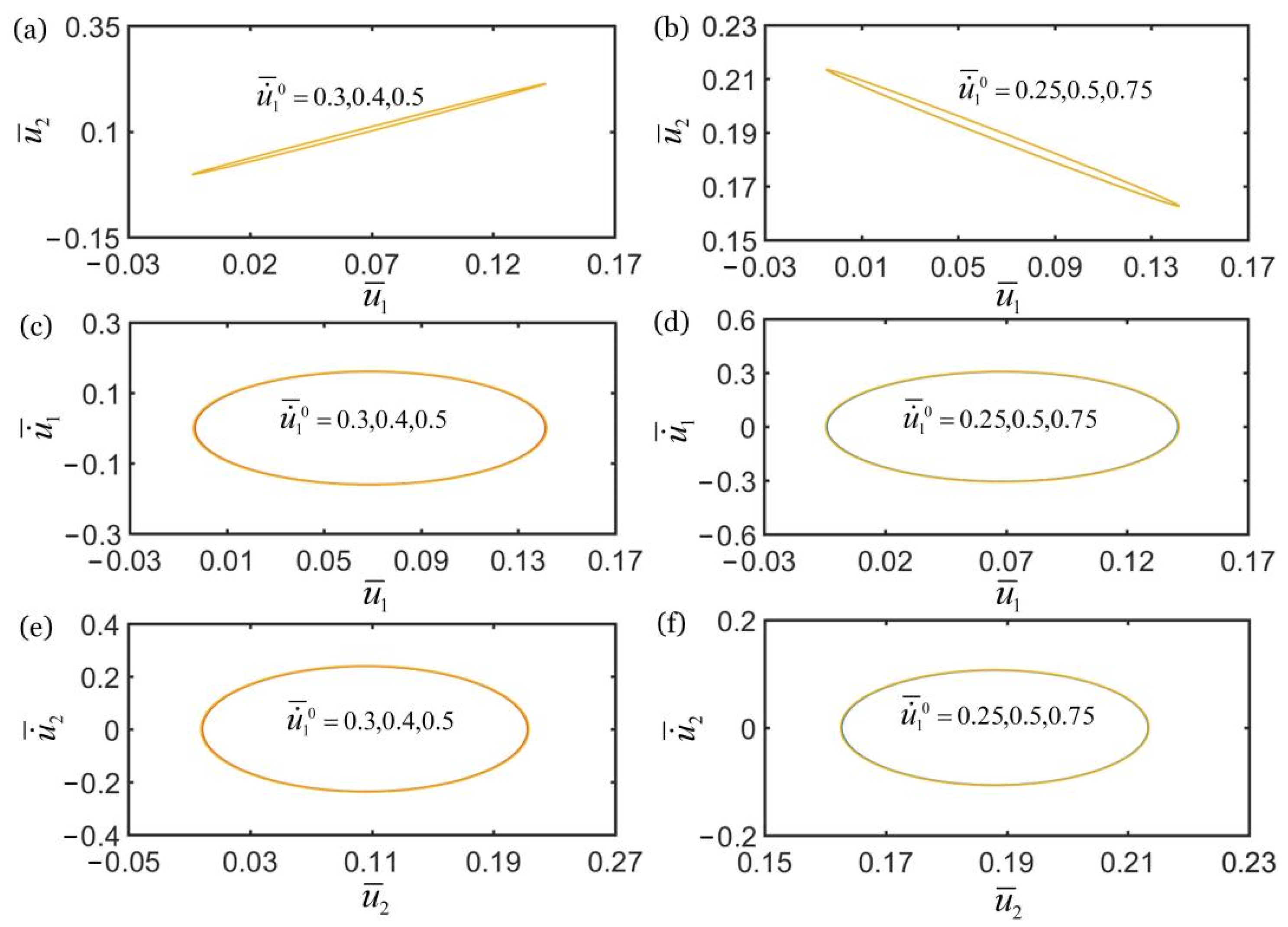
4.5. Effect of Initial Velocity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ding, W.J. Self-Excited Vibration; Tsing-Hua University Press: Beijing, China, 2009. [Google Scholar]
- Li, M.H.; Keller, P.; Li, B.; Wang, X.; Brunet, M. Light-driven side-on nematic elastomer actuators. Adv. Mater. 2003, 15, 569–572. [Google Scholar] [CrossRef]
- Wang, X.; Tan, C.F.; Chan, K.H.; Lu, X.; Zhu, L.; Kim, S.; Ho, G.W. In-built thermo-mechanical cooperative feedback mechanism for self-propelled multimodal locomotion and electricity generation. Nat. Commun. 2018, 9, 19881–19892. [Google Scholar] [CrossRef] [PubMed]
- Nocentini, S.; Parmeggiani, C.; Martella, D.; Wiersma, D.S. Optically driven soft micro robotics. Adv. Opt. Mater. 2018, 6, 1800207. [Google Scholar] [CrossRef]
- Ge, F.; Yang, R.; Tong, X.; Camerel, F.; Zhao, Y. A multifunctional dyedoped liquid crystal polymer actuator: Light-guided transportation, turning in locomotion, and autonomous motion. Angew. Chem. Int. Edit. 2018, 57, 11758. [Google Scholar] [CrossRef] [PubMed]
- Hara, Y. Function and autonomous behavior of self-oscillating polymer systems. Polymers 2014, 6, 1958–1971. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Duan, N.; Lin, C.; Hua, H. Coupled dynamic analysis of a heavily-loaded propulsion shafting system with continuous bearing-shaft friction. Int. J. Mech. Sci. 2020, 172, 105431. [Google Scholar] [CrossRef]
- Hara, Y.; Jahan, R.A. Influence of initial substrate concentration of the Belouzov-Zhabotinsky reaction on transmittance self-oscillation for a nonthermoresponsive polymer chain. Polymers 2011, 3, 330–339. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Zhang, H.; Fei, G.; Yu, B.; Tong, X.; Xia, H.; Zhao, Y. Liquid-crystalline dynamic networks doped with gold nanorods showing enhanced photocontrol of actuation. Adv. Mater. 2018, 30, 1706597. [Google Scholar] [CrossRef]
- He, Q.; Wang, Z.J.; Wang, Y.; Wang, Z.J.; Li, C.H.; Annapooranan, R.; Zeng, J.; Chen, R.K.; Cai, S. Electrospun liquid crystal elastomer microfiber actuator. Sci. Robot. 2021, 6, eabi9704. [Google Scholar] [CrossRef]
- Yang, L.; Chang, L.; Hu, Y.; Huang, M.; Ji, Q.; Lu, P.; Liu, J.; Chen, W.; Wu, Y. An autonomous soft actuator with light-driven self-sustained wavelike oscillation for phototactic self-locomotion and power generation. Adv. Funct. Mater. 2020, 30, 1908842. [Google Scholar] [CrossRef]
- Chun, S.; Pang, C.; Cho, S.B. A micropillar-assisted versatile strategy for highly sensitive and efficient triboelectric energy generation under in-plane stimuli. Adv. Mater. 2020, 32, 1905539. [Google Scholar] [CrossRef]
- Tang, R.; Liu, Z.; Xu, D.; Liu, J.; Yu, L.; Yu, H. Optical pendulum generator based on photomechanical liquid-crystalline actuators. ACS. Appl. Mater. Inter. 2015, 7, 8393–8397. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, Y. A prototype for light-electric harvester based on light sensitive liquid crystal elastomer cantilever. Energy 2020, 198, 117351. [Google Scholar] [CrossRef]
- Vantomme, G.; Gelebart, A.H.; Broer, D.J.; Meijer, E.W. A four-blade light-driven plastic mill based on hydrazone liquid-crystal networks. Tetrahedron 2017, 73, 4963–4967. [Google Scholar] [CrossRef]
- Liao, B.; Zang, H.; Chen, M.; Wang, Y.; Lang, X.; Zhu, N.; Yang, Z.; Yi, Y. Soft rod-climbing robot inspired by winding locomotion of snake. Soft Robot. 2020, 7, 500–511. [Google Scholar] [CrossRef]
- White, T.J.; Broer, D.J. Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers. Nat. Mater. 2015, 14, 1087–1098. [Google Scholar] [CrossRef]
- Lindsey, H.; Kirstin, P.; Guo, Z.L.; Metin, S. Soft Actuators for Small-Scale Robotics. Adv. Mater. 2017, 29, 1603483. [Google Scholar]
- Jenkins, A. Self-oscillation. Phys. Rep. 2013, 525, 167–222. [Google Scholar] [CrossRef] [Green Version]
- Sangwan, V.; Taneja, A.; Mukherjee, S. Design of a robust self-excited biped walking mechanism. Mech. Mach. Theory 2004, 39, 1385–1397. [Google Scholar] [CrossRef]
- Chatterjee, S. Self-excited oscillation under nonlinear feedback with time-delay. J. Sound Vib. 2011, 330, 1860–1876. [Google Scholar] [CrossRef]
- Hu, W.; Lum, G.Z.; Mastrangeli, M.; Sitti, M. Small-scale soft-bodied robot with multimodal locomotion. Nature 2018, 554, 81–85. [Google Scholar] [CrossRef]
- Huang, H.; Aida, T. Towards molecular motors in unison. Nat. Nanotechnol. 2019, 14, 407. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, P.; Yu, Y.; Li, K. Controllable vibration of liquid crystal elastomer beams under periodic illumination. Int. J. Mech. Sci. 2020, 170, 105366. [Google Scholar] [CrossRef]
- Li, K.; Su, X.; Cai, S. Self-sustained rolling of a thermally responsive rod on a hot surface. Extrem. Mech. Lett. 2021, 42, 101116. [Google Scholar] [CrossRef]
- Chávez, J.P.; Voigt, A.; Schreiter, J.; Marschner, U.; Siegmund, S.; Richter, A. A new self-excited chemo-fluidic oscillator based on stimuli-responsive hydrogels: Mathematical modeling and dynamic behavior. Appl. Math. Model. 2016, 40, 9719–9738. [Google Scholar] [CrossRef]
- SSun, B.; Jia, R.; Yang, H.; Chen, X.; Tan, K.; Deng, Q.; Tang, J. Magnetic Arthropod Millirobots Fabricated by 3D-Printed Hydrogels. Adv. Intell. Syst. 2021, 4, 2100139. [Google Scholar] [CrossRef]
- Zhu, Q.L.; Dai, C.F.; Wagner, D.; Khoruzhenko, O.; Hong, W.; Breu, J.; Zheng, Q.; Wu, Z.L. Patterned Electrode Assisted One-Step Fabrication of Biomimetic Morphing Hydrogels with Sophisticated Anisotropic Structures. Adv. Sci. 2021, 8, 2102353. [Google Scholar] [CrossRef]
- Zhao, Y.; Xuan, C.; Qian, X.; Alsaid, Y.; Hua, M.; Jin, L.; He, X. Soft phototactic swimmer based on self-sustained hydrogel oscillator. Sci. Robot. 2019, 4, eaax7112. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; Yan, H.; Zhong, Z. Deep neural networks for large deformation of photo-thermo-pH responsive cationic gels. Appl. Math. Model. 2021, 100, 549–563. [Google Scholar] [CrossRef]
- Jin, B.; Liu, J.; Shi, Y.; Chen, G.; Zhao, Q.; Yang, S. Solvent-Assisted 4D Programming and Reprogramming of Liquid Crystalline Organo-gels. Adv. Mater. 2021, 34, 2107855. [Google Scholar] [CrossRef] [PubMed]
- Ahn, C.; Li, K.; Cai, S. Light or Thermally Powered Autonomous Rolling of an Elastomer Rod. ACS. Appl. Mater. Inter. 2018, 10, 25689. [Google Scholar] [CrossRef]
- Kuenstler, A.S.; Chen, Y.; Bui, P. Blueprinting Photothermal Shape Morphing of Liquid Crystal Elastomers. Adv. Mater. 2020, 32, 2000609. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Lu, H.C.; Lee, X. Kirigami Based Light Induced Shape Morphing and Locomotion. Adv. Mater. 2020, 32, 1906233. [Google Scholar] [CrossRef] [Green Version]
- Soltani, M.; Raahemifar, K.; Nokhosteen, A.; Kashkooli, F.M.; Zoudani, E.L. Numerical Methods in Studies of Liquid Crystal Elastomers. Polymers 2021, 13, 1650. [Google Scholar] [CrossRef]
- Cheng, Y.; Lu, H.; Lee, X.; Zeng, H.; Priimagi, A. Kirigami-based light-induced shape-morphing and locomotion. Adv. Mater 2019, 32, 1906233. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Guo, S.; Tong, X.; Xia, H.; Zhao, Y. Tunable photo controlled motions using stored strain energy in malleable azobenzene liquid crystalline polymer actuators. Adv. Mater 2017, 29, 1606467. [Google Scholar] [CrossRef]
- Li, K.; Du, C.; He, Q.; Cai, S. Thermally driven self-oscillation of an elastomer fiber with a hanging weight. Extreme Mech. Lett. 2021, 50, 101547. [Google Scholar] [CrossRef]
- Baumann, A.; Sánchez-Ferrer, A.; Jacomine, L.; Martinoty, P.; Houerou, V.L.; Ziebert, F.; Kulic, I.M. Motorizing fibres with geometric zero-energy modes. Nat. Mater. 2018, 17, 523–527. [Google Scholar] [CrossRef]
- Corbett, D.; Warner, M. Deformation and rotations of free nematic elastomers in response to electric fields. Soft Matter 2009, 5, 1433–1439. [Google Scholar] [CrossRef]
- Liu, Z.; Qi, M.; Zhu, Y.; Huang, D.; Yan, X. Mechanical response of the isolated cantilever with a floating potential in steady electrostatic field. Int. J. Mech. Sci. 2019, 161, 105066. [Google Scholar] [CrossRef]
- Hwang, I.; Mun, S.; Shin, H.; Yun, S. A NIR-Light-Driven Twisted and Coiled Polymer Actuator with a PEDOT-Tos/Nylon-6 Composite for Durable and Remotely Controllable Artificial Muscle. Polymers 2022, 14, 432. [Google Scholar] [CrossRef]
- Li, Z.; Myung, N.V.; Yin, Y. Light-powered soft steam engines for self-adaptive oscillation and biomimetic swimming. Sci. Robot. 2021, 6, eabi4523. [Google Scholar] [CrossRef]
- Haber, J.M.; Sanchez-Ferrer, A.; Mihut, A.M.; Dietsch, H.; Hirt, A.M.; Mezzenga, R. Liquid-crystalline elastomer-nanoparticle hybrids with reversible switch of magnetic memory. Adv. Mater. 2013, 5, 1787–1791. [Google Scholar] [CrossRef]
- Gelebart, A.H.; Mulder, D.J.; Varga, M.; Konya, A.; Vantomme, G.; Meijer, E.W.; Selinger, R.L.B.; Broer, D.J. Making waves in a photoactive polymer film. Nature 2017, 546, 632–636. [Google Scholar] [CrossRef] [Green Version]
- Boissonade, J.; Kepper, P.D. Multiple types of spatio-temporal oscillations induced by differential diffusion in the landolt reaction. Phys. Chem. Chem. Phys. 2011, 13, 4132–4137. [Google Scholar] [CrossRef] [PubMed]
- Chakrabarti, A.; Choi, G.P.T.; Mahadevan, L. Self-excited motions of volatile drops on swellable sheets. Phys. Rev. Lett. 2020, 124, 258002. [Google Scholar] [CrossRef]
- Camacho-Lopez, M.; Finkelmann, H.; Palffy-Muhoray, P.; Shelley, M. Fast liquid-crystal elastomer swims into the dark. Nat. Mater. 2004, 3, 307–310. [Google Scholar] [CrossRef]
- Zeng, H.; Lahikainen, M.; Liu, L.; Ahmed, Z.; Wani, O.M.; Wang, M.; Priimagi, A. Light-fuelled freestyle self-oscillators. Nat. Commun. 2019, 10, 5057. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, K.; Wu, P.Y.; Cai, S. Chemomechanical oscillations in a responsive gel induced by an autocatalytic reaction. J. Appl. Phys. 2014, 116, 043523. [Google Scholar] [CrossRef]
- Strogatz, S. Synchronization: A Universal Concept in Nonlinear Science. Phys. Today 2003, 56, 47. [Google Scholar] [CrossRef]
- Vicsek, T.; Zafeiris, A. Collective motion. Phys. Rep. 2012, 517, 71–140. [Google Scholar] [CrossRef] [Green Version]
- Boccaletti, S. The Synchronized Dynamics of Complex Systems. Monograph 2008, 6, 1–239. [Google Scholar]
- O’Keeffe, K.P.; Hong, H.; Strogatz, S.H. Oscillators that sync and swarm. Nat. Commun. 2017, 8, 1504. [Google Scholar] [CrossRef] [PubMed]
- Bennett, M.; Schatz, M.F.; Rockwood, H.; Wiesenfeld, K. Huygens’s clocks. Proc. R. Soc. A. Math. Phys. Eng. Sci. 2019, 458, 563–579. [Google Scholar] [CrossRef]
- Huygens, C. Oeuvres Complètes de Christiaan Huygens. M. Nijhoff 1899, 1888–1950. [Google Scholar] [CrossRef] [Green Version]
- Du, C.; Cheng, Q.; Li, K.; Yu, Y. Self-Sustained Collective Motion of Two Joint Liquid Crystal Elastomer Spring Oscillator Powered by Steady Illumination. Micromachines 2022, 13, 271. [Google Scholar] [CrossRef]
- Ikeguchi, T.; Shimada, Y. Analysis of Synchronization of Mechanical Metronomes; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Vantomme, G.; Elands, L.C.; Gelebart, A.H.; Meijer, E.W.; Pogromsky, A.Y.; Nijmeijer, H.; Broer, D.J. Coupled liquid crystalline oscillators in Huygens’ synchrony. Nat. Mater. 2021, 18, 1–5. [Google Scholar] [CrossRef]
- Finkelmann, H.; Nishikawa, E.; Pereira, G.G.; Warner, M. A new opto-mechanical effect in solids. Phys. Rev. Lett. 2001, 87, 015501. [Google Scholar] [CrossRef]
- Brannon, R. Kinematics: The mathematics of deformation. Course Notes 2008, 6530, 10. [Google Scholar]
- Warner, M.; Terentjev, E.M. Liquid Crystal Elastomers; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Yu, Y.; Nakano, M.; Ikeda, T. Photomechanics: Directed bending of a polymer film by light. Nature 2003, 425, 145. [Google Scholar] [CrossRef]
- Hogan, P.M.; Tajbakhsh, A.R.; Terentjev, E.M. UV Manipulation of order and macroscopic shape in nematic elastomers. Phys. Rev. E 2002, 65, 041720. [Google Scholar] [CrossRef] [Green Version]
- Gan, F.; Cheng, Q.; Li, K. Light-fueled self-excited vibration of a liquid crystal elastomer spring oscillator. J. Sound Vib. 2022, 526, 116820. [Google Scholar] [CrossRef]
- Marshall, J.E.; Terentjev, E.M. Photo-sensitivity of dye-doped liquid crystal elastomers. Soft Matter 2013, 9, 8547–8551. [Google Scholar] [CrossRef]
- Nagele, T.; Hoche, R.; Zinth, W.; Wachtveitl, J. Femtosecond photoisomerization of cis-azobenzene. Chem. Phys. Lett. 1997, 272, 489–495. [Google Scholar] [CrossRef]
- Torras, N.; Zinoviev, K.E.; Marshall, J.E.; Terentjev, E.M.; Esteve, J. Bending kinetics of a photo-actuating nematic elastomer cantilever. Appl. Phys. Lett. 2011, 99, 254102. [Google Scholar]
- Gelebart, A.H.; Vantomme, G.; Meijer, E.W.; Broer, D.J. Mastering the photothermal effect in liquid crystal networks: A general approach for self-sustained mechanical oscillators. Adv. Mater. 2017, 29, 1606712. [Google Scholar] [CrossRef] [Green Version]
- Serak, S.; Tabiryan, N.V.; Vergara, R.; White, T.J.; Vaia, R.A.; Bunning, T.J. Liquid crystalline polymer cantilever oscillators fueled by light. Soft Matter 2010, 6, 779–783. [Google Scholar] [CrossRef]



| Parameter | Definition | Value | Units |
|---|---|---|---|
| Mass of each mass block | |||
| Original length of LCE fiber and spring | |||
| Gravitational acceleration | |||
| Spring constant of LCE fiber | |||
| Spring constant of spring | |||
| cis-to-trans thermal relaxation time of LCE fiber | |||
| Damping coefficient | |||
| Contraction coefficient of LCE fiber | / |
| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| Value |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Gan, F.; Du, C.; Cai, G.; Liu, J. Synchronization of a Passive Oscillator and a Liquid Crystal Elastomer Self-Oscillator Powered by Steady Illumination. Polymers 2022, 14, 3058. https://doi.org/10.3390/polym14153058
Li K, Gan F, Du C, Cai G, Liu J. Synchronization of a Passive Oscillator and a Liquid Crystal Elastomer Self-Oscillator Powered by Steady Illumination. Polymers. 2022; 14(15):3058. https://doi.org/10.3390/polym14153058
Chicago/Turabian StyleLi, Kai, Fenghui Gan, Changshen Du, Guojun Cai, and Junxiu Liu. 2022. "Synchronization of a Passive Oscillator and a Liquid Crystal Elastomer Self-Oscillator Powered by Steady Illumination" Polymers 14, no. 15: 3058. https://doi.org/10.3390/polym14153058








