Parameters Influence on the Dynamic Properties of Polymer-Matrix Composites Reinforced by Fibres, Particles, and Hybrids
Abstract
:1. Introduction
- For the fibre composites, the effects of the fibre material, fabric weaving, fibre orientation, temperature (large range: −70 to 200 °C), and frequency (1 Hz and 10 Hz);
- For the particle composites, the effects of the particle size, short-fibre-volume percentage, and type of polymer matrix.
2. Materials and Methods
2.1. Dynamic Mechanical Thermal Analysis: Forced Vibration Test
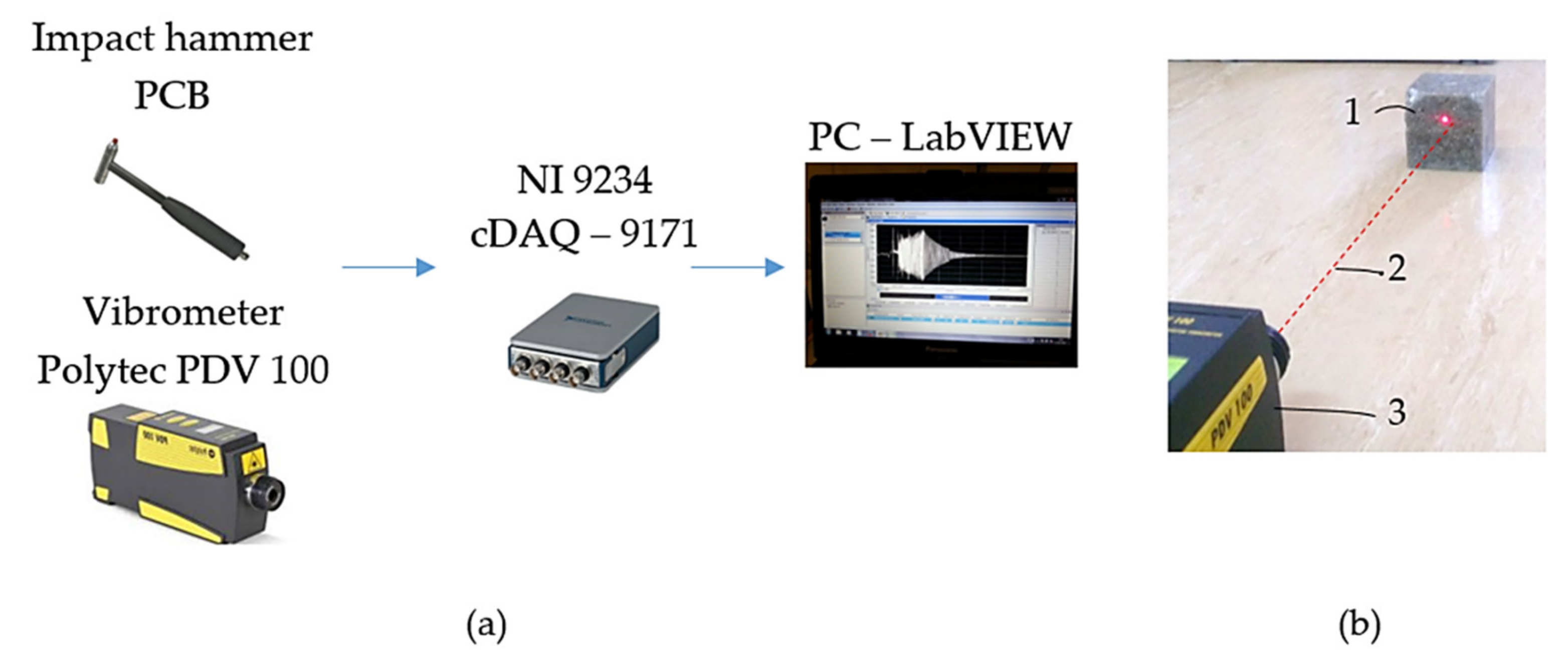
2.2. Vibration Diagnostics and Bump Test: Free-Vibration Test
- Portable Digital Vibrometer (PDV 100), for noncontact vibrational measurement in a frequency range from 0.5 Hz to 22 kHz, and at a variable working distance from 0.1 m to 30 m, and an operating temperature from +5 °C to +40 °C (Polytec GmBH, Waldbronn, Germany);
- NI 9234 Sound and Vibration Input Module, with a dynamic range of 102 dB. The input channels sample at rates as fast as 51.2 kS/s, with a 24-bit resolution, 50 g of shock, and 5 g of vibration (National Instruments Corporation, Austin, TX, USA);
- CompactDAQ Chassis cDAQ-9171 (National Instruments Corporation, Austin, TX, USA);
- An impact hammer (PCB) to mechanically impact the samples by bump force, with a sensitivity of 2.25 mV/N, and a measurement range of ±2224 N pk (PCB Piezotronics, Depew, NY, USA);
- Software for an advanced analysis of the dynamic signal based on LabView Sound and Vibration Toolkit software (National Instruments Corporation, Austin, TX, USA).
2.3. Samples and Materials
2.3.1. Multilayered Laminate Composites
2.3.2. Particle-Reinforced Composites
3. Results and Discussion
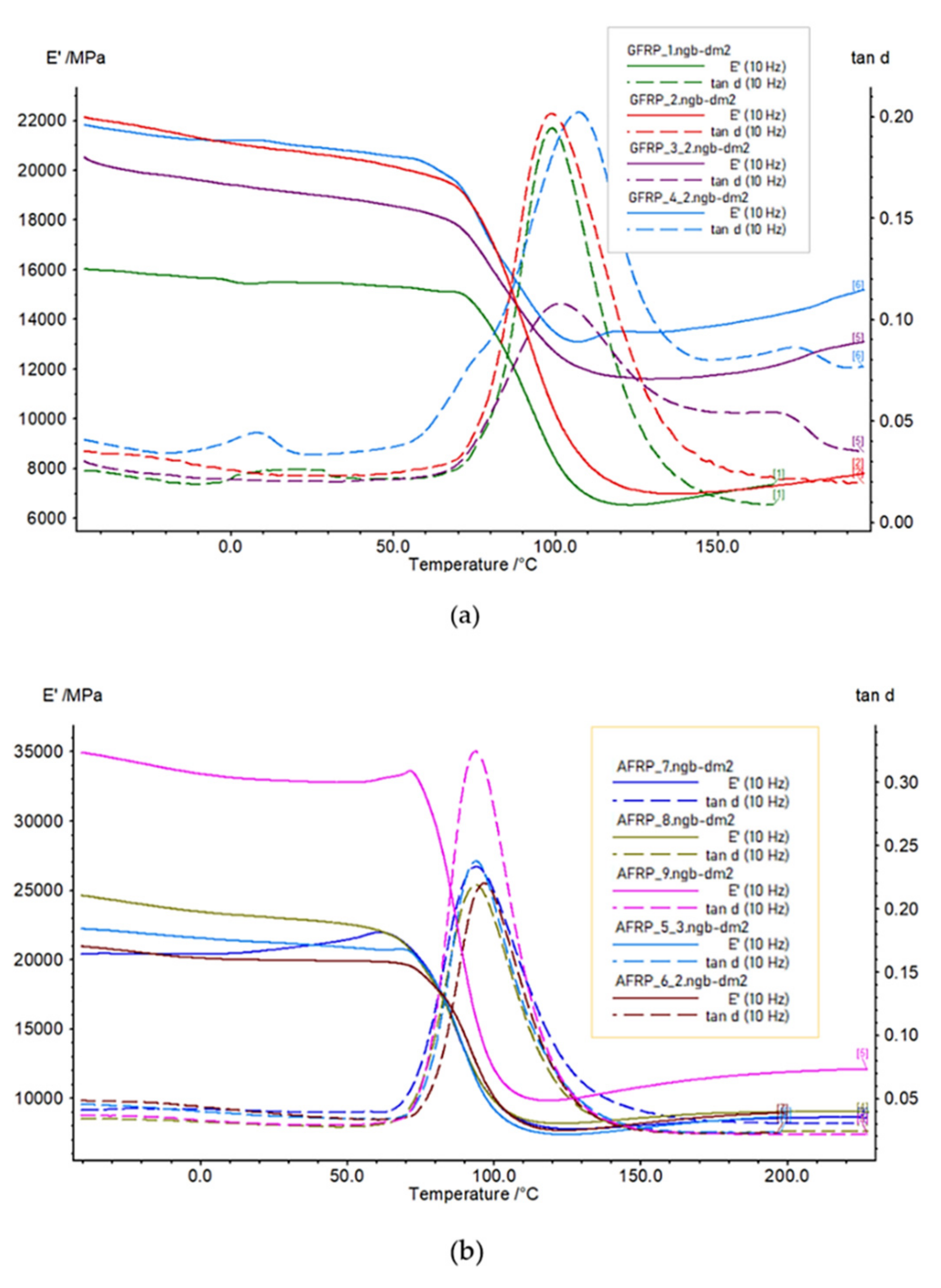
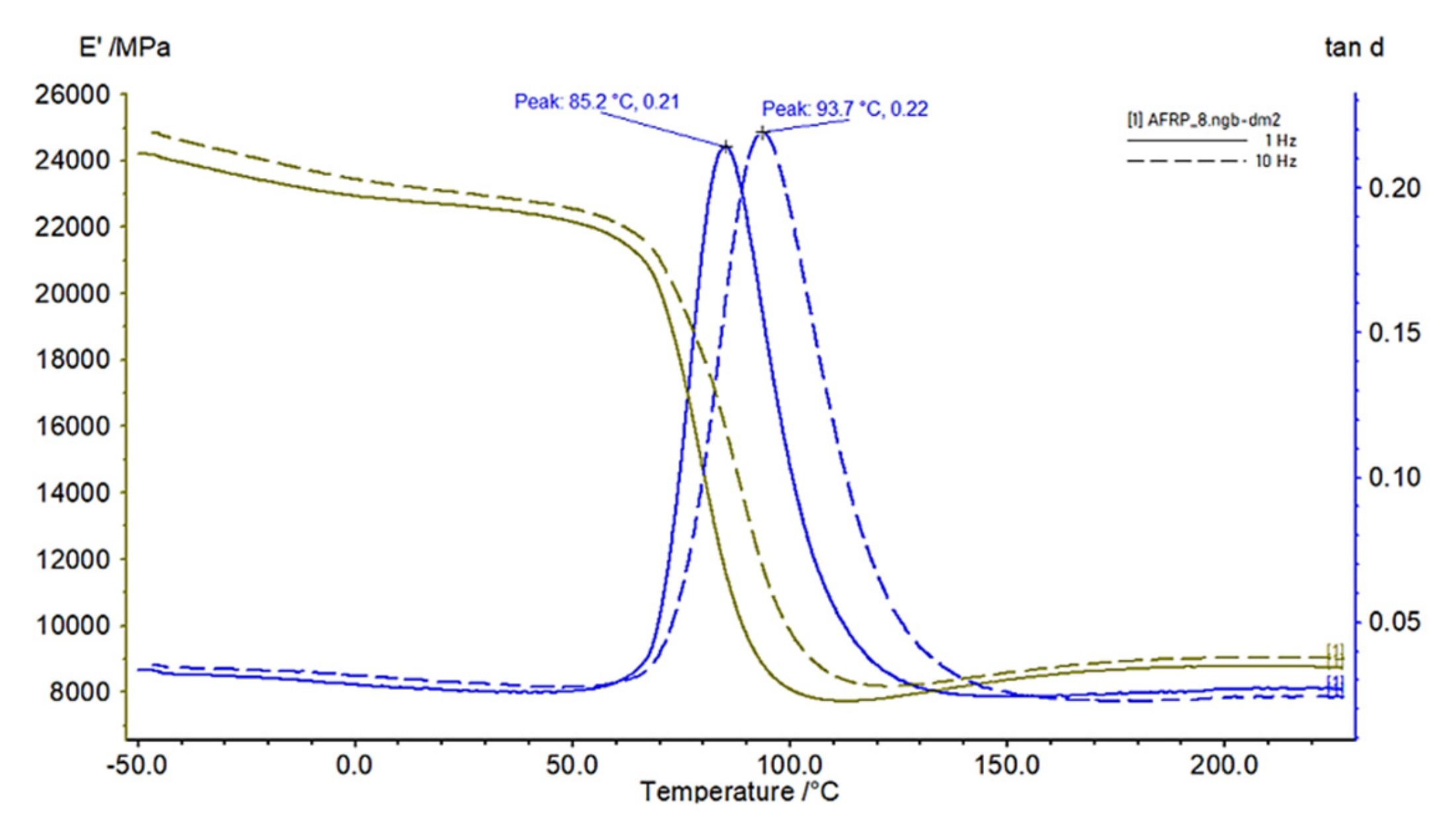
3.1. Results of DMTA Tests of Multilayered Laminates
3.2. Results of Bump Tests of Particle-Reinforced Composites
3.3. The Nature of Time-Domain-Response Curves
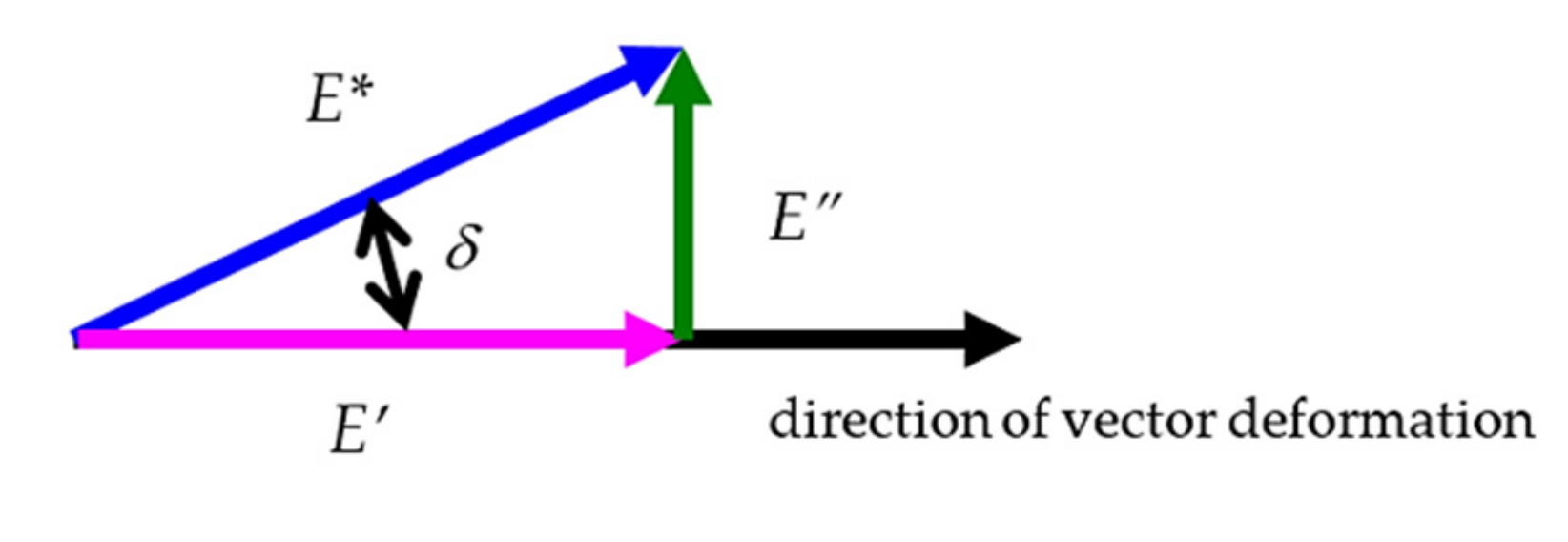
3.4. Microfield Distribution and Sources of the Composite Material Damping
4. Conclusions
- ○
- For the multilayered laminates, the fibre orientation had the greatest effect, followed by the fibre material;
- ○
- The fibre orientation had a greater effect than the type of weaving;
- ○
- The type of weaving affected the storage modulus (E′) more than the tan d;
- ○
- In the range of temperatures from −50 to 60 °C, the loss factor (tan d) was about 10-times lower than at the Tg temperature;
- ○
- The loss factor (tan d) at Tg temperature was in the range of 0–22.2% when we compared loading frequencies of 1 and 10 Hz of multilayered laminate composites samples;
- ○
- The particle size had the greatest effect on the particle composites damping.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Al-Ketan, O.; Al-Rub, R.K.A.; Rowshan, R. Mechanical properties of a new type of architected interpenetrating phase composite materials. Adv. Mater. Technol. 2017, 2, 1600235. [Google Scholar] [CrossRef]
- Bostanabad, R.; Liang, B.; Gao, J.; Liu, W.K.; Cao, J.; Zeng, D.; Su, X.; Xu, H.; Li, Y.; Chen, W. Uncertainty quantification in multiscale simulation of woven fiber composites. Comput. Methods Appl. Mech. Eng. 2018, 338, 506–532. [Google Scholar] [CrossRef]
- Frydrysek, K.; Cepica, D.; Halo, T.; Skoupy, O.; Pleva, L.; Madeja, R.; Pometlova, J.; Losertova, M.; Koutecky, J.; Michal, P.; et al. Biomechanical Analysis of Staples for Epiphysiodesis. Appl. Sci. 2022, 12, 614. [Google Scholar] [CrossRef]
- Machalla, V.; Frydrysek, K.; Mostyn, V.; Suder, J. Evaluation of tensile test for specific polymer. In Proceedings of the Applied Mechanics 2018, Myslovice, Czech Republic, 9–11 April 2018; pp. 81–86. [Google Scholar]
- Sławski, S.; Szymiczek, M.; Kaczmarczyk, J.; Domin, J.; Duda, S. Experimental and numerical investigation of striker shape influence on the destruction image in multilayered composite after low velocity impact. Appl. Sci. 2019, 10, 288. [Google Scholar] [CrossRef] [Green Version]
- Vasudevan, A.; Pandiyarajan, R.; Kumar, B.N.; Vijayarangam, J. Effect of Kevlar Ply Orientation on Mechanical Characterization of Kevlar-Glass Fiber Laminated Composites. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Hyderabad, India, 27–28 August 2020; Volume 988, p. 012088. [Google Scholar]
- Pozorski, Z.; Pozorska, J.; Kreja, I.; Smakosz, Ł. On Wrinkling in Sandwich Panels with an Orthotropic Core. Materials 2021, 14, 5043. [Google Scholar] [CrossRef]
- Falkowska, A.; Seweryn, A.; Skrodzki, M. Strength properties of a porous titanium alloy Ti6Al4V with diamond structure obtained by laser power bed fusion (LPBF). Materials 2020, 13, 5138. [Google Scholar] [CrossRef]
- Khan, S.U.; Li, C.Y.; Siddiqui, N.A.; Kim, J.K. Vibration damping characteristics of carbon fiber-reinforced composites containing multi-walled carbon nanotubes. Compos. Sci. Technol. 2011, 71, 1486–1494. [Google Scholar] [CrossRef]
- Roszkos, C.S.; Bocko, J.; Kula, T.; Sarlosi, J. Static and dynamic analyses of aluminum foam geometric models using the homogenization procedure and the FEA. Compos. Part B Eng. 2019, 171, 361–374. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, S.; Pan, F.; Zhang, J. A numerical study on electrical percolation of polymer-matrix composites with hybrid fillers of carbon nanotubes and carbon black. J. Nanomater. 2014, 2014, 614797. [Google Scholar] [CrossRef] [Green Version]
- Kormanikova, E.; Zmindak, M.; Novak, P.; Sabol, P. Tensile properties of carbon fiber reinforced polymer matrix composites: Application for the strengthening of reinforced concrete structure. Compos. Struct. 2021, 275, 114448. [Google Scholar] [CrossRef]
- Kormanikova, E.; Kotrasova, K. Micro-macro modelling of laminated composite rectangular reservoir. Compos. Struct. 2022, 279, 114701. [Google Scholar] [CrossRef]
- Krzikalla, D.; Mesicek, J.; Halama, R.; Hajnys, J.; Pagac, M.; Cegan, T.; Petru, J. On flexural properties of additive manufactured composites: Experimental, and numerical study. Compos. Sci. Technol. 2022, 218, 109182. [Google Scholar] [CrossRef]
- Ni, Q.Q.; Cheng, F.; Iwamoto, M. Development and temperature dependency of high damping sandwich laminates. Nippon. Kikai Gakkai Ronbunshu A Hen Trans. Jpn. Soc. Mech. Eng. Part A 2005, 17, 1437–1444. [Google Scholar] [CrossRef] [Green Version]
- Haddad, H.; Al Kobaisi, M. Optimization of the polymer concrete used for manufacturing bases for precision tool machines. Compos. Part B 2012, 43, 3061–3068. [Google Scholar] [CrossRef]
- Heidarnezhad, F.; Jafari, K.; Ozbakkaloglu, T. Effect of polymer content and temperature on mechanical properties of lightweight polymer concrete. Constr. Build. Mater. 2020, 260, 119853. [Google Scholar] [CrossRef]
- Zajac, J.; Petruška, O.; Radchenko, S.; Dupláková, D.; Goldyniak, D. Hardness Testing of Polymer Concrete Castings by Schmidt Hammer. Mater. Today Proc. 2020, 22, 293–299. [Google Scholar]
- Murcinkova, Z.; Zivcak, J.; Zajac, J.; Adamcik, P. Passive Multi-Layer Composite Damper of Flat Belt Tensioner Idler. Appl. Sci. 2021, 11, 3267. [Google Scholar] [CrossRef]
- Murcinkova, Z.; Adamcik, P.; Zivcak, J. Re-Design of Machine Tool Joint Components Based on Polymer Fillings for High-Speed Performance. Materials 2021, 14, 6913. [Google Scholar] [CrossRef]
- Jakubowski, A.; Dounar, S. Dynamic finite element analysis of rotor-shaft fastening into a heavy precise lathe. Sci. J. Marit. Univ. Szczec. 2021, 66, 138. [Google Scholar]
- Vivek, A.; Holla, V.; Krupashankara, M.S.; Vignesh, A.; Kulkarni, P. Effect of improving damping ratio on surface finish by filling particulate reinforced polymer composites in machine tool structures. Mater. Today Proc. 2018, 5, 13664–13673. [Google Scholar] [CrossRef]
- Yu, Y.; Gao, J.; Xu, P.; Li, Y. Multi-objective optimization design and performance analysis of machine tool worktable filled with BFPC. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Singapore, 14–16 September 2018; Volume 439, p. 042005. [Google Scholar]
- Hutyrova, Z.; Zajac, J.; Michalik, P.; Mital, D.; Duplak, J.; Gajdos, S. Study of surface roughness of machined polymer composite material. Int. J. Polym. Sci. 2015, 2015, 303517. [Google Scholar] [CrossRef] [Green Version]
- Malakova, S.; Puskar, M.; Frankovsky, P.; Sivak, S.; Palko, M.; Palko, M. Meshing Stiffness—A Parameter Affecting the Emission of Gearboxes. Appl. Sci. 2020, 10, 8678. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Y.; Gong, C.; Liu, B.; Wei, G. Production, structural design, functional control, and broad applications of carbon nanofiber-based nanomaterials: A comprehensive review. Chem. Eng. J. 2020, 402, 126189. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, F.; Zhang, X.; Liang, L.; Yang, X.; Li, Q.; Zhang, X. Vibration damping of carbon nanotube assembly materials. Adv. Eng. Mater. 2018, 20, 1700647. [Google Scholar] [CrossRef] [Green Version]
- Bocko, J.; Segla, S.; Hunady, R. Kmitanie Mechanických Sústav (Vibration of Mechanical Systems); Technical University of Kosice: Kosice, Slovakia, 2016. [Google Scholar]
- Medvec, A.; Stradiot, J.; Zahorec, O.; Caban, S. Dynamika (Dynamics); Alfa SNTL: Bratislava, Slovakia, 1988. [Google Scholar]
- Available online: http://www.grm-systems.cz/en/epoxy (accessed on 16 January 2022).
- Available online: https://r-g.com.pl/pl/p/file/7160c686048aa59257decd7ee895c247/L285-TSDS.pdf (accessed on 16 January 2022).
- Priyanka, P.; Mali, H.S.; Dixit, A. Dynamic mechanical behaviour of kevlar and carbon-kevlar hybrid fibre reinforced polymer composites. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 4181–4193. [Google Scholar] [CrossRef]
- Gardea, F.; Glaz, B.; Riddick, J.; Lagoudas, D.C.; Naraghi, M. Energy dissipation due to interfacial slip in nanocomposites reinforced with aligned carbon nanotubes. ACS Appl. Mater. Interfaces 2015, 7, 9725–9735. [Google Scholar] [CrossRef]
- Tang, X.; Yan, X. A review on the damping properties of fiber reinforced polymer composites. J. Ind. Text. 2018, 49, 693–721. [Google Scholar] [CrossRef]
- Kumar, N.P. Viscoelastic Characterization and Effective Damping of a Carbon/Polyurethane Laminate; Rochester Institute of Technology: Rochester, MN, USA, 2016. [Google Scholar]
- Budiman, B.A.; Triawan, F.; Adziman, F.; Nurprasetio, I.P. Modeling of stress transfer behavior in fiber-matrix composite under axial and transverse loadings. Compos. Interfaces 2017, 24, 677–690. [Google Scholar] [CrossRef]










| Filler:Matrix (Vol%) | Fillers Vol% | Filler Fraction | |
|---|---|---|---|
| A | 75:25 | 50 | Silica sand (0.3–1 mm) |
| 50 | Silica dust (0.1–0.3 mm) | ||
| 100:16 | epoxy resin CHS-EPOXY 324:fixative TELATIT 0492 | ||
| B | 75:25 | 50 | Silica gravel (2–4 mm) |
| 50 | Silica dust (0.1–0.3 mm) | ||
| 100:16 | epoxy resin CHS-EPOXY 324:fixative TELATIT 0492 | ||
| C | 84:16 | 35 | Danube gravel (8–16 mm) |
| 35 | Danube gravel (4–8 mm) | ||
| 30 | Silica sand (0.3–1 mm) | ||
| 100:50 | epoxy resin LH 160:fixative H 287 |
| Filler:Matrix Ratio: 75:25 Vol% Epoxy Resin LH 160:fixative H 287: 100:50 | D | E | F |
|---|---|---|---|
| Chopped carbon fibres (3 mm) (vol%) | 3 | 6 | 12 |
| Andesite gravel (4–8 mm) (vol%) | 49 | 48 | 46 |
| Silica sand (0.3–1 mm) (vol%) | 24 | 23 | 21 |
| Silica dust (0.1–0.3 mm) (vol%) | 24 | 23 | 21 |
| Filler:Matrix 78:22 Vol% | ||
|---|---|---|
| 50% | Silica gravel (2–4 mm) | |
| 30% | Silica sand (0.3–1 mm) | |
| 20% | Silica dust (0.1–0.3 mm) | |
| G | Ratio of epoxy resin LH 160:fixative H 287: 100:50 | |
| H | Ratio of epoxy resin LH 289:fixative H 287: 100:50 | |
| I | Ratio of epoxy resin CHS-EPOXY 517:fixative P11: 100:11 | |
| Sample | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequency | 1 Hz | |||||||||||
| tan d (-) | 0.19 | 0.19 | 0.09 | 0.18 | 0.23 | 0.21 | 0.23 | 0.21 | 0.32 | 0.18 | 0.31 | 0.28 |
| Tg (°C) | 89.8 | 89.5 | 91.3 | 96.4 | 86.3 | 89.1 | 84.6 | 85.2 | 85.1 | 87.8 | 85.0 | 85.7 |
| Frequency | 10 Hz | |||||||||||
| tan d (-) | 0.19 | 0.20 | 0.11 | 0.21 | 0.23 | 0.22 | 0.23 | 0.22 | 0.32 | 0.18 | 0.31 | 0.28 |
| Tg (°C) | 98.8 | 99.1 | 100.6 | 108.7 | 94.2 | 96.7 | 93.8 | 93.7 | 93.5 | 97.4 | 94.1 | 94.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murčinková, Z.; Postawa, P.; Winczek, J. Parameters Influence on the Dynamic Properties of Polymer-Matrix Composites Reinforced by Fibres, Particles, and Hybrids. Polymers 2022, 14, 3060. https://doi.org/10.3390/polym14153060
Murčinková Z, Postawa P, Winczek J. Parameters Influence on the Dynamic Properties of Polymer-Matrix Composites Reinforced by Fibres, Particles, and Hybrids. Polymers. 2022; 14(15):3060. https://doi.org/10.3390/polym14153060
Chicago/Turabian StyleMurčinková, Zuzana, Przemysław Postawa, and Jerzy Winczek. 2022. "Parameters Influence on the Dynamic Properties of Polymer-Matrix Composites Reinforced by Fibres, Particles, and Hybrids" Polymers 14, no. 15: 3060. https://doi.org/10.3390/polym14153060
APA StyleMurčinková, Z., Postawa, P., & Winczek, J. (2022). Parameters Influence on the Dynamic Properties of Polymer-Matrix Composites Reinforced by Fibres, Particles, and Hybrids. Polymers, 14(15), 3060. https://doi.org/10.3390/polym14153060








