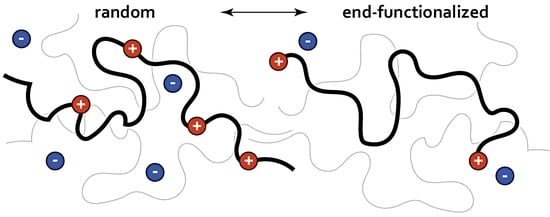
Structure and Diffusion of Ionic PDMS Melts
Abstract
:1. Introduction
2. Methodology
3. Results and Discussion
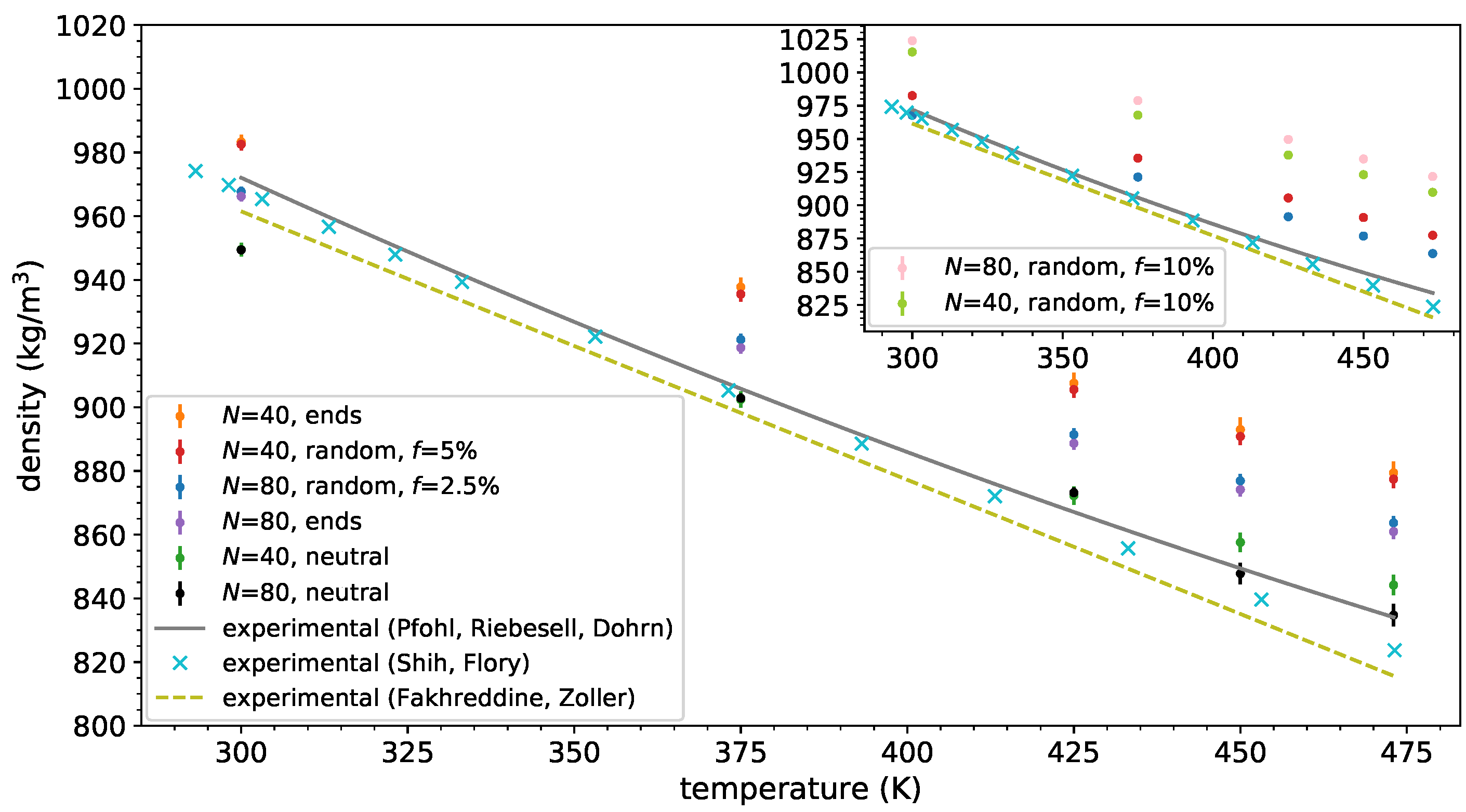
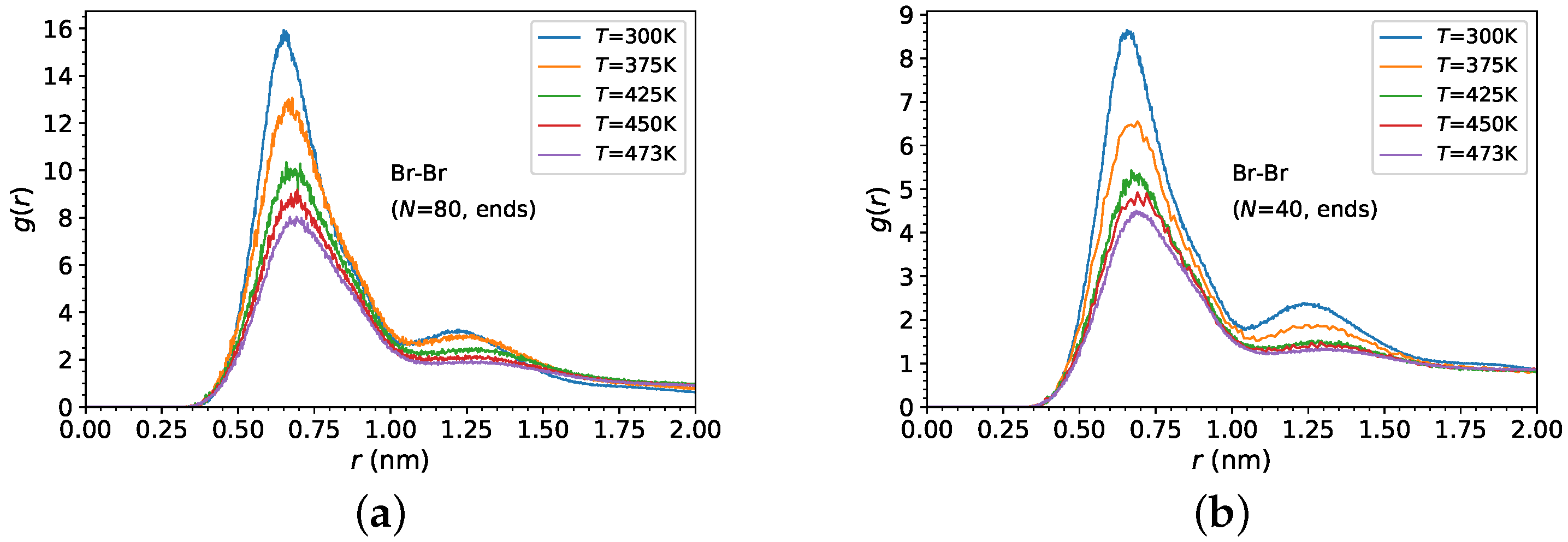
3.1. Melt Density and Structure
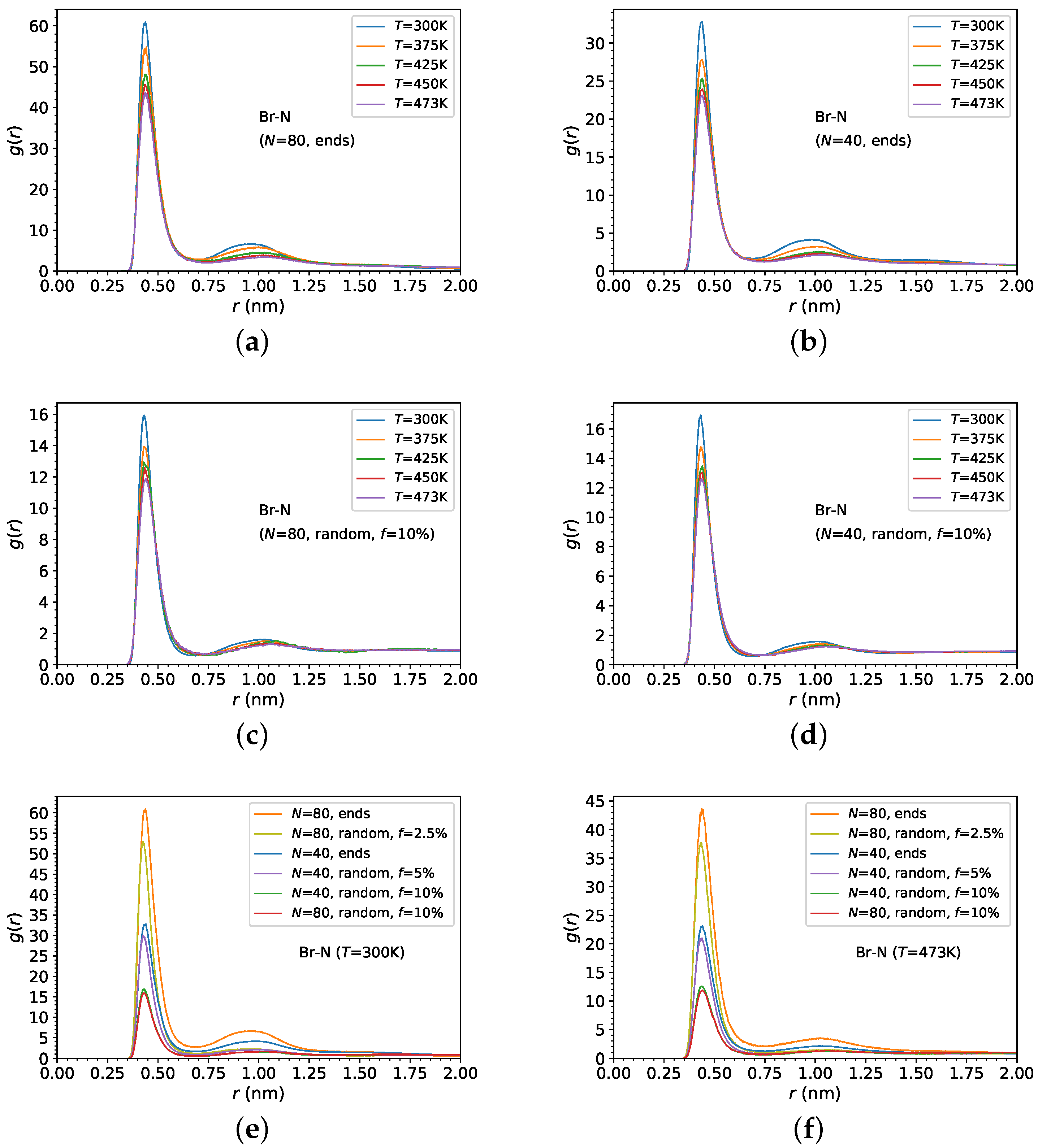
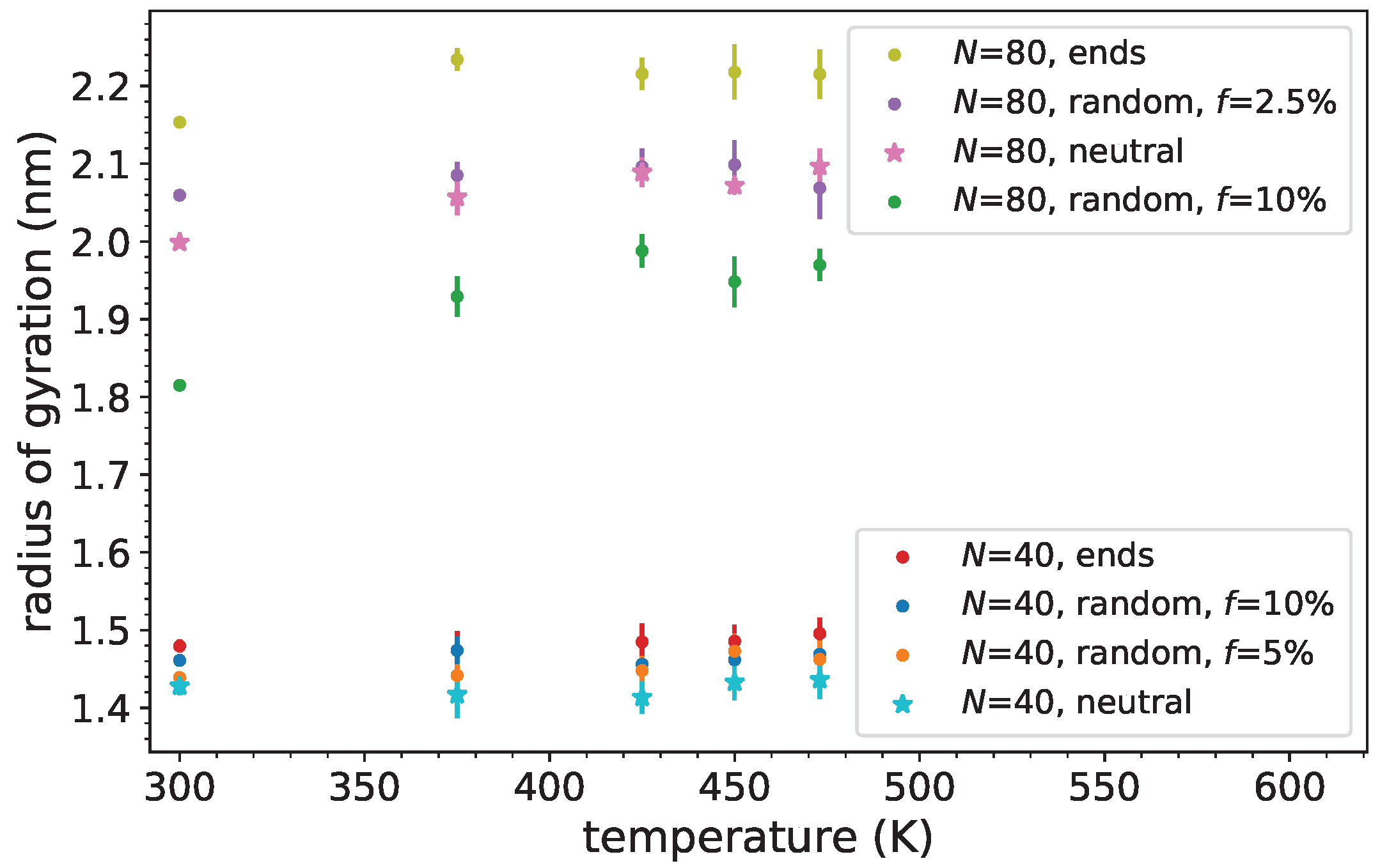
3.2. Polymer Dimensions
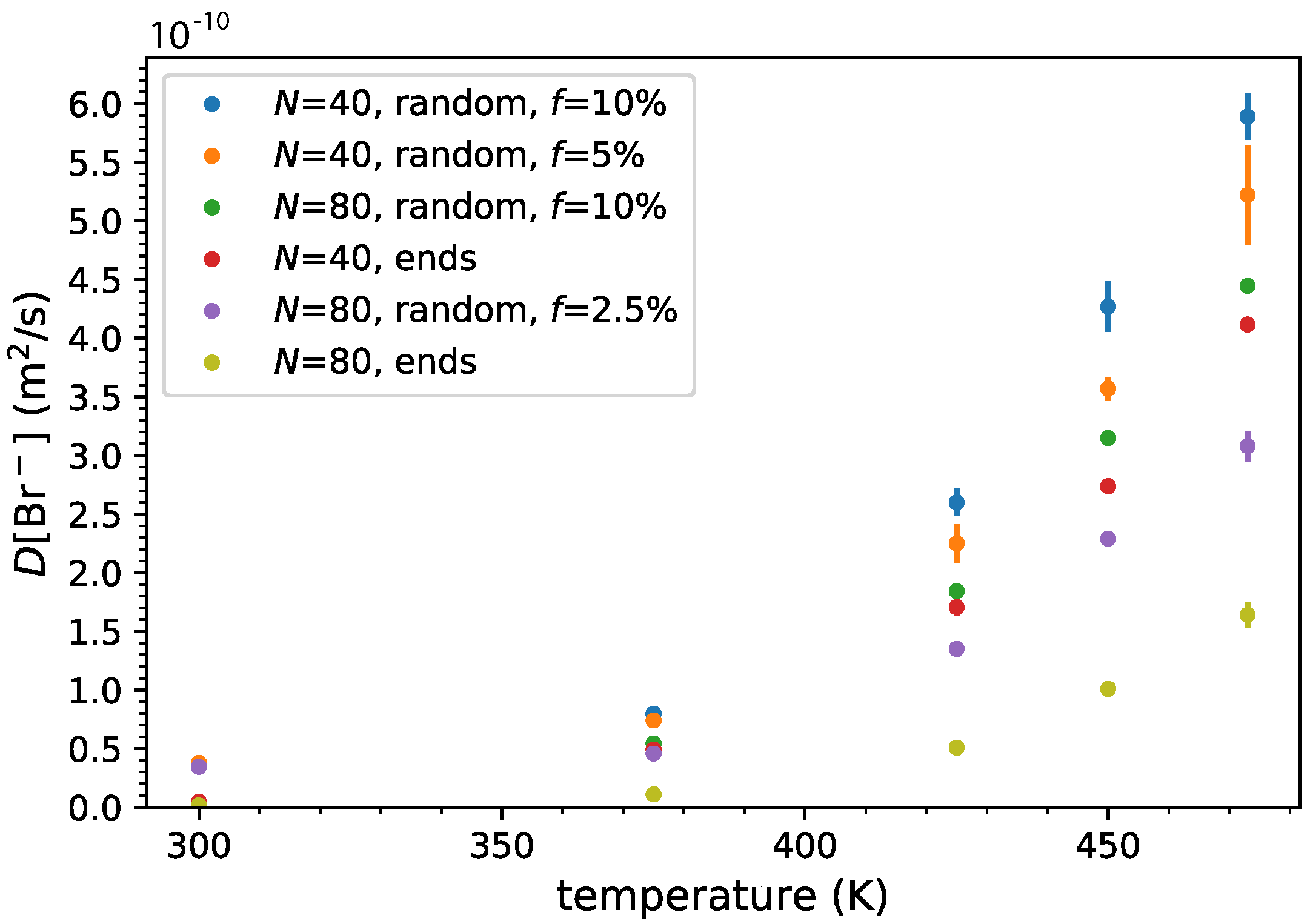
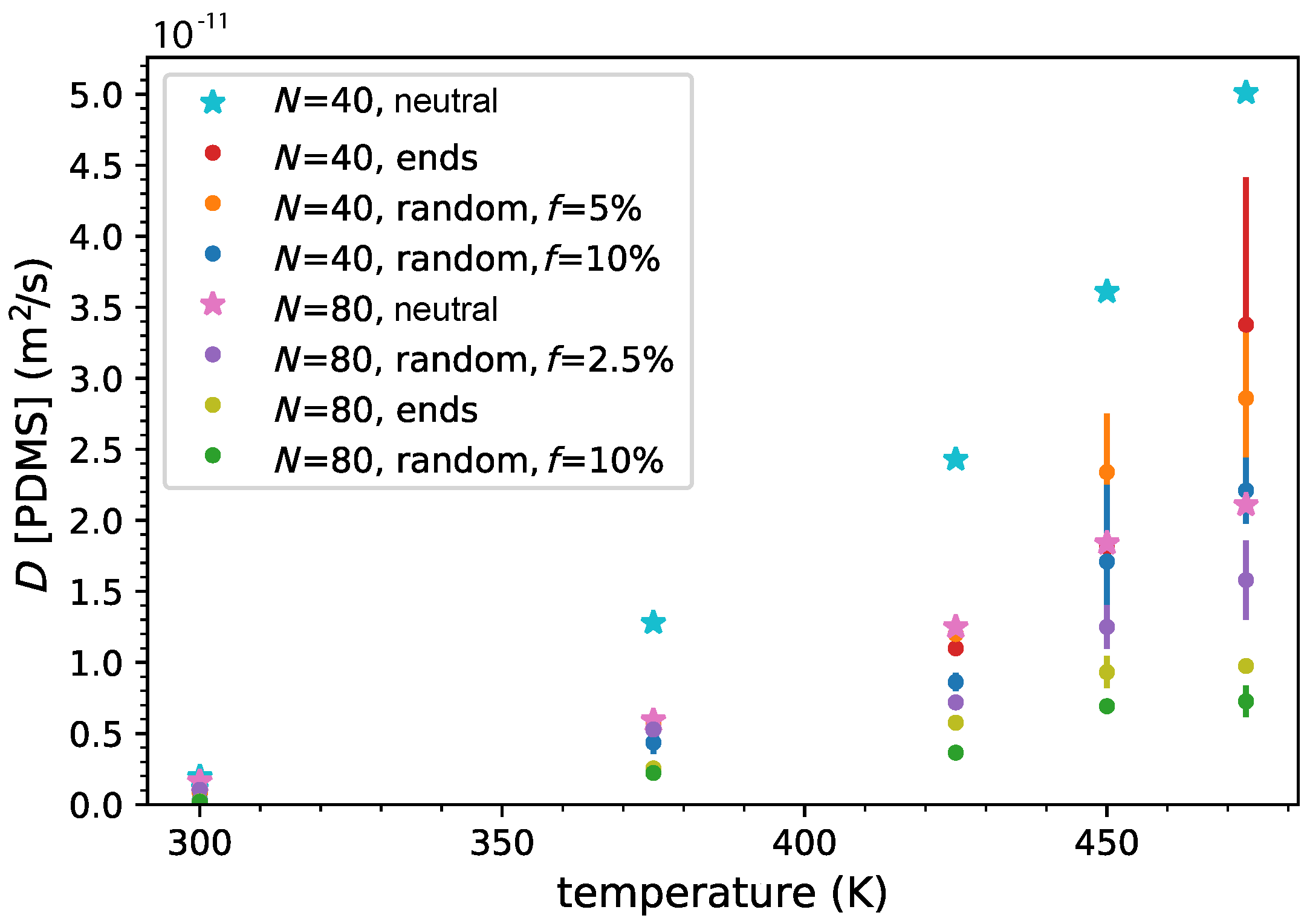
3.3. Ion and Polymer Diffusion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wolf, M.P.; Salieb-Beugelaar, G.B.; Hunziker, P. PDMS with designer functionalities—Properties, modifications strategies, and applications. Progr. Polym. Sci. 2018, 83, 97–134. [Google Scholar] [CrossRef]
- Kausar, A. Polydimethylsiloxane-based nanocomposite: Present research scenario and emergent future trends. Polym.-Plast. Technol. Mater. 2020, 59, 1148–1166. [Google Scholar] [CrossRef]
- Miranda, I.; Souza, A.; Sousa, P.; Ribeiro, J.; Castanheira, E.M.S.; Lima, R.; Minas, G. Properties and applications of PDMS for biomedical engineering: A review. J. Funct. Biomater. 2022, 13, 2. [Google Scholar] [CrossRef] [PubMed]
- Victor, A.; Ribeiro, J.E.; Araujo, F.F. Study of PDMS characterization and its applications in biomedicine: A review. J. Mech. Eng. Biomech. 2019, 4, 1–9. [Google Scholar] [CrossRef]
- Yuen, P.K.; Su, H.; Goral, V.N.; Fink, K.A. Three-dimensional interconnected microporous poly(dimethylsiloxane) microfluidic devices. Lab Chip 2011, 11, 1541–1544. [Google Scholar] [CrossRef] [PubMed]
- Toepke, M.W.; Beebe, D.J. PDMS absorption of small molecules and consequences in microfluidic applications. Lab Chip 2006, 6, 1484–1486. [Google Scholar] [CrossRef]
- Lin, L.; Chung, C.K. PDMS microfabrication and design for microfluidics and sustainable energy application: Review. Micromachines 2021, 12, 1350. [Google Scholar] [CrossRef]
- Bourbaba, J.; Achaiba, C.B.; Mohamed, B. Mechanical behavior of polymeric membrane: Comparison between PDMS and PMMA for micro fluidic Application. Energy Procedia 2013, 36, 231–237. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Shepelin, N.A.; Sherrell, P.C.; Ellis, A.V. Poly(dimethylsiloxane) for triboelectricity: From mechanisms to practical strategies. Chem. Mater. 2021, 33, 4304–4327. [Google Scholar] [CrossRef]
- Sappati, K.K.; Bhadra, S. Piezoelectric Polymer and Paper Substrates: A Review. Sensors 2018, 18, 3605. [Google Scholar] [CrossRef] [Green Version]
- Batra, A.; Cohen, C. Reversible modulus reinforcement of end-linked polydimethylsiloxane ionomer networks. Polymers 2005, 46, 12416–12421. [Google Scholar] [CrossRef]
- Batra, A.; Cohen, C.; Kim, H.; Winey, K.I.; Ando, N.; Gruner, S.M. Counterion Effect on the Rheology and Morphology of Tailored Poly(dimethylsiloxane) Ionomers. Macromolecules 2006, 39, 1630–1638. [Google Scholar] [CrossRef]
- Kohoutova, M.; Sikora, A.; Hovorka, S.; Randova, A.; Schauer, J.; Ploncarziva, M.; Izak, P. How ionic liquid changes properties of dense polydimethylsiloxane membrane? Desalin. Water Treat. 2010, 14, 78–82. [Google Scholar] [CrossRef]
- Kohoutová, M.; Sikora, A.; Hovorka, S.; Randová, A.; Schauer, J.; Tisma, M.; Setnicková, K.; Petrickovic, R.; Guernik, S.; Greenspoon, N.; et al. Influence of ionic liquid content on properties of dense polymer membranes. Eur. Polym. J. 2009, 45, 813–819. [Google Scholar] [CrossRef]
- Horowitz, A.I.; Panzer, M.J. Poly(dimethylsiloxane)-Supported Ionogels with a High Ionic Liquid Loading. Angew. Chem. Int. Ed. 2014, 53, 9780–9783. [Google Scholar] [CrossRef]
- Izák, P.; Friess, K.; Hynek, V.; Ruth, W.; Fei, Z.; Dyson, J.; Kragl, U. Separation properties of supported ionic liquid–polydimethylsiloxane membrane in pervaporation process. Desalination 2009, 241, 182–187. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, Y.; Pham, H.; Carrillo, J.M.Y.; Sumpter, B.G.; Nanda, J.; Dudney, N.J.; Saito, T.; Sokolov, A.P.; Cao, P.F. Improved Single-Ion Conductivity of Polymer Electrolyte via Accelerated Segmental Dynamics. ACS Appl. Energy Mater. 2020, 3, 12540–12548. [Google Scholar] [CrossRef]
- Poon, L.; Hum, J.R.; Weiss, R.G. Neat Linear Polysiloxane-Based Ionic Polymers: Insights into Structure-Based Property Modifications and Applications. Macromolecules 2021, 1, 2–17. [Google Scholar] [CrossRef]
- Mugemana, C.; Moghimikheirabadi, A.; Arl, D.; Addiego, F.; Schmidt, D.F.; Kröger, M.; Karatrantos, A.V. Ionic poly(dimethylsiloxane)-silica nanocomposites: Dispersion and self-healing. MRS Bull. 2022, in press. [Google Scholar] [CrossRef]
- Mo, J.; Wu, W.; Shan, S.; Wu, X.; Li, D.; Li, R.; Lin, Y.; Zhang, A. A systematic study on Zn(II)-Iminocarboxyl complexation applied in supramolecular PDMS networks. Polymers 2022, 250, 124896. [Google Scholar] [CrossRef]
- Kang, Z.; Yu, L.; Skov, A.L. A novel PDMS dielectric elastomer actuator with bis-ionic liquid as crosslinker. In Electroactive Polymer Actuators and Devices (EAPAD) XXIV; Anderson, I.A., Madden, J.D.W., Shea, H.R., Eds.; SPIE: Bellingham, WA, USA, 2022; Volume 12042, pp. 335–341. [Google Scholar]
- Verma, G.; Sheshkar, N.; Pandey, C.; Gupta, A. Recent trends of silicon elastomer-based nanocomposites and their sensing applications. J. Polym. Res. 2022, 29, 195. [Google Scholar] [CrossRef]
- Lee, Y.; Lim, S.; Song, W.J.; Lee, S.; Yoon, S.J.; Park, J.M.; Lee, M.G.; Park, Y.L.; Sun, J.Y. Triboresistive touch sensing: Grid-free touch-point recognition based on monolayered ionic power generators. Adv. Mater. 2022, 34, 2108586. [Google Scholar] [CrossRef]
- Au-Duong, A.N.; Hsu, Y.C.; Malintoi, M.; Ubaidillah, A.N.; Li, Y.T.; Lai, J.Y.; Lai, J.Y.; Chiu, Y.C. Highly transparent, stretchable, and self-healing polymers crosslinked by dynamic zinc(II)-poly(amic acid) bonds. Polym. J. 2022, 54, 305–312. [Google Scholar] [CrossRef]
- Kim, J.S.; Luqman, M.; Song, J.M. Ionomers. In Encyclopedia of Polymer Science and Technology; American Cancer Society: Atlanta, GA, USA, 2010. [Google Scholar]
- Aitken, B.S.; Buitrago, C.F.; Heffley, J.D.; Lee, M.; Gibson, H.W.; Winey, K.I.; Wagener, K.B. Precision ionomers: Synthesis and thermal/mechanical characterization. Macromolecules 2012, 45, 681–687. [Google Scholar] [CrossRef]
- Ko, K.H.; Kim, J.S. Ionomers. In Kirk Othmer Encyclopedia of Chemical Technology; American Cancer Society: Atlanta, GA, USA, 2016; pp. 1–34. [Google Scholar]
- Buitrago, C.F.; Bolintineanu, D.S.; Seitz, M.E.; Opper, K.L.; Wagener, K.B.; Stevens, M.J.; Frischknecht, A.L.; Winey, K.I. Direct comparisons of X-ray scattering and atomistic molecular dynamics simulations for precise acid copolymers and ionomers. Macromolecules 2015, 48, 1210–1220. [Google Scholar] [CrossRef]
- Shen, K.H.; Fan, M.; Hall, L.M. Molecular dynamics simulations of ion-containing polymers using generic coarse-grained models. Macromolecules 2021, 54, 2031–2052. [Google Scholar] [CrossRef]
- Ma, M.; Fu, Y. Structural and mechanical properties of ionic di-block copolymers via a molecular dynamics approach. Polymers 2019, 11, 1546. [Google Scholar] [CrossRef] [Green Version]
- Middleton, L.R.; Winey, K.I. Nanoscale aggregation in acid- and ion-containing polymers. Annu. Rev. Chem. Biomol. Eng. 2017, 8, 499–523. [Google Scholar] [CrossRef]
- Wu, S.; Xiao, C.; Zhang, Z.; Chen, Q.; Matsumiya, Y.; Watanabe, H. Molecular design of highly stretchable ionomers. Macromolecules 2018, 51, 4735–4746. [Google Scholar] [CrossRef]
- Grady, B.P. Review and critical analysis of the morphology of random ionomers across many length scales. Polym. Eng. Sci. 2008, 48, 1029–1051. [Google Scholar] [CrossRef]
- Choo, Y.; Halat, D.M.; Villaluenga, I.; Timachova, K.; Balsara, N.P. Diffusion and migration in polymer electrolytes. Progr. Polym. Sci. 2020, 103, 101220. [Google Scholar] [CrossRef] [Green Version]
- Mohottalalage, S.S.; Aryal, D.; Thurston, B.A.; Grest, G.S.; Perahia, D. Effects of ionic group distribution on the structure and dynamics of amorphous polymer melts. Macromolecules 2021, 55, 217. [Google Scholar] [CrossRef]
- Aryal, D.; Agrawal, A.; Perahia, D.; Grest, G.S. Structure and dynamics of ionic block copolymer melts: Computational study. Macromolecules 2017, 50, 7388–7398. [Google Scholar] [CrossRef]
- Yang, X.; Xu, X.; Xu, W.S. Influence of ionic interaction strength on glass formation of an ion-containing polymer melt. Macromolecules 2021, 54, 9587. [Google Scholar] [CrossRef]
- Karatrantos, A.; Koutsawa, Y.; Dubois, P.; Clarke, N.; Kröger, M. Miscibility and diffusion in ionic nanocomposites. Polymers 2018, 10, 1010. [Google Scholar] [CrossRef] [Green Version]
- Ma, B.; Olvera de la Cruz, M. A perspective on the design of ion-containing polymers for polymer electrolyte applications. J. Phys. Chem. B 2021, 125, 3015–3022. [Google Scholar] [CrossRef]
- Zhang, L.; Li, J.; Huang, X.; Zhang, Y.; Zhang, Y. Sulfonated poly(imide-siloxane) membrane as a low vanadium ion permeable separator for a vanadium redox flow battery. Polym. J. 2015, 47, 701–708. [Google Scholar] [CrossRef]
- Rogalsky, S.; Bardeau, J.F.; Makhno, S.; Tarasyuk, O.; Babkina, N.; Cherniavska, T.; Filonenko, M.; Fatyeyeva, K. New polymer electrolyte membrane for medium-temperature fuel cell applications based on cross-linked polyimide Matrimid and hydrophobic protic ionic liquid. Mater. Today Chem. 2021, 20, 100453. [Google Scholar] [CrossRef]
- Zhang, L.; Brostowitz, N.R.; Cavicchi, K.A.; Weiss, R.A. Perspective: Ionomer Research and Applications. Macromol. React. Eng. 2014, 8, 81–99. [Google Scholar] [CrossRef]
- Sides, S.W.; Curro, J.; Grest, G.S.; Stevens, M.J.; Soddemann, T.; Habenschuss, A.; Londono, J.D. Structure of poly(dimethylsiloxane) melts:. Theory, simulation, and experiment. Macromolecules 2002, 35, 6455–6465. [Google Scholar] [CrossRef]
- Hofmann, M. Mode Analysis of NMR Relaxation in a Polymer Melt. Macromolecules 2018, 51, 5742–5751. [Google Scholar] [CrossRef]
- Klonos, P.A. Crystallization, glass transition, and molecular dynamics in PDMS of low molecular weights: A calorimectric and dielectric study. Polymers 2018, 159, 169–180. [Google Scholar] [CrossRef]
- Moghimikheirabadi, A.; Mugemana, C.; Kröger, M.; Karatrantos, A.V. Polymer conformations, entanglements and dynamics in ionic nanocomposites: A molecular dynamics study. Polymers 2020, 12, 2591. [Google Scholar] [CrossRef]
- Fu, Y.; Bocharova, V.; Ma, M.; Sokolov, A.P.; Sumpter, B.G.; Kumar, R. Effects of counterion size and backbone rigidity on dynamics of ionic polymer melts and glasses. Phys. Chem. Chem. Phys. 2017, 19, 27442–27451. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; de la Cruz, O.M. Glass transition of ion-containing polymer melts in bulk and thin films. Soft Matter 2021, 17, 8420–8433. [Google Scholar] [CrossRef] [PubMed]
- Goswami, M.; Kumar, R.; Sumpter, B.G.; Mays, J. Breakdown of Inverse Morphologies in Charged Diblock Copolymers. J. Phys. Chem. B 2011, 115, 3330–3338. [Google Scholar] [CrossRef] [Green Version]
- Gartner, T.E.; Jayaraman, A. Modeling and simulations of polymers: A roadmap. Macromolecules 2019, 52, 755–786. [Google Scholar] [CrossRef] [Green Version]
- Goswami, M.; Kumar, S.K.; Bhattacharya, A.; Douglas, J.F. Computer simulations of ionomer self-assembly and dynamics. Macromolecules 2007, 40, 4113–4118. [Google Scholar] [CrossRef]
- Sampath, J.; Hall, L.M. Impact of ionic aggregate structure on ionomer mechanical properties from coarse-grained molecular dynamics simulations. J. Chem. Phys. 2017, 147, 134901. [Google Scholar] [CrossRef]
- Sampath, J.; Hall, L. Effect of neutralization on the structure and dynamics of model ionomer melts. Macromolecules 2018, 51, 626–637. [Google Scholar] [CrossRef]
- He, X.; Leo, D.J.; Akle, B. Multi-scale modeling of ion transport in high-strain ionomers with conducting powder electrodes. J. Intell. Mater. Syst. Struct. 2014, 25, 1196–1210. [Google Scholar] [CrossRef]
- Xue, K.L.; Hu, Y.F.; Yu, X.C.; Hou, J.X. Simulation of diffusion motion of ionomers using Monte Carlo algorithm. Mod. Phys. Lett. B 2020, 34, 2050271. [Google Scholar] [CrossRef]
- Bollinger, J.A.; Stevens, M.J.; Frischknecht, A.L. Quantifying Single-Ion Transport in Percolated Ionic Aggregates of Polymer Melts. ACS Macro Lett. 2020, 9, 583–587. [Google Scholar] [CrossRef]
- Frischknecht, A.L.; Paren, B.A.; Middleton, L.R.; Koski, J.P.; Tarver, J.D.; Tyagi, M.; Soles, C.L.; Winey, K.I. Chain and Ion Dynamics in Precise Polyethylene Ionomers. Macromolecules 2019, 52, 7939–7950. [Google Scholar] [CrossRef]
- Bolintineanu, D.S.; Stevens, M.J.; Frischknecht, A.L. Atomistic simulations predict a surprising variety of morphologies in precise ionomers. ACS Macro Lett. 2013, 2, 206–210. [Google Scholar] [CrossRef]
- Allahyarov, E.; Taylor, P.L. Simulation study of the equilibrium morphology in ionomers with different architectures. J. Polym. Sci. B 2011, 49, 368–376. [Google Scholar] [CrossRef]
- Marx, C.L.; Caulfield, D.F.; Cooper, S.L. Morphology of ionomers. Macromolecules 1973, 6, 344–353. [Google Scholar] [CrossRef]
- Williams, C.E.; Russell, T.P.; Jerome, R.; Horrion, J. Ionic aggregation in model ionomers. Macromolecules 1986, 19, 2877–2884. [Google Scholar] [CrossRef]
- Schué, F. Introduction to ionomers. Polym. Int. 2000, 49, 235. [Google Scholar]
- Bolintineanu, D.S.; Stevens, M.J.; Frischknecht, A.L. Influence of cation type on ionic aggregates in precise ionomers. Macromolecules 2013, 46, 5381–5392. [Google Scholar] [CrossRef]
- Hall, L.M.; Seitz, M.E.; Winey, K.I.; Opper, K.L.; Wagener, K.B.; Stevens, M.J.; Frischknecht, A.L. Ionic aggregate structure in ionomer melts: Effect of molecular architecture on aggregates and the ionomer peak. J. Am. Chem. Soc. 2012, 134, 574–587. [Google Scholar] [CrossRef]
- Ma, B.; Nguyen, T.D.; Pryamitsyn, V.A.; de la Cruz, M.O. Ionic Correlations in Random Ionomers. ACS Nano 2018, 3, 2311. [Google Scholar] [CrossRef] [PubMed]
- Hall, L.M.; Stevens, M.J.; Frischknecht, A.L. Dynamics of model ionomer melts of various architectures. Macromolecules 2012, 45, 8097–8108. [Google Scholar] [CrossRef]
- Frischknecht, A.L.; Winey, K.I. The evolution of acidic and ionic aggregates in ionomers during microsecond simulations. J. Chem. Phys. 2019, 150, 064901. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Sauer, J.A.; Hara, M. Poly(methyl methacrylate) based ionomers. 1. Dynamic mechanical properties and morphology. Macromolecules 1995, 28, 3953–3962. [Google Scholar] [CrossRef]
- Makrodimitri, Z.A.; Dohrn, R.; Economou, I.G. Atomistic Simulation of Poly(dimethylsiloxane): Force Field Development, Structure, and Thermodynamic Properties of Polymer Melt and Solubility of n-Alkanes, n-Perfluoroalkanes, and Noble and Light Gases. Macromolecules 2007, 40, 1720–1729. [Google Scholar] [CrossRef]
- Saxena, V. Molecular dynamics simulation of interhalogen compounds using two potential models 2. Liquid bromine trifluoride (BrF3)—Structure and thermodynamics. Can. J. Chem. 1993, 71, 2189–2193. [Google Scholar] [CrossRef] [Green Version]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Novel configurational-bias Monte Carlo method for branched molecules. Transferable potentials for phase equilibria. 2. United-atom description of branched alkanes. J. Phys. Chem. B 1999, 103, 4508–4517. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Madura, J.D.; Swenson, C.J. Optimized intermolecular potential functions for liquid hydrocarbons. J. Am. Chem. Soc. 1984, 106, 6638–6646. [Google Scholar] [CrossRef]
- Chen, B.; Potoff, J.J.; Siepmann, J.I. Monte Carlo Calculations for Alcohols and Their Mixtures with Alkanes. Transferable Potentials for Phase Equilibria. 5. United-Atom Description of Primary, Secondary, and Tertiary Alcohols. J. Phys. Chem. B 2001, 105, 3093–3104. [Google Scholar] [CrossRef]
- Xing, K.; Chatterjee, S.; Saito, T.; Gainaru, C.; Sokolov, A.P. Impact of Hydrogen Bonding on Dynamics of Hydroxyl-Terminated Polydimethylsiloxane. Macromolecules 2016, 49, 3138–3147. [Google Scholar] [CrossRef]
- de Jonge, J.; van Zon, A.; de Leeuw, S. Molecular dynamics study of the influence of the polarizability in PEOx–NaI polymer electrolyte systems. Solid State Ionics 2002, 147, 349–359. [Google Scholar] [CrossRef]
- Mos, B.; Verkerk, P.; Pouget, S.; van Zon, A.; Bel, G.J.; de Leeuw, S.W.; Eisenbach, C.D. The dynamics in polyethyleneoxide–alkali iodide complexes investigated by neutron spin-echo spectroscopy and molecular dynamics simulations. J. Chem. Phys. 2000, 113, 4–7. [Google Scholar] [CrossRef] [Green Version]
- de Leeuw, S.; Van Zon, A.; Bel, G. Structural relaxation in poly(ethyleneoxide) and poly(ethyleneoxide)–sodium iodide systems: A molecular dynamics study. Electrochim. Acta 2001, 46, 1419–1426. [Google Scholar] [CrossRef]
- van Zon, A.; Mos, B.; Verkerk, P.; de Leeuw, S. On the dynamics of PEO–NaI polymer electrolytes. Electrochim. Acta 2001, 46, 1717–1721. [Google Scholar] [CrossRef]
- Lin, K.J.; Maranas, J.K. Cation coordination and motion in a poly(ethylene oxide)-based single ion conductor. Macromolecules 2012, 45, 6230–6240. [Google Scholar] [CrossRef]
- Lin, K.J.; Maranas, J.K. Superionic behavior in polyethylene-oxide–based single-ion conductors. Phys. Rev. E 2013, 88, 052602. [Google Scholar] [CrossRef]
- Chen, X.; Chen, F.; Liu, M.S.; Forsyth, M. Polymer architecture effect on sodium ion transport in PSTFSI-based ionomers: A molecular dynamics study. Solid State Ionics 2016, 288, 271–276. [Google Scholar] [CrossRef]
- Gudla, H.; Zhang, C.; Brandell, D. Effects of solvent polarity on Li-ion diffusion in polymer electrolytes: An all-atom molecular dynamics study with charge scaling. J. Phys. Chem. B 2020, 124, 8124–8131. [Google Scholar] [CrossRef]
- Fang, C.E.; Tsai, Y.C.; Scheurer, C.; Chiu, C.C. Revised atomic charges for OPLS force field model of poly(ethylene oxide): Benchmarks and applications in polymer electrolyte. Polymers 2021, 13, 1131. [Google Scholar] [CrossRef]
- Bekker, H.; Berendsen, H.J.C.; Dijkstra, E.J.; Achterop, S.; van Drunen, R.; van der Spoel, D.; Sijbers, A.; Keegstra, H.; Reitsma, B.; Renardus, M.K.R. Gromacs: A parallel computer for molecular dynamics simulations. Phys. Comput. 1993, 92, 252. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Karatrantos, A.; Khan, S.; Ohba, T.; Cai, Q. The effect of different organic solvents on sodium ion storage in carbon nanopores. Phys. Chem. Chem. Phys. 2018, 20, 6307–6315. [Google Scholar] [CrossRef]
- Hatlo, M.; Karatrantos, A.; Lue, L. One-component plasma of point charges and of charged rods. Phys. Rev. E 2009, 80, 061107. [Google Scholar] [CrossRef]
- Martinez, L.; Andrade, R.; Birgin, E.G.; Martinez, J.M. packmol: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- van der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, Flexible and Free. J. Comp. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- van der Spoel, D.; Lindahl, E.; Hess, B.; Buuren, A.R.; Apol, E.; Meulenhoff, P.J.; Tielemann, P.D.; Sijbers, A.L.T.M.; Feenstra, K.A.; van Drunen, R.; et al. Gromacs User Manual; Version 3.3; University of Groningen: Groningen, The Netherlands, 2005. [Google Scholar]
- Lindahl, E.; Hess, B.; van der Spoel, D. Gromacs 3.0: A package for molecular simulation and trajectory analysis. J. Mol. Mod. 2001, 7, 306–317. [Google Scholar] [CrossRef]
- Pfohl, O.; Riebesell, C.; Dohrn, R. Measurement and calculation of phase equilibria in the system n-pentane + poly(dimethylsiloxane) at 308.15–423.15 K. Fluid Phase Equil. 2002, 202, 289–306. [Google Scholar] [CrossRef]
- Shih, H.; Flory, P.J. Equation-of-State parameters for poly(dimethylsiloxane. Macromolecules 1972, 5, 758–761. [Google Scholar] [CrossRef]
- Fakhreddine, Y.A.; Zoller, P. The equation of state of a polydimethylsiloxane fluid. J. Appl. Polym. Sci. 1990, 41, 1087–1093. [Google Scholar] [CrossRef]
- Karatrantos, A.; Composto, R.J.; Winey, K.I.; Clarke, N. Primitive path network, structure and dynamics of SWCNT/polymer nanocomposites. IOP Conf. Ser. Mat. Sci. Eng. 2012, 40, 012027. [Google Scholar] [CrossRef] [Green Version]
- Moghimikheirabadi, A.; Kröger, M.; Karatrantos, A.V. Insights from modeling into structure, entanglements, and dynamics in attractive polymer nanocomposites. Soft Matter 2021, 17, 6362–6373. [Google Scholar] [CrossRef] [PubMed]
- Karatrantos, A.; Clarke, N.; Kröger, M. Modeling of polymer structure and conformations in polymer nanocomposites from atomistic to mesoscale: A Review. Polym. Rev. 2016, 56, 385–428. [Google Scholar] [CrossRef]
- Karatrantos, A.; Clarke, N.; Composto, R.J.; Winey, K.I. Structure, entanglements and dynamics of polymer nanocomposites containing spherical nanoparticles. IOP Conf. Ser. Mat. Sci. Eng. 2014, 64, 012041. [Google Scholar] [CrossRef]
- Karatrantos, A.; Composto, R.J.; Winey, K.I.; Kröger, M.; Clarke, N. Modeling of Entangled Polymer Diffusion in Melts and Nanocomposites: A Review. Polymers 2019, 11, 876. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karatrantos, A.V.; Ohba, T.; Cai, Q. Diffusion of ions and solvent in propylene carbonate solutions for lithium-ion battery applications. J. Mol. Liq. 2020, 320, 114351. [Google Scholar] [CrossRef]
- Diachun, N.A.; Marcus, A.H.; Hussey, D.M.; Fayer, M.D. Dynamics in polydimethylsiloxane: The effect of solute polarity. J. Am. Chem. Soc. 1994, 116, 1027–1032. [Google Scholar] [CrossRef]
- Dorgan, J.R.; Rorrer, N.A.; Maupin, C.M. Parameter Free Prediction of Rheological Properties of Homopolymer Melts by Dynamic Monte Carlo Simulation. Macromolecules 2012, 45, 8833–8840. [Google Scholar] [CrossRef]
- Gouverneur, M.; Kopp, J.; van Wüllen, L.; Schönhoff, M. Direct determination of ionic transference numbers in ionic liquids by electrophoretic NMR. Phys. Chem. Chem. Phys. 2015, 17, 30680–30686. [Google Scholar] [CrossRef] [Green Version]
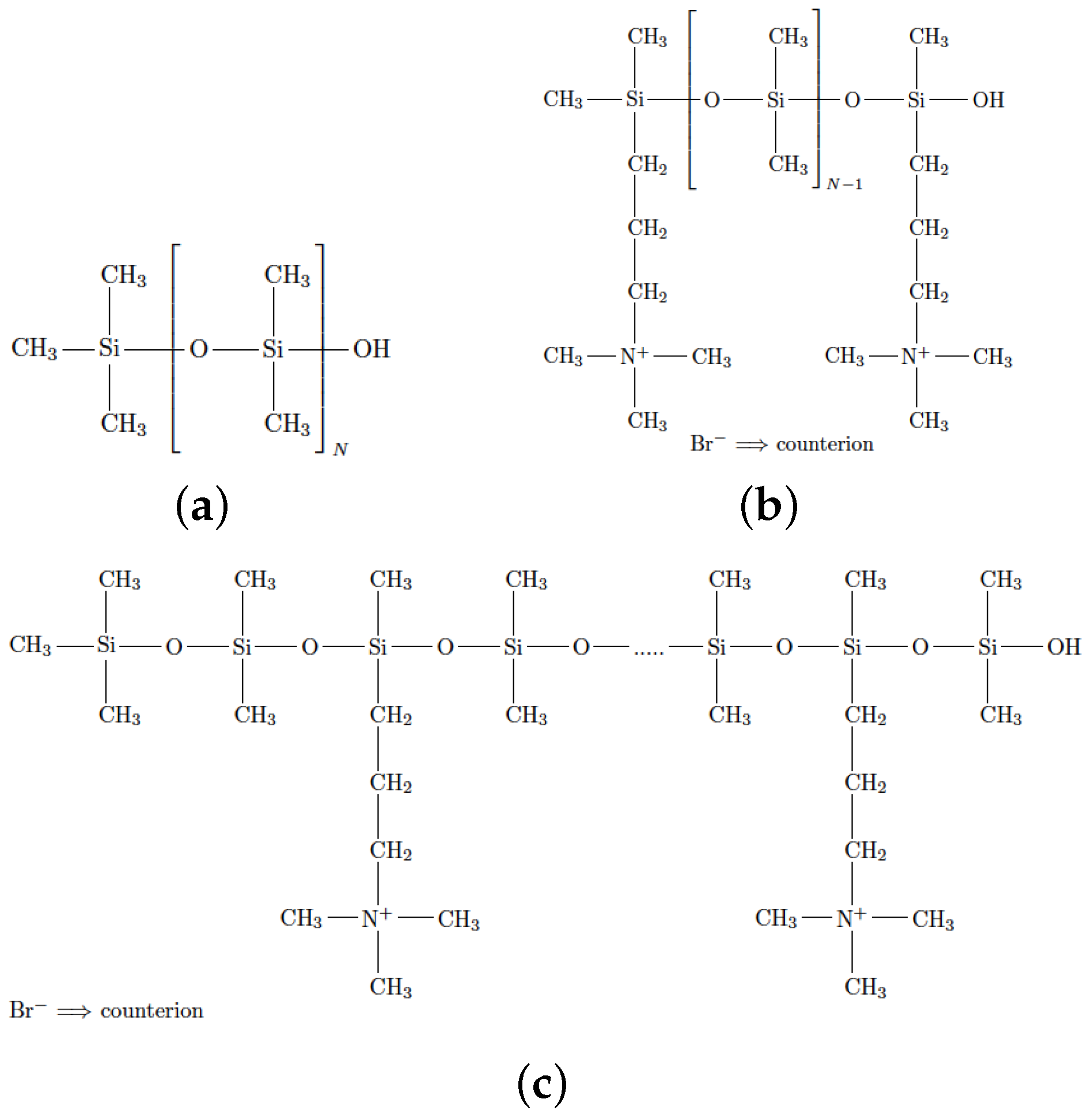

| System | f | N | Chains | Br Anions | Molecular Weight |
|---|---|---|---|---|---|
| neutral | 40 | 128 | - | 3055 g/mol | |
| 80 | 128 | - | 6095 g/mol | ||
| end-functionalized | 40 | 128 | 256 | 3277 g/mol | |
| 80 | 128 | 256 | 6268 g/mol | ||
| randomly functionalized | 40 | 128 | 512 | 3474 g/mol | |
| 80 | 128 | 1024 | 6782 g/mol | ||
| 40 | 128 | 256 | 3314 g/mol | ||
| 80 | 128 | 256 | 6256 g/mol |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karatrantos, A.V.; Khantaveramongkol, J.; Kröger, M. Structure and Diffusion of Ionic PDMS Melts. Polymers 2022, 14, 3070. https://doi.org/10.3390/polym14153070
Karatrantos AV, Khantaveramongkol J, Kröger M. Structure and Diffusion of Ionic PDMS Melts. Polymers. 2022; 14(15):3070. https://doi.org/10.3390/polym14153070
Chicago/Turabian StyleKaratrantos, Argyrios V., Jettawat Khantaveramongkol, and Martin Kröger. 2022. "Structure and Diffusion of Ionic PDMS Melts" Polymers 14, no. 15: 3070. https://doi.org/10.3390/polym14153070
APA StyleKaratrantos, A. V., Khantaveramongkol, J., & Kröger, M. (2022). Structure and Diffusion of Ionic PDMS Melts. Polymers, 14(15), 3070. https://doi.org/10.3390/polym14153070