3.1. Disappearance of the Crystal Memory during Retention in the Melt
First, we aimed to clarify the origin of the melt memory by directly observing the structure of the melt, which was generated by constant heating of the stacked lamellae.
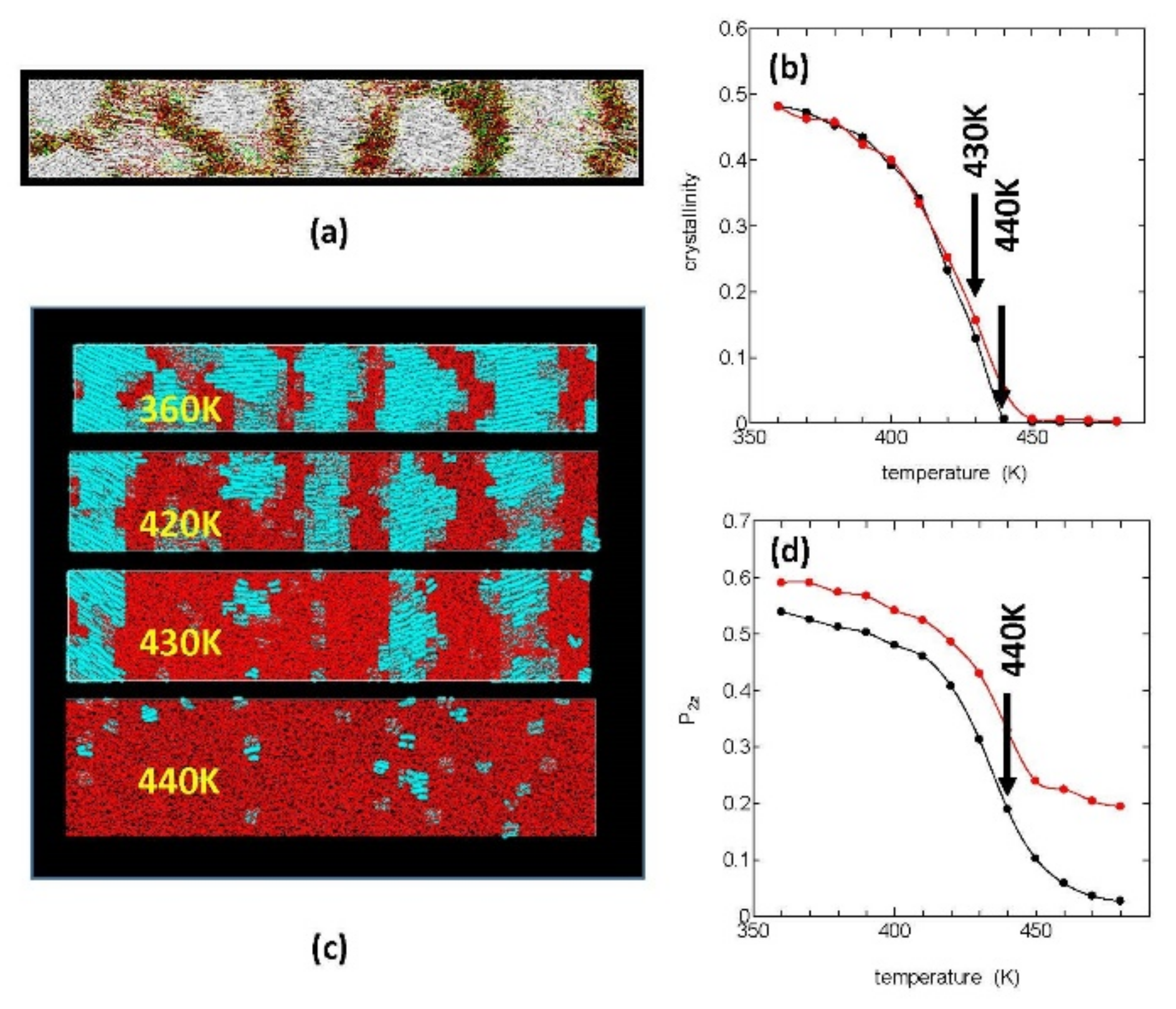
Figure 1a shows our starting crystalline structure, which was obtained in our previous MD simulation of fiber formation from the stretched PE melt [
12]. In the figure, the white areas are crystalline regions where the polymer chains are oriented in the
Z-axis direction of stretching (horizontal), and the inter-crystalline regions are filled with folds or loops (yellow), ties or bridges (red), and cilia or tails (green).
This starting crystalline system was melted by a constant heating (10 K/ns), and the melting process was investigated. In order to quantitatively evaluate the melting process, we used the crystallinity
.
Figure 1b shows the temperature changes in
during heating both under stress free condition (
) = (0, 0, 0) (black) and that under constant tension condition (
) = (0, 0, 1) (red); in both cases, the crystals were found to be completely melted around 440 K irrespective of the stress condition; by much slower heating; however, the equilibrium melting temperature (
was estimated to be between 420 and 430 K.
In
Figure 1d, we show the decrease in the order pa rameters
for the chord vectors {
} during the constant heating; the order parameters
show rapid decreases around the melting temperature, similar to the crystallinity; however, they remain finite even around 440 K where the crystallinity disappears completely.
Figure 1c is the molecular graphics of the crystallites during melting under tension free condition; the crystalline regions are here painted in blue and the amorphous regions in red, where the melting begins around 400 K with the lamella crystals gradually becoming thinner by surface melting and the crystal edges (the side surfaces of the lamellae) receding.
An essential question in the melt memory effect is how long the melt memory remains. The time period that the melt memory remains will largely depend on the holding temperature
(strictly speaking, the superheating
=
−
> 0); however, here, we only consider the case
= 440 K (
10 K).
Figure 2a shows the changes with time in the snapshots of the melt when held at 440 K under stress free condition. The small blue dots represent are the residual small crystalline areas or embryos, which gradually decrease with time. The system shows large shortening in the
Z-axis direction during retention in the melt suggesting that the initial stretched molecules in the melt are gradually relaxing and shortening in the
Z-axis direction.
Figure 2b is the orientational order
, both of the chord vectors (black dots) and of the end-to-end vectors (red dots), which show the marked loss of the melt memory during the time
held at 440 K. Both order parameters significantly reduced within a few nanoseconds, which may be related to the Rouse time
for the highly stretched polyethylene of length 500 carbons; of special interest is that the decrease of
defined from the chord vectors shows clear exponential decrease as indicated in the red circles in
Figure 2c. We also studied the changes in the radius of gyration
of the chains (
Figure 2d); the molecules initially highly stretched along the
Z-axis rapidly shrink and relax to an almost equilibrated random coil state in around 10 ns.
In addition to these and , we also studied the behavior of other order parameters, such as the trans sequence lengths and their distribution , the averaged persistence length , as well as the degree of shrinkage of the radius of gyration ( where is the radius only at the start of holding at 440 K. All these parameters for the melt state showed clear relaxation toward the equilibrium within a few nanoseconds, and they appear to have close correlations with .
The local orientation order
of the chord vectors was shown to be a main origin of the accelerated crystal nucleation under flow [
17] as will be also described in the following sections. However, the molecular mechanism of such local order in the melt dominating the nucleation or/and interfacial processes at the nucleus melt interfaces remains a mystery; the real molecular mechanism of the rapid nucleation is not easy to confirm.
Extensive research has long been done on the polymer entanglements in the melt especially focusing on rheological problems, where the number of entanglements Z per chain and the segment lengths between the adjacent entanglements are discussed. We investigated the number of entanglements Z in the melt and their possible roles in the process crystallization by using the Z1-code proposed by Kröger [
16].
Figure 3 shows the relation between the number of entanglements per chain Z and the retention time
in the melt held at 440 K.
The tendency for the number Z to slightly increase with is noticeable, which could be due to the re-entanglement of the partially disentangled melt in the initial drawn melt. However, the increase in the entanglement number Z appears to be too small to explain the remarkable changes in the crystallization rate with which will be described later; the effect of chain entanglements on crystallization does not appear to be important in the melt memory effects that we are considering here.
3.2. Crystalline Memory in the Melt and the Recrystallization Rate
The ample memory is confirmed to remain in the melt. Then, the way it affects recrystallization is the next important question.
Figure 4a shows the time dependences of the degree of crystallinity
during the early nucleation stages; the system was rapidly cooled to the crystallization temperature (350 K) from the melt, which was held for various times
at 440 K. The early stage crystallization, or the nucleation rate, is shown to depend sensitively on the retention time
at 440 K.
Figure 4b shows the evaluated initial slopes of
Figure 4a vs. the local bond orientation order
given in
Figure 2b, where we can find a clear correlation between the logarithm of the obtained nucleation rate and the bond orientation order
in the melt. This result nicely corresponds to a recent MD study showing the definite correlation between the nucleation rate
I and the degree of chain elongation in the melt
, where
was shown to be proportional to the local orientation order parameter
[
17].
We then considered the later stages of the crystal growth.
Figure 5a shows the crystallinity vs. crystallization time over several hundred of nanoseconds. The figure clearly shows that the crystallization is rapid when sufficient melt memory is retained in the case
, while it becomes significantly slower for
and actually becomes invisible when
is
. The changes in the melt structure causing such a large reduction in crystallization rate is very interesting.
Figure 5b is a log–log plot of the same crystallinity data, a so-called Avrami plot.
The crystallinity
is generally expressed as a function of crystallization time
t as
, and it reduces to a simple power law
unless the growing crystals severely overlap; the log–log plot then becomes a straight line, and its slope
n, called the Avrami exponent, represents the spatial form of the growing crystals and the birth rate of the nucleus.
Figure 5b clearly shows that the exponent
n is about 1 when the memory remains strong (
; however, the value of
n increases from 2 to 3 as the memory is being lost (
= 2~4 ns). This indicates that, as the melt memory is being lost, the mode of crystal growth relaxes to the normal three-dimensional case; here, we assumed that there are nearly constant number of embryos and neglect the time dependence of their numbers.
3.3. The Melt Memory and the Morphology Development in Recrystallization
The variation of the Avrami exponent
n with increasing retention time
in
Figure 5b suggests the change in the shape of the growing crystals by the relaxation of the melt structure with time
held in the melt. We show, in
Figure 6, the shapes of growing crystals using the molecular graphics images. Through the growth modes, the dimensionality of the crystals, are not readily noticed from the figures, the fast growing crystals for
with
n = 1 (
Figure 6a) can be seen growing predominantly in one dimension along the crystal thickness direction, while those for
= 2 and 3 ns with the exponent
n~2 (
Figure 6b,c) indicate the dominance of the lateral growth along the X–Y directions representing the usual mode of growth in the chain-folded lamellae.
The last case of the slowest possible growth
= 4 with the index n~3 (
Figure 6d) is predominantly 3D growth of the crystal; such a peculiar 3D growth mode for the chain folded crystal was already noticed in our previous MD simulation [
12] where the usual lateral growth proceeds simultaneously with crystal thickening as least for the early stage growth before inter-lamellar collisions. In addition to the changes in the 3D shape of the growing crystals, we also noticed considerable tilt of the crystalline chains.
The snapshots given in the lowest row of
Figure 6 show the final crystalline texture obtained after sufficient time of crystallization, where we notice prominent morphological changes in the texture and the orientations of the crystalline chains; the crystalline chains highly oriented along the
Z-axis (the direction of the initial elongation) gradually lose their original preference and begin to show considerable chain tilting from the
Z-axis.
Such large changes in the crystalline texture are expected to give distinct mechanical response to the elongation.
Figure 7 shows the
Z-axis elongation for the two representative textures (upper) and their mechanical properties (lower); the two textures (a) and (b) correspond to the state A and the state B defined in
Figure 5a for the retention times of
= 1 and 4 ns. The degree of uniaxial deformation along the
Z-axis (horizontal) is represented as the ratio of the length
against its original length
. In the state A (
Figure 7a), the crystals form the stacked lamellae and the molecules in the crystals retain dominant
Z-axis orientation reflecting the strong Z-orientation remaining in the melt.
On the other hand, in state B (
Figure 7c), the 3D shapes of the crystals are nearly elongated ellipsoids, and the orientations of the crystalline chains show great deviation from the
Z-axis, which corresponds to the considerable loss of the melt memory. Our preliminary studies of the stress–strain relations for the well-developed crystalline textures shows that the highly oriented crystalline structure recrystallized under strong memory gives clear cavities in the amorphous regions (
Figure 7a), which is likely due to the strong lateral constraint, leading to the brittle fracture and rapid stress drop (
Figure 7b).
On the other hand, the well-crystallized sample from the largely relaxed melt shows the crystalline texture with largely tilted chains, whose
Z-axis elongation induced considerable crystal slip and molecular reorientation leading to the nearly constant volume deformation (
Figure 7c) and the stress–strain curve showing plastic flow (
Figure 7d). The relaxation of the flow memory and of the chain orientations are suggested to give reduced crystal orientations along the
Z-axis, resulting in the facile plastic deformation; this can be a mechanism by which the sample comes to have high toughness, the details of which processes will be discussed in the following section.
3.4. Lamella Morphology and the Mechanism of Large Deformation
In the previous discussions, the varied degree of melt memory with time in the melt resulted in remarkable alteration in the mode of recrystallization, and in the crystal morphology and mechanical property. The molecular mechanism of deformation is expected to offer reasonable explanations for the improved mechanical properties of the materials crystallized from the relaxed melt. However, the relationship between the crystalline texture and their mechanical properties, such as the stress–strain relationship or fracture under large deformation, is a very difficult task to clarify due to the large complexity of the lamellar structure of crystalline polymers.
Figure 8a is a simple picture of a spherulite and the possible modes of deformation. Crystalline lamellae in the spherulite are extending radially from the spherulite center and aggregating to fill the whole spherical region. Uniaxial elongation of the spherulite along a direction (vertical in
Figure 8a) gives distinct deformation for the lamellae depending on their orientation against the draw direction. Very long polymer chains connecting the crystal regions give many complicating factors for the deformation.
We here consider the two limiting types of the deformation of lamellar crystals, one along the crystal chain axis (type P in
Figure 8c) Pand the other transverse to the chain axis (type T in
Figure 8b). Since the crystalline chains are arranged nearly perpendicular to the lamella plane, the mechanical properties of the crystals are extremely anisotropic, and therefore the polymer crystal deforms in completely different ways for these two types of deformation. We consider sufficiently large crystals made of 150,000 united atoms, where the fully crystalline states are generated in the same way as we used in our previous work [
12].
In the following subsections, we investigate the large deformation of the two type, where the deformation was constant rate elongation of the true strain rate (the Hencky-strain rate) of 0.05/ns; .
3.4.1. Uniaxial Elongation Parallel to the Chain-Axis (TYPE P Elongation)
Let us first consider the uniaxial deformation along the crystal chain axis as shown in
Figure 8c. The stacked lamellar crystals are dawn parallel to the chain axis perpendicular to the lamellar plane (
Figure 9a), where the relatively small macroscopic deformation is found to give rise to the formation of cavities in the amorphous regions. With progressive deformation, the cavity grows in size and extends in the chain axis (
Z-axis) direction. We also notice the formation of fibrils extending along the
Z-axis on both sides of the cavity.
Such a structure, consisting of cavities and neighboring fibrils, resembles that of the craze observed in the brittle fracture of amorphous polymers. When a cavity starts growing from one place, the macroscopic deformation is mainly due to the cavity with the deformation in other amorphous regions being small. The stress–strain curve in this case gives only small elongation before a sudden brittle fracture by the elongation of about 5% (
Figure 9b). One of our concern in this mode of deformation is on the structural changes in the amorphous phase.
Figure 9c,d show the molecular level details in the vicinity of the cavity, particularly focusing on the structures of folds and ties.
Within an amorphous layer, the folds that are rooted on the opposite lamellar surfaces generally do not form the so-called trapped entanglements; this is readily noticed from
Figure 9c where many folds around the cavity are seen to be well-separated.
This finding may appear somewhat strange and against previous simulation reports [
18]. However, considering the initial highly stretched melt conformations and the following crystallization by reeling in the chain tails to the crystalline regions [
12], there may not ample opportunity to form trapped entanglements between the neighboring lamellae; in fact, the entanglement analysis between the folds using the Z1 analysis gave only 10% of entanglements per fold (one entanglement per ten folds). In a similar way,
Figure 9d shows that the tie molecules seem to be pushed aside by the cavity and many of the tie molecules finally form fibrils connecting the adjacent lamellae; the abundant fibrils can serve as the residual stress transmitting components after the brittle fracture.
3.4.2. Uniaxial Elongation Transverse to the Chain Axis (Type T Elongation)
In the transverse drawing perpendicular to the chain axis (
Figure 8b), the crystalline chains initially oriented along the
Z-axis accomplish large-scale reorientation of about 90° toward the
X-axis direction [
8].
Figure 10 shows the typical molecular processes of the large deformation and reorientation.
In the early stage of deformation, we first notice the large reorientation of the crystalline chains toward the X-axis, which inevitably leads to the thinning of the lamellae along the Z-axis. The crystallites with largely tilted chains give rise to facile shear deformation by significant crystalline chain slips; the macroscopic deformation is nearly constant volume process without cavitation. The chain reorientation and crystal reorganization, which is often called “crystal breaking” or “mechanical melting”, is particularly conspicuous until 30 ns, after which many fibrils grow along the X-axis.
We here investigate the molecular processes of the transverse elongation by using various physical parameters: the level of stress, the volume of the MD cell, the crystallinity, and the degree of chain reorientations both in the crystalline and in the amorphous regions (
Figure 11). In the very early stage up to 10 ns where the Hencky strain is less than 0.5, the system shows soft elasticity and yield process.
This is then followed by an elongation under nearly constant stress level up to around 30 ns (
~1.5) (
Figure 11a), during which, the volume of the system shows slight increase suggesting the birth of small cavity-like regions (
Figure 11b); also noticed is the decrease in the crystallinity usually referred to as the “crystal breaking” or the “mechanical melting”(
Figure 11c). This stage is considered as the crystal deformation with simultaneous crystal breaking and chain reorientation, where the original stacked lamella structure is greatly perturbed.
The degree of chain reorientation during this stage is clearly seen in
Figure 11d, where it is noticed that the chain orientation along the
X-axis and that along the
Z-axis nearly replace giving complete (90 deg.) conversion of the crystal orientations.
The crystalline regions show more marked reorientation than the amorphous regions; the amorphous chains may be forced to reorient driven by the large crystal reorientation by the chain slips. After these large-scale reorientation and crystal reorganization, there follows the strain-hardening process between 30 ns < t < 60 ns (1.5 <
<3) as observed in
Figure 11a, where the crystallinity nearly recovers (
Figure 11c). The chain orientations gradually improve further (
Figure 11d) until the whole system attains the final fiber structure fully reoriented to the
X-axis direction (
Figure 11d).