Comparison and Optimization: Research on the Structure of the PET Bottle Bottom Based on the Finite Element Method
Abstract
:1. Introduction
2. Principle and Experiment
2.1. Computer-Aided Modeling of Bottle Bottom Structure
2.2. Selections of Material and Finite Element Mesh
2.3. Pressure Setting
2.4. Constraint Conditions
2.4.1. Fixed Edge
2.4.2. Free Shape Domain
2.4.3. Free Shape Boundary
2.5. Steady State Solver
2.6. Optimizations of Models
3. Results and Discussion
3.1. Results of Computer-Aided Modeling
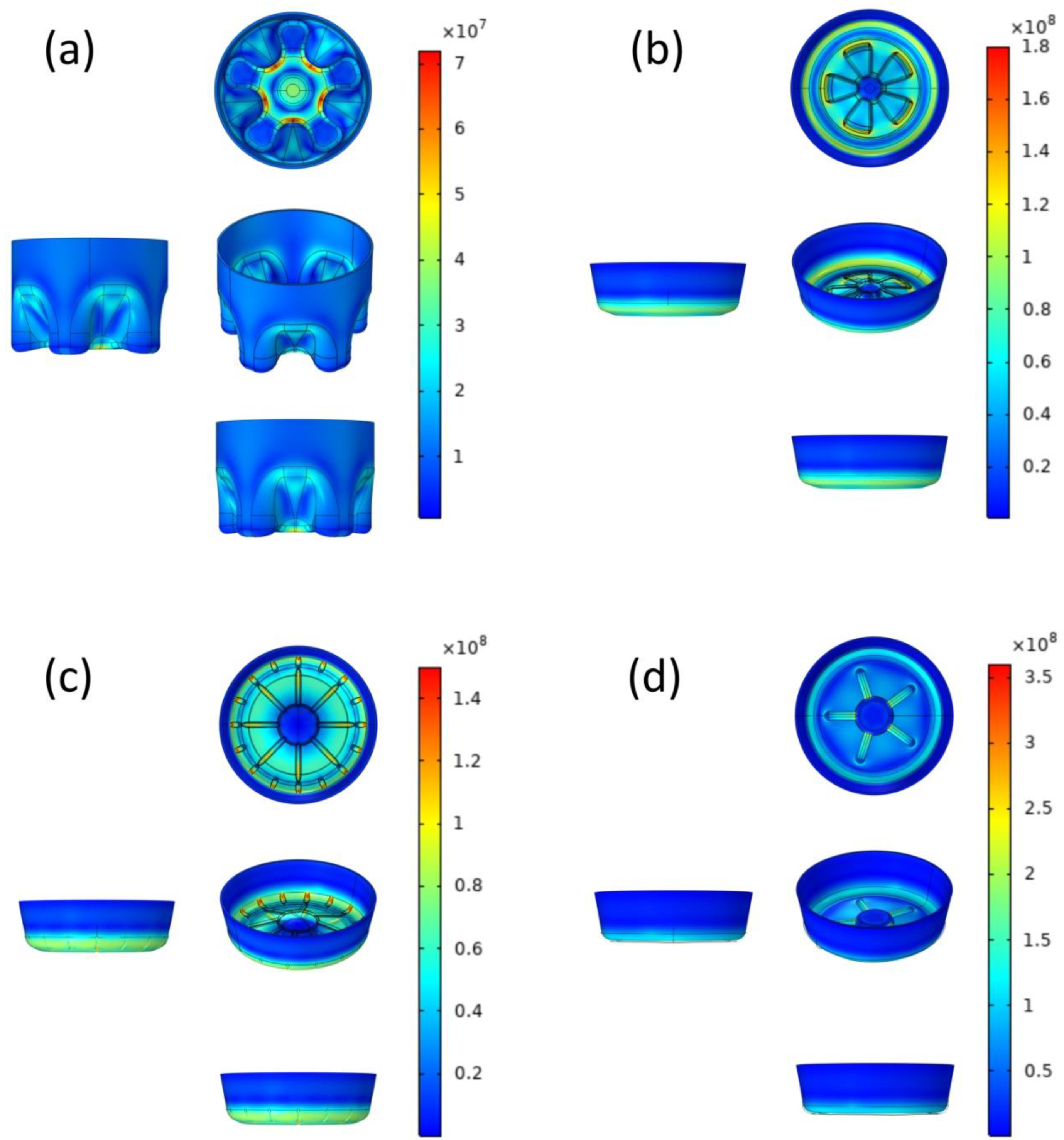
3.2. Results of von Mises Stress Surface Distribution
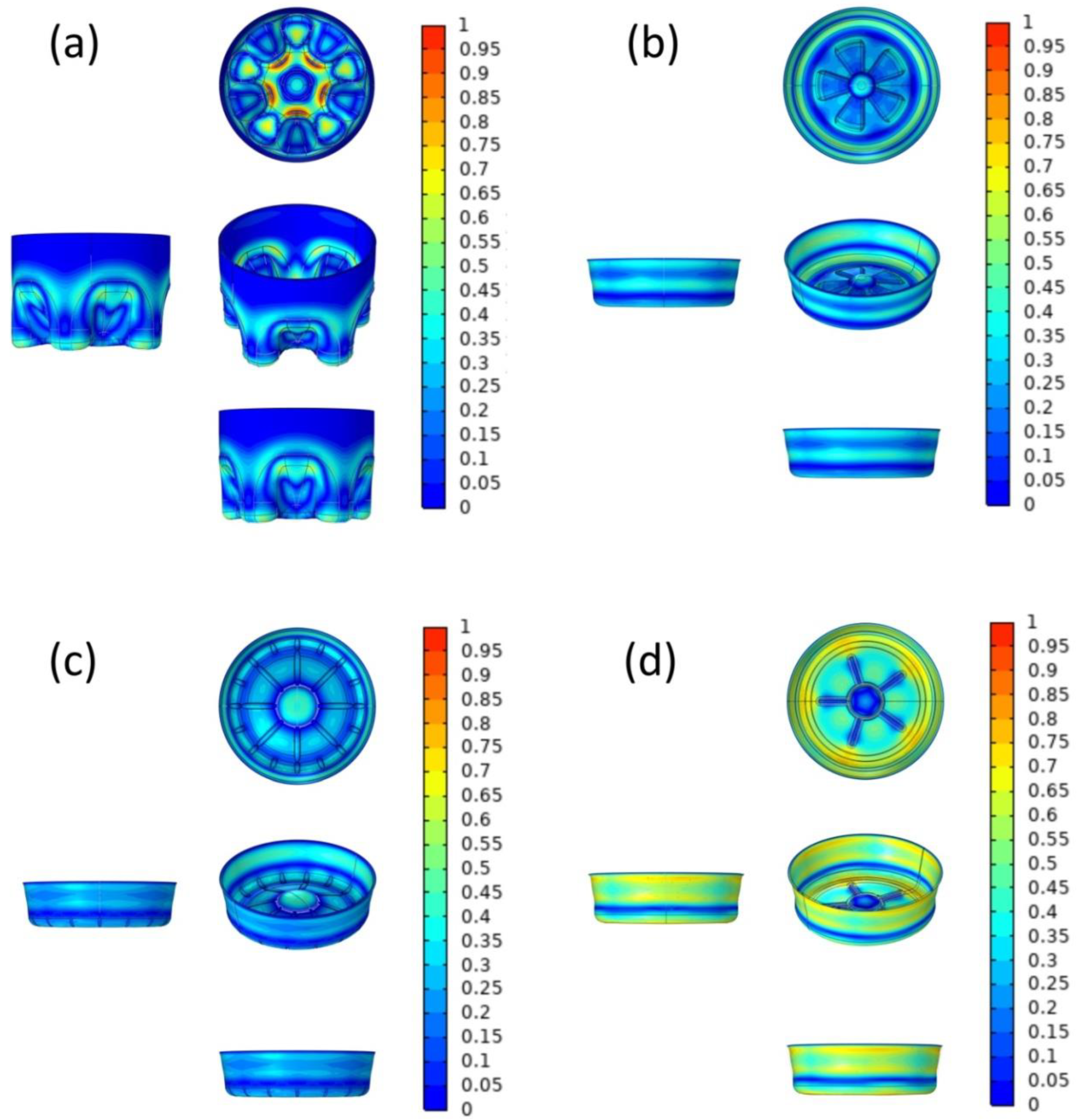
3.3. Optimization Results
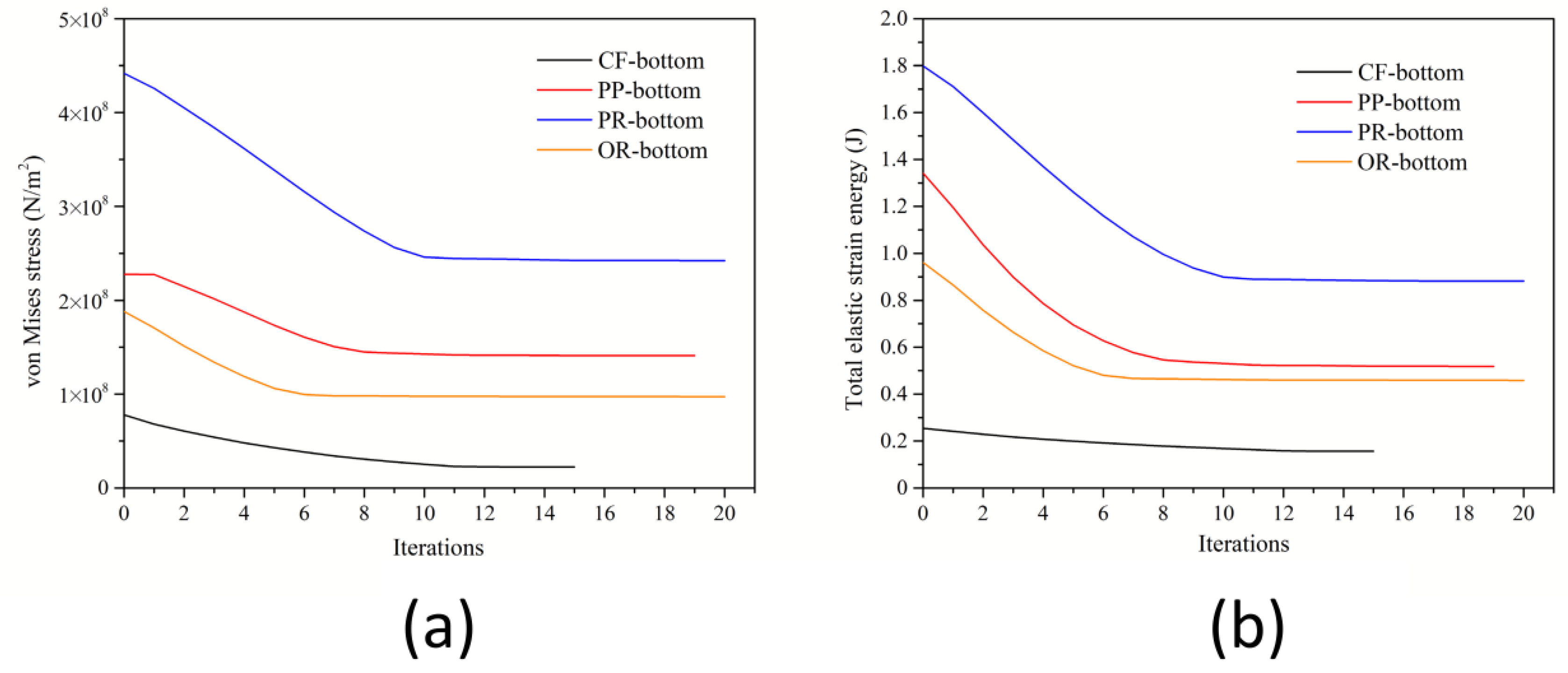
3.3.1. Reduction of Overall von Mises Stress and Total Elastic Strain Energy
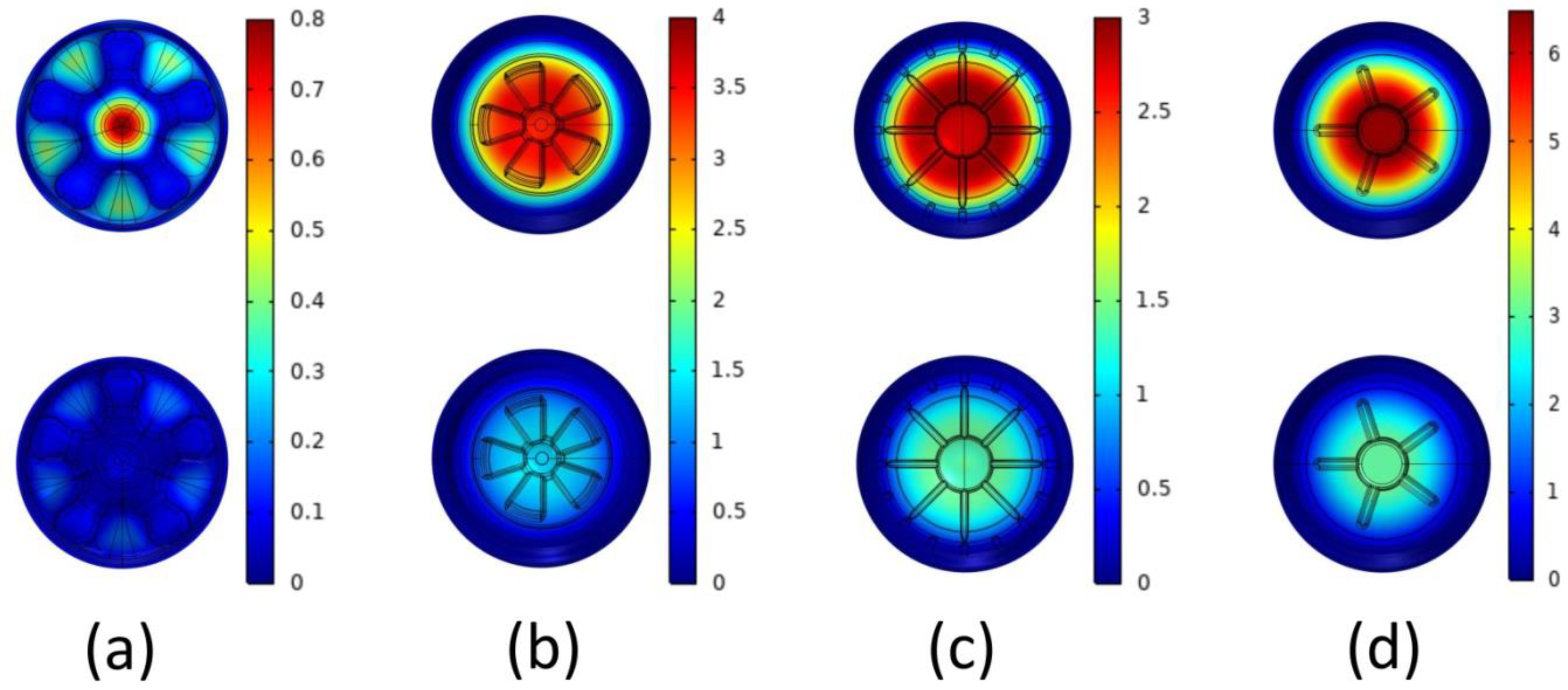
3.3.2. Comparison of Material Deformation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ihm, D.W.; Park, S.Y.; Chang, C.G.; Kim, Y.S.; Lee, H.K. Miscibility of poly (ethylene terephthalate)/poly (ethylene 2, 6-naphthalate) blends by transesterification. J. Polym. Sci. Part A Polym. Chem. 1996, 34, 2841–2850. [Google Scholar] [CrossRef]
- Avramova, N. Amorphous poly(ethylene terephthalate)/poly(butylene terephthalate) blends: Miscibility and properties. Polymer 1995, 36, 801–808. [Google Scholar] [CrossRef]
- Fakirov, S. Fundamentals of Polymer Science for Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar] [CrossRef]
- Schmidt, P.G. Polyethylene terephthalate structural studies. J. Polym. Sci. Part A Gen. Pap. 1963, 1, 1271–1292. [Google Scholar] [CrossRef]
- Beck, M.H.; Rollend, G.F.; Muszynski, J.H. Self-Standing Polyester Containers for Carbonated Beverages. U.S. Patent US5484072 A, 16 January 1996. [Google Scholar]
- Karalekas, D.; Rapti, D.; Papakaliatakis, G.; Tsartolia, E. Numerical and experimental investigation of the deformational behaviour of plastic containers. Packag. Technol. Sci. 2001, 14, 185–191. [Google Scholar] [CrossRef]
- Cho, S.H.; Hong, J.S.; Lyu, M.Y. Investigation of the Molding Conditions to Minimize Residual Stress and Shrinkage in Injection Molded Preform of PET Bottle. Polym. Korea 2011, 35, 467–471. [Google Scholar] [CrossRef]
- Wang, S.; Makinouchi, A.; Okamoto, M.; Kotaka, T.; Maeshima, M.; Ibe, N.; Nakagawa, T. Viscoplastic Material Modeling for the Stretch Blow Molding Simulation. Int. Polym. Process. 2000, 15, 166–175. [Google Scholar] [CrossRef]
- Moskala, E.J. A fracture mechanics approach to environmental stress cracking in poly(ethyleneterephthalate). Polymer 1998, 39, 675–680. [Google Scholar] [CrossRef]
- Ashford, E.; Bachmann, M.A.; Jones, D.; MacKerron, D.H. The prediction of orientation and crystallinity in drawn poly(ethylene terephthalate). Chem. Eng. Res. Des. 2000, 78, 33–38. [Google Scholar] [CrossRef]
- Lu, W.; Debelak, K.A.; Witt, A.R.; Yang, C.; Collins, W.E.; Lott, C. Structural features of crystallized poly(ethylene terephthalate) polymers. J. Polym. Sci. Part B Polym. Phys. 2001, 40, 245–254. [Google Scholar] [CrossRef]
- Siegmann, A.; Harget, P.J. Melting and crystallization of poly(ethylene terephthalate) under pressure. J. Polym. Sci. Polym. Phys. Ed. 1980, 18, 2181–2196. [Google Scholar] [CrossRef]
- Hanley, T.; Sutton, D.; Cookson, D.; Kosior, E.; Knott, R. Molecular morphology of petaloid bases of PET bottles: A small-angle X-ray scattering study. J. Appl. Polym. Sci. 2006, 99, 3328–3335. [Google Scholar] [CrossRef]
- Liu, R.Y.F.; Hu, Y.S.; Schiraldi, D.A.; Hiltner, A.; Baer, E. Crystallinity and oxygen transport properties of PET bottle walls. J. Appl. Polym. Sci. 2004, 94, 671–677. [Google Scholar] [CrossRef]
- Li, Y.; Zhen-Duo, W.; Shou-Ye, Z.; Li-Zhen, Y.; Qiang, C. The influence of the structures and compounds of DLC coatings on the barrier properties of PET bottles. Chin. Phys. B 2009, 18, 5401–5405. [Google Scholar] [CrossRef]
- Mehta, A.; Gaur, U.; Wunderlich, B. Equilibrium melting parameters of poly(ethylene terephthalate). J. Polym. Sci. Polym. Phys. Ed. 1978, 16, 289–296. [Google Scholar] [CrossRef]
- Wang, H.T.; Pan, B.R.; Du, Q.G.; Li, Y.Q. The strain in the test environmental stress cracking of plastics. Polym. Test. 2003, 22, 125–128. [Google Scholar] [CrossRef]
- Khan, S.U.; Ayub, T. Flexure and shear behaviour of self-compacting reinforced concrete beams with polyethylene terephthalate fibres and strips. Structures 2020, 25, 200–211. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some Forms of the Strain Energy Function for Rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Mooney, M. A Theory of Large Elastic Deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large elastic deformations of isotropic materials IV. Further developments of the general theory. Philos. Trans. R. Soc. A 1948, 241, 379–397. [Google Scholar] [CrossRef]
- Winslow, A.M. Magnetic Field Calculations in an Irregular Triangle Mesh; Lawrence Radiation Laboratory, University of California: Livermore, CA, USA, 1965. [Google Scholar] [CrossRef] [Green Version]
- Ogden, R.W. Nearly isochoric elastic deformations: Application to rubberlike solids. J. Mech. Phys. Solids 1978, 26, 37–57. [Google Scholar] [CrossRef]
- Yang, Z.J.; Harkin-Jones, E.; Menary, G.H.; Armstrong, C.G. A non-isothermal finite element model for injection stretch-blow molding of PET bottles with parametric studies. Polym. Eng. Sci. 2004, 44, 1379–1390. [Google Scholar] [CrossRef]
- Eringen, A.C.; Kim, B.S. Stress concentration at the tip of crack. Mech. Res. Commun. 1974, 1, 233–237. [Google Scholar] [CrossRef]
- Svanberg, K. The method of moving asymptotes—A new method for structural optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Svanberg, K. MMA and GCMMA–Fortran Versions March 2013; KTH, Royal Institute of Technology: Stockholm, Sweden, 2013; pp. 1–23. [Google Scholar]
- Zhou, X.; He, R.; Zhou, T.; Liu, Z. Crack Propagation on the Surface of the Bottleneck of a Pressure Vessel Considering the Initial Crack Angle. Appl. Sci. 2022, 12, 3913. [Google Scholar] [CrossRef]
- Yin, Z.; Su, T.; He, M. Gas Packaging Container Based on ANSYS Finite Element Analysis and Structural Optimization Design. J. Phys. Conf. Ser. 2019, 1187, 032089. [Google Scholar] [CrossRef]
- Lyu, M.-Y.; Pae, Y. Bottom design of carbonated soft drink poly(ethylene terephthalate) bottle to prevent solvent cracking. J. Appl. Polym. Sci. 2003, 88, 1145–1152. [Google Scholar] [CrossRef]
- Demirel, B.; Daver, F. The effects on the properties of PET bottles of changes to bottle-base geometry. J. Appl. Polym. Sci. 2009, 114, 3811–3818. [Google Scholar] [CrossRef]
- Dekkers, M.E.J.; Heikens, D. Crazing and shear deformation in glass bead-filled glassy polymers. J. Mater. Sci. 1985, 20, 3873–3880. [Google Scholar] [CrossRef] [Green Version]
- Lyu, M.-Y.; Kim, Y.H. Investigation of Design Parameters and Novel Design of Petaloid PET Bottles. Int. Polym. Process. 2002, 17, 279–283. [Google Scholar] [CrossRef]
- Donald, A.M.; Kramer, E.J. The competition between shear deformation and crazing in glassy polymers. J. Mater. Sci. 1982, 17, 1871–1879. [Google Scholar] [CrossRef]
- Zimmer, J.; Detrois, C.; Stommel, M. Evaluation method for stretch blow moulding simulations with process-oriented experiments. Key Eng. Mater. 2013, 554, 1658–1668. [Google Scholar] [CrossRef]
- Haddad, H.; Masood, S.; Erbulut, D.U. A study of blow moulding simulation and structural analysis for PET bottles. Aust. J. Mech. Eng. 2009, 7, 69–76. [Google Scholar] [CrossRef]
- Demirel, B.; Daver, F. Effects of preform deformation behavior on the properties of the poly(ethylene terephthalate) bottles. J. Appl. Polym. Sci. 2012, 126, 1300–1306. [Google Scholar] [CrossRef]

| Names of Beverages | Names of Models |
|---|---|
| Cola (carbonated beverage) | Claw flap bottle bottom (CF-bottom) |
| Iced tea (black tea beverage) | Pentagonal petal bottle bottom (PP-bottom) |
| Pure water (pure water) | Pentagonal radial bottle bottom (PR-bottom) |
| Natural Water (natural water) | Octagonal radial bottle bottom (OR-bottom) |
| Characteristics | Value |
|---|---|
| Density | 1190 kg m−3 |
| Young’s Modulus | 3200 MPa |
| Poisson’s Ratio | 0.35 |
| Thermal Expansion Coefficient | 7 × 10−5 K−1 |
| Intrinsic Viscosity | 0.83 dL g−1 |
| Minimum Burst Strength Requirement | 7 bar |
| Names of Models | Number of Meshes |
|---|---|
| CF-bottom | 30,137 |
| PP-bottom | 22,248 |
| PR-bottom | 126,324 |
| OR-bottom | 88,726 |
| Names of Models | Before Optimization Pa | After Optimization Pa | Decrement % |
|---|---|---|---|
| CF-bottom | 7.79 × 107 | 2.22 × 107 | 71.50% |
| PP-bottom | 2.28 × 108 | 1.41 × 108 | 38.16% |
| PR-bottom | 4.42 × 108 | 2.42 × 108 | 45.25% |
| OR-bottom | 1.88 × 108 | 9.74 × 107 | 48.19% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge-Zhang, S.; Song, M.; Huang, Z.; Li, M.; Mu, L. Comparison and Optimization: Research on the Structure of the PET Bottle Bottom Based on the Finite Element Method. Polymers 2022, 14, 3174. https://doi.org/10.3390/polym14153174
Ge-Zhang S, Song M, Huang Z, Li M, Mu L. Comparison and Optimization: Research on the Structure of the PET Bottle Bottom Based on the Finite Element Method. Polymers. 2022; 14(15):3174. https://doi.org/10.3390/polym14153174
Chicago/Turabian StyleGe-Zhang, Shangjie, Mingbo Song, Zehang Huang, Maodan Li, and Liqiang Mu. 2022. "Comparison and Optimization: Research on the Structure of the PET Bottle Bottom Based on the Finite Element Method" Polymers 14, no. 15: 3174. https://doi.org/10.3390/polym14153174
APA StyleGe-Zhang, S., Song, M., Huang, Z., Li, M., & Mu, L. (2022). Comparison and Optimization: Research on the Structure of the PET Bottle Bottom Based on the Finite Element Method. Polymers, 14(15), 3174. https://doi.org/10.3390/polym14153174






