A Simple Stochastic Reaction Model for Heterogeneous Polymerizations
Abstract
:1. Introduction
2. Models and Simulation Methods
2.1. Lattice Monte Carlo Simulation
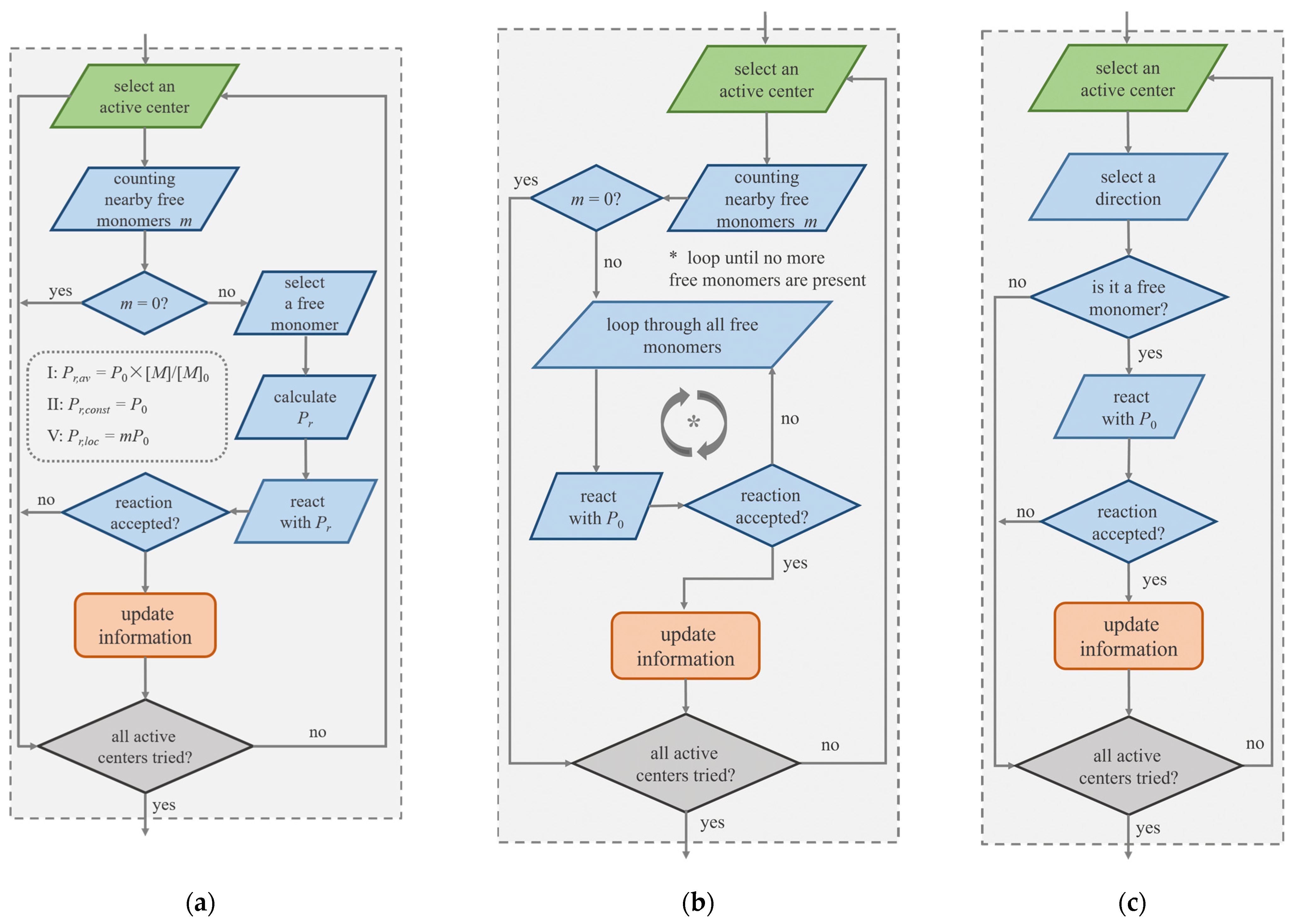
2.2. Implementation of Stochastic Reaction Model
2.3. Polymerization Kinetics
3. Results and Discussion
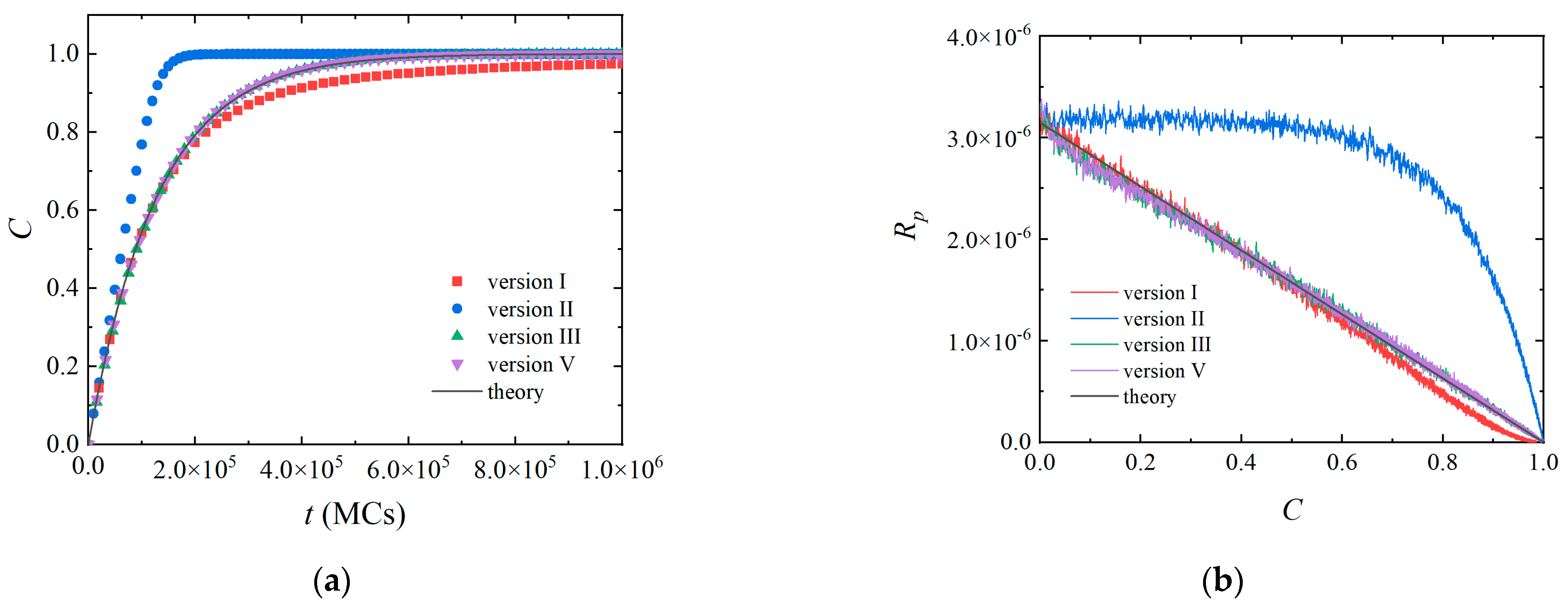
3.1. Homogeneous Polymerization
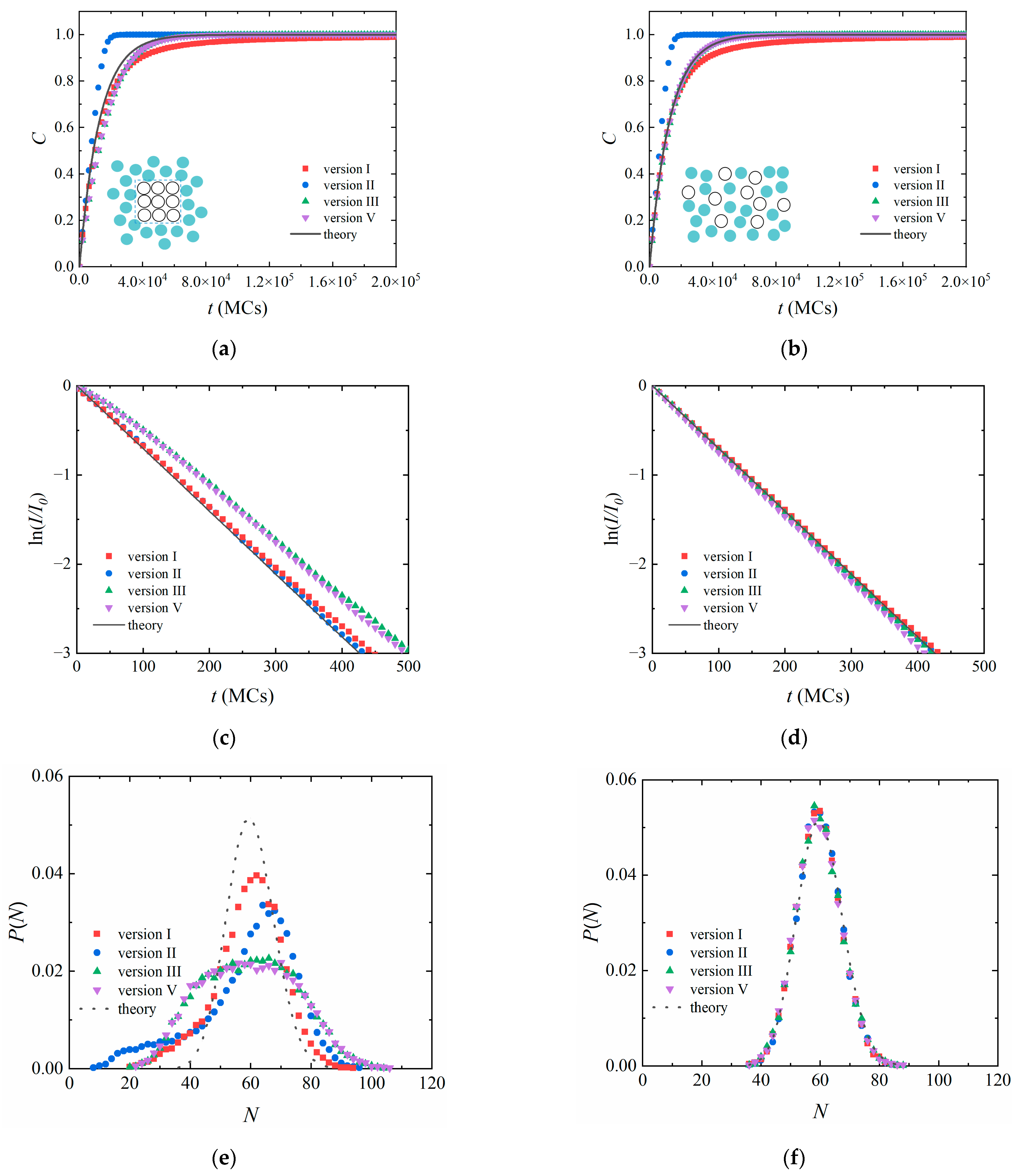
3.2. Heterogeneous Polymerization
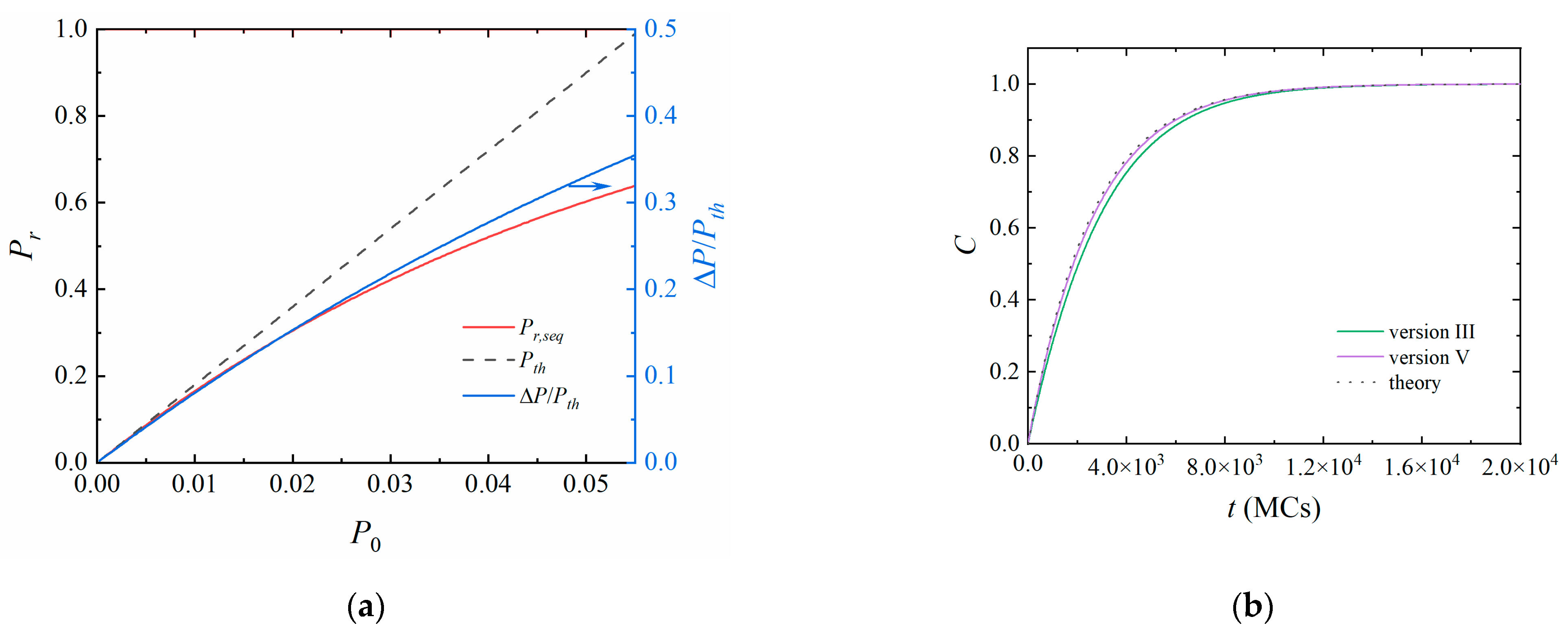
3.3. A Further Comparison between Versions III and V
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arshady, R. Suspension, emulsion, and dispersion polymerization: A methodological survey. Colloid Polym. Sci. 1992, 270, 717–732. [Google Scholar] [CrossRef]
- Qiu, J.; Charleux, B.; Matyjaszewski, K. Controlled/living radical polymerization in aqueous media: Homogeneous and heterogeneous systems. Prog. Polym. Sci. 2001, 26, 2083–2134. [Google Scholar] [CrossRef]
- Charleux, B.; Delaittre, G.; Rieger, J.; D’Agosto, F. Polymerization-induced self-assembly: From soluble macromolecules to block copolymer nano-objects in one step. Macromolecules 2012, 45, 6753–6765. [Google Scholar] [CrossRef]
- Derry, M.J.; Fielding, L.A.; Armes, S.P. Polymerization-induced self-assembly of block copolymer nanoparticles via RAFT non-aqueous dispersion polymerization. Prog. Polym. Sci. 2016, 52, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Cornel, E.J.; Jiang, J.; Chen, S.; Du, J. Principles and characteristics of polymerization-induced self-assembly with various polymerization techniques. CCS Chem. 2021, 3, 2104–2125. [Google Scholar] [CrossRef]
- Chen, W.-L.; Cordero, R.; Tran, H.; Ober, C.K. 50th anniversary perspective: Polymer brushes: Novel surfaces for future materials. Macromolecules 2017, 50, 4089–4113. [Google Scholar] [CrossRef]
- Turgman-Cohen, S.; Genzer, J. Simultaneous bulk- and surface-initiated controlled radical polymerization from planar substrates. J. Am. Chem. Soc. 2011, 133, 17567–17569. [Google Scholar] [CrossRef]
- Dai, Y.; Li, T.; Zhang, Z.; Tan, Y.; Pan, S.; Zhang, L.; Xu, H. Oxidative polymerization in living cells. J. Am. Chem. Soc. 2021, 143, 10709–10717. [Google Scholar] [CrossRef]
- Geng, J.; Li, W.; Zhang, Y.; Thottappillil, N.; Clavadetscher, J.; Lilienkampf, A.; Bradley, M. Radical polymerization inside living cells. Nat. Chem. 2019, 11, 578–586. [Google Scholar] [CrossRef] [Green Version]
- Akkermans, R.L.C.; Toxvaerd, S.R.; Briels, W.J. Molecular dynamics of polymer growth. J. Chem. Phys. 1998, 109, 2929–2940. [Google Scholar] [CrossRef]
- Deng, B.; Shi, Y. A reactive coarse-grained model for polydisperse polymers. Polymer 2016, 98, 88–99. [Google Scholar] [CrossRef] [Green Version]
- de Buyl, P.; Nies, E. A parallel algorithm for step- and chain-growth polymerization in molecular dynamics. J. Chem. Phys. 2015, 142, 134102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Biedermann, M.; Diddens, D.; Heuer, A. rs@md: Introducing reactive steps at the molecular dynamics simulation level. J. Chem. Theory Comput. 2021, 17, 1074–1085. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; DuBay, K.H. The sequence of a step-growth copolymer can be influenced by its own persistence length. J. Phys. Chem. B 2021, 125, 3426–3437. [Google Scholar] [CrossRef] [PubMed]
- Farah, K.; Karimi-Varzaneh, H.A.; Müller-Plathe, F.; Böhm, M.C. Reactive molecular dynamics with material-specific coarse-grained potentials: Growth of polystyrene chains from styrene monomers. J. Phys. Chem. B 2010, 114, 13656–13666. [Google Scholar] [CrossRef]
- Zhang, Z.; Krajniak, J.; Samaey, G.; Nies, E. A Parallel Multiscale Simulation Framework for Complex Polymerization: AB2-Type Monomer Hyperbranched Polymerization as an Example. Adv. Theory Simul. 2019, 2, 1800102. [Google Scholar] [CrossRef]
- Gao, J. An efficient method of generating dense polymer model melts by computer simulation. J. Chem. Phys. 1995, 102, 1074–1077. [Google Scholar] [CrossRef]
- Krajniak, J.; Zhang, Z.; Pandiyan, S.; Nies, E.; Samaey, G. Coarse-grained molecular dynamics simulations of polymerization with forward and backward reactions. J. Comput. Chem. 2018, 39, 1764–1778. [Google Scholar] [CrossRef]
- Xu, J.; Xue, Y.-H.; Cui, F.-C.; Liu, H.; Lu, Z.-Y. Simultaneous polymer chain growth with the coexistence of bulk and surface initiators: Insight from computer simulations. Phys. Chem. Chem. Phys. 2018, 20, 22576–22584. [Google Scholar] [CrossRef]
- Polanowski, P.; Hałagan, K.; Pietrasik, J.; Jeszka, J.K.; Matyjaszewski, K. Growth of polymer brushes by “grafting from” via ATRP–Monte Carlo simulations. Polymer 2017, 130, 267–279. [Google Scholar] [CrossRef]
- Halagan, K.; Banaszak, M.; Jung, J.; Polanowski, P.; Sikorski, A. Polymerization and structure of opposing polymer brushes studied by computer simulations. Polymers 2021, 13, 4294. [Google Scholar] [CrossRef] [PubMed]
- Polanowski, P.; Jeszka, J.K.; Matyjaszewski, K. Polymer brush relaxation during and after polymerization–Monte Carlo simulation study. Polymer 2019, 173, 190–196. [Google Scholar] [CrossRef]
- Wang, L.; He, X. Reaction kinetics of nonideal hyperbranched polymerizations: Influences of chain rigidity and reaction reversibility. J. Polym. Sci. Part A Polym. Chem. 2012, 50, 2705–2714. [Google Scholar] [CrossRef]
- Lu, W.; Ding, J. Dynamic Monte Carlo simulation of chain growth polymerization and its concentration effect. Sci. China Ser. B 2005, 48, 459–465. [Google Scholar] [CrossRef]
- Lu, W.; Ding, J. Dynamic Monte Carlo simulation of polymerization of amphiphilic macromers in a selective solvent and associated chemical gelation. Macromolecules 2006, 39, 7433–7440. [Google Scholar] [CrossRef]
- Wang, L.; He, X.; Chen, Y. Diffusion-limited hyperbranched polymers with substitution effect. J. Chem. Phys. 2011, 134, 104901. [Google Scholar] [CrossRef] [PubMed]
- Genzer, J. In Silico Polymerization: Computer simulation of controlled radical polymerization in bulk and on flat Surfaces. Macromolecules 2006, 39, 7157–7169. [Google Scholar] [CrossRef]
- Arraez, F.J.; Van Steenberge, P.H.; D’hooge, D.R. The competition of termination and shielding to evaluate the success of surface-initiated reversible deactivation radical polymerization. Polymers 2020, 12, 1409. [Google Scholar] [CrossRef] [PubMed]
- Arraez, F.J.; Van Steenberge, P.H.M.; Sobieski, J.; Matyjaszewski, K.; D’hooge, D.R. Conformational variations for surface-initiated reversible deactivation radical polymerization: From flat to curved nanoparticle surfaces. Macromolecules 2021, 54, 8270–8288. [Google Scholar] [CrossRef]
- Lísal, M.; Brennan, J.K.; Smith, W.R. Mesoscale simulation of polymer reaction equilibrium: Combining dissipative particle dynamics with reaction ensemble Monte Carlo. I. Polydispersed polymer systems. J. Chem. Phys. 2006, 125, 164905. [Google Scholar] [CrossRef]
- Yan, Y.-D.; Xue, Y.-H.; Zhao, H.-Y.; Liu, H.; Lu, Z.-Y.; Gu, F.-L. Insight into the polymerization-induced self-assembly via a realistic computer simulation strategy. Macromolecules 2019, 52, 6169–6180. [Google Scholar] [CrossRef]
- Lu, H.; Song, W.-Y.; Zou, Y.-Y.; Xu, W.-S.; Yan, Y.-D.; Liu, H.; Ma, L.-J. Kinetics and morphologies in polymerization-induced cooperative assembly: A computer simulation investigation. Polym. Int. 2021, 71, 359–365. [Google Scholar] [CrossRef]
- Liu, H.; Li, M.; Lu, Z.-Y.; Zhang, Z.-G.; Sun, C.-C. Influence of surface-initiated polymerization rate and initiator density on the properties of polymer brushes. Macromolecules 2009, 42, 2863–2872. [Google Scholar] [CrossRef]
- Liu, H.; Qian, H.-J.; Zhao, Y.; Lu, Z.-Y. Dissipative particle dynamics simulation study on the binary mixture phase separation coupled with polymerization. J. Chem. Phys. 2007, 127, 144903. [Google Scholar] [CrossRef] [PubMed]
- Berezkin, A.V.; Kudryavtsev, Y.V. Simulation of end-coupling reactions at a polymer-polymer interface: The mechanism of interfacial roughness development. Macromolecules 2011, 44, 112–121. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, Y.L.; Lu, Z.Y.; Müller-Plathe, F. A kinetic chain growth algorithm in coarse-grained simulations. J. Comput. Chem. 2016, 37, 2634–2646. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.L.; Liu, H.; Li, Z.W.; Qian, H.J.; Milano, G.; Lu, Z.Y. GALAMOST: GPU-accelerated large-scale molecular simulation toolkit. J. Comput. Chem. 2013, 34, 2197–2211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, B.; Liu, S.; Ma, J.; Yang, Y.; Li, J.; Jiang, B.-P.; Ji, S.; Shen, X.-C. A Monte Carlo simulation of surface-initiated polymerization: Heterogeneous reaction environment. Macromolecules 2022, 55, 1970–1980. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Wang, Y.; Li, Z.; Zhang, J. Polymerization-induced self-assembly of comb-like amphiphilic copolymers into onion-like vesicles. Macromolecules 2021, 54, 7448–7459. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, L.; Wang, Z.; He, X.; Chen, Y.; Müller-Plathe, F.; Böhm, M.C. A coarse-grained molecular dynamics-reactive Monte Carlo approach to simulate hyperbranched polycondensation. RSC Adv. 2014, 4, 56625–56636. [Google Scholar] [CrossRef]
- Turgman-Cohen, S.; Genzer, J. Computer simulation of controlled radical polymerization: Effect of chain confinement due to initiator grafting density and solvent quality in “grafting from” method. Macromolecules 2010, 43, 9567–9577. [Google Scholar] [CrossRef]
- DPDChem Software. Available online: https://www.researchgate.net/project/DPDChem-Software (accessed on 1 August 2022).
- Berezkin, A.V.; Kudryavtsev, Y.V. End-coupling reactions in incompatible polymer blends: From droplets to complex micelles through interfacial instability. Macromolecules 2013, 46, 5080–5089. [Google Scholar] [CrossRef]
- Guseva, D.V.; Kudryavtsev, Y.V.; Berezkin, A.V. Simulation of heterogeneous end-coupling reactions in polydisperse polymer blends. J. Chem. Phys. 2011, 135, 112. [Google Scholar] [CrossRef]
- Gavrilov, A.A.; Chertovich, A.V. Copolymerization of partly incompatible monomers: An insight from computer simulations. Macromolecules 2017, 50, 4677–4685. [Google Scholar] [CrossRef] [Green Version]
- Gavrilov, A.A.; Chertovich, A.V. Self-assembly in thin films during copolymerization on patterned surfaces. Macromolecules 2013, 46, 4684–4690. [Google Scholar] [CrossRef]
- Kozhunova, E.Y.; Gavrilov, A.A.; Zaremski, M.Y.; Chertovich, A.V. Copolymerization on selective substrates: Experimental test and computer simulations. Langmuir 2017, 33, 3548–3555. [Google Scholar] [CrossRef]
- Shao, J.; Tang, W.; Xia, R.; Feng, X.; Chen, P.; Qian, J.; Song, C. Monte Carlo simulation on kinetics of batch and semi-batch free radical polymerization. Macromol. Res. 2015, 23, 1042–1050. [Google Scholar] [CrossRef] [Green Version]
- Hałagan, K.; Banaszak, M.; Jung, J.; Polanowski, P.; Sikorski, A. Dynamics of opposing polymer brushes: A computer simulation study. Polymers 2021, 13, 2758. [Google Scholar] [CrossRef] [PubMed]
- Larson, R.; Scriven, L.; Davis, H. Monte Carlo simulation of model amphiphile-oil–water systems. J. Chem. Phys. 1985, 83, 2411–2420. [Google Scholar] [CrossRef]
- Larson, R. Monte Carlo lattice simulation of amphiphilic systems in two and three dimensions. J. Chem. Phys. 1988, 89, 1642–1650. [Google Scholar] [CrossRef]
- Ji, S.; Ding, J. Nonequilibrium Monte Carlo simulation of lattice block copolymer chains subject to oscillatory shear flow. J. Chem. Phys. 2005, 122, 164901. [Google Scholar] [CrossRef] [PubMed]
- Müller-Plathe, F. A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity. J. Chem. Phys. 1997, 106, 6082–6085. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Li, J.; Yang, B.; Liu, S.; Jiang, B.-P.; Ji, S.; Shen, X.-C. A Simple Stochastic Reaction Model for Heterogeneous Polymerizations. Polymers 2022, 14, 3269. https://doi.org/10.3390/polym14163269
Ma J, Li J, Yang B, Liu S, Jiang B-P, Ji S, Shen X-C. A Simple Stochastic Reaction Model for Heterogeneous Polymerizations. Polymers. 2022; 14(16):3269. https://doi.org/10.3390/polym14163269
Chicago/Turabian StyleMa, Jiashu, Jiahao Li, Bingbing Yang, Siwen Liu, Bang-Ping Jiang, Shichen Ji, and Xing-Can Shen. 2022. "A Simple Stochastic Reaction Model for Heterogeneous Polymerizations" Polymers 14, no. 16: 3269. https://doi.org/10.3390/polym14163269
APA StyleMa, J., Li, J., Yang, B., Liu, S., Jiang, B.-P., Ji, S., & Shen, X.-C. (2022). A Simple Stochastic Reaction Model for Heterogeneous Polymerizations. Polymers, 14(16), 3269. https://doi.org/10.3390/polym14163269






