Effect of Transversely Isotropic Elasticity on Elastohydrodynamic Lubrication of Point Contacts
Abstract
:1. Introduction
2. Methods
2.1. Contact Configuration
2.2. Materials
2.3. Lubricant
2.4. Governing Equations
2.5. Computational Domain
2.6. Operating Condition and Parametric Variations
2.7. Analytical Approximations
3. Results
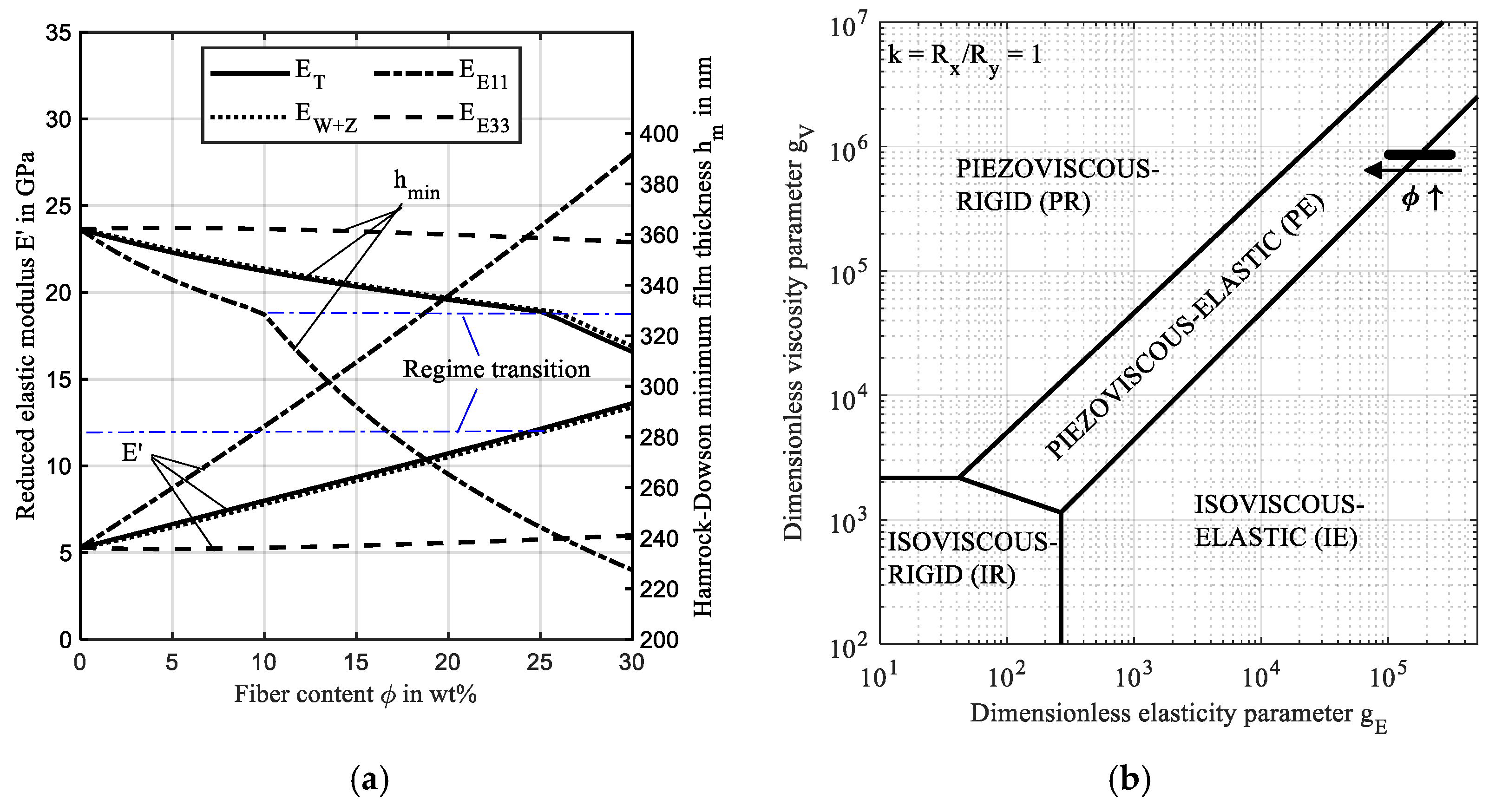
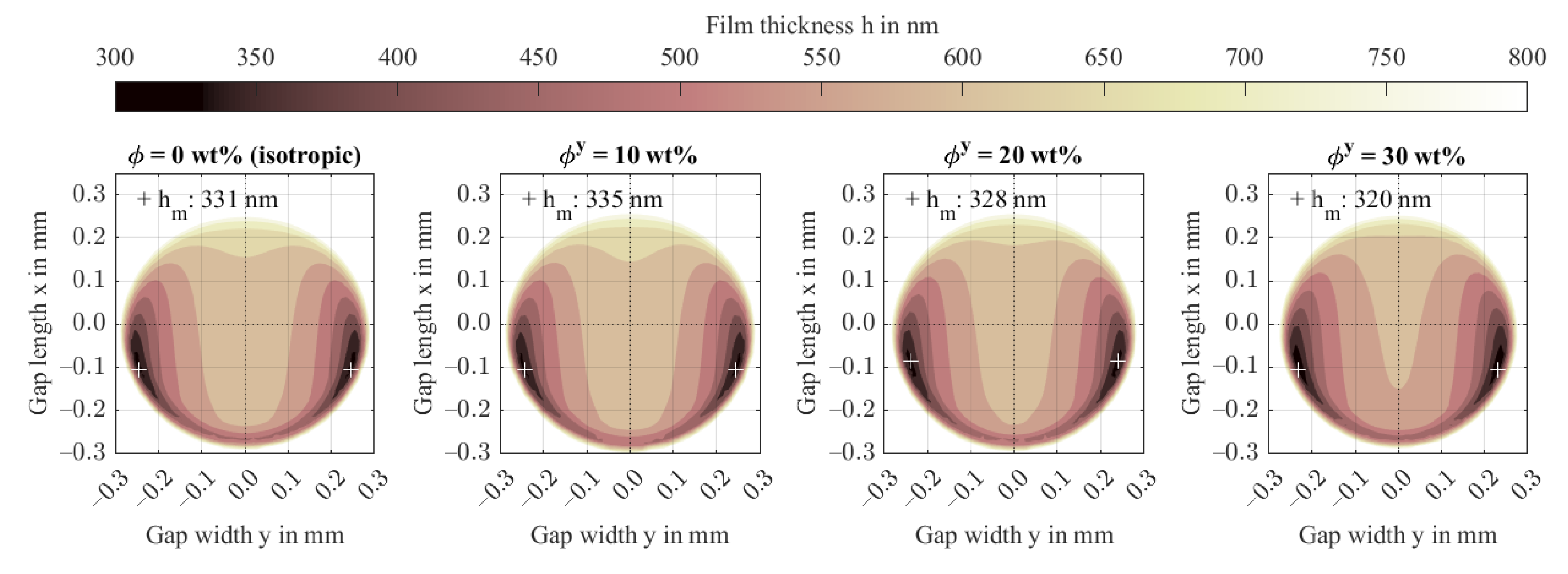
3.1. Increase in Fiber Content (Study 1)
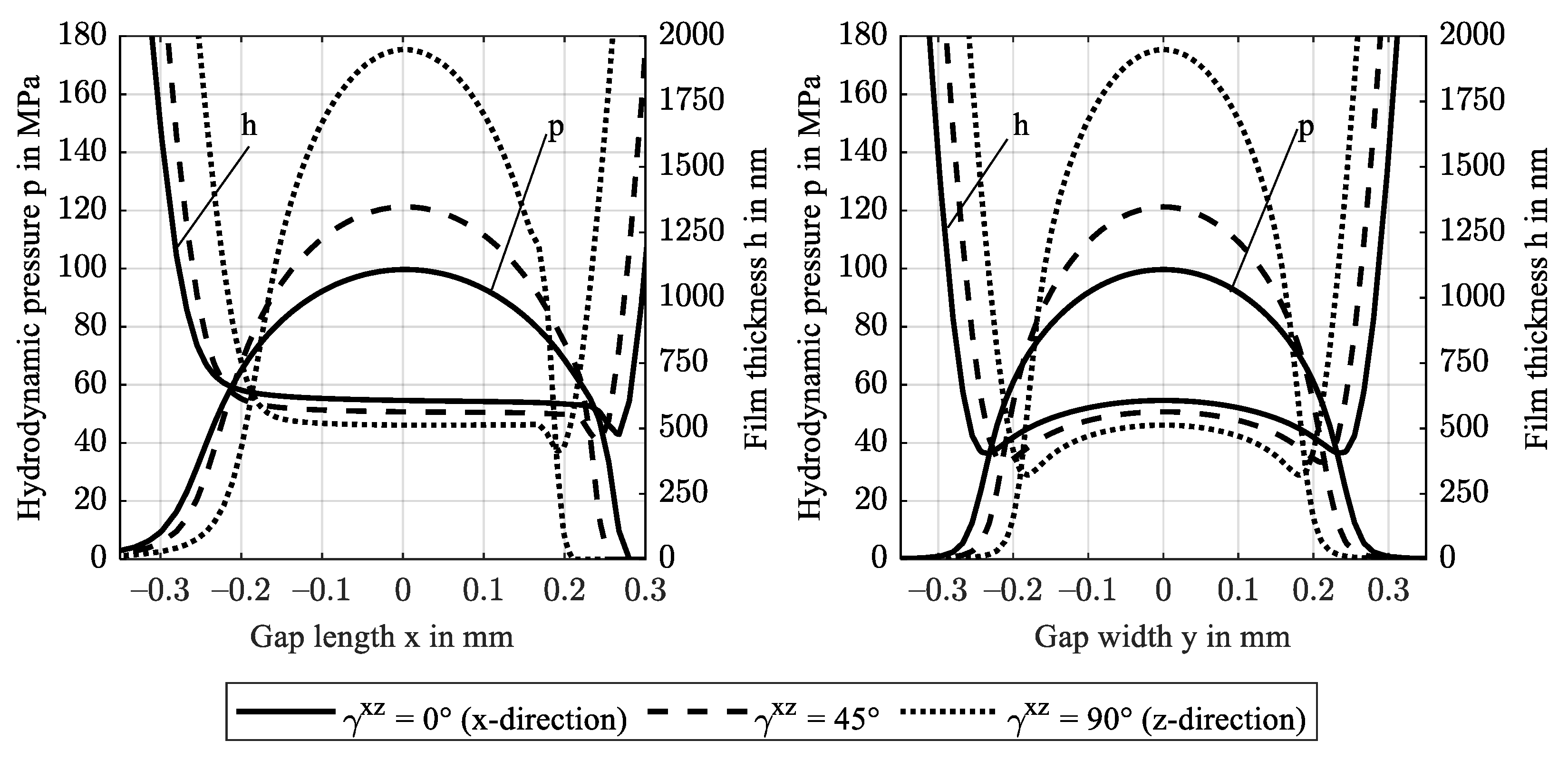
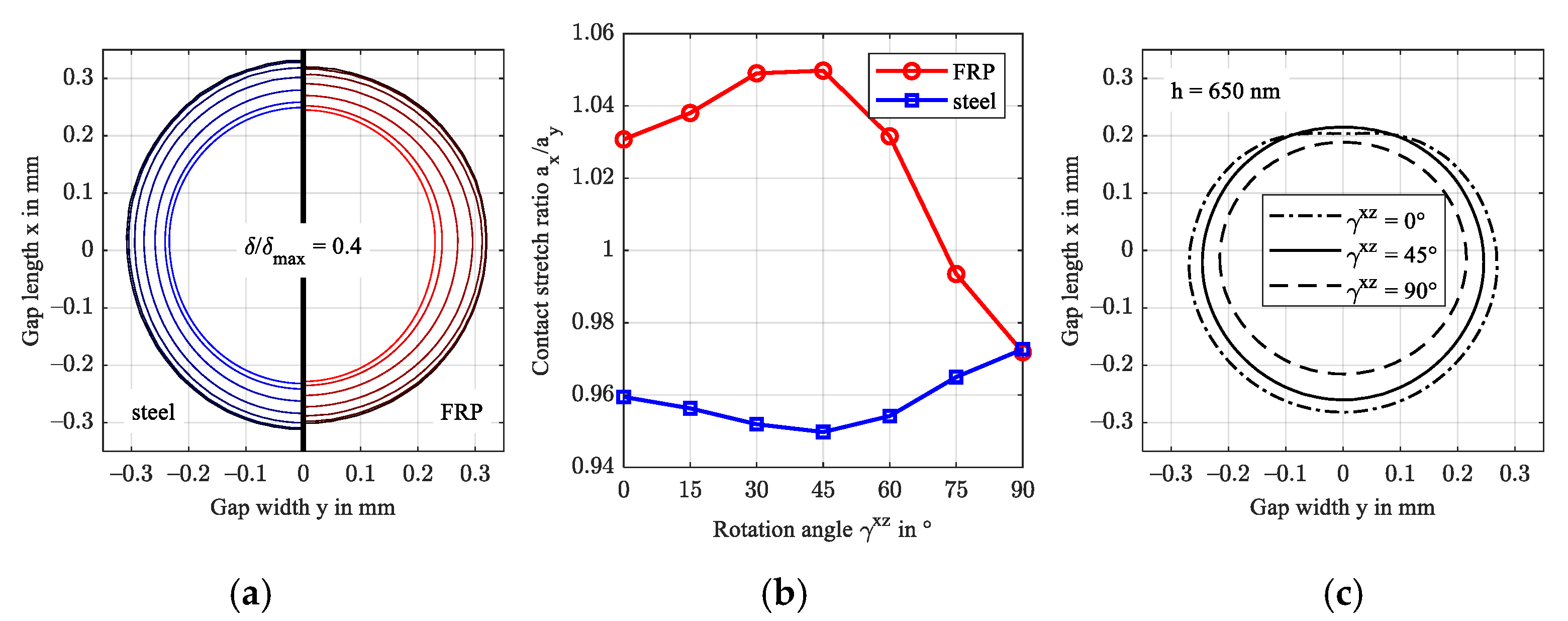
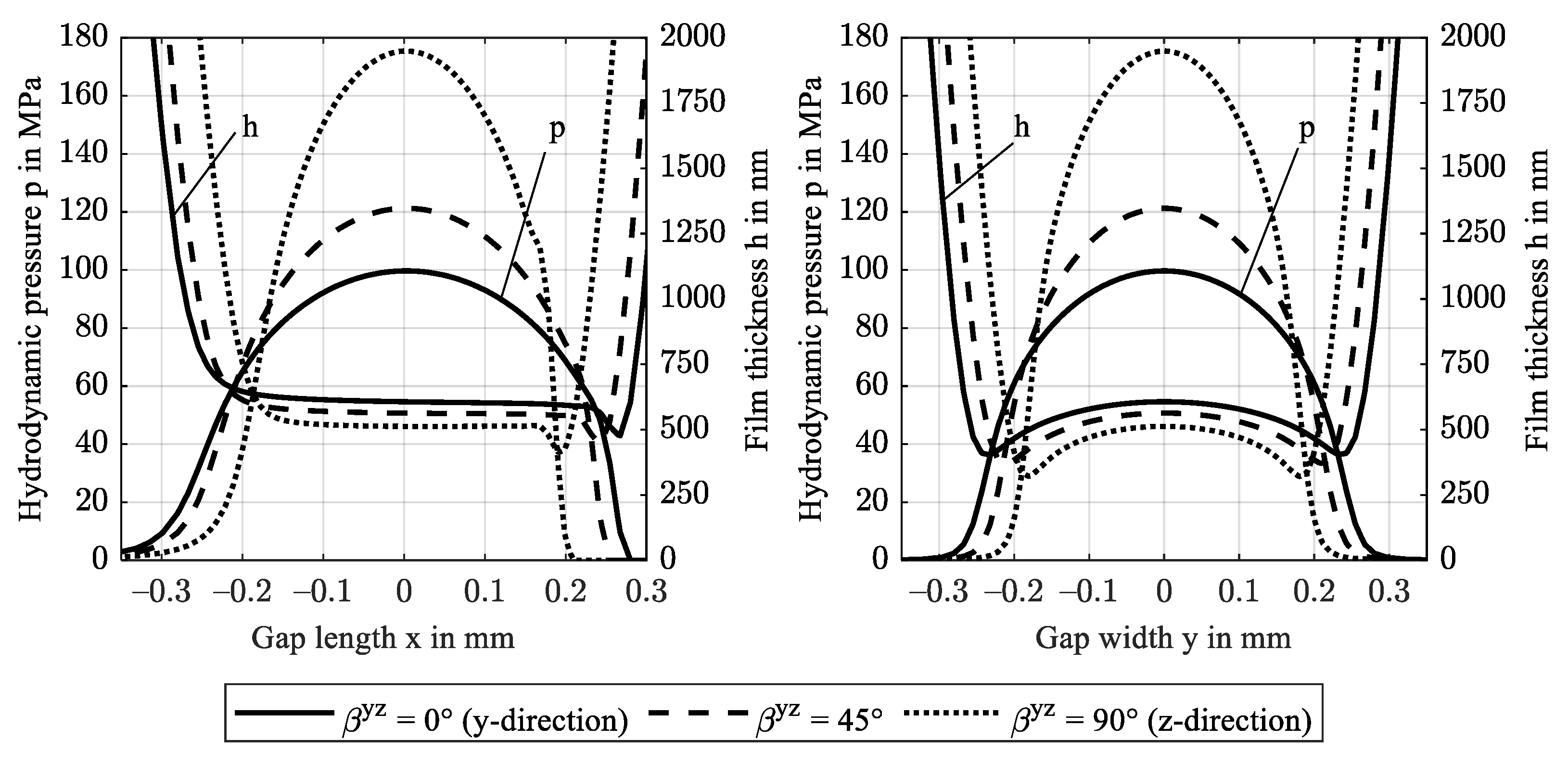
3.2. Fiber Rotation from Gap Width to Length Direction (Study 2.1)
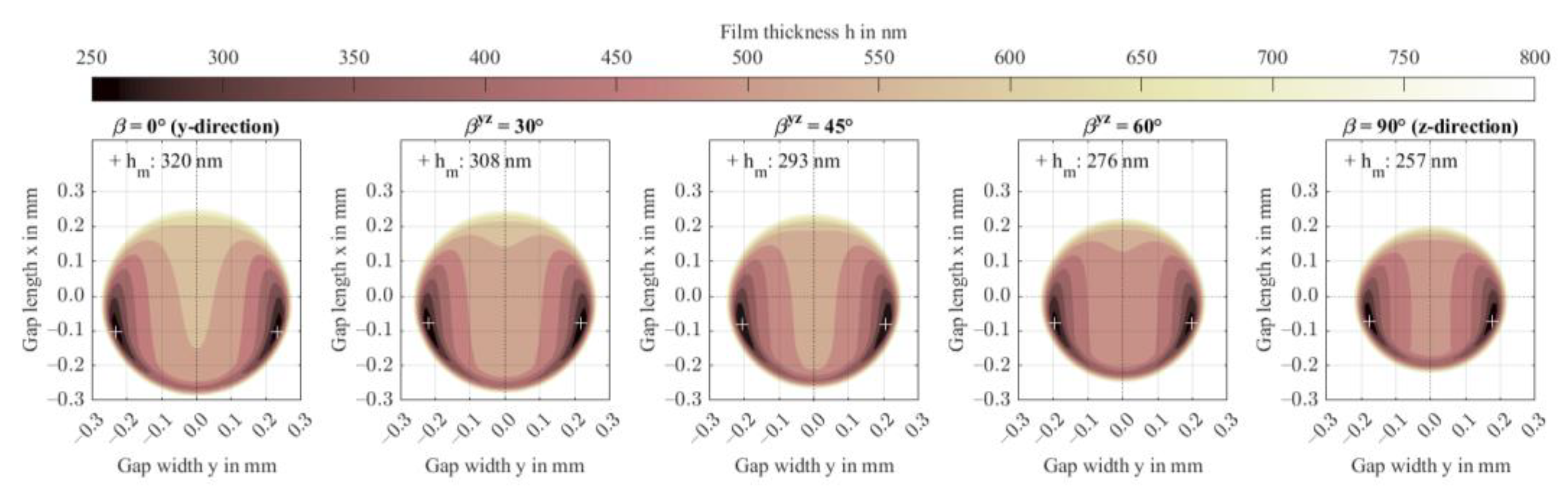
3.3. Fiber Rotation from Gap Width to Gap Normal Direction (Study 2.2)
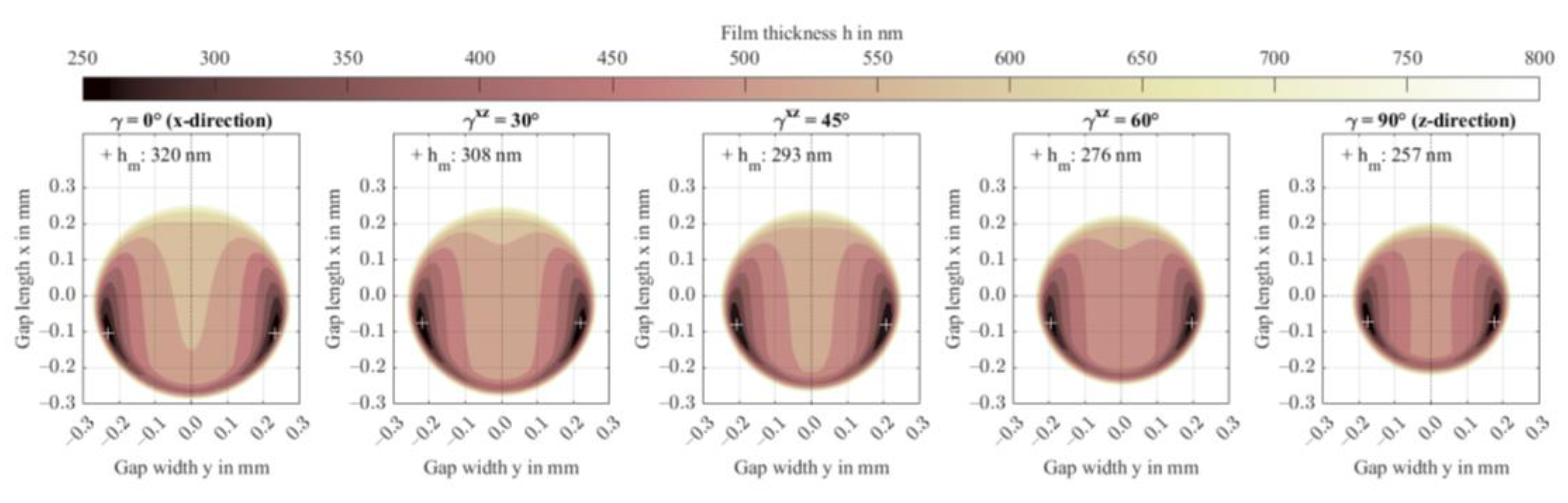
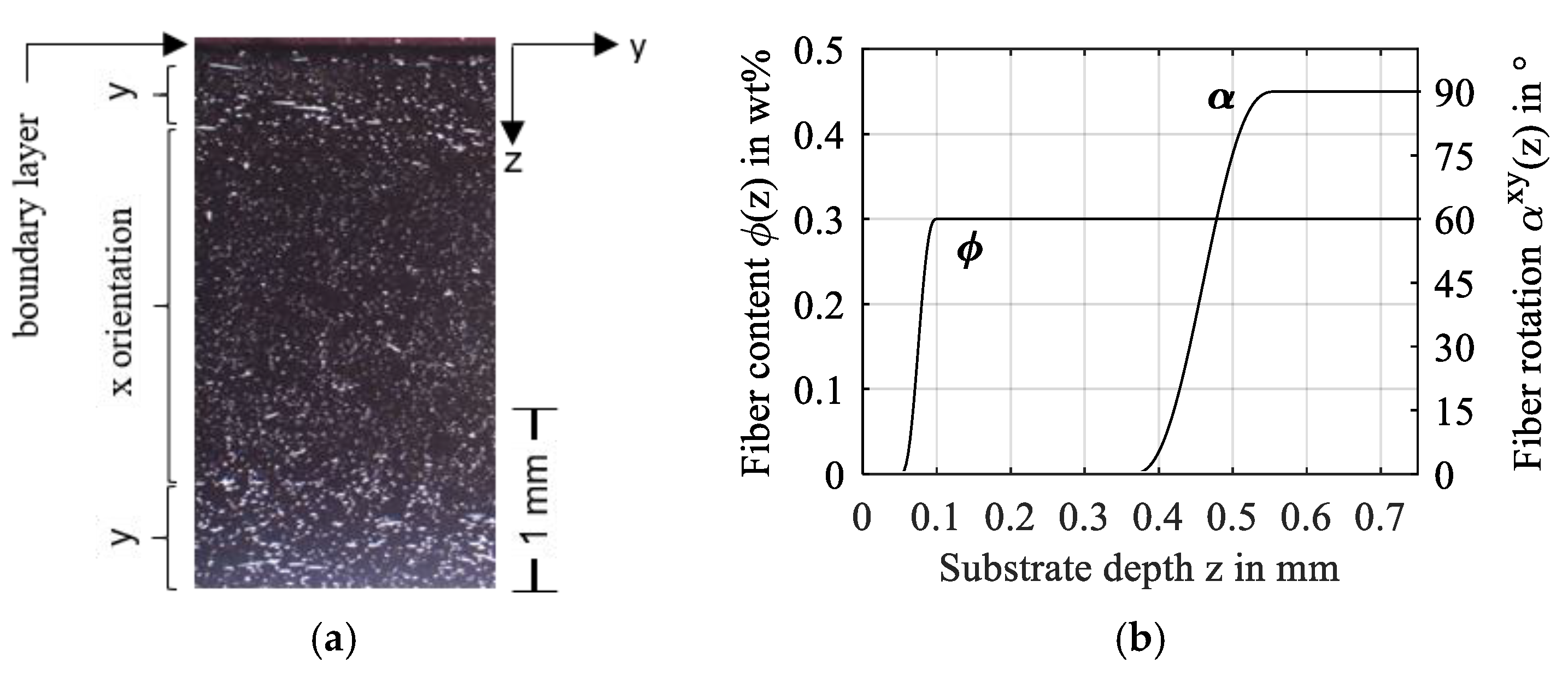
3.4. Fiber Content and Orientation Distribution (Study 3)
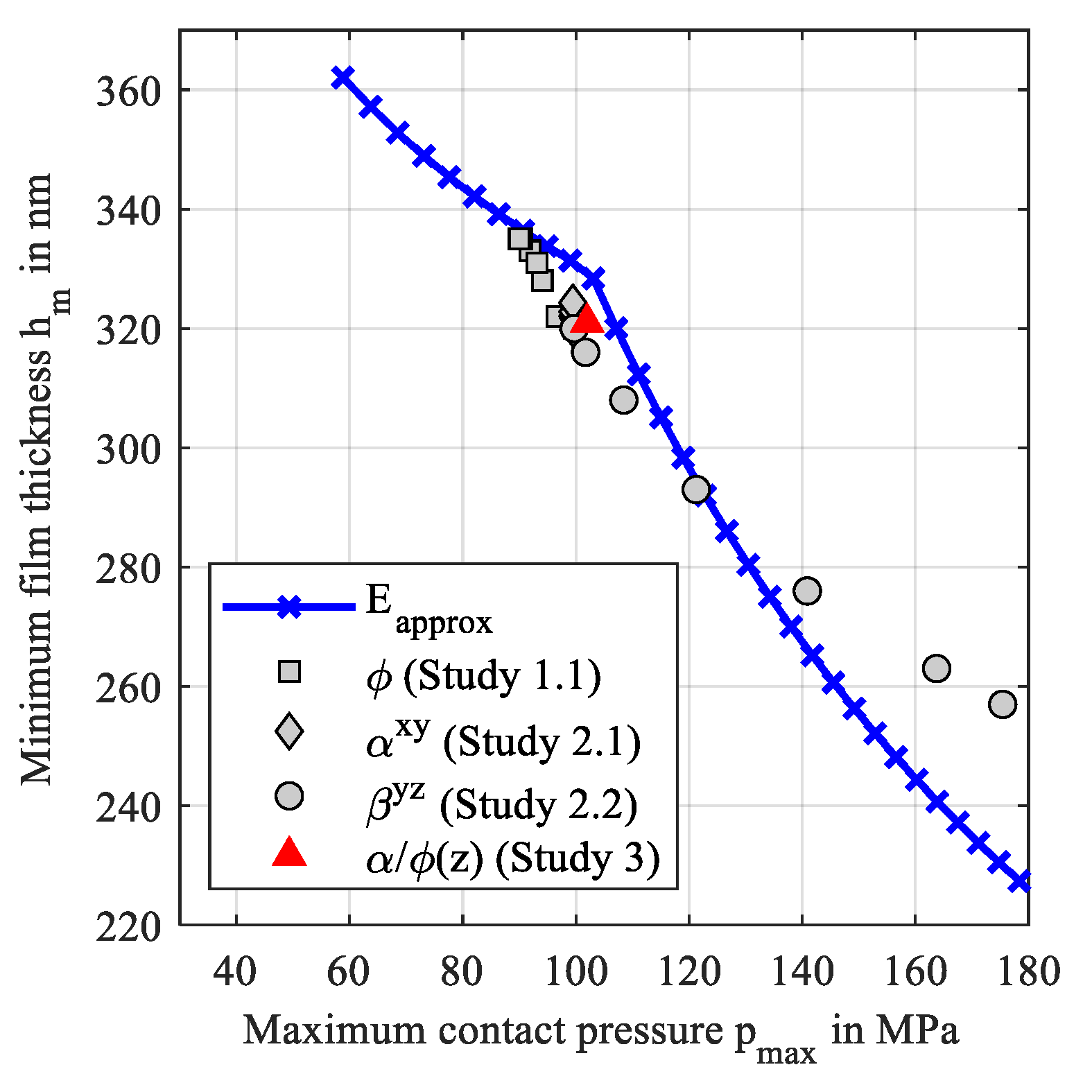
3.5. Comparison to Analytical Formulas
4. Conclusions
- The contact shape can affect the lubricant hydrodynamics. As a result, the contact regime may transition from isoviscous-elastic to piezoviscous-elastic at a threshold that depends on the operating condition.
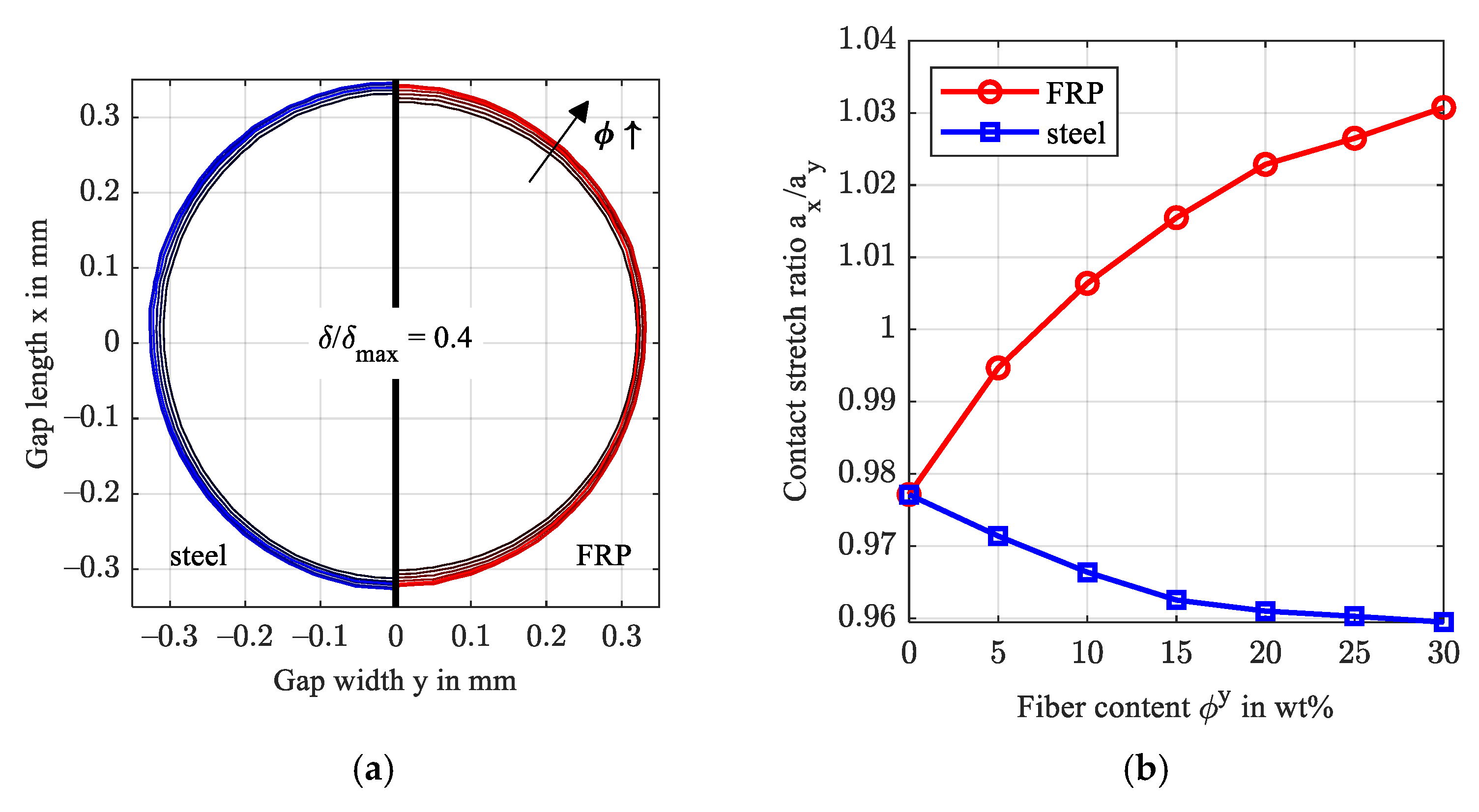
- A fiber orientation parallel to the contact plane results in a stretch of the contact area and higher film thickness compared to an orientation perpendicular to the contact plane.
- The accuracy of analytical approximations of the minimum film thickness depends strongly on the effective contact stiffness, which depends on the homogenized fiber orientation and distribution.
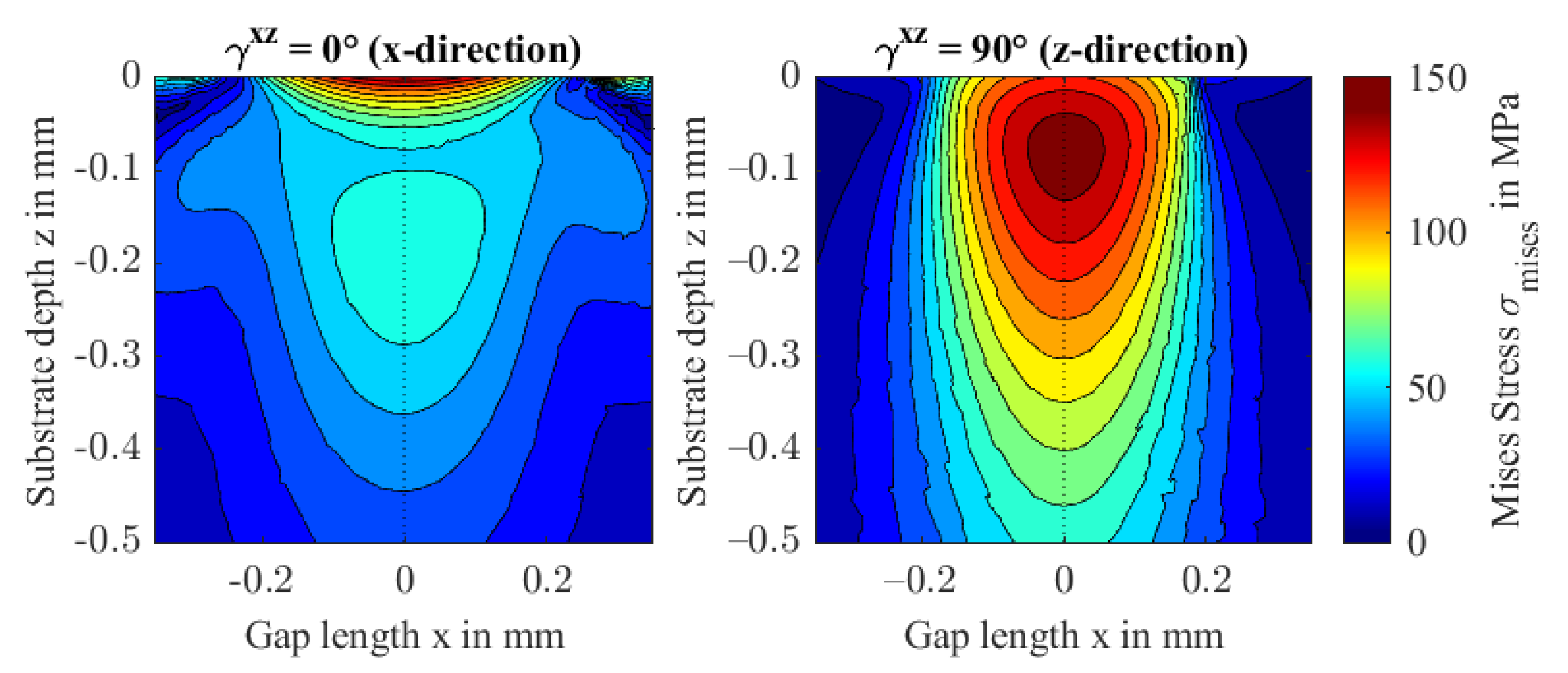
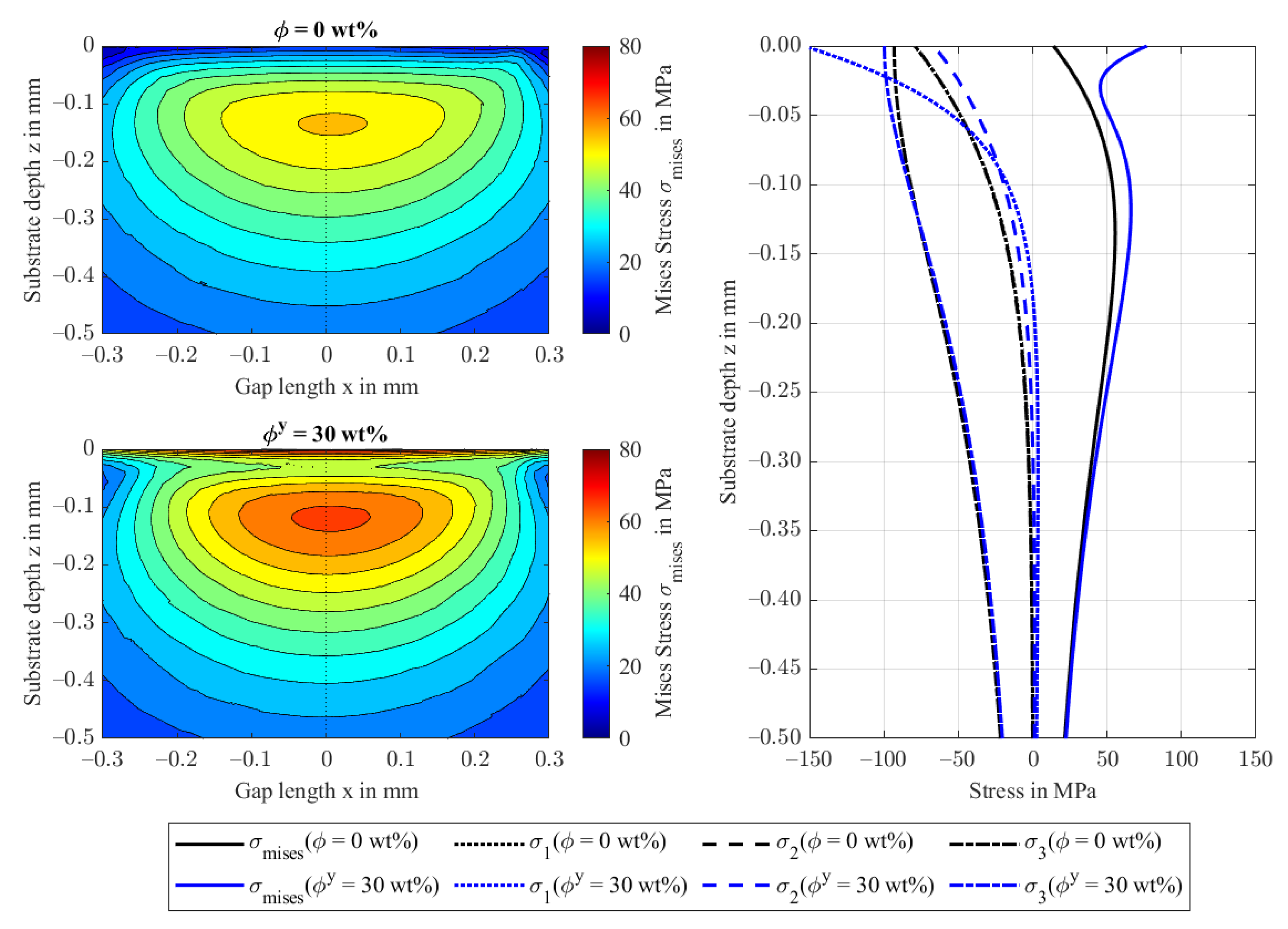
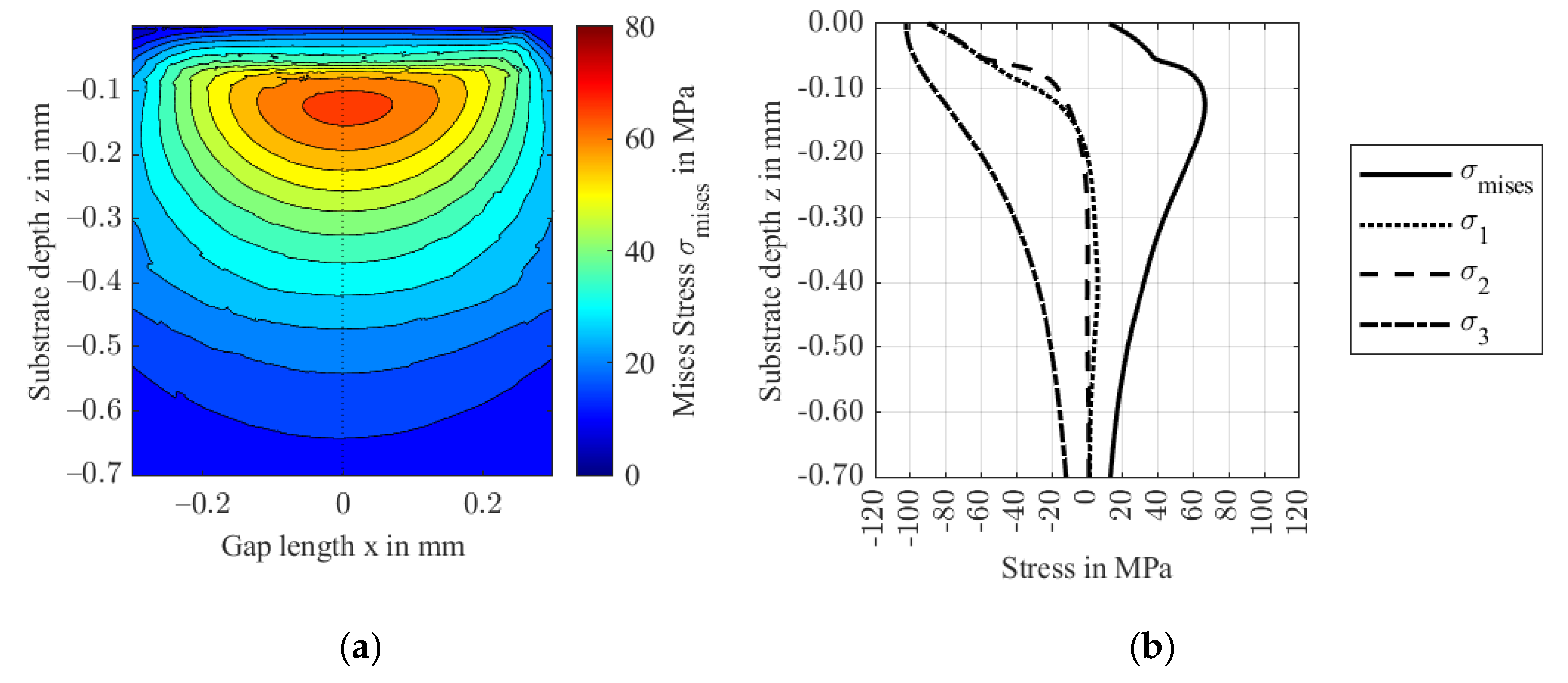
- Subsurface stresses increase with fiber content. Fiber orientations in the contact plane can cause high von Mises stress in the proximity of the surface, while fiber orientations in the contact normal direction result in maximum von Mises stress at higher depths.
- The typical fiber orientation distribution after injection molding may effectively lead to isotropic-like contact behavior.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Kurokawa, M.; Uchiyama, Y.; Iwai, T.; Nagai, S. Performance of plastic gear made of carbon fiber reinforced polyamide 12. Wear 2003, 254, 468–473. [Google Scholar] [CrossRef]
- Senthilvelan, S.; Gnanamoorthy, R. Damping characteristics of unreinforced, glass and carbon fiber reinforced nylon 6/6 spur gears. Polym. Test. 2006, 25, 56–62. [Google Scholar] [CrossRef]
- Senthilvelan, S.; Gnanamoorthy, R. Effect of rotational speed on the performance of unreinforced and glass fiber reinforced Nylon 6 spur gears. Mater. Des. 2007, 28, 765–772. [Google Scholar] [CrossRef]
- Komal, U.K.; Lila, M.K.; Chaitanya, S.; Singh, I. Fabrication of Short Fiber Reinforced Polymer Composites. In Reinforced Polymer Composites; Bajpai, P.K., Singh, I., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2019; pp. 21–38. ISBN 9783527820979. [Google Scholar]
- Valino, A.D.; Dizon, J.R.C.; Espera, A.H.; Chen, Q.; Messman, J.; Advincula, R.C. Advances in 3D printing of thermoplastic polymer composites and nanocomposites. Prog. Polym. Sci. 2019, 98, 101162. [Google Scholar] [CrossRef]
- Domininghaus, H.; Elsner, P.; Eyerer, P.; Hirth, T. Kunststoffe; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 978-3-642-16172-8. [Google Scholar]
- Hertz, H. Ueber die Berührung fester elastischer Körper. In Journal für die Reine und Angewandte Mathematik Band 92; Crelle, A.L., Borchardt, C.W., Schellbach, Eds.; De Gruyter: Berlin, Germany; Munich, Germany; Boston, MA, USA, 1882; pp. 156–171. ISBN 9783112342404. [Google Scholar]
- Willis, J.R. Hertzian contact of anisotropic bodies. J. Mech. Phys. Solids 1966, 14, 163–176. [Google Scholar] [CrossRef]
- Palmer, P.J. Theoretical Elasticity; Green, A.E., Zerna, W., Eds.; Clarendon Press: Oxford, UK, 1954; p. 442, Diagrams. 50s. J. R. Aeronaut. Soc. 1954, 58, 844. [Google Scholar] [CrossRef]
- Turner, J.R. Contact on a transversely isotropic half-space or between two transversely isotropic bodies. Int. J. Solids Struct. 1980, 16, 409–419. [Google Scholar] [CrossRef]
- Swanson, S.R. Hertzian contact of orthotropic materials. Int. J. Solids Struct. 2004, 41, 1945–1959. [Google Scholar] [CrossRef]
- Yang, S.H.; Sun, C.T. Indentation Law for Composite Laminates. In Composite Materials: Testing and Design (6th Conference); Daniel, I.M., Ed.; ASTM International: West Conshohocken, PA, USA, 1982; pp. 425–449. ISBN 978-0-8031-0695-6. [Google Scholar]
- Tan, T.M.; Sun, C.T. Use of Statical Indentation Laws in the Impact Analysis of Laminated Composite Plates. J. Appl. Mech. 1985, 52, 6–12. [Google Scholar] [CrossRef]
- Chen, C.-Y.; Tseng, Y.-F.; Chu, L.-M.; Li, W.-L. Soft EHL for transversely isotropic materials. Tribol. Int. 2013, 67, 240–253. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Y. An Efficient Numerical Model of Elastohydrodynamic Lubrication for Transversely Isotropic Materials. J. Tribol. 2019, 141, 091501. [Google Scholar] [CrossRef]
- Paulson, N.; Sadeghi, F. EHL modeling of nonhomogeneous materials: The effects of polycrystalline anisotropy on RCF. Tribol. Int. 2017, 112, 137–146. [Google Scholar] [CrossRef]
- Müller, V.; Kabel, M.; Andrä, H.; Böhlke, T. Homogenization of linear elastic properties of short-fiber reinforced composites—A comparison of mean field and voxel-based methods. Int. J. Solids Struct. 2015, 67–68, 56–70. [Google Scholar] [CrossRef]
- Gupta, M.; Wang, K. Fiber orientation and mechanical properties of short-fiber-reinforced injection-molded composites: Simulated and experimental results. Polym. Compos. 1993, 14, 367–382. [Google Scholar] [CrossRef]
- Żurawik, R.; Volke, J.; Zarges, J.-C.; Heim, H.-P. Comparison of Real and Simulated Fiber Orientations in Injection Molded Short Glass Fiber Reinforced Polyamide by X-ray Microtomography. Polymers 2021, 14, 29. [Google Scholar] [CrossRef]
- Stommel, M.; Stojek, M.; Korte, W. FEM zur Berechnung von Kunststoff-und Elastomerbauteilen; Hanser Carl: München, Germany, 2011; ISBN 9783446421240. [Google Scholar]
- Tandon, G.P.; Weng, G.J. Average stress in the matrix and effective moduli of randomly oriented composites. Compos. Sci. Technol. 1986, 27, 111–132. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 101, 55504. [Google Scholar] [CrossRef]
- Ovako Sweden AB. Material Data Sheet: 100Cr6. Available online: https://steelnavigator.ovako.com/steel-grades/100cr6/pdf?variantIDs=18 (accessed on 3 July 2022).
- CAMPUS Online Datasheets. Material Datasheet: Ultramid A3K—PA66 (BASF); M-Base Engineering + Software GmbH: Aachen, Germany, 2022. [Google Scholar]
- Kunz, J. Die Querkontraktionszahl in der Konstruktionspraxis. KunststoffXtra 2011, 6, 27–30. [Google Scholar]
- Maier, E.; Ziegltrum, A.; Lohner, T.; Stahl, K. Characterization of TEHL contacts of thermoplastic gears. Forsch. Ing. 2017, 81, 317–324. [Google Scholar] [CrossRef]
- Ziegltrum, A.; Maier, E.; Lohner, T.; Stahl, K. A Numerical Study on Thermal Elastohydrodynamic Lubrication of Coated Polymers. Tribol. Lett. 2020, 68, 361. [Google Scholar] [CrossRef]
- Tošić, M.; Larsson, R.; Lohner, T. Thermal Effects in Slender EHL Contacts. Lubricants 2022, 10, 89. [Google Scholar] [CrossRef]
- Roelands, C.J.A.; Vlugter, J.C.; Waterman, H.I. The Viscosity-Temperature-Pressure Relationship of Lubricating Oils and Its Correlation With Chemical Constitution. J. Basic Eng. 1963, 85, 601–607. [Google Scholar] [CrossRef]
- Reitschuster, S.; Maier, E.; Lohner, T.; Stahl, K. Friction and Temperature Behavior of Lubricated Thermoplastic Polymer Contacts. Lubricants 2020, 8, 67. [Google Scholar] [CrossRef]
- Bode, B. Modell zur Beschreibung des Fließverhaltens von Flüssigkeiten unter hohem Druck [Model for describing the rheological behaviour of liquids under high pressure]. Tribol. Und Schmier. 1989, 36, 182–189. [Google Scholar]
- Habchi, W. A Full-System Finite Element Approach to Elastohydrodynamic Lubrication Problems: Application to Ultra-Low-Viscosity Fluids. Ph.D. Thesis, Laboratoire de Mécanique des Contacts et des Structures, Lyon, France, 2008. [Google Scholar]
- Brooks, A.N.; Hughes, T.J. Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Comput. Methods Appl. Mech. Eng. 1982, 32, 199–259. [Google Scholar] [CrossRef]
- Hughes, T.J.; Franca, L.P.; Hulbert, G.M. A new finite element formulation for computational fluid dynamics: VIII. The galerkin/least-squares method for advective-diffusive equations. Comput. Methods Appl. Mech. Eng. 1989, 73, 173–189. [Google Scholar] [CrossRef]
- Amestoy, P.R.; Duff, I.S.; L’Excellent, J.-Y. Multifrontal parallel distributed symmetric and unsymmetric solvers. Comput. Methods Appl. Mech. Eng. 2000, 184, 501–520. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Isothermal Elastohydrodynamic Lubrication of Point Contacts: Part 1—Theoretical Formulation. J. Lubr. Technol. 1976, 98, 223–228. [Google Scholar] [CrossRef]
- Johnson, K.L. Regimes of Elastohydrodynamic Lubrication. J. Mech. Eng. Sci. 1970, 12, 9–16. [Google Scholar] [CrossRef]
- Kumar, P.; Khonsari, M.M. Lubrication Regimes: Point Contacts. In Encyclopedia of Tribology; Wang, Q.J., Chung, Y.-W., Eds.; Springer: Boston, MA, USA, 2013; pp. 2116–2121. ISBN 978-0-387-92896-8. [Google Scholar]
- Fabrikant, V.I. Contact problem for an arbitrarily oriented transversely isotropic half-space. Acta Mech. 2017, 228, 1541–1560. [Google Scholar] [CrossRef]
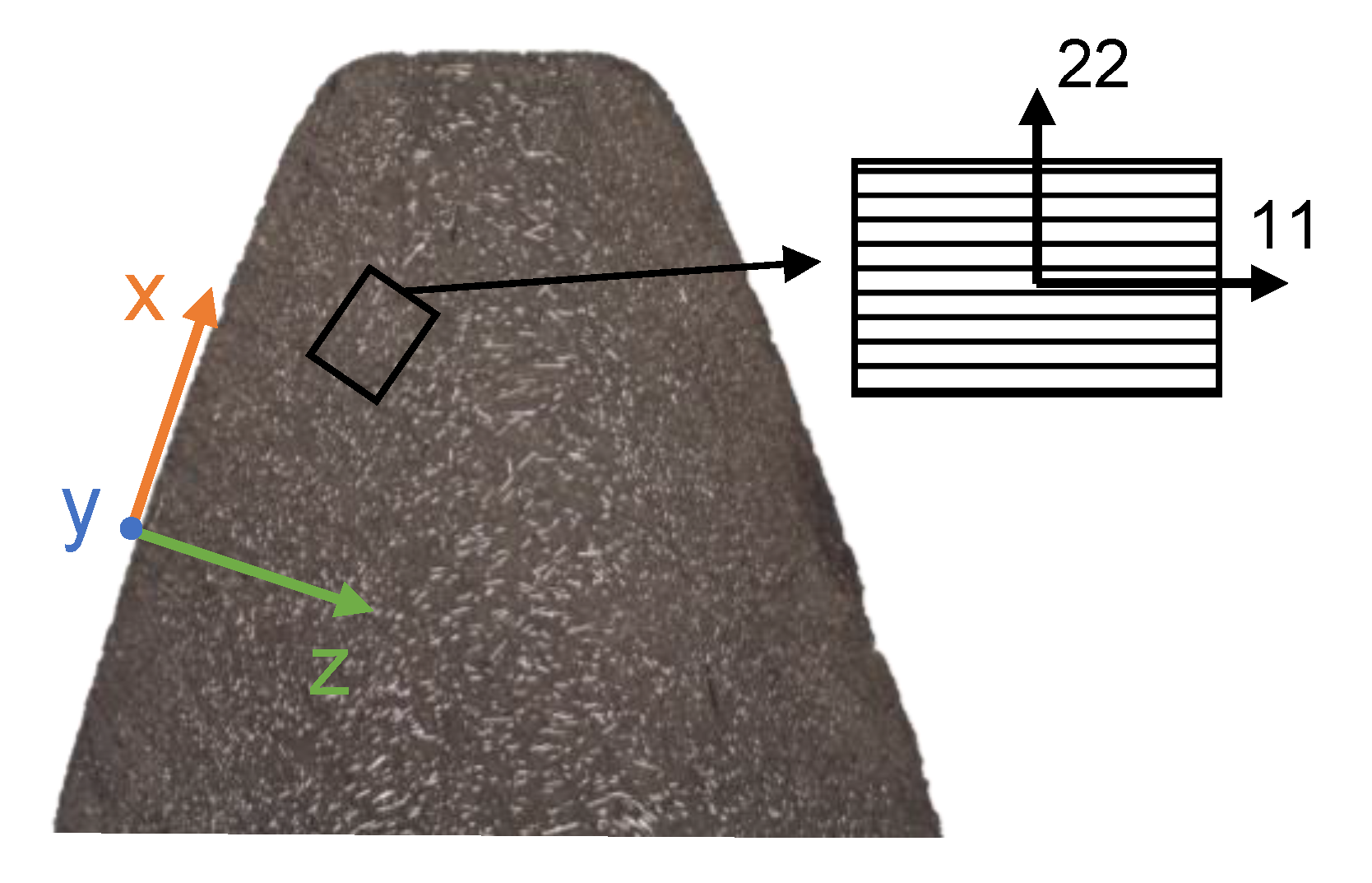
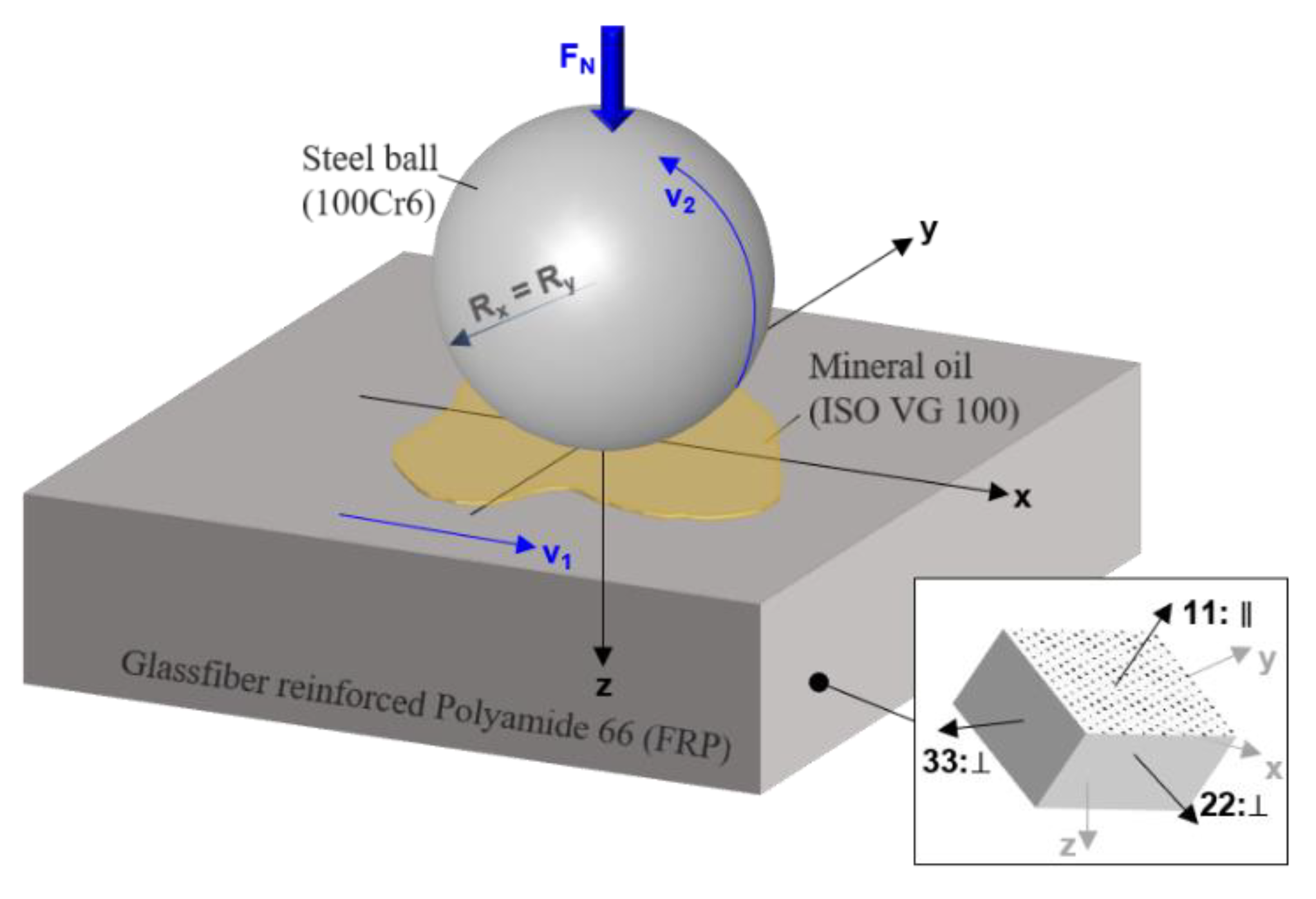
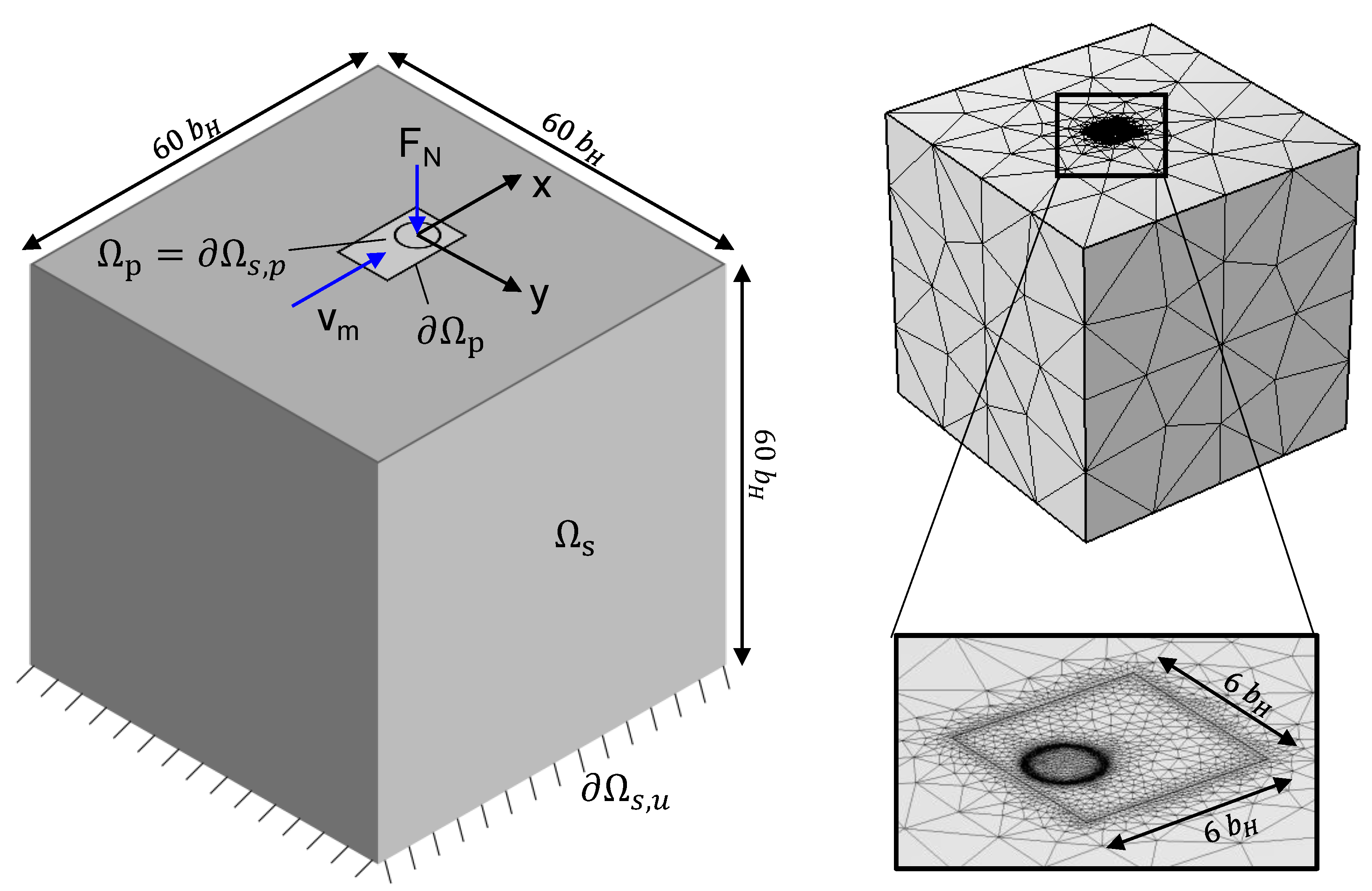
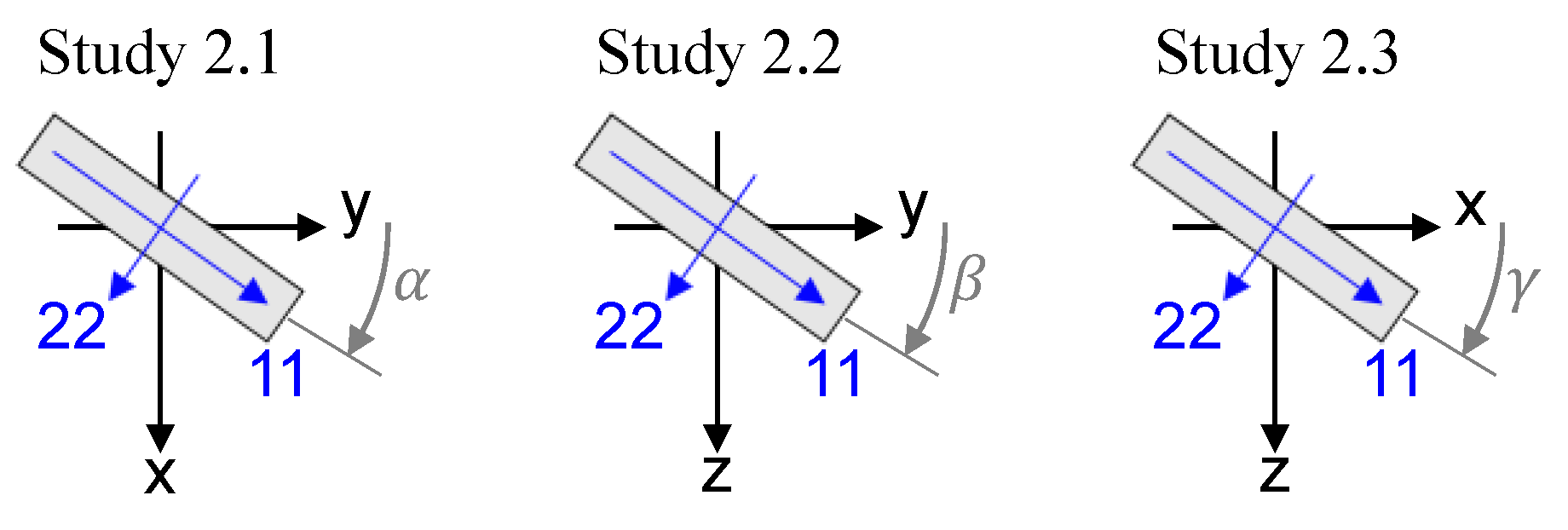








| Material | Elastic Modulus | Poisson Ratio | Density | |
|---|---|---|---|---|
| Steel | 100Cr6 | 210,000 MPa [23] | 0.30 [23] | 7800 kg/m3 [23] |
| Matrix | PA66 | 2350 MPa [24] * | 0.35 [25] | 1140 kg/m3 [6] |
| Fiber | E-Glass | 72,500 MPa [20] | 0.20 [20] | 2550 kg/m3 [20] |
| Fiber Content | E11 in MPa | E22 in MPa | G12 in MPa | G23 in MPa | AU | |
|---|---|---|---|---|---|---|
| 0 wt.% | 2350 | 2350 | 870.4 | 870.4 | 0.35 | 0.000 |
| 10 wt.% | 5576 | 2359 | 951.4 | 937.3 | 0.34 | 0.699 |
| 20 wt.% | 9214 | 2507 | 1053.0 | 1020.4 | 0.33 | 1.672 |
| 30 wt.% | 13,347 | 2724 | 1182.1 | 1126.7 | 0.32 | 2.614 |
| Unit | Ref. | Study 1 | Study 2.1 | Study 2.2 | Study 2.3 | Study 3 | ||
|---|---|---|---|---|---|---|---|---|
| Normal force | FN | N | 15 | |||||
| Mean speed | vm | m/s | 1 | |||||
| Bulk temperature | °C | 40 | ||||||
| Fiber content | wt.% | 30 | 0…30 | 30 | ||||
| Fiber orientation * | ° | 0 | 0 | 0…−90 | 0 | −90 | ||
| ° | 0 | 0 | 0 | 90 | 90 | 0 | ||
| ° | 0 | 0 | 0 | 0…−90 | 0…90 | 0 | ||
| Distribution | - | homogeneous | heterog. | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maier, E.; Lengmüller, M.; Lohner, T. Effect of Transversely Isotropic Elasticity on Elastohydrodynamic Lubrication of Point Contacts. Polymers 2022, 14, 3507. https://doi.org/10.3390/polym14173507
Maier E, Lengmüller M, Lohner T. Effect of Transversely Isotropic Elasticity on Elastohydrodynamic Lubrication of Point Contacts. Polymers. 2022; 14(17):3507. https://doi.org/10.3390/polym14173507
Chicago/Turabian StyleMaier, Enzo, Moritz Lengmüller, and Thomas Lohner. 2022. "Effect of Transversely Isotropic Elasticity on Elastohydrodynamic Lubrication of Point Contacts" Polymers 14, no. 17: 3507. https://doi.org/10.3390/polym14173507
APA StyleMaier, E., Lengmüller, M., & Lohner, T. (2022). Effect of Transversely Isotropic Elasticity on Elastohydrodynamic Lubrication of Point Contacts. Polymers, 14(17), 3507. https://doi.org/10.3390/polym14173507







