Curaua–Aramid Hybrid Laminated Composites for Impact Applications: Flexural, Charpy Impact and Elastic Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Composite Processing
2.3. Flexural Tests
2.4. Charpy Impact Test
2.5. Impulse Excitation Technique
3. Results and Discussion
3.1. Flexural Results
3.2. Charpy Impact Test and Damage Analysis
3.3. Impulse Excitation Technique (IET) Analysis
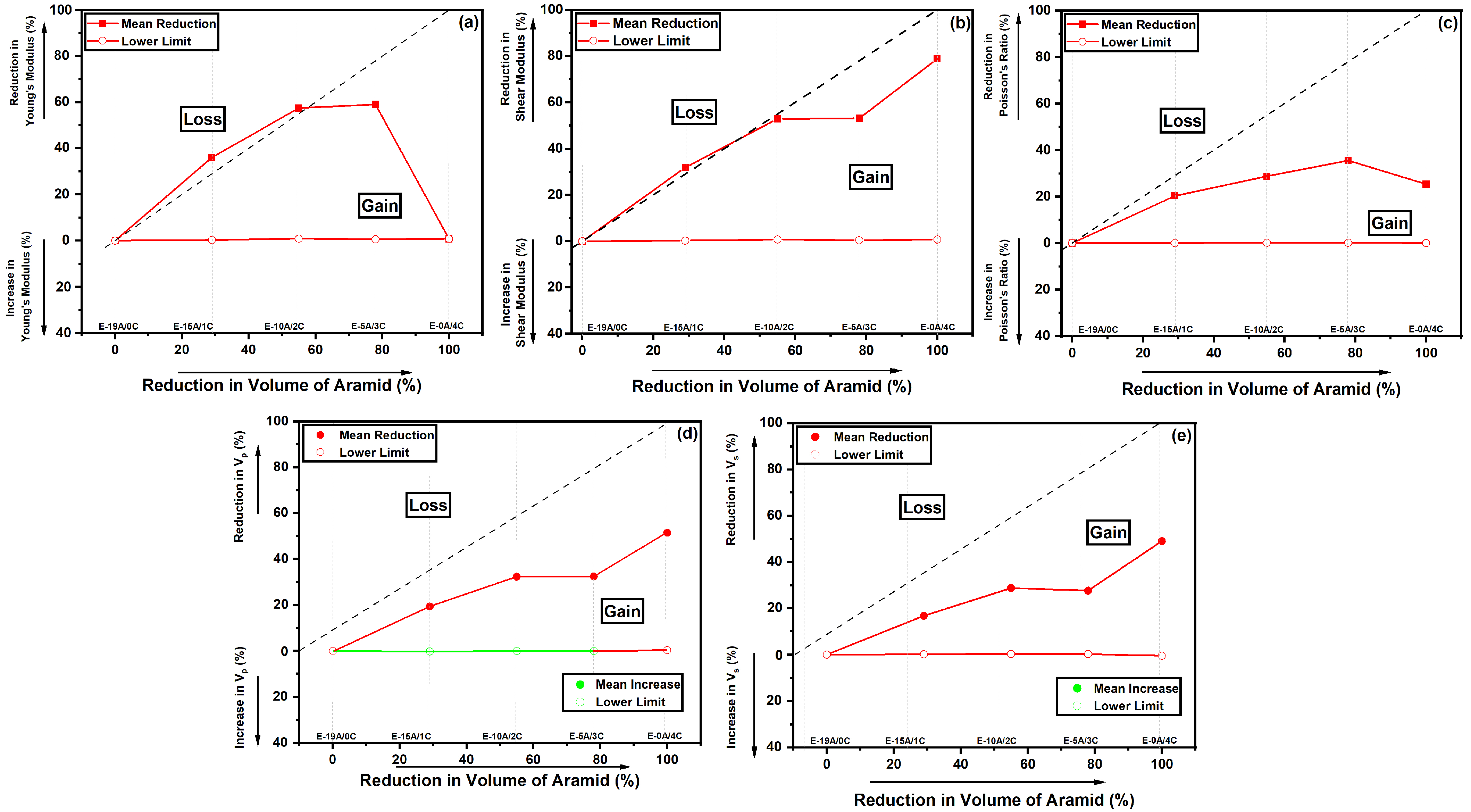
3.4. Reduction Maps
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liang, Y.; Chen, X.; Soutis, C. Review on Manufacture of Military Composite Helmet. Appl. Compos. Mater. 2022, 29, 305–323. [Google Scholar] [CrossRef]
- Li, Y.; Fan, H.; Gao, X.L. Ballistic helmets: Recent advances in materials, protection mechanisms, performance, and head injury mitigation. Compos. Part B Eng. 2022, 238, 109890. [Google Scholar] [CrossRef]
- Abdulrahim, M.; Yawas, D.; Mohammed, R.; Olatunde, A. Hybridization of Polyester/Banana stem Fiber and Cow horn particulate composite for possible production of a military helmet. Int. J. Sustain. Eng. 2021, 14, 1170–1180. [Google Scholar] [CrossRef]
- Salman, S.; Leman, Z.; Ishak, M.; Cardona, F. Effect of kenaf fibers on trauma penetration depth and ballistic impact resistance for laminated composites. Text. Res. J. 2016, 87, 2051–2065. [Google Scholar] [CrossRef]
- Laraba, S.R.; Rezzoug, A.; Halimi, R.; Wei, L.; Yang, Y.; Abdi, S.; Li, Y.; Jie, W. Development of sandwich using low-cost natural fibers: Alfa-Epoxy composite core and jute/metallic mesh-Epoxy hybrid skin composite. Ind. Crop. Prod. 2022, 184, 115093. [Google Scholar] [CrossRef]
- Singh, Y.; Singh, J.; Sharma, S.; Lam, T.D.; Nguyen, D.N. Fabrication and characterization of coir/carbon-fiber reinforced epoxy based hybrid composite for helmet shells and sports-good applications: Influence of fiber surface modifications on the mechanical, thermal and morphological properties. J. Mater. Res. Technol. 2020, 9, 15593–15603. [Google Scholar] [CrossRef]
- Yahaya, R.; Sapuan, S.; Jawaid, M.; Leman, Z.; Zainudin, E. Effect of layering sequence and chemical treatment on the mechanical properties of woven kenaf–aramid hybrid laminated composites. Mater. Des. 2015, 67, 173–179. [Google Scholar] [CrossRef]
- Murali, B.; Vijaya Ramnath, B.M.; Rajamani, D.; Nasr, E.A.; Astarita, A.; Mohamed, H. Experimental Investigations on Dry Sliding Wear Behavior of Kevlar and Natural Fiber-Reinforced Hybrid Composites through an RSM–GRA Hybrid Approach. Materials 2022, 15, 749. [Google Scholar] [CrossRef]
- Bharath, B.; Kumar, G.C.; Shivanna, G.; Hussain, S.S.; Chandrashekhar, B.; Raj, B.S.; Kumar, S.A.; Girisha, C. Fabrication and mechanical characterization of bio-composite helmet. Mater. Today Proc. 2018, 5, 2716–2720. [Google Scholar] [CrossRef]
- Ravi, Y.; Kapilan, N.; Rajole, S.; Balaji, Y.; Reddy, N.V.K.; Venkatesha, B. Damage resistance evaluation of E-glass and hybrid hemp-banana natural fiber composite helmet using drop weight impact test. Mater. Today Proc. 2022, 54, 330–335. [Google Scholar] [CrossRef]
- Qu, K.; Wu, C.; Liu, J.; Yao, Y.; Deng, Y.; Yi, C. Ballistic performance of multi-layered aluminium and UHMWPE fibre laminate targets subjected to hypervelocity impact by tungsten alloy ball. Compos. Struct. 2020, 253, 112785. [Google Scholar] [CrossRef]
- Wu, K.K.; Chen, Y.L.; Yeh, J.N.; Chen, W.L.; Lin, C.S. Ballistic impact performance of SiC ceramic-dyneema fiber composite materials. Adv. Mater. Sci. Eng. 2020, 2020, 9457489. [Google Scholar] [CrossRef]
- Bao, J.W.; Wang, Y.W.; An, R.; Cheng, H.W.; Wang, F.C. Investigation of the mechanical and ballistic properties of hybrid carbon/ aramid woven laminates. Def. Technol. 2021. [Google Scholar] [CrossRef]
- Stephen, C.; Shivamurthy, B.; Mourad, A.H.; Selvam, D.R. High-velocity impact behavior of hybrid fiber-reinforced epoxy composites. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 431. [Google Scholar] [CrossRef]
- Yahaya, R.; Sapuan, S.; Jawaid, M.; Leman, Z.; Zainudin, E.S. Effects of kenaf contents and fiber orientation on physical, mechanical, and morphological properties of hybrid laminated composites for vehicle spall liners. Polym. Compos. 2014, 36, 1469–1476. [Google Scholar] [CrossRef]
- Yue, H.; Rubalcaba, J.C.; Cui, Y.; Fernández-Blázquez, J.P.; Yang, C.; Shuttleworth, P.S. Determination of cross-sectional area of natural plant fibres and fibre failure analysis by in situ SEM observation during microtensile tests. Cellulose 2019, 26, 4693–4706. [Google Scholar]
- Ramírez, A.D.G.; Acevedo, H.S.; Cruz-Hernández, R. Correlation between cross sectional area and torsion degree of fique yarns by image analysis system. J. Phys. Conf. Ser. 2019, 1247, 012030. [Google Scholar] [CrossRef]
- da Luz, F.S.; Garcia Filho, F.d.C.; del Río, M.T.G.; Nascimento, L.F.C.; Pinheiro, W.A.; Monteiro, S.N. Graphene-Incorporated Natural Fiber Polymer Composites: A First Overview. Polymers 2020, 12, 1601. [Google Scholar] [CrossRef]
- Sarasini, F.; Tirillò, J.; D’Altilia, S.; Valente, T.; Santulli, C.; Touchard, F.; Chocinski-Arnault, L.; Mellier, D.; Lampani, L.; Gaudenzi, P. Damage tolerance of carbon/flax hybrid composites subjected to low velocity impact. Compos. Part B Eng. 2016, 91, 144–153. [Google Scholar] [CrossRef]
- Flynn, J.; Amiri, A.; Ulven, C. Hybridized carbon and flax fiber composites for tailored performance. Mater. Des. 2016, 102, 21–29. [Google Scholar] [CrossRef]
- Johnson, S.; Kang, L.; Akil, H.M. Mechanical behavior of jute hybrid bio-composites. Compos. Part B Eng. 2016, 91, 83–93. [Google Scholar] [CrossRef] [Green Version]
- Yahaya, R.; Sapuan, S.; Jawaid, M.; Leman, Z.; Zainudin, E.S. Measurement of ballistic impact properties of woven kenaf-aramid hybrid composites. Measurement 2015, 77, 335–343. [Google Scholar] [CrossRef]
- Salman, S.; Leman, Z.; Hameed Sultan, M.T.; Ishak, M.; Cardona, F. Ballistic Impact Resistance of Plain Woven KenafAramid Reinforced Polyvinyl Butyral Laminated Hybrid Composite. Bioresources 2016, 11, 7282–7295. [Google Scholar] [CrossRef]
- Salman, S.; Sharba, M.; Leman, Z.; Hameed Sultan, M.T.; Ishak, M.; Cardona, F. Tension Compression Fatigue Behavior of Plain Woven Kenaf Kevlar Hybrid Composites. Bioresources 2016, 11, 3575–3586. [Google Scholar] [CrossRef]
- Saidane, E.H.; Scida, D.; Assarar, M.; Sabhi, H.; Rezak, A. Hybridisation effect on diffusion kinetic and tensile mechanical behaviour of epoxy based flax–glass composites. Compos. Part Appl. Sci. Manuf. 2016, 87, 153–160. [Google Scholar] [CrossRef]
- Ridzuan, M.J.; Majid, M.; Afendi, M.; Mazlee, M.N.; Gibson, A. Thermal behaviour and dynamic mechanical analysis of Pennisetum purpureum/glass-reinforced epoxy hybrid composites. Compos. Struct. 2016, 152, 850–859. [Google Scholar] [CrossRef]
- Ramesh, M.; Palanikumar, K.; Hemachandra Reddy, K. Evaluation of Mechanical and Interfacial Properties of Sisal/Jute/Glass Hybrid Fiber Reinforced Polymer Composites. Trans. Indian Inst. Met. 2016, 69, 1851–1859. [Google Scholar] [CrossRef]
- Mahmud, N.; Lin, R.; Jayaraman, K. Flammability, thermal and dynamic mechanical properties of bamboo-glass hybrid composites. J. Thermoplast. Compos. Mater. 2014, 29, 1210–1228. [Google Scholar] [CrossRef]
- Yahaya, R.; Sapuan, S.; Jawaid, M.; Leman, Z.; Zainudin, E.S. Investigating ballistic impact properties of woven kenaf-aramid hybrid composites. Fibers Polym. 2016, 17, 275–281. [Google Scholar] [CrossRef]
- Hajiha, H.; Sain, M. High toughness hybrid biocomposite process optimization. Compos. Sci. Technol. 2015, 111, 44–49. [Google Scholar] [CrossRef]
- Muhammad, Y.H.; Ahmad, S.H.; Bakar, M.A.A.; Mamun, A.A.; Heim, H.P. Mechanical properties of hybrid glass/kenaf fibre-reinforced epoxy composite with matrix modification using liquid epoxidised natural rubber. J. Reinf. Plast. Compos. 2015, 34, 896–906. [Google Scholar] [CrossRef]
- Dalbehera, S.; Acharya, S. Impact of stacking sequence on tribological wear performance of woven Jute-glass hybrid epoxy composites. Tribol. Mater. Surfaces Interfaces 2015, 9, 196–201. [Google Scholar] [CrossRef]
- Gowkanapalli, R.R.; Kumar, M.; Nadadur, K.; basha, S. Tamarind Fruit Fiber and Glass Fiber Reinforced Polyester Composites. Mech. Adv. Mater. Struct. 2015, 22, 770–775. [Google Scholar] [CrossRef]
- Atiqah, A.; Maleque, M.; Jawaid, M.; Iqbal, M.S. Development of kenaf-glass reinforced unsaturated polyester hybrid composite for structural applications. Compos. Part B Eng. 2013, 56, 68–73. [Google Scholar] [CrossRef]
- Yahaya, R.; Sapuan, S.; Jawaid, M.; Leman, Z.; Zainudin, E.S. Quasi-Static Penetration and Ballistic Properties of Kenaf-Aramid Hybrid Composites. Mater. Des. 2014, 63, 775–782. [Google Scholar] [CrossRef]
- Bakkal, M.; Savas, M. Development of Natural Fiber Reinforced Laminated Hybrid Composites. In Advanced Materials Research, Proceedings of the Manufacturing Engineering and Technology for Manufacturing Growth, San Diego, CA, USA, 1–2 November 2012; Trans Tech Publications Ltd.: Wollerau, Switzerland, 2013; Volume 628, pp. 15–20. [Google Scholar] [CrossRef]
- Delgado-Aguilar, M.; Tarrés, Q.; Marques, M.d.F.V.; Espinach, F.X.; Julián, F.; Mutjé, P.; Vilaseca, F. Explorative study on the use of Curauá reinforced polypropylene composites for the automotive industry. Materials 2019, 12, 4185. [Google Scholar] [CrossRef]
- Teixeira, R.S.; Santos, S.F.d.; Christoforo, A.L.; Payá, J.; Savastano, H., Jr.; Lahr, F.R. Impact of content and length of curauá fibers on mechanical behavior of extruded cementitious composites: Analysis of variance. Cem. Concr. Compos. 2019, 102, 134–144. [Google Scholar] [CrossRef]
- Teixeira, F.P.; de Andrade Silva, F. On the use of natural curauá reinforced cement based composites for structural applications. Cem. Concr. Compos. 2020, 114, 103775. [Google Scholar] [CrossRef]
- Braga, F.d.O.; Bolzan, L.T.; Lima Jr., E. P.; Monteiro, S.N. Performance of natural curaua fiber-reinforced polyester composites under 7.62mm bullet impact as a stand-alone ballistic armor. J. Mater. Res. Technol. 2017, 6, 323–328. [Google Scholar] [CrossRef]
- Monteiro, S.N.; Braga, F.d.O.; Lima, E.P.; Louro, L.H.L.; Drelich, J.W. Promising curaua fiber-reinforced polyester composite for high-impact ballistic multilayered armor. Polym. Eng. Sci. 2017, 57, 947–954. [Google Scholar] [CrossRef]
- Tomczak, F.; Satyanarayana, K.G.; Sydenstricker, T.H.D. Studies on lignocellulosic fibers of Brazil: Part III–Morphology and properties of Brazilian curauá fibers. Compos. Part Appl. Sci. Manuf. 2007, 38, 2227–2236. [Google Scholar] [CrossRef]
- Hattalli, S.; Benaboura, A.; Ham-Pichavant, F.; Nourmamode, A.; Castellan, A. Adding value to Alfa grass (Stipa tenacissima L.) soda lignin as phenolic resins 1. Lignin characterization. Polym. Degrad. Stab. 2002, 76, 259–264. [Google Scholar] [CrossRef]
- Hoareau, W.; Trindade, W.G.; Siegmund, B.; Castellan, A.; Frollini, E. Sugar cane bagasse and curaua lignins oxidized by chlorine dioxide and reacted with furfuryl alcohol: Characterization and stability. Polym. Degrad. Stab. 2004, 86, 567–576. [Google Scholar] [CrossRef]
- Malkapuram, R.; Kumar, V.; Negi, Y.S. Recent development in natural fiber reinforced polypropylene composites. J. Reinf. Plast. Compos. 2009, 28, 1169–1189. [Google Scholar] [CrossRef]
- Martí-Ferrer, F.; Vilaplana, F.; Ribes-Greus, A.; Benedito-Borrás, A.; Sanz-Box, C. Flour rice husk as filler in block copolymer polypropylene: Effect of different coupling agents. J. Appl. Polym. Sci. 2006, 99, 1823–1831. [Google Scholar] [CrossRef]
- Summerscales, J.; Dissanayake, N.P.; Virk, A.S.; Hall, W. A review of bast fibres and their composites. Part 1—Fibres as reinforcements. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1329–1335. [Google Scholar] [CrossRef]
- Khan, T.; Hameed Sultan, M.T.B.; Ariffin, A.H. The challenges of natural fiber in manufacturing, material selection, and technology application: A review. J. Reinf. Plast. Compos. 2018, 37, 770–779. [Google Scholar] [CrossRef]
- Rubio, I.; Rodríguez-Millán, M.; Marco, M.; Olmedo, A.; Loya, J. Ballistic performance of aramid composite combat helmet for protection against small projectiles. Compos. Struct. 2019, 226, 111153. [Google Scholar] [CrossRef]
- da Silva, A.O.; de Castro Monsores, K.G.; de Sant’ Ana Oliveira, S.; Weber, R.P.; Monteiro, S.N. Ballistic behavior of a hybrid composite reinforced with curaua and aramid fabric subjected to ultraviolet radiation. J. Mater. Res. Technol. 2018, 7, 584–591. [Google Scholar] [CrossRef]
- Ray, R.; Das, S.N.; Mohapatra, A. Study on Physical and Mechanical Behavior of Bauhinia Vahlii Fiber Filled Glass–Epoxy Hybrid Composites. In Lecture Notes in Mechanical Engineering; Springer: Singapore, 2022; pp. 587–595. [Google Scholar] [CrossRef]
- Meliande, N.M.; Silveira, P.H.P.M.d.; Monteiro, S.N.; Nascimento, L.F.C. Tensile Properties of Curaua–Aramid Hybrid Laminated Composites for Ballistic Helmet. Polymers 2022, 14, 2588. [Google Scholar] [CrossRef]
- Palta, E.; Fang, H.; Weggel, D.C. Finite element analysis of the Advanced Combat Helmet under various ballistic impacts. Int. J. Impact Eng. 2018, 112, 125–143. [Google Scholar] [CrossRef]
- Popov, I.; Shitikova, M. Impulse excitation technique and its application for identification of material damping: An overview. IOP Conf. Ser. Mater. Sci. Eng. 2020, 962, 022025. [Google Scholar] [CrossRef]
- Othman, A.R.; Hassan, M. Effect of different construction designs of aramid fabric on the ballistic performances. Mater. Des. 2013, 44, 407–413. [Google Scholar] [CrossRef]
- Walsh, S.M.; Scott, B.R.; Jones, T.L.; Cho, K.; Wolbert, J. A Materials Approach in the Development of Multi-Threat Warfighter Head Protection; Technical report; Army Research Lab: Aberdeen Proving Ground, MD, USA, 2008. [Google Scholar]
- ASTM D790; Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials. American Society For Testing Materials: West Conshohocken, PA, USA,, 2017.
- ASTM D6110; Standard Test Method for Determining the Charpy Impact Resistance of Notched Specimens of Plastics. American Society For Testing Materials: West Conshohocken, PA, USA, 2018.
- Roebben, G.; Bollen, B.; Brebels, A.; Van Humbeeck, J.; Van der Biest, O. Impulse excitation apparatus to measure resonant frequencies, elastic moduli, and internal friction at room and high temperature. Rev. Sci. Instrum. 1997, 68, 4511–4515. [Google Scholar] [CrossRef]
- ASTM E1876-09; Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration. American Society For Testing Materials: West Conshohocken, PA, USA, 2016.
- Sood, M.; Dwivedi, G. Effect of fiber treatment on flexural properties of natural fiber reinforced composites: A review. Egypt. J. Pet. 2018, 27, 775–783. [Google Scholar] [CrossRef]
- Liang, Q.; Liu, J.; Wang, X.; Liu, X.; Zhang, D.; Qian, K. Flexural progressive failure mechanism of hybrid 3D woven composites: Combination of X-ray tomography, acoustic emission and digital image correlation. Compos. Struct. 2022, 280, 114894. [Google Scholar] [CrossRef]
- Subagia, I.A.; Kim, Y.; Tijing, L.D.; Kim, C.S.; Shon, H.K. Effect of stacking sequence on the flexural properties of hybrid composites reinforced with carbon and basalt fibers. Compos. Part B Eng. 2014, 58, 251–258. [Google Scholar] [CrossRef]
- Neto, J.; Queiroz, H.; Aguiar, R.; Lima, R.; Cavalcanti, D.; Banea, M.D. A Review of Recent Advances in Hybrid Natural Fiber Reinforced Polymer Composites. J. Renew. Mater. 2022, 10, 561. [Google Scholar] [CrossRef]
- Pai, A.R.; Jagtap, R.N. Surface morphology & mechanical properties of some unique natural fiber reinforced polymer composites—A review. J. Mater. Environ. Sci. 2015, 6, 902–917. [Google Scholar]
- Park, R.; Jang, J. Performance improvement of carbon fiber/polyethylene fiber hybrid composites. J. Mater. Sci. 1999, 34, 2903–2910. [Google Scholar] [CrossRef]
- Zachariah, A.S.; Shenoy, B.S.; Jayan, J.; Pai, K.D. Experimental investigation on dynamic and static transverse behaviour of thin woven Carbon/Aramid hybrid laminates. J. King Saud Univ. Eng. Sci. 2022, 34, 273–281. [Google Scholar] [CrossRef]
- Yi, S.; Xu, S.; Li, Y.; Gan, W.; Yi, X.; Liu, W.; Wang, Q.; Wang, H.; Ou, R. Synergistic toughening effects of grafting modification and elastomer-olefin block copolymer addition on the fracture resistance of wood particle/polypropylene/elastomer composites. Mater. Des. 2019, 181, 107918. [Google Scholar] [CrossRef]
- Feng, X.; Sheng, Y.; Ge, X.; Wu, Z.; Huang, Q. Evaluation of the properties of hybrid yellow poplar (Liriodendron sino-americanum): A comparison study with yellow poplar (Liriodendron tulipifera). Maderas Cienc. Tecnol. 2021, 23. [Google Scholar] [CrossRef]
- Yu, C.; Yu, P.; Ma, G.; Zhou, L.; Deng, F.; Wang, F.; Zhu, X. Preparation of aramid-based epoxy resin from low-grade aramid. RSC Adv. 2021, 11, 36265–36272. [Google Scholar] [CrossRef]
- Safri, S.N.A.; Sultan, M.T.H.; Jawaid, M.; Jayakrishna, K. Impact behaviour of hybrid composites for structural applications: A review. Compos. Part Eng. 2018, 133, 112–121. [Google Scholar] [CrossRef]
- Sridharan, S. Introduction. In Delamination Behaviour of Composites; Sridharan, S., Ed.; Woodhead Publishing Series in Composites Science and Engineering; Woodhead Publishing: Sawston, UK, 2008; pp. 21–23. [Google Scholar] [CrossRef]
- Ogihara, S.; Takeda, N.; Kobayashi, A. Transverse cracking in CFRP cross-ply laminates with interlaminar resin layers. Adv. Compos. Mater. 1998, 7, 347–363. [Google Scholar] [CrossRef]
- Wang, A. Chapter 2—Fracture Analysis of Interlaminar Cracking. In Interlaminar Response of Composite Materials; Pagano, N., Ed.; Composite Materials Series; Elsevier: Amsterdam, The Netherlands, 1989; Volume 5, pp. 69–109. [Google Scholar] [CrossRef]
- Kumar, S.; Gupta, D.S.; Singh, I.; Sharma, A. Behavior of Kevlar/Epoxy Composite Plates Under Ballistic Impact. J. Reinf. Plast. Compos. 2010, 29, 2048–2064. [Google Scholar] [CrossRef]
- Singh, T.J.; Samanta, S. Effect of stacking sequence on mechanical strength of bamboo/kevlar K29 inter-ply laminated hybrid composite. Indian J. Fibre Text. Res. 2017, 42, 230–234. [Google Scholar]




| Curaua | Cellulose (wt%) | Hemicellulose (wt%) | Lignin (wt%) | Wax (wt%) | Pectin (wt%) | Ash (wt%) |
| 73.6 | 9.9 | 7.5 | - | - | - | |
| Microfibril Angle () | Density (g/cm3) | Fiber Diameter (m) | Tensile Strength (MPa) | Specific Strength (S/) | Elongation at Break (%) | |
| 15 | 1.4 | 170 | 158–729 | 113–521 | 5 |
| Composite Configuration | Number of Layers | |
|---|---|---|
| Aramid Woven Fabric (A) | Curaua Non-Woven Mat (C) | |
| E-19A/0C | 19 | 0 |
| E-15A/1C | 15 | 1 |
| E-10A/2C | 10 | 2 |
| E-5A/3C | 5 | 3 |
| E-0A/4C | 0 | 4 |
| Composite | Weight (g) | Thickness (mm) | Vol.% Total Reinforcement | Vol.% Aramid | Vol.% Curaua | Areal Density (Kg/m2) |
|---|---|---|---|---|---|---|
| PASGT-based | ~200 | ~ 8–10 | ~70 | - | - | 11.24 |
| E-19A/0C | 197.78 ± 1.41 | 8.32 ± 0.03 | 73.29 ± 0.58 | 73.29 ± 0.58 | 0 | 10.99 ± 0.07 |
| E-15A/1C | 204.65 ± 0.92 | 9.06 ± 0.04 | 68.52 ± 0.63 | 52.06 ± 0.39 | 16.47 ± 0.44 | 11.37 ± 0.51 |
| E-10A/2C | 200.47 ± 2.83 | 9.37 ± 0.08 | 65.00 ± 0.83 | 33.27 ± 0.40 | 31.73 ± 0.76 | 11.14 ± 0.16 |
| E-5A/3C | 196.14 ± 2.17 | 9.61 ± 0.13 | 61.22 ± 0.59 | 15.96 ± 0.15 | 45.26 ± 0.72 | 10.90 ± 0.12 |
| E-0A/4C | 192.41 ± 2.21 | 9.98 ± 0.12 | 57.97 ± 0.86 | 0 | 57.97 ± 0.86 | 10.69 ± 0.12 |
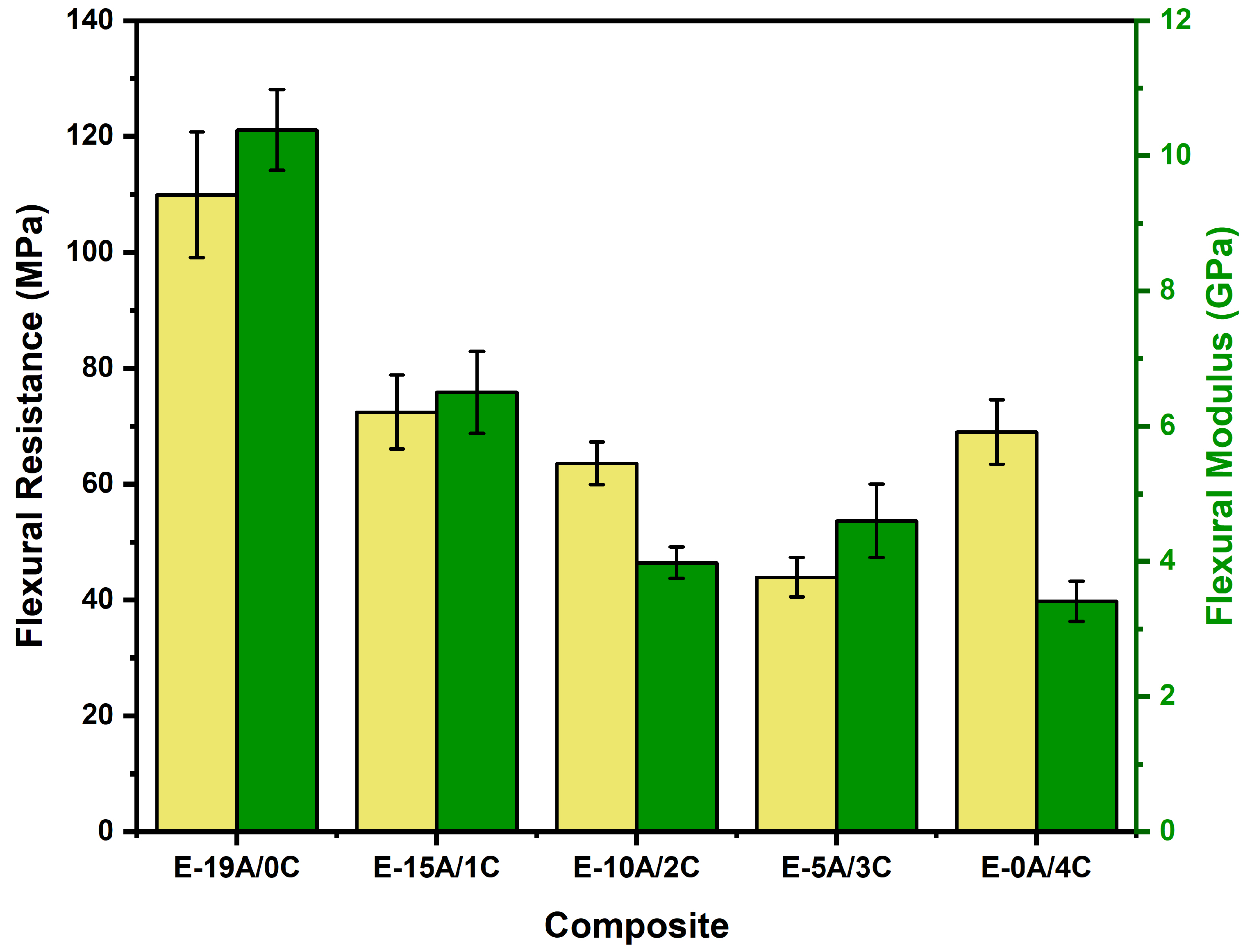
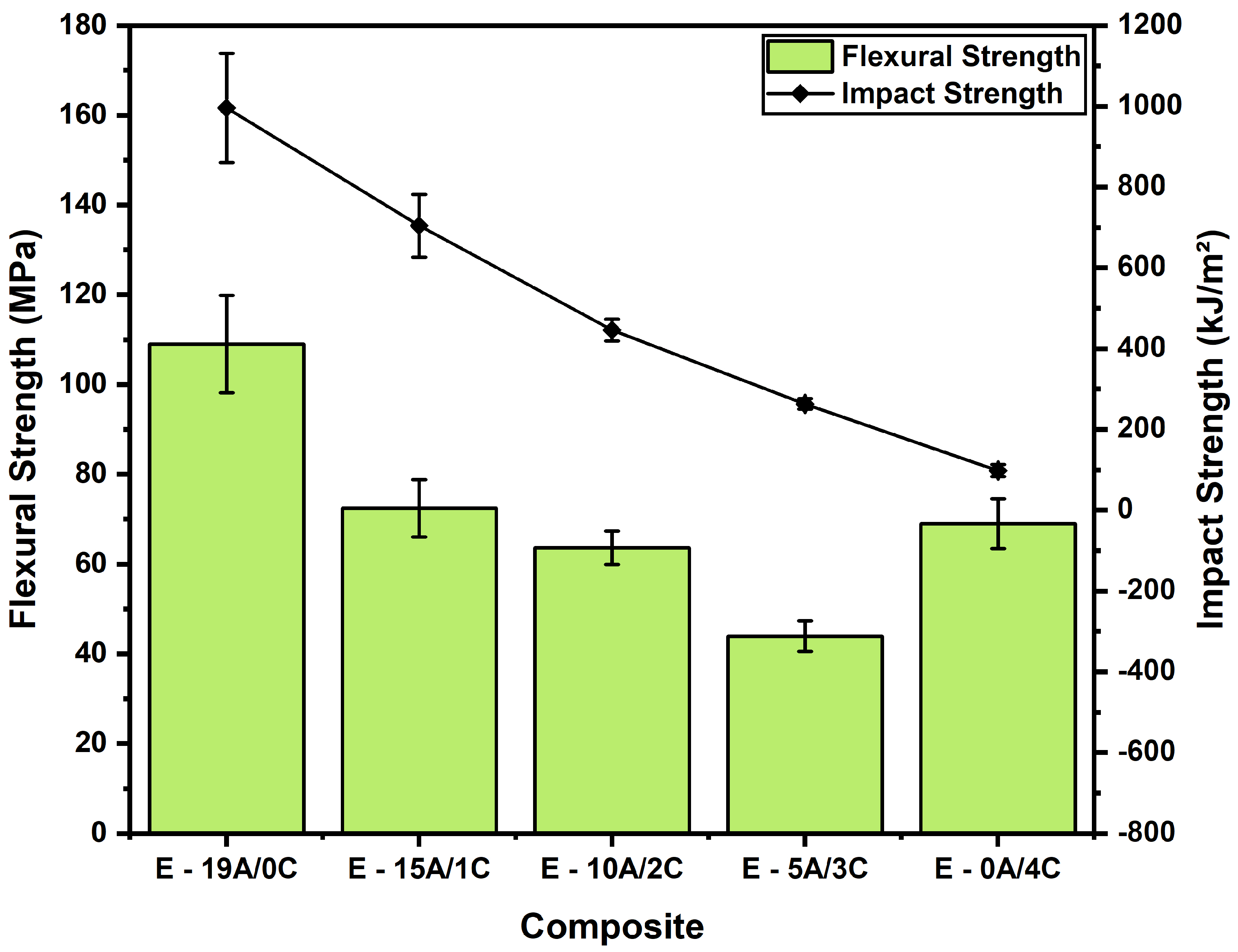
| Composite | Aramid Volume Reduction (%) | (MPa) | Ef (GPa) |
|---|---|---|---|
| E-19A/0C | 0 | 109.02 ± 10.83 | 10.38 ± 0.60 |
| E-15A/1C | 29 | 72.44 ± 6.38 | 6.50 ± 0.60 |
| E-10A/2C | 55 | 63.60 ± 3.71 | 3.98 ± 0.23 |
| E-5A/3C | 78 | 43.94 ± 3.42 | 4.60 ± 0.54 |
| E-0A/4C | 100 | 68.98 ± 5.58 | 3.41 ± 0.30 |
| Mean Treatment Squares | Mean Residue Squares | F (Calculated) | Fcritic (Tabulated 1) | q (Tabulated 2) | MSD |
|---|---|---|---|---|---|
| 4473.80 | 42.92 | 104.24 | 2.65 | 4.07 | 9.43 |
| Mean Treatment Squares | Mean Residue Squares | F (Calculated) | Fcritic (Tabulated 1) | q (Tabulated 2) | MSD |
|---|---|---|---|---|---|
| 63.86 | 0.231 | 276.19 | 2.65 | 4.07 | 0.69 |
| Mean Treatment Squares | Mean Residue Squares | F (Calculated) | Fcritic (Tabulated 1) | q (Tabulated 2) | MSD |
|---|---|---|---|---|---|
| 142,858,001 | 825,184 | 173.12 | 2.69 | 4.10 | 1.41 |
| Composite | Young’s Modulus E (GPa) | Shear Modulus G (GPa) | Poisson’s Ratio | Longitudinal Wave Velocity Vp (m/s) | Shear Wave Velocity Vs (m/s) |
|---|---|---|---|---|---|
| E-19A/0C | 17.64 ± 0.54 | 5.59 ± 0.14 | 0.59 ± 0.05 | 4110 ± 960 | 2111 ± 63 |
| E-15A/1C | 11.28 ± 0.36 | 3.81 ± 0.08 | 0.47 ± 0.04 | 3314 ± 774 | 1756 ± 41 |
| E-10A/2C | 7.49 ± 0.25 | 2.63 ± 0.04 | 0.42 ± 0.04 | 2783 ± 652 | 1504 ± 25 |
| E-5A/3C | 7.22 ± 0.35 | 2.62 ± 0.08 | 0.38 ± 0.07 | 2778 ± 660 | 1527 ± 55 |
| E-0A/4C | 3.41 ± 0.22 | 1.18 ± 0.03 | 0.44 ± 0.08 | 1994 ± 332 | 1075 ± 31 |
| Mean Treatment Squares | Mean Residue Squares | F (Calculated) | Fcritic (Tabulated 1) | q (Tabulated 2) | MSD |
|---|---|---|---|---|---|
| 289.28 | 0.13 | 2208 | 2.58 | 4.02 | 0.46 |
| Mean Treatment Squares | Mean Residue Squares | F (Calculated) | Fcritic (Tabulated 1) | q (Tabulated 2) | MSD |
|---|---|---|---|---|---|
| 27.05 | 0.01 | 3875 | 2.58 | 4.02 | 0.11 |
| Mean Treatment Squares | Mean Residue Squares | F (Calculated) | Fcritic (Tabulated 1) | q (Tabulated 2) | MSD |
|---|---|---|---|---|---|
| 0.06 | 0.01 | 18.68 | 2.58 | 4.02 | 0.07 |
| Mean Treatment Squares | Mean Residue Squares | F (Calculated) | Fcritic (Tabulated 1) | q (Tabulated 2) | MSD |
|---|---|---|---|---|---|
| 6,097,543 | 498,321 | 12.24 | 2.58 | 4.02 | 899 |
| Mean Treatment Squares | Mean Residue Squares | F (Calculated) | Fcritic (Tabulated 1) | q (Tabulated 2) | MSD |
|---|---|---|---|---|---|
| 1,438,705 | 2052 | 701 | 2.58 | 4.02 | 57.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meliande, N.M.; Oliveira, M.S.; Silveira, P.H.P.M.d.; Dias, R.R.; Marçal, R.L.S.B.; Monteiro, S.N.; Nascimento, L.F.C. Curaua–Aramid Hybrid Laminated Composites for Impact Applications: Flexural, Charpy Impact and Elastic Properties. Polymers 2022, 14, 3749. https://doi.org/10.3390/polym14183749
Meliande NM, Oliveira MS, Silveira PHPMd, Dias RR, Marçal RLSB, Monteiro SN, Nascimento LFC. Curaua–Aramid Hybrid Laminated Composites for Impact Applications: Flexural, Charpy Impact and Elastic Properties. Polymers. 2022; 14(18):3749. https://doi.org/10.3390/polym14183749
Chicago/Turabian StyleMeliande, Natalin Michele, Michelle Souza Oliveira, Pedro Henrique Poubel Mendonça da Silveira, Rafael Rodrigues Dias, Rubens Lincoln Santana Blazutti Marçal, Sergio Neves Monteiro, and Lucio Fabio Cassiano Nascimento. 2022. "Curaua–Aramid Hybrid Laminated Composites for Impact Applications: Flexural, Charpy Impact and Elastic Properties" Polymers 14, no. 18: 3749. https://doi.org/10.3390/polym14183749
APA StyleMeliande, N. M., Oliveira, M. S., Silveira, P. H. P. M. d., Dias, R. R., Marçal, R. L. S. B., Monteiro, S. N., & Nascimento, L. F. C. (2022). Curaua–Aramid Hybrid Laminated Composites for Impact Applications: Flexural, Charpy Impact and Elastic Properties. Polymers, 14(18), 3749. https://doi.org/10.3390/polym14183749









