Predictive Shapes of Ellipsoid PPDL-PTHF Copolymer Particles Prepared by the Phantom Stretching Technique
Abstract
:1. Introduction
2. Materials and Methods
2.1. Microparticle Preparation and Characterization
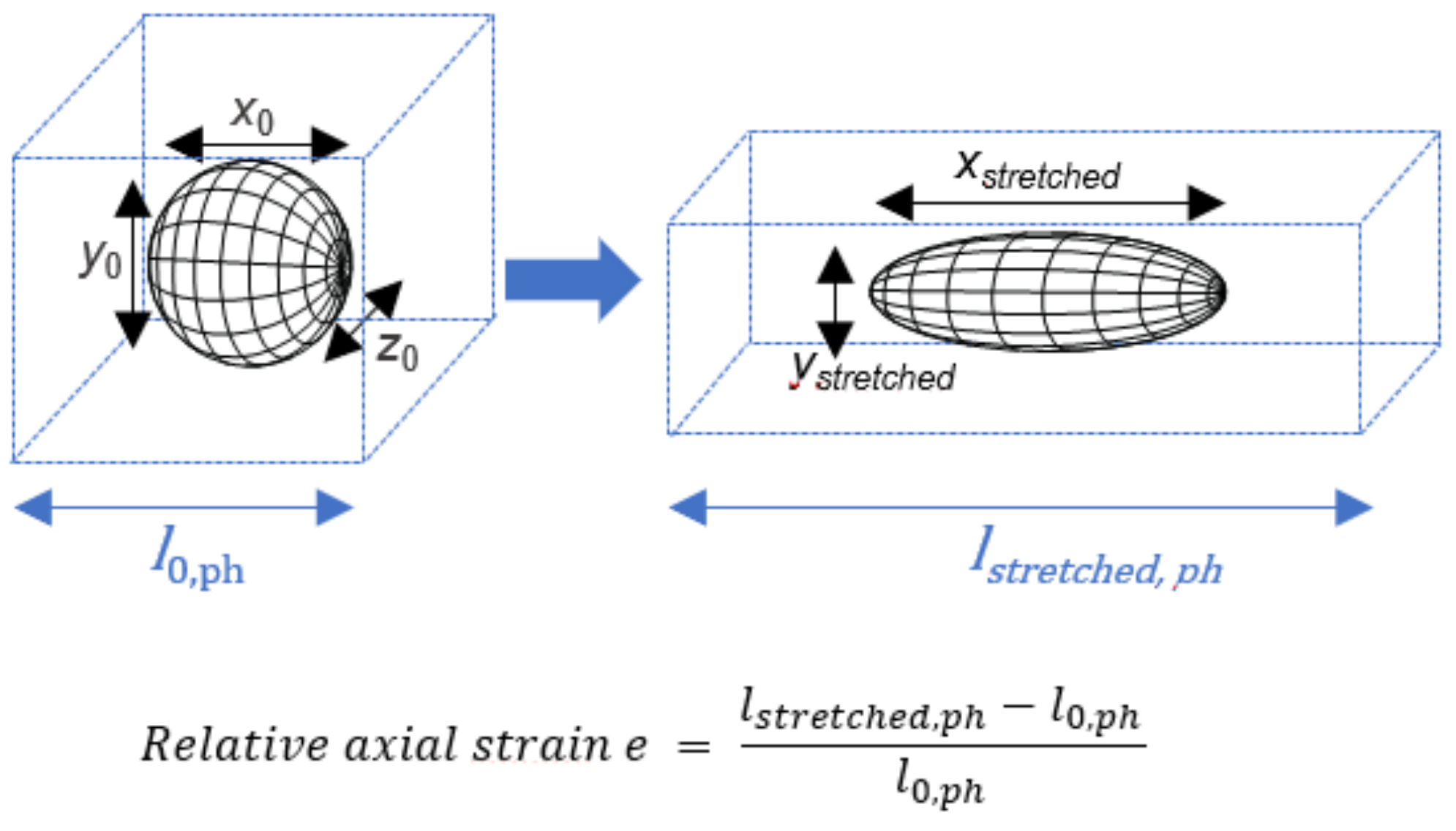
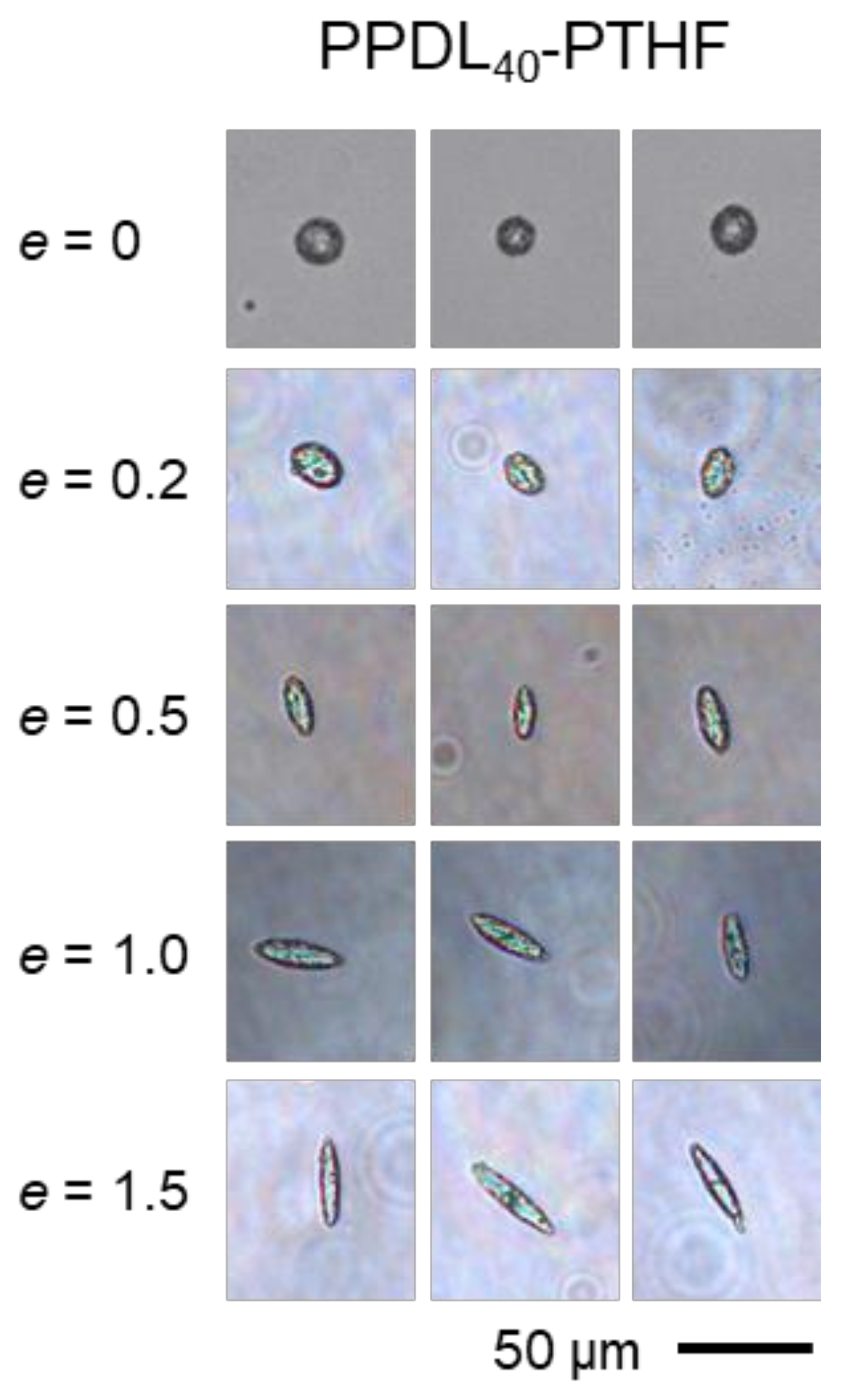
2.2. Particle Embedding in PVA Phantoms, Stretching, and Microscopic Evaluation of Aspect Ratios
2.3. Thermomechanical Tests
2.4. Model Evaluation
3. Results and Discussion
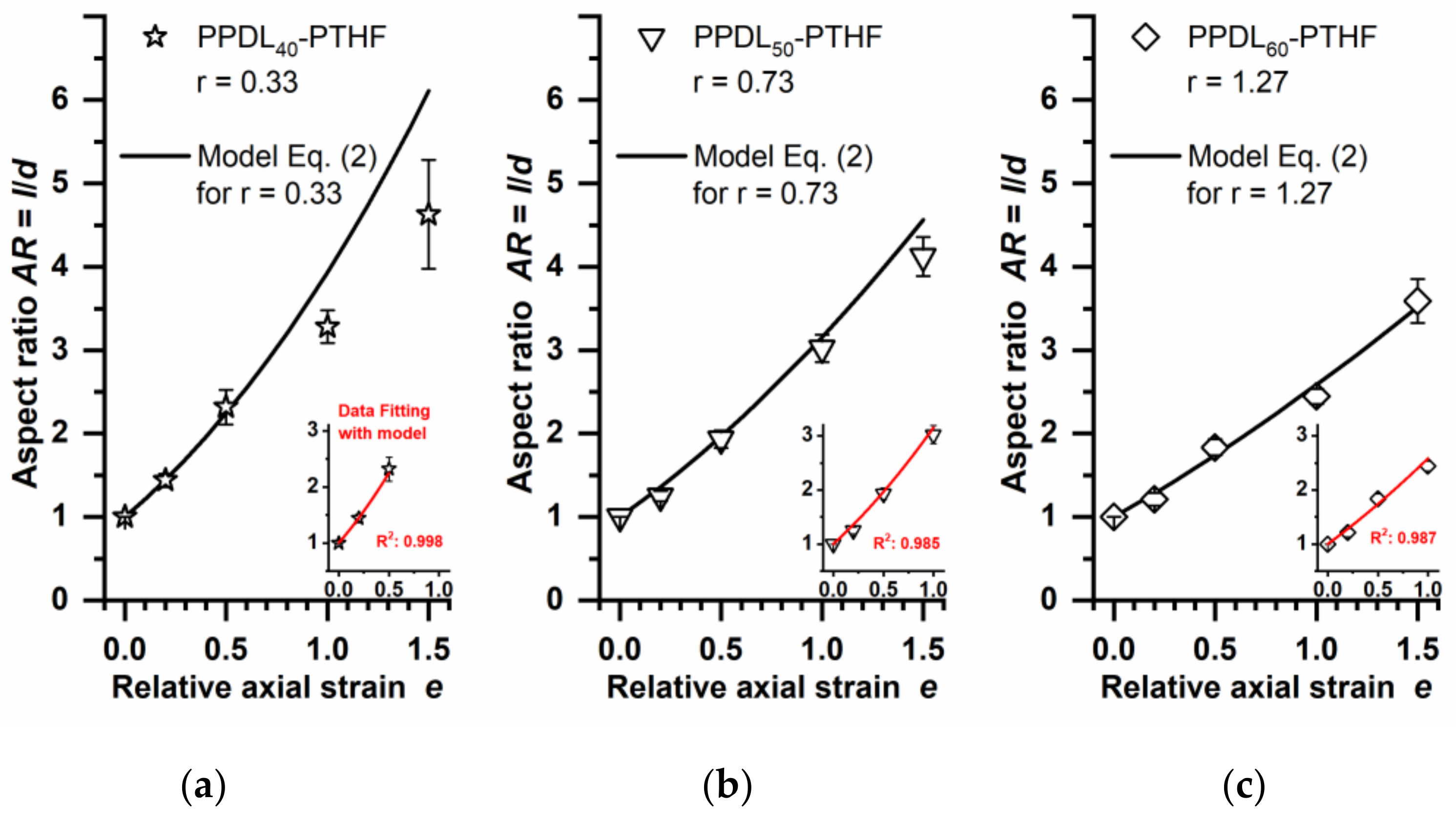
3.1. Deformation Models to Predict Aspect Ratios
3.2. Applicability of the Elastic Deformation Model to Multiblock Copolymer Microparticles
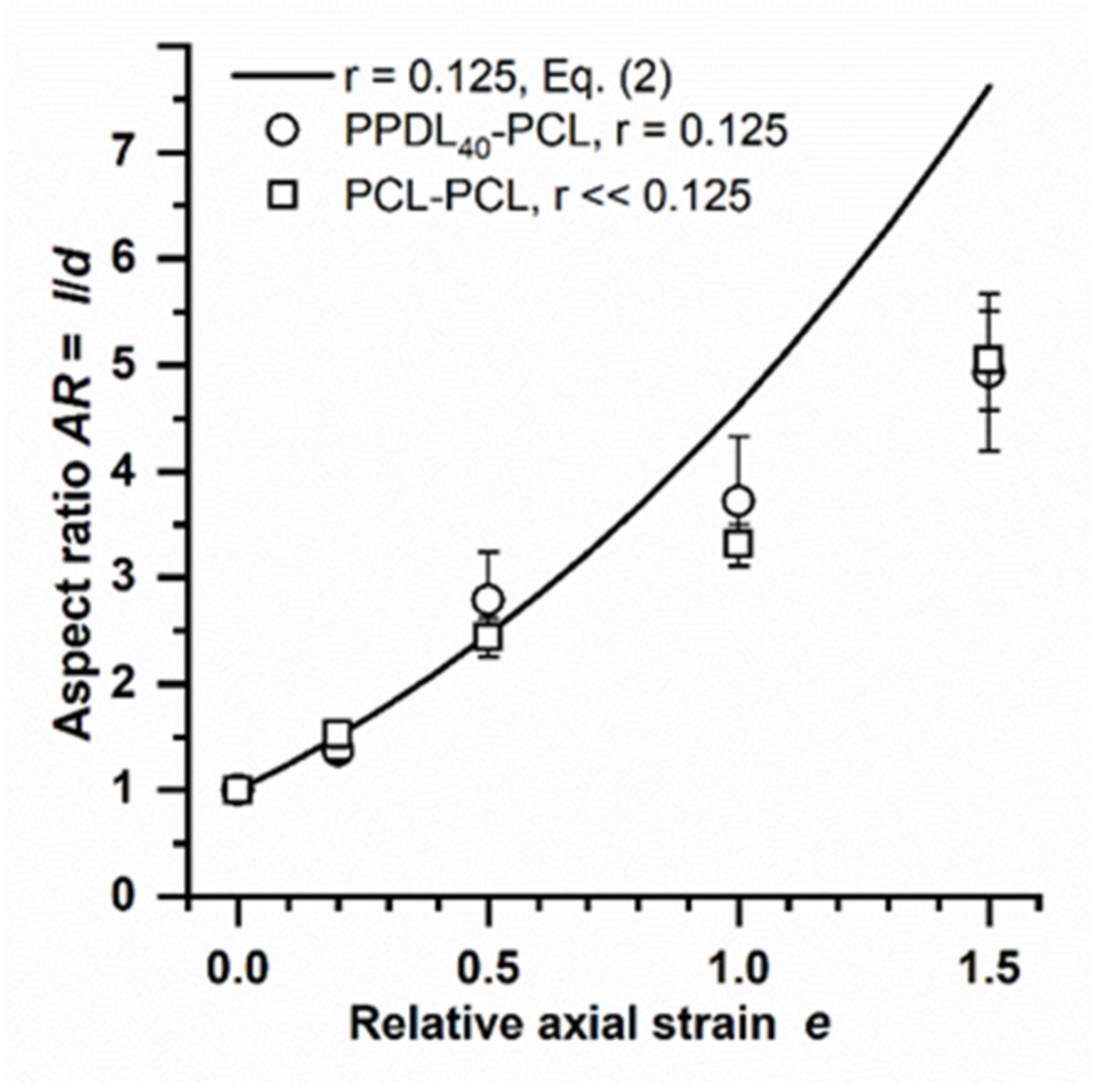
3.3. Investigation of Limitations of the Deformation Model for the Multiblock Copolymers
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meng, C.; Pollard, D.D. Eshelby’s solution for ellipsoidal inhomogeneous inclusions with applications to compaction bands. J. Struct. Geol. 2014, 67, 1–19. [Google Scholar] [CrossRef]
- Nikishina, M.A.; Alexandrov, D.V. Nucleation and growth dynamics of ellipsoidal crystals in metastable liquids. Philos. Trans. R. Soc. 2021, 379, 20200306. [Google Scholar] [CrossRef] [PubMed]
- Wischke, C.; Schossig, M.; Lendlein, A. Shape-Memory Effect of Micro-/Nanoparticles from Thermoplastic Multiblock Copolymers. Small 2014, 10, 83–87. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Haghnegahdar, A.; Feng, Y.; Patil, A.; Kulkarni, N.; Singh, G.J.P.; Malhotra, G.; Bharadwaj, R. Prediction of the carrier shape effect on particle transport, interaction and deposition in two dry powder inhalers and a mouth-to-G13 human respiratory system: A CFD-DEM study. J. Aerosol Sci. 2022, 160, 105899. [Google Scholar] [CrossRef]
- Bhide, A.R.; Jindal, A.B. Fabrication and evaluation of artemether loaded polymeric nanorods obtained by mechanical stretching of nanospheres. Int. J. Pharm. 2021, 605, 120820. [Google Scholar] [CrossRef] [PubMed]
- Champion, J.A.; Mitragotri, S. Role of target geometry in phagocytosis. Proc. Natl. Acad. Sci. USA 2006, 103, 4930–4934. [Google Scholar] [CrossRef]
- Decuzzi, P.; Ferrari, M. The adhesive strength of non-spherical particles mediated by specific interactions. Biomaterials 2006, 27, 5307–5314. [Google Scholar] [CrossRef]
- Arnida; Janát-Amsbury, M.M.; Ray, A.; Peterson, C.M.; Ghandehari, H. Geometry and surface characteristics of gold nanoparticles influence their biodistribution and uptake by macrophages. Eur. J. Pharm. Biopharm. 2011, 77, 417–423. [Google Scholar] [CrossRef]
- Hadji, H.; Bouchemal, K. Effect of micro- and nanoparticle shape on biological processes. J. Control. Release 2022, 342, 93–110. [Google Scholar] [CrossRef]
- Castoldi, A.; Empting, M.; De Rossi, C.; Mayr, K.; Dersch, P.; Hartmann, R.; Müller, R.; Gordon, S.; Lehr, C.-M. Aspherical and Spherical InvA497-Functionalized Nanocarriers for Intracellular Delivery of Anti-Infective Agents. Pharm. Res. 2018, 36, 22. [Google Scholar] [CrossRef] [Green Version]
- Schwarzer, M.; Brehm, J.; Vollmer, M.; Jasinski, J.; Xu, C.; Zainuddin, S.; Fröhlich, T.; Schott, M.; Greiner, A.; Scheibel, T.; et al. Shape, size, and polymer dependent effects of microplastics on Daphnia magna. J. Hazard. Mater. 2022, 426, 128136. [Google Scholar] [CrossRef]
- Haryadi, B.M.; Hafner, D.; Amin, I.; Schubel, R.; Jordan, R.; Winter, G.; Engert, J. Nonspherical Nanoparticle Shape Stability Is Affected by Complex Manufacturing Aspects: Its Implications for Drug Delivery and Targeting. Adv. Healthc. Mater. 2019, 8, 1900352. [Google Scholar] [CrossRef]
- Gadzinowski, M.; Mickiewicz, D.; Basinska, T. Spherical versus prolate spheroidal particles in biosciences: Does the shape make a difference? Polym. Adv. Technol. 2021, 32, 3867–3876. [Google Scholar] [CrossRef]
- Sutera, S.P.; Mehrjardi, M.H. Deformation and Fragmentation of Human Red Blood-Cells in Turbulent Shear-Flow. Biophys. J. 1975, 15, 1–10. [Google Scholar] [CrossRef]
- Heslinga, M.J.; Mastria, E.M.; Eniola-Adefeso, O. Fabrication of biodegradable spheroidal microparticles for drug delivery applications. J. Control. Release 2009, 138, 235–242. [Google Scholar] [CrossRef]
- Snoeks, E.; van Blaaderen, A.; van Dillen, T.; van Kats, C.M.; Brongersma, M.L.; Polman, A. Colloidal ellipsoids with continuously variable shape. Adv. Mater. 2000, 12, 1511–1514. [Google Scholar] [CrossRef]
- Jiang, P.; Bertone, J.F.; Colvin, V.L. A lost-wax approach to monodisperse colloids and their crystals. Science 2001, 291, 453–457. [Google Scholar] [CrossRef]
- Dendukuri, D.; Tsoi, K.; Hatton, T.A.; Doyle, P.S. Controlled synthesis of nonspherical microparticles using microfluidics. Langmuir 2005, 21, 2113–2116. [Google Scholar] [CrossRef]
- Hwang, D.K.; Oakey, J.; Toner, M.; Arthur, J.A.; Anseth, K.S.; Lee, S.; Zeiger, A.; Van Vliet, K.J.; Doyle, P.S. Stop-Flow Lithography for the Production of Shape-Evolving Degradable Microgel Particles. J. Am. Chem. Soc. 2009, 131, 4499–4504. [Google Scholar] [CrossRef]
- Rolland, J.P.; Maynor, B.W.; Euliss, L.E.; Exner, A.E.; Denison, G.M.; DeSimone, J.M. Direct fabrication and harvesting of monodisperse, shape-specific nanobiomaterials. J. Am. Chem. Soc. 2005, 127, 10096–10100. [Google Scholar] [CrossRef]
- Franses, E.L.; Caruthers, J.M.; Keville, K.M. Nonsperical Particles and Methods Thereof. U.S. Patent 4,743,507, 10 May 1988. [Google Scholar]
- Nagy, M.; Keller, A. Ellipsoidal Polymer Particles with Predesigned Axial-Ratio. Polym. Commun. 1989, 30, 130–132. [Google Scholar]
- Li, Z.; Chen, Z.; Gao, Y.; Xing, Y.; Zhou, Y.; Luo, Y.; Xu, W.; Chen, Z.; Gao, X.; Gupta, K.; et al. Shape memory micro-anchors with magnetic guidance for precision micro-vascular deployment. Biomaterials 2022, 283, 121426. [Google Scholar] [CrossRef] [PubMed]
- Guha, S.; Jindal, A.B. An insight into obtaining of non-spherical particles by mechanical stretching of micro- and nanospheres. J. Drug Deliv. Sci. Technol. 2020, 59, 101860. [Google Scholar] [CrossRef]
- Keville-Polizopoulus, K.M. Preparation, Characterization, and Flow Behavior of Dispersions of Monodisperse Microspheroids. PhD Thesis, Prudue University, West Lafayette, IN, USA, 1988. [Google Scholar]
- Friess, F.; Roch, T.; Seifert, B.; Lendlein, A.; Wischke, C. Phagocytosis of spherical and ellipsoidal micronetwork colloids from crosslinked poly(epsilon-caprolactone). Int. J. Pharm. 2019, 567, 118461. [Google Scholar] [CrossRef]
- Motokucho, S.; Furukawa, M.; Kawashima, M.; Kojio, K.; Yoshinaga, K. Physical properties of poly(tetrahydrofuran)-block-poly(2-ethyl-2-oxazoline) triblock copolymer. Polym. J. 2013, 45, 1115–1119. [Google Scholar] [CrossRef]
- Champion, J.A.; Katare, Y.K.; Mitragotri, S. Making polymeric micro- and nanoparticles of complex shapes. Proc. Natl. Acad. Sci. USA 2007, 104, 11901–11904. [Google Scholar] [CrossRef]
- Friess, F.; Lendlein, A.; Wischke, C. Switching microobjects from low to high aspect ratios using a shape-memory effect. Soft Matter 2021, 17, 9326–9331. [Google Scholar] [CrossRef]
- Keville, K.; Franses, E.; Caruthers, J. Preparation and characterization of monodisperse polymer microspheroids. J. Colloid Interface Sci. 1991, 144, 103–126. [Google Scholar] [CrossRef]
- Lu, Y.; Yin, Y.; Xia, Y. A Self-Assembly Approach to the Fabrication of Patterned, Two-Dimensional Arrays of Microlenses of Organic Polymers. Adv. Mater. 2001, 13, 34–37. [Google Scholar] [CrossRef]
- Lu, Y.; Yin, Y.; Li, Z.-Y.; Xia, Y. Colloidal Crystals Made of Polystyrene Spheroids: Fabrication and Structural/Optical Characterization. Langmuir 2002, 18, 7722–7727. [Google Scholar] [CrossRef]

| Sample | E at 70 °C 1 (MPa) | r = E Inclusion/E Phantom |
|---|---|---|
| Multiblock copolymers | ||
| PPDL40-PTHF | 16 | 0.33 |
| PPDL50-PTHF | 35 | 0.73 |
| PPDL60-PTHF | 61 | 1.27 |
| PPDL40-PCL | 6 | 0.125 |
| PCL-PCL | − 2 | − 2 |
| Phantom matrix | ||
| PVA | 48 | n.a. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wischke, C.; Hofmann, D. Predictive Shapes of Ellipsoid PPDL-PTHF Copolymer Particles Prepared by the Phantom Stretching Technique. Polymers 2022, 14, 3762. https://doi.org/10.3390/polym14183762
Wischke C, Hofmann D. Predictive Shapes of Ellipsoid PPDL-PTHF Copolymer Particles Prepared by the Phantom Stretching Technique. Polymers. 2022; 14(18):3762. https://doi.org/10.3390/polym14183762
Chicago/Turabian StyleWischke, Christian, and Dieter Hofmann. 2022. "Predictive Shapes of Ellipsoid PPDL-PTHF Copolymer Particles Prepared by the Phantom Stretching Technique" Polymers 14, no. 18: 3762. https://doi.org/10.3390/polym14183762





