Theoretical Modeling of Magnetoactive Elastomers on Different Scales: A State-of-the-Art Review
Abstract
:1. Introduction
2. Basic Mechanisms behind Magneto-Mechanical Coupling
3. Main MAE Modeling Approaches
3.1. Microscopic and Mesoscopic Modeling
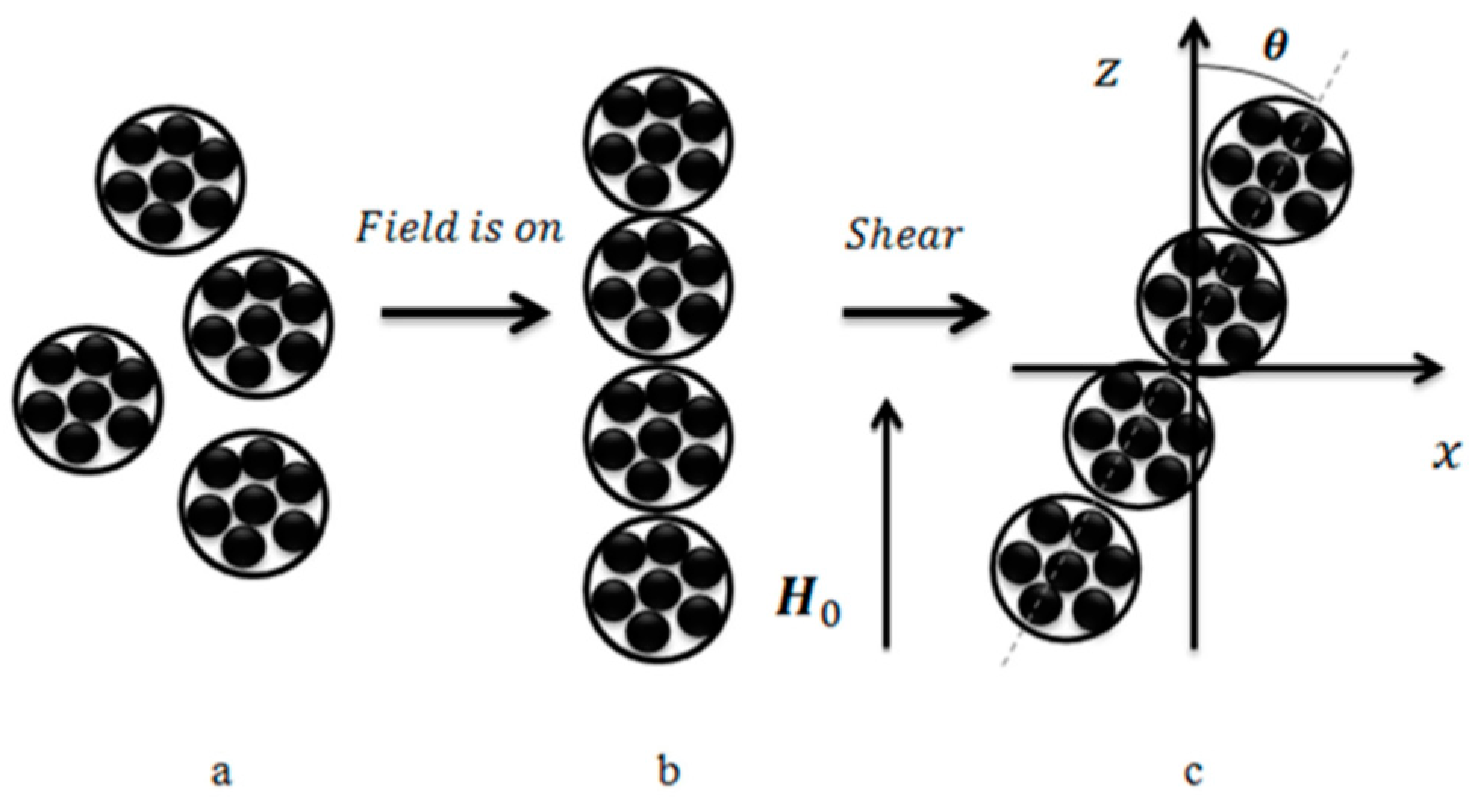
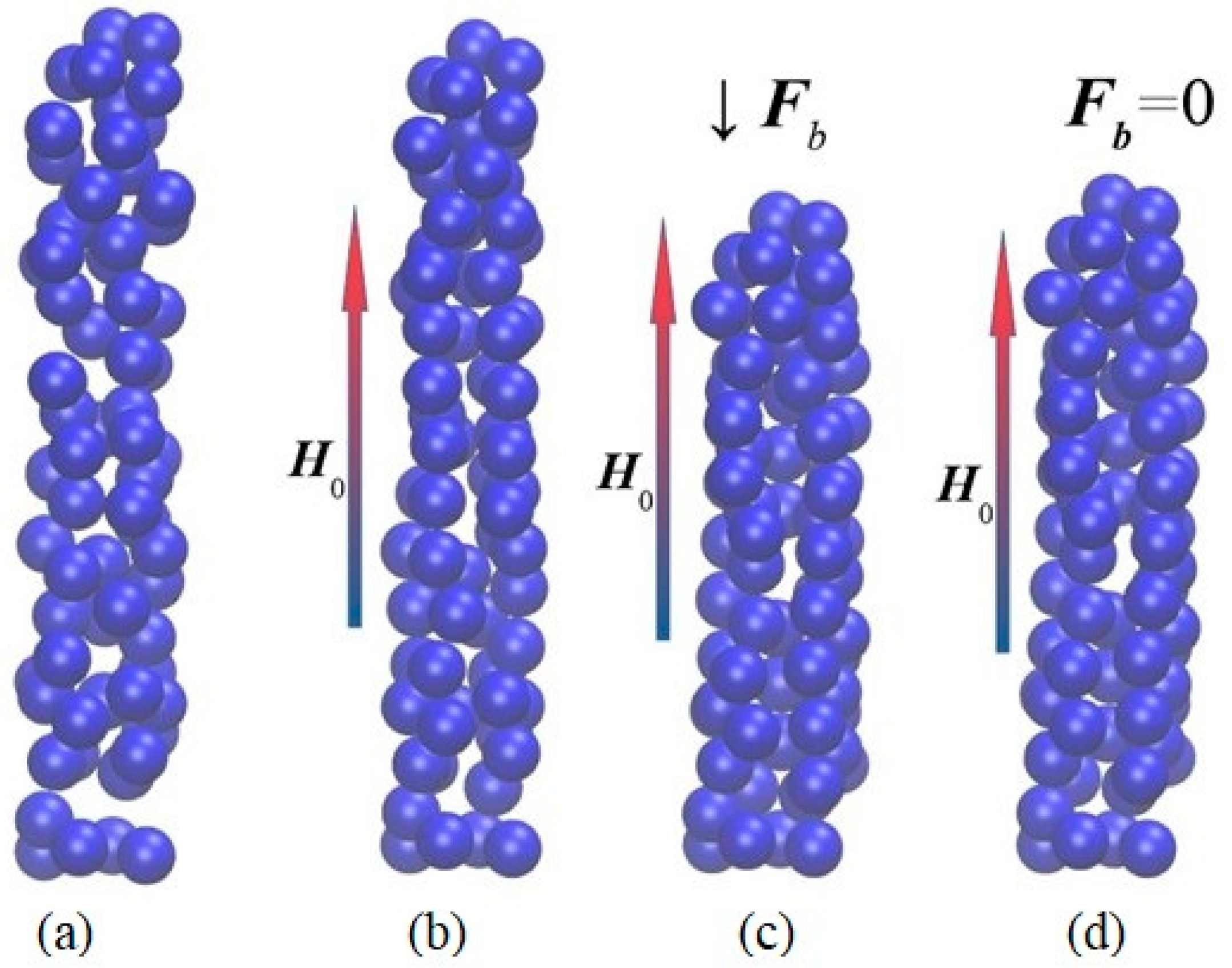
3.1.1. Molecular Dynamics Simulations
MD Simulations of Magnetic Gels
Refined MD Models of MAEs
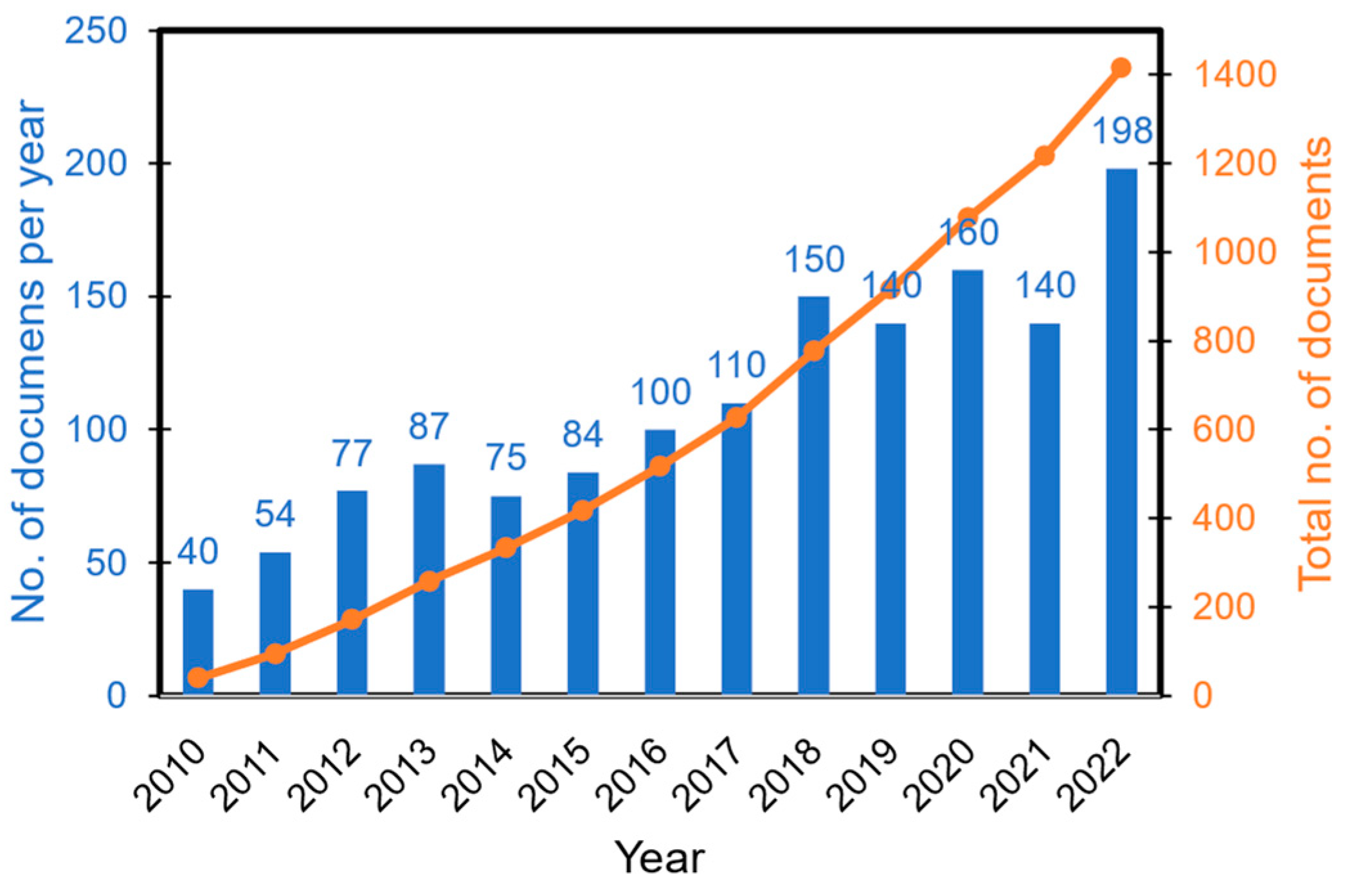
Stress-Strain Behavior and Elastic Modulus of MAEs via DPD Simulation
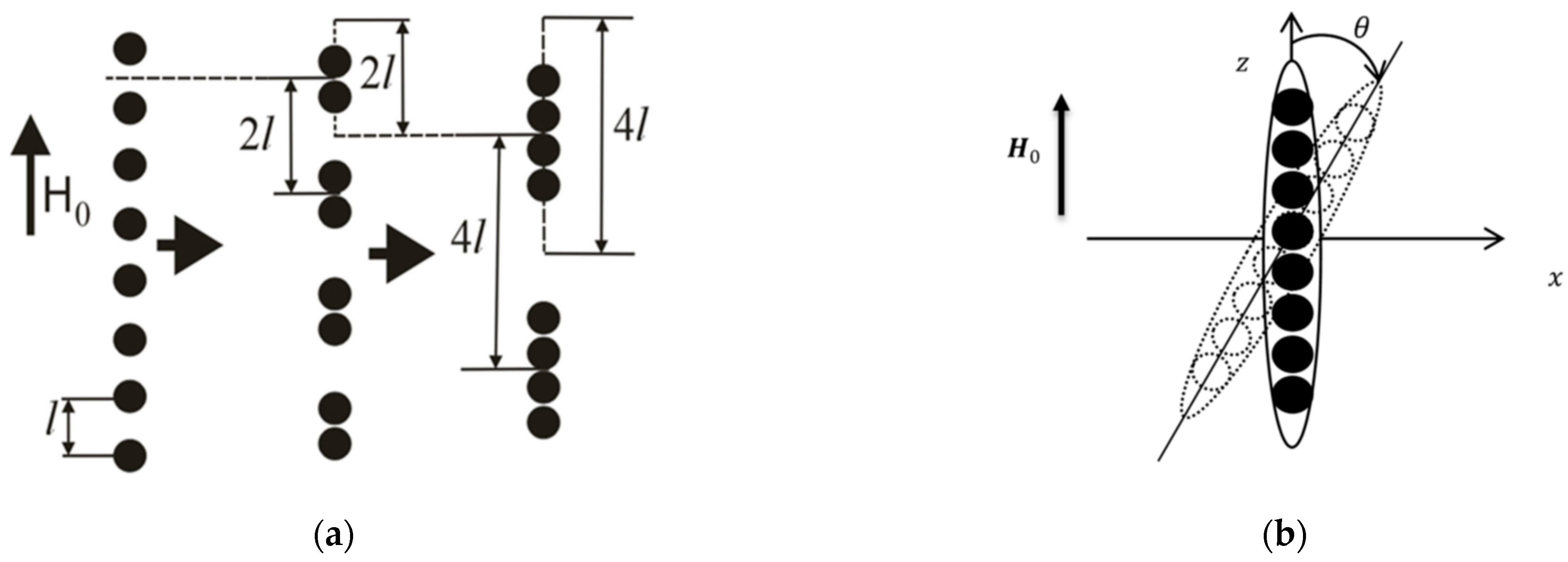
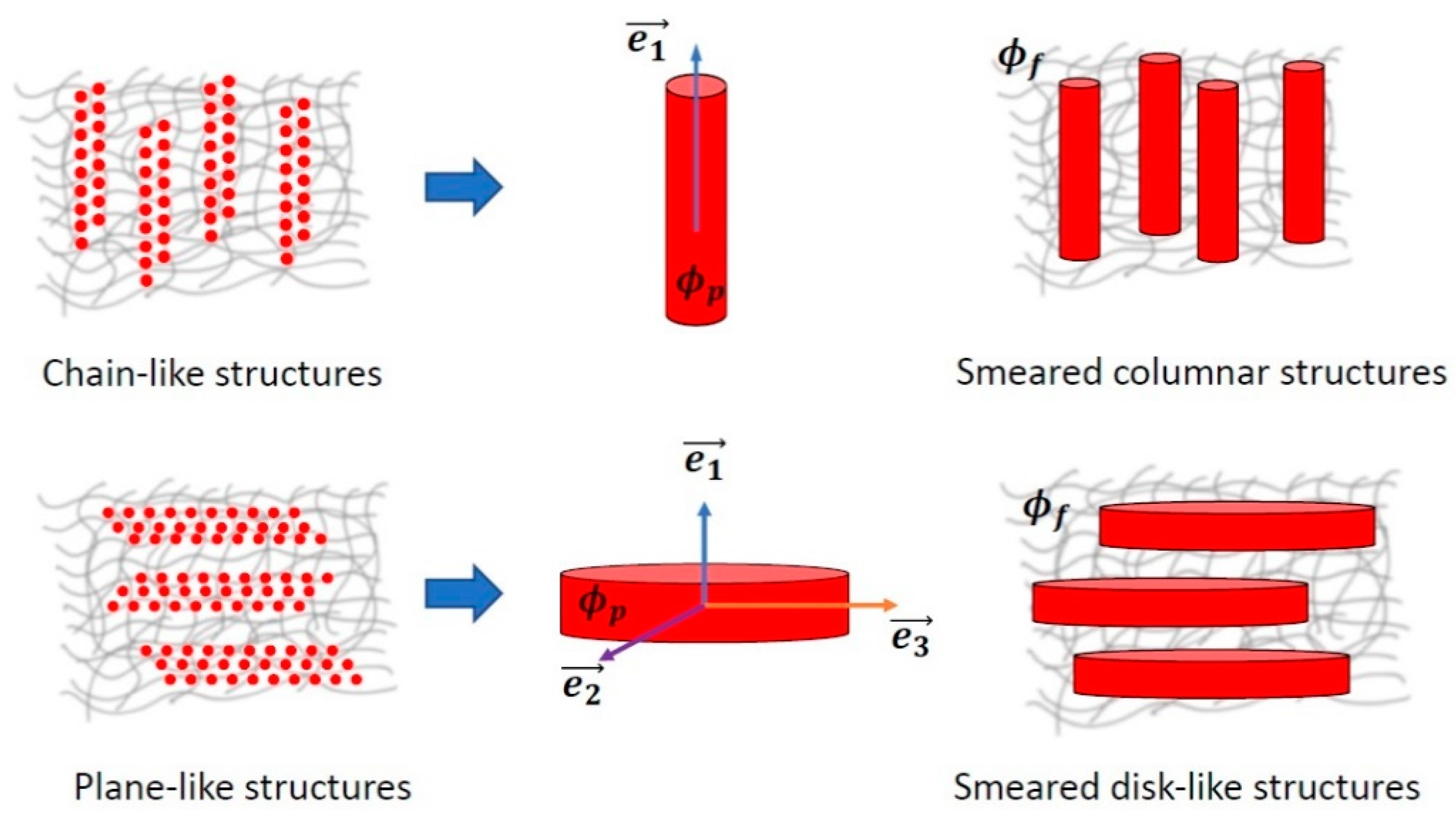
3.1.2. Mesoscopic Structure Modeling: Analytical and Numerical Approaches
Calculation of Elastic Moduli
Calculation of Magnetostriction
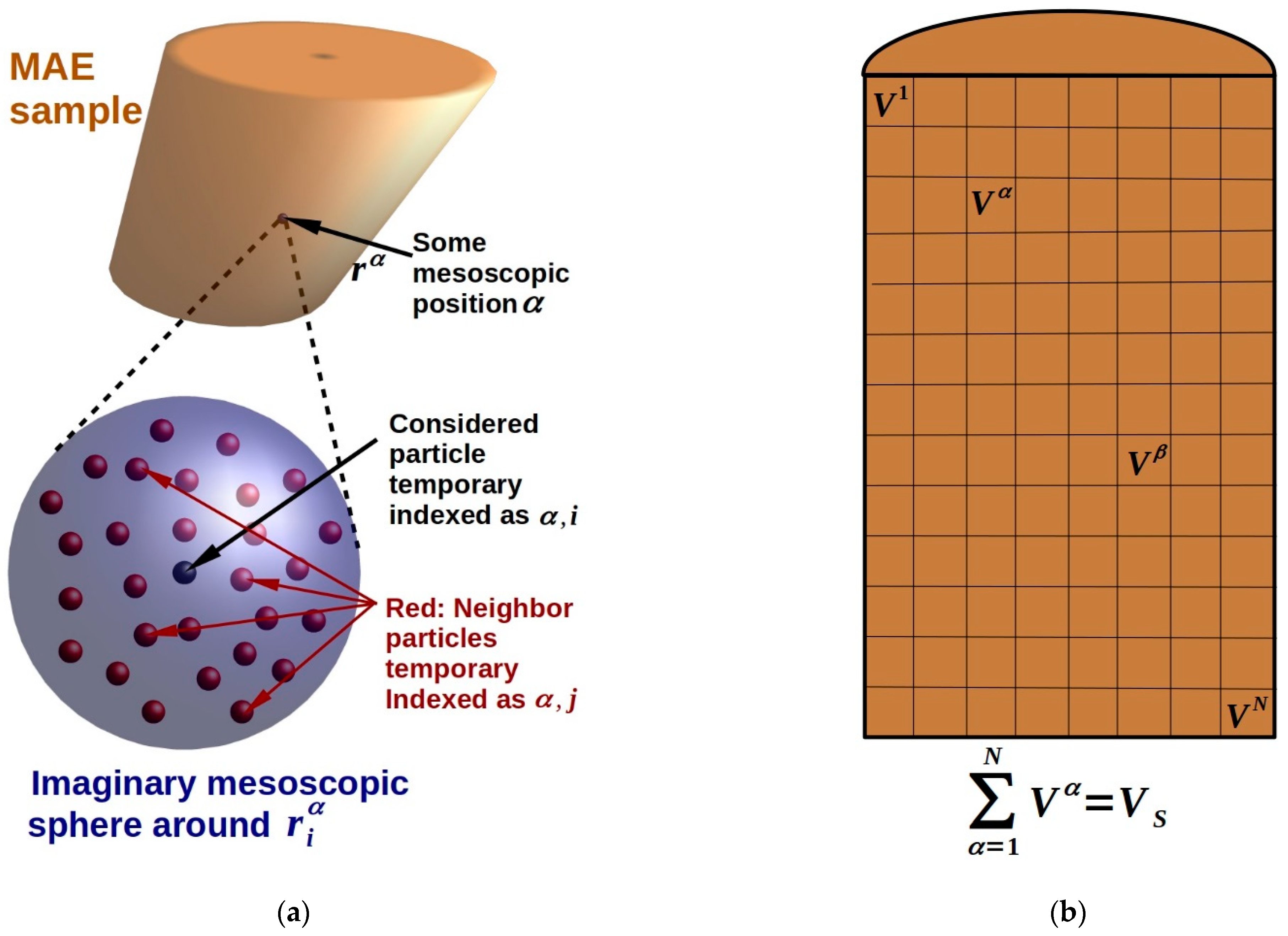
3.1.3. Mesoscopic Cell Modeling
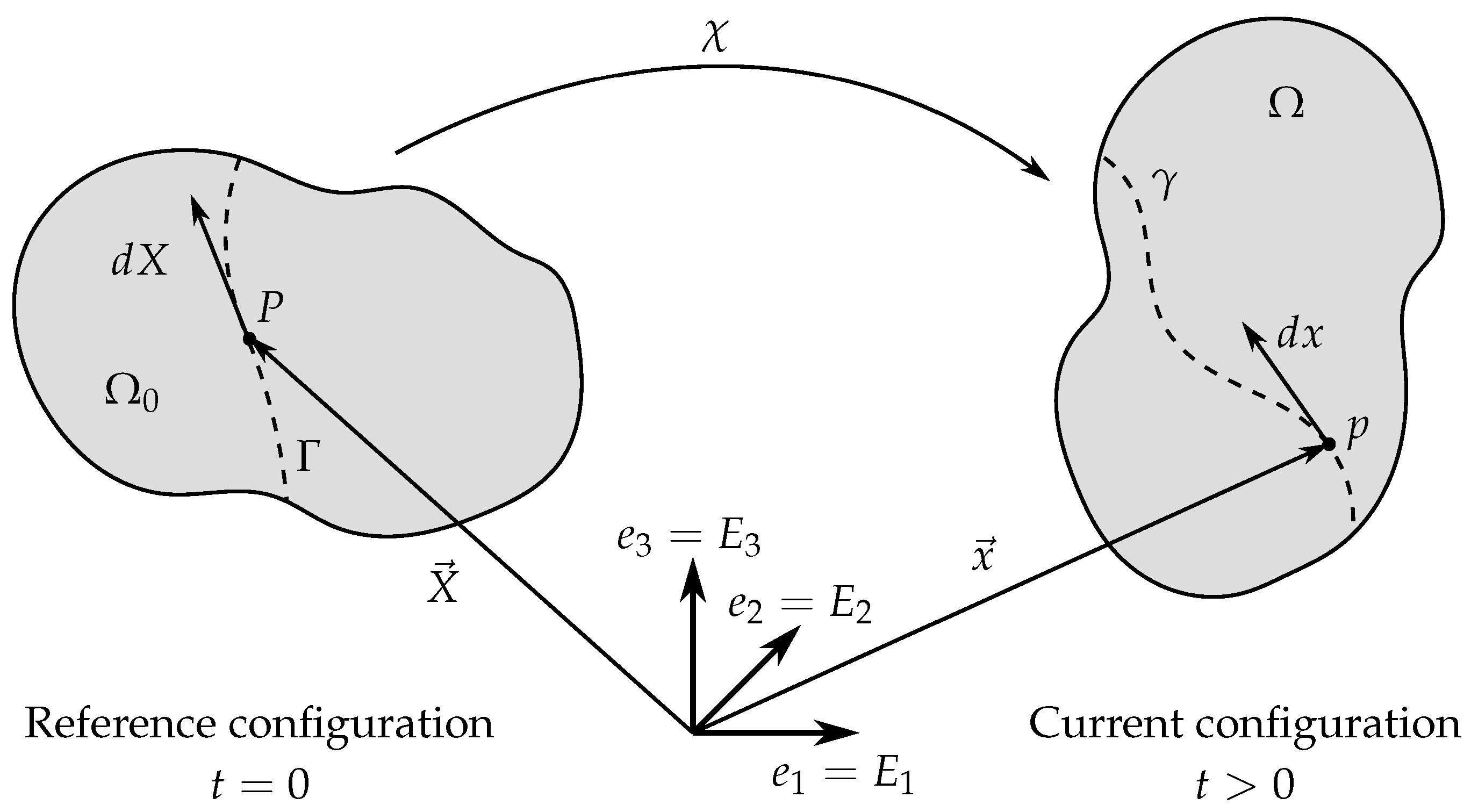
3.2. Continuum Modeling
3.2.1. Mechanical Engineering Approach
3.2.2. Invariant Theory
3.2.3. Effective Medium Theory
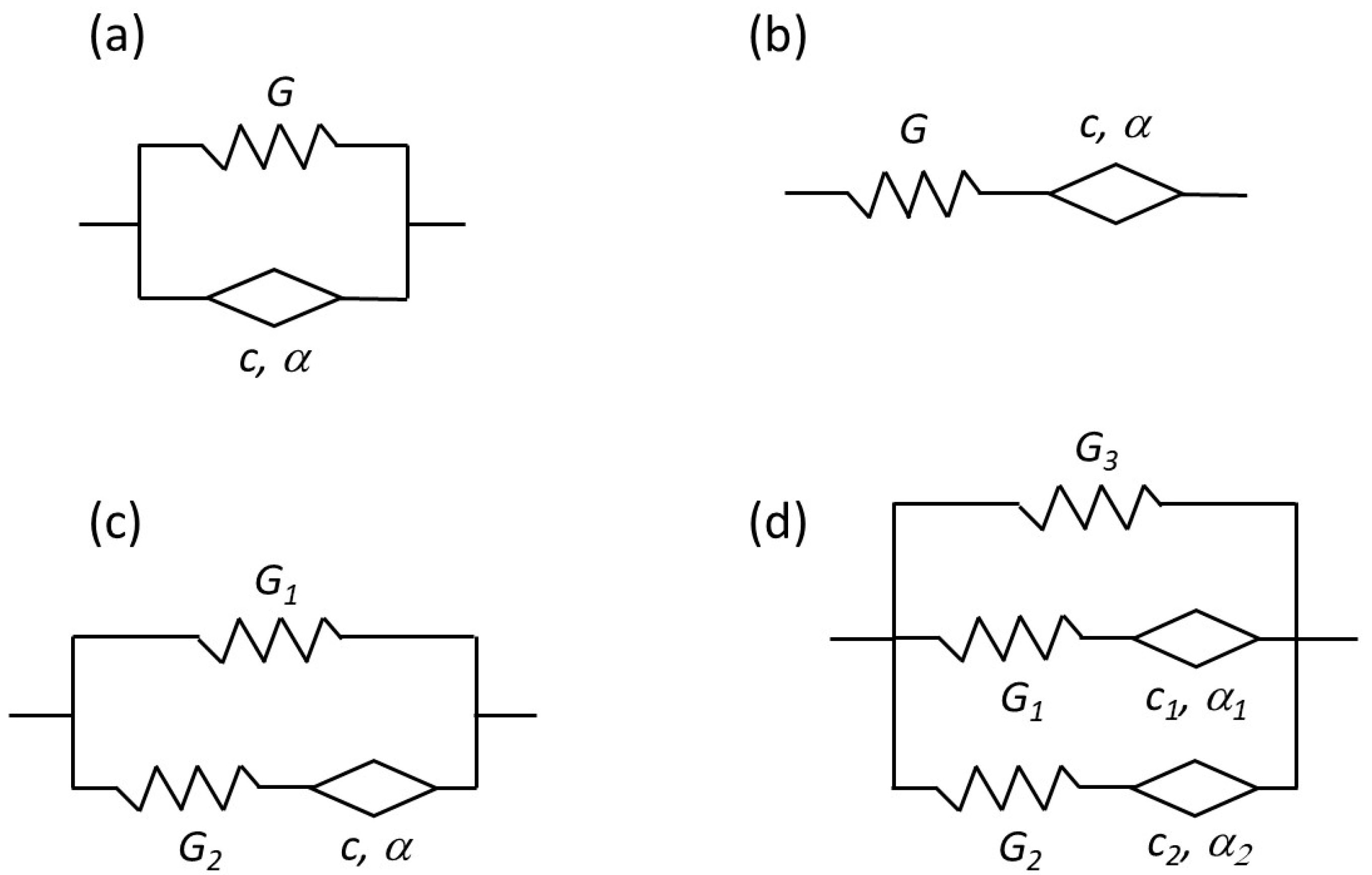
3.3. Rheological Modeling
4. Multi-Scale Modeling Approaches
4.1. Representative Element Homogenization Approaches
4.2. FE2-Approach
4.3. Mean Field Approach
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BL | Bruggeman-Landauer |
| BVP | Boundary value problem |
| DPD | Dissipative particle dynamics |
| EMT | Effective medium theory |
| FE | Ferroelectric |
| FEM | Finite element method |
| FM | Ferromagnetic |
| FORC | First order reversal curve |
| MAE | Magnetoactive elastomer |
| MD | Molecular dynamics |
| HM | Hard magnetic |
| MNG | Magnetic nanogel |
| MR | Magnetorheological |
| SM | Soft magnetic |
| RVE | Representative volume element |
| SV | Sarychev and Vinogradov |
References
- Filipcsei, G.; Csetneki, I.; Szilágyi, A.; Zrínyi, M. Magnetic Field-Responsive Smart Polymer Composites. In Oligomers-Polymer Composites-Molecular Imprinting; Gong, B., Sanford, A.R., Ferguson, J.S., Eds.; Advances in Polymer Science; Springer: Berlin/Heidelberg, Germany, 2007; pp. 137–189. ISBN 978-3-540-46830-1. [Google Scholar]
- Li, Y.; Li, J.; Li, W.; Du, H. A State-of-the-Art Review on Magnetorheological Elastomer Devices. Smart Mater. Struct. 2014, 23, 123001. [Google Scholar] [CrossRef]
- Menzel, A.M. Tuned, Driven, and Active Soft Matter. Phys. Rep. 2015, 554, 1–45. [Google Scholar] [CrossRef]
- Ubaidillah; Sutrisno, J.; Purwanto, A.; Mazlan, S.A. Recent Progress on Magnetorheological Solids: Materials, Fabrication, Testing, and Applications. Adv. Eng. Mater. 2015, 17, 563–597. [Google Scholar] [CrossRef]
- Odenbach, S. Microstructure and Rheology of Magnetic Hybrid Materials. Arch. Appl. Mech. 2016, 86, 269–279. [Google Scholar] [CrossRef]
- López-López, M.; Durán, J.; Iskakova, L.; Zubarev, A. Mechanics of Magnetopolymer Composites: A Review. J. Nanofluids 2016, 5, 479–495. [Google Scholar] [CrossRef]
- Cantera, M.A.; Behrooz, M.; Gibson, R.F.; Gordaninejad, F. Modeling of Magneto-Mechanical Response of Magnetorheological Elastomers (MRE) and MRE-Based Systems: A Review. Smart Mater. Struct. 2017, 26, 023001. [Google Scholar] [CrossRef]
- Shamonin, M.; Kramarenko, E.Y. Chapter 7—Highly Responsive Magnetoactive Elastomers. In Novel Magnetic Nanostructures; Domracheva, N., Caporali, M., Rentschler, E., Eds.; Advanced Nanomaterials; Elsevier: Amsterdam, The Netherlands, 2018; pp. 221–245. ISBN 978-0-12-813594-5. [Google Scholar]
- Kramarenko, E.Y.; Stepanov, G.V.; Khokhlov, A.R. Magnetically Active Silicone Elastomers: Twenty Years of Development. INEOS OPEN 2020, 2, 178–184. [Google Scholar] [CrossRef]
- Odenbach, S. Magnetic Hybrid-Materials: Multi-Scale Modelling, Synthesis, and Applications, 1st ed.; De Gruyter: Berlin, Germany, 2021; ISBN 978-3-11-056963-6. [Google Scholar]
- Kostrov, S.A.; Shamonin, M.; Stepanov, G.V.; Kramarenko, E.Y. Magnetodielectric Response of Soft Magnetoactive Elastomers: Effects of Filler Concentration and Measurement Frequency. Int. J. Mol. Sci. 2019, 20, 2230. [Google Scholar] [CrossRef]
- Moreno-Mateos, M.A.; Hossain, M.; Steinmann, P.; Garcia-Gonzalez, D. Hybrid Magnetorheological Elastomers Enable Versatile Soft Actuators. Npj Comput. Mater. 2022, 8, 162. [Google Scholar] [CrossRef]
- Li, M.; Pal, A.; Aghakhani, A.; Pena-Francesch, A.; Sitti, M. Soft Actuators for Real-World Applications. Nat. Rev. Mater. 2022, 7, 235–249. [Google Scholar] [CrossRef]
- Moreno-Mateos, M.A.; Gonzalez-Rico, J.; Nunez-Sardinha, E.; Gomez-Cruz, C.; Lopez-Donaire, M.L.; Lucarini, S.; Arias, A.; Muñoz-Barrutia, A.; Velasco, D.; Garcia-Gonzalez, D. Magneto-Mechanical System to Reproduce and Quantify Complex Strain Patterns in Biological Materials. Appl. Mater. Today 2022, 27, 101437. [Google Scholar] [CrossRef]
- Böse, H.; Rabindranath, R.; Ehrlich, J. Soft Magnetorheological Elastomers as New Actuators for Valves. J. Intell. Mater. Syst. Struct. 2012, 23, 989–994. [Google Scholar] [CrossRef]
- Kashima, S.; Miyasaka, F.; Hirata, K. Novel Soft Actuator Using Magnetorheological Elastomer. IEEE Trans. Magn. 2012, 48, 1649–1652. [Google Scholar] [CrossRef]
- Cvek, M.; Moucka, R.; Sedlacik, M.; Babayan, V.; Pavlinek, V. Enhancement of Radio-Absorbing Properties and Thermal Conductivity of Polysiloxane-Based Magnetorheological Elastomers by the Alignment of Filler Particles. Smart Mater. Struct. 2017, 26, 095005. [Google Scholar] [CrossRef]
- Shevchenko, V.G.; Stepanov, G.V.; Kramarenko, E.Y. Dielectric Spectroscopy of Hybrid Magnetoactive Elastomers. Polymers 2021, 13, 2002. [Google Scholar] [CrossRef]
- Sorokin, V.V.; Sokolov, B.O.; Stepanov, G.V.; Kramarenko, E.Y. Controllable Hydrophobicity of Magnetoactive Elastomer Coatings. J. Magn. Magn. Mater. 2018, 459, 268–271. [Google Scholar] [CrossRef]
- Glavan, G.; Salamon, P.; Belyaeva, I.A.; Shamonin, M.; Drevenšek-Olenik, I. Tunable Surface Roughness and Wettability of a Soft Magnetoactive Elastomer. J. Appl. Polym. Sci. 2018, 135, 46221. [Google Scholar] [CrossRef]
- Watanabe, M.; Tanaka, Y.; Murakami, D.; Tanaka, M.; Kawai, M.; Mitsumata, T. Optimal Plasticizer Content for Magnetic Elastomers Used for Cell Culture Substrate. Chem. Lett. 2020, 49, 280–283. [Google Scholar] [CrossRef]
- Chen, S.; Zhu, M.; Zhang, Y.; Dong, S.; Wang, X. Magnetic-Responsive Superhydrophobic Surface of Magnetorheological Elastomers Mimicking from Lotus Leaves to Rose Petals. Langmuir 2021, 37, 2312–2321. [Google Scholar] [CrossRef]
- Sánchez, P.A.; Minina, E.S.; Kantorovich, S.S.; Kramarenko, E.Y. Surface Relief of Magnetoactive Elastomeric Films in a Homogeneous Magnetic Field: Molecular Dynamics Simulations. Soft Matter 2019, 15, 175–189. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Wang, D.; Yang, P.; Tang, X.; Liu, J.; Li, X. Improved Magneto-Sensitive Adhesion Property of Magnetorheological Elastomers Modified Using Graphene Nanoplatelets. Ind. Eng. Chem. Res. 2020, 59, 9143–9151. [Google Scholar] [CrossRef]
- Kovalev, A.; Belyaeva, I.A.; von Hofen, C.; Gorb, S.; Shamonin, M. Magnetically Switchable Adhesion and Friction of Soft Magnetoactive Elastomers. Adv. Eng. Mater. 2022, 2200372. [Google Scholar] [CrossRef]
- Li, R.; Wang, D.; Li, X.; Liao, C.; Yang, P.; Ruan, H.; Shou, M.; Luo, J.; Wang, X. Study on Sliding Friction Characteristics of Magnetorheological Elastomer—Copper Pair Affected by Magnetic-Controlled Surface Roughness and Elastic Modulus. Smart Mater. Struct. 2021, 31, 015030. [Google Scholar] [CrossRef]
- Bastola, A.K.; Paudel, M.; Li, L.; Li, W. Recent Progress of Magnetorheological Elastomers: A Review. Smart Mater. Struct. 2020, 29, 123002. [Google Scholar] [CrossRef]
- Bastola, A.K.; Hossain, M. A Review on Magneto-Mechanical Characterizations of Magnetorheological Elastomers. Compos. Part B Eng. 2020, 200, 108348. [Google Scholar] [CrossRef]
- Lucarini, S.; Hossain, M.; Garcia-Gonzalez, D. Recent Advances in Hard-Magnetic Soft Composites: Synthesis, Characterisation, Computational Modelling, and Applications. Compos. Struct. 2022, 279, 114800. [Google Scholar] [CrossRef]
- Makarova, L.A.; Isaev, D.A.; Omelyanchik, A.S.; Alekhina, I.A.; Isaenko, M.B.; Rodionova, V.V.; Raikher, Y.L.; Perov, N.S. Multiferroic Coupling of Ferromagnetic and Ferroelectric Particles through Elastic Polymers. Polymers 2022, 14, 153. [Google Scholar] [CrossRef]
- Weeber, R.; Kantorovich, S.; Holm, C. Deformation Mechanisms in 2D Magnetic Gels Studied by Computer Simulations. Soft Matter 2012, 8, 9923–9932. [Google Scholar] [CrossRef]
- Weeber, R.; Kantorovich, S.; Holm, C. Ferrogels Cross-Linked by Magnetic Nanoparticles—Deformation Mechanisms in Two and Three Dimensions Studied by Means of Computer Simulations. J. Magn. Magn. Mater. 2015, 383, 262–266. [Google Scholar] [CrossRef]
- Weeber, R.; Kantorovich, S.; Holm, C. Ferrogels Cross-Linked by Magnetic Particles: Field-Driven Deformation and Elasticity Studied Using Computer Simulations. J. Chem. Phys. 2015, 143, 154901. [Google Scholar] [CrossRef] [Green Version]
- Ryzhkov, A.V.; Raikher, Y.L. Structural Changes in Microferrogels Cross-Linked by Magnetically Anisotropic Particles. J. Magn. Magn. Mater. 2017, 431, 192–195. [Google Scholar] [CrossRef]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Sánchez, P.A.; Gundermann, T.; Dobroserdova, A.; Kantorovich, S.S.; Odenbach, S. Importance of Matrix Inelastic Deformations in the Initial Response of Magnetic Elastomers. Soft Matter 2018, 14, 2170–2183. [Google Scholar] [CrossRef]
- Dobroserdova, A.B.; Sánchez, P.A.; Shapochkin, V.E.; Smagin, D.A.; Zverev, V.S.; Odenbach, S.; Kantorovich, S.S. Measuring FORCs Diagrams in Computer Simulations as a Mean to Gain Microscopic Insight. J. Magn. Magn. Mater. 2020, 501, 166393. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Melenev, P.V.; Holm, C.; Raikher, Y.L. Coarse-Grained Molecular Dynamics Simulation of Small Ferrogel Objects. J. Magn. Magn. Mater. 2015, 383, 277–280. [Google Scholar] [CrossRef]
- Minina, E.S.; Sánchez, P.A.; Likos, C.N.; Kantorovich, S.S. The Influence of the Magnetic Filler Concentration on the Properties of a Microgel Particle: Zero-Field Case. J. Magn. Magn. Mater. 2018, 459, 226–230. [Google Scholar] [CrossRef]
- Novikau, I.S.; Minina, E.S.; Sánchez, P.A.; Kantorovich, S.S. Suspensions of Magnetic Nanogels at Zero Field: Equilibrium Structural Properties. J. Magn. Magn. Mater. 2020, 498, 166152. [Google Scholar] [CrossRef]
- Novikau, I.S.; Sánchez, P.A.; Kantorovich, S.S. The Influence of an Applied Magnetic Field on the Self-Assembly of Magnetic Nanogels. J. Mol. Liq. 2020, 307, 112902. [Google Scholar] [CrossRef]
- Alekhina, I.; Kramarenko, E.; Makarova, L.; Perov, N. Chapter 17—Magnetorheological Composites for Biomedical Applications. In Magnetic Materials and Technologies for Medical Applications; Tishin, A.M., Ed.; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publishing: Sawston, UK, 2022; pp. 501–526. ISBN 978-0-12-822532-5. [Google Scholar]
- Ryzhkov, A.V.; Melenev, P.V.; Balasoiu, M.; Raikher, Y.L. Structure Organization and Magnetic Properties of Microscale Ferrogels: The Effect of Particle Magnetic Anisotropy. J. Chem. Phys. 2016, 145, 074905. [Google Scholar] [CrossRef]
- Novikau, I.S.; Novak, E.V.; Pyanzina, E.S.; Kantorovich, S.S. Behaviour of a Magnetic Nanogel in a Shear Flow. J. Mol. Liq. 2022, 346, 118056. [Google Scholar] [CrossRef]
- Dobroserdova, A.; Schümann, M.; Borin, D.; Novak, E.; Odenbach, S.; Kantorovich, S. Magneto-Elastic Coupling as a Key to Microstructural Response of Magnetic Elastomers with Flake-like Particles. Soft Matter 2022, 18, 496–506. [Google Scholar] [CrossRef]
- Makarova, L.A.; Alekhina, Y.A.; Isaev, D.A.; Khairullin, M.F.; Perov, N.S. Tunable Layered Composites Based on Magnetoactive Elastomers and Piezopolymer for Sensors and Energy Harvesting Devices. J. Phys. Appl. Phys. 2020, 54, 015003. [Google Scholar] [CrossRef]
- Komarov, P.V.; Khalatur, P.G.; Khokhlov, A.R. Magnetoresponsive Smart Nanocomposites with Highly Cross-Linked Polymer Matrix. Polym. Adv. Technol. 2021, 32, 3922–3933. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative Particle Dynamics: Bridging the Gap between Atomistic and Mesoscopic Simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Gavrilov, A.A.; Komarov, P.V.; Khalatur, P.G. Thermal Properties and Topology of Epoxy Networks: A Multiscale Simulation Methodology. Macromolecules 2015, 48, 206–212. [Google Scholar] [CrossRef]
- Ivaneyko, D.; Toshchevikov, V.; Saphiannikova, M. Dynamic Moduli of Magneto-Sensitive Elastomers: A Coarse-Grained Network Model. Soft Matter 2015, 11, 7627–7638. [Google Scholar] [CrossRef]
- Jolly, M.R.; Carlson, J.D.; Muñoz, B.C. A Model of the Behaviour of Magnetorheological Materials. Smart Mater. Struct. 1996, 5, 607–614. [Google Scholar] [CrossRef]
- Zhu, Y.; Gong, X.; Dang, H.; Zhang, X.; Zhang, P. Numerical Analysis on Magnetic-Induced Shear Modulus of Magnetorheological Elastomers Based on Multi-Chain Model. Chin. J. Chem. Phys. 2006, 19, 126. [Google Scholar] [CrossRef]
- Yin, H.M.; Sun, L.Z.; Chen, J.S. Micromechanics-Based Hyperelastic Constitutive Modeling of Magnetostrictive Particle-Filled Elastomers. Mech. Mater. 2002, 34, 505–516. [Google Scholar] [CrossRef]
- Zhang, W.; Gong, X.L.; Chen, L. A Gaussian Distribution Model of Anisotropic Magnetorheological Elastomers. J. Magn. Magn. Mater. 2010, 322, 3797–3801. [Google Scholar] [CrossRef]
- Yang, J.; Gong, X.; Deng, H.; Qin, L.; Xuan, S. Investigation on the Mechanism of Damping Behavior of Magnetorheological Elastomers. Smart Mater. Struct. 2012, 21, 125015. [Google Scholar] [CrossRef]
- Biller, A.M.; Stolbov, O.V.; Raikher, Y.L. Modeling of Particle Interactions in Magnetorheological Elastomers. J. Appl. Phys. 2014, 116, 114904. [Google Scholar] [CrossRef]
- Ivaneyko, D.; Toshchevikov, V.P.; Saphiannikova, M.; Heinrich, G. Magneto-Sensitive Elastomers in a Homogeneous Magnetic Field: A Regular Rectangular Lattice Model. Macromol. Theory Simul. 2011, 20, 411–424. [Google Scholar] [CrossRef]
- Kalita, V.M.; Snarskii, A.A.; Shamonin, M.; Zorinets, D. Effect of Single-Particle Magnetostriction on the Shear Modulus of Compliant Magnetoactive Elastomers. Phys. Rev. E 2017, 95, 032503. [Google Scholar] [CrossRef]
- Kalita, V.M.; Dzhezherya, Y.I.; Levchenko, G.G. Anomalous Magnetorheological Effect in Unstructured Magnetoisotropic Magnetoactive Elastomers. Appl. Phys. Lett. 2020, 116, 063701. [Google Scholar] [CrossRef]
- Kalita, V.M.; Snarskii, A.A.; Zorinets, D.; Shamonin, M. Single-Particle Mechanism of Magnetostriction in Magnetoactive Elastomers. Phys. Rev. E 2016, 93, 062503. [Google Scholar] [CrossRef]
- Borin, D.; Stepanov, G.; Musikhin, A.; Zubarev, A.; Bakhtiiarov, A.; Storozhenko, P. Magnetorheological Effect of Magnetoactive Elastomer with a Permalloy Filler. Polymers 2020, 12, 2371. [Google Scholar] [CrossRef]
- Gila-Vilchez, C.; Duran, J.D.G.; Gonzalez-Caballero, F.; Zubarev, A.; Lopez-Lopez, M.T. Magnetorheology of Alginate Ferrogels. Smart Mater. Struct. 2019, 28, 035018. [Google Scholar] [CrossRef]
- Gila-Vilchez, C.; Bonhome-Espinosa, A.B.; Kuzhir, P.; Zubarev, A.; Duran, J.D.G.; Lopez-Lopez, M.T. Rheology of Magnetic Alginate Hydrogels. J. Rheol. 2018, 62, 1083–1096. [Google Scholar] [CrossRef]
- Menzel, A.M.; Löwen, H. Modeling and Theoretical Description of Magnetic Hybrid Materials—Bridging from Meso- to Macro-Scales. Phys. Sci. Rev. 2020. [Google Scholar] [CrossRef]
- Schümann, M.; Odenbach, S. In-Situ Observation of the Particle Microstructure of Magnetorheological Elastomers in Presence of Mechanical Strain and Magnetic Fields. J. Magn. Magn. Mater. 2017, 441, 88–92. [Google Scholar] [CrossRef]
- Pessot, G.; Löwen, H.; Menzel, A.M. Dynamic Elastic Moduli in Magnetic Gels: Normal Modes and Linear Response. J. Chem. Phys. 2016, 145, 104904. [Google Scholar] [CrossRef]
- Pessot, G.; Schümann, M.; Gundermann, T.; Odenbach, S.; Löwen, H.; Menzel, A.M. Tunable Dynamic Moduli of Magnetic Elastomers: From Characterization by x-Ray Micro-Computed Tomography to Mesoscopic Modeling. J. Phys. Condens. Matter 2018, 30, 125101. [Google Scholar] [CrossRef]
- Stolbov, O.V.; Raikher, Y.L. Magnetostriction Effect in Soft Magnetic Elastomers. Arch. Appl. Mech. 2019, 89, 63–76. [Google Scholar] [CrossRef]
- Sánchez, P.A.; Stolbov, O.V.; Kantorovich, S.S.; Raikher, Y.L. Modeling the Magnetostriction Effect in Elastomers with Magnetically Soft and Hard Particles. Soft Matter 2019, 15, 7145–7158. [Google Scholar] [CrossRef]
- Zubarev, A.Y.; Borin, D.Y. Effect of Particle Concentration on Ferrogel Magnetodeformation. J. Magn. Magn. Mater. 2015, 377, 373–377. [Google Scholar] [CrossRef]
- Morozov, K.; Shliomis, M.; Yamaguchi, H. Magnetic Deformation of Ferrogel Bodies: Procrustes Effect. Phys. Rev. E 2009, 79, 040801. [Google Scholar] [CrossRef]
- Fischer, L.; Menzel, A.M. Magnetostriction in Magnetic Gels and Elastomers as a Function of the Internal Structure and Particle Distribution. J. Chem. Phys. 2019, 151, 114906. [Google Scholar] [CrossRef]
- Gollwitzer, C.; Turanov, A.; Krekhova, M.; Lattermann, G.; Rehberg, I.; Richter, R. Measuring the Deformation of a Ferrogel Sphere in a Homogeneous Magnetic Field. J. Chem. Phys. 2008, 128, 164709. [Google Scholar] [CrossRef]
- Filipcsei, G.; Zrínyi, M. Magnetodeformation Effects and the Swelling of Ferrogels in a Uniform Magnetic Field. J. Phys. Condens. Matter 2010, 22, 276001. [Google Scholar] [CrossRef]
- Biller, A.M.; Stolbov, O.V.; Raikher, Y.L. Two-Particle Element of a Magnetorheological Elastomer under a Cyclic Magnetic Field. J. Phys. Conf. Ser. 2018, 994, 012001. [Google Scholar] [CrossRef]
- Stolbov, O.V.; Raikher, Y.L. Mesostructural Origin of the Field-Induced Pseudo-Plasticity Effect in a Soft Magnetic Elastomer. IOP Conf. Ser. Mater. Sci. Eng. 2019, 581, 012003. [Google Scholar] [CrossRef]
- Becker, T.I.; Stolbov, O.V.; Borin, D.Y.; Zimmermann, K.; Raikher, Y.L. Basic Magnetic Properties of Magnetoactive Elastomers of Mixed Content. Smart Mater. Struct. 2020, 29, 075034. [Google Scholar] [CrossRef]
- Bayat, A.; Gordaninejad, F. Characteristic Volume Element for Randomly Particulate Magnetoactive Composites. J. Eng. Mater. Technol. 2017, 140, 011003. [Google Scholar] [CrossRef]
- Vaganov, M.V.; Borin, D.Y.; Odenbach, S.; Raikher, Y.L. Modeling the Magnetomechanical Behavior of a Multigrain Magnetic Particle in an Elastic Environment. Soft Matter 2019, 15, 4947–4960. [Google Scholar] [CrossRef]
- Vaganov, M.V.; Borin, D.Y.; Odenbach, S.; Raikher, Y.L. Mesomagnetomechanics of Hybrid Elastomer Composites: Magnetization of Elastically Trapped Particles. J. Magn. Magn. Mater. 2020, 499, 166249. [Google Scholar] [CrossRef]
- Vaganov, M.V.; Linke, J.; Odenbach, S.; Raikher, Y.L. Model FORC Diagrams for Hybrid Magnetic Elastomers. J. Magn. Magn. Mater. 2017, 431, 130–133. [Google Scholar] [CrossRef]
- Timoshenko, S.P. LXVI. On the Correction for Shear of the Differential Equation for Transverse Vibrations of Prismatic Bars. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1921, 41, 744–746. [Google Scholar] [CrossRef]
- Timoshenko, S.P.X. On the Transverse Vibrations of Bars of Uniform Cross-Section. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1922, 43, 125–131. [Google Scholar] [CrossRef]
- Von Lockette, P.; Lofland, S.E.; Biggs, J.; Roche, J.; Mineroff, J.; Babcock, M. Investigating New Symmetry Classes in Magnetorheological Elastomers: Cantilever Bending Behavior. Smart Mater. Struct. 2011, 20, 105022. [Google Scholar] [CrossRef] [Green Version]
- Brown, W.F. Magnetostatic Principles in Ferromagnetism, 1st ed.; Interscience Publishers: Amsterdam, The Netherlands; New York, NY, USA, 1962. [Google Scholar]
- Cosserat, E.M.P.; Cosserat, F. Theorie des Corps Deformables; A. Hermann et Fils: Paris, France, 1909. [Google Scholar]
- Kalita, V.; Dzhezherya, Y.I.; Cherepov, S.V.; Skirta, Y.B.; Bodnaruk, A.; Levchenko, G. Critical Bending and Shape Memory Effect in Magnetoactive Elastomers. Smart Mater. Struct. 2020, 30, 025020. [Google Scholar] [CrossRef]
- Brisbois, C.A.; Tasinkevych, M.; Vázquez-Montejo, P.; Olvera de la Cruz, M. Actuation of Magnetoelastic Membranes in Precessing Magnetic Fields. Proc. Natl. Acad. Sci. USA 2019, 116, 2500–2505. [Google Scholar] [CrossRef]
- Ali, M.N.; Wahi, S.K.; Santapuri, S. Modeling and Analysis of a Magnetoelastic Annular Membrane Placed in an Azimuthal Magnetic Field. Math. Mech. Solids 2021, 26, 1614–1634. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, J.; Salehizadeh, M.; Onaizah, O.; Diller, E. Millimeter-Scale Flexible Robots with Programmable Three-Dimensional Magnetization and Motions. Sci. Robot. 2019, 4, eaav4494. [Google Scholar] [CrossRef]
- Shinoda, H.; Azukizawa, S.; Maeda, K.; Tsumori, F. Bio-Mimic Motion of 3D-Printed Gel Structures Dispersed with Magnetic Particles. J. Electrochem. Soc. 2019, 166, B3235–B3239. [Google Scholar] [CrossRef]
- Zhang, W.; Saad, A.; Masters, S.; Hong, J.; Ounaies, Z.; Frecker, M. Finite Element Analysis of Electroactive and Magnetoactive Coupled Behaviors in Multi-Field Origami Structures. Intern. J. Intell. Mat. Sys. Struct. 2018, 29, 3983–4000. [Google Scholar] [CrossRef]
- Ren, Z.; Hu, W.; Dong, X.; Sitti, M. Multi-Functional Soft-Bodied Jellyfish-like Swimming. Nat. Commun. 2019, 10, 2703. [Google Scholar] [CrossRef]
- Khaderi, S.N.; Craus, C.B.; Hussong, J.; Schorr, N.; Belardi, J.; Westerweel, J.; Prucker, O.; Rühe, J.; den Toonder, J.M.J.; Onck, P.R. Magnetically-Actuated Artificial Cilia for Microfluidic Propulsion. Lab. Chip 2011, 11, 2002–2010. [Google Scholar] [CrossRef]
- Gu, H.; Boehler, Q.; Cui, H.; Secchi, E.; Savorana, G.; De Marco, C.; Gervasoni, S.; Peyron, Q.; Huang, T.-Y.; Pane, S.; et al. Magnetic Cilia Carpets with Programmable Metachronal Waves. Nat. Commun. 2020, 11, 2637. [Google Scholar] [CrossRef]
- Yan, D.; Abbasi, A.; Reis, P.M. A Comprehensive Framework for Hard-Magnetic Beams: Reduced-Order Theory, 3D Simulations, and Experiments. Int. J. Solids Struct. 2021, 111319. [Google Scholar] [CrossRef]
- Sano, T.G.; Pezzulla, M.; Reis, P.M. A Kirchhoff-like Theory for Hard Magnetic Rods under Geometrically Nonlinear Deformation in Three Dimensions. J. Mech. Phys. Solids 2022, 160, 104739. [Google Scholar] [CrossRef]
- Volkova, T.I.; Böhm, V.; Kaufhold, T.; Popp, J.; Becker, F.; Borin, D.Y.; Stepanov, G.V.; Zimmermann, K. Motion Behaviour of Magneto-Sensitive Elastomers Controlled by an External Magnetic Field for Sensor Applications. J. Magn. Magn. Mater. 2017, 431, 262–265. [Google Scholar] [CrossRef]
- Hu, W.; Lum, G.Z.; Mastrangeli, M.; Sitti, M. Small-Scale Soft-Bodied Robot with Multimodal Locomotion. Nature 2018, 554, 81–85. [Google Scholar] [CrossRef]
- Brigadnov, I.A.; Dorfmann, A. Mathematical Modeling of Magneto-Sensitive Elastomers. Int. J. Solids Struct. 2003, 40, 4659–4674. [Google Scholar] [CrossRef]
- Dorfmann, A.; Ogden, R.W. Nonlinear Magnetoelastic Deformations of Elastomers. Acta Mech. 2004, 167, 13–28. [Google Scholar] [CrossRef]
- Danas, K.; Kankanala, S.V.; Triantafyllidis, N. Experiments and Modeling of Iron-Particle-Filled Magnetorheological Elastomers. J. Mech. Phys. Solids 2012, 60, 120–138. [Google Scholar] [CrossRef]
- Dorfmann, A.; Ogden, R.W. Magnetoelastic Modelling of Elastomers. Eur. J. Mech.-A/Solids 2003, 22, 497–507. [Google Scholar] [CrossRef]
- Spencer, A.J.M. Part III—Theory of Invariants. In Mathematics; Eringen, A.C., Ed.; Academic Press: Cambridge, MA, USA, 1971; pp. 239–353. ISBN 978-0-12-240801-4. [Google Scholar]
- Dohmen, E.; Kraus, B. Coupled Anisotropic Magneto-Mechanical Material Model for Structured Magnetoactive Materials. Polymers 2020, 12, 2710. [Google Scholar] [CrossRef]
- Coleman, B.D.; Noll, W. The Thermodynamics of Elastic Materials with Heat Conduction and Viscosity. Arch. Ration. Mech. Anal. 1963, 13, 167–178. [Google Scholar] [CrossRef]
- Zhao, R.; Kim, Y.; Chester, S.A.; Sharma, P.; Zhao, X. Mechanics of Hard-Magnetic Soft Materials. J. Mech. Phys. Solids 2019, 124, 244–263. [Google Scholar] [CrossRef]
- Galipeau, E.; Ponte Castañeda, P. A Finite-Strain Constitutive Model for Magnetorheological Elastomers: Magnetic Torques and Fiber Rotations. J. Mech. Phys. Solids 2013, 61, 1065–1090. [Google Scholar] [CrossRef]
- Agirre-Olabide, I.; Lion, A.; Elejabarrieta, M.J. A New Three-Dimensional Magneto-Viscoelastic Model for Isotropic Magnetorheological Elastomers. Smart Mater. Struct. 2017, 26, 035021. [Google Scholar] [CrossRef]
- Kankanala, S.V.; Triantafyllidis, N. On Finitely Strained Magnetorheological Elastomers. J. Mech. Phys. Solids 2004, 52, 2869–2908. [Google Scholar] [CrossRef]
- Metsch, P.; Kalina, K.A.; Spieler, C.; Kästner, M. A Numerical Study on Magnetostrictive Phenomena in Magnetorheological Elastomers. Comput. Mater. Sci. 2016, 124, 364–374. [Google Scholar] [CrossRef]
- de Groot, S.R.; Suttorp, L.G. Foundations of Electrodynamics; Noord-Hollandsche U.M: Amsterdam, The Netherlands, 1972; ISBN 978-0-444-10370-3. [Google Scholar]
- Eringen, A.C.; Maugin, G.A. Electrodynamics of Continua I: Foundations and Solid Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; ISBN 978-1-4612-3226-1. [Google Scholar]
- Spieler, C.; Kästner, M.; Goldmann, J.; Brummund, J.; Ulbricht, V. XFEM Modeling and Homogenization of Magnetoactive Composites. Acta Mech. 2013, 224, 2453–2469. [Google Scholar] [CrossRef]
- Vogel, F.; Bustamante, R.; Steinmann, P. On Some Mixed Variational Principles in Magneto-Elastostatics. Int. J. Non-Linear Mech. 2013, 51, 157–169. [Google Scholar] [CrossRef]
- Stolbov, O.; Raikher, Y. Large-Scale Shape Transformations of a Sphere Made of a Magnetoactive Elastomer. Polymers 2020, 12, 2933. [Google Scholar] [CrossRef]
- Chougale, S.; Romeis, D.; Saphiannikova, M. Transverse Isotropy in Magnetoactive Elastomers. J. Magn. Magn. Mater. 2021, 523, 167597. [Google Scholar] [CrossRef]
- Chougale, S.; Romeis, D.; Saphiannikova, M. Field-Induced Transversely Isotropic Shear Response of Ellipsoidal Magnetoactive Elastomers. Materials 2021, 14, 3958. [Google Scholar] [CrossRef]
- Lefèvre, V.; Danas, K.; Lopez-Pamies, O. A General Result for the Magnetoelastic Response of Isotropic Suspensions of Iron and Ferrofluid Particles in Rubber, with Applications to Spherical and Cylindrical Specimens. J. Mech. Phys. Solids 2017, 107, 343–364. [Google Scholar] [CrossRef] [Green Version]
- Lefèvre, V.; Danas, K.; Lopez-Pamies, O. Two Families of Explicit Models Constructed from a Homogenization Solution for the Magnetoelastic Response of MREs Containing Iron and Ferrofluid Particles. Int. J. Non-Linear Mech. 2020, 119, 103362. [Google Scholar] [CrossRef]
- Lefèvre, V.; Lopez-Pamies, O. Nonlinear Electroelastic Deformations of Dielectric Elastomer Composites: I—Ideal Elastic Dielectrics. J. Mech. Phys. Solids 2017, 99, 409–437. [Google Scholar] [CrossRef]
- Lefèvre, V.; Lopez-Pamies, O. Nonlinear Electroelastic Deformations of Dielectric Elastomer Composites: II—Non-Gaussian Elastic Dielectrics. J. Mech. Phys. Solids 2017, 99, 438–470. [Google Scholar] [CrossRef]
- Akbari, E.; Khajehsaeid, H. A Continuum Magneto-Mechanical Model for Magnetorheological Elastomers. Smart Mater. Struct. 2020, 30, 015008. [Google Scholar] [CrossRef]
- Shariff, M.H.B.M.; Bustamante, R.; Hossain, M.; Steinmann, P. A Novel Spectral Formulation for Transversely Isotropic Magneto-Elasticity. Math. Mech. Solids 2017, 22, 1158–1176. [Google Scholar] [CrossRef]
- Snarskii, A.A.; Zorinets, D.; Shamonin, M.; Kalita, V.M. Theoretical Method for Calculation of Effective Properties of Composite Materials with Reconfigurable Microstructure: Electric and Magnetic Phenomena. Phys. Stat. Mech. Its Appl. 2019, 535, 122467. [Google Scholar] [CrossRef]
- Snarskii, A.A.; Shamonin, M.; Yuskevich, P.; Saveliev, D.V.; Belyaeva, I.A. Induced Anisotropy in Composite Materials with Reconfigurable Microstructure: Effective Medium Model with Movable Percolation Threshold. Phys. Stat. Mech. Its Appl. 2020, 560, 125170. [Google Scholar] [CrossRef]
- Snarskii, A.A.; Shamonin, M.; Yuskevich, P. Effective Medium Theory for the Elastic Properties of Composite Materials with Various Percolation Thresholds. Materials 2020, 13, 1243. [Google Scholar] [CrossRef]
- Snarskii, A.A.; Shamonin, M.; Yuskevich, P. Effect of Magnetic-Field-Induced Restructuring on the Elastic Properties of Magnetoactive Elastomers. J. Magn. Magn. Mater. 2021, 517, 167392. [Google Scholar] [CrossRef]
- Mitsumata, T.; Ohori, S.; Honda, A.; Kawai, M. Magnetism and Viscoelasticity of Magnetic Elastomers with Wide Range Modulation of Dynamic Modulus. Soft Matter 2012, 9, 904–912. [Google Scholar] [CrossRef]
- Bruggeman, V.D. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen. Ann. Phys. 1935, 416, 636–664. [Google Scholar] [CrossRef]
- Landauer, R. The Electrical Resistance of Binary Metallic Mixtures. J. Appl. Phys. 1952, 23, 779–784. [Google Scholar] [CrossRef]
- Sarychev, A.K.; Vinogradov, A.P. Effective Medium Theory for the Magnetoconductivity Tensor of Disordered Materials. Phys. Status Solidi B 1983, 117, K113–K118. [Google Scholar] [CrossRef]
- Budiansky, B. On the Elastic Moduli of Some Heterogeneous Materials. J. Mech. Phys. Solids 1965, 13, 223–227. [Google Scholar] [CrossRef]
- Hill, R. A Self-Consistent Mechanics of Composite Materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Chougale, S.; Romeis, D.; Saphiannikova, M. Magneto-Mechanical Enhancement of Elastic Moduli in Magnetoactive Elastomers with Anisotropic Microstructures. Materials 2022, 15, 645. [Google Scholar] [CrossRef]
- Belyaeva, I.A.; Kramarenko, E.Y.; Stepanov, G.V.; Sorokin, V.V.; Stadler, D.; Shamonin, M. Transient Magnetorheological Response of Magnetoactive Elastomers to Step and Pyramid Excitations. Soft Matter 2016, 12, 2901–2913. [Google Scholar] [CrossRef]
- Stolbov, O.; Raikher, Y.; Stepanov, G.; Chertovich, A.; Kramarenko, E.; Khokhlov, A. Low-Frequency Rheology of Magnetically Controlled Elastomers with Isotropic Structure. Polym. Sci. Ser. A 2010, 52, 1344–1354. [Google Scholar] [CrossRef]
- Li, W.H.; Zhou, Y.; Tian, T.F. Viscoelastic Properties of MR Elastomers under Harmonic Loading. Rheol. Acta 2010, 49, 733–740. [Google Scholar] [CrossRef]
- Spencer, B.F.; Dyke, S.J.; Sain, M.K.; Carlson, J.D. Phenomenological Model for Magnetorheological Dampers. J. Eng. Mech. 1997, 123, 230–238. [Google Scholar] [CrossRef]
- Chen, L.; Jerrams, S. A Rheological Model of the Dynamic Behavior of Magnetorheological Elastomers. J. Appl. Phys. 2011, 110, 013513. [Google Scholar] [CrossRef]
- Yu, Y.; Li, J.; Li, Y.; Li, S.; Li, H.; Wang, W. Comparative Investigation of Phenomenological Modeling for Hysteresis Responses of Magnetorheological Elastomer Devices. Int. J. Mol. Sci. 2019, 20, 3216. [Google Scholar] [CrossRef] [PubMed]
- Qiao, Y.; Zhang, J.; Zhang, M.; Liu, L.; Zhai, P. A Magnetic Field- and Frequency-Dependent Dynamic Shear Modulus Model for Isotropic Silicone Rubber-Based Magnetorheological Elastomers. Compos. Sci. Technol. 2021, 204, 108637. [Google Scholar] [CrossRef]
- Nadzharyan, T.A.; Kostrov, S.A.; Stepanov, G.V.; Kramarenko, E.Y. Fractional Rheological Models of Dynamic Mechanical Behavior of Magnetoactive Elastomers in Magnetic Fields. Polymer 2018, 142, 316–329. [Google Scholar] [CrossRef]
- Nadzharyan, T.A.; Sorokin, V.V.; Stepanov, G.V.; Bogolyubov, A.N.; Kramarenko, E.Y. A Fractional Calculus Approach to Modeling Rheological Behavior of Soft Magnetic Elastomers. Polymer 2016, 92, 179–188. [Google Scholar] [CrossRef]
- Nam, T.H.; Petríková, I.; Marvalová, B. Experimental Characterization and Viscoelastic Modeling of Isotropic and Anisotropic Magnetorheological Elastomers. Polym. Test. 2020, 81, 106272. [Google Scholar] [CrossRef]
- Zhu, G.; Xiong, Y.; Li, Z.; Li, M.; Bai, X. ‘Frank’ A Fractional-Order Model on the Dynamic Mechanical Behavior of Magnetorheological Elastomers. Smart Mater. Struct. 2020, 29, 025020. [Google Scholar] [CrossRef]
- Huu Nam, T.; Petríková, I.; Marvalová, B. Effects of Loading Rate, Applied Shear Strain, and Magnetic Field on Stress Relaxation Behavior of Anisotropic Magnetorheological Elastomer. Mech. Adv. Mater. Struct. 2022, 29, 2984–2998. [Google Scholar] [CrossRef]
- Poojary, U.R.; Gangadharan, K.V. Integer and Fractional Order-Based Viscoelastic Constitutive Modeling to Predict the Frequency and Magnetic Field-Induced Properties of Magnetorheological Elastomer. J. Vib. Acoust. 2018, 140, 041007. [Google Scholar] [CrossRef]
- Nguyen, X.B.; Komatsuzaki, T.; Zhang, N. A Nonlinear Magnetorheological Elastomer Model Based on Fractional Viscoelasticity, Magnetic Dipole Interactions, and Adaptive Smooth Coulomb Friction. Mech. Syst. Signal Process. 2020, 141, 106438. [Google Scholar] [CrossRef]
- Wang, B.; Kari, L. A Visco-Elastic-Plastic Constitutive Model of Isotropic Magneto-Sensitive Rubber with Amplitude, Frequency and Magnetic Dependency. Int. J. Plast. 2020, 132, 102756. [Google Scholar] [CrossRef]
- Poojary, U.R.; Gangadharan, K.V. Material Modeling of Frequency, Magnetic Field and Strain Dependent Response of Magnetorheological Elastomer. J. Mater. Sci. 2021, 56, 15752–15766. [Google Scholar] [CrossRef]
- Lewandowski, D. Modeling of Magnetorheological Elastomers Using the Elastic–Plastic Model with Kinematic Hardening. Materials 2019, 12, 892. [Google Scholar] [CrossRef]
- Romeis, D.; Saphiannikova, M. A Cascading Mean-Field Approach to the Calculation of Magnetization Fields in Magnetoactive Elastomers. Polymers 2021, 13, 1372. [Google Scholar] [CrossRef] [PubMed]
- Ponte Castañeda, P.; Galipeau, E. Homogenization-Based Constitutive Models for Magnetorheological Elastomers at Finite Strain. J. Mech. Phys. Solids 2011, 59, 194–215. [Google Scholar] [CrossRef]
- Galipeau, E.; Rudykh, S.; deBotton, G.; Ponte Castañeda, P. Magnetoactive Elastomers with Periodic and Random Microstructures. Int. J. Solids Struct. 2014, 51, 3012–3024. [Google Scholar] [CrossRef]
- Danas, K. Effective Response of Classical, Auxetic and Chiral Magnetoelastic Materials by Use of a New Variational Principle. J. Mech. Phys. Solids 2017, 105, 25–53. [Google Scholar] [CrossRef]
- Mukherjee, D.; Rambausek, M.; Danas, K. An Explicit Dissipative Model for Isotropic Hard Magnetorheological Elastomers. J. Mech. Phys. Solids 2021, 151, 104361. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Hossain, M. Microstructural Modelling of Hard-Magnetic Soft Materials: Dipole–Dipole Interactions versus Zeeman Effect. Extreme Mech. Lett. 2021, 48, 101382. [Google Scholar] [CrossRef]
- Dadgar-Rad, F.; Hossain, M. Finite Deformation Analysis of Hard-Magnetic Soft Materials Based on Micropolar Continuum Theory. Int. J. Solids Struct. 2022, 251, 111747. [Google Scholar] [CrossRef]
- Eringen, A.C. Microcontinuum Field Theories; Springer: New York, NY, USA, 1999; ISBN 978-1-4612-6815-4. [Google Scholar]
- Keip, M.-A.; Rambausek, M. A Multiscale Approach to the Computational Characterization of Magnetorheological Elastomers. Int. J. Numer. Methods Eng. 2016, 107, 338–360. [Google Scholar] [CrossRef]
- Hori, M.; Nemat-Nasser, S. On Two Micromechanics Theories for Determining Micro–Macro Relations in Heterogeneous Solids. Mech. Mater. 1999, 31, 667–682. [Google Scholar] [CrossRef]
- Zohdi, T.; Wriggers, P. An Introduction to Computational Micromechanics, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 978-3-540-77482-2. [Google Scholar]
- Schröder, J.; Labusch, M.; Keip, M.-A. Algorithmic Two-Scale Transition for Magneto-Electro-Mechanically Coupled Problems: FE2-Scheme: Localization and Homogenization. Comput. Methods Appl. Mech. Eng. 2016, 302, 253–280. [Google Scholar] [CrossRef]
- Keip, M.-A.; Rambausek, M. Computational and Analytical Investigations of Shape Effects in the Experimental Characterization of Magnetorheological Elastomers. Int. J. Solids Struct. 2017, 121, 1–20. [Google Scholar] [CrossRef]
- Rambausek, M.; Göküzüm, F.S.; Nguyen, L.T.K.; Keip, M.-A. A Two-Scale FE-FFT Approach to Nonlinear Magneto-Elasticity. Int. J. Numer. Methods Eng. 2019, 117, 1117–1142. [Google Scholar] [CrossRef]
- Ivaneyko, D.; Toshchevikov, V.; Saphiannikova, M.; Heinrich, G. Mechanical Properties of Magneto-Sensitive Elastomers: Unification of the Continuum-Mechanics and Microscopic Theoretical Approaches. Soft Matter 2014, 10, 2213–2225. [Google Scholar] [CrossRef]
- Romeis, D.; Metsch, P.; Kästner, M.; Saphiannikova, M. Theoretical Models for Magneto-Sensitive Elastomers: A Comparison between Continuum and Dipole Approaches. Phys. Rev. E 2017, 95, 042501. [Google Scholar] [CrossRef]
- Romeis, D.; Toshchevikov, V.; Saphiannikova, M. Effects of Local Rearrangement of Magnetic Particles on Deformation in Magneto-Sensitive Elastomers. Soft Matter 2019, 15, 3552–3564. [Google Scholar] [CrossRef]
- Romeis, D.; Toshchevikov, V.; Saphiannikova, M. Elongated Micro-Structures in Magneto-Sensitive Elastomers: A Dipolar Mean Field Model. Soft Matter 2016, 12, 9364–9376. [Google Scholar] [CrossRef]
- Romeis, D.; Kostrov, S.A.; Kramarenko, E.Y.; Stepanov, G.V.; Shamonin, M.; Saphiannikova, M. Magnetic-Field-Induced Stress in Confined Magnetoactive Elastomers. Soft Matter 2020, 16, 9047–9058. [Google Scholar] [CrossRef]
- Metsch, P.; Romeis, D.; Kalina, K.A.; Raßloff, A.; Saphiannikova, M.; Kästner, M. Magneto-Mechanical Coupling in Magneto-Active Elastomers. Materials 2021, 14, 434. [Google Scholar] [CrossRef] [PubMed]
- Puljiz, M.; Huang, S.; Auernhammer, G.K.; Menzel, A.M. Forces on Rigid Inclusions in Elastic Media and Resulting Matrix-Mediated Interactions. Phys. Rev. Lett. 2016, 117, 238003. [Google Scholar] [CrossRef] [PubMed] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nadzharyan, T.A.; Shamonin, M.; Kramarenko, E.Y. Theoretical Modeling of Magnetoactive Elastomers on Different Scales: A State-of-the-Art Review. Polymers 2022, 14, 4096. https://doi.org/10.3390/polym14194096
Nadzharyan TA, Shamonin M, Kramarenko EY. Theoretical Modeling of Magnetoactive Elastomers on Different Scales: A State-of-the-Art Review. Polymers. 2022; 14(19):4096. https://doi.org/10.3390/polym14194096
Chicago/Turabian StyleNadzharyan, Timur A., Mikhail Shamonin, and Elena Yu. Kramarenko. 2022. "Theoretical Modeling of Magnetoactive Elastomers on Different Scales: A State-of-the-Art Review" Polymers 14, no. 19: 4096. https://doi.org/10.3390/polym14194096





