A Fully Implicit Log-Conformation Tensor Coupled Algorithm for the Solution of Incompressible Non-Isothermal Viscoelastic Flows
Abstract
1. Introduction
2. Governing Equations
2.1. Stress-Tensor-Based Formulation
2.2. Log-Conformation Tensor-Based Formulation
3. Numerical Method
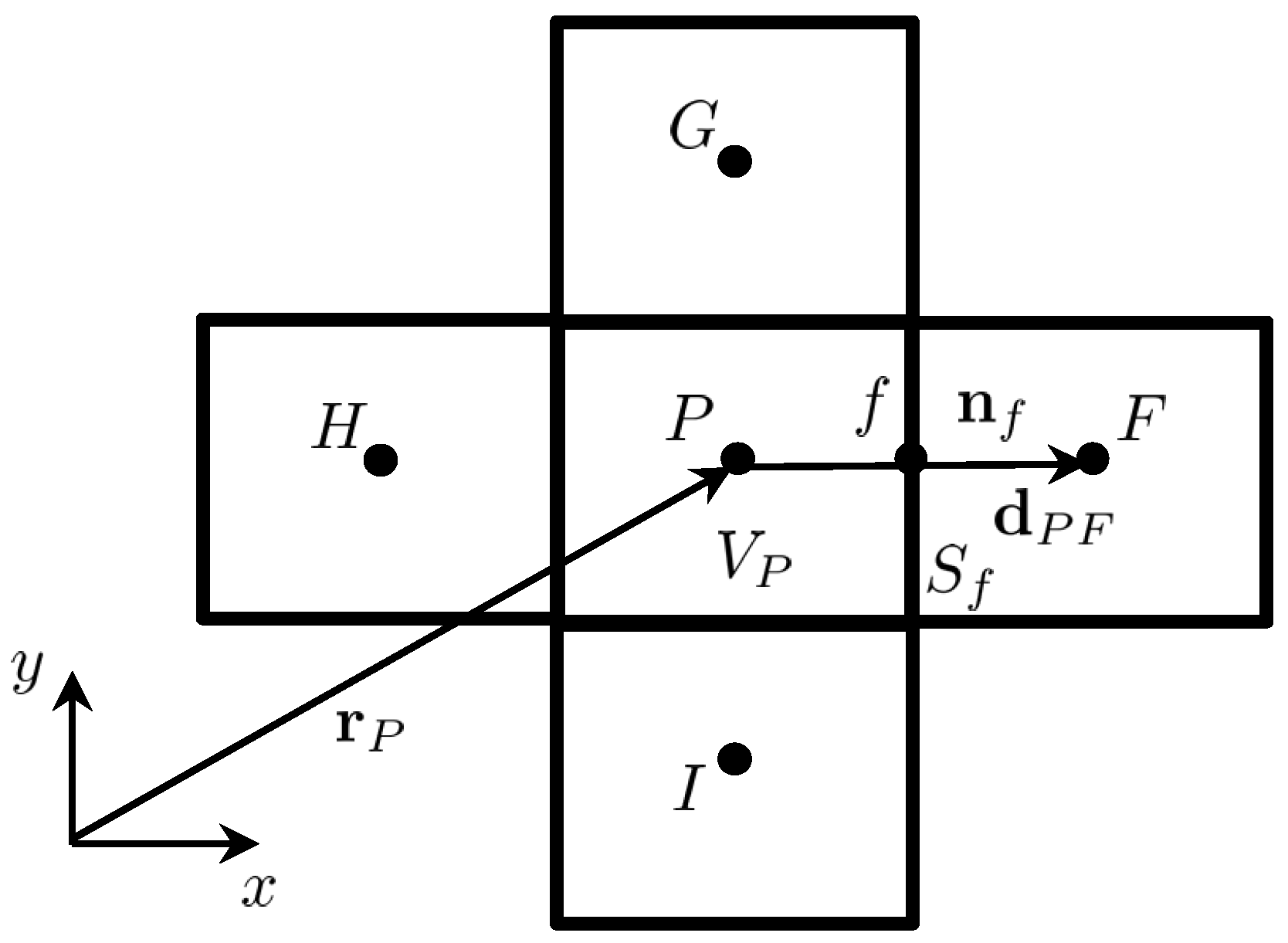
3.1. Discretization of the Equations for Conservation of Linear Momentum
3.2. Discretization of the Equation for Conservation of Mass
3.3. Discretization of the Log-Conformation Tensor Constitutive Equations
3.4. Discretization of the Equation for Conservation of Energy
3.5. Block-Coupled Algorithm
- Initialize the fluid variables with the latest known values .
- Iterate until convergence.
4. Results and Discussion
4.1. Geometry, Meshes, and Initial and Boundary Conditions
- For velocity, no-slip at the walls, symmetry at the centerline, parabolic velocity profile at the inlet (with average velocity m/s), and a zero-gradient condition at the outlet, i.e., assuming a fully developed flow;
- For pressure, the inlet and wall boundary conditions were set as zero-gradient and the centerline as symmetry boundary condition. At the outlet Dirichlet boundary condition was used, with a fixed value . Notice that, although the zero-pressure gradient specified at the inlet did not match the fully developed Poiseuille flow with the average velocity , this inconsistency did not affect the results, because the length of the upstream channel was sufficiently large to achieve fully developed flow conditions;
- For the log-conformation tensor components, zero values were assumed at the inlet, a symmetry boundary condition was used at the centerline, a linear extrapolation of the tensor components to the boundary was used at the walls, and a zero-gradient condition was imposed at the outlet;
- For the temperature, a Dirichlet condition was imposed at the inlet ( K), a symmetry boundary condition was used at the centerline, at the upstream wall, , K, while, for the downstream wall, the temperature was chosen such as to give temperature jumps of . A zero-gradient condition was imposed at the outlet;
- All fields were set to zero at the initial time.
4.2. Numerical Parameters
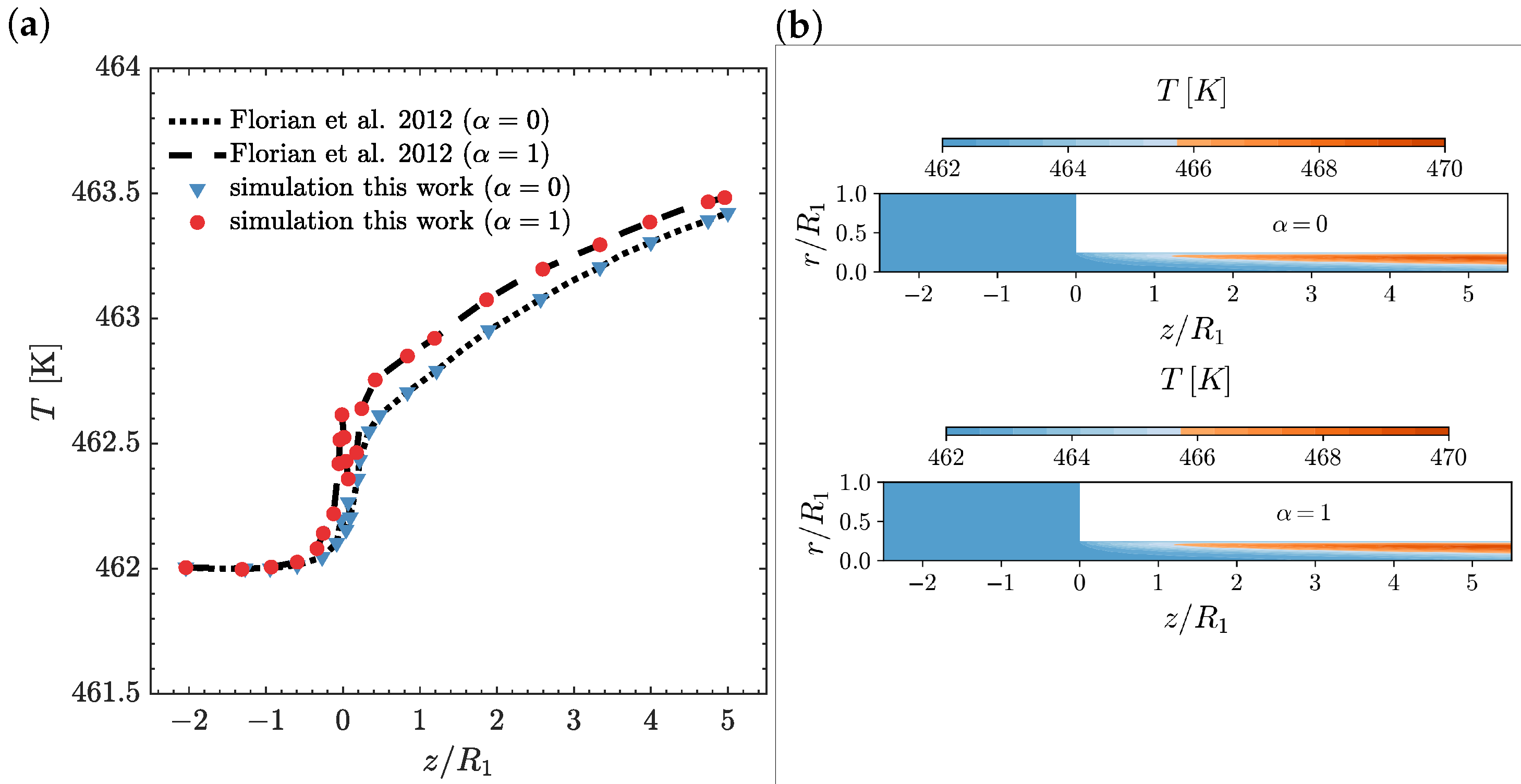
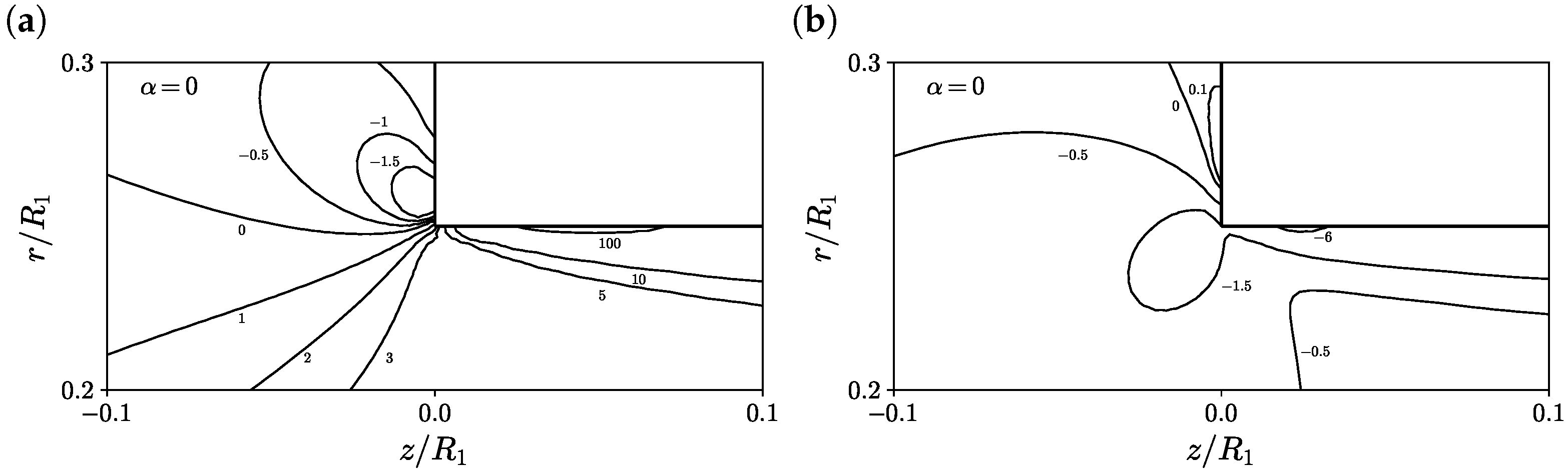
4.3. Effects of the Energy Partitioning Parameter
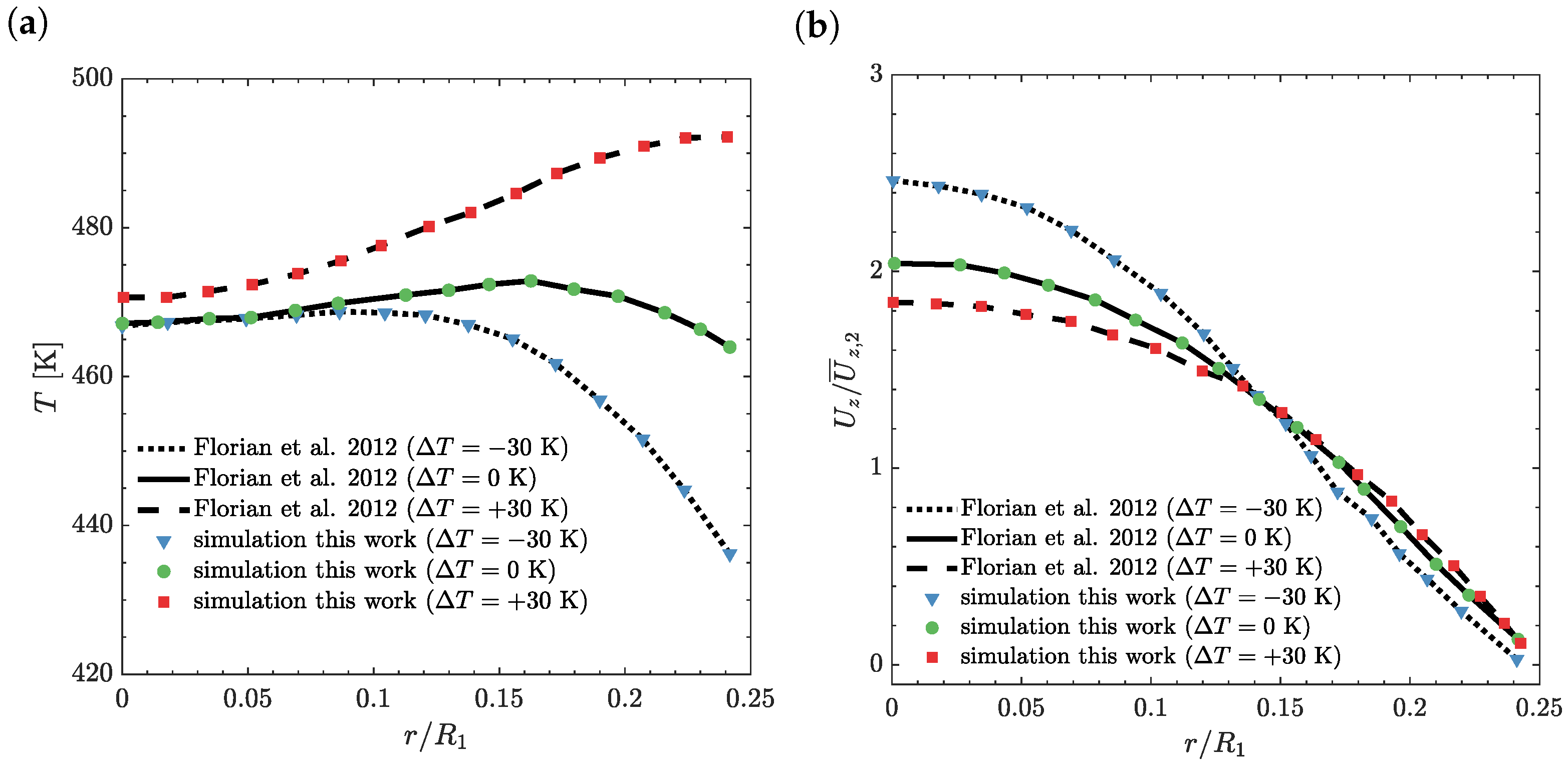
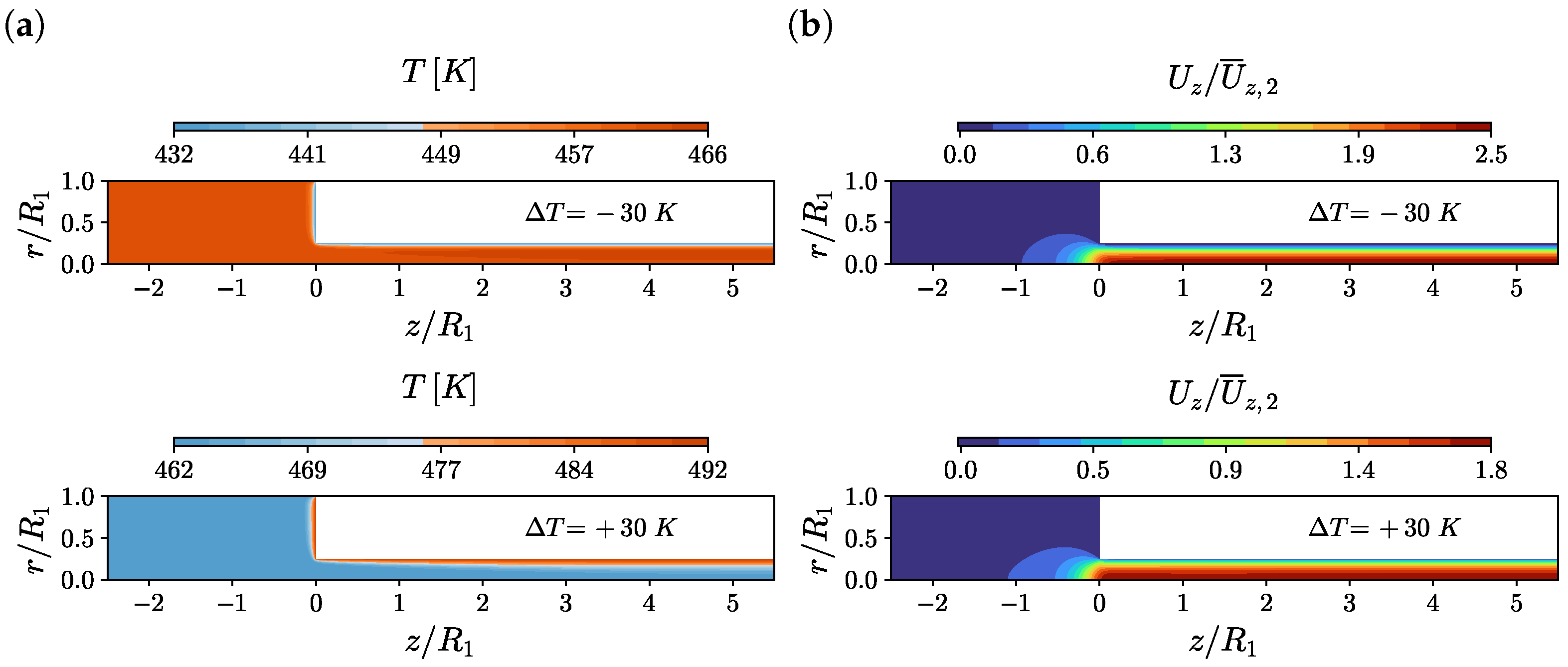
4.4. Effects of Wall Temperature Jumps
5. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, R.Y.; Yang, W.H. Numerical simulation of mold filling in injection molding using a three-dimensional finite volume approach. J. Numer. Methods Fluids 2001, 37, 125–148. [Google Scholar] [CrossRef]
- Zhou, J.; Turng, L.S. Three-dimensional numerical simulation of injection mold filling with a finite-volume method and parallel computing. Adv. Polym. Technol. 2007, 25, 247–258. [Google Scholar] [CrossRef]
- Pedro, J.; Ramôa, B.; Nóbrega, J.; Fernandes, C. Verification and Validation of openInjMoldSim, an Open-Source Solver to Model the Filling Stage of Thermoplastic Injection Molding. Fluids 2020, 5, 84. [Google Scholar] [CrossRef]
- Habla, F.; Fernandes, C.; Maier, M.; Densky, L.; Ferrás, L.; Rajkumar, A.; Carneiro, O.; Hinrichsen, O.; Nóbrega, J.M. Development and validation of a model for the temperature distribution in the extrusion calibration stage. Appl. Therm. Eng. 2016, 100, 538–552. [Google Scholar] [CrossRef]
- Pimenta, F.; Alves, M. Conjugate heat transfer in the unbounded flow of a viscoelastic fluid past a sphere. Int. J. Heat Fluid Flow 2021, 89, 108784. [Google Scholar] [CrossRef]
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Nóbrega, J.M.; Gaspar-Cunha, A. Modeling of Plasticating Injection Molding-Experimental Assessment. Int. Polym. Proc. 2014, 29, 558–569. [Google Scholar] [CrossRef]
- Fernandes, C.; Fakhari, A.; Tukovic, Ž. Non-Isothermal Free-Surface Viscous Flow of Polymer Melts in Pipe Extrusion Using an Open-Source Interface Tracking Finite Volume Method. Polymers 2021, 13, 4454. [Google Scholar] [CrossRef]
- Meburger, S.; Niethammer, M.; Bothe, D.; Schäfer, M. Numerical simulation of non-isothermal viscoelastic flows at high Weissenberg numbers using a finite volume method on general unstructured meshes. J.-Non-Newton. Fluid Mech. 2021, 287, 104451. [Google Scholar] [CrossRef]
- Bird, R. Constitutive equations for polymeric liquids. Annu. Rev. Fluid Mech. 1995, 27, 169–193. [Google Scholar] [CrossRef]
- Williams, M.; Landel, R.; Ferry, J. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Ferry, J. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Bird, R.; Armstrong, R.; Hassager, O. Dynamics of Polymeric Liquids, Volume 1: Fluid Mechanics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
- Peters, G.; Baaijens, F. Modelling of non-isothermal viscoelastic flows. J.-Non-Newton. Fluid Mech. 1997, 68, 205–224. [Google Scholar] [CrossRef]
- Hütter, M.; Luap, C.; Öttinger, H. Energy elastic effects and the concept of temperature in flowing polymeric liquids. Rheol. Acta 2009, 48, 301–316. [Google Scholar] [CrossRef]
- Braun, H. A model for the thermorheological behavior of viscoelastic fluids. Rheol. Acta 1991, 30, 523–529. [Google Scholar] [CrossRef]
- Wachs, A.; Clermont, J.R. Non-isothermal viscoelastic flow computations in an axisymmetric contraction at high Weissenberg numbers by a finite volume method. J.-Non-Newton. Fluid Mech. 2000, 95, 147–184. [Google Scholar] [CrossRef]
- Wachs, A.; Clermont, J.R.; Khalifeh, A. Computations of non-isothermal viscous and viscoelastic flows in abrupt contractions using a finite volume method. Eng. Comput. 2002, 19, 874–901. [Google Scholar] [CrossRef]
- Habla, F.; Woitalka, A.; Neuner, S.; Hinrichsen, O. Development of a methodology for numerical simulation of non-isothermal viscoelastic fluid flows with application to axisymmetric 4:1 contraction flows. Chem. Eng. J. 2012, 207–208, 772–784. [Google Scholar] [CrossRef]
- Fernandes, C.; Faroughi, S.A.; Ribeiro, R.; Isabel, A.; McKinley, G.H. Finite volume simulations of particle-laden viscoelastic fluid flows: Application to hydraulic fracture processes. Eng. Comput. 2022. [Google Scholar] [CrossRef]
- Zheng, Z.Y.; Li, F.C.; Yang, J.C. Modeling Asymmetric Flow of Viscoelastic Fluid in Symmetric Planar Sudden Expansion Geometry Based on User-Defined Function in FLUENT CFD Package. Adv. Mech. Eng. 2013, Volume 2013, 795937. [Google Scholar] [CrossRef]
- Shahbani-Zahiri, A.; Shahmardan, M.; Hassanzadeh, H.; Norouzi, M. Effects of fluid inertia and elasticity and expansion angles on recirculation and thermal regions of viscoelastic flow in the symmetric planar gradual expansions. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 480–492. [Google Scholar] [CrossRef]
- Kunisch, K.; Marduel, X. Optimal control of non-isothermal viscoelastic fluid flow. J.-Non-Newton. Fluid Mech. 2000, 88, 261–301. [Google Scholar] [CrossRef]
- Spanjaards, M.; Hulsen, M.; Anderson, P. Computational analysis of the extrudate shape of three-dimensional viscoelastic, non-isothermal extrusion flows. J.-Non-Newton. Fluid Mech. 2020, 282, 104310. [Google Scholar] [CrossRef]
- Patankar, S.; Spalding, D. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Darwish, M.; Sraj, I.; Moukalled, F. A coupled incompressible flow solver on structured grid. Numer. Heat Transf. Part B Fundam. 2007, 52, 353–371. [Google Scholar] [CrossRef]
- Darwish, M.; Sraj, I.; Moukalled, F. A coupled finite volume solver for the solution of incompressible flows on unstructured grids. J. Comput. Phys. 2009, 228, 180–201. [Google Scholar] [CrossRef]
- Mangani, L.; Buchmayr, M.; Darwish, M. Development of a novel fully coupled solver in OpenFOAM: Steady-state incompressible turbulent flows. Numer. Heat Transf. Part B Fundam. 2014, 66, 1–20. [Google Scholar] [CrossRef]
- Fernandes, C.; Cević, V.V.; Uroić, T.; Simoes, R.; Carneiro, O.; Jasak, H.; Nóbrega, J. A coupled finite volume flow solver for the solution of incompressible viscoelastic flows. J.-Non-Newton. Fluid Mech. 2019, 265, 99–115. [Google Scholar] [CrossRef]
- Ferreira, G.; Lage, P.; Silva, L.; Jasak, H. Implementation of an implicit pressure-velocity coupling for the Eulerian multi-fluid model. Comput. Fluids 2002, 181, 188–207. [Google Scholar] [CrossRef]
- Pimenta, F.; Alves, M.A. A coupled finite-volume solver for numerical simulation of electrically-driven flows. Comput. Fluids 2019, 193, 104279. [Google Scholar] [CrossRef]
- Kim, J.; Kim, C.; Kim, J.; Chung, C.; Ahn, K.; Lee, S. High-resolution finite element simulation of 4:1 planar contraction flow of viscoelastic fluid. J.-Non-Newton. Fluid Mech. 2005, 129, 23–37. [Google Scholar] [CrossRef]
- Oliveira, M.; Oliveira, P.; Pinho, F.; Alves, M. Effect of contraction ratio upon viscoelastic flow in contractions: The axisymmetric case. J.-Non-Newton. Fluid Mech. 2007, 147, 92–108. [Google Scholar] [CrossRef]
- Xue, S.C.; Phan-Thien, N.; Tanner, R. Three dimensional numerical simulations of viscoelastic flows through planar contractions. J.-Non-Newton. Fluid Mech. 1998, 74, 195–245. [Google Scholar] [CrossRef]
- Shaw, M. Introduction to Polymer Rheology; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Fattal, R.; Kupferman, R. Time-dependent simulation of viscoelastic flows at high Weissenberg number using the log-conformation representation. J.-Non-Newton. Fluid Mech. 2005, 126, 23–37. [Google Scholar] [CrossRef]
- Balci, N.; Thomases, B.; Renardy, M.; Doering, C. Symmetric factorization of the conformation tensor in viscoelastic fluid models. J.-Non-Newton. Fluid Mech. 2011, 166, 546–553. [Google Scholar] [CrossRef]
- Afonso, A.; Pinho, F.; Alves, M. The kernel-conformation constitutive laws. J.-Non-Newton. Fluid Mech. 2012, 167–168, 30–37. [Google Scholar] [CrossRef]
- Knechtges, P. Simulation of Viscoelastic Free-Surface Flows. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2018. [Google Scholar]
- Spahn, M. Modeling High Weissenberg Number Flows in OpenFOAM: Implementation of a Novel Log-Conf Approach in the Context of Finite Volumes. Master’s Thesis, RWTH Aachen University, Aachen, Germany, 2019. [Google Scholar]
- Oldroyd, J.G. On the formulation of rheological equations of state. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1950, 200, 523–541. [Google Scholar]
- Giesekus, H. A simple constitutive equation for polymer fluids based on the concept of deformation-dependent tensorial mobility. J.-Non-Newton. Fluid Mech. 1982, 11, 69–109. [Google Scholar] [CrossRef]
- Phan-Thien, N.; Tanner, R. A new constitutive equation derived from network theory. J.-Non-Newton. Fluid Mech. 1977, 2, 353–365. [Google Scholar] [CrossRef]
- Phan-Thien, N. A nonlinear network viscoelastic model. J. Rheol. 1978, 22, 259–283. [Google Scholar] [CrossRef]
- Wapperom, P.; Hulsen, M. Thermodynamics of viscoelastic fluids: The temperature equation. J. Rheol. 1998, 42, 999–1019. [Google Scholar] [CrossRef]
- Moreno, L.; Codina, R.; Baiges, J. Numerical simulation of non-isothermal viscoelastic fluid flows using a VMS stabilized finite element formulation. J.-Non-Newton. Fluid Mech. 2021, 296, 104640. [Google Scholar] [CrossRef]
- Fernandes, C.; Araujo, M.; Ferrás, L.; Nóbrega, J. Improved both sides diffusion (iBSD): A new and straightforward stabilization approach for viscoelastic fluid flows. J.-Non-Newton. Fluid Mech. 2017, 249, 63–78. [Google Scholar] [CrossRef]
- Rhie, C.; Chow, W. Numerical Study of Turbulent Flow Past an Isolated Airfol with Trailing Edge Separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. Ph.D. Thesis, Imperial College University of London, London, UK, 1996. [Google Scholar]
- Knechtges, P. The fully-implicit log-conformation formulation and its application to three-dimensional flows. J.-Non-Newton. Fluid Mech. 2015, 223, 209–220. [Google Scholar] [CrossRef]
- van der Vorst, H. Bi-CGSTAB: A fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 1992, 13, 631–644. [Google Scholar] [CrossRef]




| Block | Mesh 1 (M1) | Mesh 2 (M2) | ||||
|---|---|---|---|---|---|---|
| Block I | ||||||
| Block II | ||||||
| Block III | ||||||
| Block IV | ||||||
| Block V | ||||||
| NC | 4293 | 17172 | ||||
| Mesh | Number of Iterations | Execution Time [s] | ||||
|---|---|---|---|---|---|---|
| C | S | S/C | C | S | S/C | |
| M1 | 827 | 357,681 | 432 | 103 | 1760 | 17 |
| M2 | 1484 | 778,344 | 524 | 689 | 13,102 | 19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernandes, C. A Fully Implicit Log-Conformation Tensor Coupled Algorithm for the Solution of Incompressible Non-Isothermal Viscoelastic Flows. Polymers 2022, 14, 4099. https://doi.org/10.3390/polym14194099
Fernandes C. A Fully Implicit Log-Conformation Tensor Coupled Algorithm for the Solution of Incompressible Non-Isothermal Viscoelastic Flows. Polymers. 2022; 14(19):4099. https://doi.org/10.3390/polym14194099
Chicago/Turabian StyleFernandes, Célio. 2022. "A Fully Implicit Log-Conformation Tensor Coupled Algorithm for the Solution of Incompressible Non-Isothermal Viscoelastic Flows" Polymers 14, no. 19: 4099. https://doi.org/10.3390/polym14194099
APA StyleFernandes, C. (2022). A Fully Implicit Log-Conformation Tensor Coupled Algorithm for the Solution of Incompressible Non-Isothermal Viscoelastic Flows. Polymers, 14(19), 4099. https://doi.org/10.3390/polym14194099







