Magnetic Field Influence on the Microwave Characteristics of Composite Samples Based on Polycrystalline Y-Type Hexaferrite
Abstract
:1. Introduction
2. Materials and Methods
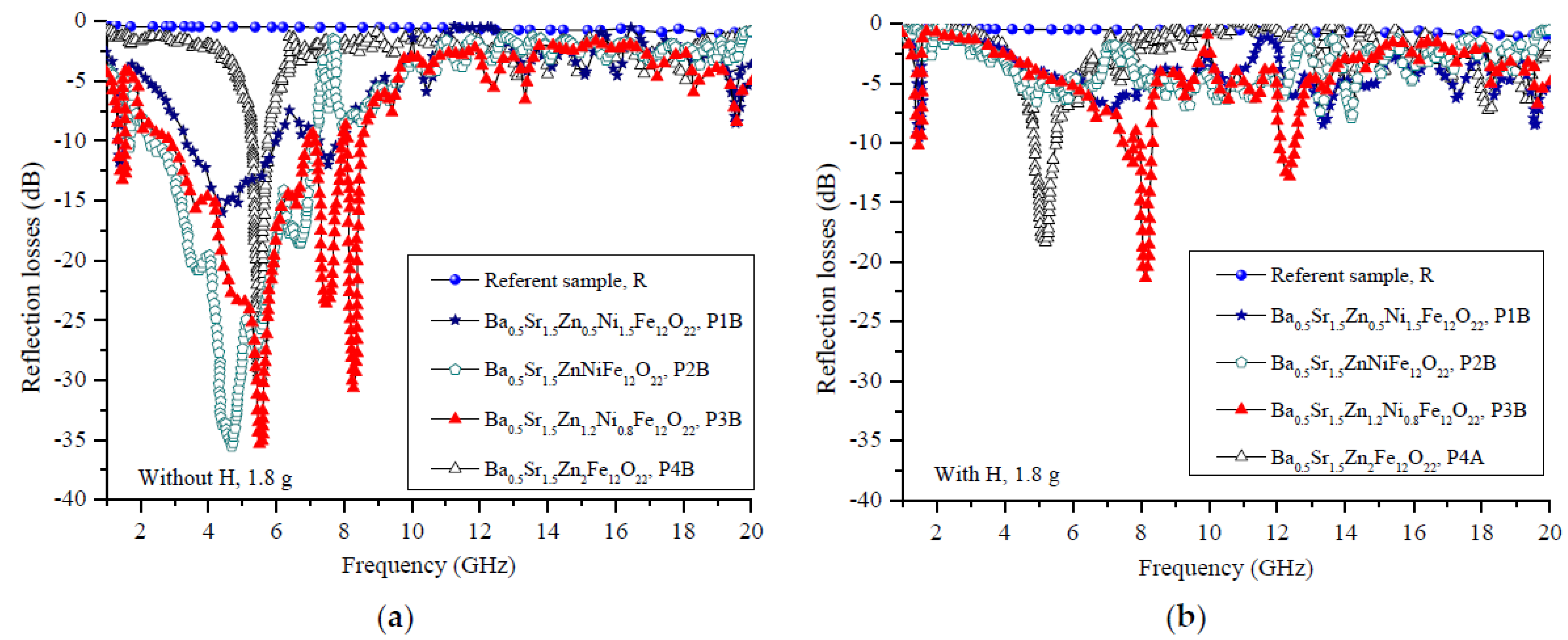
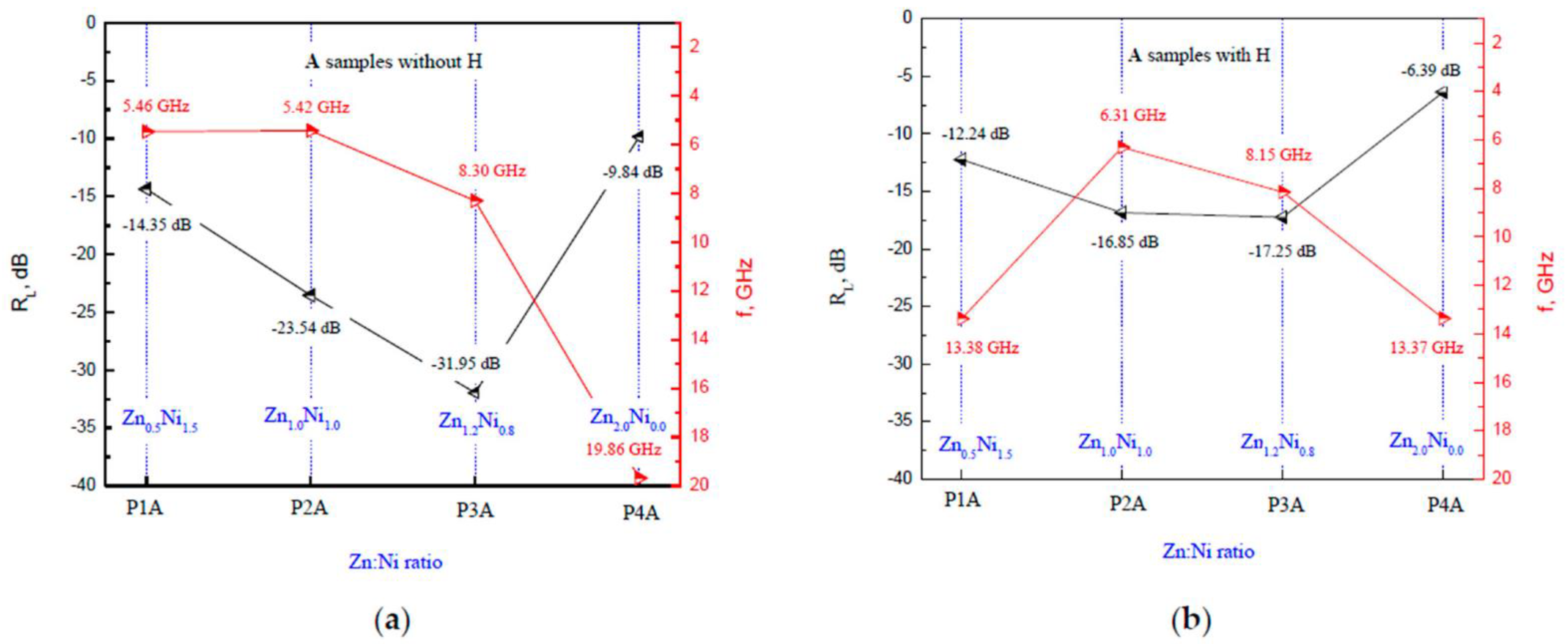
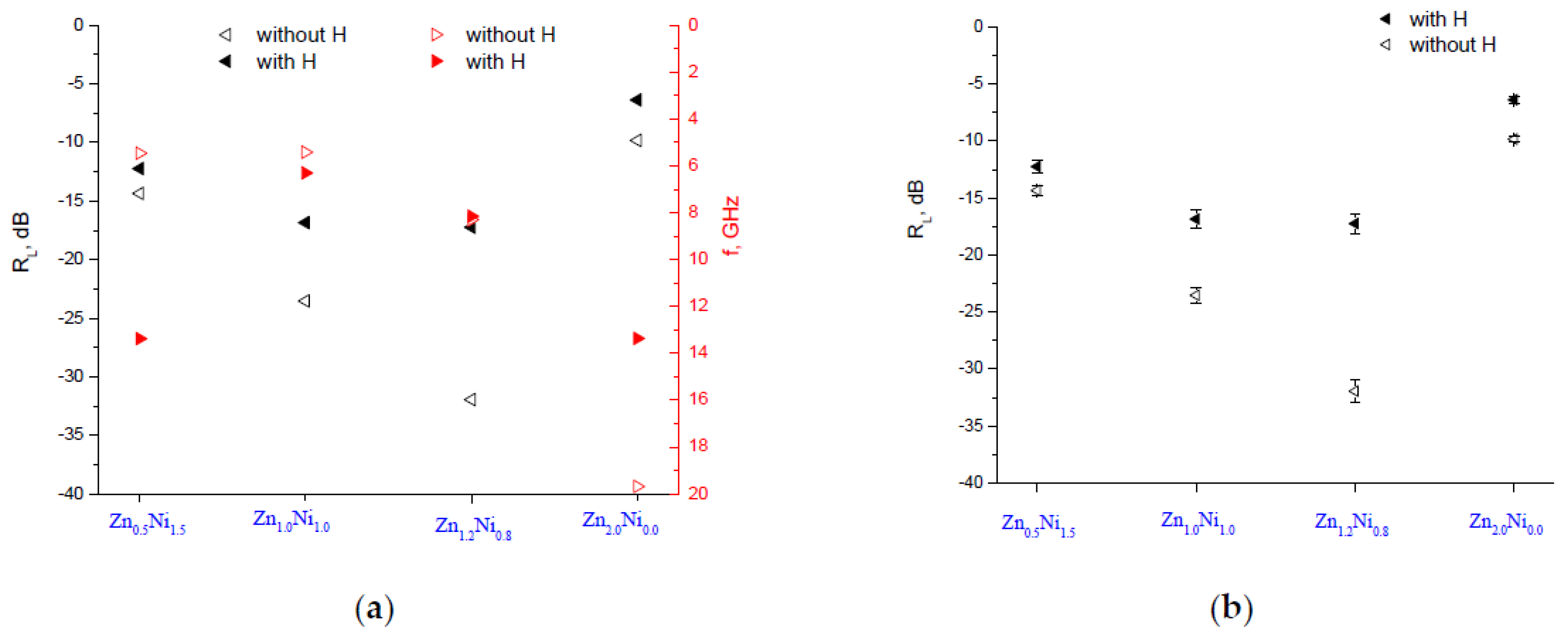
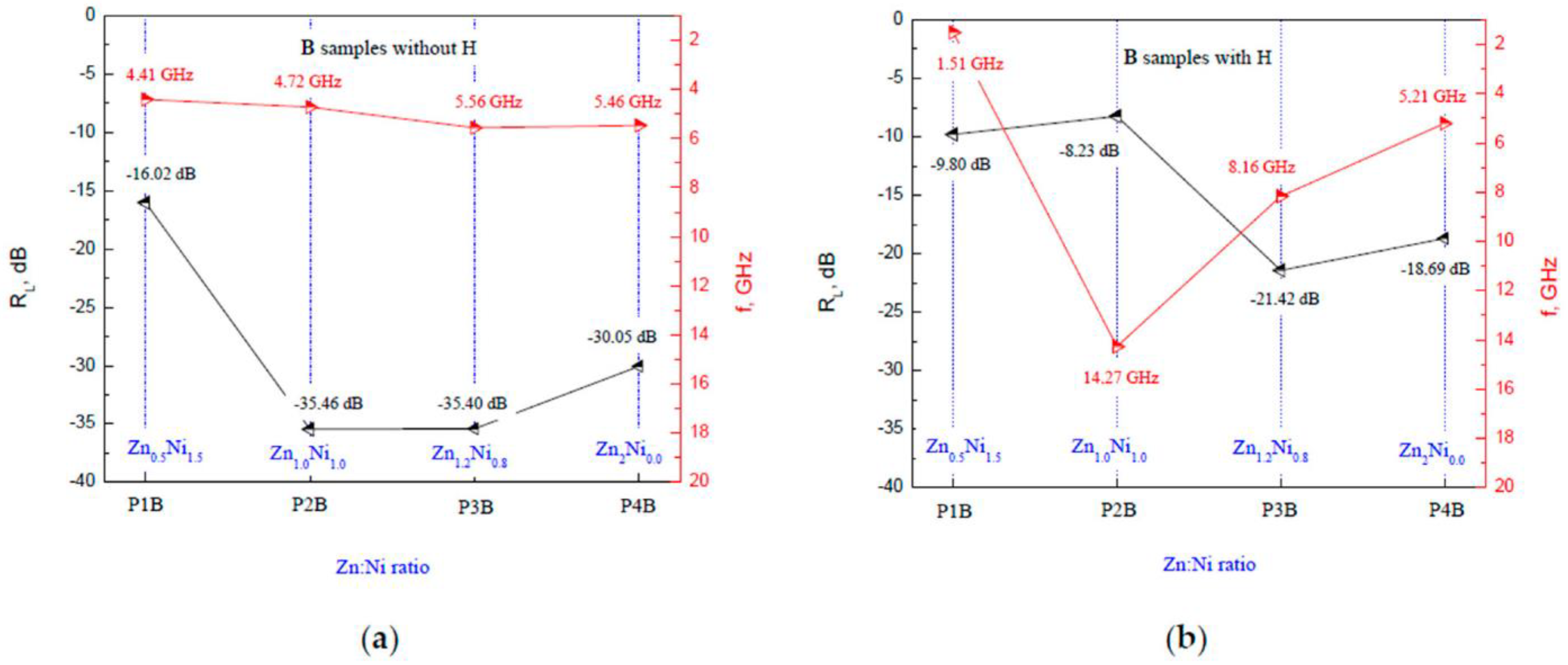
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dankov, P. Material characterization in the microwave range, when the materials become composite, reinforced, 3d-printed, artificially mixed, nanomaterials and metamaterials, Nanomaterials and Metamaterials. Forum Electromagn. Res. Methods Appl. Technol. (FERMAT J.) 2020, 41, 1–37. Available online: https://www.e-fermat.org/articles.php (accessed on 20 December 2020).
- Miszczyk, A. Protective and suppressing electromagnetic interference properties of epoxy coatings containing nano-sized NiZn ferrites. Front. Mater. 2020, 7, 183. [Google Scholar] [CrossRef]
- Bera, S.C. Microwave Active Devices and Circuits for Communication, 1st ed.; Springer: Singapore, 2019. [Google Scholar]
- Houbi, A.; Aldashevich, Z.A.; Atassi, Y.; Bagasharova Telmanovna, Z.; Saule, M.; Kubanych, K. Microwave absorbing properties of ferrites and their composites: A review. J. Magn. Magn. Mater. 2021, 529, 167839. [Google Scholar] [CrossRef]
- Zeng, X.J.; Cheng, X.Y.; Yu, R.H.; Stucky, G.D. Electromagnetic microwave absorption theory and recent achievements in microwave absorbers. Carbon 2020, 168, 606–623. [Google Scholar] [CrossRef]
- Cao, M.S.; Wang, X.X.; Zhang, M.; Cao, W.Q.; Fang, X.Y.; Yuan, J. Variable-temperature electron transport and dipole polarization turning flexible multifunctional microsensor beyond electrical and optical energy. Adv. Mater. 2020, 32, 1907156. [Google Scholar] [CrossRef]
- Lee, S.; Jo, I.; Kang, S.; Jang, B.; Moon, J.; Park, J.B.; Lee, S.; Rho, S.; Kim, Y.; Hong, B.H. Smart contact lenses with graphene coating for electromagnetic interference shielding and dehydration protection. ACS Nano 2017, 11, 5318–5324. [Google Scholar] [CrossRef]
- Wang, Z.; Mao, B.Y.; Wang, Q.L.; Yu, J.; Dai, J.X.; Song, R.G.; Pu, Z.H.; He, D.P.; Wu, Z.; Mu, S.C. Ultrahigh conductive copper/large flake size graphene heterostructure thin-film with remarkable electromagnetic interference shielding effectiveness. Small 2018, 14, 1704332. [Google Scholar] [CrossRef]
- Meng, F.B.; Wang, H.G.; Huang, F.; Guo, Y.F.; Wang, Z.Y.; Hui, D.; Zhou, Z.W. Graphene-based microwave absorbing composites: A review and prospective. Compos. Part B Eng. 2018, 137, 260–277. [Google Scholar] [CrossRef]
- Wang, F.Y.; Sun, Y.Q.; Li, D.R.; Zhong, B.; Wu, Z.G.; Zuo, S.Y.; Yan, D.; Zhuo, R.F.; Feng, J.J.; Yan, P.X. Core-shell FeCo@carbon nanoparticles encapsulated in polydopamine-derived carbon nanocages for efficient microwave absorption. Carbon 2018, 134, 264–273. [Google Scholar] [CrossRef]
- Wang, L.N.; Jia, X.L.; Li, Y.F.; Yang, F.; Zhang, L.Q.; Liu, L.P.; Ren, X.; Yang, H.T. Synthesis and microwave absorption property of flexible magnetic film based on graphene oxide/carbon nanotubes and Fe3O4 nanoparticles. J. Mater. Chem. A 2014, 2, 14940–14946. [Google Scholar] [CrossRef]
- Li, W.; Wei, J.; Wang, W.; Hu, D.; Li, Y.; Guan, J. Ferrite-based metamaterial microwave absorber with absorption frequency magnetically tunable in a wide range. Mater. Des. 2016, 110, 27–34. [Google Scholar] [CrossRef]
- Pang, Y.; Li, Y.; Wang, J.; Yan, M.; Qu, S.; Xia, S.; Xu, Z. Electromagnetic reflection reduction of carbon composite materials mediated by collaborative mechanisms. Carbon 2019, 147, 112–119. [Google Scholar] [CrossRef]
- Zhao, B.; Zhao, W.Y.; Shao, G.; Fan, B.B.; Zhang, R. Morphology-control synthesis of a core–shell structured NiCu alloy with tunable electromagnetic-wave absorption capabilities. ACS Appl. Mater. Interfaces 2015, 7, 12951–12960. [Google Scholar] [CrossRef]
- Li, H.; Cao, Z.M.; Lin, J.Y.; Zhao, H.; Jiang, Q.R.; Jiang, Z.Y.; Liao, H.G.; Kuang, Q.; Xie, Z.X. Synthesis of u-channelled spherical Fex(CoyNi1-y)100-xJanus colloidal particles with excellent electromagnetic wave absorption performance. Nanoscale 2018, 10, 1930–1938. [Google Scholar] [CrossRef]
- Wang, C.H.; Ding, Y.J.; Yuan, Y.; He, X.D.; Wu, S.T.; Hu, S.; Zou, M.C.; Zhao, W.Q.; Yang, L.S.; Cao, A.Y.; et al. Graphene aerogel composites derived from recycled cigarette filters for electromagnetic wave absorption. J. Mater. Chem. C 2015, 3, 11893–11901. [Google Scholar] [CrossRef]
- Zhou, X.F.; Jia, Z.R.; Feng, A.L.; Wang, X.X.; Liu, J.J.; Zhang, M.; Cao, H.J.; Wu, G.L. Synthesis of fish skin-derived 3D carbon foams with broadened bandwidth and excellent electromagnetic wave absorption performance. Carbon 2019, 152, 827–836. [Google Scholar] [CrossRef]
- Xiang, J.; Li, J.L.; Zhang, X.H.; Ye, Q.; Xu, J.H.; Sheng, X.Q. Magnetic carbon nanofibers containing uniformly dispersed Fe/Co/Ni nanoparticles as stable and highperformance electromagnetic wave absorbers. J. Mater. Chem. A 2014, 2, 16905–16914. [Google Scholar] [CrossRef]
- Li, X.A.; Du, D.X.; Wang, C.S.; Wang, H.Y.; Xu, Z.P. In situ synthesis of hierarchical rose-like porous Fe@C with enhanced electromagnetic wave absorption. J. Mater. Chem. C 2018, 6, 558–567. [Google Scholar] [CrossRef]
- Kolev, S.; Peneva, P.; Krezhov, K.; Malakova, T.; Ghelev, C.; Koutzarova, T.; Kovacheva, D.; Vertruyen, B.; Closset, R.; Tran, L.-M.; et al. Structural, magnetic and microwave characterization of polycrystalline Z-type Sr3Co2Fe24O41 hexaferrite. Materials 2020, 13, 2355. [Google Scholar] [CrossRef] [PubMed]
- Almessiere, M.; Genc, F.; Sozeri, H.; Baykal, A.; Trukhanov, S.V.; Trukhanov, A.V. Influence of charge disproportionation on microwave characteristics of Zn–Nd substituted Sr-hexaferrites. J. Mater. Sci. Mater. Electron. 2019, 30, 6776–6785. [Google Scholar] [CrossRef]
- Kong, L.B.; Li, Z.W.; Liu, L.; Huang, R.; Abshinova, M.; Yang, Z.H.; Tang, C.B.; Tan, P.K.; Deng, C.R.; Matitsine, S. Recent progress in some composite materials and structures for specific electromagnetic applications. Int. Mater. Rev. 2013, 58, 203–259. [Google Scholar] [CrossRef]
- Pullar, R.C. Hexagonal Ferrite Fibres and Nanofibres. Solid State Phenom. 2016, 241, 1–68. [Google Scholar] [CrossRef]
- Kong, L.B.; Liu, L.; Yang, Z.; Li, S.; Zhang, T.; Wang, C. Ferrite-based composites for microwave absorbing applications. In Metal Oxides, Magnetic, Ferroelectric, and Multiferroic Metal Oxides; Stojanovic, B.D., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 361–385. [Google Scholar] [CrossRef]
- Bahadur, A.; Saeed, A.; Iqbal, S.; Shoaib, M.; Ahmad, I.; ur Rahman, M.S.; Bashir, M.I.; Yaseen, M.; Hussain, W. Morphological and magnetic properties of BaFe12O19 nanoferrite: A promising microwave absorbing material. Ceram. Int. 2017, 43, 7346–7350. [Google Scholar] [CrossRef]
- Wei, S.C.; Liu, Y.; Tian, H.L.; Tong, H.; Liu, Y.X.; Xu, B.S. Microwave absorption property of plasma spray W-type hexagonal ferrite coating. J. Magn. Magn. Mater. 2015, 377, 419–423. [Google Scholar] [CrossRef]
- Kumar, S.; Meena, R.S.; Chatterjee, R. Microwave absorption studies of Cr-doped Co–U type hexaferrites over 2–18 GHz frequency range. J. Magn. Magn. Mater. 2016, 418, 194–199. [Google Scholar] [CrossRef]
- Singh, J.; Singh, C.; Kaur, D.; Narang, S.B.; Jotania, R.; Joshi, R. Investigation on structural and microwave absorption property of Co2+ and Y3+ substituted M-type Ba-Sr hexagonal ferrites prepared by a ceramic method. J. Alloy. Comp. 2017, 695, 792–798. [Google Scholar] [CrossRef]
- Tang, X.T.; Wei, G.T.; Zhu, T.X.; Sheng, L.M.; An, K.; Yu, L.M.; Liu, Y.; Zhao, X.L. Microwave absorption performance enhanced by high-crystalline graphene and BaFe12O19 nanocomposites. J. Appl. Phys. 2016, 119, 204301. [Google Scholar] [CrossRef]
- Stergiou, C.A.; Litsardakis, G. Y-type hexagonal ferrites for microwave absorber and antenna applications. J. Magn. Magn. Mater. 2016, 405, 54–61. [Google Scholar] [CrossRef]
- Koutzarova, T.; Kolev, S.; Krezhov, K.; Georgieva, B.; Ghelev, C.; Kovacheva, D.; Vertruyen, B.; Closset, R.; Tran, L.-M.; Babij, M.; et al. Ni-substitution effect on the properties of Ba0.5Sr1.5Zn2−xNixFe12O22 powders. J. Magn. Magn. Mater. 2020, 505, 166725. [Google Scholar] [CrossRef]
- Koutzarova, T.; Kolev, S.; Krezhov, K.; Georgieva, B.; Ghelev, C.; Kovacheva, D.; Vertruyen, B.; Closset, R.; Tran, L.-M.; Babij, M.; et al. Data supporting the results of the characterization of the phases and structures appearing during the synthesis process of Ba0.5Sr1.5Zn2-xNixFe12O22 by auto-combustion. Data Brief 2020, 31, 105803. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Jo, S.; Gueon, K.; Choi, K.; Kim, J.; Churn, K. Complex permeability and permittivity and microwave absorption of ferrite-rubber composite at X-band frequencies. IEEE Trans. Magn. 1991, 27, 5462–5464. [Google Scholar] [CrossRef]
- Georgieva, B.; Kolev, S.; Krezhov, K.; Ghelev, C.; Kovacheva, D.; Vertruyen, B.; Closset, R.; Tran, L.-M.; Babij, M.; Zaleski, A.J.; et al. Structural and magnetic characterization of Y-type hexaferrite powders prepared by sol-gel auto-combustion and sonochemistry. J. Magn. Magn. Mater. 2019, 477, 131–135. [Google Scholar] [CrossRef]
- El Hiti, M.; Abo El Ata, A. Semiconductivity in Ba2Ni2−xZnxFe12O22 Y-type hexaferrites. J. Magn. Magn. Mater. 1999, 195, 667–678. [Google Scholar] [CrossRef]
- Kolev, S.; Yanev, A.; Nedkov, I. Microwave absorption of ferrite powders in a polymer matrix. Phys. Stat. Sol. 2006, 3, 1308–1315. [Google Scholar] [CrossRef]
- Kolev, S.; Koutzarova, T. Nanosized ferrite materials for absorption and protection from microwave radiation. In Advanced Nanotechnologies for Detection and Defence against CBRN Agents NATO Science for Peace and Security Series B: Physics and Biophysics; Petkov, P., Tsiulyanu, D., Popov, C., Kulisch, W., Eds.; Springer: Dordrecht, The Netherlands, 2018; pp. 273–283. [Google Scholar] [CrossRef]
- Naito, Y.; Suetake, K. Application of ferrite to electromagnetic wave absorber and its characteristics. IEEE Trans. Microw. Theory Tech. 1971, 19, 65–72. [Google Scholar] [CrossRef]
- Liu, W.; Liu, L.; Yang, Z.; Xu, J.; Hou, Y.; Ji, G. A versatile route toward the electromagnetic functionalization of metal–organic framework-derived three-dimensional nanoporous carbon composites. ACS Appl. Mater. Interfaces 2018, 10, 8965–8975. [Google Scholar] [CrossRef] [PubMed]
- Quan, B.; Shi, W.H.; Ong, S.J.H.; Lu, X.C.; Wang, P.L.Y.; Ji, G.B.; Guo, Y.F.; Zheng, L.R.; Xu, Z.C.J. Defect engineering in two common types of dielectric materials for electromagnetic absorption applications. Adv. Funct. Mater. 2019, 29, 1901236. [Google Scholar] [CrossRef]
- Wang, G.Z.; Gao, Z.; Tang, S.W.; Chen, C.Q.; Duan, F.F.; Zhao, S.C.; Lin, S.W.; Feng, Y.H.; Zhou, L.; Qin, Y. Microwave absorption properties of carbon nanocoils coated with highly controlled magnetic materials by atomic layer deposition. ACS Nano 2012, 6, 11009–11017. [Google Scholar] [CrossRef]
- Qiao, L.; Wang, T.; Mei, Z.L.; Li, X.L.; Sui, W.B.; Tang, L.Y.; Li, F.S. Analyzing bandwidth on the microwave absorber by the interface reflection model. Chin. Phys. Lett. 2016, 33, 027502. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, S.Y.; Tang, D.M.; Yang, Y.; Zhang, B.S. Thin magnetic coating for low-frequency broadband microwave absorption. J. Appl. Phys. 2014, 116, 243911. [Google Scholar] [CrossRef]
- Kong, I.; Ahmad, S.H.; Abdullah, M.H.; Hui, D.; Yusoff, A.N.; Puryanti, D. Magnetic and microwave absorbing properties of magnetite thermoplastic natural rubber nanocomposites. J. Magn. Magn. Mater. 2010, 322, 3401–3409. [Google Scholar] [CrossRef]
- Cao, M.S.; Song, W.L.; Hou, Z.L.; Wen, B.; Yuan, J. The effects of temperature and frequency on the dielectric properties, electromagnetic interference shielding and microwave-absorption of short carbon fiber/silica composites. Carbon 2010, 48, 788–796. [Google Scholar] [CrossRef]
- Zhu, L.Y.; Zeng, X.J.; Li, X.P.; Yang, B.; Yu, R.H. Hydrothermal synthesis of magnetic Fe3O4/graphene composites with good electromagnetic microwave absorbing performances. J. Magn. Magn. Mater. 2017, 426, 114–120. [Google Scholar] [CrossRef]
- Smit, J.; Wijn, H.P.J. Ferrites: Physical Properties of Ferrimagnetic Oxides in Relation to Their Technical Applications; Wiley: New York, NY, USA, 1959. [Google Scholar]


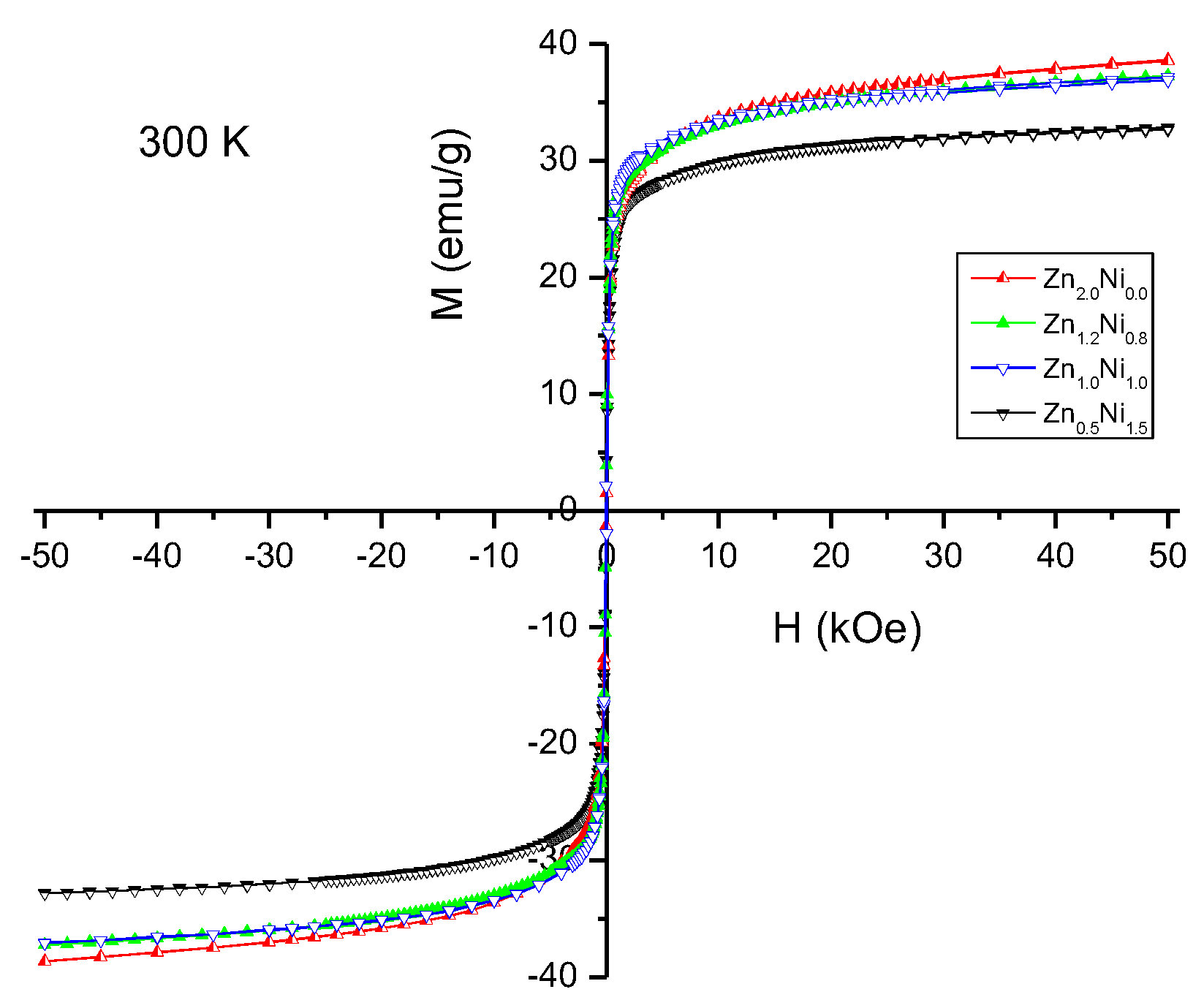


| 300 K | Zn0.5Ni1.5 | ZnNi | Zn1.2Ni0.8 | Zn2Ni0 |
|---|---|---|---|---|
| saturation magnetization, emu/g | 32.82 | 37.07 | 37.25 | 38.56 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolev, S.; Georgieva, B.; Koutzarova, T.; Krezhov, K.; Ghelev, C.; Kovacheva, D.; Vertruyen, B.; Closset, R.; Tran, L.M.; Babij, M.; et al. Magnetic Field Influence on the Microwave Characteristics of Composite Samples Based on Polycrystalline Y-Type Hexaferrite. Polymers 2022, 14, 4114. https://doi.org/10.3390/polym14194114
Kolev S, Georgieva B, Koutzarova T, Krezhov K, Ghelev C, Kovacheva D, Vertruyen B, Closset R, Tran LM, Babij M, et al. Magnetic Field Influence on the Microwave Characteristics of Composite Samples Based on Polycrystalline Y-Type Hexaferrite. Polymers. 2022; 14(19):4114. https://doi.org/10.3390/polym14194114
Chicago/Turabian StyleKolev, Svetoslav, Borislava Georgieva, Tatyana Koutzarova, Kiril Krezhov, Chavdar Ghelev, Daniela Kovacheva, Benedicte Vertruyen, Raphael Closset, Lan Maria Tran, Michal Babij, and et al. 2022. "Magnetic Field Influence on the Microwave Characteristics of Composite Samples Based on Polycrystalline Y-Type Hexaferrite" Polymers 14, no. 19: 4114. https://doi.org/10.3390/polym14194114
APA StyleKolev, S., Georgieva, B., Koutzarova, T., Krezhov, K., Ghelev, C., Kovacheva, D., Vertruyen, B., Closset, R., Tran, L. M., Babij, M., & Zaleski, A. J. (2022). Magnetic Field Influence on the Microwave Characteristics of Composite Samples Based on Polycrystalline Y-Type Hexaferrite. Polymers, 14(19), 4114. https://doi.org/10.3390/polym14194114







