Analysis of Mechanical Property Degradation of Outdoor Weather-Exposed Polymers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Methods
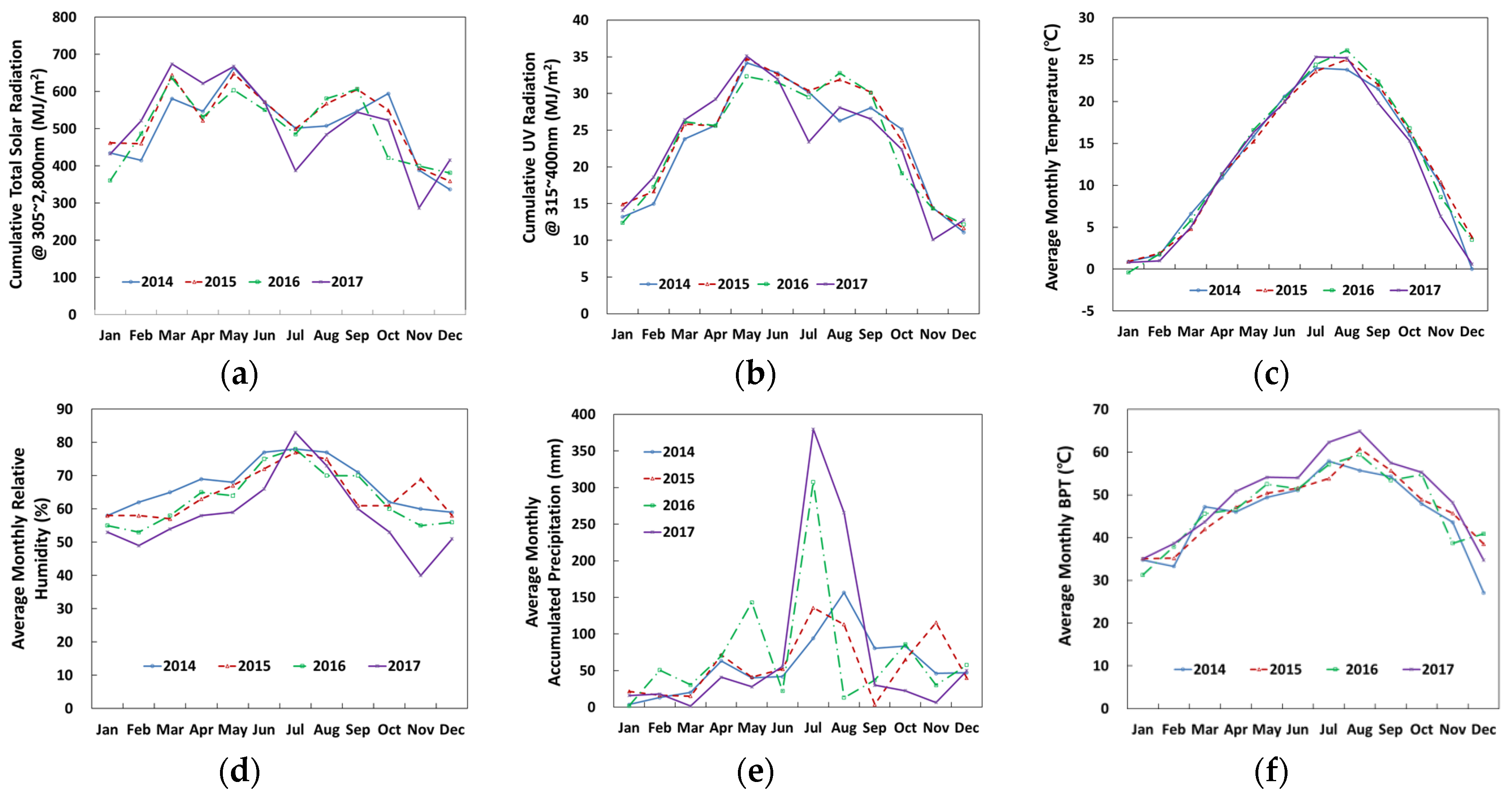
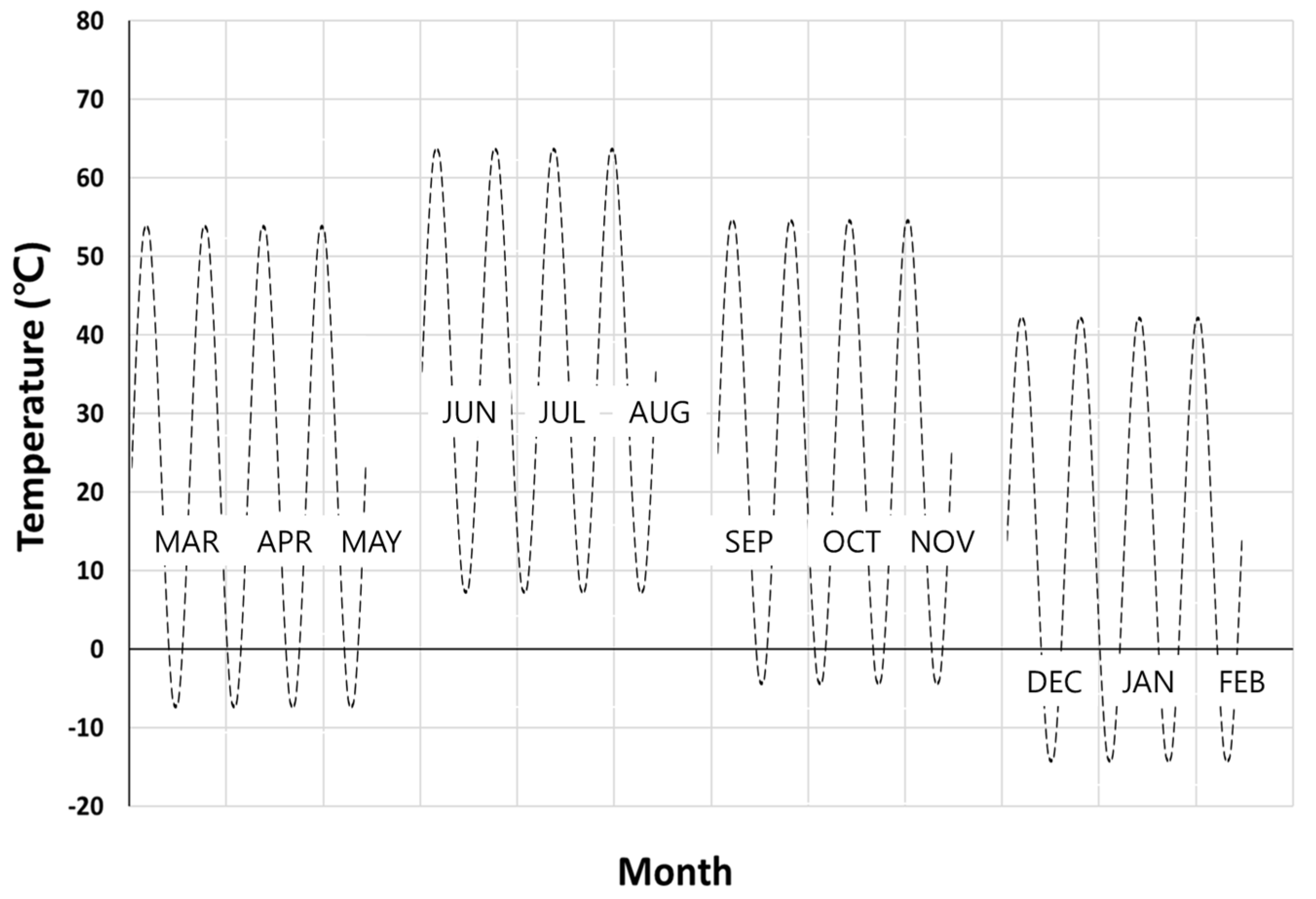
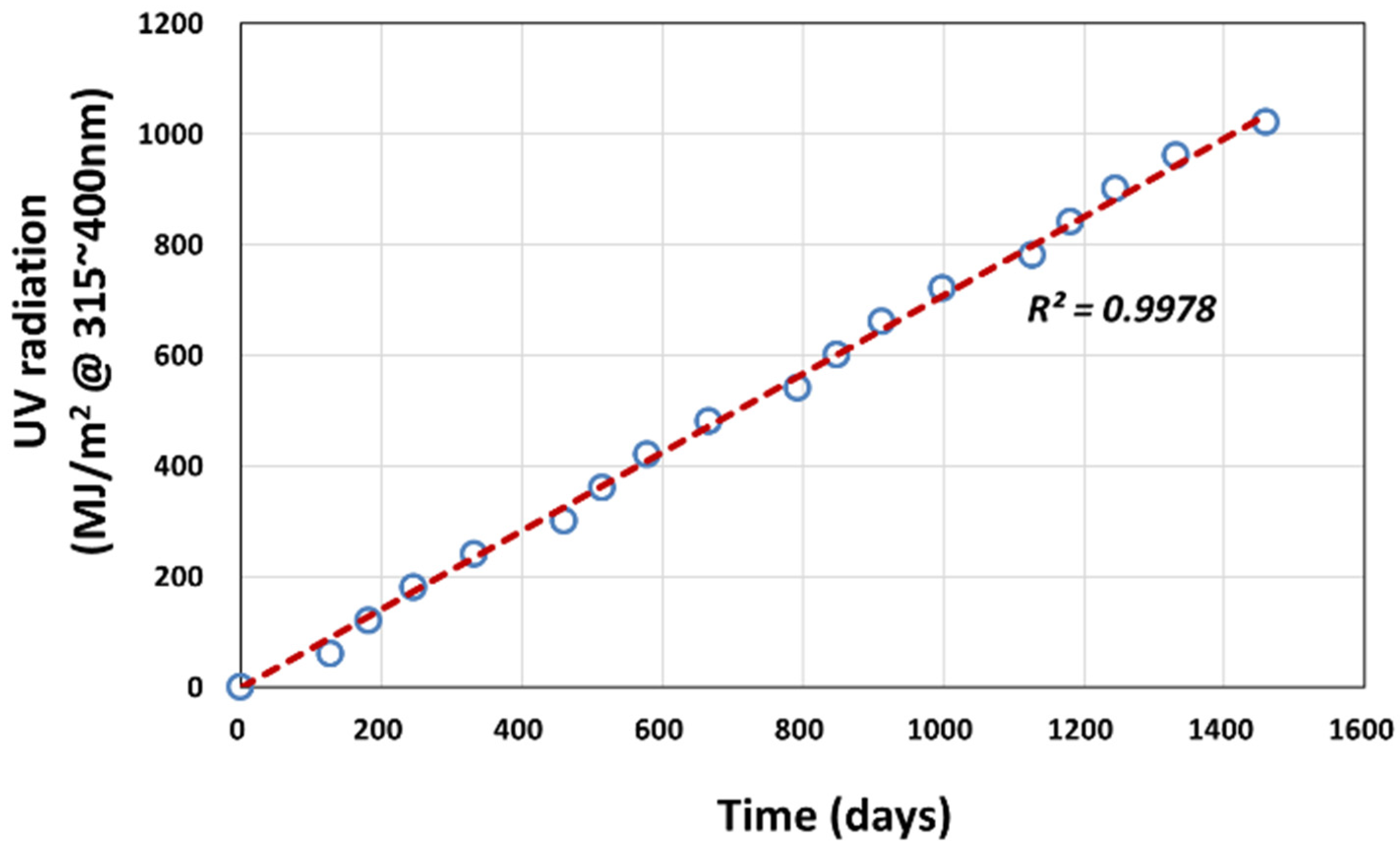
2.2.1. Outdoor Weathering
2.2.2. Tensile Testing
3. Results and Discussion
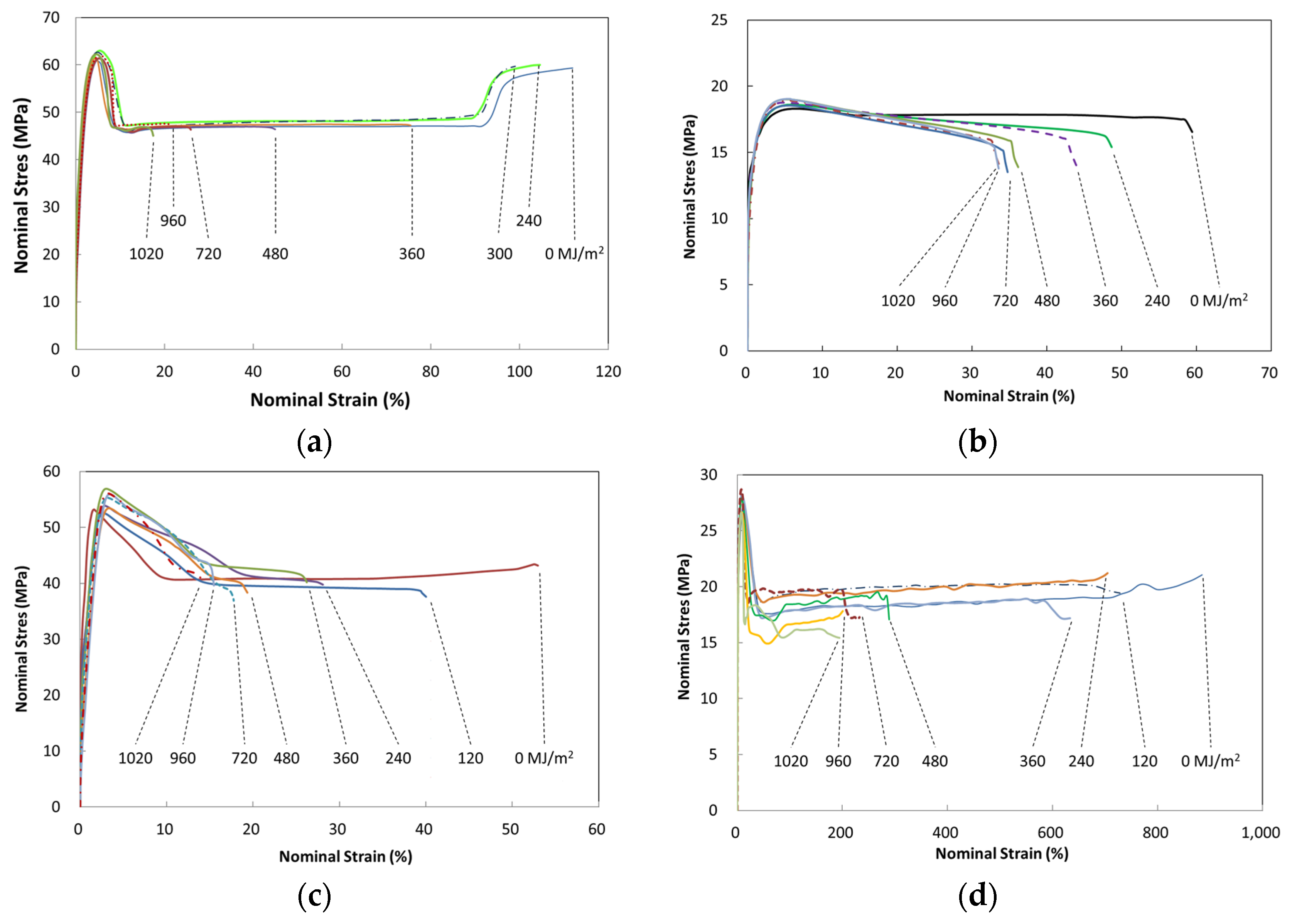
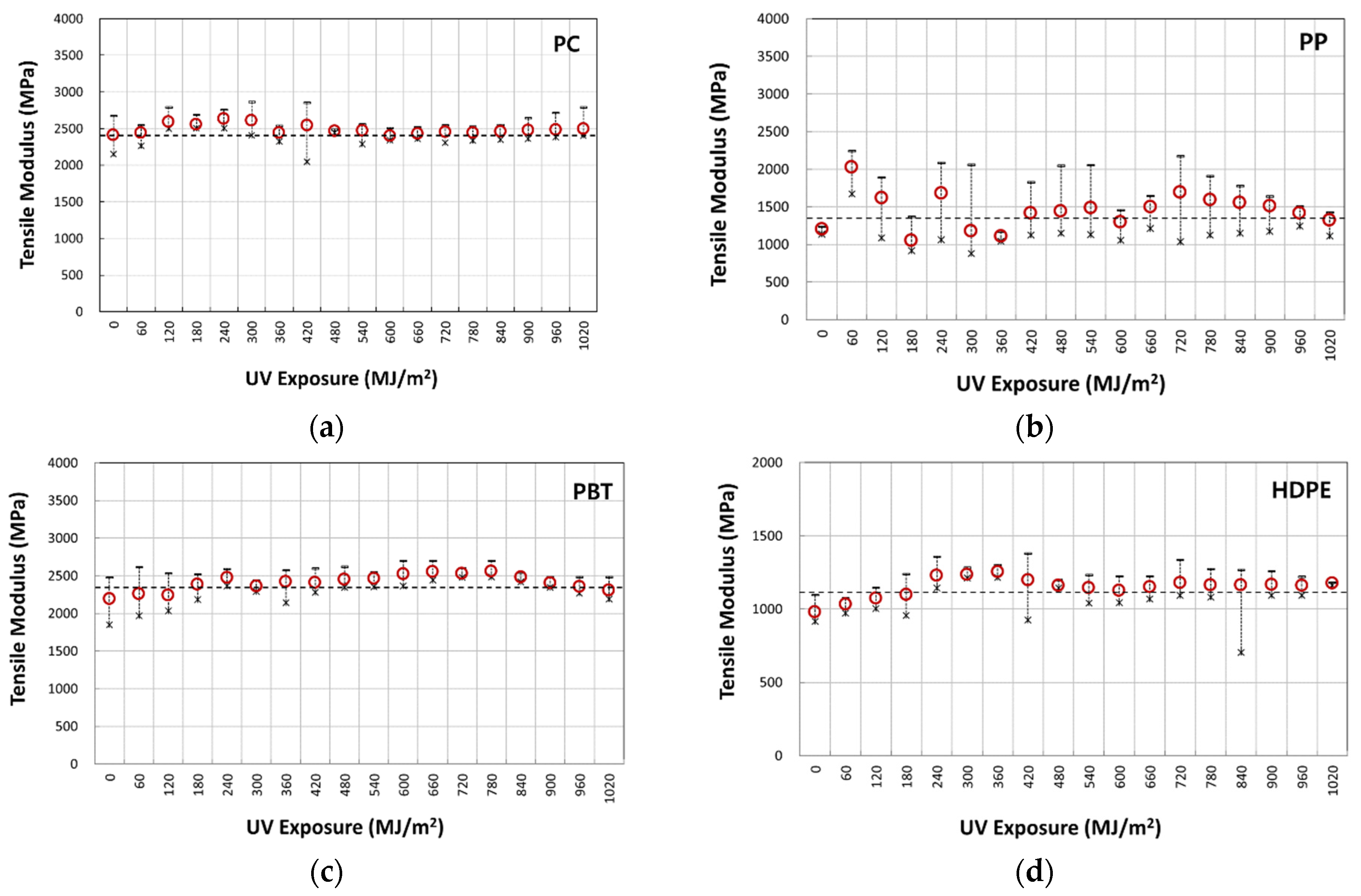
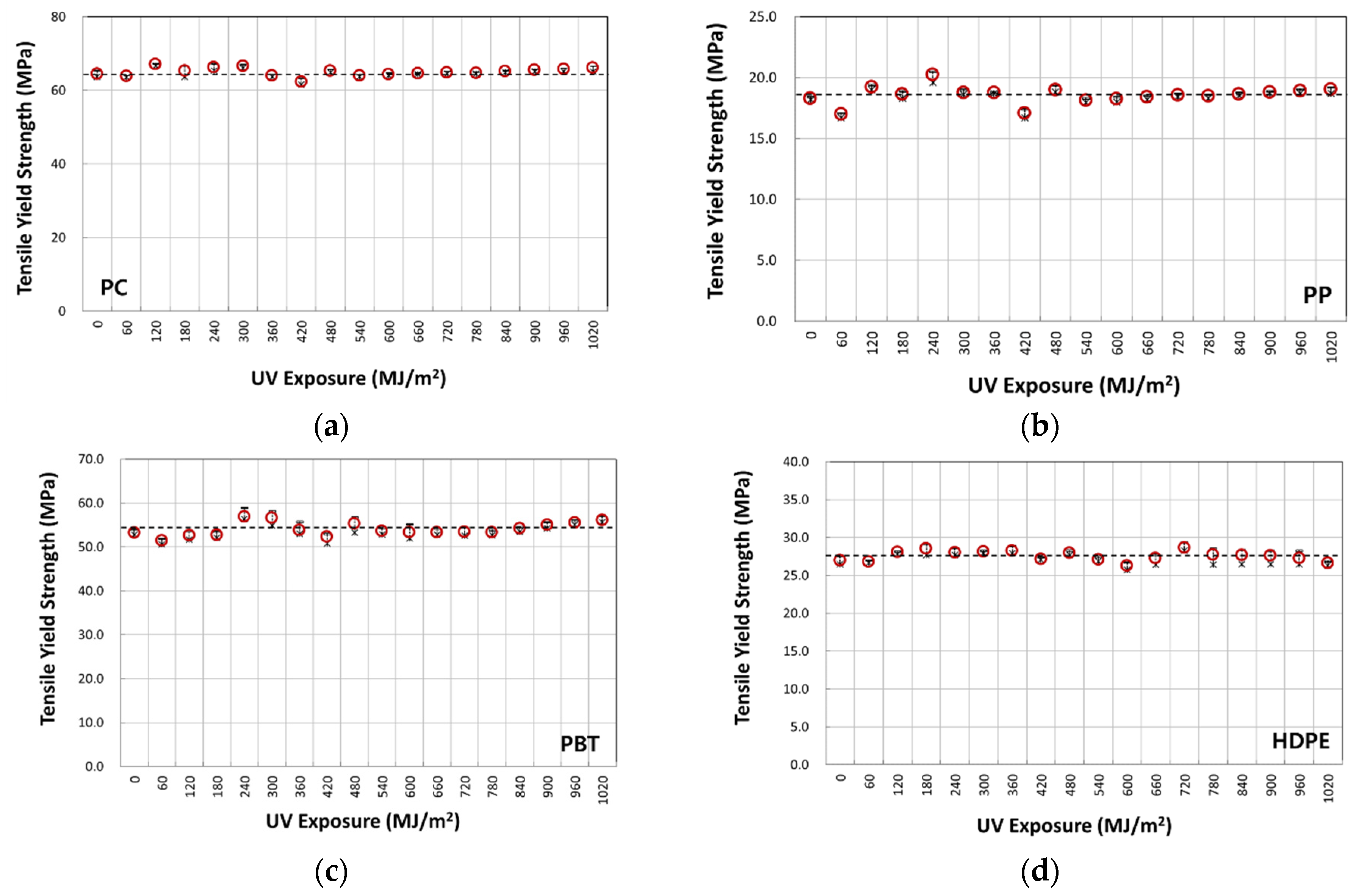
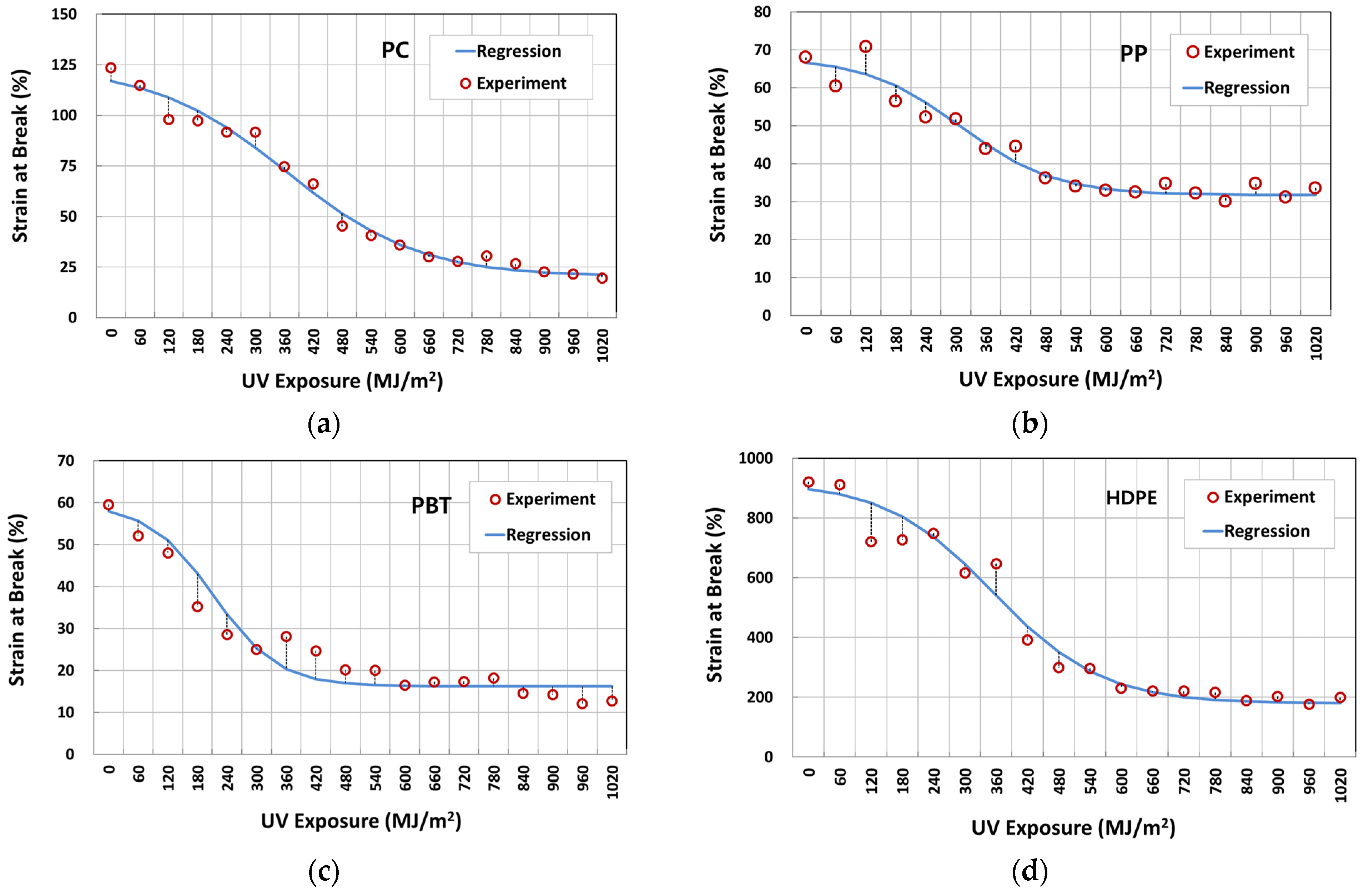
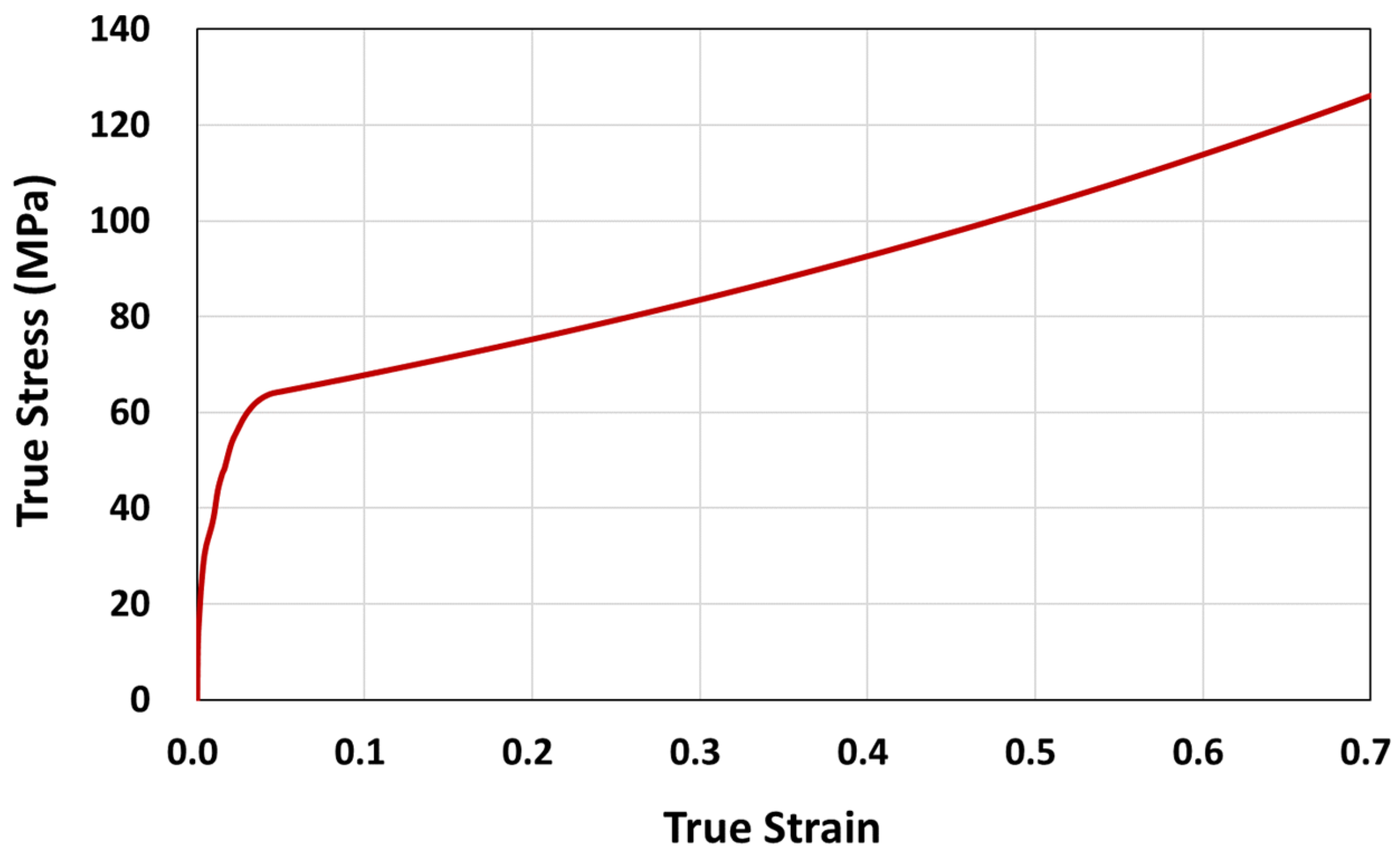
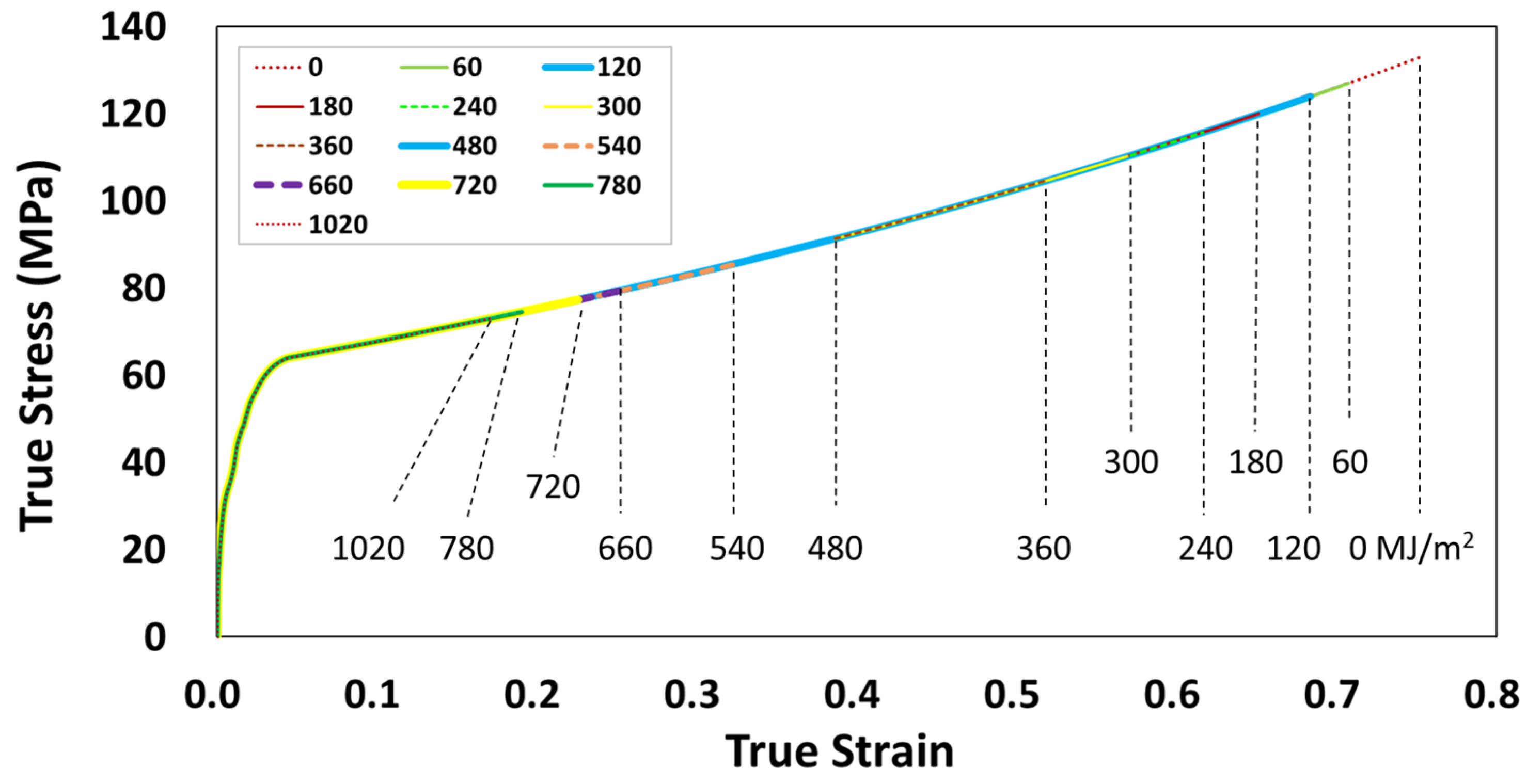
3.1. Tensile Behavior
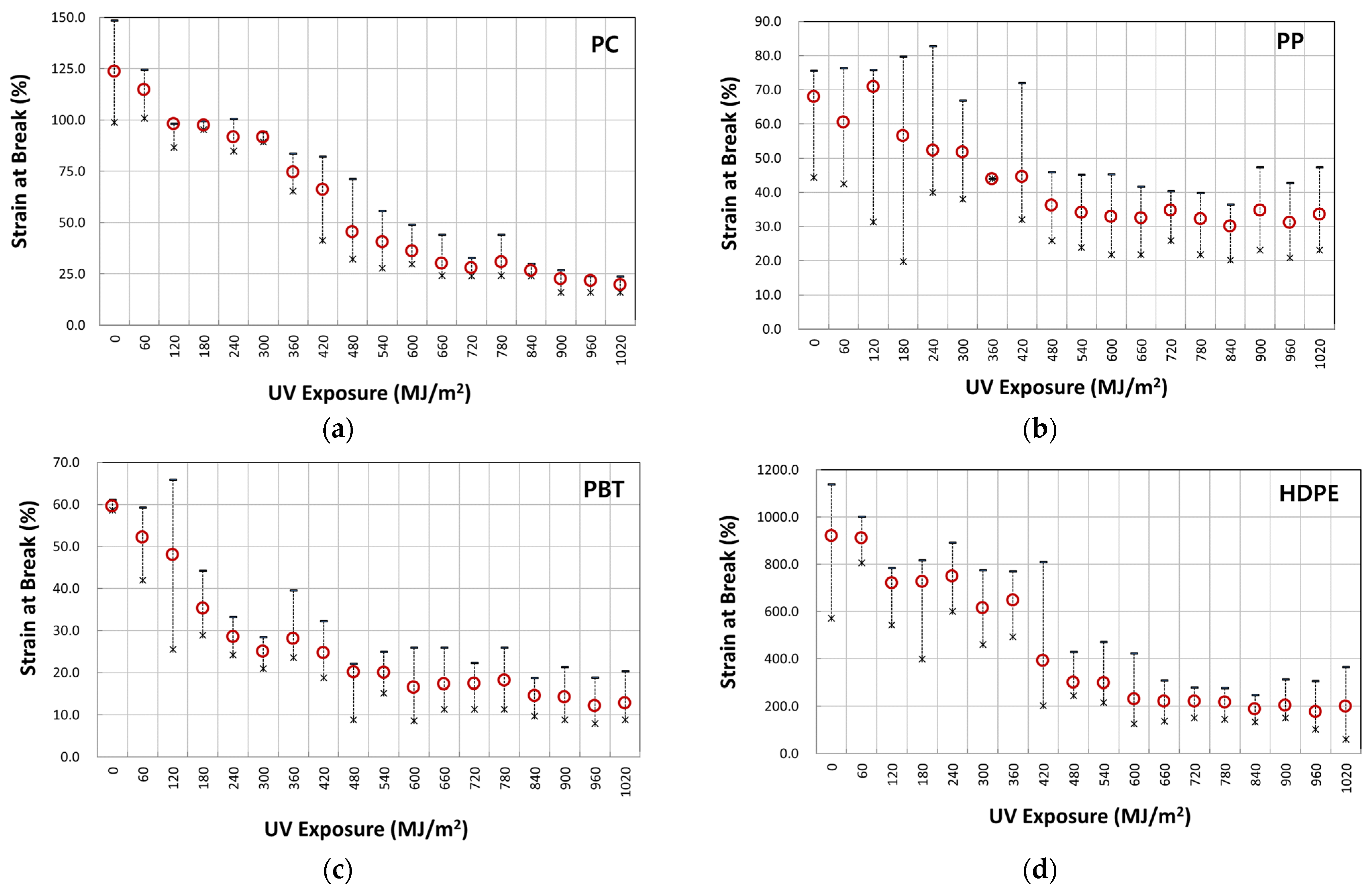
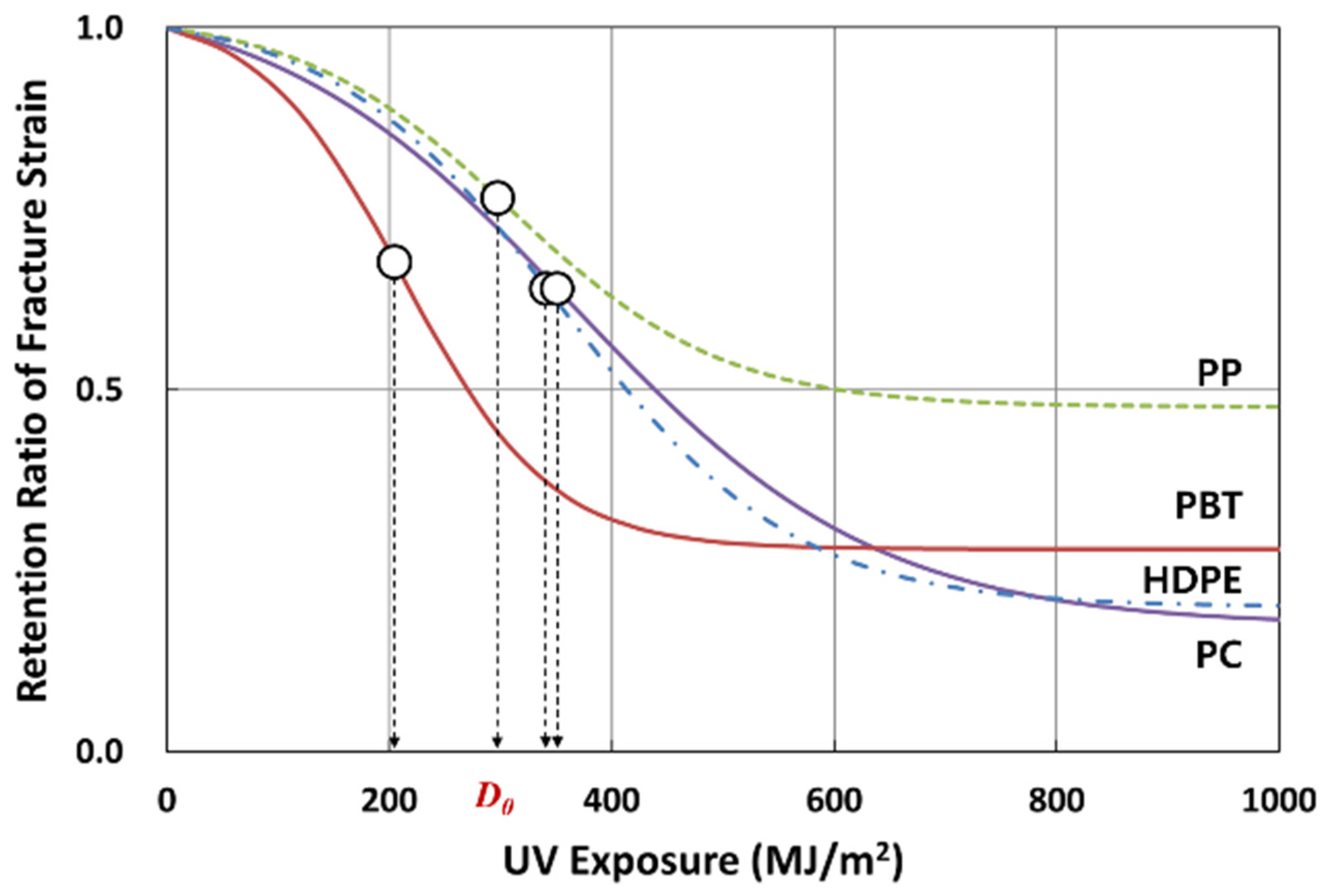
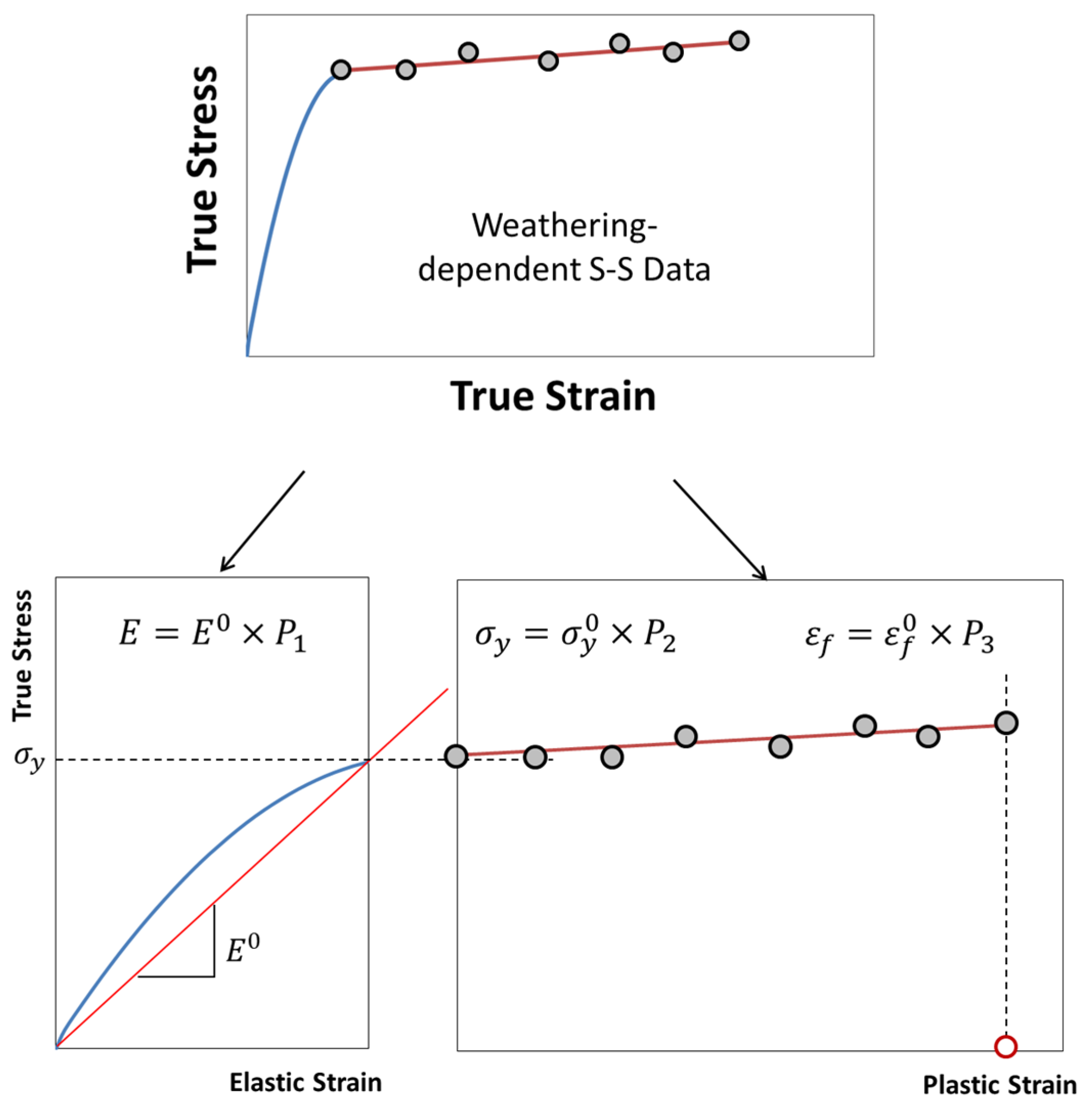
3.2. Logistic Regression Analysis of Fracture Strain Retention
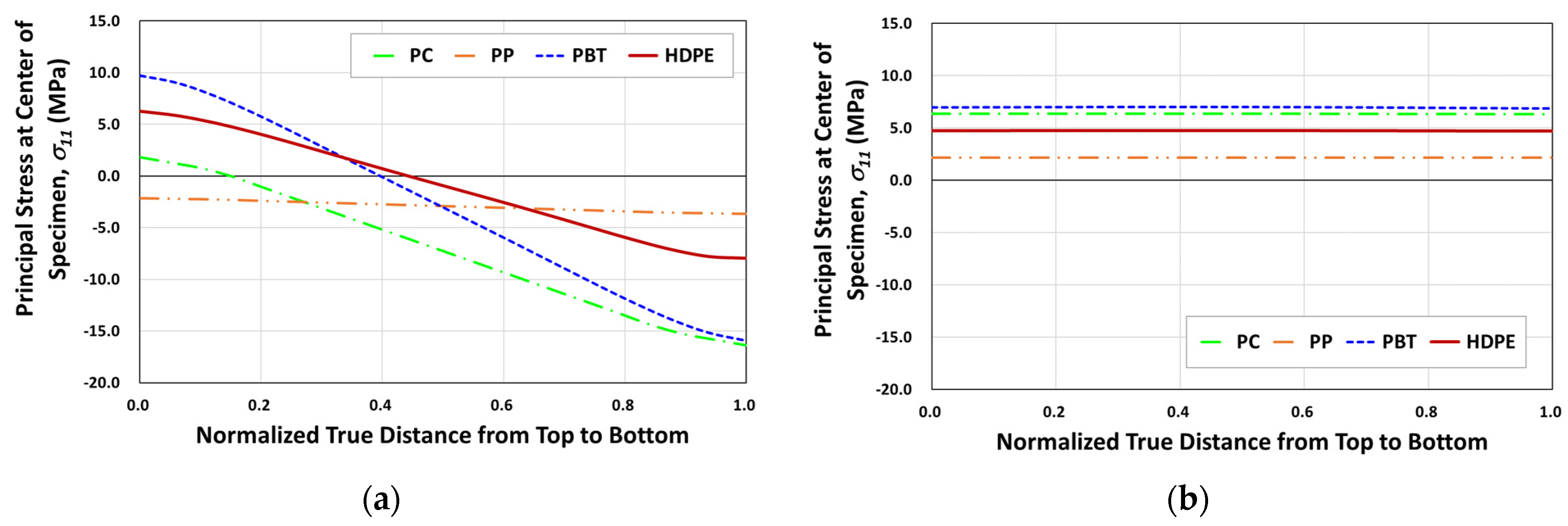
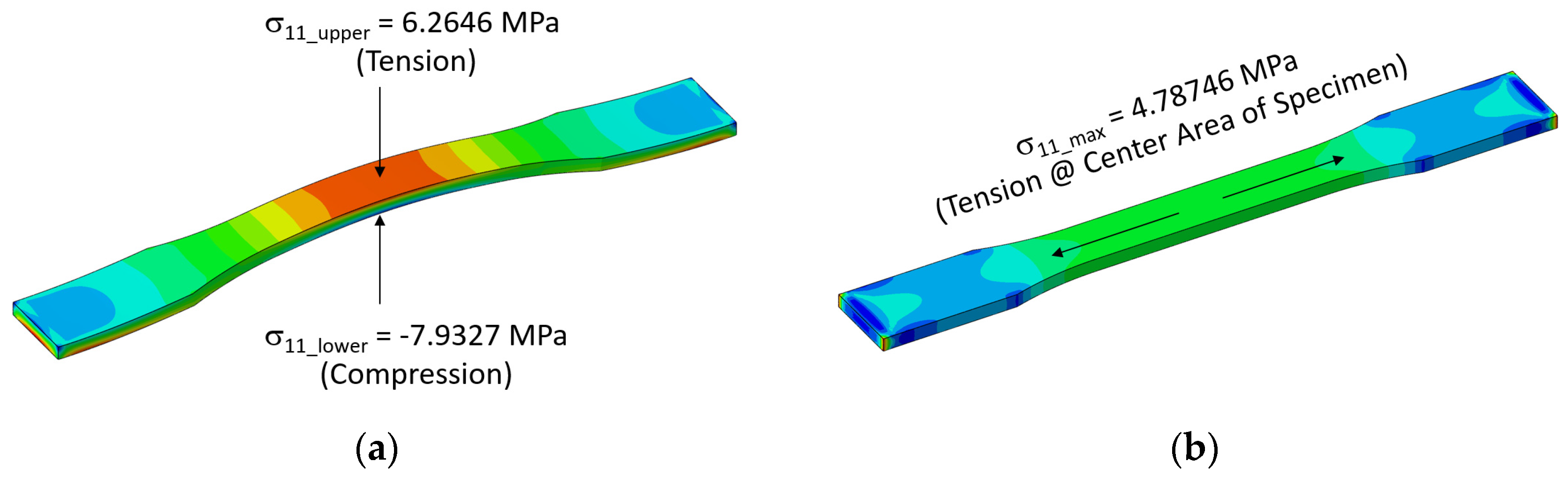
3.3. Weathering FE Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Henshaw, J.M.; Wood, V.; Hall, A.C. Failure of automobile seat belts caused by polymer degradation. Eng. Fail. Anal. 1999, 6, 13–25. [Google Scholar] [CrossRef]
- Dunn, R.F.; McSwain, R.H.; Mills, T.; Malone, B. Failure of plastic press release buttons in automobile seat belts. Eng. Fail. Anal. 2005, 12, 81–98. [Google Scholar] [CrossRef]
- Diepens, M.; Gijsman, P. Outdoor and accelerated weathering studies of bisphenol A polycarbonate. Polym. Degrad. Stab. 2011, 96, 649–652. [Google Scholar] [CrossRef] [Green Version]
- Sherman, E.S.; Ram, A.; Kenig, S. Tensile failure of weathered polycarbonate. Polym. Eng. Sci. 1982, 22, 457–465. [Google Scholar] [CrossRef]
- Benzarti, K.; Colin, X. Consequences of thermo-and photo-oxidation on end-use properties of pure PE. AIP Conf. Proc. 2010, 101, 1255. [Google Scholar]
- Lv, Y.; Huang, Y.; Yang, J.; Kong, M.; Yang, H.; Zhao, J.; Li, G. Outdoor and accelerated laboratory weathering of polypropylene: A comparison and correlation study. Polym. Degrad. Stab. 2015, 112, 145–159. [Google Scholar] [CrossRef]
- José Pabiot, J.V. The change in mechanical behavior of linear polymers during photochemical aging. Polym. Eng. Sci. 1981, 21, 32–38. [Google Scholar] [CrossRef]
- Al-Shabanat, M. Study of the effect of weathering in natural environment on polypropylene and its composites: Morphological and mechanical properties. Int. J. Chem. 2011, 3, 129. [Google Scholar] [CrossRef] [Green Version]
- Mendes, L.; Rufino, E.; De Paula, F.O.; Torres, A., Jr. Mechanical, thermal and microstructure evaluation of HDPE after weathering in Rio de Janeiro City. Polym. Degrad. Stab. 2003, 79, 371–383. [Google Scholar] [CrossRef]
- Hsueh, H.-C.; Kim, J.H.; Orski, S.; Fairbrother, A.; Jacobs, D.; Perry, L.; Hunston, D.; White, C.; Sung, L. Micro and macroscopic mechanical behaviors of high-density polyethylene under UV irradiation and temperature. Polym. Degrad. Stab. 2020, 174, 109098. [Google Scholar] [CrossRef]
- Tjandraatmadja, G.; Burn, L.; Jollands, M. Evaluation of commercial polycarbonate optical properties after QUV-A radiation—The role of humidity in photodegradation. Polym. Degrad. Stab. 2002, 78, 435–448. [Google Scholar] [CrossRef]
- Pickett, J.; Gibson, D.; Rice, S.; Gardner, M. Effects of temperature on the weathering of engineering thermoplastics. Polym. Degrad. Stab. 2008, 93, 684–691. [Google Scholar] [CrossRef]
- Nichols, M.E. Anticipating paint cracking: The application of fracture mechanics to the study of paint weathering. J. Coat. Technol. 2002, 74, 39–46. [Google Scholar] [CrossRef]
- Broutman, L.J. Surface Embrittlement of Polyethylene Pipe Grade Resin; Report No. GRI-81-0030; Gas Research Institute: Chicago, IL, USA, 1981. [Google Scholar]
- Choi, S.W.; Broutman, L.J. Ductile-Brittle Transitions for Polyethylene Pipe Grade Resins. In Proceedings of the 11th Plastic Fuel Gas Pipe Symposium, San Francisco, CA, USA, 3–5 October 1989; American Gas Association: Washington, DC, USA; pp. 296–320. [Google Scholar]
- Choi, S.W. Surface Embrittlement of Polyethylene. Ph.D. Thesis, Illinois Institute of Technology, Chicago, IL, USA, 1992. [Google Scholar]
- Lamnii, H.; Abdelaziz, M.N.; Ayoub, G.; Gloaguen, J.-M.; Maschke, U.; Mansoor, B. Effect of UV Ageing on the fatigue life of bulk polyethylene. In Proceedings of the FATIGUE 2018, Poitiers, France, 27 May–1 June 2018. [Google Scholar]
- Lamnii, H.; Abdelaziz, M.N.; Ayoub, G.; Colin, X.; Maschke, U. Experimental investigation and modeling attempt on the effects of ultraviolet aging on the fatigue behavior of an LDPE semi-crystalline polymer. Int. J. Fatigue 2021, 142, 105952. [Google Scholar] [CrossRef]
- Iizuka, T.; Ohtake, Y.; Tanaka, K. A effect of moisture on photo-degradation for polypropylene. Zair./J. Soc. Mater. Sci. Jpn. 2016, 65, 812–817. [Google Scholar] [CrossRef]
- Erdmann, M.; Niebergall, U.; Wachtendorf, V.; Böhning, M. Evaluation of UV-induced embrittlement of PE-HD by Charpy impact test. J. Appl. Polym. Sci. 2020, 137, 49069. [Google Scholar] [CrossRef]
- Jiang, L.; Zhou, M.; Ding, Y.; Zhou, Y.; Dan, Y. Aging induced ductile-brittle-ductile transition in bisphenol A polycarbonate. J. Polym. Res. 2018, 25, 39. [Google Scholar] [CrossRef]
- Blaga, A.; Yamasaki, R. Surface microcracking induced by weathering of polycarbonate sheet. J. Mater. Sci. 1976, 11, 1513–1520. [Google Scholar] [CrossRef] [Green Version]
- McKeen, L.W. The Effect of UV Light and Weather on Plastics and Elastomers; William Andrew: Amsterdam, The Netherlands, 2019. [Google Scholar]
- World Maps of Köppen-Geiger Climate Classification. Available online: http://koeppen-geiger.vu-wien.ac.at/ (accessed on 10 November 2021).
- Rajakumar, K.; Sarasvathy, V.; Chelvan, A.T.; Chitra, R.; Vijayakumar, C. Natural weathering studies of polypropylene. J. Polym. Environ. 2009, 17, 191–202. [Google Scholar] [CrossRef]
- Lasdon, L.S.; Waren, A.D.; Jain, A.; Ratner, M.W. Design and Testing of a Generalized Reduced Gradient Code for Nonlinear Optimization; Case Western Reserve University: Cleveland, OH, USA, 1975. [Google Scholar]
- Lasdon, L.S.; Waren, A.D.; Jain, A.; Ratner, M. Design and testing of a generalized reduced gradient code for nonlinear programming. ACM Trans. Math. Softw. (TOMS) 1978, 4, 34–50. [Google Scholar] [CrossRef]
- ABAQUS Document Manual, Version 6.14; Dassault Systemes: Velizy-Villacoublay, France, 2010.
- Grassia, L.; D’Amore, A.; Simon, S.L. On the viscoelastic Poisson’s ratio in amorphous polymers. J. Rheol. 2010, 54, 1009–1022. [Google Scholar] [CrossRef]
- Polymer Properties Database. Available online: http://polymerdatabase.com/polymer%20physics/Poisson%20Table.html (accessed on 10 November 2021).
- Hooputra, H.; Gese, H.; Dell, H.; Werner, H. A comprehensive failure model for crashworthiness simulation of aluminium extrusions. Int. J. Crashworthiness 2004, 9, 449–464. [Google Scholar] [CrossRef]
- Performance Based Standard for Accelerated Exposure of Automotive Exterior Materials Using a Controlled Irradiance Xenon-Arc Apparatus; Society of Automotive Engineers: Warrendale, PA, USA, 2017; SAE J2527.
- Frigione, M.; Rodríguez-Prieto, A. Can Accelerated Aging Procedures Predict the Long Term Behavior of Polymers Exposed to Different Environments? Polymers 2021, 13, 2688. [Google Scholar] [CrossRef] [PubMed]







| Material | UV Stabilizer | Tensile Modulus (MPa) | Tensile Yield Strength (MPa) | Fracture Strain (%) | MFR 1 (g/10 min) | Density (g/cc) | CTE 2, ×10−5 (mm/mm/°C) |
|---|---|---|---|---|---|---|---|
| PC | Yes | 2340 | 60 | 150 | 15 (300 °C/1.2 kg) | 1.2 | 6.80 |
| PP | Yes | 1200 | 19 | 30 | 25 (230 °C/2.16 kg) | 1.03 | 4.50 |
| PBT | Yes | 2200 | 50 | >50 | 15 (250 °C/5.0 kg) | 1.33 | 8.00 |
| HDPE | None | 800 | 28 | >600 | 2 (190 °C/2.16 kg) | 0.952 | 15.00 |
| Black Panel Temperature @ 37° Facing South (°C) | December | January | February | March | April | May | June | July | August | September | October | November | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Highest temp. (Tmax) | 40.9 | 35.1 | 38.6 | 47.2 | 50.8 | 54.1 | 54.0 | 62.3 | 64.9 | 57.5 | 55.3 | 48.2 | |
| Avg. temp. | 3.7 | 2.5 | 4.0 | 8.9 | 14.6 | 20.0 | 24.4 | 27.1 | 28.9 | 25.1 | 19.0 | 10.4 | |
| Lowest temp. (Tmin) | −11.6 | −13.3 | −11.4 | −9.6 | −3.9 | 2.6 | 8.6 | 13.7 | 16.0 | 0.0 | 0.2 | −5.8 | |
| ΔT | 52.5 | 48.4 | 50.0 | 56.8 | 54.7 | 51.5 | 45.4 | 48.6 | 48.9 | 57.5 | 55.1 | 54.0 | |
| Seasonal temp. | Tmax | 40.9 | 54.1 | 64.9 | 57.5 | ||||||||
| Tmin | −13.3 | −9.6 | 8.6 | −5.8 | |||||||||
| Daily temp. cycle | (Tmax + Tmin)/2 | 13.8 | 22.3 | 36.8 | 25.9 | ||||||||
| (Tmax − Tmin)/2 | 27.1 | 31.9 | 28.2 | 31.7 | |||||||||
| Seasonal temp. cycle | (Tmax + Tmin)/2 | 25.8 = (64.9 + (−13.3))/2 | |||||||||||
| (Tmax − Tmin)/2 | 39.1 = (64.9 − (−13.3))/2 | ||||||||||||
| D (MJ/m2) | 0 | 60 | 180 | 300 | 420 | 540 | 660 | 780 | 900 | 1020 |
|---|---|---|---|---|---|---|---|---|---|---|
| t (days) | 0 | 128 | 246 | 461 | 579 | 794 | 913 | 1127 | 1246 | 1460 |
| Material | Tensile Modulus (MPa) | Tensile Yield Strength (MPa) | Strain at Yield (%) | |||
|---|---|---|---|---|---|---|
| Average | Standard Dev. | Average | Standard Dev. | Average | Standard Dev. | |
| PC | 2489.17 | 69.75 | 65.01 | 1.14 | 2.64 | 0.08 |
| PP | 1465.53 | 248.72 | 18.56 | 0.73 | 3.40 | 0.90 |
| PBT | 2409.32 | 108.27 | 54.04 | 1.52 | 4.09 | 0.32 |
| HDPE | 1105.20 | 96.11 | 27.55 | 0.67 | 3.96 | 0.41 |
| PC | PP | PBT | HDPE | ||
|---|---|---|---|---|---|
| Regression Parameters | Pmax | 1.000 | 1.000 | 1.000 | 1.000 |
| k | 7.3182 × 10−3 | 1.0493 × 10−2 | 1.5251 × 10−2 | 9.6216 × 10−3 | |
| Pmid = D0 | 365.357 | 309.338 | 212.623 | 355.052 | |
| Pmin | 0.165 | 0.467 | 0.272 | 0.195 | |
| 0.984 | 0.952 | 0.933 | 0.968 | ||
| D50% (MJ/m2) | 420.199 | 567.934 | 264.246 | 406.344 | |
| (%) | 116.91 | 66.64 | 57.93 | 897.26 | |
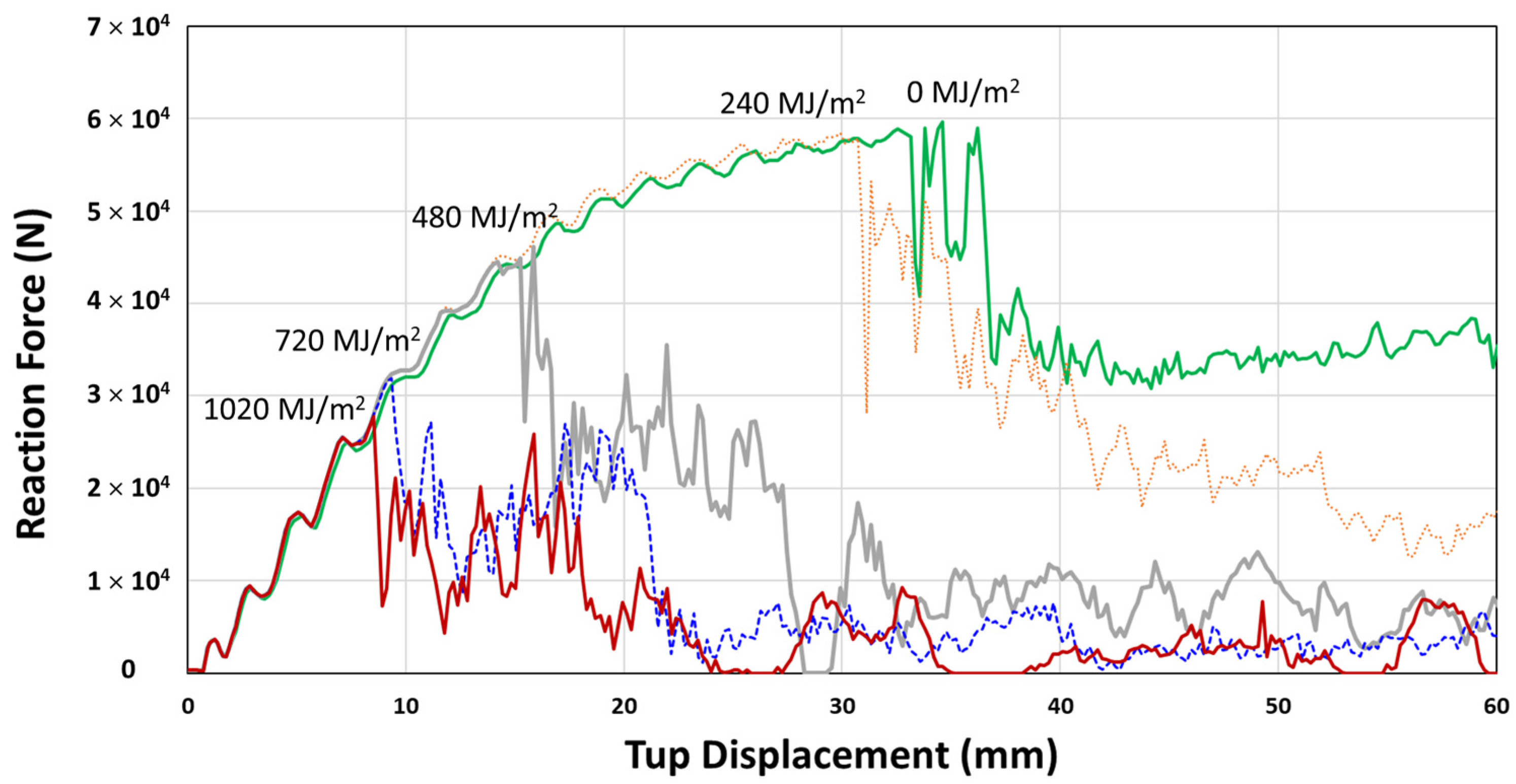
| Cumulative UV Irradiation (MJ/m2 @ 315~400 nm) | Tup Displacement (mm) @ Max. R.F. | Max. R.F. (N) | Fracture Initiation Energy (J) | Fracture Propagation Energy (J) | Total Energy (J) @ 60 mm Tup Displacement | Reduction of Tup Displacement (%) | Reduction of Max. R.F. (%) | Reduction of Fracture Initiation Energy (%) | Reduction of Fracture Propagation Energy (%) | Reduction of Total Energy @ 60 mm Tup Displacement (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 34.6 | 59,597.1 | 1391.26 | 916.78 | 2308.04 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 240 | 29.91 | 58,412.8 | 1157.57 | 808.32 | 1965.89 | 13.6 | 2.0 | 16.8 | 11.8 | 14.8 |
| 480 | 15.85 | 46,087.6 | 389.43 | 531.51 | 920.94 | 54.2 | 22.7 | 72.0 | 42.0 | 60.1 |
| 720 | 9.34 | 31,882.0 | 136.76 | 367.58 | 504.34 | 73.0 | 46.5 | 90.2 | 59.9 | 78.1 |
| 1020 | 8.52 | 27,809.2 | 111.87 | 264.89 | 376.76 | 75.4 | 53.3 | 92.0 | 71.1 | 83.7 |
| Step | Water Spray | Irradiance (W/m2 @ 340 nm) | Humidity (%) | Air Temperature (°C) | Black Panel Temperature (°C) | Duration (min) |
|---|---|---|---|---|---|---|
| 1 | Off | 0.55 | 50 | 47 | 70 | 40 |
| 2 | On | 0.55 | 95 | 47 | 70 | 20 |
| 3 | Off | 0.55 | 50 | 47 | 70 | 60 |
| 4 | On | 0 | 95 | 38 | 38 | 60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Lee, Y.; Kim, C.; Choi, S. Analysis of Mechanical Property Degradation of Outdoor Weather-Exposed Polymers. Polymers 2022, 14, 357. https://doi.org/10.3390/polym14020357
Kim S, Lee Y, Kim C, Choi S. Analysis of Mechanical Property Degradation of Outdoor Weather-Exposed Polymers. Polymers. 2022; 14(2):357. https://doi.org/10.3390/polym14020357
Chicago/Turabian StyleKim, Sunwoo, Youngmin Lee, Changhwan Kim, and Sunwoong Choi. 2022. "Analysis of Mechanical Property Degradation of Outdoor Weather-Exposed Polymers" Polymers 14, no. 2: 357. https://doi.org/10.3390/polym14020357
APA StyleKim, S., Lee, Y., Kim, C., & Choi, S. (2022). Analysis of Mechanical Property Degradation of Outdoor Weather-Exposed Polymers. Polymers, 14(2), 357. https://doi.org/10.3390/polym14020357







