A Multiscale Simulation of Polymer Melt Injection Molding Filling Flow Using SPH Method with Slip-Link Model
Abstract
:1. Introduction
2. Formulations
2.1. Smoothed Particle Hydrodynamics
2.1.1. Governing Equations
2.1.2. Improved SPH Algorithm for the Polymer Melt Injection Molding Filling Flow
2.2. Clustered Fixed Slip-Link Model
2.3. Multiscale Simulation Solution Procedure
3. Numerical Simulation Cases
3.1. Poiseuille Flow
3.2. Injection Molding Filling in a Simple Long Rectangular Cavity
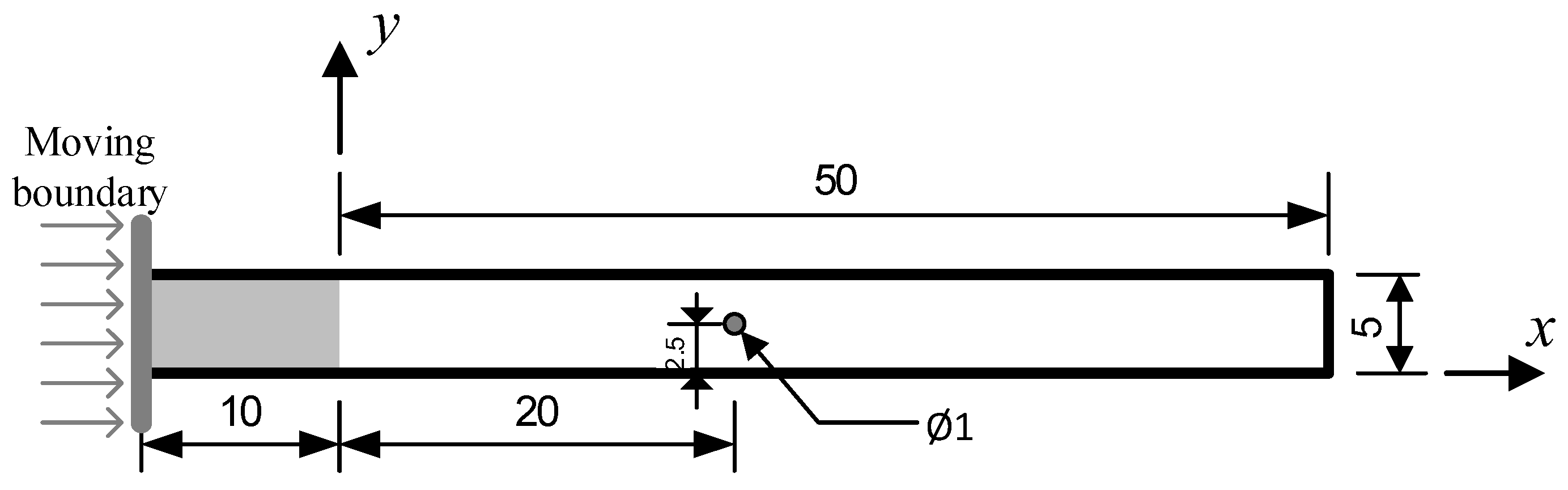
3.3. Injection Molding Filling in a Rectangular Cavity with a Circular Obstacle
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, R.; Tanner, R.I.; Fan, X.-J. Injection Molding; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Zhou, H. Computer Modeling for Injection Molding: Simulation, Optimization, and Control; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Zhou, H.; Yan, B.; Zhang, Y. 3D Filling Simulation of Injection Molding Based on the PG Method. J. Mater. Process. Technol. 2008, 204, 475–480. [Google Scholar] [CrossRef]
- Zhang, S.; Hua, S.; Cao, W.; Min, Z.; Liu, Y.; Wang, Y.; Shen, C. 3D Viscoelastic Simulation of Jetting in Injection Molding. Polym. Eng. Sci. 2019, 59, E397–E405. [Google Scholar] [CrossRef]
- Bernal, F.; Kindelan, M. An RBF Meshless Method for Injection Molding Modelling. In Meshfree Methods for Partial Differential Equations III; Griebel, M., Schweitzer, M.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 57, pp. 41–56. [Google Scholar] [CrossRef]
- Veltmaat, L.; Mehrens, F.; Endres, H.-J.; Kuhnert, J.; Suchde, P. Mesh-Free Simulations of Injection Molding Processes. Phys. Fluids 2022, 34, 033102. [Google Scholar] [CrossRef]
- Noii, N.; Khodadadian, A.; Wick, T. Bayesian Inversion Using Global-Local Forward Models Applied to Fracture Propagation in Porous Media. Int. J. Multiscale Comput. 2022, 20, 57–79. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M.; Khodadadian, A.; Noii, N.; Heitzinger, C.; Wick, T. A Reduced-Order Variational Multiscale Interpolating Element Free Galerkin Technique Based on Proper Orthogonal Decomposition for Solving Navier–Stokes Equations Coupled with a Heat Transfer Equation: Nonstationary Incompressible Boussinesq Equations. J. Comput. Phys. 2021, 426, 109875. [Google Scholar] [CrossRef]
- Lucy, L.B. A Numerical Approach to the Testing of the Fission Hypothesis. Astron. J. 1977, 82, 1013. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed Particle Hydrodynamics: Theory and Application to Non-Spherical Stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating Free Surface Flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Becker, M.; Teschner, M. Weakly Compressible SPH for Free Surface Flows. In Proceedings of the Eurographics/SIGGRAPH Symposium on Computer Animation, San Diego, CA, USA, 2–4 August 2007; pp. 209–217. [Google Scholar] [CrossRef]
- Fang, J.; Parriaux, A.; Rentschler, M.; Ancey, C. Improved SPH Methods for Simulating Free Surface Flows of Viscous Fluids. Appl. Numer. Math. 2009, 59, 251–271. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Ouyang, J.; Yang, B.; Liu, Z. SPH Simulations of Three-Dimensional Non-Newtonian Free Surface Flows. Comput. Methods Appl. Mech. Eng. 2013, 256, 101–116. [Google Scholar] [CrossRef]
- Johnson, G.R.; Petersen, E.H.; Stryk, R.A. Incorporation of an SPH Option into the EPIC Code for a Wide Range of High Velocity Impact Computations. Int. J. Impact Eng. 1993, 14, 385–394. [Google Scholar] [CrossRef]
- Marrone, S.; Antuono, M.; Colagrossi, A.; Colicchio, G.; Le Touzé, D.; Graziani, G. δ-SPH Model for Simulating Violent Impact Flows. Comput. Methods Appl. Mech. Eng. 2011, 200, 1526–1542. [Google Scholar] [CrossRef]
- Giannaros, E.; Kotzakolios, A.; Kostopoulos, V.; Campoli, G. Hypervelocity Impact Response of CFRP Laminates Using Smoothed Particle Hydrodynamics Method: Implementation and Validation. Int. J. Impact Eng. 2019, 123, 56–69. [Google Scholar] [CrossRef]
- Swegle, J.W.; Attaway, S.W. On the Feasibility of Using Smoothed Particle Hydrodynamics for Underwater Explosion Calculations. Comput. Mech. 1995, 17, 151–168. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R.; Lam, K.Y.; Zong, Z. Smoothed Particle Hydrodynamics for Numerical Simulation of Underwater Explosion. Comput. Mech. 2003, 30, 106–118. [Google Scholar] [CrossRef]
- Chen, J.-Y.; Lien, F.-S. Simulations for Soil Explosion and Its Effects on Structures Using SPH Method. Int. J. Impact Eng. 2018, 112, 41–51. [Google Scholar] [CrossRef]
- Wang, Y.; Tran, H.T.; Nguyen, G.D.; Ranjith, P.G.; Bui, H.H. Simulation of Mixed-mode Fracture Using SPH Particles with an Embedded Fracture Process Zone. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 1417–1445. [Google Scholar] [CrossRef]
- Mu, D.; Tang, A.; Li, Z.; Qu, H.; Huang, D. A Bond-Based Smoothed Particle Hydrodynamics Considering Frictional Contact Effect for Simulating Rock Fracture. Acta Geotech. 2022. [Google Scholar] [CrossRef]
- Bonet, J.; Kulasegaram, S. Correction and Stabilization of Smooth Particle Hydrodynamics Methods with Applications in Metal Forming Simulations. Int. J. Numer. Methods Eng. 2000, 47, 1189–1214. [Google Scholar] [CrossRef]
- Prakash, M.; Cleary, P.W. Modelling Highly Deformable Metal Extrusion Using SPH. Comput. Part. Mech. 2015, 2, 19–38. [Google Scholar] [CrossRef] [Green Version]
- Niu, X.; Zhao, J.; Wang, B. Application of Smooth Particle Hydrodynamics (SPH) Method in Gravity Casting Shrinkage Cavity Prediction. Comput. Part. Mech. 2019, 6, 803–810. [Google Scholar] [CrossRef]
- Fan, X.-J.; Tanner, R.I.; Zheng, R. Smoothed Particle Hydrodynamics Simulation of Non-Newtonian Moulding Flow. J. Non-Newton. Fluid Mech. 2010, 165, 219–226. [Google Scholar] [CrossRef]
- He, L.; Lu, G.; Chen, D.; Li, W.; Lu, C. Three-Dimensional Smoothed Particle Hydrodynamics Simulation for Injection Molding Flow of Short Fiber-Reinforced Polymer Composites. Model. Simul. Mater. Sci. Eng. 2017, 25, 055007. [Google Scholar] [CrossRef]
- Wu, K.; Wan, L.; Zhang, H.; Yang, D. Numerical Simulation of the Injection Molding Process of Short Fiber Composites by an Integrated Particle Approach. Int. J. Adv. Manuf. Technol. 2018, 97, 3479–3491. [Google Scholar] [CrossRef]
- Xu, X.; Yu, P. Extension of SPH to Simulate Non-Isothermal Free Surface Flows during the Injection Molding Process. Appl. Math. Model. 2019, 73, 715–731. [Google Scholar] [CrossRef]
- Ren, M.; Gu, J.; Li, Z.; Ruan, S.; Shen, C. Simulation of Polymer Melt Injection Molding Filling Flow Based on an Improved SPH Method with Modified Low-Dissipation Riemann Solver. Macromol. Theory Simul. 2022, 31, 2100029. [Google Scholar] [CrossRef]
- Brini, E.; Algaer, E.A.; Ganguly, P.; Li, C.; Rodríguez-Ropero, F.; van der Vegt, N.F.A. Systematic Coarse-Graining Methods for Soft Matter Simulations—A Review. Soft Matter 2013, 9, 2108–2119. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of Concentrated Polymer Systems. Part 1.—Brownian Motion in the Equilibrium State. J. Chem. Soc. Faraday Trans. 2 1978, 74, 1789–1801. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of Concentrated Polymer Systems. Part 2.—Molecular Motion under Flow. J. Chem. Soc. Faraday Trans. 2 1978, 74, 1802–1817. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of Concentrated Polymer Systems. Part 3.—The Constitutive Equation. J. Chem. Soc. Faraday Trans. 2 1978, 74, 1818–1832. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of Concentrated Polymer Systems. Part 4.—Rheological Properties. J. Chem. Soc. Faraday Trans. 2 1979, 75, 38–54. [Google Scholar] [CrossRef]
- Schieber, J.D.; Neergaard, J.; Gupta, S. A Full-Chain, Temporary Network Model with Sliplinks, Chain-Length Fluctuations, Chain Connectivity and Chain Stretching. J. Rheol. 2003, 47, 213–233. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Takimoto, J.-I.; Koyama, K.; Ianniruberto, G.; Marrucci, G.; Greco, F. Brownian Simulations of a Network of Reptating Primitive Chains. J. Chem. Phys. 2001, 115, 4387–4394. [Google Scholar] [CrossRef]
- Andreev, M.; Feng, H.; Yang, L.; Schieber, J.D. Universality and Speedup in Equilibrium and Nonlinear Rheology Predictions of the Fixed Slip-Link Model. J. Rheol. 2014, 58, 723–736. [Google Scholar] [CrossRef] [Green Version]
- Feng, H.; Andreev, M.; Pilyugina, E.; Schieber, J.D. Smoothed Particle Hydrodynamics Simulation of Viscoelastic Flows with the Slip-Link Model. Mol. Syst. Des. Eng. 2016, 1, 99–108. [Google Scholar] [CrossRef]
- Murashima, T.; Taniguchi, T. Flow-History-Dependent Behavior of Entangled Polymer Melt Flow Analyzed by Multiscale Simulation. J. Phys. Soc. Jpn. 2012, 81, SA013. [Google Scholar] [CrossRef]
- Sato, T.; Harada, K.; Taniguchi, T. Multiscale Simulations of Flows of a Well-Entangled Polymer Melt in a Contraction–Expansion Channel. Macromolecules 2019, 52, 547–564. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics and Its Diverse Applications. Annu. Rev. Fluid Mech. 2012, 44, 323–346. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S. Numerical Diffusive Terms in Weakly-Compressible SPH Schemes. Comput. Phys. Commun. 2012, 183, 2570–2580. [Google Scholar] [CrossRef]
- Rodgers, P.A. Pressure–Volume–Temperature Relationships for Polymeric Liquids: A Review of Equations of State and Their Characteristic Parameters for 56 Polymers. J. Appl. Polym. Sci. 1993, 48, 1061–1080. [Google Scholar] [CrossRef]
- Morris, J.P.; Fox, P.J.; Zhu, Y. Modeling Low Reynolds Number Incompressible Flows Using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]
- Zheng, X.; Ma, Q.; Shao, S. Study on SPH Viscosity Term Formulations. Appl. Sci. 2018, 8, 249. [Google Scholar] [CrossRef] [Green Version]
- Oger, G.; Doring, M.; Alessandrini, B.; Ferrant, P. An Improved SPH Method: Towards Higher Order Convergence. J. Comput. Phys. 2007, 225, 1472–1492. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Feng, J.J. Pressure Boundary Conditions for Computing Incompressible Flows with SPH. J. Comput. Phys. 2011, 230, 7473–7487. [Google Scholar] [CrossRef]
- Lind, S.J.; Xu, R.; Stansby, P.K.; Rogers, B.D. Incompressible Smoothed Particle Hydrodynamics for Free-Surface Flows: A Generalised Diffusion-Based Algorithm for Stability and Validations for Impulsive Flows and Propagating Waves. J. Comput. Phys. 2012, 231, 1499–1523. [Google Scholar] [CrossRef]
- Xu, X.; Yu, P. A Technique to Remove the Tensile Instability in Weakly Compressible SPH. Comput. Mech. 2018, 62, 963–990. [Google Scholar] [CrossRef]
- Khaliullin, R.N.; Schieber, J.D. Application of the Slip-Link Model to Bidisperse Systems. Macromolecules 2010, 43, 6202–6212. [Google Scholar] [CrossRef]
- Valadez-Pérez, N.E.; Taletskiy, K.; Schieber, J.D.; Shivokhin, M. Efficient Determination of Slip-Link Parameters from Broadly Polydisperse Linear Melts. Polymers 2018, 10, 908. [Google Scholar] [CrossRef] [Green Version]
- Fang, J.; Owens, R.G.; Tacher, L.; Parriaux, A. A Numerical Study of the SPH Method for Simulating Transient Viscoelastic Free Surface Flows. J. Non-Newton. Fluid Mech. 2006, 139, 68–84. [Google Scholar] [CrossRef] [Green Version]
- Taletskiy, K.; Andreev, M. ktaletsk/gpu_dsm: Release for Archiving with Zenodo. 2018. Available online: https://doi.org/10.5281/zenodo.1158749 (accessed on 14 October 2019).
- Guzmán, J.D.; Schieber, J.D.; Pollard, R. A Regularization-Free Method for the Calculation of Molecular Weight Distributions from Dynamic Moduli Data. Rheol. Acta 2005, 44, 342–351. [Google Scholar] [CrossRef]









| Parameter | Value | |
|---|---|---|
| SPH | Initial melt density, ρ0 (kg/m3) | 742.93 |
| Melt temperature, T (K) | 463.15 | |
| Zero-shear viscosity, μ0 (Pa·s) | 1254.18 | |
| Critical stress level at the transition to shear thinning, τ* (Pa) | 192,149 | |
| Power law index in the high shear rate regime, n | 0.2411 | |
| Compressibility parameter of the Tait model, B (Pa) | 7.9344 × 107 | |
| GEX | Shape parameter, a | 1.39 |
| Shape parameter, b | 0.26 | |
| Localization parameter, mp (g/mol) | 20.54 | |
| CFSM | Molecular weight of a Kuhn step cluster, Mc (g/mol) | 1089.12 |
| Characteristic time for a Kuhn step cluster, τc (s) | 1.5 × 10−7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, M.; Gu, J.; Li, Z.; Ruan, S.; Shen, C. A Multiscale Simulation of Polymer Melt Injection Molding Filling Flow Using SPH Method with Slip-Link Model. Polymers 2022, 14, 4334. https://doi.org/10.3390/polym14204334
Ren M, Gu J, Li Z, Ruan S, Shen C. A Multiscale Simulation of Polymer Melt Injection Molding Filling Flow Using SPH Method with Slip-Link Model. Polymers. 2022; 14(20):4334. https://doi.org/10.3390/polym14204334
Chicago/Turabian StyleRen, Mengke, Junfeng Gu, Zheng Li, Shilun Ruan, and Changyu Shen. 2022. "A Multiscale Simulation of Polymer Melt Injection Molding Filling Flow Using SPH Method with Slip-Link Model" Polymers 14, no. 20: 4334. https://doi.org/10.3390/polym14204334






