Multiscale Progressive Failure Analysis of 3D Woven Composites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Material Characterization
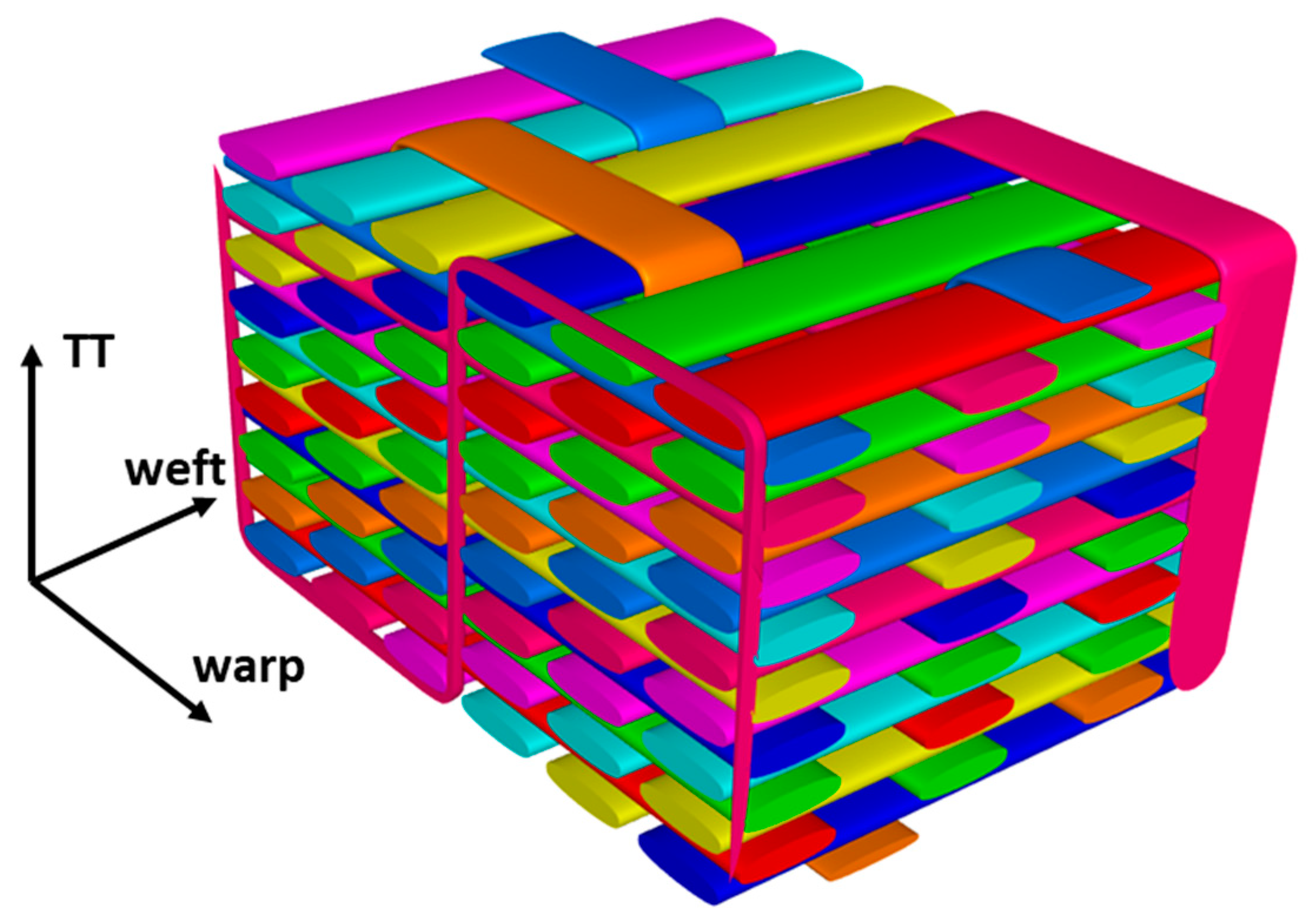
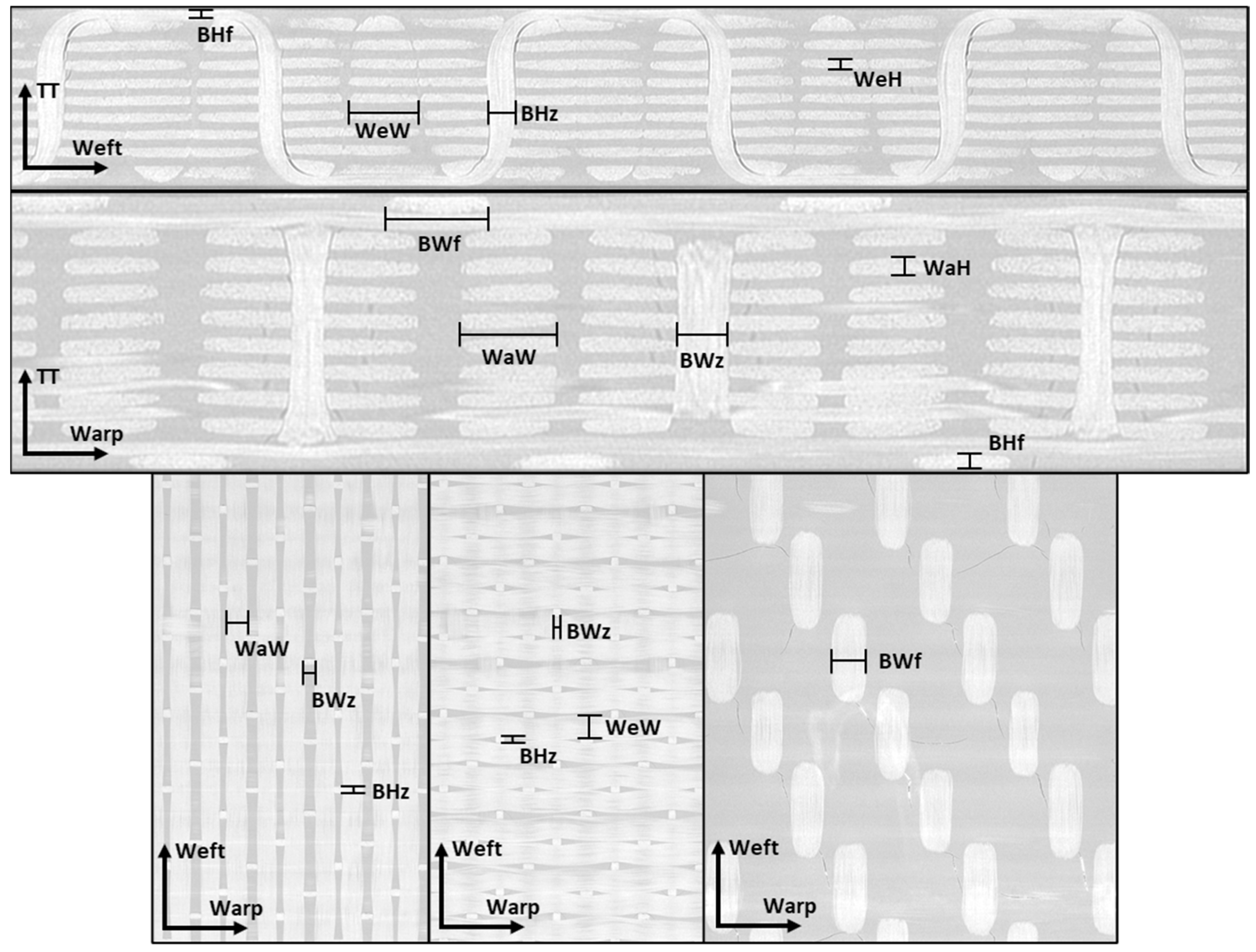
2.2.1. Geometric Characterization Based on X-ray CT and SEM
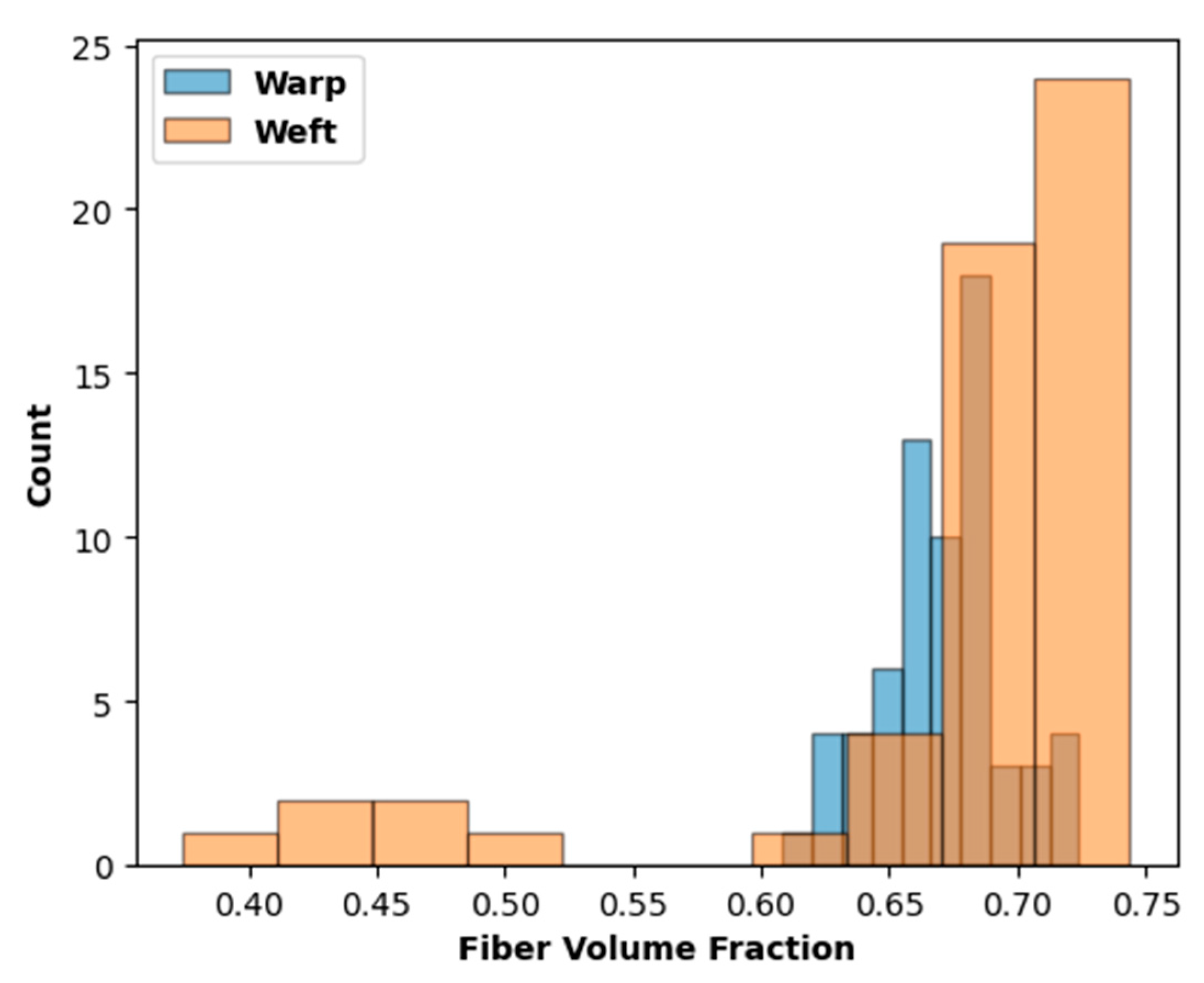
2.2.2. Acid-Digestion Tests
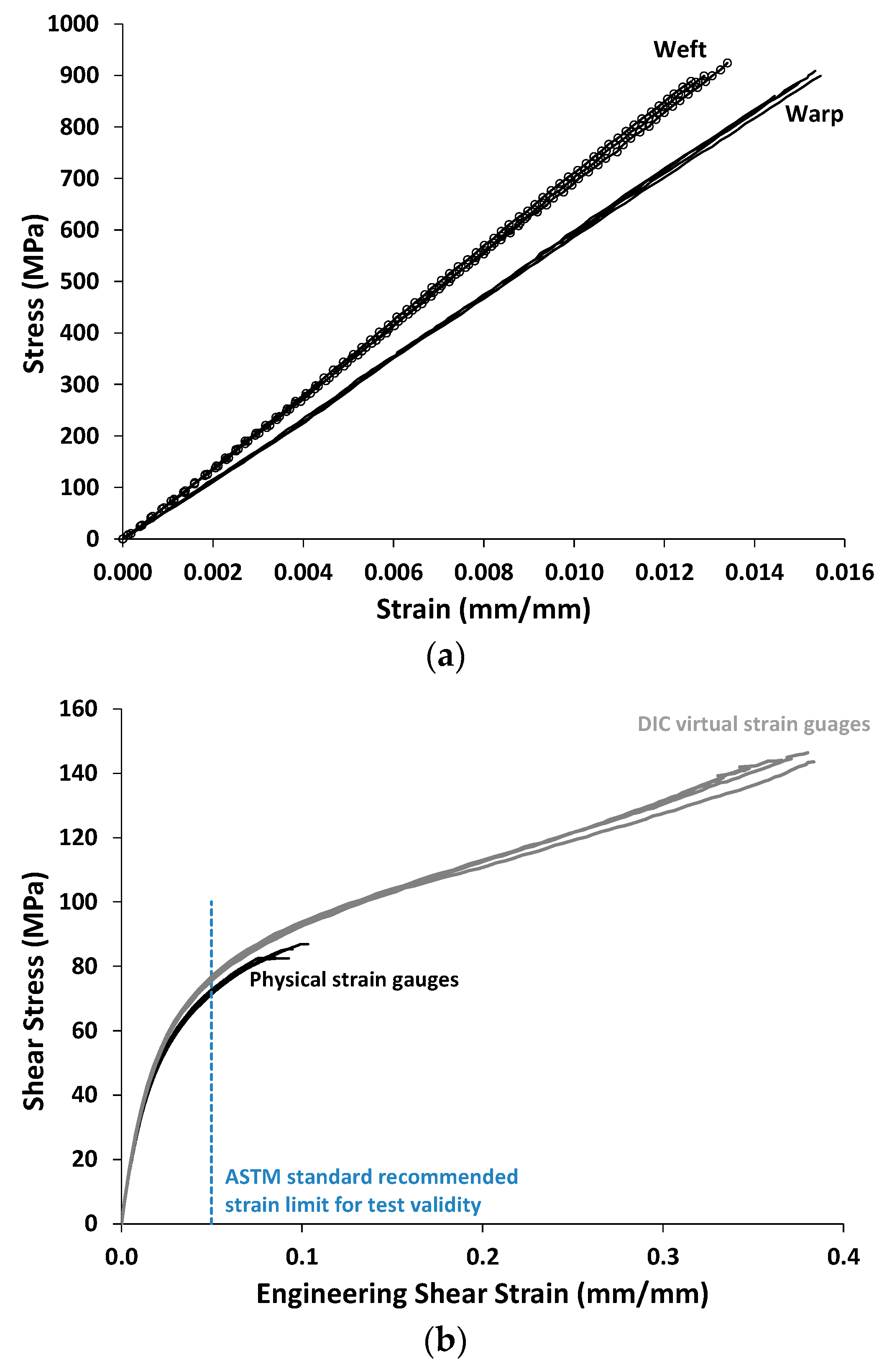
2.2.3. Warp and Weft Tensile and In-Plane Shear Tests
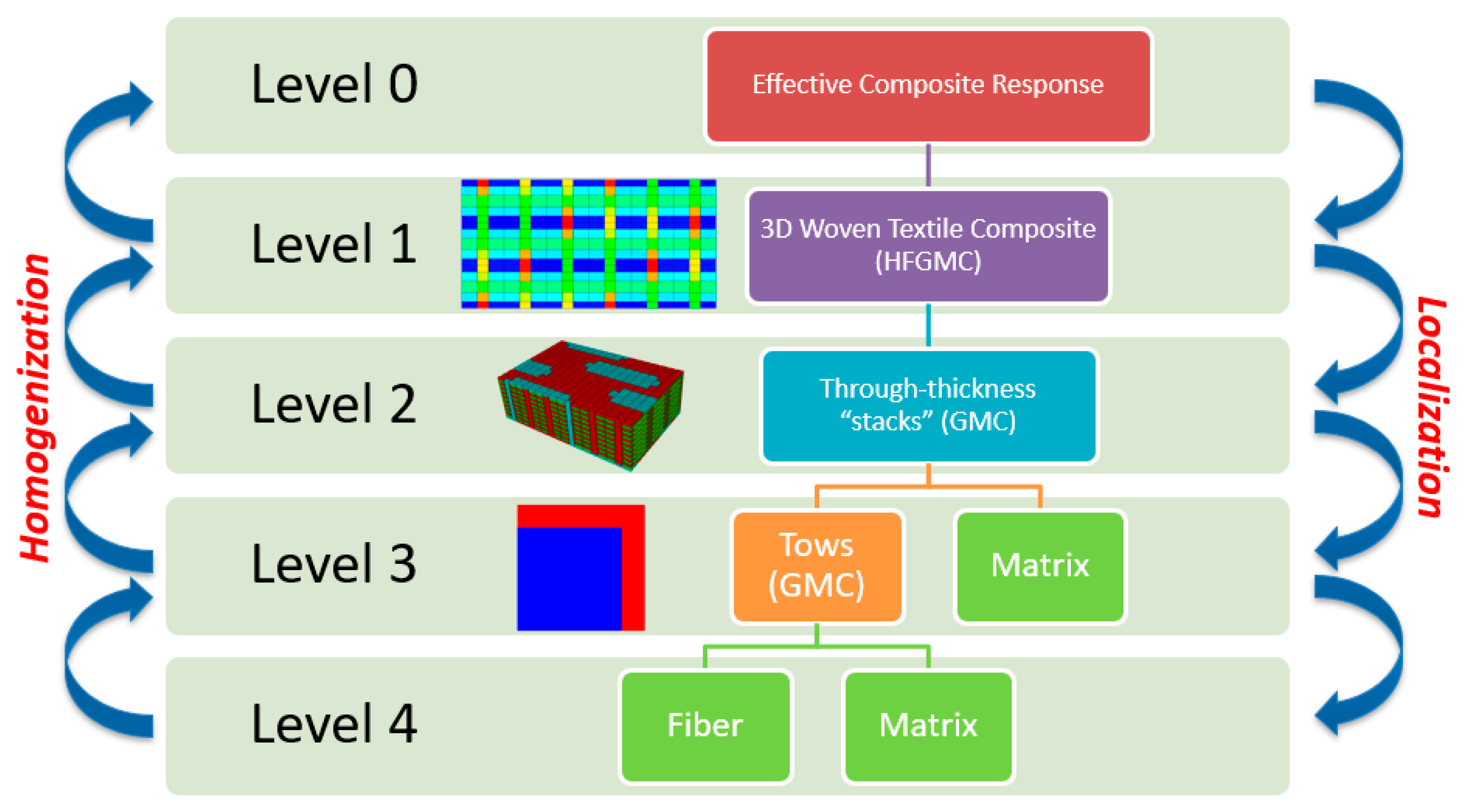
2.3. Multiscale Modeling Procedure
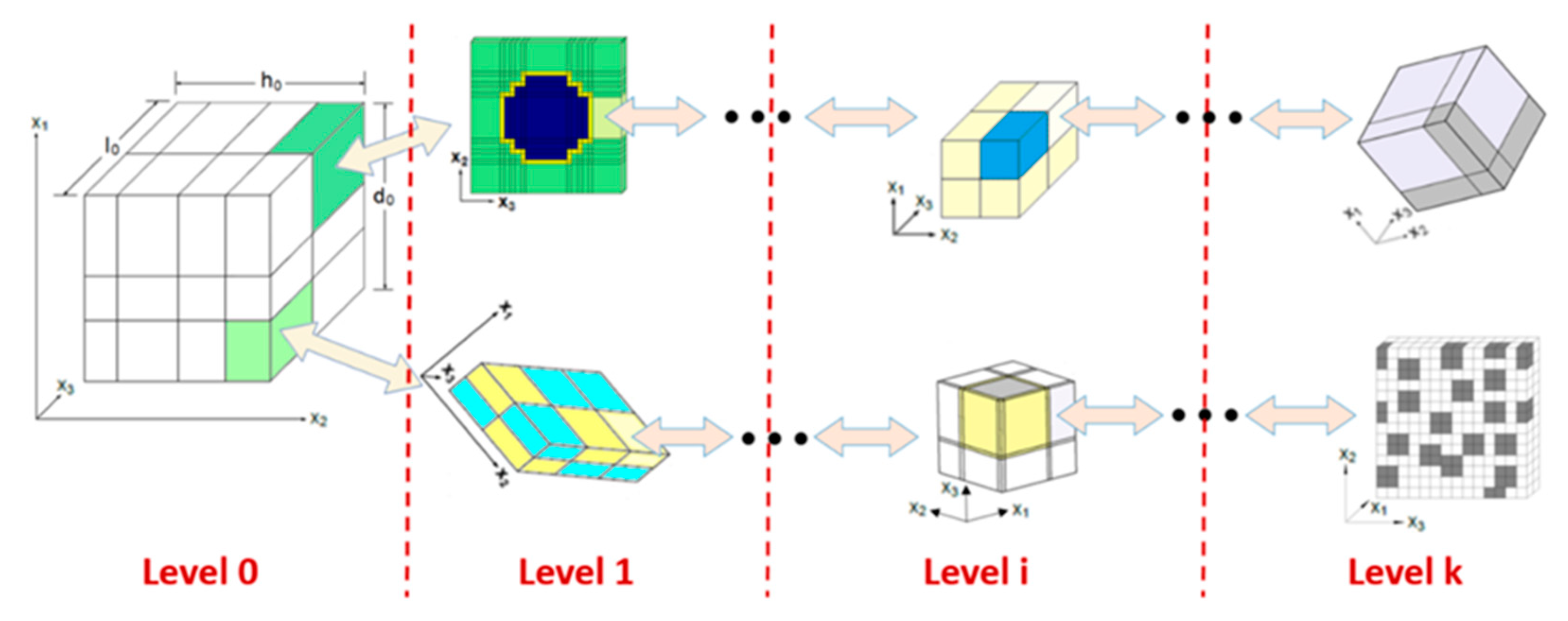
2.3.1. Multiscale Recursive Micromechanics
2.3.2. Crack-Band Progressive Damage Model
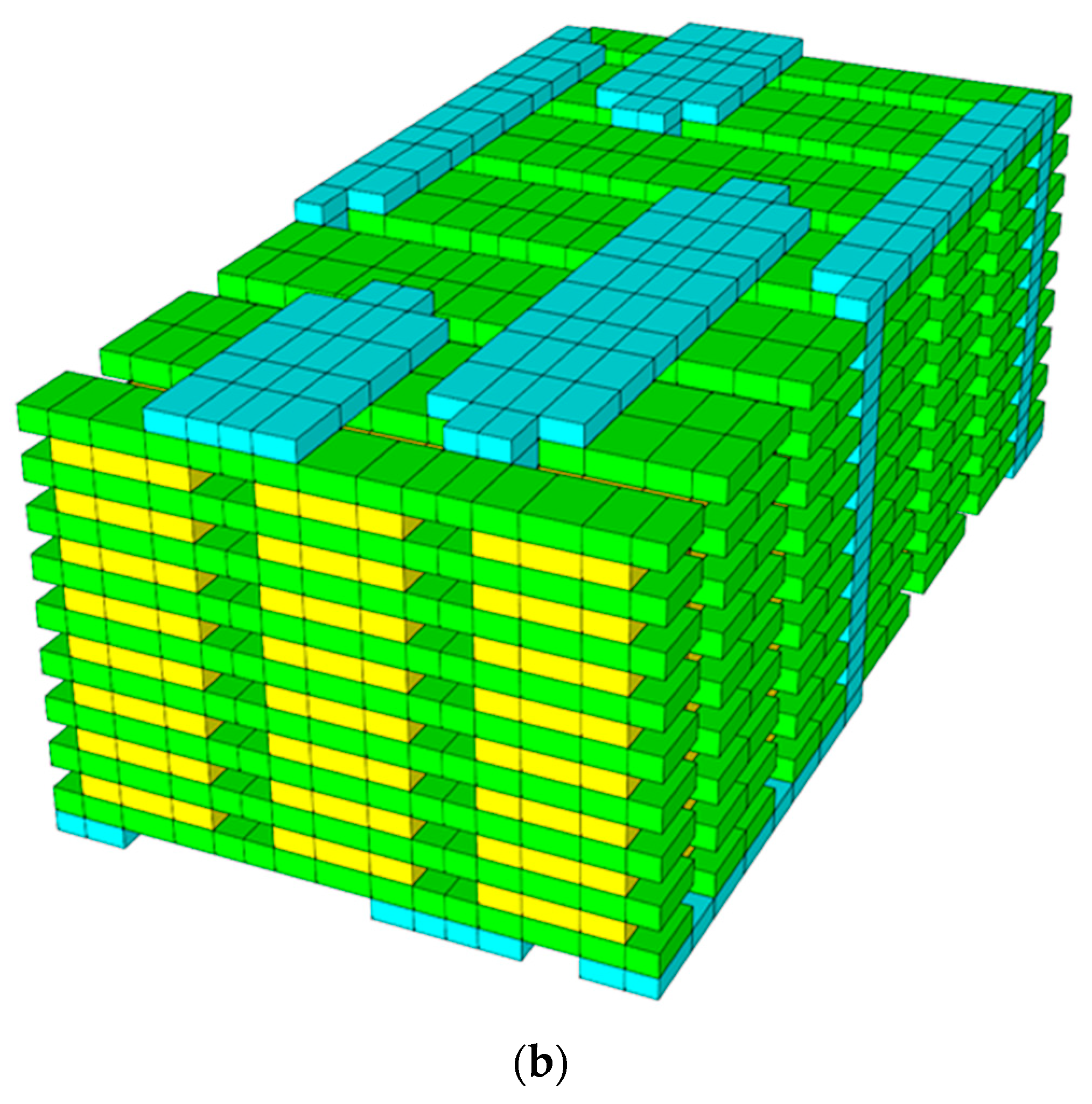
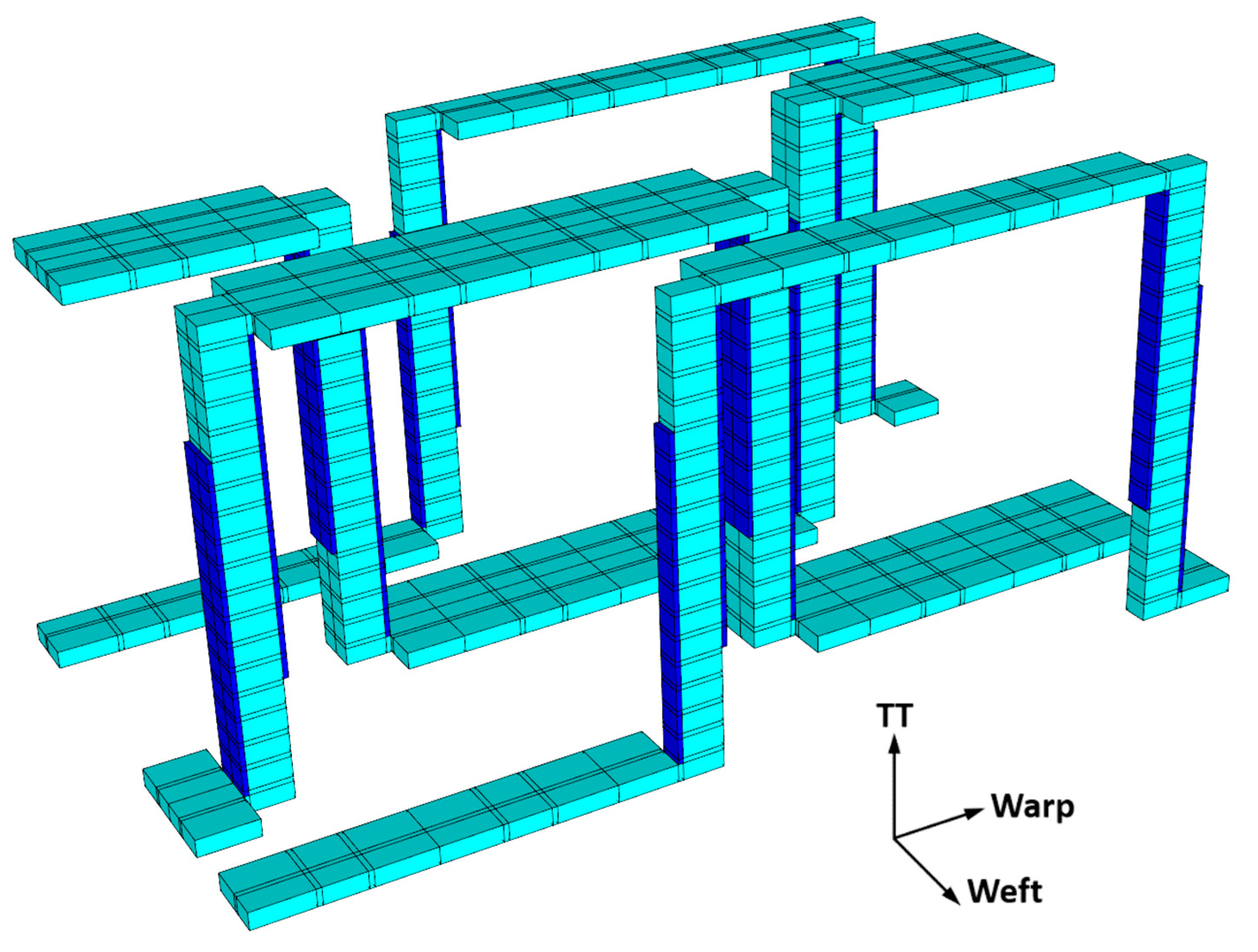
2.3.3. Multiscale 3D Woven-Composite Model
3. Experimental Results
3.1. Geometic Characterization
3.2. Warp and Weft Tensile and In-Plane Shear Tests
4. Multiscale Modeling Results and Discussion
4.1. Effect of Binder-Tow Disbonds
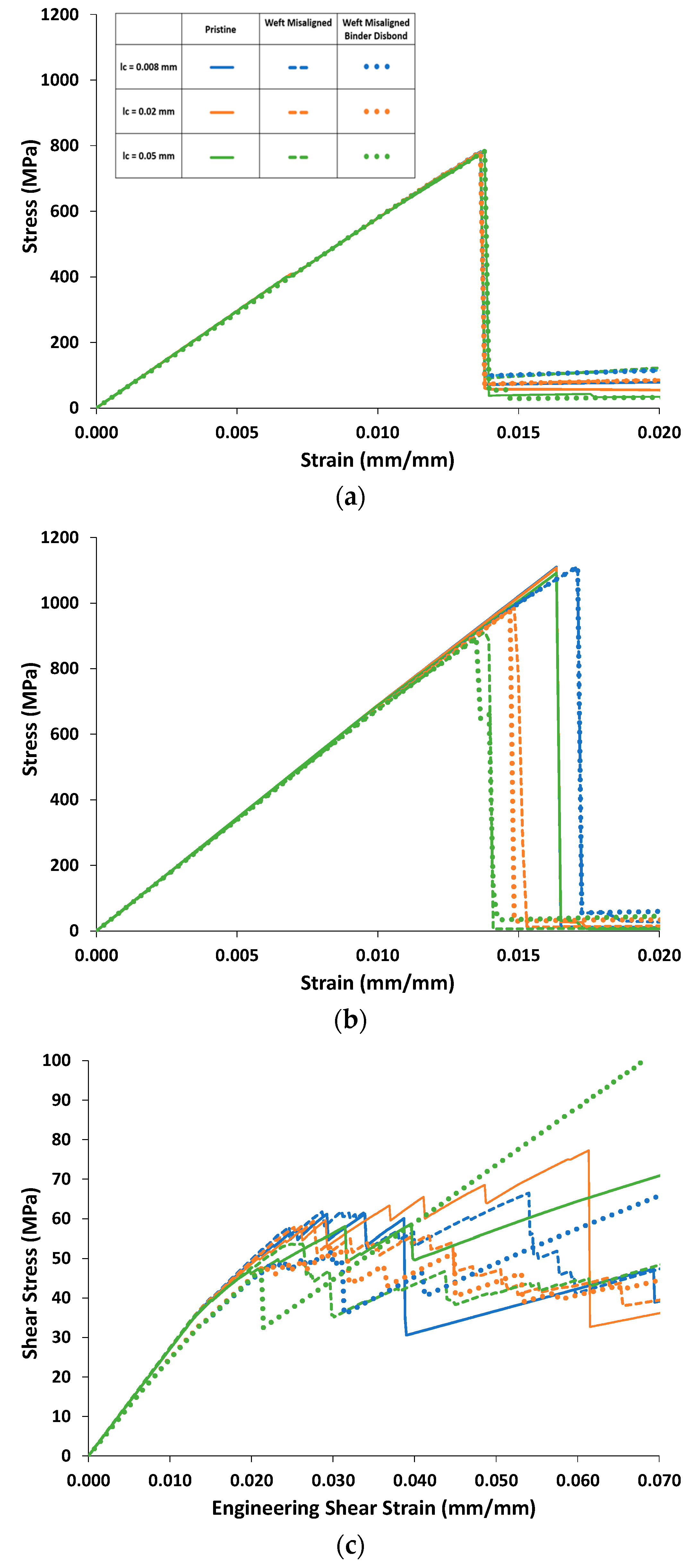
4.2. Effect of Weft-Tow Waviness
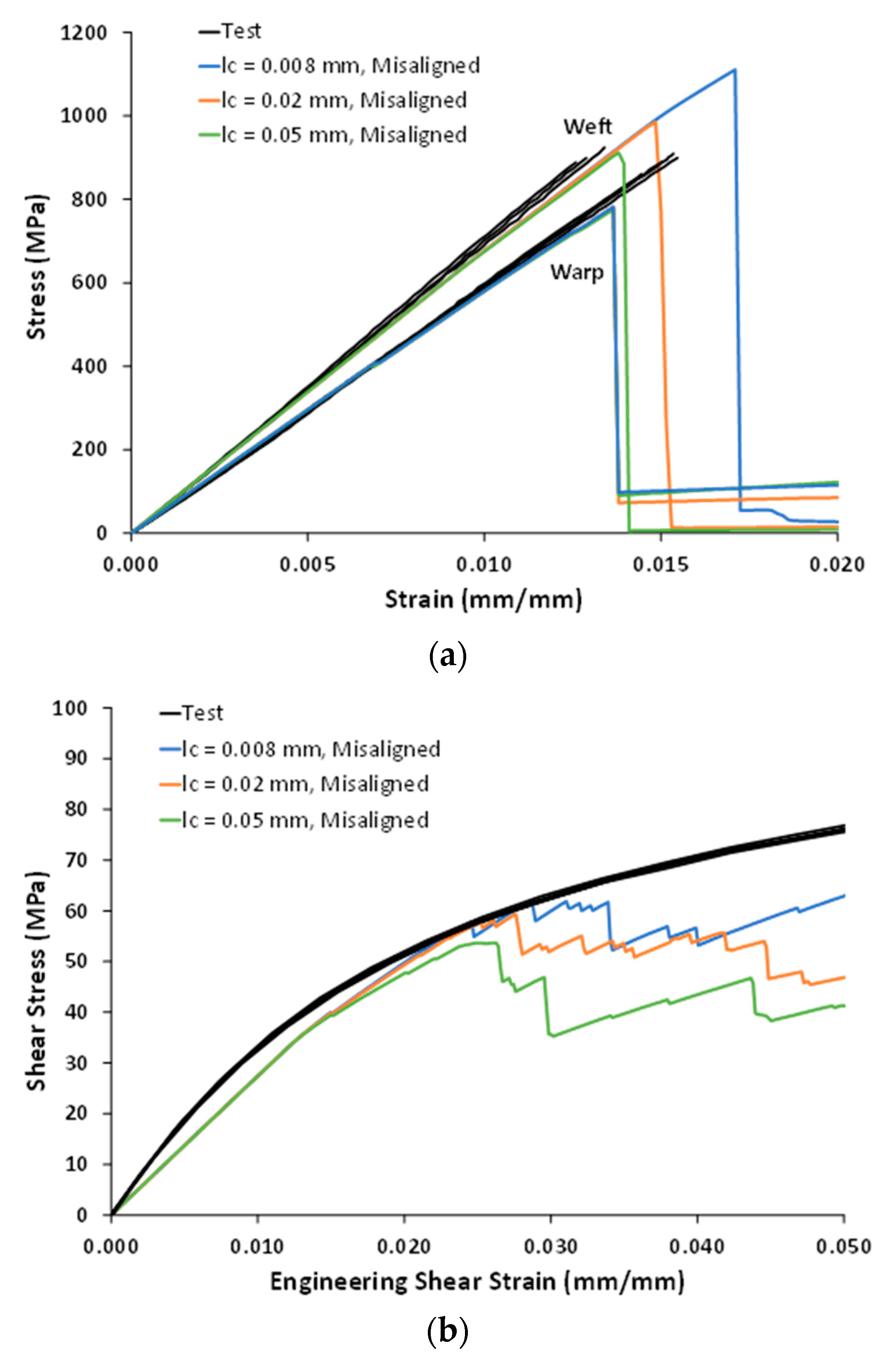
4.3. Correlations with Test Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Variable | Description |
| Strain concentration and stiffness tensors for subvolume αi, respectively | |
| Effective stiffness tensor for an RUC at Level i | |
| BHf, BWf | Binder-tow height and width, flat warp-aligned region, respectively |
| BHz, BWz | Binder-tow height and width, mid-thickness region, respectively |
| DM | Scalar damage variable |
| E, G | Undamaged matrix Young’s and shear moduli, respectively |
| E11f, E22f, G12f, ν12f, ν23f | Transversely isotropic fiber elastic constants |
| E11, E22, E33 | Orthotropic elastic Young’s moduli |
| G23, G13, G12 | Orthotropic elastic shear moduli |
| lc | Characteristic length |
| GI, GII | Mode-I- and mode-II-strain energy-release rates, respectively |
| GIC, GIIC | Mode-I and mode-II fracture toughnesses, respectively |
| Total number of subvolumes | |
| Damaged compliance matrix | |
| , | Mode-I and mode-II crack-band tractions, respectively |
| tM, εM | Mixed-mode traction and strain, respectively |
| , | Mixed-mode traction and strain when damage initiates, respectively |
| Second- and fourth-order coordinate transformation tensors for RUC at Level i, respectively | |
| Volume fraction of subvolume αi | |
| WaH, WaW | Warp-tow height and width, respectively |
| WeH, WeW | Weft-tow height and width, respectively |
| , | Normal and shear cohesive strength (matrixes), respectively |
| αi | Subvolume located at Level i |
| Subvolume αi strain and stress tensors, respectively | |
| Average strain and stress tensors for an RUC at Level i, respectively | |
| Mode-I and mode-II crack-band strains, respectively | |
| , | Mixed-mode damage initiation and failure strains, respectively |
| ii normal and ij shear stresses for matrix subvolume , respectively | |
| ν | Poisson ratio for isotropic matrix |
| ν23,ν23,ν12 | Orthotropic elastic Poisson ratios |
References
- Bogdanovich, A.E. Multi-scale modeling, stress and failure analyses of 3-D woven composites. J. Mater. Sci. 2006, 41, 6547–6590. [Google Scholar] [CrossRef]
- Gao, Z.; Chen, L. A review of multi-scale numerical modeling of three-dimensional woven fabric. Compos. Struct. 2021, 263, 113685. [Google Scholar] [CrossRef]
- Patel, D.K.; Waas, A.M.; Yen, C.-F. Direct numerical simulation of 3D woven textile composites subjected to tensile loading: An experimentally validated multiscale approach. Compos. B. Eng. 2018, 152, 102–115. [Google Scholar] [CrossRef]
- Dewangan, M.K.; Panigrahi, S.K. Finite element analysis of hybrid 3D orthogonal woven composite subjected to ballistic impact with multi-scale modeling. Polym. Adv. Technol. 2021, 32, 964–979. [Google Scholar] [CrossRef]
- Wang, Q.; Li, T.; Yang, X.; Huang, Q.; Wang, B.; Ren, M. Multiscale numerical and experimental investigation into the evolution of process-induced residual strain/stress in 3D woven composite. Compos. A Appl. Sci. and Manuf. 2020, 135, 105913. [Google Scholar] [CrossRef]
- Pineda, E.J.; Bednarcyk, B.A.; Ricks, T.M.; Farrokh, B.; Jackson, W. Multiscale failure analysis of a 3D woven composite containing manufacturing induced voids and disbonds. Compos. A Appl. Sci. and Manuf. 2022, 156, 106844. [Google Scholar] [CrossRef]
- Ricks, T.M.; Pineda, E.J.; Bednarcyk, B.A.; Arnold, S.M. Progressive failure analysis of 3D woven composites via multiscale recursive micromechanics. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11 January 2021. [Google Scholar]
- Ge, L.; Li, H.; Zhang, Y.L.; Zhong, J.; Chen, Y.; Fang, D. Multiscale viscoelastic behavior of 3D braided composites with pore defects. Compos. Sci. Technol. 2022, 217, 109114. [Google Scholar] [CrossRef]
- Zhu, L.; Lyu, L.; Wang, Y.; Qian, Y.; Zhao, Y.; Wei, C.; Guo, J. Axial-compression performance and finite element analysis of a tubular three-dimensional-woven composite from a meso-structural approach. Thin-Wall. Struct. 2020, 157, 107074. [Google Scholar] [CrossRef]
- Ewert, A.; Drach, B.; Vasylevskyi, K.; Tsukrov, I. Predicting the overall response of an orthogonal 3D woven composite using simulated and tomography-derived geometry. Compos. Struct. 2020, 243, 112169. [Google Scholar] [CrossRef]
- Mendoza, A.; Schneider, J.; Parra, E.; Roux, S. The correlation framework: Bridging the gap between modeling and analysis for 3D woven composites. Compos. Struct. 2019, 229, 111468. [Google Scholar] [CrossRef]
- Wintiba, B.; Sonon, B.; Kamel, K.E.M.; Massart, T.J. An automated procedure for the generation and conformal discretization of 3D woven composites RVEs. Compos. Struct. 2017, 180, 955–971. [Google Scholar] [CrossRef]
- Isart, N.; el Said, B.; Ivanov, D.S.; Hallett, S.R.; Mayugo, J.A.; Blanco, N. Internal Geometric Modelling of 3D Woven Composites: A Comparison Between Different Approaches. Compos. Struct. 2015, 132, 1219–1230. [Google Scholar] [CrossRef]
- Drach, A.; Drach, B.; Tsukrov, I. Processing of fiber architecture data for finite element modeling of 3D woven composites. Adv. Eng. Softw. 2014, 72, 18–27. [Google Scholar] [CrossRef]
- Ballard, M.K.; Whitcomb, J.D. Stress analysis of 3D textile composites using high performance computing: New insights and challenges. IOP Conf. Series: Mater. Sci. Eng. 2018, 406, 012004. [Google Scholar] [CrossRef] [Green Version]
- Joglekar, S.; Pankow, M. Modeling of 3D Woven Composites Using the Digital Element Approach for Accurate Prediction of Kinking under Compressive Loads. Compos. Struct. 2017, 160, 547–559. [Google Scholar] [CrossRef]
- Green, S.D.; Matveev, M.Y.; Long, A.C.; Ivanov, D.; Hallett, S.R. Mechanical modelling of 3D woven composites considering realistic unit cell geometry. Compos. Struct. 2014, 118, 284–293. [Google Scholar] [CrossRef] [Green Version]
- Rahali, Y.; Goda, I.; Ganghoffer, J.F. Numerical identification of classical and nonclassical moduli of 3D woven textile and analysis of scale effects. Compos. Struct. 2016, 135, 122–139. [Google Scholar] [CrossRef]
- Bergan, A.C. An Automated Meshing Framework for Progressive Damage Analysis of Fabrics Using CompDam. In Proceedings of the American Society for Composites—35th Technical Conference, Virtual, 14 September 2020. [Google Scholar]
- Ballard, M.K.; Iarve, E.V.; Whitcomb, J.D.; Mollenhauer, D.H. An Extended Critical Failure Volume Method for Strength Prediction in 3D Woven Textile Composites. In Proceedings of the AIAA Scitech 2022 Forum, San Diego, CA, USA, 3 January 2022. [Google Scholar]
- Hoos, K.H.; Ballard, M.K.; Adluru, H.K.; Iarve, E.V.L.; Zhou, E.; Mollenhauer, D.H. Determination of Effective Elastic Properties of Realistic 3D Textile Mesoscale Models Using Periodic Cluster Method. In Proceedings of the AIAA Scitech 2022 Forum, San Diego, CA, USA, 3 January 2022. [Google Scholar]
- Mazumder, A.; Liu, Q.; Wang, Y.; Yen, C.-F. A non-linear material model for progressive damage analysis of woven composites using a conformal meshing framework. J. Compos. Mater. 2022, 56, 3323–3340. [Google Scholar] [CrossRef]
- Wielhorski, Y.; Mendoza, A.; Rubino, M.; Roux, S. Numerical modeling of 3D woven composite reinforcements: A review. Compos. A Appl. Sci. and Manuf. 2022, 154, 106729. [Google Scholar] [CrossRef]
- Zeng, X.; Brown, L.P.; Endruweit, A.; Matveev, M.; Long, A.C. Geometrical modelling of 3D woven reinforcements for polymer composites: Prediction of fabric permeability and composite mechanical properties. Compos. A Appl. Sci. and Manuf. 2014, 56, 150–160. [Google Scholar] [CrossRef]
- Pineda, E.J.; Bednarcyk, B.A.; Ricks, T.M.; Arnold, S.M.; Henson, G. Efficient multiscale recursive micromechanics of composites for engineering applications. Int. J. Multiscale Comput. Eng. 2021, 19, 77–105. [Google Scholar] [CrossRef]
- Aboudi, J.; Arnold, S.M.; Bednarcyk, B.A. Practical Micromechanics of Composite Materials; Elsevier: Oxford, UK, 2021. [Google Scholar]
- Bažant, Z.P.; Oh, B.H. Crack band theory for fracture of concrete. Mater. Struct. 1983, 16, 155–177. [Google Scholar] [CrossRef] [Green Version]
- Pineda, E.J.; Bednarcyk, B.A.; Waas, A.M.; Arnold, S.M. Progressive failure of a unidirectional fiber reinforced composite using the method of cells: Discretization objective computational results. Int. J. Solids Struct. 2013, 50, 1203–1216. [Google Scholar] [CrossRef] [Green Version]
- Camanho, P.P.; Dávila, C.G. Mixed-Mode Decohesion Finite Elements for the Simulation of Delamination in Composite Materials. NASA/TM-2002-211737. 2002. Available online: https://ntrs.nasa.gov/citations/20020053651 (accessed on 1 October 2022).
- Jackson, W.C.; Bergan, A.; Rose, C.A.; Segal, K.N.; Gardner, N.W.; Waas, N.W. Experimental Observations of Damage States in Unnotched and Notched 3D Orthogonal Woven Coupons Loaded in Tension. In Proceedings of the AIAA Scitech 2022 Forum, San Diego, CA, USA, 3 January 2022. [Google Scholar]
- Naresh, K.; Khan, K.A.; Umer, R.; Cantwell, W.J. The use of X-ray computed tomography for design and process modeling of aerospace composites: A review. Mater. Des. 2020, 190, 108553. [Google Scholar] [CrossRef]
- Wintiba, B.; Vasiukov, D.; Panier, S.; Lomov, S.V.; Kamel, K.E.M.; Massart, T.J. Automated reconstruction and conformal discretization of 3D woven composite CT scans with local fiber volume fraction control. Compos. Struct. 2020, 248, 112438. [Google Scholar] [CrossRef]
- Semeraro, F.; Ferguson, J.C.; Panerai, F.; King, R.J.; Mansour, N.N. Anisotropic analysis of fibrous and woven materials part 1: Estimation of local orientation. Comput. Mater. Sci. 2020, 178, 109631. [Google Scholar] [CrossRef]
- Naouar, N.; Vidal-Sallé, E.; Schneider, J.; Maire, E.; Boisse, P. Meso-scale FE analyses of textile composite reinforcement deformation based on X-ray computed tomography. Compos. Struct. 2014, 116, 165–176. [Google Scholar] [CrossRef]
- Sinchuk, Y.; Shishkina, O.; Gueguen, M.; Signor, L.; Nadot-Martin, C.; Trumel, H.; Van Paepegem, W. X-ray CT based multi-layer unit cell modeling of carbon fiber-reinforced textile composites: Segmentation, meshing and elastic property homogenization. Compos. Struct. 2022, 298, 116003. [Google Scholar] [CrossRef]
- ASTM International. Standard Test Methods for Constituent Content of Composite Materials-D3171–22; ASTM International: West Conshohocken, PA, USA, 2022. [Google Scholar]
- National Institute for Aviation Research, Wichita State University. Available online: https://www.wichita.edu/industry_and_defense/NIAR/ (accessed on 2 September 2022).
- ASTM International. Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials-D3039/D3039M–08; ASTM International: West Conshohocken, PA, USA, 2008. [Google Scholar]
- ASTM International. Standard Test Method for Shear Properties of Composite Materials by V-Notched Rail Shear Method. D7078/D7078M–12; ASTM International: West Conshohocken, PA, USA, 2012. [Google Scholar]
- Hobbiebrunken, T.; Hojo, M.; Fiedler, B.; Tanaka, M.; Ochiai, S.; Schulte, K. Thermomechanical analysis of micromechanical formation of residual stresses and initial matrix failure in CFRP. JSME Int. J. A-Solid Mech. Mater. Eng. 2004, 47, 349–356. [Google Scholar] [CrossRef]








| IM7 Carbon Fiber [26] | RTM6 Epoxy Resin | |||
|---|---|---|---|---|
| Property | Value | Property | Value | Source |
| E11f (GPa) | 262.2 | E (GPa) | 2.755 | [40] |
| E22f (GPa) | 11.8 | ν | 0.38 | [40] |
| G12f (GPa) | 18.9 | Xm (MPa) | 87 | [40] |
| ν12f | 0.17 | Ym (MPa) | 76.1 | [40] |
| ν23f | 0.21 | GIC (N-mm/mm) | 0.216 | [19] |
| X11f (MPa) | 4335 | GIIC (N-mm/mm) | 0.857 | [19] |
| X22f (MPa) | 113 | |||
| Y11f (MPa) | 2608 | |||
| Y22f (MPa) | 354 | |||
| Z12f (MPa) | 138 | |||
| Z23f (MPa) | 128 | |||
| Variable | Description | Mean (mm) | Standard Deviation (mm) |
|---|---|---|---|
| WaW | Warp-tow width | 1.108 | 0.068 |
| WaH | Warp-tow height | 0.186 | 0.022 |
| WeW | Weft-tow width | 1.186 | 0.118 |
| WeH | Weft-tow height | 0.202 | 0.026 |
| BWf | Binder-tow width (flat region) | 1.171 | 0.081 |
| BHf | Binder-tow height (flat region) | 0.174 | 0.017 |
| BWz | Binder-tow width (TT region) | 0.501 | 0.105 |
| BHz | Binder-tow height (TT region) | 0.413 | 0.052 |
| Number of Measurements | Mean Vf | Vf Standard Deviation | |
|---|---|---|---|
| Warp Tows | 66 | 0.6705 | 0.0249 |
| Weft Tows | 54 | 0.6738 | 0.0876 |
| Combined | 120 | 0.6720 | 0.0617 |
| Strain Gauge Tensile Modulus (GPa) | DIC Tensile Modulus (GPa) | Strength (MPa) | |
|---|---|---|---|
| 58.066 | 57.549 | 915 | |
| 58.497 | 56.173 | 892 | |
| 59.778 | 56.537 | 906 | |
| 58.575 | 57.864 | 871 | |
| 58.960 | - | 924 | |
| Avg. | 58.775 | 57.031 | 902 |
| St. Dev. | 0.644 | 0.805 | 21 |
| Strain Gauge Tensile Modulus (GPa) | DIC Tensile Modulus (GPa) | Strength (MPa) | |
|---|---|---|---|
| 67.754 | - | 970 | |
| 67.088 | 68.137 | 933 | |
| 66.680 | - | 905 | |
| 69.624 | 70.919 | 894 | |
| 69.198 | 70.481 | 909 | |
| Avg. | 68.069 | 69.846 | 922 |
| St. Dev. | 1.293 | 1.496 | 30 |
| Strain Gauge Shear Modulus (GPa) | Shear Stress at 5% Strain (MPa) | |
|---|---|---|
| 3.369 | 71.881 | |
| 3.425 | 72.802 | |
| 3.271 | 71.360 | |
| 3.326 | 71.808 | |
| Avg. | 3.348 | 71.968 |
| St. Dev. | 0.065 | 0.599 |
| Pristine | Disbonded Binder Tow | Difference | |
|---|---|---|---|
| E11 (GPa) | 8.51 | 8.46 | −0.6% |
| E22 (GPa) | 68.9 | 68.9 | 0% |
| E33 (GPa) | 59.2 | 58.5 | −1.2% |
| G23 (GPa) | 2.71 | 2.49 | −8.1% |
| G13 (GPa) | 1.88 | 1.72 | −8.5% |
| G12 (GPa) | 1.95 | 1.94 | −0.5% |
| ν23 | 0.0315 | 0.0291 | −7.6% |
| ν13 | 0.0492 | 0.0483 | −1.8% |
| ν12 | 0.0411 | 0.0410 | −0.2% |
| lc (mm) | Warp UTS (MPa) | Weft UTS (MPa) | In-Plane Shear Stress at 5% Strain (MPa) | |
|---|---|---|---|---|
| Pristine | 0.008 | 782 | 1110 | 36.7 |
| 0.02 | 780 | 1107 | 65.2 | |
| 0.05 | 781 | 1092 | 57.2 | |
| Disbonded | 0.008 | 781 | 1109 | 48.2 |
| Binder | 0.02 | 788 | 1107 | 49.0 |
| Tow | 0.05 | 780 | 1091 | 41.9 |
| Pristine | Weft Misalignment | Difference vs. Pristine | Weft Misalignment and Binder Disbond | Difference vs. Pristine | |
|---|---|---|---|---|---|
| E11 (GPa) | 8.51 | 8.52 | 0.1% | 8.46 | −0.6% |
| E22 (GPa) | 68.9 | 67.9 | −1.5% | 67.8 | −1.6% |
| E33 (GPa) | 59.2 | 59.3 | 0.2% | 58.6 | −1.0% |
| G23 (GPa) | 2.71 | 2.75 | 1.3% | 2.52 | −7.0% |
| G13 (GPa) | 1.88 | 1.89 | 0.5% | 1.73 | −8.0% |
| G12 (GPa) | 1.95 | 1.95 | 0% | 1.95 | 0% |
| ν23 | 0.0315 | 0.0320 | 1.6% | 0.0296 | −6.3% |
| ν13 | 0.0492 | 0.0491 | −0.2% | 0.0482 | −2.0% |
| ν12 | 0.0411 | 0.0418 | 1.7% | 0.0416 | 1.2% |
| lc (mm) | Warp UTS (MPa) | Weft UTS (MPa) | In-Plane Shear Stress at 5% Strain (MPa) | |
|---|---|---|---|---|
| Pristine | 0.008 | 782 | 1110 | 36.7 |
| 0.02 | 780 | 1107 | 65.2 | |
| 0.05 | 781 | 1092 | 57.2 | |
| Misaligned Weft | 0.008 | 782 | 1111 | 62.9 |
| Tows | 0.02 | 781 | 985 | 46.8 |
| 0.05 | 775 | 912 | 41.3 | |
| Misaligned Weft | 0.008 | 782 | 1111 | 48.7 |
| Tows and Binder | 0.02 | 781 | 974 | 44.0 |
| Disbond | 0.05 | 783 | 894 | 73.5 |
| Test Avg. | Model | Difference | |
|---|---|---|---|
| Warp Tensile Modulus (GPa) | 57.031 | 59.3 | 4.0% |
| Weft Tensile Modulus (GPa) | 69.846 | 67.9 | −2.8% |
| In-Plane Shear Modulus (GPa) | 3.348 | 2.75 | −17.9% |
| Test Avg. | Model lc = 0.008 mm | Difference | Model lc = 0.02 mm | Difference | Model lc = 0.05 mm | Difference | |
|---|---|---|---|---|---|---|---|
| Warp UTS (MPa) | 902 | 782 | −13.3% | 781 | −13.4% | 775 | −14.1% |
| Weft UTS (MPa) | 922 | 1111 | 20.5% | 985 | 6.8% | 912 | −1.1% |
| In-Plane Shear Stress at 5% Strain (MPa) | 71.968 | 62.9 | −12.6% | 46.8 | −35.0% | 41.3 | −42.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ricks, T.M.; Pineda, E.J.; Bednarcyk, B.A.; McCorkle, L.S.; Miller, S.G.; Murthy, P.L.N.; Segal, K.N. Multiscale Progressive Failure Analysis of 3D Woven Composites. Polymers 2022, 14, 4340. https://doi.org/10.3390/polym14204340
Ricks TM, Pineda EJ, Bednarcyk BA, McCorkle LS, Miller SG, Murthy PLN, Segal KN. Multiscale Progressive Failure Analysis of 3D Woven Composites. Polymers. 2022; 14(20):4340. https://doi.org/10.3390/polym14204340
Chicago/Turabian StyleRicks, Trenton M., Evan J. Pineda, Brett A. Bednarcyk, Linda S. McCorkle, Sandi G. Miller, Pappu L. N. Murthy, and Kenneth N. Segal. 2022. "Multiscale Progressive Failure Analysis of 3D Woven Composites" Polymers 14, no. 20: 4340. https://doi.org/10.3390/polym14204340
APA StyleRicks, T. M., Pineda, E. J., Bednarcyk, B. A., McCorkle, L. S., Miller, S. G., Murthy, P. L. N., & Segal, K. N. (2022). Multiscale Progressive Failure Analysis of 3D Woven Composites. Polymers, 14(20), 4340. https://doi.org/10.3390/polym14204340





