Influence of PVB Interlayer Mechanical Properties on Laminated Glass Elements Design in Dependence of Real Time-Temperature Changes
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Background
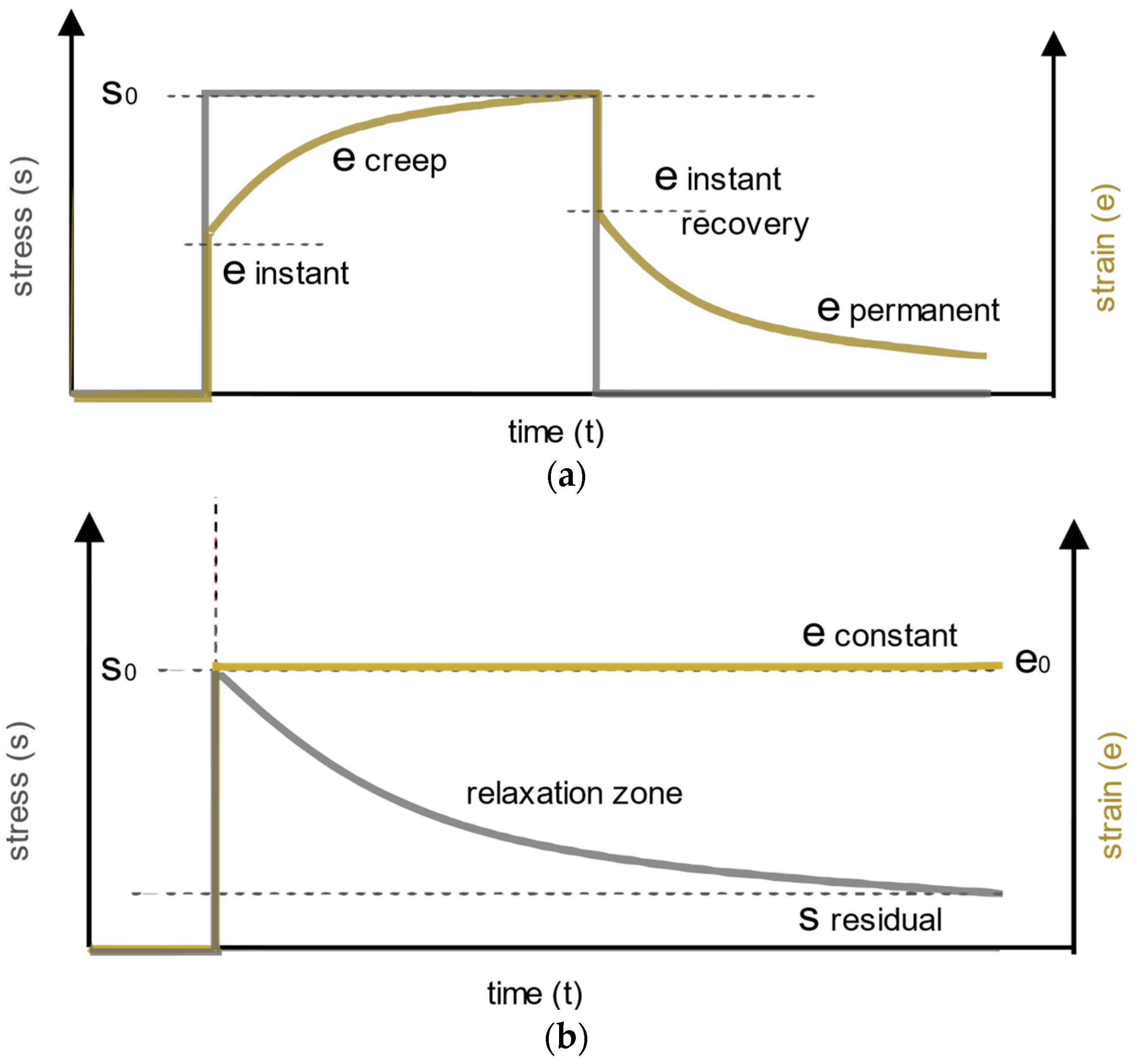
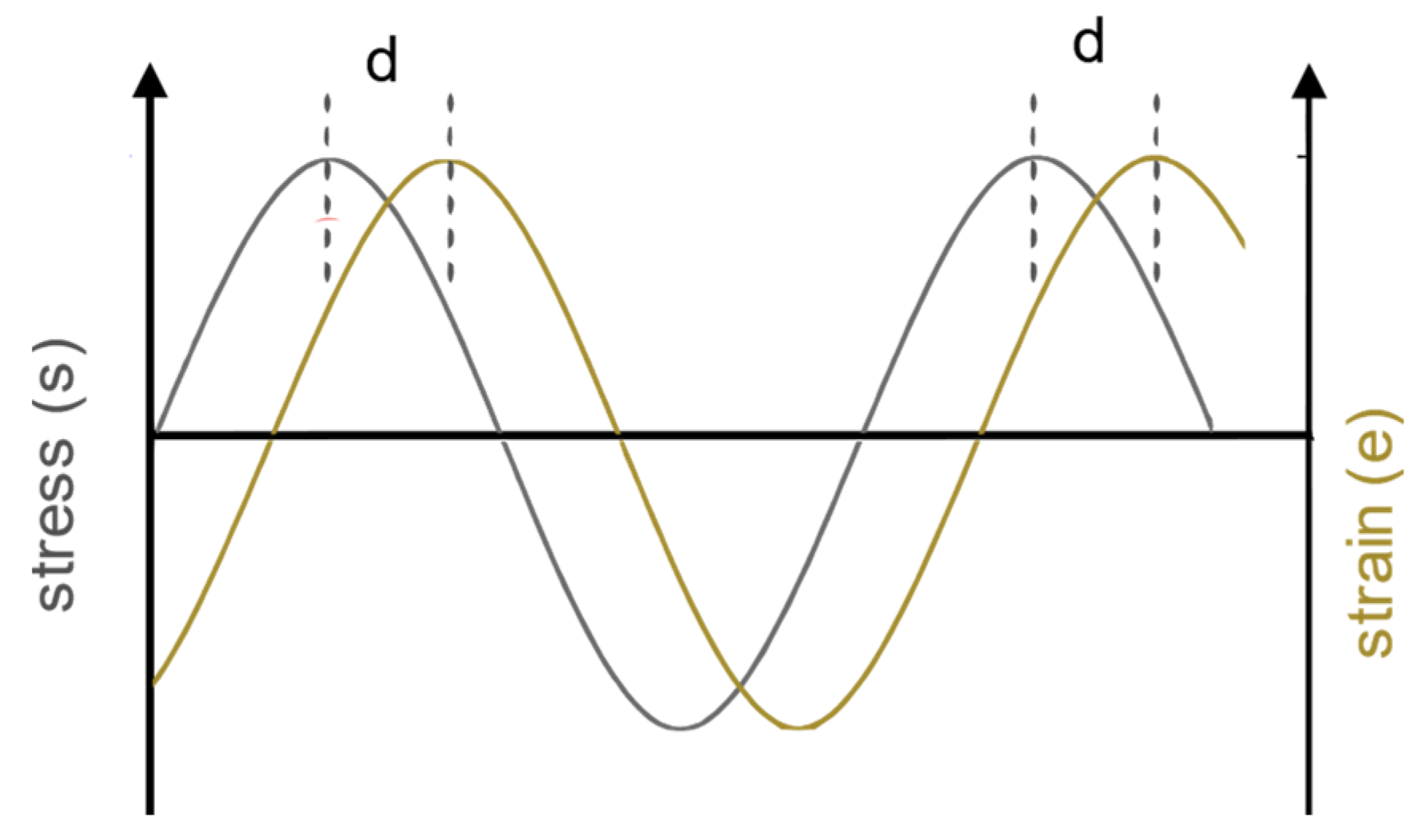
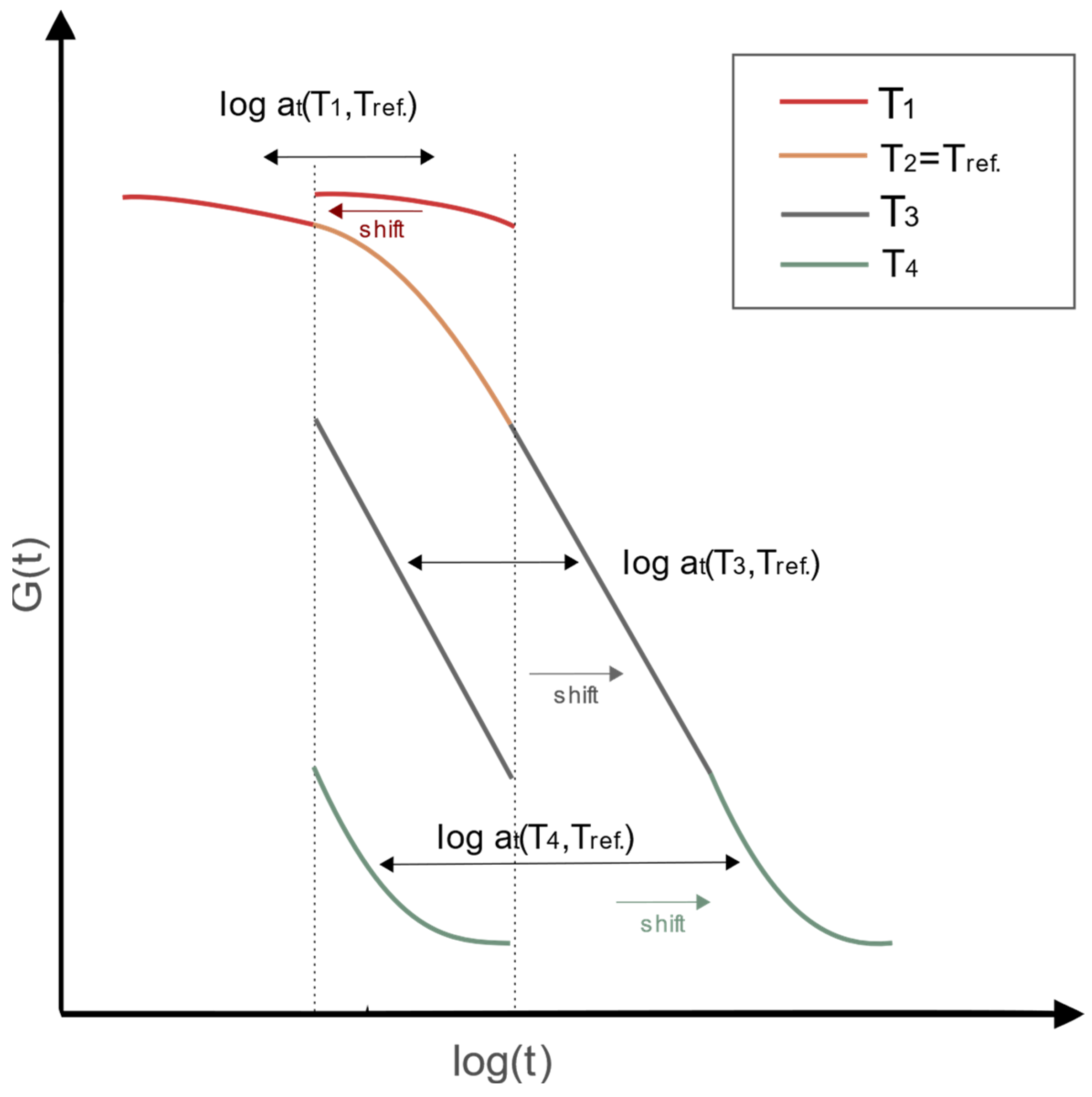
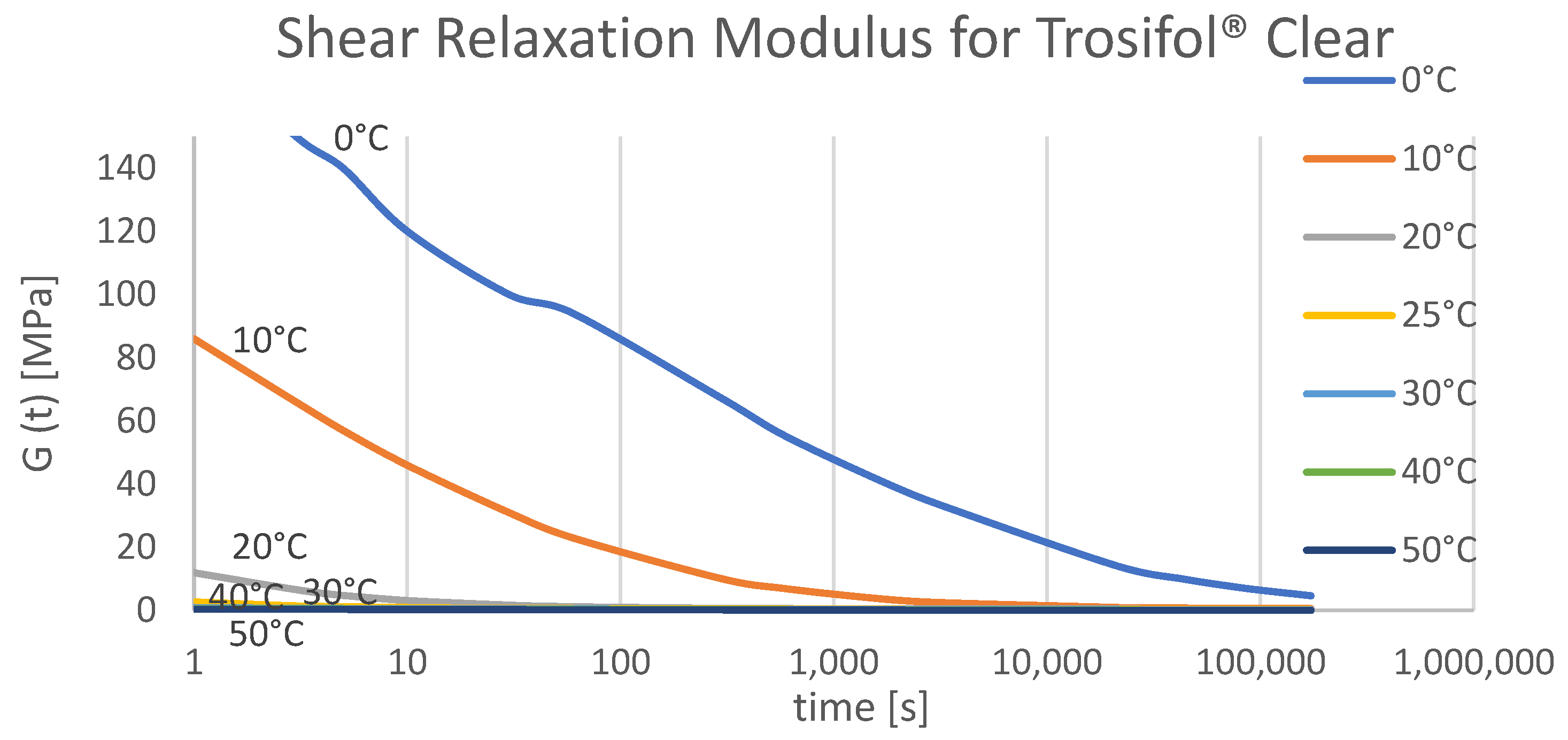
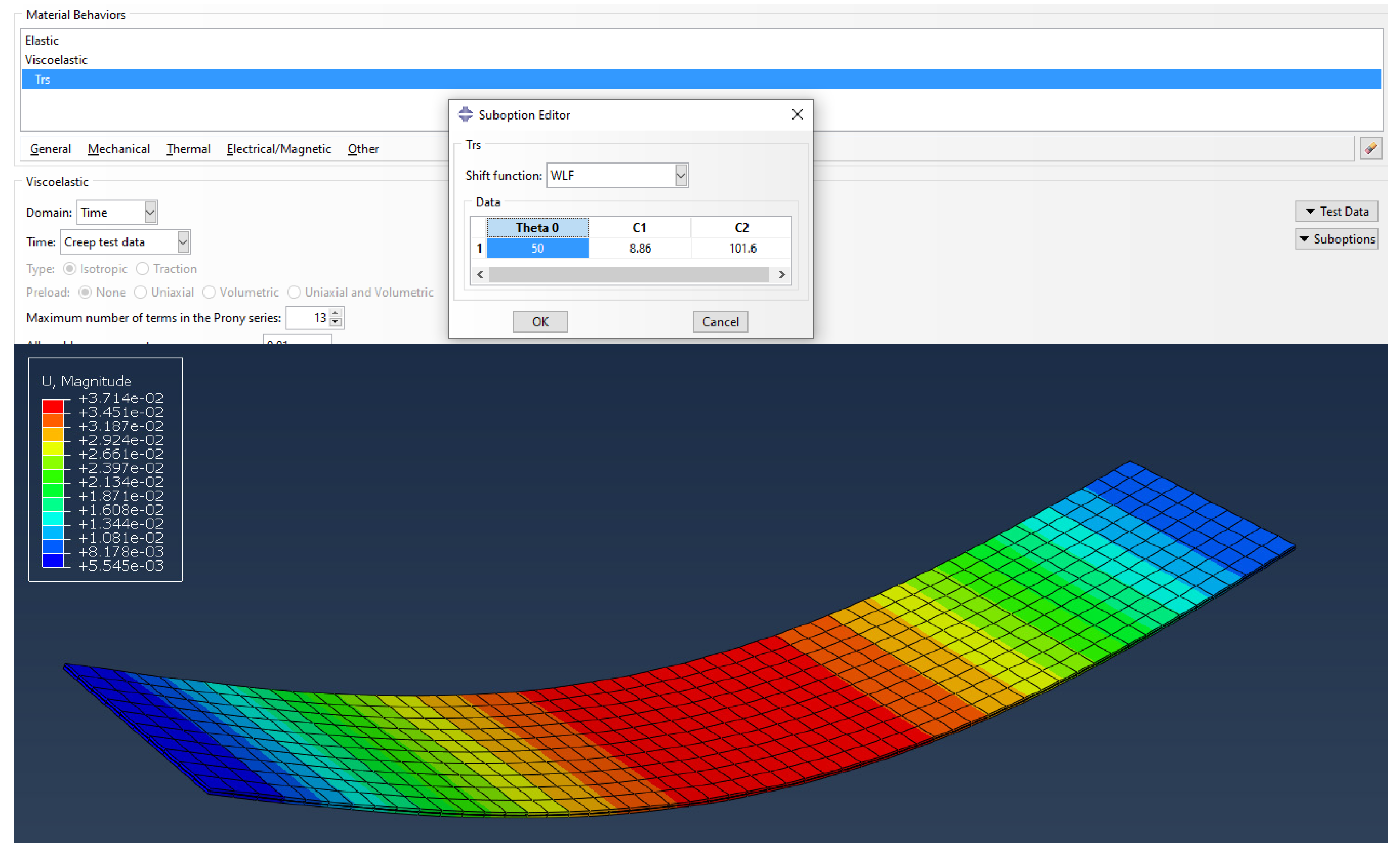
2.1.1. Viscoelastic Response of the Interlayer
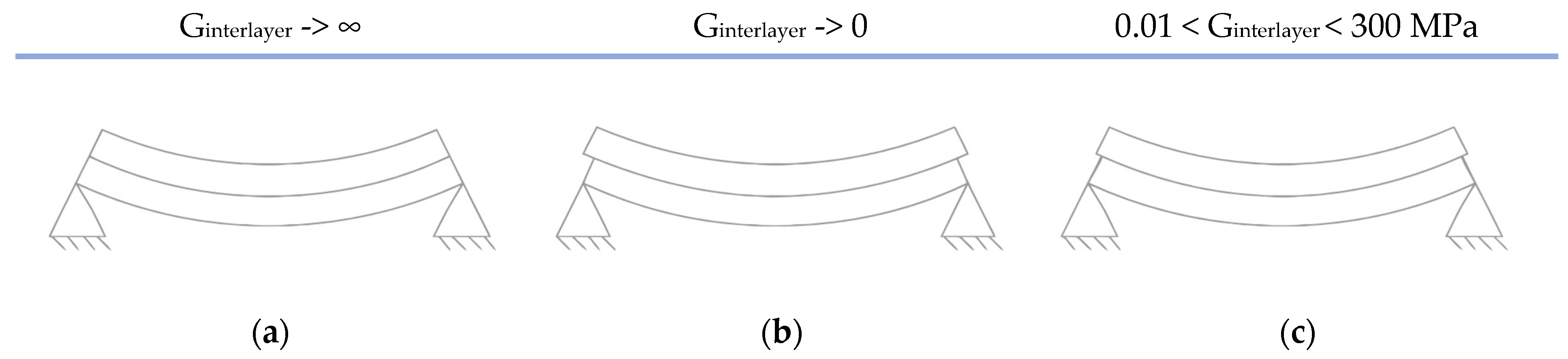
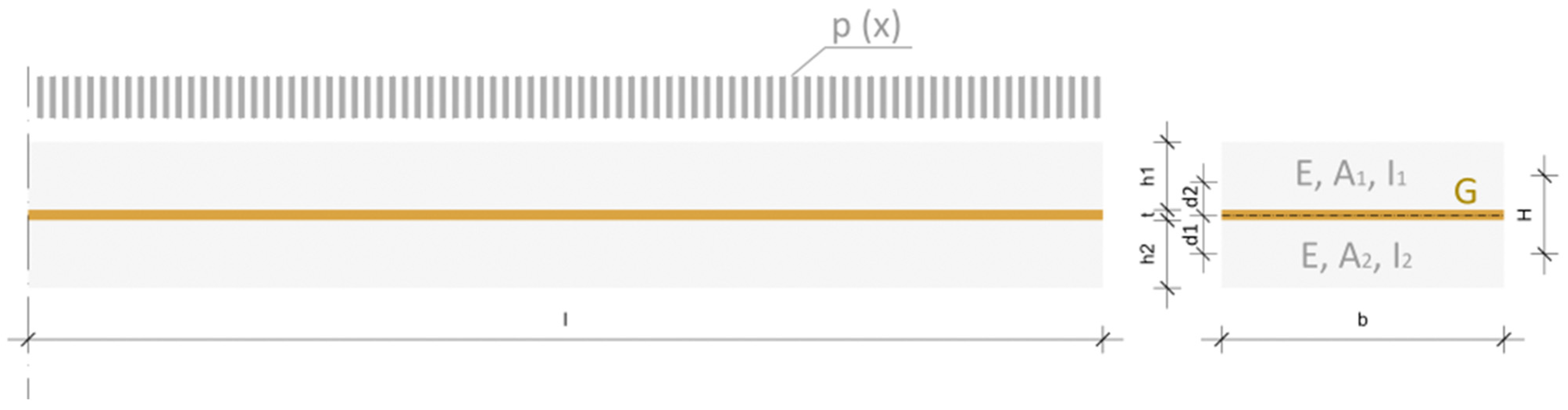
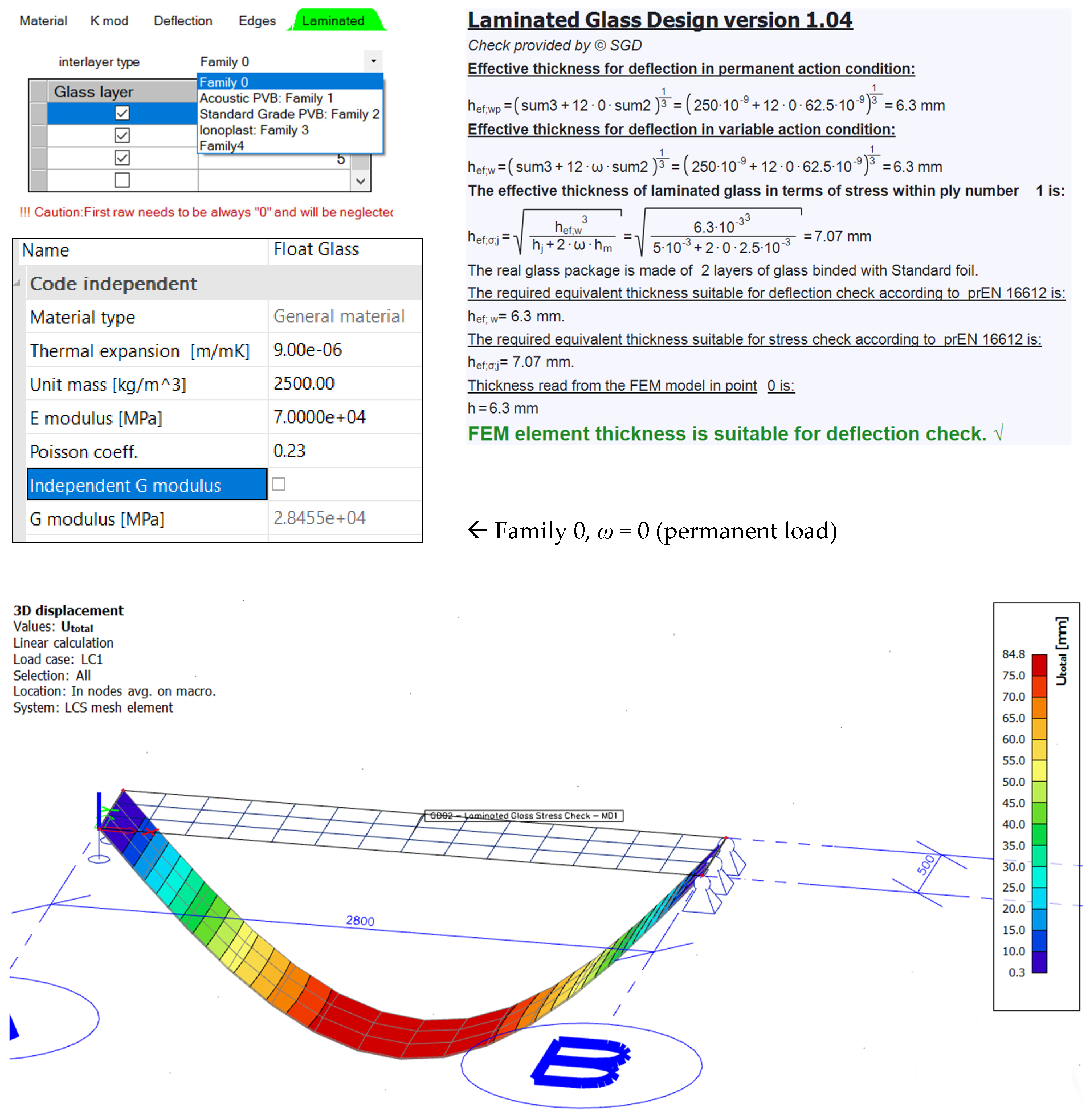
2.1.2. Effective Thickness Methods
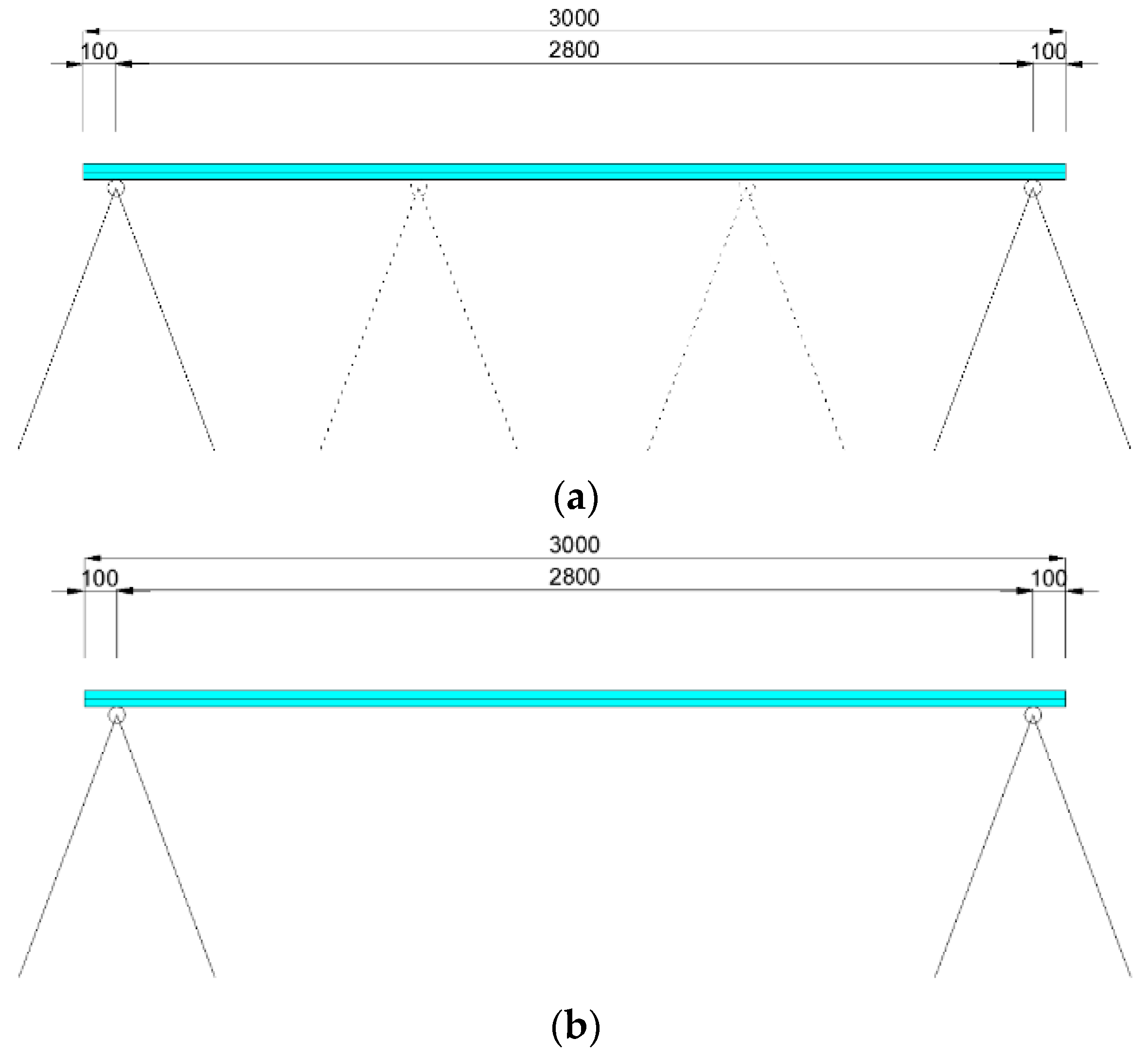
2.2. Experimental Research
2.3. Numerical Modeling
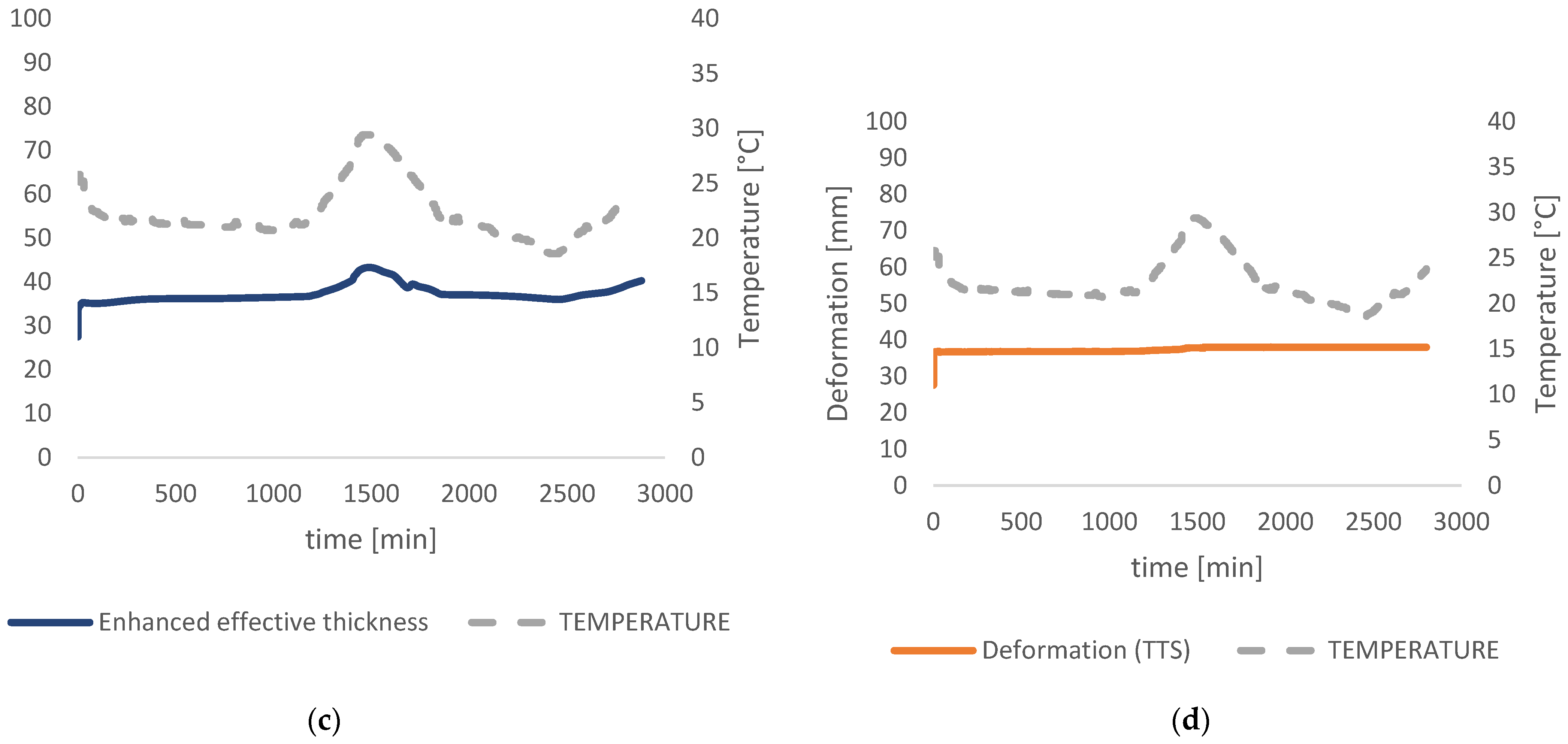
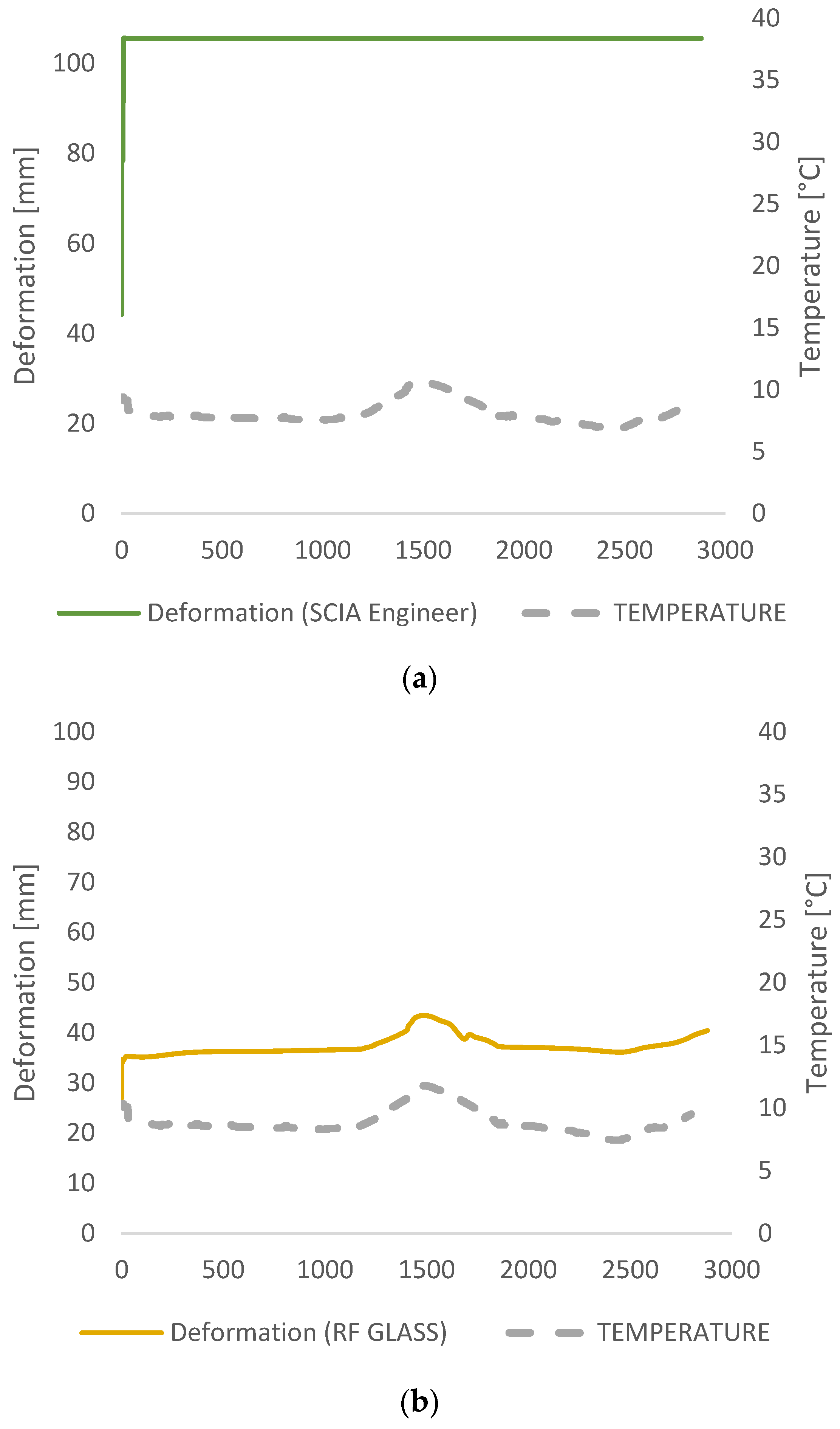
3. Results
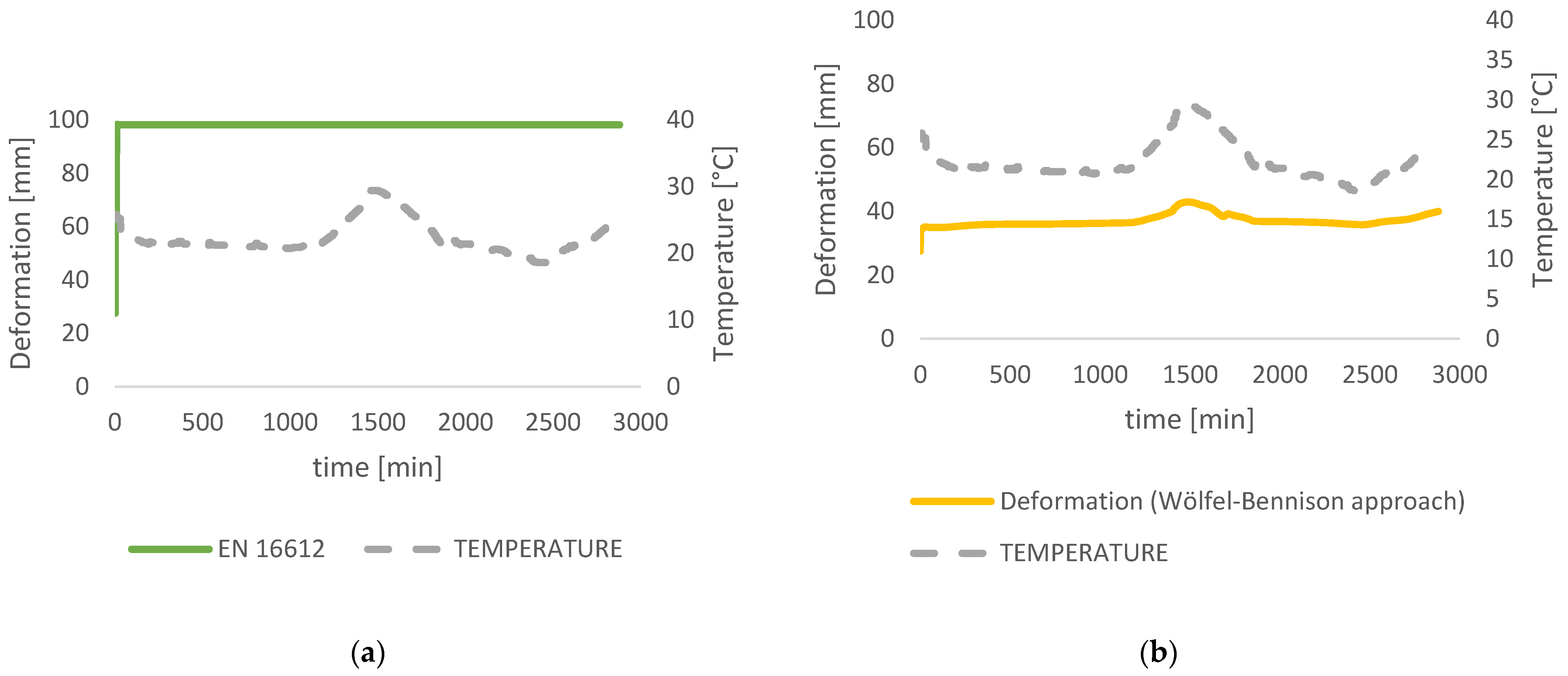
3.1. Analytical Calculations
3.2. Numerical Analysis
4. Conclusions
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pantelides, C.P.; Horst, A.D.; Minor, J.E. Post-breakage behavior of architectural glazing in Windstorms. J. Wind. Eng. Ind. Aerodyn. 1992, 44, 2425–2435. [Google Scholar] [CrossRef]
- Galuppi, L.; Royer-Carfagni, G. The effective thickness of laminated glass plates. J. Mech. Mater. Struct. 2012, 7, 375–400. [Google Scholar] [CrossRef]
- Aenlle, M.L.; Pelayo, F.; Ismael, G. Calculation of displacements and stresses in laminated glass beams under dynamic loadings using an effective Young modulus. Procedia Eng. 2017, 199, 1405–1410. [Google Scholar] [CrossRef]
- Wurm, J. Glass Structures: Design and Construction of self-Supporting Skins; Birkhäuser Verlag AG: Basel, Switzerland, 2007; ISBN 9783764376079. [Google Scholar]
- Trosifol Elastic Properties. Available online: https://www.trosifol.com/fileadmin/user_upload/TROSIFOL/support/downloads/technical_information/kuraray-Elastic-Properties.pdf (accessed on 16 August 2022).
- Biolzi, L.; Cagnacci, E.; Orlando, M.; Piscitelli, L.; Rosati, G. Long term response of glass-PVB double-lap joints. Compos. Part B Eng. 2014, 63, 41–49. [Google Scholar] [CrossRef]
- Behr, B.R.A.; Minor, J.E.; Asce, F.; Linden, M.P. Laminated glass units under uniform lateral pressure. J. Struct. Eng. 1985, I, 1037–1050. [Google Scholar] [CrossRef]
- Behr, R.A.; Minor, J.E.; Norville, H.S. Structural behavior of architectural laminated glass. J. Struct. Eng. 1993, 119, 202–222. [Google Scholar] [CrossRef]
- Jalham, I.S.; Alsaed, O. The Effect of Glass Plate Thickness and Type and Thickness of the Bonding Interlayer on the Mechanical Behavior of Laminated Glass. New J. Glass Ceram. 2011, 1, 40–48. [Google Scholar] [CrossRef]
- Seo, D.K.; You, J.B.; Im, S.G.; Kim, J.; Kim, K.K.; Jung, Y.K.; Li, M.; Park, C.P.; Kim, D.P. Laminated film composites of multilayered plastic film and inorganic polymer binder as an alternative to transparent and hard glass. Polym. J. 2013, 45, 685–689. [Google Scholar] [CrossRef]
- Foraboschi, P. Optimal design of glass plates loaded transversally. Mater. Des. 2014, 62, 443–458. [Google Scholar] [CrossRef]
- HRN EN 16612:2019; Glass in Building-Determination of the Lateral Load Resistance of Glass Panes by Calculation. Croatian Institute for Standards: Zagreb, Croatia, 2019.
- Galuppi, L.; Manara, G.; Royer Carfagni, G. Practical expressions for the design of laminated glass. Compos. Part B Eng. 2013, 45, 1677–1688. [Google Scholar] [CrossRef]
- Pelayo, F.; Lamela-Rey, M.J.; Muniz-Calvente, M.; López-Aenlle, M.; Álvarez-Vázquez, A.; Fernández-Canteli, A. Study of the time-temperature-dependent behaviour of PVB: Application to laminated glass elements. Thin-Walled Struct. 2017, 119, 324–331. [Google Scholar] [CrossRef]
- RF-GLASS; Design of Single Layer, Laminated, and Insulating Glass. Dlubal Software GmbH: Tiefenbach, Germany, 2013.
- SCIA Engineering 18.0 New Features. Available online: https://www.scia.net/en/system/files/documents/se18_whats_new_-_en.pdf (accessed on 15 August 2022).
- Feldmann, M.; Kasper, R. Guidance for European Structural Design of Glass Components; Publications Office of the European Union: Luxembourg, 2014; ISBN 9789279350948. [Google Scholar]
- prEN 13474; Glass in Building-Determination of the Strength of Glass Panes. CEN European Committee for Standardization: Brussels, Belgium, 2009.
- DIN 18008-5; Glass in Building-Design and Construction Rules. European Standards: Pilsen, Czech Republic, 2013.
- Haese, A.; Siebert, G. DIN 18008–Experience after one year of applying the new German glass design standard. In Proceedings of the Challenging Glass Conference Proceedings-Challenging Glass 5: Conference on Architectural and Structural Applications of Glass, CGC 2016, Ghent, Belgium, 16–17 June 2016. [Google Scholar]
- Abaqus Example Problems. 5.1.7.Coupled Thermomechanical Analysis of Viscoelastic Dampers, Abaqus/Standard. Available online: http://130.149.89.49:2080/v2016/books/exa/default.htm?startat=ch05s01aex123.html (accessed on 29 August 2022).
- Tomizawa, T.; Okumura, K. Visco- and plastoelastic fracture of nanoporous polymer sheets. Polym. J. 2019, 51, 845–850. [Google Scholar] [CrossRef]
- Centelles, X.; Pelayo, F.; Lamela-Rey, M.J.; Fernández, A.I.; Salgado-Pizarro, R.; Castro, J.R.; Cabeza, L.F. Viscoelastic characterization of seven laminated glass interlayer materials from static tests. Constr. Build. Mater. 2021, 279, 122503. [Google Scholar] [CrossRef]
- Barrientos, E.; Pelayo, F.; Noriega, Á.; Lamela, M.J.; Fernández-Canteli, A.; Tanaka, E. Optimal discrete-time Prony series fitting method for viscoelastic materials. Mech. Time-Depend. Mater. 2019, 23, 193–206. [Google Scholar] [CrossRef]
- Li, R. Time-temperature superposition method for glass transition temperature of plastic materials. Mater. Sci. Eng. A 2000, 278, 36–45. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons: Hoboken, NJ, USA, 1980. [Google Scholar]
- ASTM D3418-99; Standard Test Method for Transition Temperatures of Polymers by Differential Scanning Calorimetry. ASTM International: West Conshohocken, PA, USA, 1999.
- Hána, T.; Janda, T.; Schmidt, J.; Zemanová, A.; Šejnoha, M.; Eliášová, M.; Vokáč, M. Experimental and numerical study of viscoelastic properties of polymeric interlayers used for laminated glass: Determination of material parameters. Materials 2019, 12, 2241. [Google Scholar] [CrossRef] [PubMed]
- Brinson, H.F.; Brinson, L.C. Polymer Engineering Science and Viscoelasticity: An Introduction, 2nd ed.; Springer: New York, NY, USA, 2015; ISBN 9781489974853. [Google Scholar]
- Trosifol Classification According to EN16612:2019 and EN16613:2019-Simplified Method. Available online: https://www.trosifol.com/fileadmin/user_upload/TROSIFOL/support/downloads/technical_information/trosifol-interlayers-classification-according-to-en-16612-2019-and-en-16613-2019-simplified-method-technical-data.pdf (accessed on 3 August 2022).
- HRN EN 16613:2019; Glass in Building. Laminated Glass and Laminated Safety Glass. Determination of Interlayer Viscoelastic Properties. Croatian Institute for Standards: Zagreb, Croatia, 2019.
- Stevels, W.; D’Haene, P. Determination and Verification of PVB Interlayer Modulus Properties. In Proceedings of the Conference on Architectural and Structural Applications of Glass, Ghent, Belgium, 4 September 2020. [Google Scholar]
- Galuppi, L.; Royer-Carfagni, G. Enhanced Effective Thickness of multi-layered laminated glass. Compos. Part B Eng. 2014, 64, 202–213. [Google Scholar] [CrossRef]
- Galuppi, L.; Royer-Carfagni, G. Enhanced Effective Thickness (EET) of curved laminated glass. Ann. Solid Struct. Mech. 2015, 7, 71–92. [Google Scholar] [CrossRef]
- Galuppi, L.; Nizich, A. Enhanced Effective Thickness Method for Cantilevered Laminated Glass Balustrades; GPD Glass Performance Days: Tampere, Finland, 2019. [Google Scholar]
- WA-T: Inductive Displacement Transducer (Probe). Available online: https://www.hbm.com/en/3059/wa-t-inductive-displacement-transducer-probe/?product_type_no=WA-T:%20Inductive%20Displacement%20Transducer%20(Probe) (accessed on 22 August 2022).
- Hána, T.; Vokáč, M.; Eliášová, M.; Machalická, K.V. Advanced computational methods of perpendicularly loaded laminated glass panes. In Proceedings of the 13th International Conference ‘Modern Building Materials, Structures and Techniques’ (MBMST 2019), Vilnius, Lithuania, 16–17 May 2019. [Google Scholar] [CrossRef]
- Hána, T.; Machalická, K.V.; Vokáč, M.; Eliášová, M. Current analytical computational methods of laminated glass panels in comparison to FEM simulation. In Structures and Architecture-Bridging the Gap and Crossing Borders; CRC Press: London, UK, 2019. [Google Scholar]
- Gwóźdź, M.; Woźniczka, P. New static analysis methods for plates made of monolithic and laminated glass. Arch. Civ. Eng. 2020, 66, 593–609. [Google Scholar] [CrossRef]
- Shitanoki, Y.; Bennison, S.J.; Koike, Y. A practical, nondestructive method to determine the shear relaxation modulus behavior of polymeric interlayers for laminated glass. Polym. Test. 2014, 37, 59–67. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galić, J.; Stepinac, L.; Bošnjak, A.; Zovko, I. Influence of PVB Interlayer Mechanical Properties on Laminated Glass Elements Design in Dependence of Real Time-Temperature Changes. Polymers 2022, 14, 4402. https://doi.org/10.3390/polym14204402
Galić J, Stepinac L, Bošnjak A, Zovko I. Influence of PVB Interlayer Mechanical Properties on Laminated Glass Elements Design in Dependence of Real Time-Temperature Changes. Polymers. 2022; 14(20):4402. https://doi.org/10.3390/polym14204402
Chicago/Turabian StyleGalić, Josip, Lucija Stepinac, Antonia Bošnjak, and Ivana Zovko. 2022. "Influence of PVB Interlayer Mechanical Properties on Laminated Glass Elements Design in Dependence of Real Time-Temperature Changes" Polymers 14, no. 20: 4402. https://doi.org/10.3390/polym14204402
APA StyleGalić, J., Stepinac, L., Bošnjak, A., & Zovko, I. (2022). Influence of PVB Interlayer Mechanical Properties on Laminated Glass Elements Design in Dependence of Real Time-Temperature Changes. Polymers, 14(20), 4402. https://doi.org/10.3390/polym14204402





