Polymorphism and Perfection in Crystallization of Hard Sphere Polymers
Abstract
:1. Introduction
2. Methodology
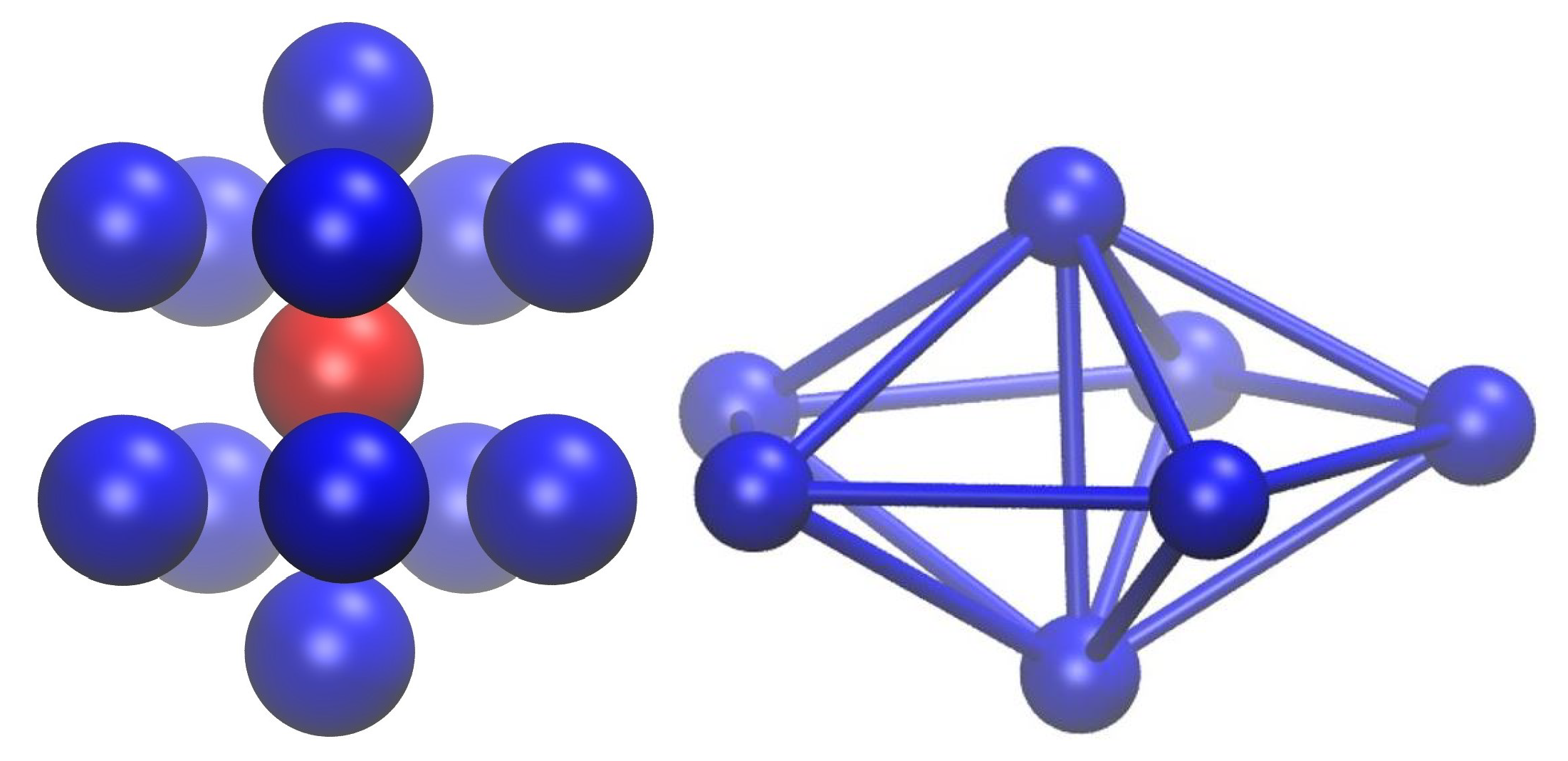
- Monomers with first neighbors whose arrangement conforms to the point symmetry group of the face centered cubic crystal (FCC sites),
- Monomers with first neighbors whose positions conform to the point group of the hexagonal close packed crystal (HCP sites),
- Monomers whose first neighbors conform to the point group 5 of a non-crystallographic fivefold axis (FIV sites),
- Monomers with first neighbors that are not arranged according to any kind of symmetry (apart from the identity E), either crystallographic or non-crystallographic (amorphous, denoted AMO).
3. Results
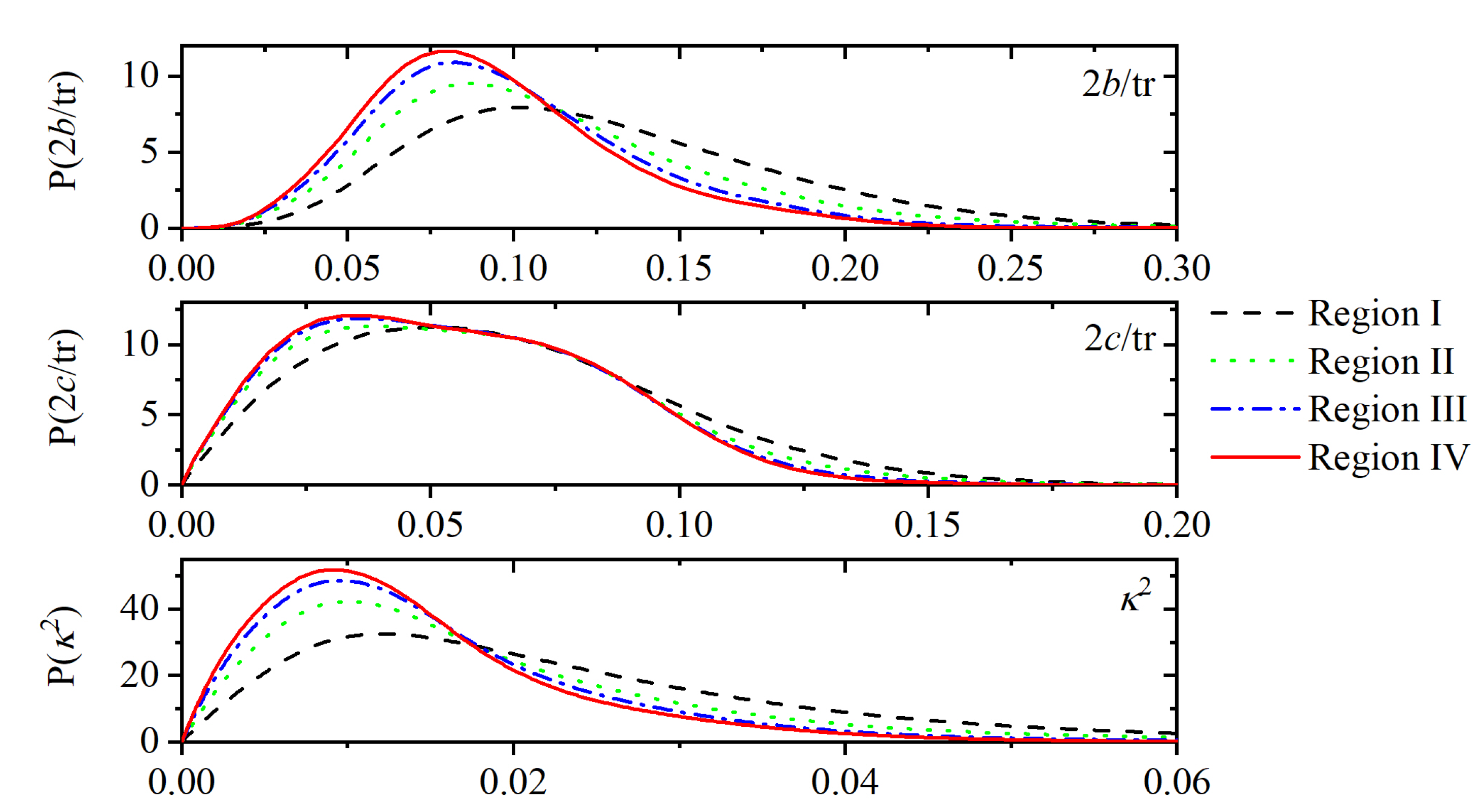
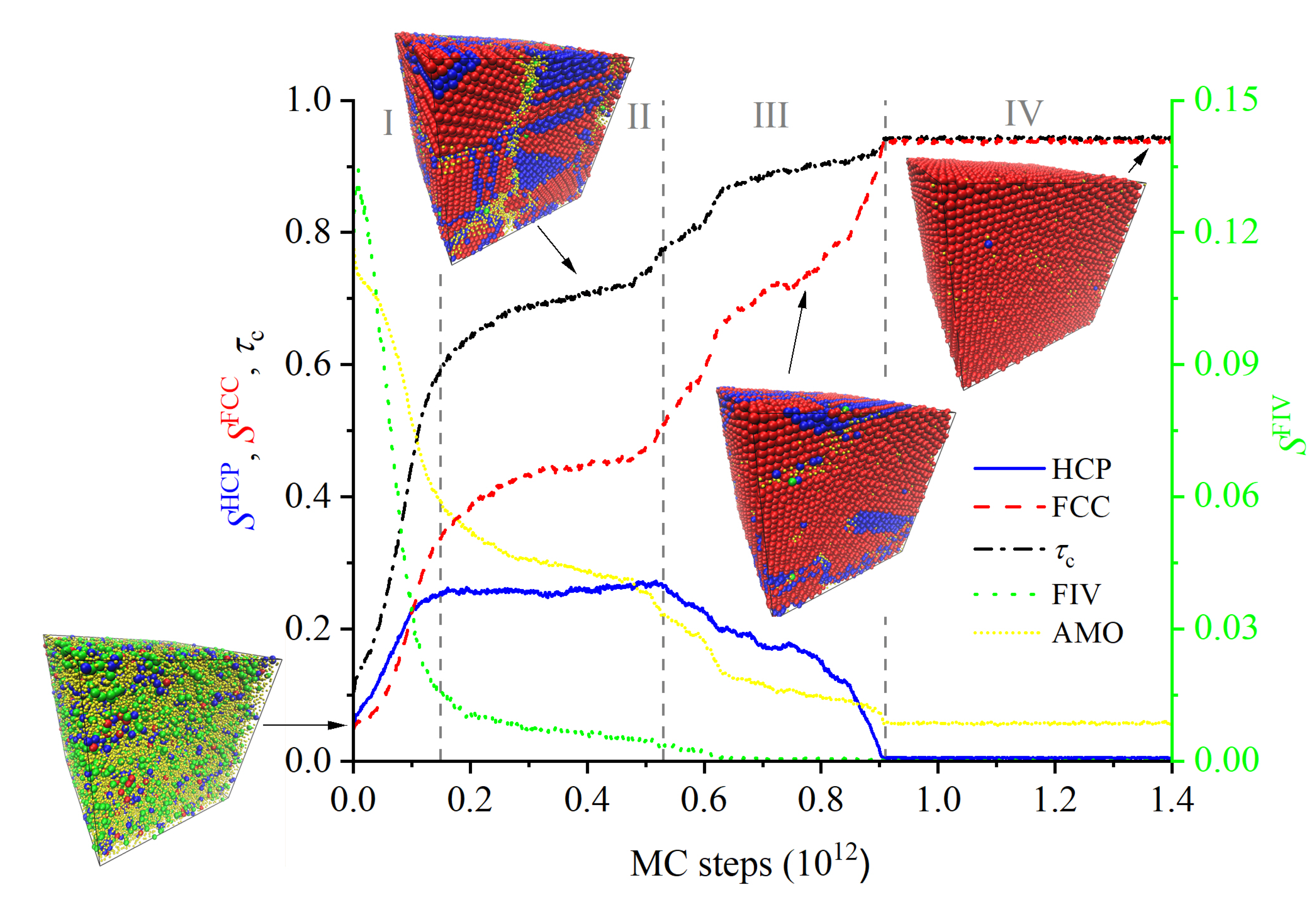
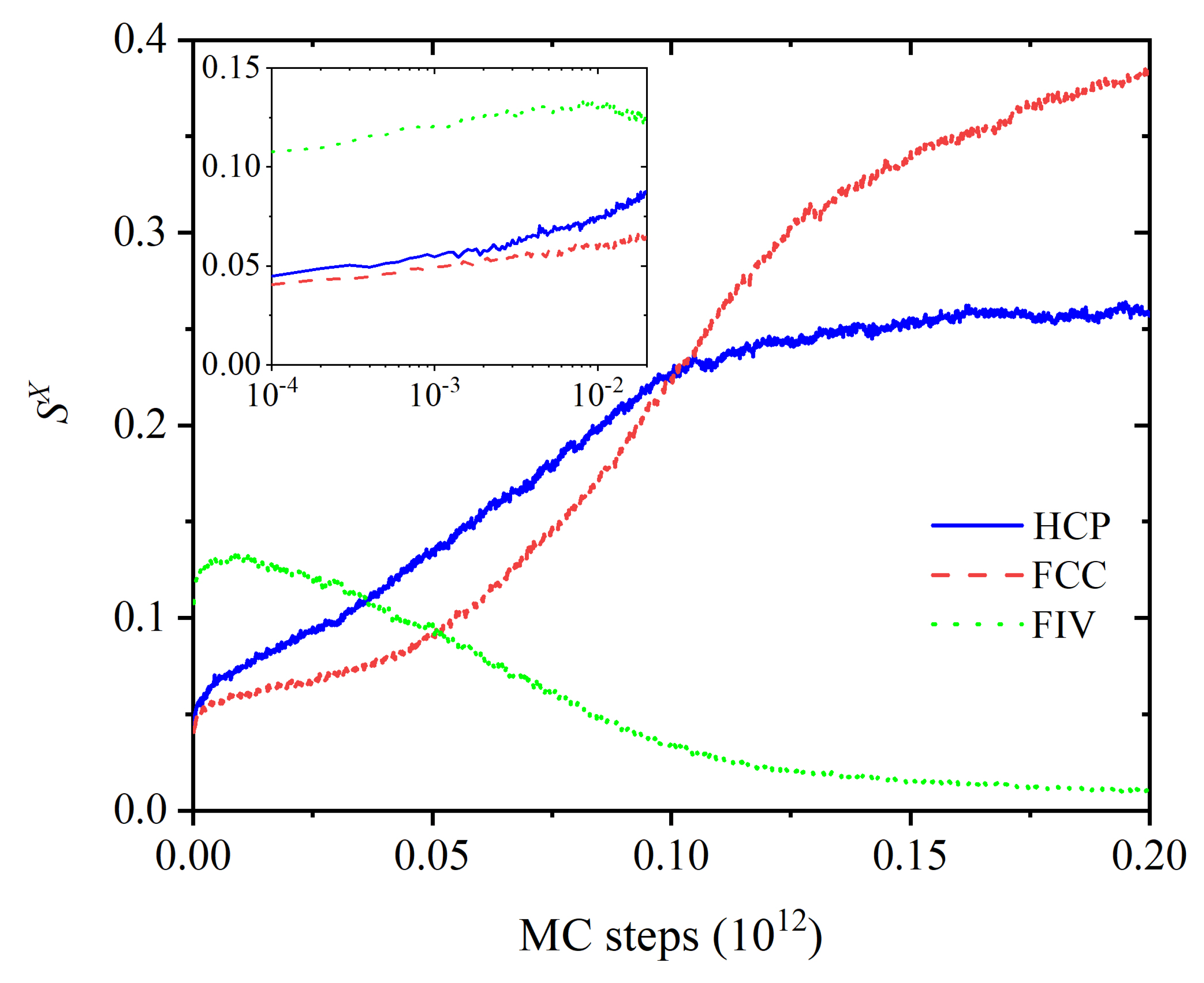
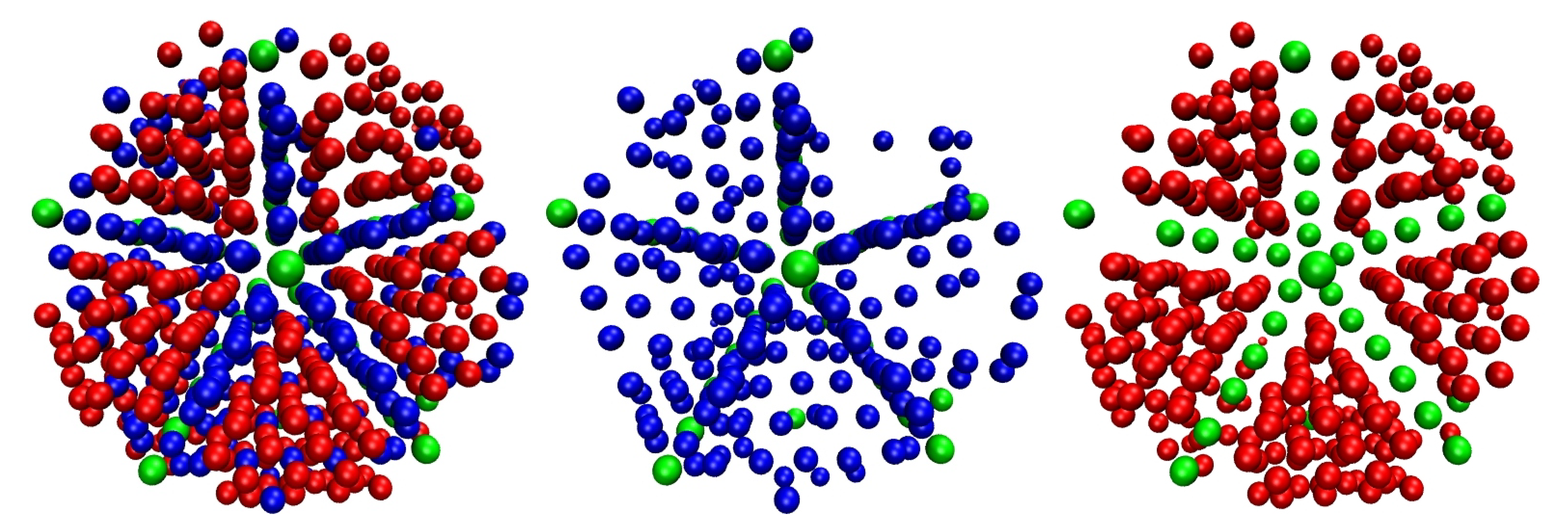
3.1. Evolution of Crystallinity
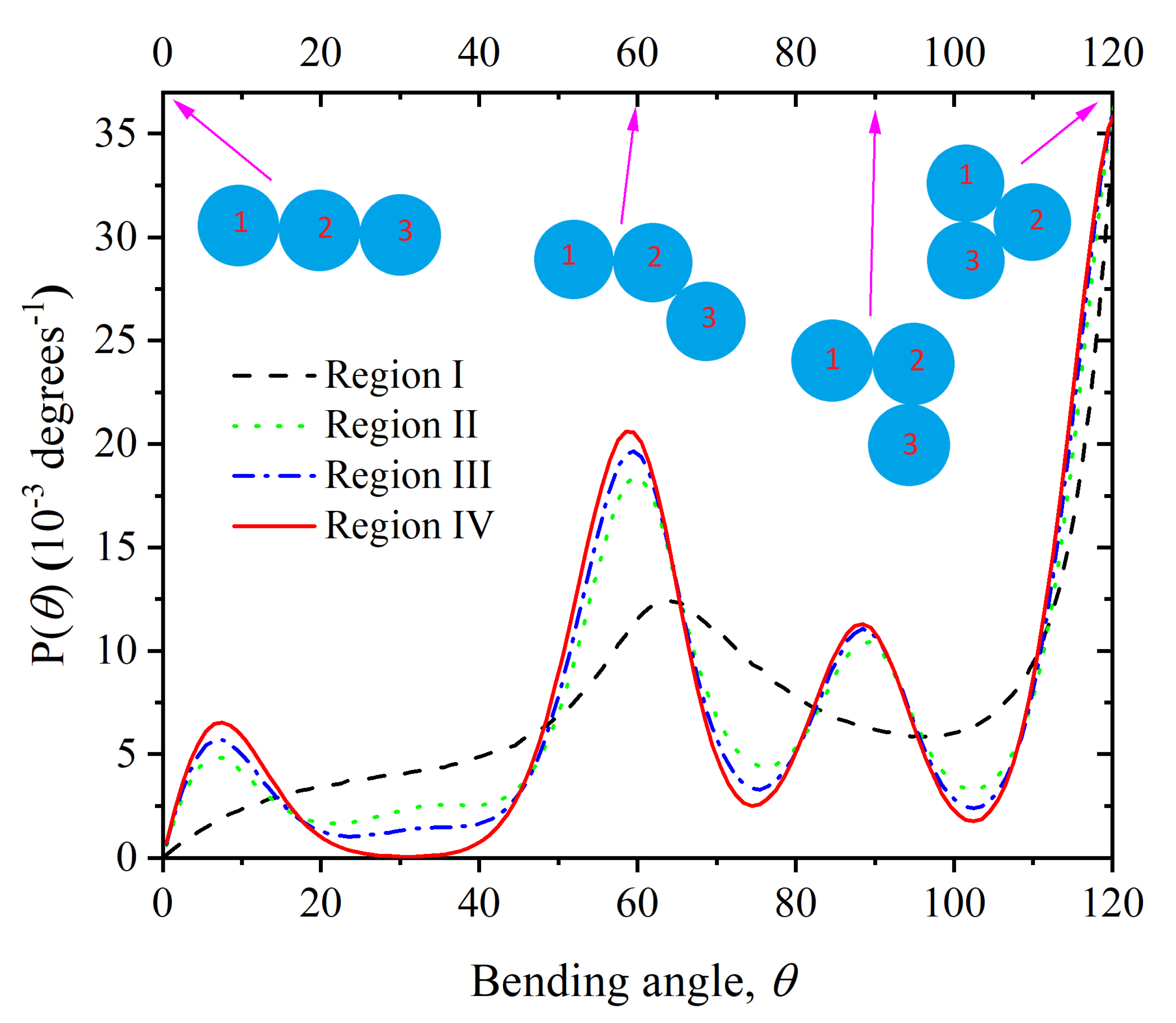
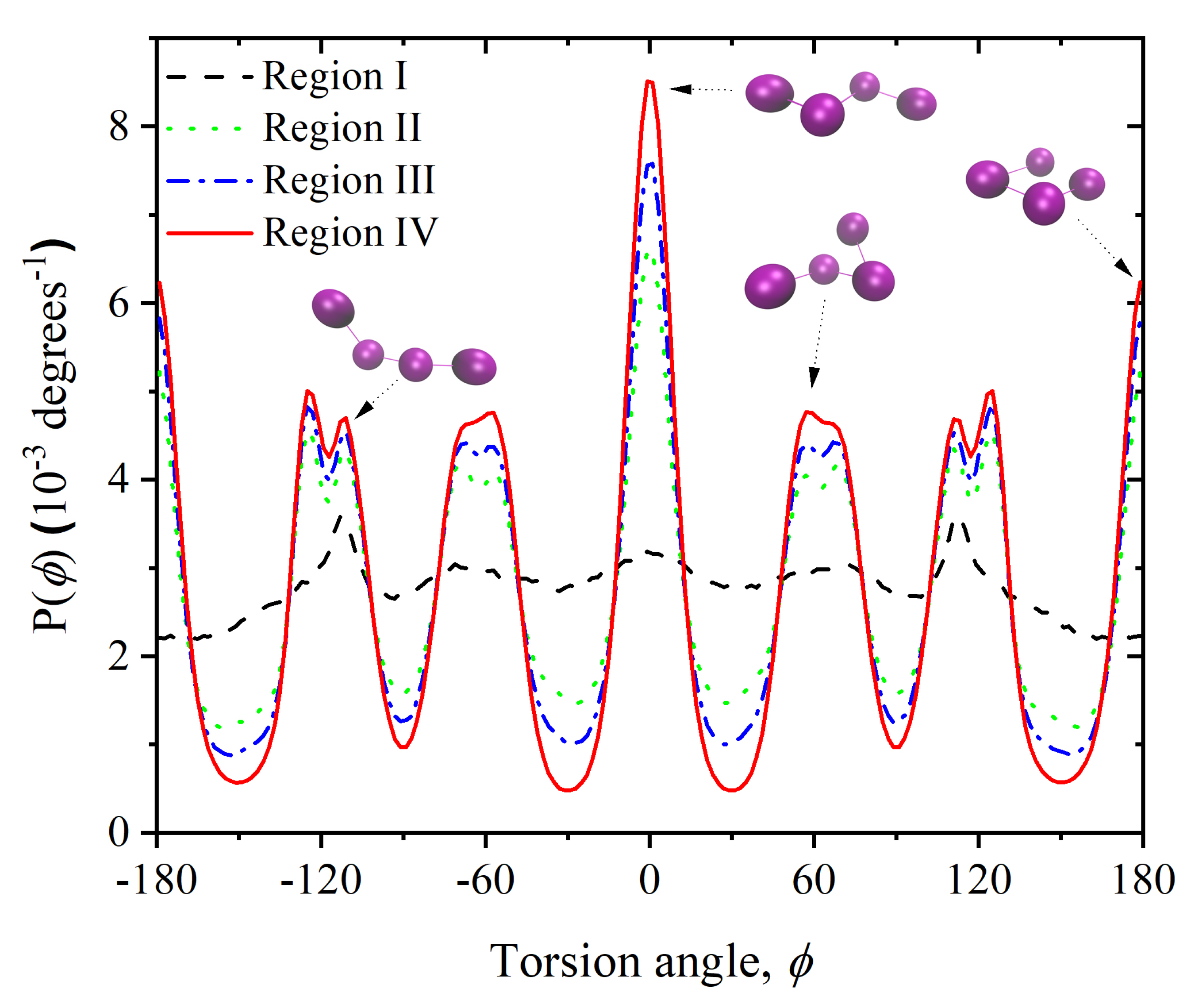
3.2. Chain Statistics and Conformations
3.3. Entropic Origins of Crystallization
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMO | Amorphous |
| BCC | Body-Centered Cubic |
| CCAMs | Chain-Connectivity-Altering Moves |
| CCE | Characteristic Crystallographic Element (norm) |
| FCC | Face Centered Cubic |
| FIV | Fivefold |
| HCP | Hexagonal Close Packed |
| HS | Hard Sphere |
| KMC | Kinetic Monte Carlo |
| MC | Monte Carlo |
| MD | Molecular Dynamics |
| PBC | Periodic Boundary Condition |
| rHCP | Random Hexagonal Close Packed |
| VC | Voronoi Cell |
| List of variables | |
| b | asphericity |
| bond length | |
| Kuhn length | |
| c | acylindricity |
| mumerical tolerance in bond length | |
| second-order gyration tensor | |
| I | position index |
| k | Boltzmann constant |
| chain length, average, minimum-, maximum chain length | |
| number of trials in configurational bias schemes | |
| number of fivefold sites | |
| N | number of polymer chains |
| number of frames | |
| total number of monomeric sites | |
| number of vertices of the Voronoi polyhedron | |
| distance between monomers i and j | |
| position vector of a monomer. | |
| displacement from Voronoi Cell centroid vector | |
| radius of gyration | |
| end-to-end distance | |
| s | entropy |
| order parameter for crystal type X | |
| T | temperature |
| hard sphere interaction energy | |
| U | internal energy |
| volume, accessible volume, monomer volume, Voronoi cell volume | |
| accessible volume | |
| Greek symbols | |
| conformational entropy difference per monomer | |
| translational entropy difference per monomer | |
| CCE-norm with respect to crystal type X | |
| torsion angle | |
| relative shape anisotropy | |
| eigenvalues of | |
| volume fraction | |
| volume fraction relative to maximum HS packing density | |
| monomer diameter | |
| chemical potential | |
| Flory exponent | |
| total crystallinity | |
| bending angle |
Appendix A
Appendix A.1. Definition of Bending and Torsion Angles
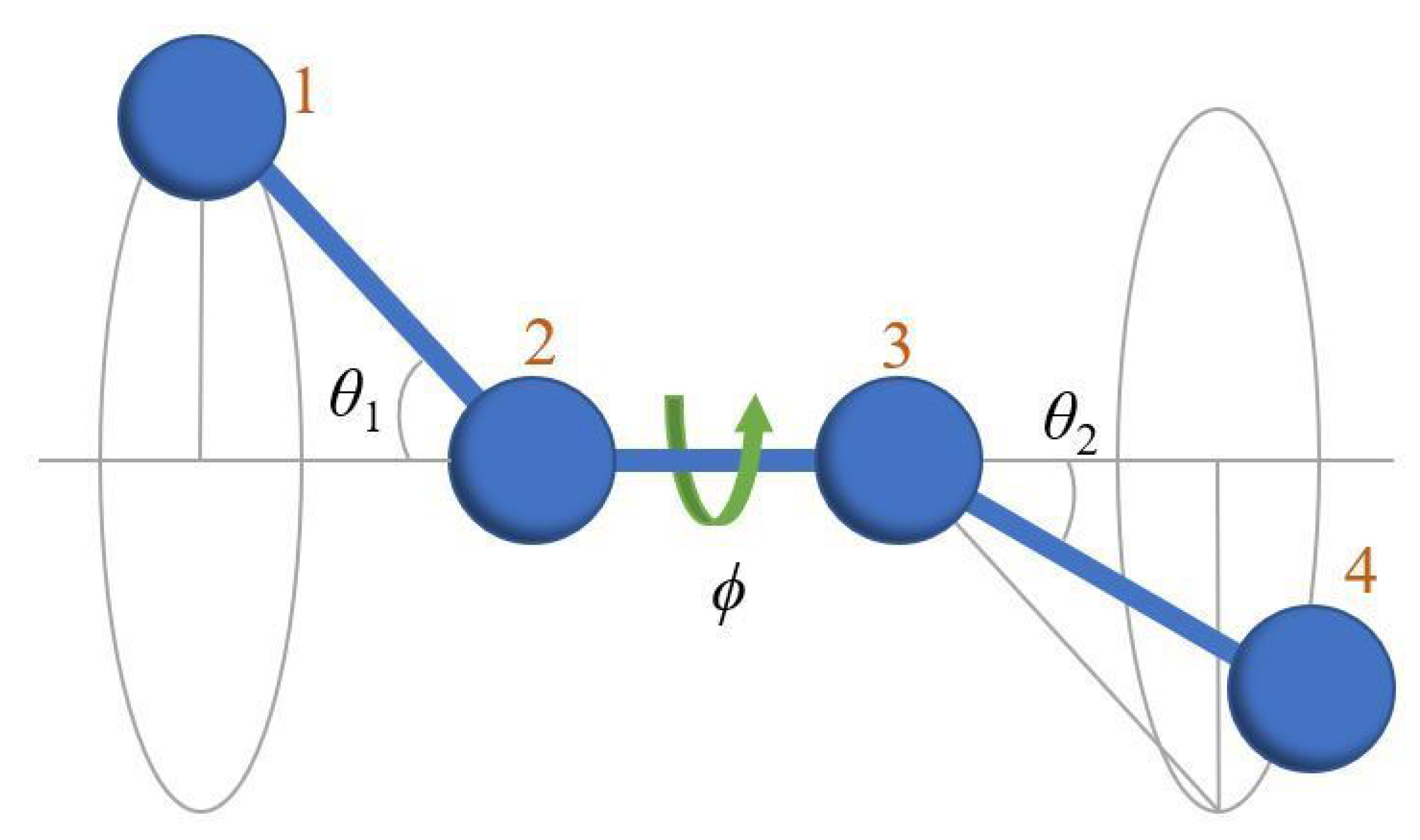
Appendix A.2. Kuhn Length and Ideal Chain Statistics

Appendix A.3. Shape Measures of the Voronoi Polyhedra

References
- Gao, Z.G.; Rohani, S.; Gong, J.B.; Wang, J.K. Recent Developments in the Crystallization Process: Toward the Pharmaceutical Industry. Engineering 2017, 3, 343–353. [Google Scholar] [CrossRef]
- Murray, L.J.; Dinca, M.; Long, J.R. Hydrogen storage in metal-organic frameworks. Chem. Soc. Rev. 2009, 38, 1294–1314. [Google Scholar] [CrossRef] [PubMed]
- Janiak, C. Engineering coordination polymers towards applications. Dalton Trans. 2003, 14, 2781–2804. [Google Scholar] [CrossRef]
- Wang, T.; Lu, H.J.; Wang, J.K.; Xiao, Y.; Zhou, Y.A.; Bao, Y.; Hao, H.X. Recent progress of continuous crystallization. J. Ind. Eng. Chem. 2017, 54, 14–29. [Google Scholar] [CrossRef]
- Li, G.; Zhu, R.; Yang, Y. Polymer solar cells. Nat. Photonics 2012, 6, 153–161. [Google Scholar] [CrossRef]
- Koch, F.P.V.; Rivnay, J.; Foster, S.; Muller, C.; Downing, J.M.; Buchaca-Domingo, E.; Westacott, P.; Yu, L.Y.; Yuan, M.J.; Baklar, M.; et al. The impact of molecular weight on microstructure and charge transport in semicrystalline polymer Semiconductors poly(3-hexylthiophene), a model study. Prog. Polym. Sci. 2013, 38, 1978–1989. [Google Scholar] [CrossRef]
- Meyers, M.A.; Chen, P.Y.; Lin, A.Y.M.; Seki, Y. Biological materials: Structure and mechanical properties. Prog. Mater. Sci. 2008, 53, 1–206. [Google Scholar] [CrossRef] [Green Version]
- Mileva, D.; Tranchida, D.; Gahleitner, M. Designing polymer crystallinity: An industrial perspective. Polym. Cryst. 2018, 1. [Google Scholar] [CrossRef]
- Reiter, G.; Sommer, J. Polymer Crystallization: Obervations, Concepts and Interpretations; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Russo, J.; Tanaka, H. The microscopic pathway to crystallization in supercooled liquids. Sci. Rep. 2012, 2, 505. [Google Scholar] [CrossRef] [Green Version]
- Erdemir, D.; Lee, A.Y.; Myerson, A.S. Nucleation of Crystals from Solution: Classical and Two-Step Models. Accounts Chem. Res. 2009, 42, 621–629. [Google Scholar] [CrossRef]
- Manoharan, V.N. Colloidal matter: Packing, geometry, and entropy. Science 2015, 349, 1253751. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palberg, T. Crystallization kinetics of colloidal model suspensions: Recent achievements and new perspectives. J. Phys. Condens. Matter 2014, 26, 333101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pusey, P.N.; Vanmegen, W.; Bartlett, P.; Ackerson, B.J.; Rarity, J.G.; Underwood, S.M. Structure of crystals of hard colloidal spheres. Phys. Rev. Lett. 1989, 63, 2753–2756. [Google Scholar] [CrossRef] [PubMed]
- Gasser, U.; Weeks, E.R.; Schofield, A.; Pusey, P.N.; Weitz, D.A. Real-space imaging of nucleation and growth in colloidal crystallization. Science 2001, 292, 258–262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, J.X.; Li, M.; Rogers, R.; Meyer, W.; Ottewill, R.H.; Russell, W.B.; Chaikin, P.M. Crystallization of hard-sphere colloids in microgravity. Nature 1997, 387, 883–885. [Google Scholar] [CrossRef]
- Verhaegh, N.A.M.; Vanduijneveldt, J.S.; Vanblaaderen, A.; Lekkerkerker, H.N.W. Direct observation of stacking disorder in a colloidal crystal. J. Chem. Phys. 1995, 102, 1416–1421. [Google Scholar] [CrossRef] [Green Version]
- Petukhov, A.V.; Dolbnya, I.P.; Aarts, D.; Vroege, G.J.; Lekkerkerker, H.N.W. Bragg rods and multiple x-ray scattering in random-stacking colloidal crystals. Phys. Rev. Lett. 2003, 90, 028304. [Google Scholar] [CrossRef] [Green Version]
- Vanmegen, W.; Underwood, S.M. Change in crystallization mechanism at the glass-transition of colloidal spheres. Nature 1993, 362, 616–618. [Google Scholar] [CrossRef]
- Pusey, P.N.; Vanmegen, W. Phase-behavior of concentrated suspensions of nearly hard colloidal spheres. Nature 1986, 320, 340–342. [Google Scholar] [CrossRef]
- Russel, W.B.; Chaikin, P.M.; Zhu, J.; Meyer, W.V.; Rogers, R. Dendritic growth of hard sphere crystals. Langmuir 1997, 13, 3871–3881. [Google Scholar] [CrossRef]
- Cheng, Z.D.; Zhu, J.X.; Russel, W.B.; Meyer, W.V.; Chaikin, P.M. Colloidal hard-sphere crystallization kinetics in microgravity and normal gravity. Appl. Opt. 2001, 40, 4146–4151. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.D.; Chaikin, P.M.; Zhu, J.X.; Russel, W.B.; Meyer, W.V. Crystallization kinetics of hard spheres in microgravity in the coexistence regime: Interactions between growing crystallites. Phys. Rev. Lett. 2002, 88, 015501. [Google Scholar] [CrossRef] [Green Version]
- Martelozzo, V.C.; Schofield, A.B.; Poon, W.C.K.; Pusey, P.N. Structural aging of crystals of hard-sphere colloids. Phys. Rev. E 2002, 66, 021408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kegel, W.K.; Dhont, J.K.G. “Aging” of the structure of crystals of hard colloidal spheres. J. Chem. Phys. 2000, 112, 3431–3436. [Google Scholar] [CrossRef]
- Dolbnya, I.P.; Petukhov, A.V.; Aarts, D.; Vroege, G.J.; Lekkerkerker, H.N.W. Coexistence of rHCP and FCC phases in hard-sphere colloidal crystals. Europhys. Lett. 2005, 72, 962–968. [Google Scholar] [CrossRef] [Green Version]
- Rintoul, M.D.; Torquato, S. Metastability and crystallization in hard-sphere systems. Phys. Rev. Lett. 1996, 77, 4198–4201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Medvedev, N.N.; Bezrukov, A.; Shtoyan, D. From amorphous solid to defective crystal. A study of structural peculiarities in close packings of hard spheres. J. Struct. Chem. 2004, 45, S23–S30. [Google Scholar] [CrossRef]
- van Meel, J.A.; Frenkel, D.; Charbonneau, P. Geometrical frustration: A study of four-dimensional hard spheres. Phys. Rev. E 2009, 79, 030201. [Google Scholar] [CrossRef] [Green Version]
- O’Malley, B.; Snook, I. Crystal nucleation in the hard sphere system. Phys. Rev. Lett. 2003, 90, 085702. [Google Scholar] [CrossRef]
- Punnathanam, S.; Monson, P.A. Crystal nucleation in binary hard sphere mixtures: A Monte Carlo simulation study. J. Chem. Phys. 2006, 125, 024508. [Google Scholar] [CrossRef]
- Russo, J.; Tanaka, H. Crystal nucleation as the ordering of multiple order parameters. J. Chem. Phys. 2016, 145, 211801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lam, M.A.; Khusid, B.; Kondic, L.; Meyer, W.V. Role of diffusion in crystallization of hard-sphere colloids. Phys. Rev. E 2021, 104, 054607. [Google Scholar] [CrossRef] [PubMed]
- Pronk, S.; Frenkel, D. Can stacking faults in hard-sphere crystals anneal out spontaneously? J. Chem. Phys. 1999, 110, 4589–4592. [Google Scholar] [CrossRef]
- Auer, S.; Frenkel, D. Numerical prediction of absolute crystallization rates in hard-sphere colloids. J. Chem. Phys. 2004, 120, 3015–3029. [Google Scholar] [CrossRef]
- Sanchez-Burgos, I.; Sanz, E.; Vega, C.; Espinosa, J.R. FCC vs. HCP competition in colloidal hard-sphere nucleation: On their relative stability, interfacial free energy and nucleation rate. Phys. Chem. Chem. Phys. 2021, 23, 19611–19626. [Google Scholar] [CrossRef]
- Leoni, F.; Russo, J. Nonclassical Nucleation Pathways in Stacking-Disordered Crystals. Phys. Rev. X 2021, 11, 031006. [Google Scholar] [CrossRef]
- Bolhuis, P.G.; Frenkel, D.; Mau, S.C.; Huse, D.A. Entropy difference between crystal phases. Nature 1997, 388, 235–236. [Google Scholar] [CrossRef] [Green Version]
- Bruce, A.D.; Wilding, N.B.; Ackland, G.J. Free energy of crystalline solids: A lattice-switch Monte Carlo method. Phys. Rev. Lett. 1997, 79, 3002–3005. [Google Scholar] [CrossRef] [Green Version]
- Mau, S.C.; Huse, D.A. Stacking entropy of hard-sphere crystals. Phys. Rev. E 1999, 59, 4396–4401. [Google Scholar] [CrossRef] [Green Version]
- Woodcock, L.V. Entropy difference between the face-centred cubic and hexagonal close-packed crystal structures. Nature 1997, 385, 141–143. [Google Scholar] [CrossRef]
- de Miguel, E.; Marguta, R.G.; del Rio, E.M. System-size dependence of the free energy of crystalline solids. J. Chem. Phys. 2007, 127, 54512. [Google Scholar] [CrossRef] [PubMed]
- Koch, H.; Radin, C.; Sadun, L. Most stable structure for hard spheres. Phys. Rev. E 2005, 72, 016708. [Google Scholar] [CrossRef] [Green Version]
- Auer, S.; Frenkel, D. Prediction of absolute crystal-nucleation rate in hard-sphere colloids. Nature 2001, 409, 1020–1023. [Google Scholar] [CrossRef] [Green Version]
- Radin, C.; Sadun, L. Structure of the hard sphere solid. Phys. Rev. Lett. 2005, 94, 015502. [Google Scholar] [CrossRef] [Green Version]
- Noya, E.G.; Almarza, N.G. Entropy of hard spheres in the close-packing limit. Mol. Phys. 2015, 113, 1061–1068. [Google Scholar] [CrossRef] [Green Version]
- Zaccarelli, E.; Valeriani, C.; Sanz, E.; Poon, W.C.K.; Cates, M.E.; Pusey, P.N. Crystallization of Hard-Sphere Glasses. Phys. Rev. Lett. 2009, 103, 135704. [Google Scholar] [CrossRef] [Green Version]
- Valeriani, C.; Sanz, E.; Pusey, P.N.; Poon, W.C.K.; Cates, M.E.; Zaccarelli, E. From compact to fractal crystalline clusters in concentrated systems of monodisperse hard spheres. Soft Matter 2012, 8, 4960–4970. [Google Scholar] [CrossRef] [Green Version]
- Karayiannis, N.C.; Malshe, R.; de Pablo, J.J.; Laso, M. Fivefold symmetry as an inhibitor to hard-sphere crystallization. Phys. Rev. E 2011, 83, 061505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karayiannis, N.C.; Malshe, R.; Kroger, M.; de Pablo, J.J.; Laso, M. Evolution of fivefold local symmetry during crystal nucleation and growth in dense hard-sphere packings. Soft Matter 2012, 8, 844–858. [Google Scholar] [CrossRef]
- Luchnikov, V.; Gervois, A.; Richard, P.; Oger, L.; Troadec, J.P. Crystallization of dense hard sphere packings—Competition of HCP and FCC close order. J. Mol. Liq. 2002, 96–97, 185–194. [Google Scholar] [CrossRef]
- Richard, P.; Gervois, A.; Oger, L.; Troadec, J.P. Order and disorder in hard-sphere packings. Europhys. Lett. 1999, 48, 415–420. [Google Scholar] [CrossRef]
- Chen, H.Y.; Ma, H.R. The density profile of hard sphere liquid system under gravity. J. Chem. Phys. 2006, 125, 024510. [Google Scholar] [CrossRef] [PubMed]
- Marechal, M.; Hermes, M.; Dijkstra, M. Stacking in sediments of colloidal hard spheres. J. Chem. Phys. 2011, 135, 034510. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dasgupta, T.; Edison, J.R.; Dijkstra, M. Growth of defect-free colloidal hard-sphere crystals using colloidal epitaxy. J. Chem. Phys. 2017, 146, 074903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoogenboom, J.P.; van Langen-Suurling, A.K.; Romijn, J.; van Blaaderen, A. Epitaxial growth of a colloidal hard-sphere hcp crystal and the effects of epitaxial mismatch on crystal structure. Phys. Rev. E 2004, 69, 051602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- vanBlaaderen, A.; Ruel, R.; Wiltzius, P. Template-directed colloidal crystallization. Nature 1997, 385, 321–324. [Google Scholar] [CrossRef]
- Senger, B.; Bafaluy, F.J.; Schaaf, P.; Schmitt, A.; Voegel, J.C. Configurations of adsorbed hard-spheres after diffusion in a gravitational-field. Proc. Natl. Acad. Sci. USA 1992, 89, 9449–9453. [Google Scholar] [CrossRef] [Green Version]
- Hernandez-Guzman, J.; Weeks, E.R. The equilibrium intrinsic crystal-liquid interface of colloids. Proc. Natl. Acad. Sci. USA 2009, 106, 15198–15202. [Google Scholar] [CrossRef] [Green Version]
- Kosinski, P.; Hoffmann, A.C. Extension of the hard-sphere particle-wall collision model to account for particle deposition. Phys. Rev. E 2009, 79, 061302. [Google Scholar] [CrossRef] [Green Version]
- McMullen, A.; Holmes-Cerfon, M.; Sciortino, F.; Grosberg, A.Y.; Brujic, J. Freely Jointed Polymers Made of Droplets. Phys. Rev. Lett. 2018, 121, 138002. [Google Scholar] [CrossRef]
- Verweij, R.W.; Moerman, P.G.; Huijnen, L.P.P.; Ligthart, N.E.G.; Chakraborty, I.; Groenewold, J.; Kegel, W.K.; van Blaaderen, A.; Kraft, D.J. Conformations and diffusion of flexibly linked colloidal chains. J. Phys.-Mater. 2021, 4, 035002. [Google Scholar] [CrossRef]
- Zou, L.N.; Cheng, X.; Rivers, M.L.; Jaeger, H.M.; Nagel, S.R. The Packing of Granular Polymer Chains. Science 2009, 326, 408–410. [Google Scholar] [CrossRef] [Green Version]
- Brown, E.; Nasto, A.; Athanassiadis, A.G.; Jaeger, H.M. Strain Stiffening in Random Packings of Entangled Granular Chains. Phys. Rev. Lett. 2012, 108, 108302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Z.G.; Yang, Z.; Chen, X.; Tan, R.; Li, G.; Gan, Z.H.; Shao, Y.; He, J.L.; Zhang, Z.B.; Li, W.H.; et al. Discrete Giant Polymeric Chains Based on Nanosized Monomers. Jacs Au 2021, 1, 79–86. [Google Scholar] [CrossRef] [PubMed]
- Sushko, N.; van der Schoot, P.; Michels, M.A.J. Density-functional theory of the crystallization of hard polymeric chains. J. Chem. Phys. 2001, 115, 7744–7752. [Google Scholar] [CrossRef] [Green Version]
- Vega, C.; McBride, C. Scaling laws for the equation of state of flexible and linear tangent hard sphere chains. Phys. Rev. E 2002, 65, 052501. [Google Scholar] [CrossRef]
- Shakirov, T. Crystallisation in Melts of Short, Semi-Flexible Hard-Sphere Polymer Chains: The Role of the Non-Bonded Interaction Range. Entropy 2019, 21, 856. [Google Scholar] [CrossRef] [Green Version]
- Shakirov, T.; Paul, W. Crystallization in melts of short, semiflexible hard polymer chains: An interplay of entropies and dimensions. Phys. Rev. E 2018, 97, 042501. [Google Scholar] [CrossRef]
- Dietz, J.D.; Hoy, R.S. Two-stage athermal solidification of semiflexible polymers and fibers. Soft Matter 2020, 16, 6206–6217. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Entropy-Driven Crystallization in Dense Systems of Athermal Chain Molecules. Phys. Rev. Lett. 2009, 103, 045703. [Google Scholar] [CrossRef]
- Ni, R.; Dijkstra, M. Effect of bond length fluctuations on crystal nucleation of hard bead chains. Soft Matter 2013, 9, 365–369. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.T.; Chen, C.Y.; Chen, H.L. FCC or HCP: The stable close-packed lattice of crystallographically equivalent spherical micelles in block copolymer/homopolymer blend. Polymer 2019, 169, 131–137. [Google Scholar] [CrossRef]
- Zhang, C.; Vigil, D.L.; Sun, D.; Bates, M.W.; Loman, T.; Murphy, E.A.; Barbon, S.M.; Song, J.A.; Yu, B.H.; Fredrickson, G.H.; et al. Emergence of Hexagonally Close-Packed Spheres in Linear Block Copolymer Melts. J. Am. Chem. Soc. 2021, 143, 14106–14114. [Google Scholar] [CrossRef] [PubMed]
- Hsu, N.W.; Nouri, B.; Chen, L.T.; Chen, H.L. Hexagonal Close-Packed Sphere Phase of Conformationally Symmetric Block Copolymer. Macromolecules 2020, 53, 9665–9675. [Google Scholar] [CrossRef]
- Mahynski, N.A.; Kumar, S.K.; Panagiotopoulos, A.Z. Relative stability of the FCC and HCP polymorphs with interacting polymers. Soft Matter 2015, 11, 280–289. [Google Scholar] [CrossRef]
- Mahynski, N.A. Entropic control over nanoscale colloidal crystals. Mol. Phys. 2016, 114, 2586–2596. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Mavrantzas, V.G.; Theodorou, D.N. A novel Monte Carlo scheme for the rapid equilibration of atomistic model polymer systems of precisely defined molecular architecture. Phys. Rev. Lett. 2002, 88, 105503. [Google Scholar] [CrossRef]
- Pant, P.V.K.; Theodorou, D.N. Variable Connectivity Method For The Atomistic Monte-Carlo Simulation Of Polydisperse Polymer Melts. Macromolecules 1995, 28, 7224–7234. [Google Scholar] [CrossRef]
- Bortz, A.B.; Kalos, M.H.; Lebowitz, J.L. A new algorithm for Monte Carlo simulation of Ising spin systems. J. Comput. Phys. 1975, 17, 10–18. [Google Scholar] [CrossRef]
- Fichthorn, K.A.; Weinberg, W.H. Theoretical foundations of dynamical Monte Carlo simulations. J. Chem. Phys. 1991, 95, 1090. [Google Scholar] [CrossRef]
- Siepmann, J.I.; Frenkel, D. Configurational bias Monte Carlo—A new sampling scheme for flexible chains. Mol. Phys. 1992, 75, 59–70. [Google Scholar] [CrossRef] [Green Version]
- de Pablo, J.J.; Laso, M.; Suter, U.W. Simulation of Polyethylene above and below the melting-point. J. Chem. Phys. 1992, 96, 2395–2403. [Google Scholar] [CrossRef]
- Kroger, M. Efficient hybrid algorithm for the dynamic creation of wormlike chains in solutions, brushes, melts and glasses. Comput. Phys. Commun. 2019, 241, 178–179. [Google Scholar] [CrossRef]
- Shi, W.; Maginn, E.J. Improvement in Molecule Exchange Efficiency in Gibbs Ensemble Monte Carlo: Development and Implementation of the Continuous Fractional Component Move. J. Comput. Chem. 2008, 29, 2520–2530. [Google Scholar] [CrossRef]
- Kampmann, T.A.; Boltz, H.H.; Kierfeld, J. Monte Carlo simulation of dense polymer melts using event chain algorithms. J. Chem. Phys. 2015, 143, 044105. [Google Scholar] [CrossRef] [Green Version]
- Auhl, R.; Everaers, R.; Grest, G.S.; Kremer, K.; Plimpton, S.J. Equilibration of long chain polymer melts in computer simulations. J. Chem. Phys. 2003, 119, 12718–12728. [Google Scholar] [CrossRef] [Green Version]
- Subramanian, G. A topology preserving method for generating equilibrated polymer melts in computer simulations. J. Chem. Phys. 2010, 133, 164902. [Google Scholar] [CrossRef]
- Herranz, M.; Martínez-Fernández, D.; Ramos, P.M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Simu-D: A Simulator-Descriptor Suite for Polymer-Based Systems under Extreme Conditions. Int. J. Mol. Sci. 2021, 22, 12464. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Abrams, C.F.; Laso, M. Modeling of crystal nucleation and growth in athermal polymers: Self-assembly of layered nano-morphologies. Soft Matter 2010, 6, 2160–2173. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The role of bond tangency and bond gap in hard sphere crystallization of chains. Soft Matter 2015, 11, 1688–1700. [Google Scholar] [CrossRef]
- Ramos, P.M.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Entropy-Driven Heterogeneous Crystallization of Hard-Sphere Chains under Unidimensional Confinement. Polymers 2021, 13, 1352. [Google Scholar] [CrossRef] [PubMed]
- Ramos, P.M.; Herranz, M.; Martinez-Fernandez, D.; Foteinopoulou, K.; Laso, M.; Karayiannis, N.C. Crystallization of Flexible Chains of Tangent Hard Spheres under Full Confinement. J. Phys. Chem. B 2022, 126, 5931–5947. [Google Scholar] [CrossRef] [PubMed]
- Herranz, M.; Benito, J.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Thermodynamic stability of crystals of hard sphere polymers. under consideration.
- Laso, M.; Karayiannis, N.C. Flexible chain molecules in the marginal and concentrated regimes: Universal static scaling laws and cross-over predictions. J. Chem. Phys. 2008, 128, 174901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karayiannis, N.C.; Laso, M. Monte Carlo scheme for generation and relaxation of dense and nearly jammed random structures of freely jointed hard-sphere chains. Macromolecules 2008, 41, 1537–1551. [Google Scholar] [CrossRef]
- Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Monte Carlo simulations of densely-packed athermal polymers in the bulk and under confinement. Chem. Eng. Sci. 2015, 121, 118–132. [Google Scholar] [CrossRef] [Green Version]
- Ramos, P.M.; Karayiannis, N.C.; Laso, M. Off-lattice simulation algorithms for athermal chain molecules under extreme confinement. J. Comput. Phys. 2018, 375, 918–934. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Laso, M. Dense and nearly jammed random packings of freely jointed chains of tangent hard spheres. Phys. Rev. Lett. 2008, 100, 050602. [Google Scholar] [CrossRef]
- Herranz, M.; Santiago, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Crystal, Fivefold and Glass Formation in Clusters of Polymers Interacting with the Square Well Potential. Polymers 2020, 12, 1111. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The characteristic crystallographic element norm: A descriptor of local structure in atomistic and particulate systems. J. Chem. Phys. 2009, 130, 074704. [Google Scholar] [CrossRef]
- Ramos, P.M.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Identification of Local Structure in 2-D and 3-D Atomic Systems through Crystallographic Analysis. Crystals 2020, 10, 1008. [Google Scholar] [CrossRef]
- Rycroft, C.H. VORO++: A three-dimensional Voronoi cell library in C++. Chaos Interdiscip. J. Nonlinear Sci. 2009, 19, 041111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoy, R.S.; Karayiannis, N.C. Simple model for chain packing and crystallization of soft colloidal polymers. Phys. Rev. E 2013, 88, 012601. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.T.; Smith, T.B.; Hoy, R.S.; Karayiannis, N.C. Effect of chain stiffness on the competition between crystallization and glass-formation in model unentangled polymers. J. Chem. Phys. 2015, 143, 144901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mckay, A.L. A dense non-crystallographic packing of equal spheres. Acta Crystallogr. 1962, 15, 916–918. [Google Scholar] [CrossRef]
- Bagley, B.G. A Dense Packing of Hard Spheres with Five-fold Symmetry. Nature 1965, 208, 674–675. [Google Scholar] [CrossRef]
- Bagley, B.G. 5-Fold Pseudosymmetry. Nature 1970, 225, 1040. [Google Scholar] [CrossRef] [PubMed]
- Anikeenko, A.V.; Medvedev, N.N.; Bezrukov, A.; Stoyan, D. Observation of fivefold symmetry structures in computer models of dense packing of hard spheres. J. Non-Cryst. Solids 2007, 353, 3545–3549. [Google Scholar] [CrossRef]
- Kuo, K.H. Mackay, Anti-Mackay, Double-Mackay, Pseudo-Mackay, and Related Icosahedral Shell Clusters. Struct. Chem. 2002, 13, 221–230. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. Model. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Anikeenko, A.V.; Medvedev, N.N. Polytetrahedral nature of the dense disordered packings of hard spheres. Phys. Rev. Lett. 2007, 98, 235504. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Twinning of Polymer Crystals Suppressed by Entropy. Symmetry 2014, 6, 758–780. [Google Scholar] [CrossRef] [Green Version]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Spontaneous Crystallization in Athermal Polymer Packings. Int. J. Mol. Sci. 2013, 14, 332–358. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salcedo, E.D.; Nguyen, H.T.; Hoy, R.S. Factors influencing thermal solidification of bent-core trimers. J. Chem. Phys. 2019, 151, 134501. [Google Scholar] [CrossRef] [PubMed]
- Ashcroft, N.W.; Mermin, D.N. Solid State Physics, 1st ed.; Brooks/Cole: Pacific Grove, CA, USA, 1976. [Google Scholar]
- Dove, M.T. Introduction to Lattice Dynamics; Cambridge Topics in Mineral Physics and Chemistry 4; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Hoover, W.G.; Ree, F.H. Melting Transition And Communal Entropy For Hard Spheres. J. Chem. Phys. 1968, 49, 3609. [Google Scholar] [CrossRef] [Green Version]
- Dodd, L.R.; Theodorou, D.N. Analytical treatment of the volume and surface area of molecules formed by an arbitrary collection of unequal spheres intersected by planes. Mol. Phys. 1991, 72, 1313–1345. [Google Scholar] [CrossRef]
- Irving, J.H.; Kirkwood, J.G. The statistical mechanical theory of transport processes. IV. The equations of hydrodynamics. J. Chem. Phys. 1950, 18, 817–829. [Google Scholar] [CrossRef]
- Kumar, V.S.; Kumaran, V. Voronoi neighbor statistics of hard-disks and hard-spheres. J. Chem. Phys. 2005, 123, 074502. [Google Scholar] [CrossRef] [Green Version]
- Kumar, V.S.; Kumaran, V. Voronoi cell volume distribution and configurational entropy of hard-spheres. J. Chem. Phys. 2005, 123, 114501. [Google Scholar] [CrossRef]
- Flory, P.J. Statistical Mechanics of Chain Molecules; Hanser-Verlag: Munchen, Germany, 1989. [Google Scholar]




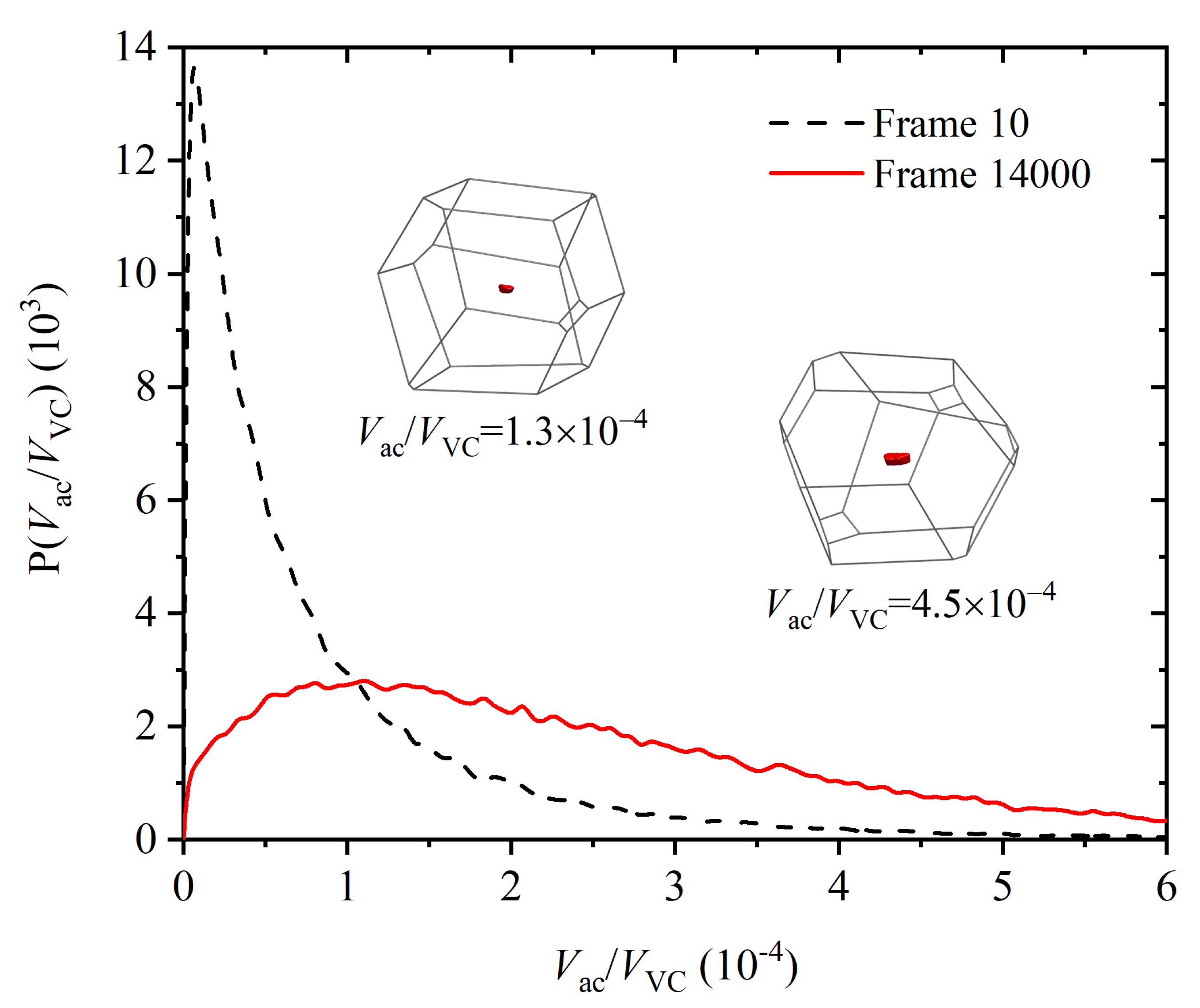

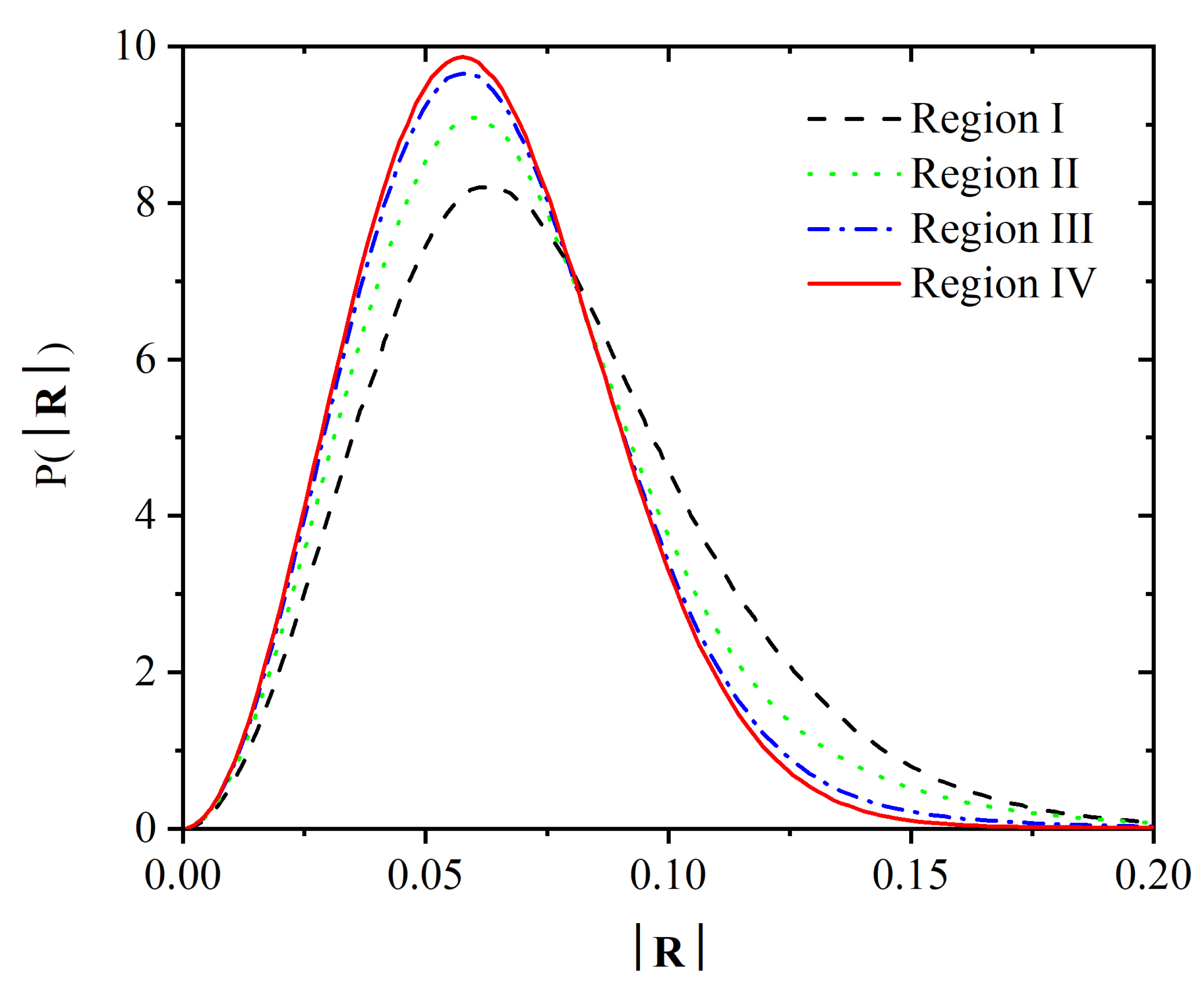
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Polymorphism and Perfection in Crystallization of Hard Sphere Polymers. Polymers 2022, 14, 4435. https://doi.org/10.3390/polym14204435
Herranz M, Foteinopoulou K, Karayiannis NC, Laso M. Polymorphism and Perfection in Crystallization of Hard Sphere Polymers. Polymers. 2022; 14(20):4435. https://doi.org/10.3390/polym14204435
Chicago/Turabian StyleHerranz, Miguel, Katerina Foteinopoulou, Nikos Ch. Karayiannis, and Manuel Laso. 2022. "Polymorphism and Perfection in Crystallization of Hard Sphere Polymers" Polymers 14, no. 20: 4435. https://doi.org/10.3390/polym14204435
APA StyleHerranz, M., Foteinopoulou, K., Karayiannis, N. C., & Laso, M. (2022). Polymorphism and Perfection in Crystallization of Hard Sphere Polymers. Polymers, 14(20), 4435. https://doi.org/10.3390/polym14204435








