Coarse-Grained Simulations of Release of Drugs Housed in Flexible Nanogels: New Insights into Kinetic Parameters
Abstract
1. Introduction
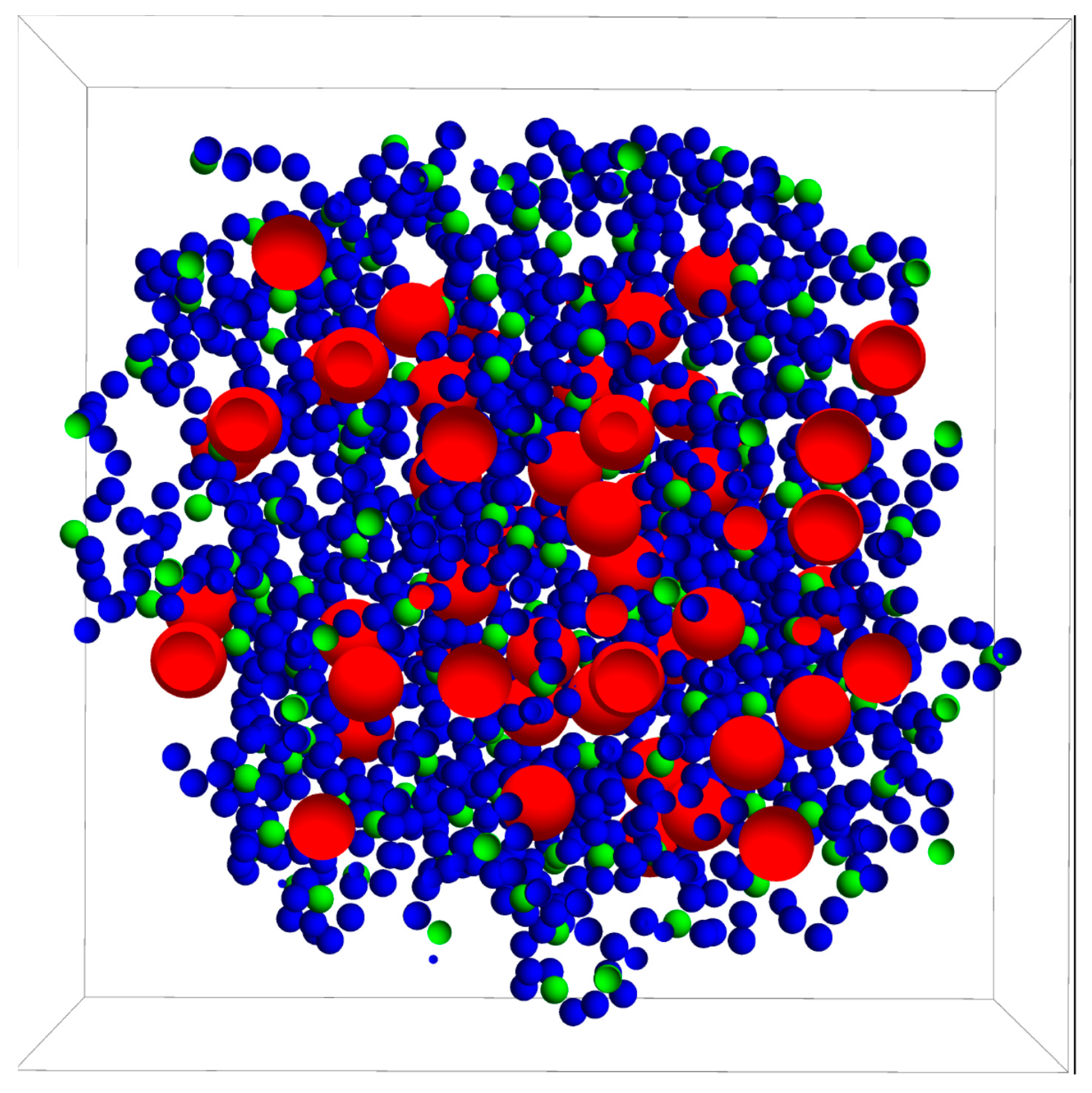
2. Model and Simulations
3. Results and Discussion
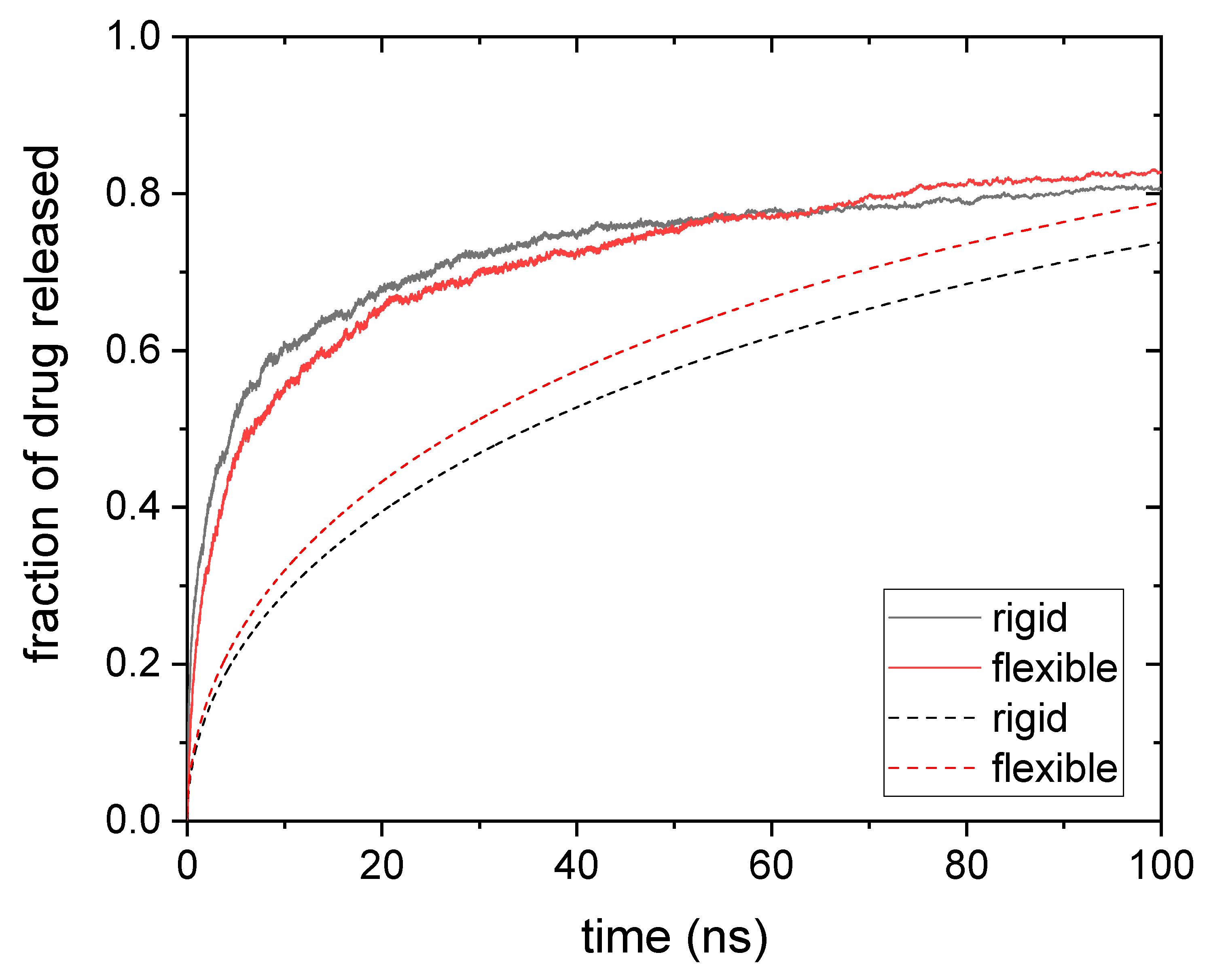
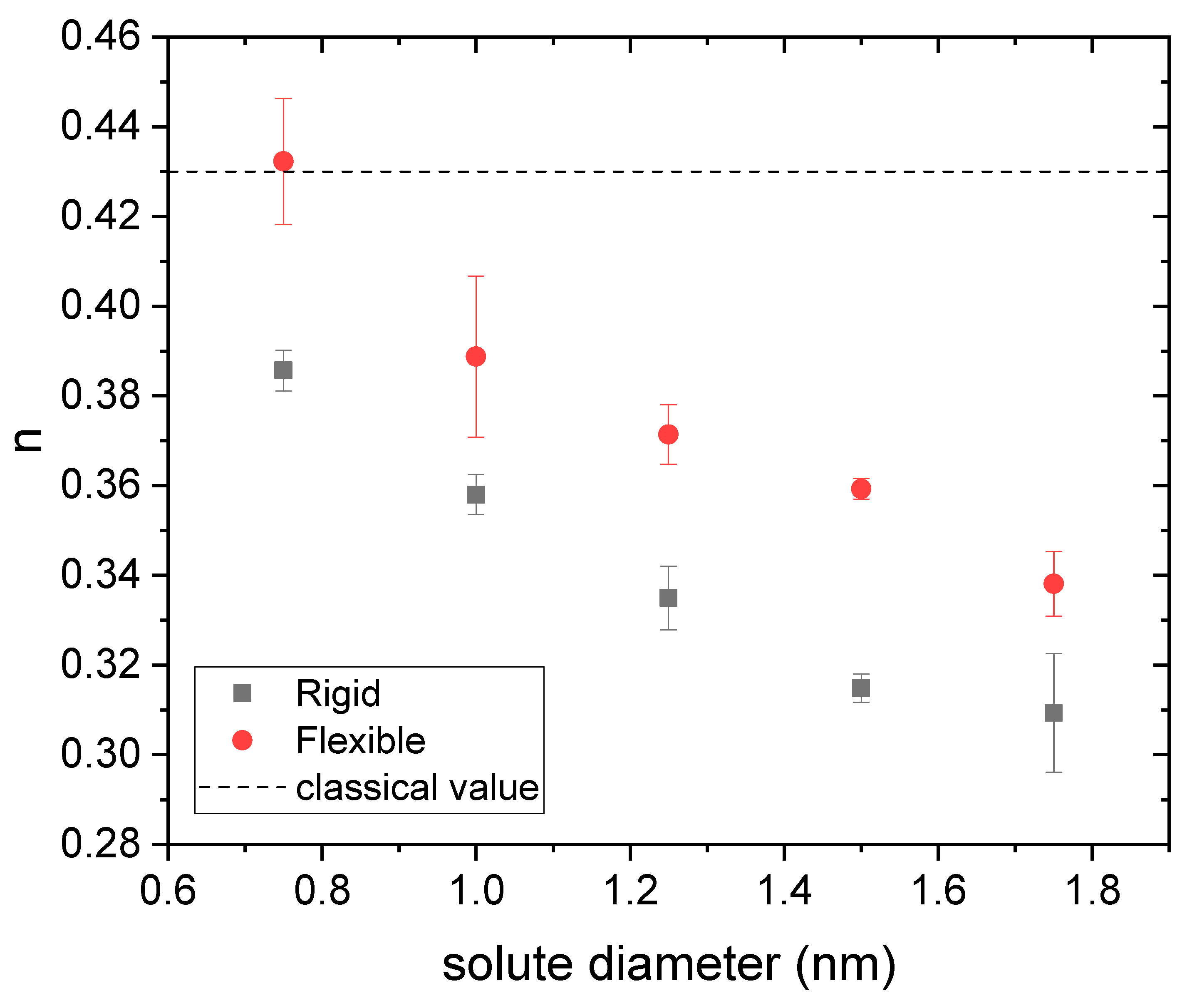
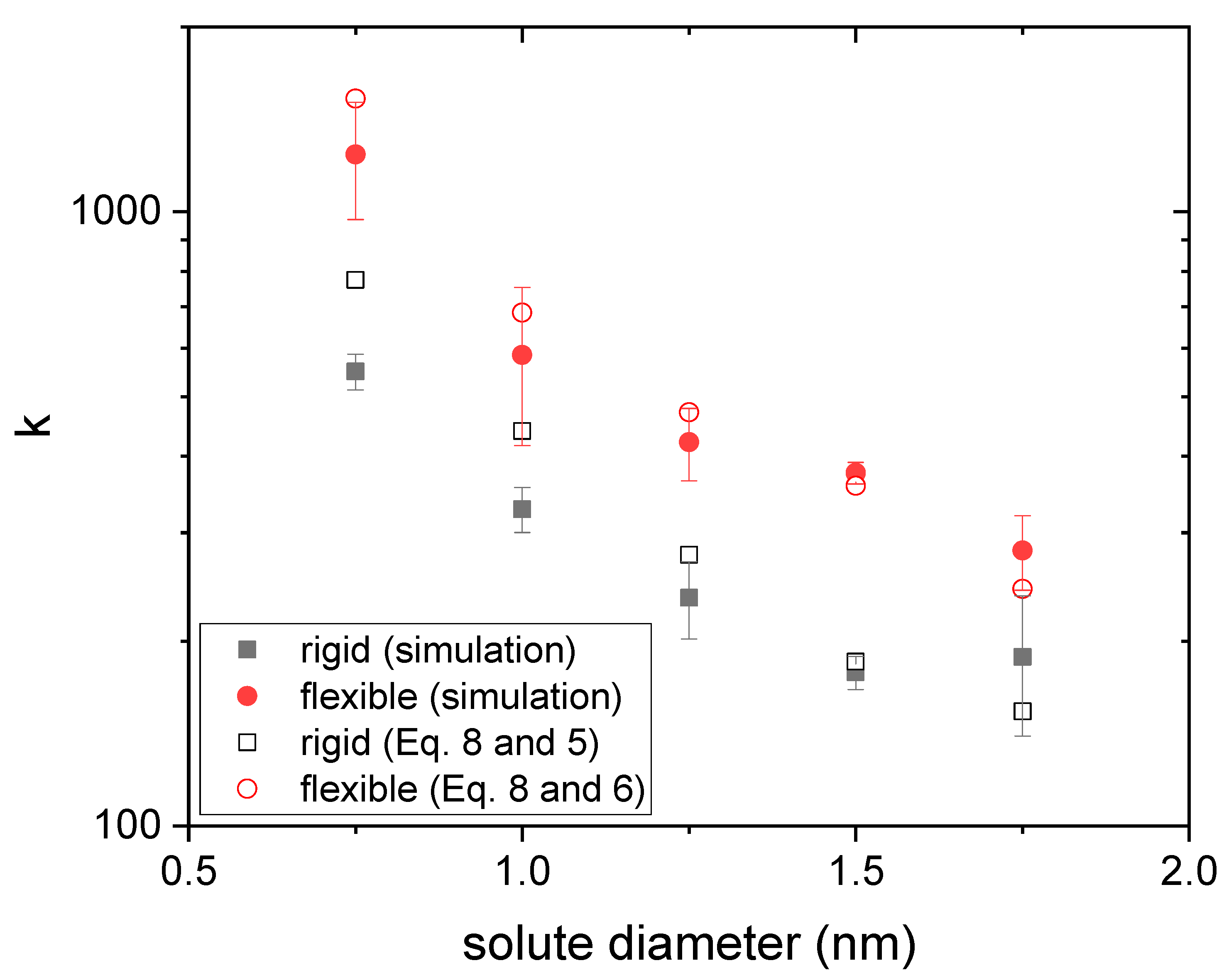
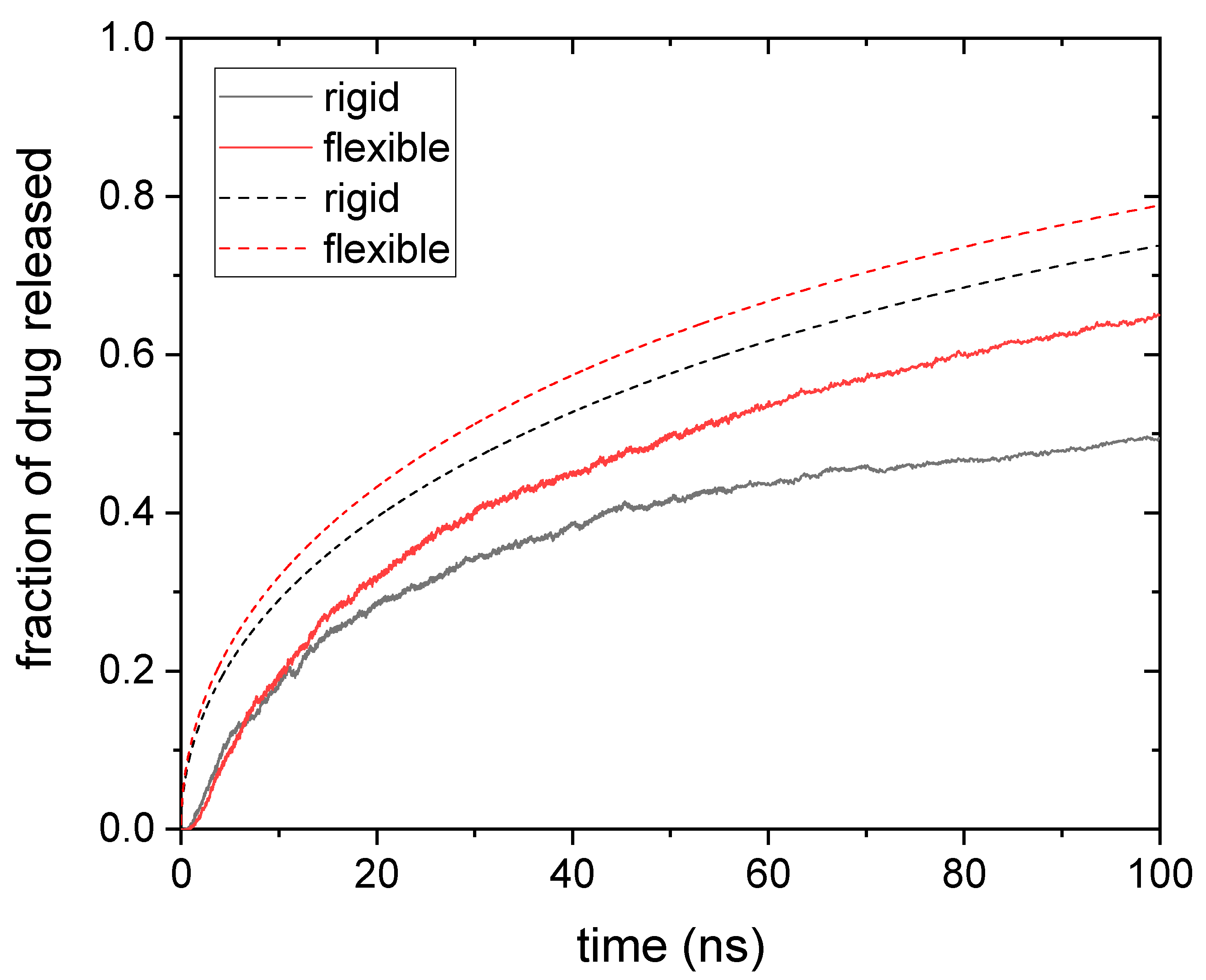
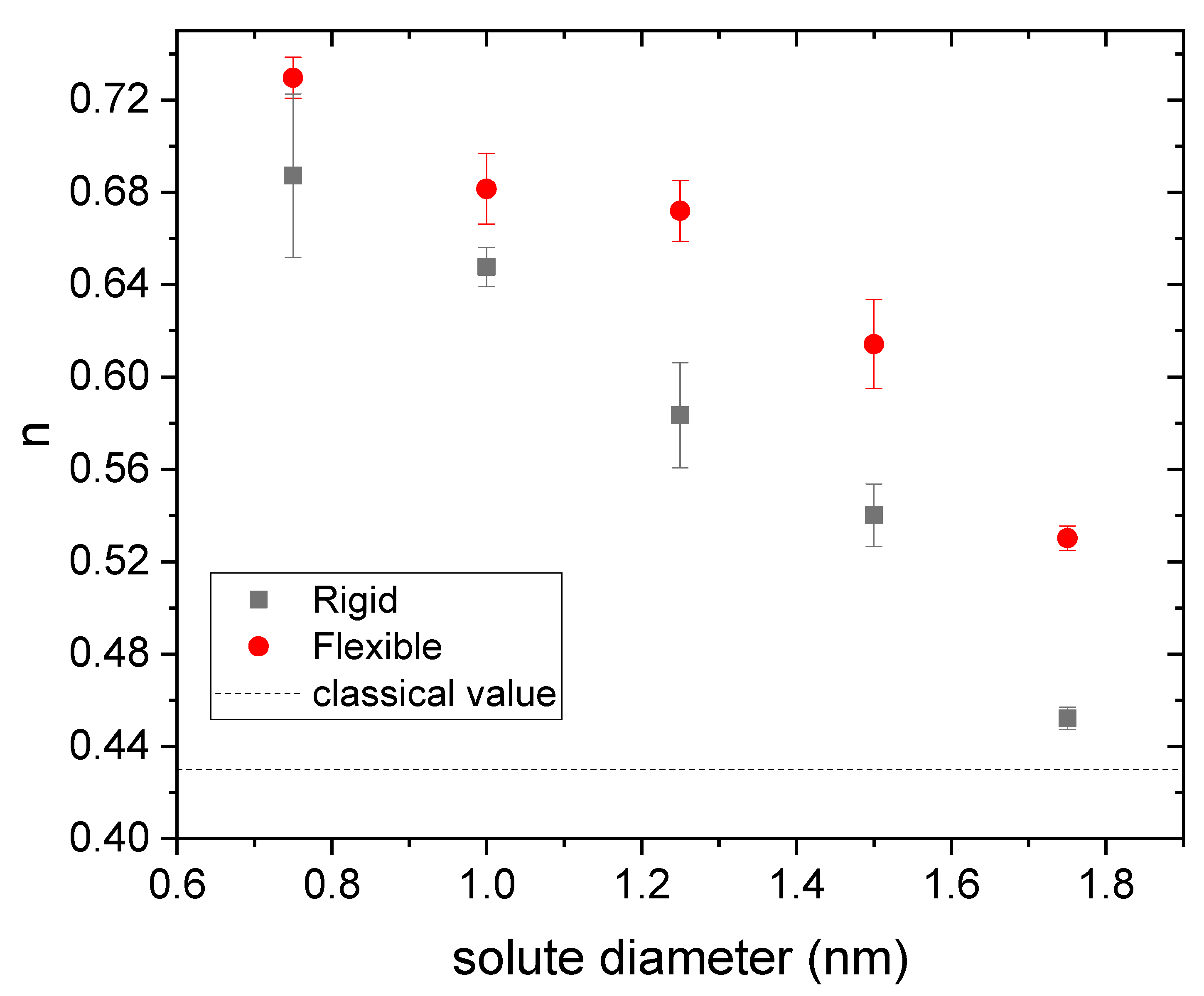
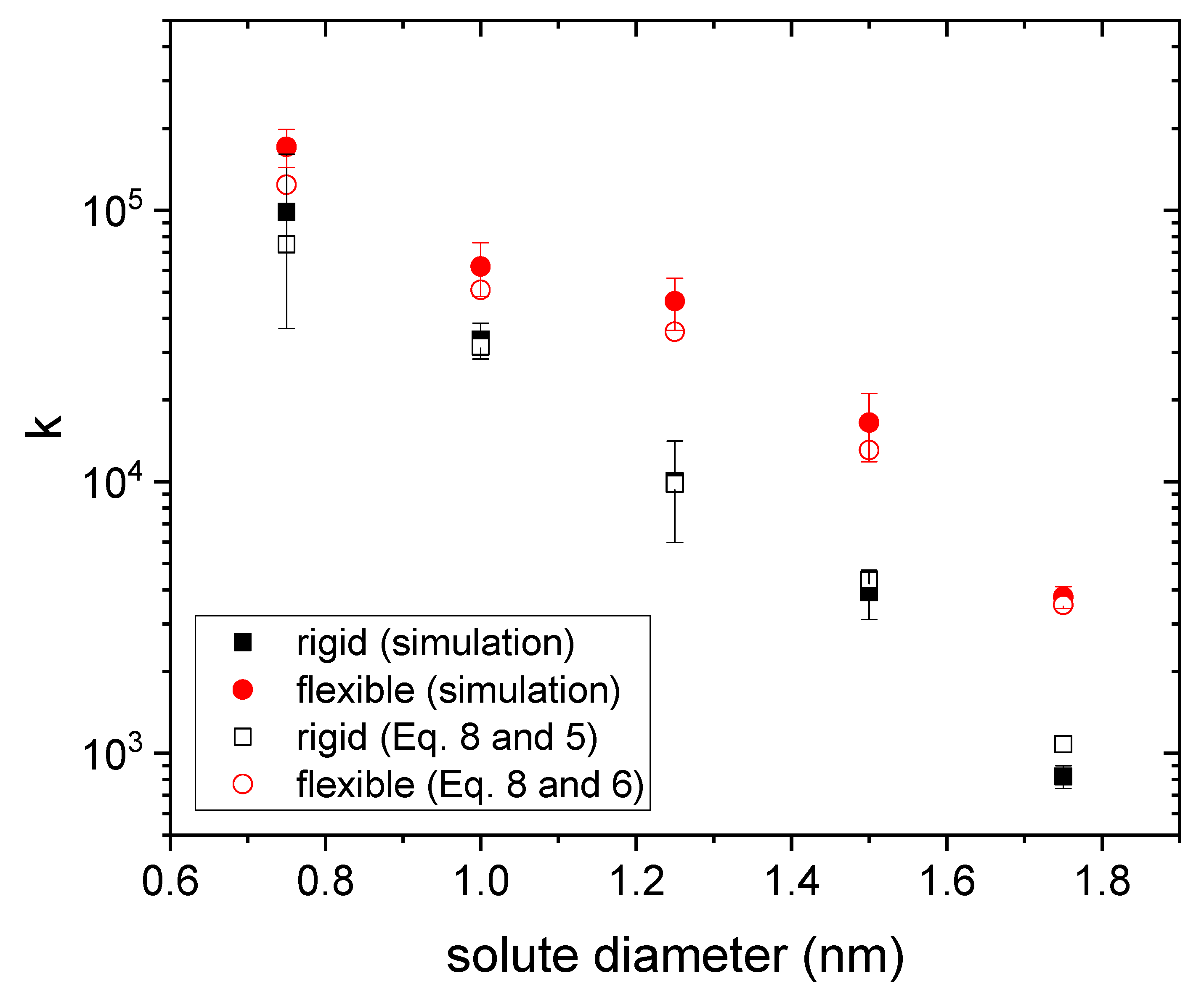
3.1. Drug Distributed throughout the Nanogel
3.2. Drug Distributed in the Core of the Nanogel
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pinelli, F.; Perale, G.; Rossi, F. Coating and Functionalization Strategies for Nanogels and Nanoparticles for Selective Drug Delivery. Gels 2020, 6, 6. [Google Scholar] [CrossRef]
- Stawicki, B.; Schacher, T.; Cho, H. Nanogels as a Versatile Drug Delivery System for Brain Cancer. Gels 2021, 7, 63. [Google Scholar] [CrossRef]
- Zhou, W.; Yang, G.; Ni, X.; Diao, S.; Xie, C.; Fan, Q. Recent Advances in Crosslinked Nanogel for Multimodal Imaging and Cancer Therapy. Polymers 2020, 12, 1902. [Google Scholar] [CrossRef]
- Papagiannopoulos, A.; Sotiropoulos, K. Current Advances of Polysaccharide-Based Nanogels and Microgels in Food and Biomedical Sciences. Polymers 2022, 14, 813. [Google Scholar] [CrossRef]
- Patnaik, S.; Sharma, A.K.; Garg, B.S.; Gandhi, R.P.; Gupta, K.C. Photoregulation of Drug Release in Azo-Dextran Nanogels. Int. J. Pharm. 2007, 342, 184–193. [Google Scholar] [CrossRef]
- Oh, N.M.; Oh, K.T.; Baik, H.J.; Lee, B.R.; Lee, A.H.; Youn, Y.S.; Lee, E.S. A Self-Organized 3-Diethylaminopropyl-Bearing Glycol Chitosan Nanogel for Tumor Acidic PH Targeting: In Vitro Evaluation. C Colloids Surf. B Biointerfaces 2010, 78, 120–126. [Google Scholar] [CrossRef]
- Cazares-Cortes, E.; Espinosa, A.; Guigner, J.-M.; Michel, A.; Griffete, N.; Wilhelm, C.; Menager, C. Doxorubicin Intracellular Remote Release from Biocompatible Oligo(Ethylene Glycol) Methyl Ether Methacrylate-Based Magnetic Nanogels Triggered by Magnetic Hyperthermia. ACS Appl. Mater. Interfaces 2017, 9, 25775–25788. [Google Scholar] [CrossRef]
- Aguirre, G.; Villar-Alvarez, E.; Gonzalez, A.; Ramos, J.; Taboada, P.; Forcada, J. Biocompatible Stimuli-Responsive Nanogels for Controlled Antitumor Drug Delivery. J. Polym. Sci. Part A-Polym. Chem. 2016, 54, 1694–1705. [Google Scholar] [CrossRef]
- Hsiao, M.-H.; Larsson, M.; Larsson, A.; Evenbratt, H.; Chen, Y.-Y.; Chen, Y.-Y.; Liu, D.-M. Design and Characterization of a Novel Amphiphilic Chitosan Nanocapsule-Based Thermo-Gelling Biogel with Sustained in Vivo Release of the Hydrophilic Anti-Epilepsy Drug Ethosuximide. J. Control. Release 2012, 161, 942–948. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, X.; Guo, H.; Li, C.; Yu, D. An Injectable and Glucose-Sensitive Nanogel for Controlled Insulin Release. J. Mater. Chem. 2012, 22, 22788–22796. [Google Scholar] [CrossRef]
- Alvarez-Bautista, A.; Duarte, C.M.M.; Mendizabal, E.; Katime, I. Controlled Delivery of Drugs through Smart PH-Sensitivenanohydrogels for Anti-Cancer Therapies: Synthesis, Drug Release and Cellular Studies. Des. Monomers Polym. 2016, 19, 319–329. [Google Scholar] [CrossRef]
- Xue, Z.; Fu, R.; Duan, Z.; Chi, L.; Zhu, C.; Fan, D. Inhibitory Effect of PH-Responsive Nanogel Encapsulating Ginsenoside CK against Lung Cancer. Polymers 2021, 13, 1784. [Google Scholar] [CrossRef] [PubMed]
- Zambito, Y.; Pedreschi, E.; Di Colo, G. Is Dialysis a Reliable Method for Studying Drug Release from Nanoparticulate Systems?—A Case Study. Int. J. Pharm. 2012, 434, 28–34. [Google Scholar] [CrossRef] [PubMed]
- Klinger, D.; Landfester, K. Stimuli-Responsive Microgels for the Loading and Release of Functional Compounds: Fundamental Concepts and Applications. Polymer 2012, 53, 5209–5231. [Google Scholar] [CrossRef]
- Casalini, T.; Perale, G. From Microscale to Macroscale: Nine Orders of Magnitude for a Comprehensive Modeling of Hydrogels for Controlled Drug Delivery. Gels 2019, 5, 28. [Google Scholar] [CrossRef]
- Casalini, T. Not Only in Silico Drug Discovery: Molecular Modeling towards in Silico Drug Delivery Formulations. J. Control. Release 2021, 332, 390–417. [Google Scholar] [CrossRef]
- Bunde, A.; Havlin, S.; Nossal, R.; Stanley, H.E.; Weiss, G.H. On Controlled Diffusion-Limited Drug Release from a Leaky Matrix. J. Chem. Phys. 1985, 83, 5909–5913. [Google Scholar] [CrossRef]
- Kosmidis, K.; Argyrakis, P.; Macheras, P. A Reappraisal of Drug Release Laws Using Monte Carlo Simulations: The Prevalence of the Weibull Function. Pharm. Res. 2003, 20, 988–995. [Google Scholar] [CrossRef]
- Villalobos, R.; Garcia, E.V.; Quintanar, D.; Young, P.M. Drug Release from Inert Spherical Matrix Systems Using Monte Carlo Simulations. Curr. Drug Deliv. 2017, 14, 65–72. [Google Scholar] [CrossRef]
- Maroto-Centeno, J.A.; Quesada-Pérez, M. Coarse-Grained Simulations of Diffusion Controlled Release of Drugs from Neutral Nanogels: Effect of Excluded Volume Interactions. J. Chem. Phys. 2020, 152, 024107. [Google Scholar] [CrossRef]
- Martín-Molina, A.; Quesada-Pérez, M. A Review of Coarse-Grained Simulations of Nanogel and Microgel Particles. J. Mol. Liq. 2019, 280, 374–381. [Google Scholar] [CrossRef]
- Rovigatti, L.; Gnan, N.; Tavagnacco, L.; Moreno, A.J.; Zaccarelli, E. Numerical Modelling of Non-Ionic Microgels: An Overview. Soft Matter 2019, 15, 1108–1119. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, H.; Winkler, R.G. Universal Conformational Properties of Polymers in Ionic Nanogels. Sci. Rep. 2016, 6, 19836. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, H.; Halver, R.; Sutmann, G.; Winkler, R.G. Polymer Conformations in Ionic Microgels in the Presence of Salt: Theoretical and Mesoscale Simulation Results. Polymers 2017, 9, 15. [Google Scholar] [CrossRef] [PubMed]
- Kamerlin, N.; Elvingson, C. Tracer Diffusion in a Polymer Gel: Simulations of Static and Dynamic 3D Networks Using Spherical Boundary Conditions. J. Phys. Condens. Matter 2016, 28, 475101. [Google Scholar] [CrossRef]
- Cho, H.W.; Kim, H.; Sung, B.J.; Kim, J.S. Tracer Diffusion in Tightly-Meshed Homogeneous Polymer Networks: A Brownian Dynamics Simulation Study. Polymers 2020, 12, 2067. [Google Scholar] [CrossRef]
- Kim, Y.; Joo, S.; Kim, W.K.; Jeon, J.-H. Active Diffusion of Self-Propelled Particles in Flexible Polymer Networks. Macromolecules 2022, 55, 7136–7147. [Google Scholar] [CrossRef]
- Zhao, B.-R.; Li, B. Molecular Simulation of Hopping Mechanisms of Nanoparticles in Regular Cross-Linked Polymer Networks. J. Chem. Phys. 2022, 157, 104901. [Google Scholar] [CrossRef]
- Quesada-Pérez, M.; Maroto-Centeno, J.A.; Ramos-Tejada, M.D.M.; Martín-Molina, A. Coarse-Grained Simulations of Solute Diffusion in Crosslinked Flexible Hydrogels. Macromolecules 2022, 55, 1495–1504. [Google Scholar] [CrossRef]
- Caccavo, D. An Overview on the Mathematical Modeling of Hydrogels’ Behavior for Drug Delivery Systems. Int. J. Pharm. 2019, 560, 175–190. [Google Scholar] [CrossRef]
- Kim, W.K.; Chudoba, R.; Milster, S.; Roa, R.; Kanduč, M.; Dzubiella, J. Tuning the Selective Permeability of Polydisperse Polymer Networks. Soft Matter 2020, 16, 8144–8154. [Google Scholar] [CrossRef] [PubMed]
- Milster, S.; Kim, W.K.; Kanduč, M.; Dzubiella, J. Tuning the Permeability of Regular Polymeric Networks by the Cross-Link Ratio. J. Chem. Phys. 2021, 154, 154902. [Google Scholar] [CrossRef] [PubMed]
- Samanta, N.; Chakrabarti, R. Tracer Diffusion in a Sea of Polymers with Binding Zones: Mobile vs. Frozen Traps. Soft Matter 2016, 12, 8554–8563. [Google Scholar] [CrossRef] [PubMed]
- Quesada-Pérez, M.; Adroher-Benítez, I.; Maroto-Centeno, J.A. Size-Exclusion Partitioning of Neutral Solutes in Crosslinked Polymer Networks: A Monte Carlo Simulation Study. J. Chem. Phys. 2014, 140, 204910. [Google Scholar] [CrossRef]
- Daeihamed, M.; Haeri, A.; Ostad, S.N.; Akhlaghi, M.F.; Dadashzadeh, S. Doxorubicin-Loaded Liposomes: Enhancing the Oral Bioavailability by Modulation of Physicochemical Characteristics. Nanomedicine 2017, 12, 1187–1202. [Google Scholar] [CrossRef]
- Quesada-Perez, M.; Martin-Molina, A. Monte Carlo Simulation of Thermo-Responsive Charged Nanogels in Salt-Free Solutions. Soft Matter 2013, 9, 7086–7094. [Google Scholar] [CrossRef]
- Ahualli, S.; Martin-Molina, A.; Alberto Maroto-Centeno, J.; Quesada-Perez, M. Interaction between Ideal Neutral Nanogels: A Monte Carlo Simulation Study. Macromolecules 2017, 50, 2229–2238. [Google Scholar] [CrossRef]
- Cichoki, B.; Hinsen, K. Dynamic Computer-Simulation of Concentrated Hard-Sphere Suspensions.1. Simulation Technique and Mean-Square Displacement Data. Physica A 1990, 166, 473–491. [Google Scholar] [CrossRef]
- Wieczorek, G.; Zielenkiewicz, P. Influence of Macromolecular Crowding on Protein-Protein Association Rates—A Brownian Dynamics Study. Biophys. J. 2008, 95, 5030–5036. [Google Scholar] [CrossRef]
- Rothman, J.S.; Kocsis, L.; Herzog, E.; Nusser, Z.; Silver, R.A. Physical Determinants of Vesicle Mobility and Supply at a Central Synapse. Elife 2016, 5, e15133. [Google Scholar] [CrossRef]
- Houser, J.R.; Busch, D.J.; Bell, D.R.; Li, B.; Ren, P.; Stachowiak, J.C. The Impact of Physiological Crowding on the Diffusivity of Membrane Bound Proteins. Soft Matter 2016, 12, 2127–2134. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.; Grima, R. Fast Simulation of Brownian Dynamics in a Crowded Environment. J. Chem. Phys. 2017, 146, 024105. [Google Scholar] [CrossRef] [PubMed]
- Perez-Mas, L.; Martin-Molina, A.; Quesada-Perez, M. Coarse-Grained Monte Carlo Simulations of Nanogel-Polyelectrolyte Complexes: Electrostatic Effects. Soft Matter 2020, 16, 3022–3028. [Google Scholar] [CrossRef] [PubMed]
- Ermak, D.L. A Computer Simulation of Charged Particles in Solution. I. Technique and Equilibrium Properties. J. Chem. Phys. 1975, 62, 4189–4196. [Google Scholar] [CrossRef]
- Johansson, L.; LLöfroth, J. Diffusion and Interaction in Gels and Solutions. 4. Hard Sphere Brownian Dynamics Simulations. J. Chem. Phys. 1993, 98, 7471–7479. [Google Scholar] [CrossRef]
- Quesada-Pérez, M.; Maroto-Centeno, J.A.; Ramos-Tejada, M.D.M.; Martín-Molina, A. Universal Description of Steric Hindrance in Flexible Polymer Gels. Phys. Chem. Chem. Phys. 2021, 23, 14997–15002. [Google Scholar] [CrossRef]
- Moncho-Jorda, A.; Jodar-Reyes, A.B.; Kanduc, M.; German-Bellod, A.; Lopez-Romero, J.M.; Contreras-Caceres, R.; Sarabia, F.; García-Castro, M.; Perez-Ram írez, H.A.; Odriozola, G. Scaling Laws in the Diffusive Release of Neutral Cargo from Hollow Hydrogel Nanoparticles: Paclitaxel-Loaded Poly(4vinylpyridine). ACS Nano 2020, 14, 15227–15240. [Google Scholar] [CrossRef]
- Ritger, P.L.; Peppas, N.A. A Simple Equation for Description of Solute Release I. Fickian and Non-Fickian Release from Non-Swellable Devices in the Form of Slabs, Spheres, Cylinders or Discs. J. Control. Release 1987, 5, 23–36. [Google Scholar] [CrossRef]
- Blanco, M.D.; Guerrero, S.; Teijón, C.; Olmo, R.; Pastrana, L.; Katime, I.; Teijón, J.M. Preparation and Characterization of Nanoparticulate Poly(N-Isopropylacryl- Amide) Hydrogel for the Controlled Release of Anti-Tumour Drugs. Polym. Int. 2008, 57, 1215–1225. [Google Scholar] [CrossRef]
- Lu, C.; Li, B.; Liu, N.; Wu, G.; Gao, H.; Ma, J. A Hydrazone Crosslinked Zwitterionic Polypeptide Nanogel as a Platform for Controlled Drug Delivery. RSC Adv. 2014, 4, 50301–50311. [Google Scholar] [CrossRef]
- Ignacio, M.; Slater, G.W. Using Fitting Functions to Estimate the Diffusion Coefficient of Drug Molecules in Diffusion-Controlled Release Systems. Phys. A Stat. Mech. Its Appl. 2021, 567, 125681. [Google Scholar] [CrossRef]
- Cheng, X.; Jin, Y.; Qi, R.; Fan, W.; Li, H.; Sun, X.; Lai, S. Dual PH and Oxidation-Responsive Nanogels Crosslinked by Diselenide Bonds for Controlled Drug Delivery. Polymer 2016, 101, 370–378. [Google Scholar] [CrossRef]
- Vigata, M.; Meinert, C.; Hutmacher, D.W.; Bock, N. Hydrogels as Drug Delivery Systems: A Review of Current Characterization and Evaluation Techniques. Pharmaceutics 2020, 12, 1188. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quesada-Pérez, M.; Pérez-Mas, L.; Carrizo-Tejero, D.; Maroto-Centeno, J.-A.; Ramos-Tejada, M.d.M.; Martín-Molina, A. Coarse-Grained Simulations of Release of Drugs Housed in Flexible Nanogels: New Insights into Kinetic Parameters. Polymers 2022, 14, 4760. https://doi.org/10.3390/polym14214760
Quesada-Pérez M, Pérez-Mas L, Carrizo-Tejero D, Maroto-Centeno J-A, Ramos-Tejada MdM, Martín-Molina A. Coarse-Grained Simulations of Release of Drugs Housed in Flexible Nanogels: New Insights into Kinetic Parameters. Polymers. 2022; 14(21):4760. https://doi.org/10.3390/polym14214760
Chicago/Turabian StyleQuesada-Pérez, Manuel, Luis Pérez-Mas, David Carrizo-Tejero, José-Alberto Maroto-Centeno, María del Mar Ramos-Tejada, and Alberto Martín-Molina. 2022. "Coarse-Grained Simulations of Release of Drugs Housed in Flexible Nanogels: New Insights into Kinetic Parameters" Polymers 14, no. 21: 4760. https://doi.org/10.3390/polym14214760
APA StyleQuesada-Pérez, M., Pérez-Mas, L., Carrizo-Tejero, D., Maroto-Centeno, J.-A., Ramos-Tejada, M. d. M., & Martín-Molina, A. (2022). Coarse-Grained Simulations of Release of Drugs Housed in Flexible Nanogels: New Insights into Kinetic Parameters. Polymers, 14(21), 4760. https://doi.org/10.3390/polym14214760







