Effective Tensile Strength Estimation of Natural Fibers through Micromechanical Models: The Case of Henequen Fiber Reinforced-PP Composites
Abstract
:1. Introduction
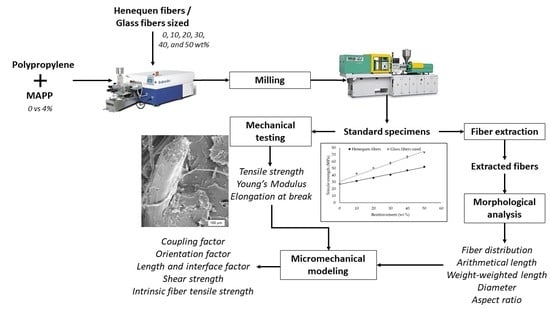
2. Materials and Methods
2.1. Materials
2.2. Methods
3. Results and Discussion
3.1. Macromechanical Analysis of Tensile Properties
3.2. Interface, Shear Strength, and Intrinsic Tensile Strength of Henequen Fibers Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tarrés, Q.; Vilaseca, F.; Herrera-Franco, P.J.; Espinach, F.X.; Delgado-Aguilar, M.; Mutjé, P. Interface and Micromechanical Characterization of Tensile Strength of Bio-Based Composites from Polypropylene and Henequen Strands. Ind. Crops Prod. 2019, 132, 319–326. [Google Scholar] [CrossRef]
- Kim, J.; Cho, D. Effects of Alkali-Treatment and Feeding Route of Henequen Fiber on the Heat Deflection Temperature, Mechanical, and Impact Properties of Novel Henequen Fiber/Polyamide 6 Composites. J. Compos. Sci. 2022, 6, 89. [Google Scholar] [CrossRef]
- Agaliotis, E.M.; Ake-Concha, B.D.; May-Pat, A.; Morales-Arias, J.P.; Bernal, C.; Valadez-Gonzalez, A.; Herrera-Franco, P.J.; Proust, G.; Koh-Dzul, J.F.; Carrillo, J.G.; et al. Tensile Behavior of 3D Printed Polylactic Acid (PLA) Based Composites Reinforced with Natural Fiber. Polymers 2022, 14, 3976. [Google Scholar] [CrossRef] [PubMed]
- Castillo-Lara, J.F.; Flores-Johnson, E.A.; Valadez-Gonzalez, A.; Herrera-Franco, P.J.; Carrillo, J.G.; Gonzalez-Chi, P.I.; Agaliotis, E.; Li, Q.M. Mechanical Behaviour of Composite Sandwich Panels with Foamed Concrete Core Reinforced with Natural Fibre in Four-Point Bending. Thin-Walled Struct. 2021, 169, 108457. [Google Scholar] [CrossRef]
- Castillo-Lara, J.F.; Flores-Johnson, E.A.; Valadez-Gonzalez, A.; Herrera-Franco, P.J.; Carrillo, J.G.; Gonzalez-Chi, P.I.; Li, Q.M. Mechanical Properties of Natural Fiber Reinforced Foamed Concrete. Materials 2020, 13, 3060. [Google Scholar] [CrossRef]
- Le Baillif, M.; Oksman, K. The Effect of Processing on Fiber Dispersion, Fiber Length, and Thermal Degradation of Bleached Sulfite Cellulose Fiber Polypropylene Composites. J. Thermoplast. Compos. Mater. 2009, 22, 115–133. [Google Scholar] [CrossRef]
- De Albuquerque, A.C.; Joseph, K.; Hecker De Carvalho, L.; Morais D’almeida, J.R. Effect of Wettability and Ageing Conditions on the Physical and Mechanical Properties of Uniaxially Oriented Jute-Roving-Reinforced Polyester Composites. Compos. Sci. Technol. 2000, 60, 833–844. [Google Scholar] [CrossRef]
- Mishra, S.; Mohanty, A.K.; Drzal, L.T.; Misra, M.; Parija, S.; Nayak, S.K.; Tripathy, S.S. Studies on Mechanical Performance of Biofibre/Glass Reinforced Polyester Hybrid Composites. Compos. Sci. Technol. 2003, 63, 1377–1385. [Google Scholar] [CrossRef]
- Hassan, M.L.; Nada, A.A.M.A. Utilization of Lignocellulosic Fibers in Molded Polyester Composites. J. Appl. Polym. Sci. 2003, 87, 653–660. [Google Scholar] [CrossRef]
- Joshi, S.V.; Drzal, L.T.; Mohanty, A.K.; Arora, S. Are Natural Fiber Composites Environmentally Superior to Glass Fiber Reinforced Composites? Compos. Part A-Appl. Sci. Manuf. 2004, 35, 371–376. [Google Scholar] [CrossRef]
- Kumar, R.; Ul Haq, M.I.; Raina, A.; Anand, A. Industrial Applications of Natural Fibre-Reinforced Polymer Composites–Challenges and Opportunities. Int. J. Sustain. Eng. 2019, 12, 212–220. [Google Scholar] [CrossRef]
- Toriz, G.; Denes, F.; Young, R.A. Lignin-Polypropylene Composites. Part 1: Composites from Unmodified Lignin and Polypropylene. Polym. Compos. 2002, 23, 806–813. [Google Scholar] [CrossRef]
- Pil, L.; Bensadoun, F.; Pariset, J.; Verpoest, I. Why Are Designers Fascinated by Flax and Hemp Fibre Composites? Compos. Part A-Appl. Sci. Manuf. 2016, 83, 193–205. [Google Scholar] [CrossRef]
- Mäder, E. Glass Fibers: Quo Vadis? Fibers 2017, 5, 10. [Google Scholar] [CrossRef] [Green Version]
- Tjong, S.C.; Xu, S.A.; Kwok-Yiu Li, R.; Mai, Y.W. Short Glass Fiber-Reinforced Polyamide 6,6 Composites Toughened with Maleated SEBS. Compos. Sci. Technol. 2002, 62, 2017–2027. [Google Scholar] [CrossRef]
- Dai, Q.; Kelly, J.; Sullivan, J.; Elgowainy, A. Life-Cycle Analysis Update of Glass and Glass Fiber for the GREET Model; Argonne National Laboratory: Lemont, IL, USA, 2015; p. 25. [Google Scholar]
- Wu, Y.; Xia, C.; Cai, L.; Garcia, A.C.; Shi, S.Q. Development of Natural Fiber-Reinforced Composite with Comparable Mechanical Properties and Reduced Energy Consumption and Environmental Impacts for Replacing Automotive Glass-Fiber Sheet Molding Compound. J. Clean. Prod. 2018, 184, 92–100. [Google Scholar] [CrossRef]
- Serrano, A.; Espinach, F.X.; Tresserras, J.; Pellicer, N.; Alcala, M.; Mutje, P. Study on the Technical Feasibility of Replacing Glass Fibers by Old Newspaper Recycled Fibers as Polypropylene Reinforcement. J. Clean. Prod. 2014, 65, 489–496. [Google Scholar] [CrossRef]
- Rouger, J.; Mutje, P. Correlation between the Cellulose Fibers Beating and the Fixation of a Soluble Cationic Polymer. Br. Polym. J. 1984, 16, 83–86. [Google Scholar] [CrossRef]
- Sahu, P.; Gupta, M.K. A Review on the Properties of Natural Fibres and Its Bio-Composites: Effect of Alkali Treatment. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 234, 198–217. [Google Scholar] [CrossRef]
- Zaman, H.U.; Khan, R.A. Acetylation Used for Natural Fiber/Polymer Composites. J. Thermoplast. Compos. Mater. 2021, 34, 3–23. [Google Scholar] [CrossRef]
- Xie, Y.; Hill, C.A.S.; Xiao, Z.; Militz, H.; Mai, C. Silane Coupling Agents Used for Natural Fiber/Polymer Composites: A Review. Compos. Part A Appl. Sci. Manuf. 2010, 41, 806–819. [Google Scholar] [CrossRef]
- Enciso, B.; Abenojar, J.; Martínez, M.A. Influence of Plasma Treatment on the Adhesion between a Polymeric Matrix and Natural Fibres. Cellulose 2017, 24, 1791–1801. [Google Scholar] [CrossRef]
- Terayama, H. Method of Colloid Titration (a New Titration between Polymer Ions). J. Polym. Sci. 1952, 8, 243–253. [Google Scholar] [CrossRef]
- Zhou, Y.; Fan, M.; Chen, L. Interface and Bonding Mechanisms of Plant Fibre Composites: An Overview; Elsevier Ltd.: Amsterdam, The Netherlands, 2016; Volume 101, ISBN 7790390554. [Google Scholar]
- Colom, X.; Carrasco, F.; Pagès, P.; Canavate, J. Effects of Different Treatments on the Interface of HDPE/Lignocellulosic Fiber Composites. Compos. Sci. Technol. 2003, 63, 161–169. [Google Scholar] [CrossRef]
- Tarrés, Q.; Hernández-díaz, D.; Ardanuy, M. Interface Strength and Fiber Content Influence on Corn Stover Fibers Reinforced Bio-polyethylene Composites Stiffness. Polymers 2021, 13, 768. [Google Scholar] [CrossRef] [PubMed]
- Fukuda, H.; Kawata, K. On Young’s Modulus of Short Fibre Composites. Fibre Sci. Technol. 1974, 7, 207–222. [Google Scholar] [CrossRef]
- Jiménez, A.M.; Delgado-Aguilar, M.; Tarrés, Q.; Quintana, G.; Fullana-i-Palmer, P.; Mutjè, P.; Espinach, F.X. Sugarcane Bagasse Reinforced Composites: Studies on the Young’s Modulus and Macro and Micro-Mechanics. Bioresources 2017, 12, 3618–3629. [Google Scholar] [CrossRef] [Green Version]
- Granda, L.A.; Espinach, F.X.; Méndez, J.A.; Tresserras, J.; Delgado-Aguilar, M.; Mutjé, P. Semichemical Fibres of Leucaena Collinsii Reinforced Polypropylene Composites: Young’s Modulus Analysis and Fibre Diameter Effect on the Stiffness. Compos. B Eng. 2016, 92, 332–337. [Google Scholar] [CrossRef]
- Arbelaiz, A.; Fernández, B.; Cantero, G.; Llano-Ponte, R.; Valea, A.; Mondragon, I. Mechanical Properties of Flax Fibre/Polypropylene Composites. Influence of Fibre/Matrix Modification and Glass Fibre Hybridization. Compos. Part A Appl. Sci. Manuf. 2005, 36, 1637–1644. [Google Scholar] [CrossRef]
- Arrakhiz, F.Z.; el Achaby, M.; Malha, M.; Bensalah, M.O.; Fassi-Fehri, O.; Bouhfid, R.; Benmoussa, K.; Qaiss, A. Mechanical and Thermal Properties of Natural Fibers Reinforced Polymer Composites: Doum/Low Density Polyethylene. Mater. Des. 2013, 43, 200–205. [Google Scholar] [CrossRef]
- Alonso-Montemayor, F.J.; Tarrés, Q.; Oliver-Ortega, H.; Espinach, F.X.; Narro-Céspedes, R.I.; Castañeda-Facio, A.O.; Delgado-Aguilar, M. Enhancing the Mechanical Performance of Bleached Hemp Fibers Reinforced Polyamide 6 Composites: A Competitive Alternative to Commodity Composites. Polymers 2020, 12, 1041. [Google Scholar] [CrossRef] [PubMed]
- Tarrés, Q.; Ardanuy, M. Evolution of Interfacial Shear Strength and Mean Intrinsic Single Strength in Biobased Composites from Bio-Polyethylene and Thermo-Mechanical Pulp-Corn Stover Fibers. Polymers 2020, 12, 1308. [Google Scholar] [CrossRef] [PubMed]
- Serra, A.; Tarrés, Q.; Claramunt, J.; Mutjé, P.; Ardanuy, M.; Espinach, F.X. Behavior of the Interphase of Dyed Cotton Residue Flocks Reinforced Polypropylene Composites. Compos. B Eng. 2017, 128, 200–207. [Google Scholar] [CrossRef] [Green Version]
- López, J.P.; Boufi, S.; el Mansouri, N.E.; Mutjé, P.; Vilaseca, F. PP Composites Based on Mechanical Pulp, Deinked Newspaper and Jute Strands: A Comparative Study. Compos. B Eng. 2012, 43, 3453–3461. [Google Scholar] [CrossRef]
- Oushabi, A.; Sair, S.; Oudrhiri Hassani, F.; Abboud, Y.; Tanane, O.; el Bouari, A. The Effect of Alkali Treatment on Mechanical, Morphological and Thermal Properties of Date Palm Fibers (DPFs): Study of the Interface of DPF–Polyurethane Composite. S. Afr. J. Chem. Eng. 2017, 23, 116–123. [Google Scholar] [CrossRef]
- Mahesh, A.; Rudresh, B.M.; Reddappa, H.N. Potential of Natural Fibers in the Modification of Mechanical Behavior of Polypropylene Hybrid Composites. Mater. Today Proc. 2022, 54, 131–136. [Google Scholar] [CrossRef]
- Bhagat, A.B.; Ghosh, A.K. Performance Properties of PP/Sisal Fibre Composites Having Near Critical Fibre Length and Prediction of Their Properties. Fibers Polym. 2022, 23, 1983–1994. [Google Scholar] [CrossRef]
- Keener, T.J.; Stuart, R.K.; Brown, T.K. Maleated Coupling Agents for Natural Fibre Composites. Compos. Part A Appl. Sci. Manuf. 2004, 35, 357–362. [Google Scholar] [CrossRef]
- Ndiaye, D.; Gueye, M.; Malang Badji, A.; Thiandoume, C.; Dasylva, A.; Tidjani, A. Effects of reinforcing fillers and coupling agents on performances of wood–polymer composites. In Bio-Based Composites for High-Performance Materials: From Strategy to Industrial Application; CRC Press: Boca Raton, FL, USA, 2014; pp. 113–132. [Google Scholar]
- Wong, K.H.; Syed Mohammed, D.; Pickering, S.J.; Brooks, R. Effect of Coupling Agents on Reinforcing Potential of Recycled Carbon Fibre for Polypropylene Composite. Compos. Sci. Technol. 2012, 72, 835–844. [Google Scholar] [CrossRef]
- Franco-Marquès, E.; Méndez, J.; Pèlach, M.A.; Vilaseca, F.; Bayer, J.; Mutjé, P. Influence of Coupling Agents in the Preparation of Polypropylene Composites Reinforced with Recycled Fibers. Chem. Eng. J. 2011, 166, 1170–1178. [Google Scholar] [CrossRef]
- Poornima, C.; Uthamballi Shivanna, M.; Sathyanarayana, S. Influence of Basalt Fiber and Maleic Anhydride on the Mechanical and Thermal Properties of Polypropylene. Polym. Compos. 2022. early view. [Google Scholar] [CrossRef]
- Aguado, R.; Espinach, F.X.; Vilaseca, F.; Tarrés, Q.; Mutjé, P.; Delgado-Aguilar, M. Approaching a Zero-Waste Strategy in Rapeseed (Brassica Napus) Exploitation: Sustainably Approaching Bio-Based Polyethylene Composites. Sustainability 2022, 14, 7942. [Google Scholar] [CrossRef]
- Shi, S.; Yang, C.; Nie, M. Enhanced Interfacial Strength of Natural Fiber/Polypropylene Composite with Mechanical-Interlocking Interface. ACS Sustain. Chem. Eng. 2017, 5, 10413–10420. [Google Scholar] [CrossRef]
- López, J.P.; Méndez, J.A.; Espinach, F.X.; Julián, F.; Mutjé, P.; Vilaseca, F. Tensile Strength Characteristics of Polypropylene Composites Reinforced with Stone Groundwood Fibers from Softwood. BioResource 2012, 7, 3188–3200. [Google Scholar] [CrossRef]
- Mohanty, S.; Nayak, S.K.; Verma, S.K.; Tripathy, S.S. Effect of MAPP as a Coupling Agent on the Performance of Jute-PP Composites. J. Reinf. Plast. Compos. 2004, 23, 625–637. [Google Scholar] [CrossRef]
- Pregi, E.; Faludi, G.; Kun, D.; Móczó, J.; Pukánszky, B. Three-Component Polypropylene/Lignin/Flax Composites with High Natural Additive Content for Structural Applications. Ind. Crops Prod. 2022, 182, 114890. [Google Scholar] [CrossRef]
- Fu, S.-Y.; Lauke, B.; Mäder, E.; Yue, C.-Y.; Hu, X. Tensile Properties of Short-Glass-Fiber-and Short-Carbon-Fiber-Reinforced Polypropylene Composites. Compos. Part A Appl. Sci. Manuf. 2000, 31, 1117–1125. [Google Scholar] [CrossRef]
- Rao, K.M.M.; Rao, K.M. Extraction and Tensile Properties of Natural Fibers: Vakka, Date and Bamboo. Compos. Struct. 2007, 77, 288–295. [Google Scholar] [CrossRef]
- Ku, H.; Wang, H.; Pattarachaiyakoop, N.; Trada, M. A Review on the Tensile Properties of Natural Fiber Reinforced Polymer Composites. Compos. B Eng. 2011, 42, 856–873. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Richards, C.; Watson, J. High-Performance Glass Fiber Development for Composite Applications. Int. J. Appl. Glass Sci. 2014, 5, 65–81. [Google Scholar] [CrossRef]
- Richely, E.; Bourmaud, A.; Placet, V.; Guessasma, S.; Beaugrand, J. A Critical Review of the Ultrastructure, Mechanics and Modelling of Flax Fibres and Their Defects. Prog. Mater. Sci. 2022, 124, 100851. [Google Scholar] [CrossRef]
- Kelly, A.; Tyson, W.R. Tensile Properties of Fibre-Reinforced Metals: Copper/Tungsten and Copper/Molybdenum. J. Mech. Phys. Solids 1965, 13, 329–350. [Google Scholar] [CrossRef]
- Janowski, G.; Frącz, W.; Bąk, Ł. The Mechanical Properties Prediction of Poly [(3-Hydroxybutyrate)-Co-(3-Hydroxyvalerate)] (PHBV) Biocomposites on a Chosen Example. Materials 2022, 15, 7531. [Google Scholar] [CrossRef]
- Tucker, C.L.; Liang, E. Stiffness Predictions for Unidirectional Short-Fiber Composites: Review and Evaluation. Compos. Sci. Technol. 1999, 59, 655–671. [Google Scholar] [CrossRef]
- Li, Y.; Pickering, K.L.; Farrell, R.L. Determination of Interfacial Shear Strength of White Rot Fungi Treated Hemp Fibre Reinforced Polypropylene. Compos. Sci. Technol. 2009, 69, 1165–1171. [Google Scholar] [CrossRef]
- Bowyer, W.H.; Bader, H.G. On the Reinforcement of Thermoplastics by Imperfectly Aligned Discontinuous Fibres. J. Mater. Sci. 1972, 7, 1315–1321. [Google Scholar] [CrossRef]
- Hirsch, T.J. Modulus of Elasticity of Concrete Affected by Elastic Moduli of Cement Paste Matrix and Aggregate. J. Proc. 1962, 59, 427–452. [Google Scholar]
- Fu, S.-Y.; Lauke, B. Effects of Fiber Length and Fiber Orientation Distributions on the Tensile Strength of Short-Fiber-Reinforced Polymers. Compos. Sci. Technol. 1996, 56, 1179–1190. [Google Scholar] [CrossRef]
- Thomason, J.L. Interfacial Strength in Thermoplastic Composites—At Last an Industry Friendly Measurement Method? Compos. Part A Appl. Sci. Manuf. 2002, 33, 1283–1288. [Google Scholar] [CrossRef] [Green Version]
- Inceoglu, F.; Ville, J.; Ghamrin, N.; Pradel, J.L.; Durin, A.; Valette, R.; Vergnes, B. Correlation between Processing Conditions and Fiber Breakage during Compunding of Glass Fiber-Reinforced Polyamide. Polym. Compos. 2011, 32, 1842–1850. [Google Scholar] [CrossRef]
- Al-Oqla, F.M.; Alothman, O.Y.; Jawaid, M.; Sapuan, S.M.; Es-Saheb, M.H. Processing and properties of date palm fibers and its composites. In Biomass and Bioenergy: Processing and Properties; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; Volume 9783319076, pp. 1–25. ISBN 9783319075785. [Google Scholar]
- Thomason, J.L. The Influence of Fibre Properties on the Properties of Glass-Fibre-Reinforced Polyamide 6,6. J. Compos. Mater. 2000, 34, 158–172. [Google Scholar] [CrossRef]
- Amuthakkannan, P.; Manikandan, V.; Jappes, J.T.W.; Uthayakumar, M. Effect of Fibre Length and Fibre Content on Mechanical Properties of Short Basalt Fibre Reinforced Polymer Matrix Composites. Mater. Phys. Mech. 2013, 16, 107–117. [Google Scholar]
- Alves Fidelis, M.E.; Pereira, T.V.C.; Gomes, O.D.F.M.; de Andrade Silva, F.; Toledo Filho, R.D. The Effect of Fiber Morphology on the Tensile Strength of Natural Fibers. J. Mater. Res. Technol. 2013, 2, 149–157. [Google Scholar] [CrossRef] [Green Version]
- López, J.P.; Méndez, J.A.; Mansouri, N.; Mutjé, P.; Vilaseca, F. Mean Intrinsic Tensile Properties of Stone Groundwood Fibers from Softwood. Bioresources 2011, 6, 5037–5049. [Google Scholar] [CrossRef]
- Pegoretti, A.; della Volpe, C.; Detassis, M.; Migliaresi, C.; Wagner, H.D. Thermomechanical Behaviour of Interfacial Region in Carbon Fibre/Epoxy Composites. Compos. Part A Appl. Sci. Manuf. 1996, 27, 1067–1074. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Gassan, J. Composites Reinforced with Cellulose_Bledzki_1999.Pdf. Prog. Polym. Sci. 1999, 24, 221–274. [Google Scholar] [CrossRef]
- Kompella, M.K.; Lambros, J. Micromechanical Characterization of Cellulose Fibers. Polym. Test. 2002, 21, 523–530. [Google Scholar] [CrossRef]



| Without MAPP | With 4% MAPP | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Henequen Content (wt.%) | (MPa) | (GPa) | (%) | (MPa) | (MPa) | (GPa) | (%) | (MPa) | |
| 0 | 0 | 27.6 ± 0.5 | 1.5 ± 0.1 | 9.3 ± 0.2 | - | 27.6 ± 0.5 | 1.5 ± 0.1 | 9.3 ± 0.2 | - |
| 10 | 0.064 | 27.5 ± 0.3 | 2.4 ± 0.1 | 3.8 ± 0.1 | 22.5 | 31.7 ± 0.9 | 2.3 ± 0.1 | 4.2 ± 0.2 | 23.5 |
| 20 | 0.133 | 29.2 ± 0.5 | 3.1 ± 0.1 | 3.5 ± 0.2 | 21.8 | 36.4 ± 0.7 | 3.1 ± 0.2 | 3.7 ± 0.1 | 22.3 |
| 30 | 0.208 | 30.7 ± 0.4 | 4.3 ± 0.2 | 2.5 ± 0.1 | 18.7 | 40.8 ± 1.1 | 4.2 ± 0.2 | 3.4 ± 0.2 | 21.5 |
| 40 | 0.290 | 35.0 ± 0.7 | 5.2 ± 0.1 | 1.9 ± 0.1 | 16.2 | 47.2 ± 1.1 | 5.3 ± 0.2 | 3.3 ± 0.2 | 21.2 |
| 50 | 0.379 | 38.2 ± 1.1 | 6.4 ± 0.2 | 1.3 ± 0.2 | 12.8 | 52.4 ± 1.3 | 6.4 ± 0.2 | 3.1 ± 0.1 | 20.7 |
| Material | MGCh (µeq/g) |
|---|---|
| PP | 4.56 |
| MAPP | 4.67 |
| Henequen | 20.67 |
| Jute | 12.16 |
| Sisal | 23.10 |
| Bleached Kraft pulp | 8.40 |
| Composite Material | FTSF | Ratio 1 |
|---|---|---|
| Henequen/PP/without MAPP | 79.82 | 1 |
| Henequen/PP/with 4% MAPP | 109.79 | 1.4 |
| GF/PP | 258.99 | 3.2 |
| Henequen Content (wt.%) | (µm) | (µm) | (µm) | Aspect Ratio |
|---|---|---|---|---|
| 10 | 509.1 | 826.3 ± 10.6 | 25.5 ± 0.1 | 32.4 |
| 20 | 496.4 | 784.2 ± 12.3 | 25.6 ± 0.1 | 29.2 |
| 30 | 477.2 | 741.9 ± 5.9 | 25.3 ± 0.2 | 29.3 |
| 40 | 432.4 | 708.1 ± 17.2 | 25.4 ± 0.2 | 27.9 |
| 50 | 434.0 | 674.3 ± 7.2 | 25.5 ± 0.1 | 26.4 |
| Henequen Content (wt.%) | τ | ||||
|---|---|---|---|---|---|
| 10 | 0.20 | 0.306 | 0.66 | 14.99 | 421.5 |
| 20 | 0.25 | 0.313 | 0.79 | 14.11 | 364.7 |
| 30 | 0.24 | 0.306 | 0.79 | 14.58 | 365.8 |
| 40 | 0.23 | 0.304 | 0.77 | 14.74 | 331.9 |
| 50 | 0.20 | 0.300 | 0.68 | 14.75 | 510.2 |
| 0.22 | 0.306 | 0.74 | 14.63 | 398.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espinach, F.X.; Julian, F.; Alcalà, M.; Vilaseca, F.; Carrasco, F.; Mutjé, P. Effective Tensile Strength Estimation of Natural Fibers through Micromechanical Models: The Case of Henequen Fiber Reinforced-PP Composites. Polymers 2022, 14, 4890. https://doi.org/10.3390/polym14224890
Espinach FX, Julian F, Alcalà M, Vilaseca F, Carrasco F, Mutjé P. Effective Tensile Strength Estimation of Natural Fibers through Micromechanical Models: The Case of Henequen Fiber Reinforced-PP Composites. Polymers. 2022; 14(22):4890. https://doi.org/10.3390/polym14224890
Chicago/Turabian StyleEspinach, Francesc Xavier, Fernando Julian, Manel Alcalà, Fabiola Vilaseca, Félix Carrasco, and Pere Mutjé. 2022. "Effective Tensile Strength Estimation of Natural Fibers through Micromechanical Models: The Case of Henequen Fiber Reinforced-PP Composites" Polymers 14, no. 22: 4890. https://doi.org/10.3390/polym14224890
APA StyleEspinach, F. X., Julian, F., Alcalà, M., Vilaseca, F., Carrasco, F., & Mutjé, P. (2022). Effective Tensile Strength Estimation of Natural Fibers through Micromechanical Models: The Case of Henequen Fiber Reinforced-PP Composites. Polymers, 14(22), 4890. https://doi.org/10.3390/polym14224890