Evaluation of Microscopic Damage of PEEK Polymers under Cyclic Loadings Using Molecular Dynamics Simulations
Abstract
:1. Introduction
2. Method
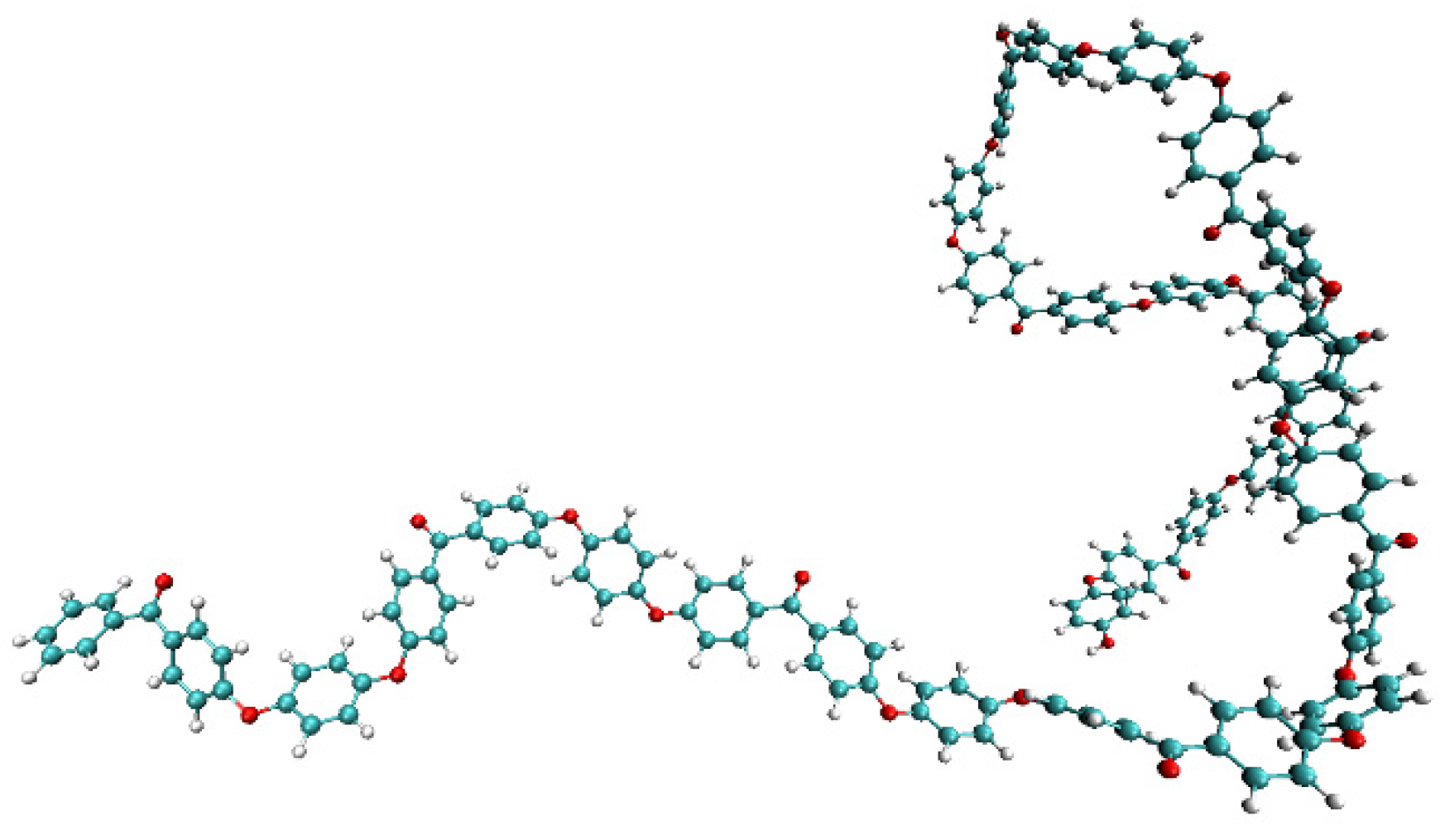
2.1. Modeling and Relaxation Process
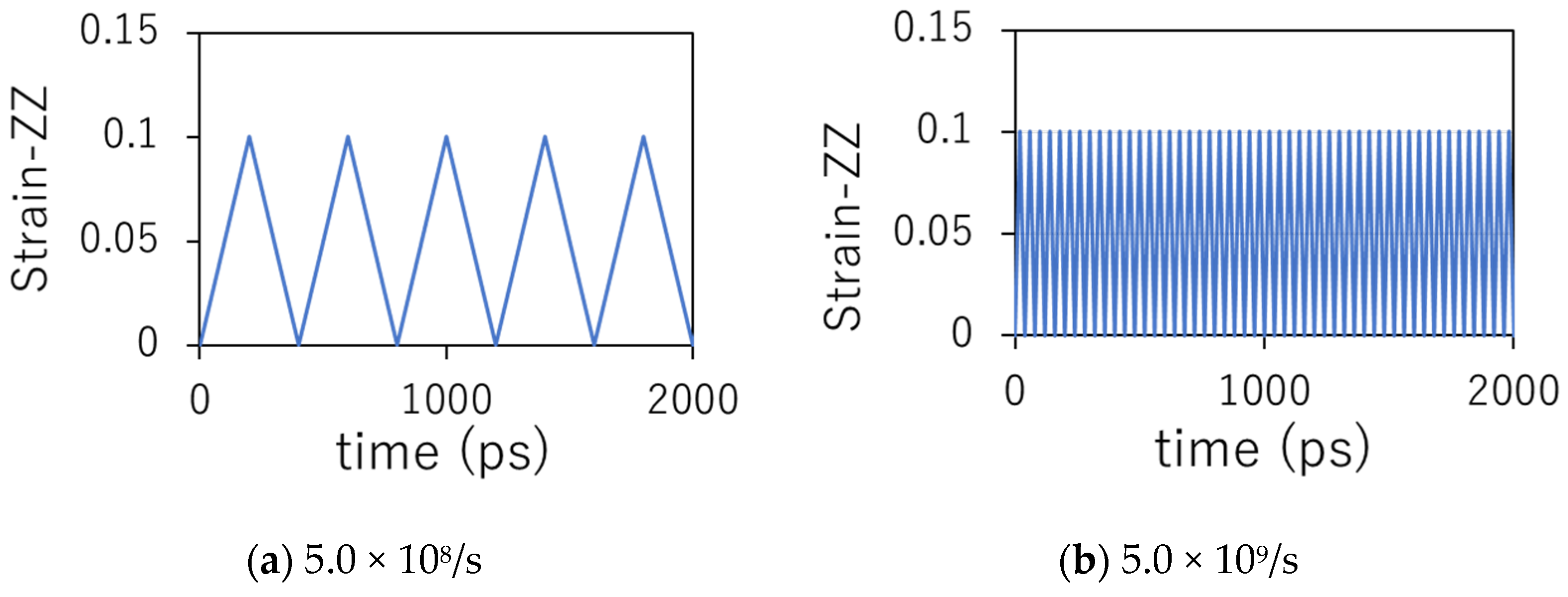
2.2. Cyclic Loading
2.3. Evaluation of Resin Damage
3. Results and Discussion
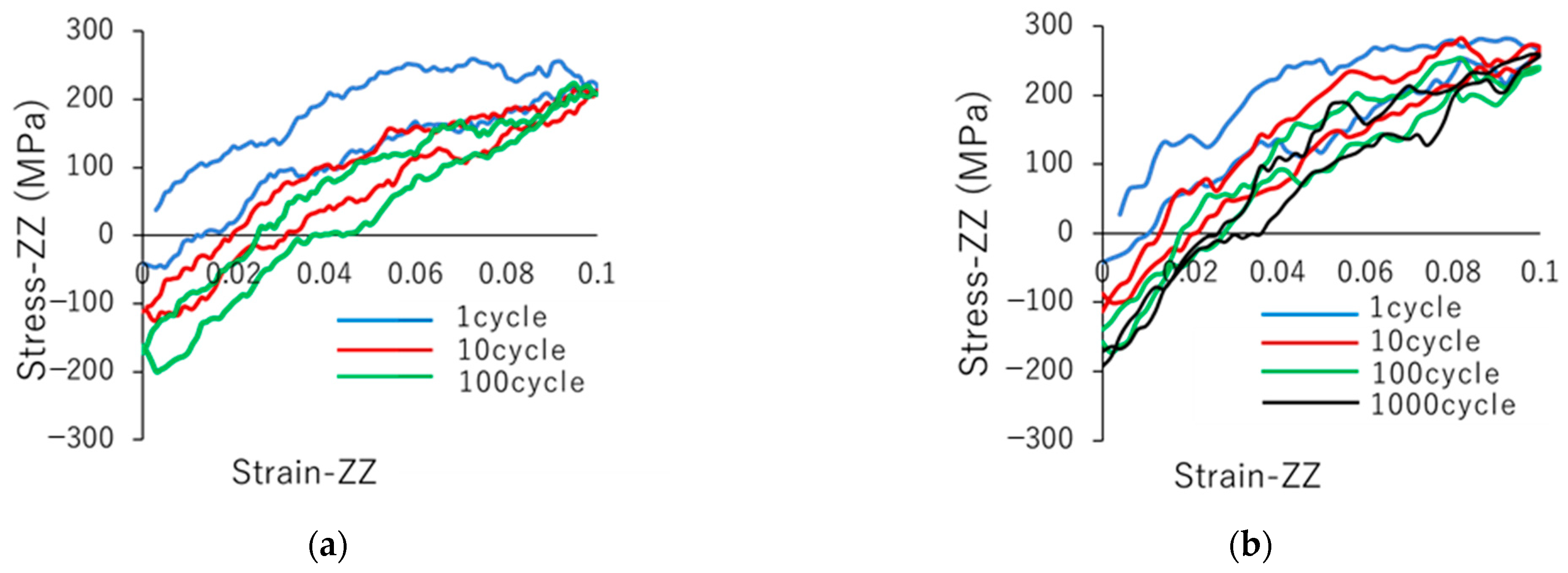
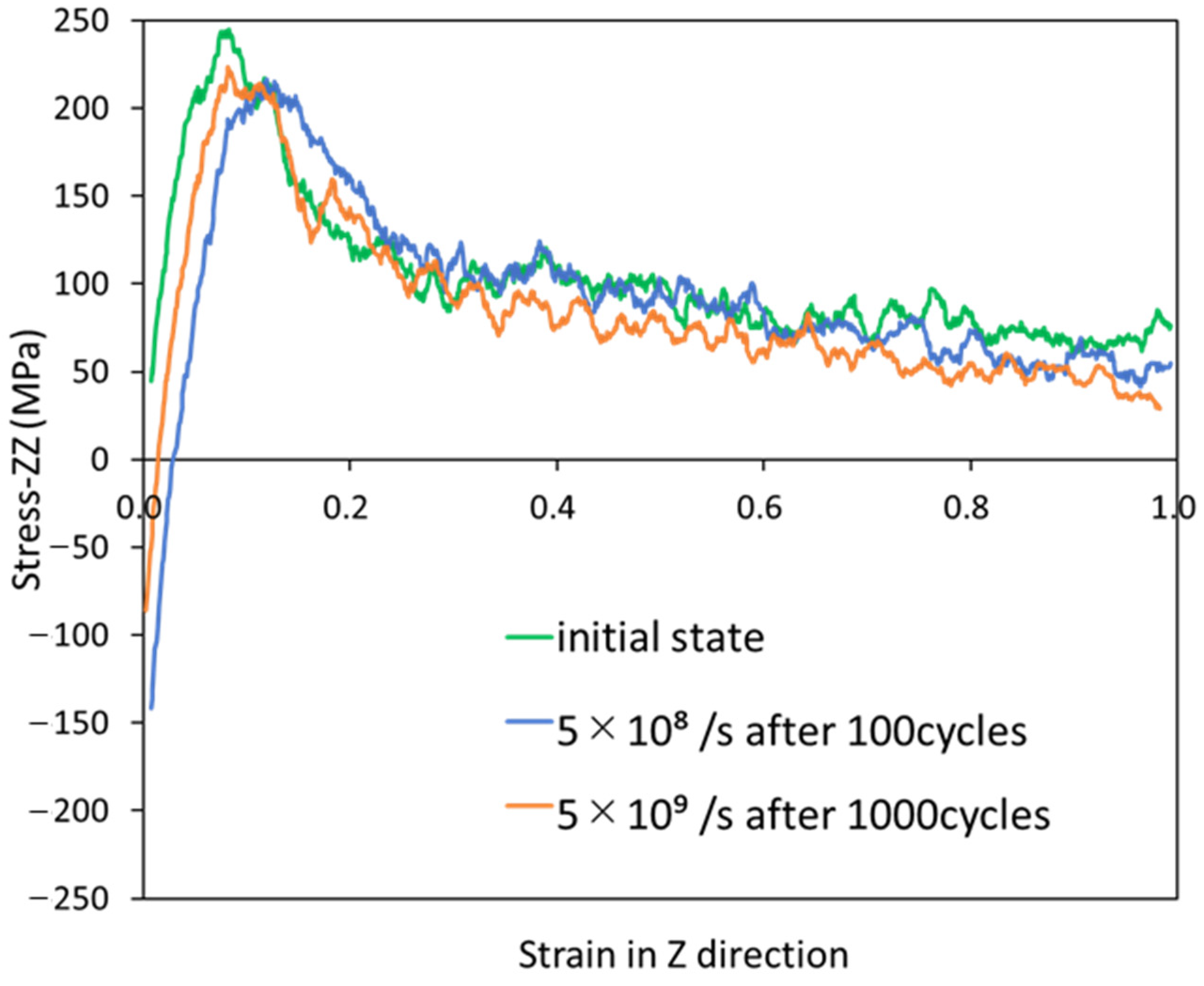
3.1. Stress–Strain Curves
3.2. Entropy Generation
3.3. End-to-End Distance Distribution
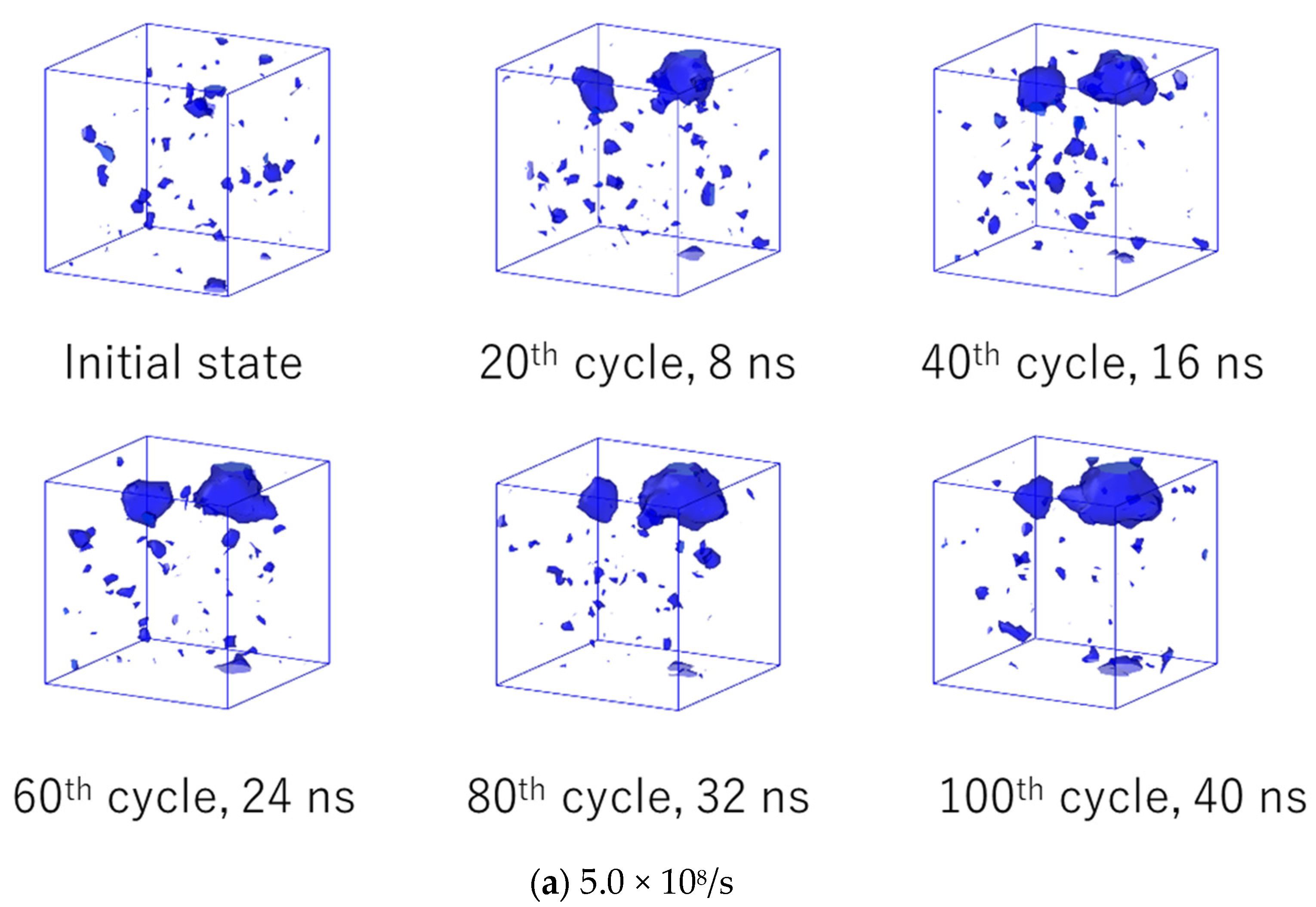
3.4. Void Analysis
3.5. Residual Strength
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, M.S.; Seo, H.Y.; Kang, C.G. Comparative study on mechanical properties of CR340/CFRP composites through three point bending test by using theoretical and experimental methods. Int. J. Precis Eng. Manuf. Green Technol. 2016, 3, 359–365. [Google Scholar] [CrossRef]
- Alshammari, B.A.; Alsuhybani, M.S.; Almushaikeh, A.M.; Alotaibi, B.M.; Alenad, A.M.; Alqahtani, N.B.; Alharbi, A.G. Comprehensive review of the properties and modifications of carbon fiber-reinforced thermoplastic composites. Polymers 2021, 13, 2474. [Google Scholar] [CrossRef] [PubMed]
- Sawamura, Y.; Yamazaki, Y.; Yoneyama, S.; Koyanagi, J. Multi-scale numerical simulation of impact failure for cylindrical CFRP. Adv. Compos. Mater. 2021, 30 (Suppl. 1), 19–38. [Google Scholar] [CrossRef]
- Takase, N.; Koyanagi, J.; Mori, K.; Sakai, T. Molecular Dynamics Simulation for Evaluating Fracture Entropy of a Polymer Material under Various Combined Stress States. Materials 2021, 14, 1884. [Google Scholar] [CrossRef] [PubMed]
- Kawai, T.; Soeno, S.; Kuroda, S.I.; Koido, S.; Nemoto, T.; Tamada, M. Deformation induced void formation and growth in β nucleated isotactic polypropylene. Polymer 2019, 178, 121523. [Google Scholar] [CrossRef]
- Tamboura, S.; Laribi, M.A.; Fitoussi, J.; Shirinbayan, M.; Bi, R.T.; Tcharkhtchi, A.; Dali, H.B. Damage and fatigue life prediction of short fiber reinforced composites submitted to variable temperature loading: Application to Sheet Molding Compound composites. Int. J. Fatigue 2020, 138, 105676. [Google Scholar] [CrossRef]
- Movahedi-Rad, A.V.; Eslami, G.; Keller, T. A novel fatigue life prediction methodology based on energy dissipation in viscoelastic materials. Int. J. Fatigue 2021, 152, 106457. [Google Scholar] [CrossRef]
- Aoki, R.; Higuchi, R.; Yokozeki, T. Fatigue simulation for progressive damage in CFRP laminates using intra-laminar and inter-laminar fatigue damage models. Int. J. Fatigue 2021, 143, 106015. [Google Scholar] [CrossRef]
- Brod, M.; Dean, A.; Rolfes, R. Numerical life prediction of unidirectional fiber composites under block loading conditions using a progressive fatigue damage model. Int. J. Fatigue 2021, 147, 106159. [Google Scholar] [CrossRef]
- Di Maio, D.; Voudouris, G.; Sever, I.A. Investigation of fatigue damage growth and selfheating behaviour of cross-ply laminates using simulation-driven dynamic test. Int. J. Fatigue 2022, 155, 106617. [Google Scholar] [CrossRef]
- Vassilopoulos, A.P. The history of fiber-reinforced polymer composite laminate fatigue. Int. J. Fatigue 2020, 134, 105512. [Google Scholar] [CrossRef]
- Koyanagi, J.; Mochizuki, A.; Higuchi, R.; Tan, V.B.C.; Tay, T.E. Finite element model for simulating entropy-based strength-degradation of carbon-fiber-reinforced plastics subjected to cyclic loadings. Int. J. Fatigue 2022, 165, 107204. [Google Scholar] [CrossRef]
- Jiang, B.; Zhang, M.; Fu, L.; Zhou, M.; Zhai, Z. Molecular dynamics simulation on the interfacial behavior of over-molded hybrid fiber reinforced thermoplastic composites. Polymers 2020, 12, 1270. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Liu, J.; Zhang, M.; Zhai, Z.; Jiang, B. Molecular Dynamics Simulation on the effect of self-resistance electric heating on carbon fiber surface chemical properties and fiber/PP interfacial behavior. Polymers 2022, 14, 1043. [Google Scholar] [CrossRef] [PubMed]
- Morita, M.; Oya, Y.; Kato, N.; Mori, K.; Koyanagi, J. Effect of Electrostatic Interactions on the Interfacial Energy between Thermoplastic Polymers and Graphene Oxide: A Molecular Dynamics study. Polymers 2022, 14, 2579. [Google Scholar] [CrossRef]
- Oya, Y.; Inuyama, K.; Okabe, T.; Koyanagi, J.; Matsuzaki, R. Analysis of structure characteristics in laminated graphene oxide nanocomposites using molecular dynamics simulation. Adv. Compos. Mater. 2018, 27 (Suppl. 4), 427–438. [Google Scholar] [CrossRef]
- Hossain, D.; Tschopp, M.A.; Ward, D.K.; Bouvard, J.L.; Wang, P.; Horstemeyer, M.F. Molecular dynamics simulations of deformation mechanisms of amorphous polyethylene. Polymer 2010, 51, 6071–6083. [Google Scholar] [CrossRef]
- Bao, Q.; Yang, Z.; Lu, Z. Molecular dynamics simulation of amorphous polyethylene (PE) under cyclic tensile-compressive loading below the glass transition temperature. Polymer 2020, 186, 121968. [Google Scholar] [CrossRef]
- Yashiro, K.; Naito, M.; Ueno, S.; Jie, F. Molecular dynamics simulation of polyethylene under cyclic loading: Effect of loading condition and chain length. Int. J. Mech. Sci. 2010, 52, 136–145. [Google Scholar] [CrossRef]
- Li, C.; Jaramillo, E.; Strachan, A. Molecular dynamics simulations on cyclic deformation of an epoxy thermoset. Polymer 2013, 54, 881–890. [Google Scholar] [CrossRef]
- Hagita, K.; Morita, H.; Doi, M.; Takano, H. Coarse-grained molecular dynamics simulation of filled polymer nanocomposites under uniaxial elongation. Macromolecules 2016, 49, 1972–1983. [Google Scholar] [CrossRef] [Green Version]
- Chawla, R.; Sharma, S. Molecular dynamics simulation of carbon nanotube pull-out from polyethylene matrix. Compos. Sci. Technol. 2017, 144, 169–177. [Google Scholar] [CrossRef]
- Sato, M.; Hasegawa, K.; Koyanagi, J.; Higuchi, R.; Ishida, Y. Residual strength prediction for unidirectional CFRP using a nonlinear viscoelastic constitutive equation considering entropy damage. Compos. A 2021, 141, 106178. [Google Scholar] [CrossRef]
- Sakai, T.; Takase, N.; Oya, Y.; Koyanagi, J. A Possibility for Quantitative Detection of Mechanically-Induced Invisible Damage by Thermal Property Measurement via Entropy Generation for a Polymer Material. Materials 2022, 15, 737. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Yang, H.; Liu, W.; Zhang, K.; Huang, A. Confidence level and reliability analysis of the fatigue life of CFRP laminates predicted based on fracture fatigue entropy. Int. J. Fatigue 2022, 156, 106659. [Google Scholar] [CrossRef]
- Basaran, C.; Nie, S. An irreversible thermodynamics theory for damage mechanics of solids. Int. J. Damage Mech. 2004, 13, 205–223. [Google Scholar] [CrossRef]
- Zhang, M.H.; Shen, X.H.; He, L.; Zhang, K.S. Application of differential entropy in characterizing the deformation inhomogeneity and life prediction of low-cycle fatigue of metals. Materials 2018, 11, 1917. [Google Scholar] [CrossRef] [Green Version]
- Ontiveros, V.; Amiri, M.; Kahirdeh, A.; Modarres, M. Thermodynamic entropy generation in the course of the fatigue crack initiation. Fatigue Fract. Engng. Mater Struct. 2017, 40, 423–434. [Google Scholar] [CrossRef]
- Yun, H.; Modarres, M. Measures of Entropy to Characterize Fatigue Damage in Metallic Materials. Entropy 2019, 21, 804. [Google Scholar] [CrossRef] [Green Version]
- Sosnovskiy, L.A.; Sherbakov, S.S. Mechanothermodynamic entropy and analysis of damage state of complex systems. Entropy 2016, 18, 268. [Google Scholar] [CrossRef]
- Suarez, E.; Díaz, N.; Suarez, D. Entropy calculations of single molecules by combining the rigid–rotor and harmonic-oscillator approximations with conformational entropy estimations from molecular dynamics simulations. Chem. Theor. Comput. 2011, 7, 2638–2653. [Google Scholar] [CrossRef] [PubMed]
- Suárez, D.; Díaz, N. Direct methods for computing single-molecule entropies from molecular simulations. Wiley Interdiscip. Rev. Comp. Mol. Sci. 2015, 5, 1–26. [Google Scholar] [CrossRef]
- PolyParGen. Available online: http://polypargen.com/ (accessed on 24 May 2022).
- Yabe, I.; Mori, K.; Koyanagi, J. Development of PolyParGenv2 Software for Determination of Molecular Dynamics Simulation Parameters for Molecules with Crosslinked or Condensed Ring Structures. J. Comput. Chem. Jpn. Int. Ed. 2020, 6, 2019–2031. [Google Scholar] [CrossRef]
- Pisani, W.A.; Radue, M.S.; Chinkanjanarot, S.; Bednarcyk, B.A.; Pineda, E.J.; Waters, K.; Pandey, R.; King, J.A.; Odegard, G.M. Multiscale modeling of PEEK using reactive molecular dynamics modeling and micromechanics. Polymer 2019, 163, 96–105. [Google Scholar] [CrossRef] [Green Version]
- Solvay. KetaSpire PEEK Design & Processing Guide; Solvay: Brussels, Belgium, 2015. [Google Scholar]
- GROMACS [Soft]. Available online: https://www.gromacs.org/ (accessed on 24 May 2022).
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Kollman, P.A. Application of RESP charges to calculate conformational energies, hydrogen bond energies, and free energies of solvation. J. Am. Chem. Soc. 1993, 115, 9620–9631. [Google Scholar] [CrossRef]
- Valiev, M.; Bylaska, E.J.; Govind, N.; Kowalski, K.; Straatsma, T.P.; Van Dam, H.J.J.; Wang, D.; Nieplocha, J.; Aprà, E.; Windus, T.L.; et al. NWChem: A comprehensive and scalable open-source solution for large scale molecular simulations. Comput. Phys. Commun. 2010, 181, 1477–1489. [Google Scholar] [CrossRef] [Green Version]
- Naderi, M.; Amiri, M.; Khonsari, M.M. On the thermodynamic entropy of fatigue fracture. Proc. R Soc. A. 2010, 466, 423–438. [Google Scholar] [CrossRef] [Green Version]
- de Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University: Cornell, NY, USA, 1979. [Google Scholar]
- OVITO [Soft]. Available online: https://www.ovito.org/ (accessed on 27 September 2022).
- ParaView [Soft]. Available online: https://www.paraview.org/ (accessed on 27 September 2022).
- Stukowski, A. Computational Analysis Methods in Atomistic Modeling of Crystals. JOM 2014, 66, 399–407. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iwamoto, S.; Oya, Y.; Koyanagi, J. Evaluation of Microscopic Damage of PEEK Polymers under Cyclic Loadings Using Molecular Dynamics Simulations. Polymers 2022, 14, 4955. https://doi.org/10.3390/polym14224955
Iwamoto S, Oya Y, Koyanagi J. Evaluation of Microscopic Damage of PEEK Polymers under Cyclic Loadings Using Molecular Dynamics Simulations. Polymers. 2022; 14(22):4955. https://doi.org/10.3390/polym14224955
Chicago/Turabian StyleIwamoto, Shun, Yutaka Oya, and Jun Koyanagi. 2022. "Evaluation of Microscopic Damage of PEEK Polymers under Cyclic Loadings Using Molecular Dynamics Simulations" Polymers 14, no. 22: 4955. https://doi.org/10.3390/polym14224955
APA StyleIwamoto, S., Oya, Y., & Koyanagi, J. (2022). Evaluation of Microscopic Damage of PEEK Polymers under Cyclic Loadings Using Molecular Dynamics Simulations. Polymers, 14(22), 4955. https://doi.org/10.3390/polym14224955





