Mechanism of Morphology Development in HDGEBA/PAMS Hybrid Thermosets: Monte Carlo Simulation and LSCM Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Samples Preparation
2.2. Measurements
3. Results
3.1. Gelation, Viscosity Measurements, and Glass Transition Temperatures
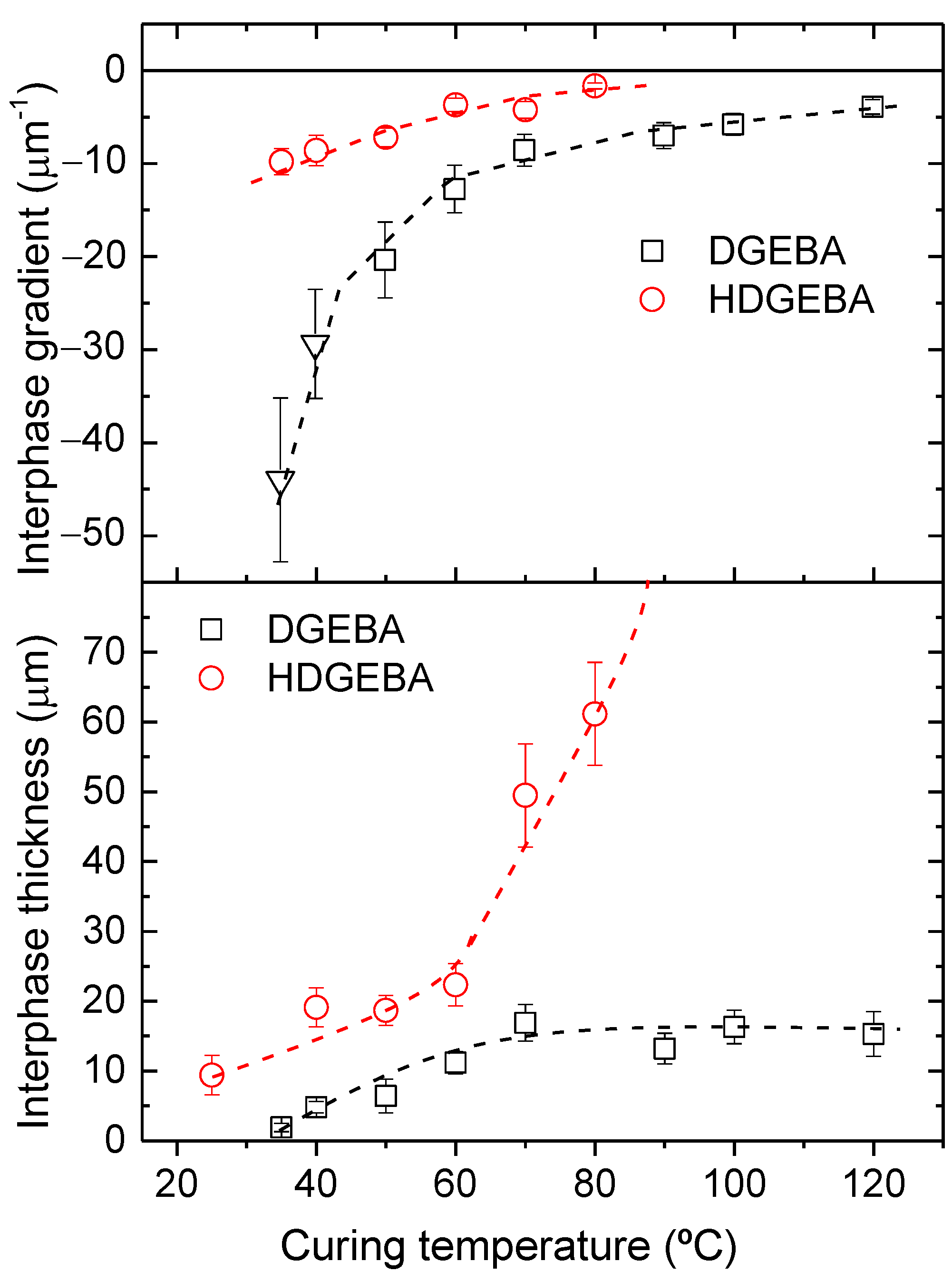
3.2. Morphology Analysis of Cured Samples
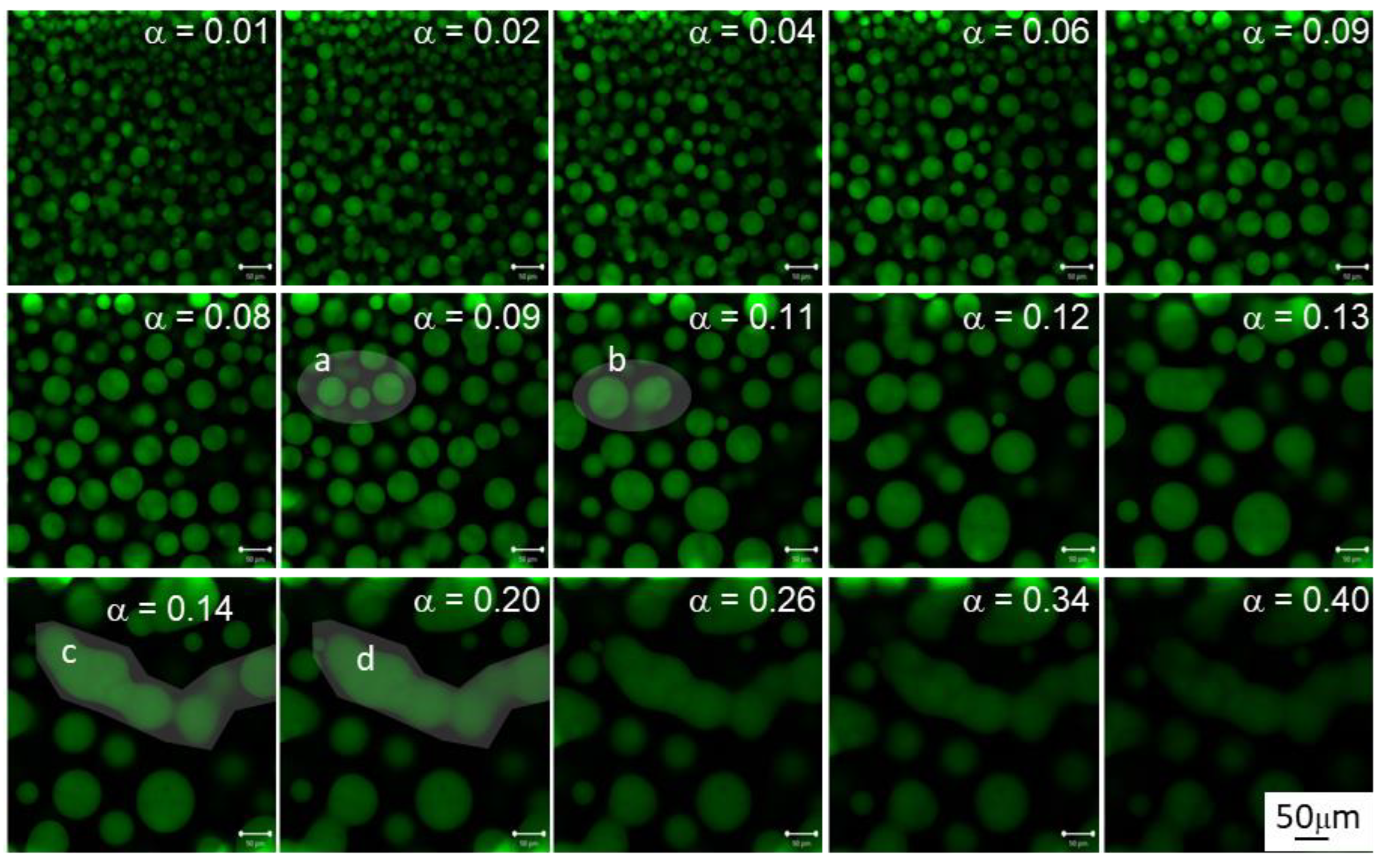
3.3. Morphology Evolution with Conversion at 40 °C
3.4. 0-Time Distribution
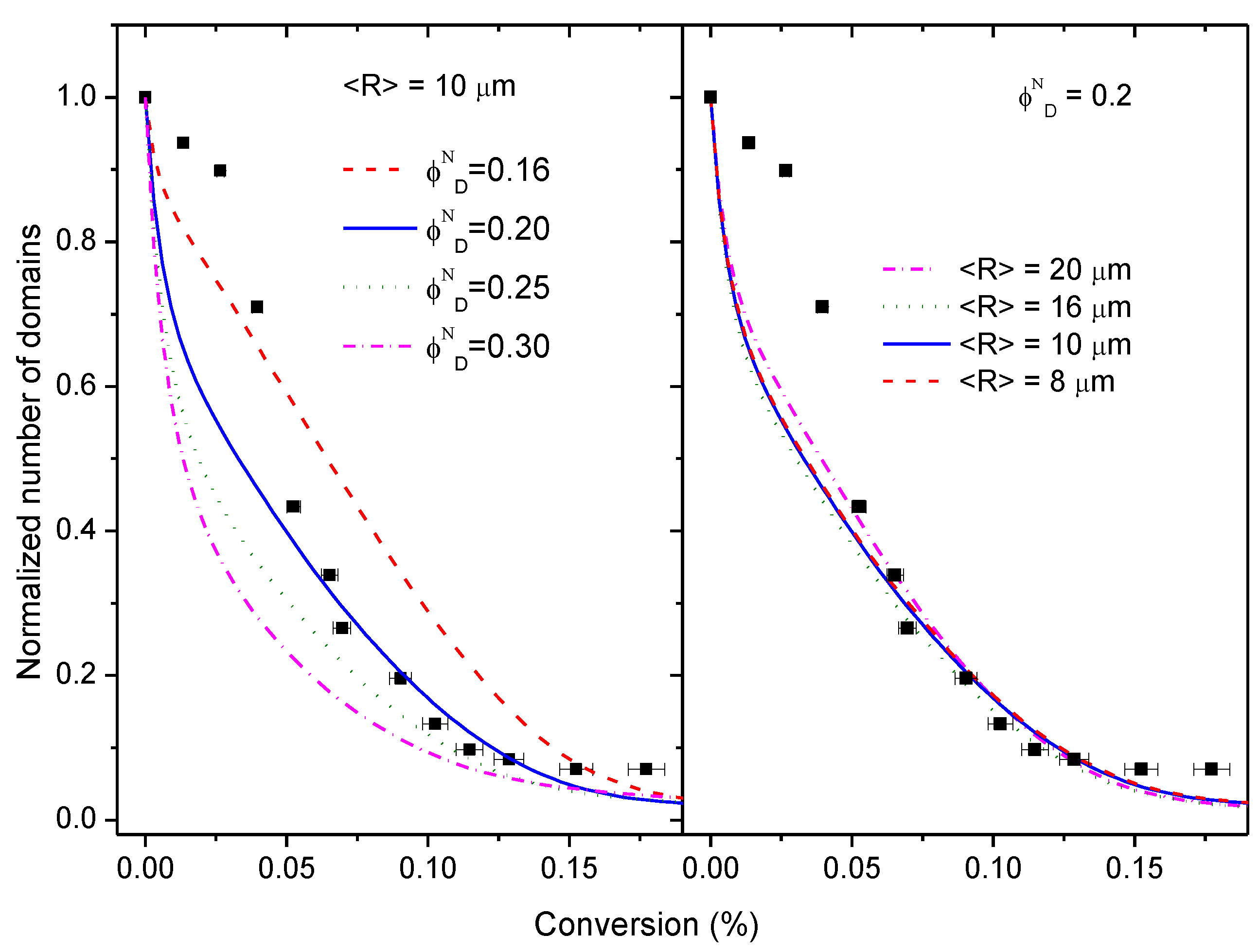
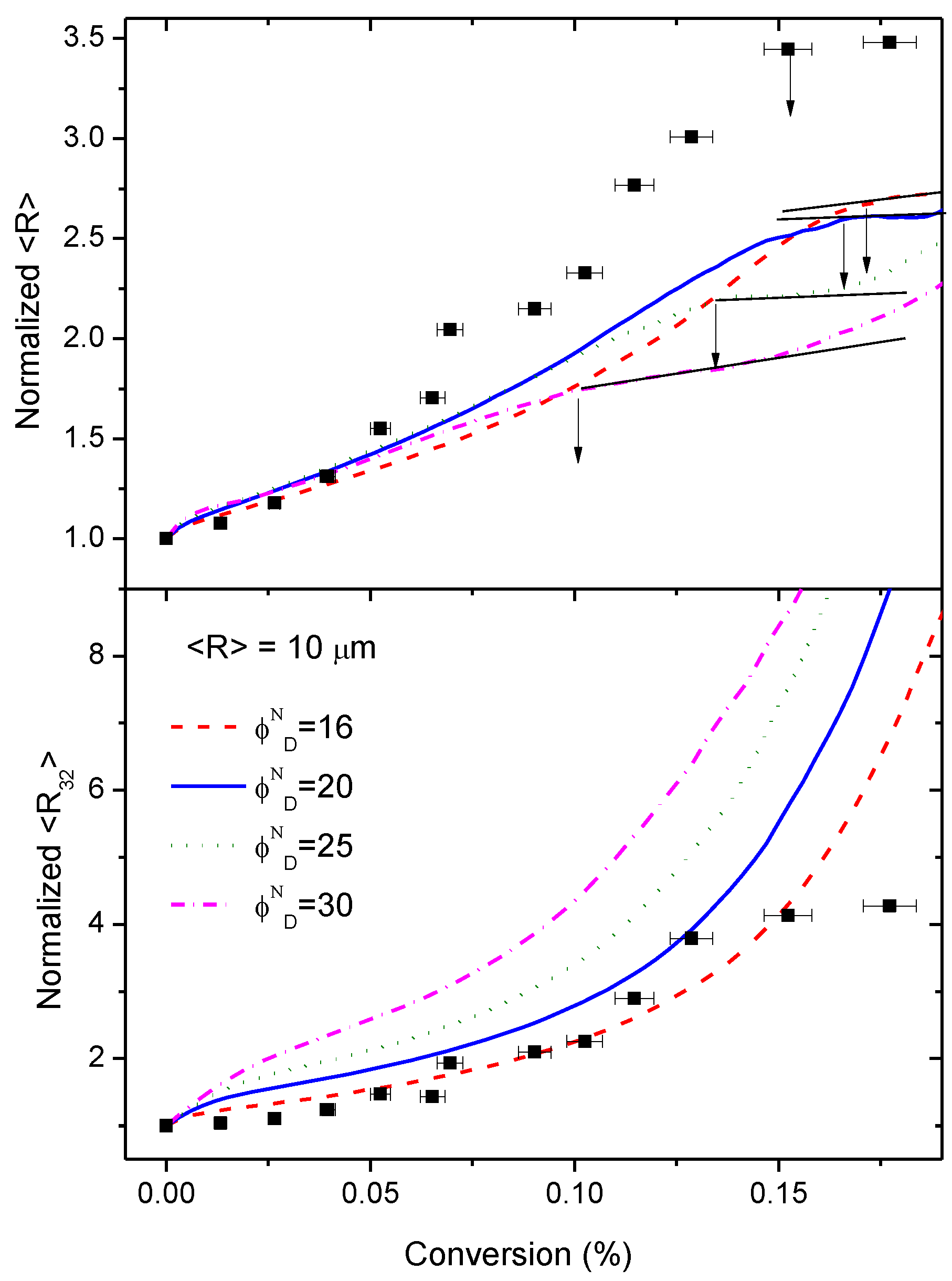
3.5. Simulation of the Coalescence and Growth of PAMS-Rich Domains
- (i)
- The diffusion rate of epoxy fluid through the domains must be almost the same as the reaction rate. This assumption seems to be rather stringent, but it is based on experimental observations. If the diffusion rate is much higher than the reaction rate, after some induction period, the domains would grow independently of conversion and this has not been observed (see Figure 5). On the other hand, if the diffusion rate is lower than the reaction rate, the reaction becomes diffusion-controlled and the rates of diffusion and reaction of the HDGEBA molecules will be equal.
- (ii)
- The spherical shape of the particles remains after collisions. This is a common assumption in all coalescence models [49,50] and it has also been observed experimentally (see Figure 4) before microgelation. Consequently, once an encounter takes place, the volume of the daughter particle is the sum of the volumes of the parent molecules, and its centre of mass changes accordingly. An encounter takes place when the distance between two particles is equal to the sum of their radii.
- (iii)
- Initial PAMS-rich domains consist only of pure PAMS. This assumption appears to be contradictory to the observed glass transition temperature of the PAMS phase in the initial mixture. Since the volume fraction of PAMS-rich domains is uncertain, we will explore some other values of the initial volume fraction keeping constant the equivalent ratio.
- (iv)
- The initial distribution of sizes is taken as a monomodal Gaussian distribution centred around a given average radius with a standard deviation and upper and lower cut-offs as observed experimentally. This assumption excludes both very small and very big particles that have not been observed experimentally (see Figure S7). Several initial average sizes will be explored to analyse their influence on the coalescence process.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- May, C. Epoxy Resins: Chemistry and Technology, 2nd ed.; Marcel Dekker: New York, NY, USA, 1988; p. 1. ISBN 10: 0824776909. [Google Scholar]
- Pascault, J.-P.; Williams, R.J.J. Overview of Thermosets: Present and Future. In Thermosets, 2nd ed.; Guo, Q., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 3–34. ISBN 978-0-08-101021-1. [Google Scholar]
- Incerti, D.; Wang, T.; Carolan, D.; Fergusson, A. Curing Rate Effects on the Toughness of Epoxy Polymers. Polymer 2018, 159, 116–123. [Google Scholar] [CrossRef]
- González, M.; Cabanelas, J.C.; Baselga, J. Applications of FTIR on Epoxy Resins—Identification, Monitoring the Curing Process, Phase Separation and Water Uptake. In Infrared Spectroscopy—Materials Science, Engineering and Technology; Theophanides, D.T., Ed.; InTech: London, UK, 2012; Volume 2, Chapter 13. [Google Scholar]
- Ramos, V.D.; da Costa, H.M.; Soares, V.L.P.; Nascimento, R.S.V. Modification of Epoxy Resin: A Comparison of Different Types of Elastomer. Polym. Test 2005, 24, 387–394. [Google Scholar] [CrossRef]
- Chen, D.; Li, J.; Yuan, Y.; Gao, C.; Cui, Y.; Li, S.; Wang, H.; Peng, C.; Liu, X.; Wu, Z.; et al. A New Strategy to Improve the Toughness of Epoxy Thermosets by Introducing the Thermoplastic Epoxy. Polymer 2022, 240, 124518. [Google Scholar] [CrossRef]
- Ma, J.; Mo, M.S.; Du, X.S.; Rosso, P.; Friedrich, K.; Kuan, H.C. Effect of Inorganic Nanoparticles on Mechanical Property, Fracture Toughness and Toughening Mechanism of Two Epoxy Systems. Polymer 2008, 49, 3510–3523. [Google Scholar] [CrossRef]
- Cha, J.; Kim, J.; Ryu, S.; Hong, S.H. Comparison to Mechanical Properties of Epoxy Nanocomposites Reinforced by Functionalized Carbon Nanotubes and Graphene Nanoplatelets. Compos. B Eng. 2019, 162, 283–288. [Google Scholar] [CrossRef]
- Zhang, D.; Huang, Y.; Chia, L. Effects of Carbon Nanotube (CNT) Geometries on the Dispersion Characterizations and Adhesion Properties of CNT Reinforced Epoxy Composites. Compos. Struct. 2022, 296, 115942. [Google Scholar] [CrossRef]
- Kontaxis, L.C.; Kozaniti, F.K.; Papanicolaou, G.C. Mechanical Behavior Modelling and Filler Geometry Effect of Glass Filler Reinforced Starch-epoxy Hybrid Matrix Composites. Materials 2021, 14, 6587. [Google Scholar] [CrossRef]
- Gojny, F.H.; Wichmann, M.H.G.; Köpke, U.; Fiedler, B.; Schulte, K. Carbon Nanotube-Reinforced Epoxy-Composites: Enhanced Stiffness and Fracture Toughness at Low Nanotube Content. Compos. Sci. Technol. 2004, 64, 2363–2371. [Google Scholar] [CrossRef]
- Domun, N.; Paton, K.R.; Hadavinia, H.; Sainsbury, T.; Zhang, T.; Mohamud, H. Enhancement of Fracture Toughness of Epoxy Nanocomposites by Combining Nanotubes and Nanosheets as Fillers. Materials 2017, 10, 1179. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zamanian, M.; Mortezaei, M.; Salehnia, B.; Jam, J.E. Fracture Toughness of Epoxy Polymer Modified with Nanosilica Particles: Particle Size Effect. Eng. Fract. Mech. 2013, 97, 193–206. [Google Scholar] [CrossRef]
- Adachi, T.; Osaki, M.; Araki, W.; Kwon, S.C. Fracture Toughness of Nano- and Micro-Spherical Silica-Particle-Filled Epoxy Composites. Acta Mater. 2008, 56, 2101–2109. [Google Scholar] [CrossRef]
- Rosetti, Y.; Alcouffe, P.; Pascault, J.P.; Gérard, J.F.; Lortie, F. Polyether Sulfone-Based Epoxy Toughening: From Micro- to Nano-Phase Separation via PES End-Chain Modification and Process Engineering. Materials 2018, 11, 1960. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Domun, N.; Hadavinia, H.; Zhang, T.; Sainsbury, T.; Liaghat, G.H.; Vahid, S. Improving the Fracture Toughness and the Strength of Epoxy Using Nanomaterials—A Review of the Current Status. Nanoscale 2015, 7, 10294–10329. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mi, X.; Liang, N.; Xu, H.; Wu, J.; Jiang, Y.; Nie, B.; Zhang, D. Toughness and Its Mechanisms in Epoxy Resins. Prog. Mater. Sci. 2022, 130, 100977. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Sato, N.; Tölle, F.; Mülhaupt, R.; Fiedler, B.; Schulte, K. Fracture Toughness and Failure Mechanism of Graphene Based Epoxy Composites. Compos. Sci. Technol. 2014, 97, 90–99. [Google Scholar] [CrossRef]
- Yahyaei, H.; Ebrahimi, M.; Tahami, H.V.; Mafi, E.R.; Akbarinezhad, E. Toughening Mechanisms of Rubber Modified Thin Film Epoxy Resins: Part 2—Study of Abrasion, Thermal and Corrosion Resistance. Prog. Org. Coat. 2017, 113, 136–142. [Google Scholar] [CrossRef]
- Mathew, V.S.; Sinturel, C.; George, S.C.; Thomas, S. Epoxy Resin/Liquid Natural Rubber System: Secondary Phase Separation and Its Impact on Mechanical Properties. J. Mater. Sci. 2010, 45, 1769–1781. [Google Scholar] [CrossRef]
- Chruściel, J.J.; Leśniak, E. Modification of Epoxy Resins with Functional Silanes, Polysiloxanes, Silsesquioxanes, Silica and Silicates. Prog. Polym. Sci. 2015, 14, 67–121. [Google Scholar] [CrossRef]
- Byczyński, Ł.; Dutkiewicz, M.; Januszewski, R.; Wrona, P.; Pilch-Pitera, B. Epoxy Coatings with Increased Hydrophobicity Modified by Isocyanurate Containing Siloxane. Mater. Today Commun. 2020, 24, 101001. [Google Scholar] [CrossRef]
- Tao, Z.; Yang, S.; Chen, J.; Fan, L. Synthesis and Characterization of Imide Ring and Siloxane-Containing Cycloaliphatic Epoxy Resins. Eur. Polym. J. 2007, 43, 1470–1479. [Google Scholar] [CrossRef]
- Ahmad, S.; Gupta, A.P.; Sharmin, E.; Alam, M.; Pandey, S.K. Synthesis, Characterization and Development of High Performance Siloxane-Modified Epoxy Paints. Prog. Org. Coat. 2005, 54, 248–255. [Google Scholar] [CrossRef]
- Cabanelas, J.C.; Prolongo, S.G.; Serrano, B.; Bravo, J.; Baselga, J. Water Absorption in Polyaminosiloxane-Epoxy Thermosetting Polymers. J. Mater. Process. Technol. 2003, 143–144, 311–315. [Google Scholar] [CrossRef] [Green Version]
- Sung, P.H.; Lin, C.Y. Polysiloxane Modified Epoxy Polymer Network-I. Graft Interpenetrating Polymeric Networks. Eur. Polym. J. 1997, 33, 903–906. [Google Scholar] [CrossRef]
- Cabanelas, J.C.; Serrano, B.; Baselga, J. Development of Cocontinuous Morphologies in Initially Heterogeneous Thermosets Blended with Poly(Methyl Methacrylate). Macromolecules 2005, 38, 961–970. [Google Scholar] [CrossRef] [Green Version]
- Ma, S.; Liu, W.; Yu, D.; Wang, Z. Modification of Epoxy Resin with Polyether-Grafted-Polysiloxane and Epoxy-Miscible Polysiloxane Particles. Macromol. Res. 2010, 18, 22–28. [Google Scholar] [CrossRef]
- Wu, D.; Zhao, B.; Dai, Z.; Qin, J.; Lin, B. Grafting Epoxy-Modified Hydrophilic Polymers onto Poly(Dimethylsiloxane) Microfluidic Chip to Resist Nonspecific Protein Adsorption. Lab Chip 2006, 6, 942–947. [Google Scholar] [CrossRef]
- Zhou, C.; Li, R.; Luo, W.; Chen, Y.; Zou, H.; Liang, M.; Li, Y. The Preparation and Properties Study of Polydimethylsiloxane-Based Coatings Modified by Epoxy Resin. J. Polym. Res. 2016, 23, 14. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, H.; Chen, Z.; Zhou, S.; Chen, Y.; Liang, M.; Zou, H. Silicone-Epoxy Block Hybrid Network to Achieve High-Performance and Transparent Polydimethylsiloxane Materials. React. Funct. Polym. 2020, 150, 104537. [Google Scholar] [CrossRef]
- Shon, M.Y.; Kwon, H.S. Comparison of Surface Modification with Amino Terminated Polydimethylsiloxane and Amino Branched Polydimethylsiloxane on the Corrosion Protection of Epoxy Coating. Corros. Sci. 2009, 51, 650–657. [Google Scholar] [CrossRef]
- Yang, Y.; Li, W.; Chen, K.; Gan, W.; Wang, C. Epoxy Terminated Polysiloxane Blended with Diglycidyl Ether of Bisphenol-A. 1: Curing Behavior and Compatibility. J. Appl. Polym. Sci. 2018, 135, 46891. [Google Scholar] [CrossRef]
- Huang, Z.; Huang, Y.; Yu, Y. Modification of Epoxy Resin with Polysiloxane Bearing Pendant Quaternary Ammonium Groups. Chin. J. Poly. Sci. 2002, 20, 537–541. [Google Scholar]
- Cabanelas, J.C.; Serrano, B.; Gonzalez-Benito, J.; Bravo, J.; Baselga, J. Morphology of Epoxy/Polyorganosiloxane Reactive Blends. Macromol. Rapid Commun. 2001, 22, 694–699. [Google Scholar] [CrossRef]
- Sobhani, S.; Jannesari, A.; Bastani, S. Effect of Molecular Weight and Content of PDMS on Morphology and Properties of Silicone-Modified Epoxy Resin. J. Appl. Polym. Sci. 2012, 123, 162–178. [Google Scholar] [CrossRef]
- Leguizamon, S.C.; Ahn, J.; Lee, S.; Jones, B.H. Tuneable Phase Behaviour and Glass Transition via Polymerization-Induced Phase Separation in Crosslinked Step-Growth Polymers. Soft Matter 2022, 18, 4455–4463. [Google Scholar] [CrossRef] [PubMed]
- Canto, C.F.; Prado, L.D.A.; Radovanovic, E.; Yoshida, I.V.P. Organic-Inorganic Hybrid Materials Derived from Epoxy Resin and Polysiloxanes: Synthesis and Characterization. Polym. Eng. Sci. 2008, 48, 141–148. [Google Scholar] [CrossRef]
- Hsu, C.W.; Ma, C.C.M.; Tan, C.S.; Li, H.T.; Huang, S.C.; Lee, T.M.; Tai, H. Effect of Thermal Aging on the Optical, Dynamic Mechanical, and Morphological Properties of Phenylmethylsiloxane-Modified Epoxy for Use as an LED Encapsulant. Mater. Chem. Phys. 2012, 134, 789–796. [Google Scholar] [CrossRef]
- Li, H.T.; Lin, M.S.; Chuang, H.R.; Wang, M.W. Siloxane- and Imide-Modified Epoxy Resin Cured with Siloxane-Containing Dianhydride. J. Polym. Res. 2005, 12, 385–391. [Google Scholar] [CrossRef]
- Prolongo, S.G.; Cabanelas, J.C.; Baselga, J. Reactive compatibilization of epoxy/polyorganosiloxane blends. Macromol. Symp. 2003, 198, 283–294. [Google Scholar] [CrossRef] [Green Version]
- Pascault, J.P.; Sautereau, H.; Verdu, J.; Williams, R.J.J. Thermosetting Polymers; Marcel Dekker Inc.: New York, NY, USA, 2002; ISBN 0-8247-0670-6. [Google Scholar]
- Paul, D.R.; Newman, S. Polymer Blends I; Academic Press: London, UK, 1978; ISBN 10.0125468016. [Google Scholar]
- Consiglio, R.; Baker, D.R.; Paul, G.; Stanley, H.E. Continuum Percolation Thresholds for Mixtures of Spheres of Different Sizes. Phys. A 2003, 319, 49–55. [Google Scholar] [CrossRef]
- Cabanelas, J.C.; Serrano, B.; Gonzalez, M.G.; Baselga, J. Confocal Microscopy Study of Phase Morphology Evolution in Epoxy/Polysiloxane Thermosets. Polymer 2005, 46, 6633–6639. [Google Scholar] [CrossRef] [Green Version]
- Lemenand, T.; della Valle, D.; Zellouf, Y.; Peerhossaini, H. Droplets Formation in Turbulent Mixing of Two Immiscible Fluids in a New Type of Static Mixer. Int. J. Multiph. Flow 2003, 29, 813–840. [Google Scholar] [CrossRef]
- Halász, G.; Gyüre, B.; Jánosi, I.M.; Szabó, K.G.; Tél, T. Vortex Flow Generated by a Magnetic Stirrer. Am. J. Phys. 2007, 75, 1092–1098. [Google Scholar] [CrossRef] [Green Version]
- Leiva, J.M.; Geffroy, E. Evolution of the Size Distribution of an Emulsion under a Simple Shear Flow. Fluids 2018, 3, 46. [Google Scholar] [CrossRef] [Green Version]
- Smoluchowski, M. Von Drei Vortrage Uber Diffusion, Brownsche Bewegung Und Koagulation von Kolloidteilchen. Zeitschrift fur Physik 1916, 17, 557–585. [Google Scholar]
- Laurençot, P.; Mischler, S. On Coalescence Equations and Related Models. In Modeling and Computational Methods for Kinetic Equations. Modeling and Simulation in Science, Engineering and Technology; Degond, P., Pareschi, L., Russo, G., Eds.; Birkhäuser: Boston, MA, USA, 2004; p. 321. [Google Scholar] [CrossRef]



| Compound | HDGEBA | PAMS |
|---|---|---|
 | 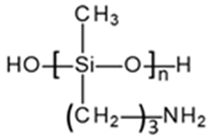 | |
| 411 | 1190 ± 150 | |
| −41 | −68 | |
| 2 | 20.3 ± 2.7 | |
| 1.055 | ||
| 0.53 |
| Temperature (°C) | (min) | (min) | |||
|---|---|---|---|---|---|
| 40 | 0.60 | 66.7 | 0.30 | ||
| 60 | 0.90 | 19.4 | 0.28 | ||
| 70 | 0.93 | 10.5 | 0.23 | ||
| 80 | 0.97 | - | - | - | - |
| 90 | 0.99 | - | - | - | - |
| Run | |||||
|---|---|---|---|---|---|
| 1–8 | 14–40 | 8.0 | 2.5 | 2 | 16 |
| 9–16 | 14–40 | 10.0 | 2.5 | 4 | 18 |
| 17–24 | 14–40 | 12.0 | 2.5 | 6 | 20 |
| 25–32 | 14–40 | 14.0 | 2.5 | 8 | 22 |
| 33–40 | 14–40 | 16.0 | 2.5 | 10 | 24 |
| 41–48 | 14–40 | 18.0 | 2.5 | 12 | 26 |
| 49–56 | 14–40 | 20.0 | 2.5 | 14 | 28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González, M.G.; Pozuelo, J.; Cabanelas, J.C.; Serrano, M.B.; Baselga, J. Mechanism of Morphology Development in HDGEBA/PAMS Hybrid Thermosets: Monte Carlo Simulation and LSCM Study. Polymers 2022, 14, 5375. https://doi.org/10.3390/polym14245375
González MG, Pozuelo J, Cabanelas JC, Serrano MB, Baselga J. Mechanism of Morphology Development in HDGEBA/PAMS Hybrid Thermosets: Monte Carlo Simulation and LSCM Study. Polymers. 2022; 14(24):5375. https://doi.org/10.3390/polym14245375
Chicago/Turabian StyleGonzález, María G., Javier Pozuelo, Juan C. Cabanelas, María B. Serrano, and Juan Baselga. 2022. "Mechanism of Morphology Development in HDGEBA/PAMS Hybrid Thermosets: Monte Carlo Simulation and LSCM Study" Polymers 14, no. 24: 5375. https://doi.org/10.3390/polym14245375
APA StyleGonzález, M. G., Pozuelo, J., Cabanelas, J. C., Serrano, M. B., & Baselga, J. (2022). Mechanism of Morphology Development in HDGEBA/PAMS Hybrid Thermosets: Monte Carlo Simulation and LSCM Study. Polymers, 14(24), 5375. https://doi.org/10.3390/polym14245375






