Linear and Nonlinear Elastic Properties of Polystyrene-Based Nanocomposites with Allotropic Carbon Fillers and Binary Mixtures
Abstract
1. Introduction
2. Materials and Methods
2.1. Fabrication of Nanocomposite Samples
2.2. Analysis of Linear Elastic Properties
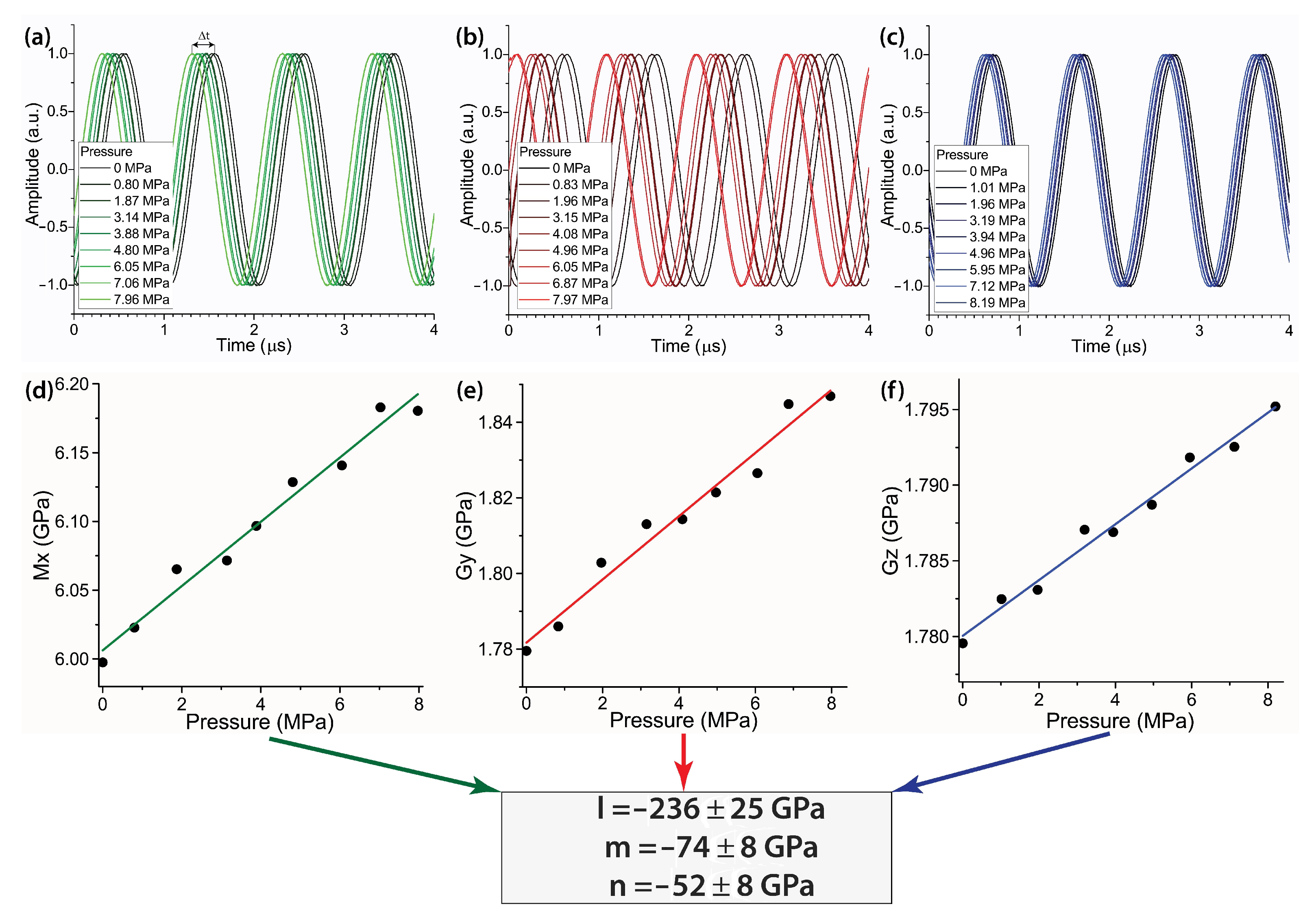
2.3. Measurements of Nonlinear Elastic Moduli
3. Results and Discussion
3.1. Linear Elastic Properties of PS-Based Nanocomposites
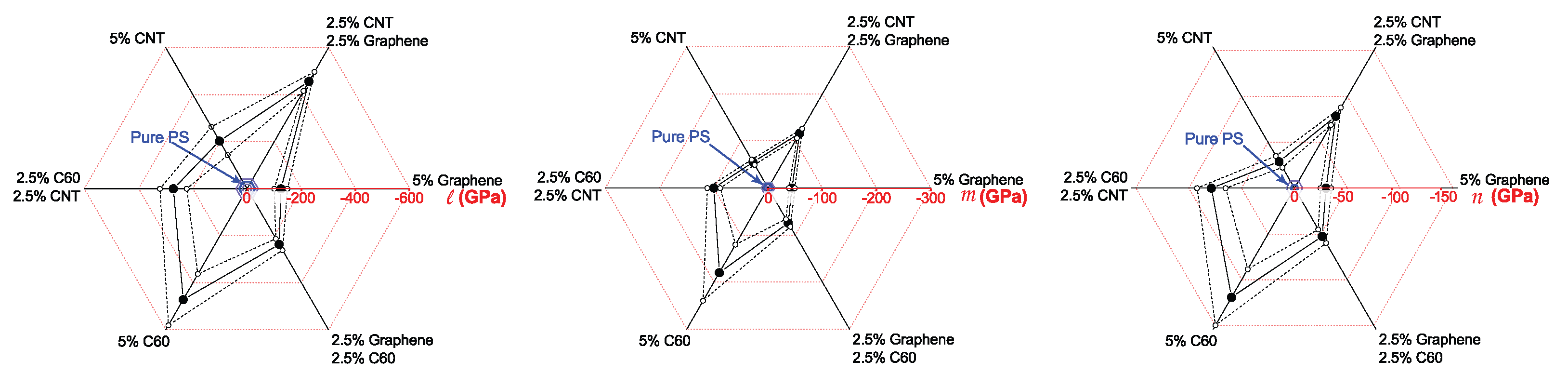
3.2. Nonlinear Elastic Moduli
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mittal, V. (Ed.) Optimization of Polymer Nanocomposite Properties; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Fu, S.; Sun, Z.; Huang, P.; Li, Y.; Hu, N. Some basic aspects of polymer nanocomposites: A critical review. Nano Mater. Sci. 2019, 1, 2–30. [Google Scholar] [CrossRef]
- Guerder, P.Y.; Giordano, S.; Matar, O.B.; Vasseur, J.O. Tuning the elastic nonlinearities in composite nanomaterials. J. Phys. Condens. Matter 2015, 27, 145304. [Google Scholar] [CrossRef] [PubMed]
- Mermet-Guyennet, M.R.B.; de Castro, J.G.; Varol, H.S.; Habibi, M.; Hosseinkhani, B.; Martzel, N.; Sprik, R.; Denn, M.M.; Zaccone, A.; Parekh, S.H.; et al. Size-dependent reinforcement of composite rubbers. Polymer 2015, 73, 170–173. [Google Scholar] [CrossRef]
- Li, Y.; Huang, X.; Zeng, L.; Li, R.; Tian, H.; Fu, X.; Wang, Y.; Zhong, W.H. A review of the electrical and mechanical properties of carbon nanofiller-reinforced polymer composites. J. Mater. Sci. 2019, 54, 1036–1076. [Google Scholar] [CrossRef]
- Yeh, S.K.; Su, C.C.; Huang, J.M.; Ke, M.Q.; Bogale, D.; Anbarasan, R.; Tung, K.L.; Wang, S.F. Fabrication of polystyrene/carbon nanocomposites with superior mechanical properties. Polym. Eng. Sci. 2020, 60, 2046–2056. [Google Scholar] [CrossRef]
- Papageorgiou, D.G.; Kinloch, I.A.; Young, R.J. Mechanical properties of graphene and graphene-based nanocomposites. Prog. Mater. Sci. 2017, 90, 75–127. [Google Scholar] [CrossRef]
- Spitalsky, Z.; Tasis, D.; Papagelis, K.; Galiotis, C. Carbon nanotube–polymer composites: Chemistry, processing, mechanical and electrical properties. Prog. Polym. Sci. 2010, 35, 357–401. [Google Scholar] [CrossRef]
- Moskalyuk, O.A.; Belashov, A.V.; Beltukov, Y.M.; Ivan’kova, E.M.; Popova, E.N.; Semenova, I.V.; Yelokhovskii, V.Y.; Yudin, V.E. Polystyrene-based nanocomposites with different fillers: Fabrication and mechanical properties. Polymers 2020, 12, 2457. [Google Scholar] [CrossRef]
- Zha, J.W.; Li, W.K.; Liao, R.J.; Bai, J.; Dang, Z.M. High performance hybrid carbon fillers/binary–polymer nanocomposites with remarkably enhanced positive temperature coefficient effect of resistance. J. Mater. Chem. A 2013, 1, 843. [Google Scholar] [CrossRef]
- Nikolaeva, A.L.; Gofman, I.V.; Yakimansky, A.V.; Ivan’kova, E.M.; Abalov, I.V.; Baranchikov, A.E.; Ivanov, V.K. Polyimide-Based Nanocomposites with Binary CeO2/Nanocarbon Fillers: Conjointly Enhanced Thermal and Mechanical Properties. Polymers 2020, 12, 1952. [Google Scholar] [CrossRef]
- Zambrzycki, M.; Fraczek-Szczypta, A. Conductive hybrid polymer composites based on recycled carbon fibres and carbon nanofillers. J. Mater. Sci. 2018, 53, 7403–7416. [Google Scholar] [CrossRef]
- Szeluga, U.; Kumanek, B.; Trzebicka, B. Synergy in hybrid polymer/nanocarbon composites. A review. Compos. Part A Appl. Sci. Manuf. 2015, 73, 204–231. [Google Scholar] [CrossRef]
- Jen, Y.M.; Huang, J.C.; Zheng, K.Y. Synergistic Effect of Multi-Walled Carbon Nanotubes and Graphene Nanoplatelets on the Monotonic and Fatigue Properties of Uncracked and Cracked Epoxy Composites. Polymers 2020, 12, 1895. [Google Scholar] [CrossRef]
- Murnaghan, E.D. Finite Deformation of an Elastic Solid; Wiley: New York, NY, USA, 1951. [Google Scholar]
- Takahashi, S. Measurement of third-order elastic constants and stress dependent coefficients for steels. Mech. Adv. Mater. Mod. Process. 2018, 4, 2. [Google Scholar] [CrossRef]
- Kurashkin, K.V. Changes in linear and nonlinear elastic properties of aluminium alloy under static deformation. J. Phys. Conf. Ser. 2018, 1129, 012021. [Google Scholar] [CrossRef]
- Egle, D.M.; Bray, D.E. Measurement of acoustoelastic and third-order elastic constants for rail steel. J. Acoust. Soc. Am. 1976, 60, 741. [Google Scholar] [CrossRef]
- Winkler, K.W.; Liu, X. Measurements of third-order elastic constants in rocks. J. Acoust. Soc. Am. 1996, 100, 1392. [Google Scholar] [CrossRef]
- Bateman, T.; Mason, W.P.; McSkimin, H.J. Third-Order Elastic Moduli of Germanium. J. Appl. Phys. 1961, 32, 928. [Google Scholar] [CrossRef]
- Korobov, A.I.; Prokhorov, V.M.; Mekhedov, D.M. Second-order and third-order elastic constants of B95 aluminum alloy and B95/nanodiamond composite. Phys. Solid State 2013, 55, 8–11. [Google Scholar] [CrossRef]
- Belashov, A.V.; Beltukov, Y.M.; Moskalyuk, O.A.; Semenova, I.V. Relative variations of nonlinear elastic moduli in polystyrene-based nanocomposites. Polym. Test. 2021, 95, 107132. [Google Scholar] [CrossRef]
- Hughes, D.S.; Kelly, J.L. Second-order elastic deformation of solids. Phys. Rev. 1953, 92, 1145–1149. [Google Scholar] [CrossRef]
- Dreiden, G.V.; Khusnutdinova, K.R.; Samsonov, A.M.; Semenova, I.V. Comparison of the effect of cyanoacrylate- and polyurethane-based adhesives on a longitudinal strain solitary wave in layered polymethylmethacrylate waveguides. J. Appl. Phys. 2008, 104, 086106. [Google Scholar] [CrossRef]
- Belashov, A.V.; Zhikhoreva, A.A.; Beltukov, Y.M.; Moskalyuk, O.A.; Semenova, I.V. Third-order elastic moduli of polystyrene samples fabricated by different technologies. Tech. Phys. 2021, 66, 1085–1091. [Google Scholar] [CrossRef]
- Nielsen, L.E. Simple theory of stress-strain properties of filled polymers. J. Appl. Polym. Sci. 1966, 10, 97–103. [Google Scholar] [CrossRef]
- Kausar, A. Technical viewpoint on polystyrene/ graphene nanocomposite. J. Thermoplast. Compos. Mater. 2022, 35, 1757–1771. [Google Scholar] [CrossRef]
- Yu, Y.H.; Lin, Y.Y.; Lin, C.H.; Chan, C.C.; Huang, Y.C. High-performance polystyrene/graphene-based nanocomposites with excellent anti-corrosion properties. Polym. Chem. 2014, 5, 535–550. [Google Scholar] [CrossRef]
- Tu, Z.; Wang, J.; Yu, C.; Xiao, H.; Jiang, T.; Yang, Y.; Shi, D.; Mai, Y.W.; Li, R.K. A facile approach for preparation of polystyrene/graphene nanocomposites with ultra-low percolation threshold through an electrostatic assembly process. Compos. Sci. Technol. 2016, 134, 49–56. [Google Scholar] [CrossRef]
- Chang, T.E.; Kisliuk, A.; Rhodes, S.M.; Brittain, W.J.; Sokolov, A.P. Conductivity and mechanical properties of well-dispersed single-wall carbon nanotube/polystyrene composite. Polymer 2006, 47, 7740–7746. [Google Scholar] [CrossRef]
- Bansal, S.A.; Singh, A.P.; Kumar, S. Synergistic effect of graphene and carbon nanotubes on mechanical and thermal performance of polystyrene. Mater. Res. Express 2018, 5, 075602. [Google Scholar] [CrossRef]
- Liu, Y.T.; Dang, M.; Xie, X.M.; Wang, Z.F.; Ye, X.Y. Synergistic effect of Cu2+-coordinated carbon nanotube/graphene network on the electrical and mechanical properties of polymer nanocomposites. J. Mater. Chem. 2011, 21, 18723–18729. [Google Scholar] [CrossRef]
- Semenov, A.A.; Beltukov, Y.M. Nonlinear elastic moduli of composite materials with nonlinear spherical inclusions dispersed in a nonlinear matrix. Int. J. Solids Struct. 2020, 191–192, 333–340. [Google Scholar] [CrossRef]
- Semenova, I.V.; Belashov, A.V.; Zhikhoreva, A.A.; Moskalyuk, O.A.; Beltukov, Y.M. Frequency Dependence of Nonlinear Elastic Moduli of Polystyrene-Based Nanocomposites in the Range of 1.5–2.5 MHz. Macromol. Symp. 2022, 405, 2100252. [Google Scholar] [CrossRef]




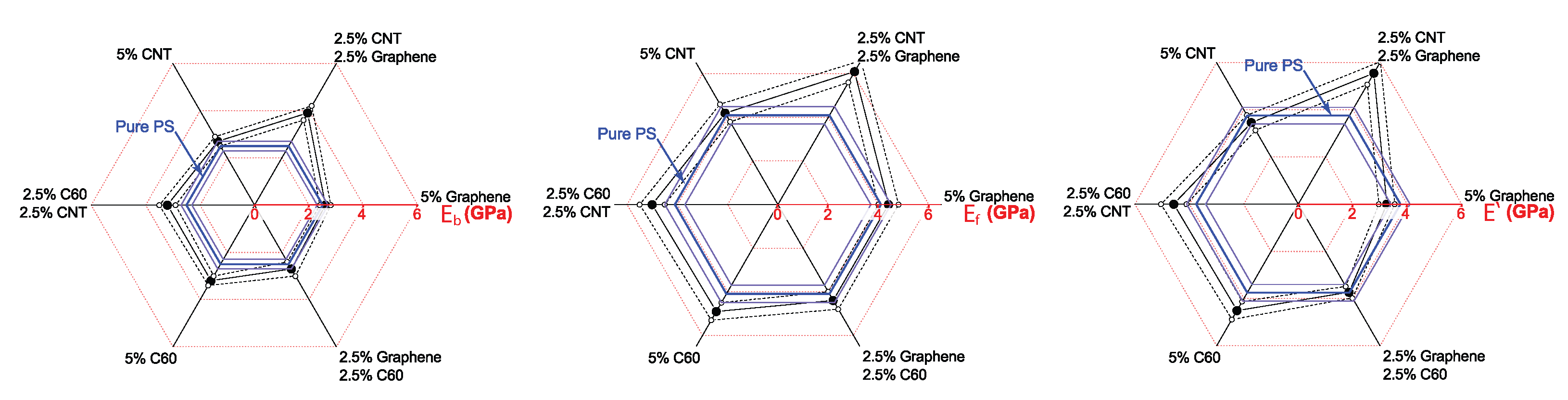
| Sample | Tensile | Flexural | ||||
|---|---|---|---|---|---|---|
| , MPa | , % | , GPa | , MPa | , % | , GPa | |
| PS pure | ||||||
| PS + C | ||||||
| PS + CNT | ||||||
| PS + Gr | ||||||
| PS + C + CNT | ||||||
| PS + C + Gr | ||||||
| PS + CNT + Gr | ||||||
| Sample | (g/cm) | l (GPa) | m (GPa) | n (GPa) |
|---|---|---|---|---|
| PS pure | 1.00 | −29 ± 10 | −8 ± 4 | −3.5 ± 1.4 |
| PS + C | 1.04 | −471 ± 178 | −179 ± 59 | −119 ± 30 |
| PS + CNT | 1.07 | −203 ± 88 | −55 ± 5 | −29 ± 6 |
| PS + Gr | 1.11 | −124 ± 24 | −44 ± 5 | −30 ± 5 |
| PS + C + CNT | 1.05 | −271 ± 49 | −99 ± 11 | −78 ± 14 |
| PS + C + Gr | 1.06 | −236 ± 24 | −74±8 | −53 ± 7 |
| PS + CNT + Gr | 1.09 | −456 ± 40 | −116 ± 10 | −79 ± 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belashov, A.V.; Zhikhoreva, A.A.; Moskalyuk, O.A.; Beltukov, Y.M.; Semenova, I.V. Linear and Nonlinear Elastic Properties of Polystyrene-Based Nanocomposites with Allotropic Carbon Fillers and Binary Mixtures. Polymers 2022, 14, 5462. https://doi.org/10.3390/polym14245462
Belashov AV, Zhikhoreva AA, Moskalyuk OA, Beltukov YM, Semenova IV. Linear and Nonlinear Elastic Properties of Polystyrene-Based Nanocomposites with Allotropic Carbon Fillers and Binary Mixtures. Polymers. 2022; 14(24):5462. https://doi.org/10.3390/polym14245462
Chicago/Turabian StyleBelashov, Andrey V., Anna A. Zhikhoreva, Olga A. Moskalyuk, Yaroslav M. Beltukov, and Irina V. Semenova. 2022. "Linear and Nonlinear Elastic Properties of Polystyrene-Based Nanocomposites with Allotropic Carbon Fillers and Binary Mixtures" Polymers 14, no. 24: 5462. https://doi.org/10.3390/polym14245462
APA StyleBelashov, A. V., Zhikhoreva, A. A., Moskalyuk, O. A., Beltukov, Y. M., & Semenova, I. V. (2022). Linear and Nonlinear Elastic Properties of Polystyrene-Based Nanocomposites with Allotropic Carbon Fillers and Binary Mixtures. Polymers, 14(24), 5462. https://doi.org/10.3390/polym14245462





