Mechanical and Imaging Properties of a Clinical-Grade Kidney Phantom Based on Polydimethylsiloxane and Elastomer
Abstract
:1. Introduction
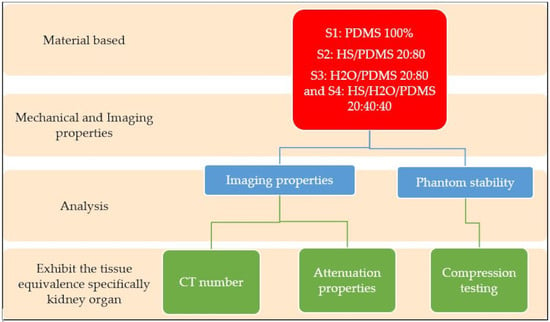
2. Materials and Methods
2.1. Fabrication of PDMS Phantom
2.2. Compression Testing
2.3. Radiation Attenuation Properties
2.4. Imaging Properties
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mat Radzi, S.F.; Abdul Karim, M.K.; Saripan, M.I.; Abd Rahman, M.A.; Osman, N.H.; Dalah, E.Z.; Mohd Noor, N. Impact of Image Contrast Enhancement on Stability of Radiomics Feature Quantification on a 2D Mammogram Radiograph. IEEE Access 2020, 8, 127720–127731. [Google Scholar] [CrossRef]
- Mut, N.A.I.C.; Bakar, N.H.A.; Kamal, I.; Suhaimi, S.A.A.; Mohammad, N.M.; Ahmad, R.; Zain, N.M. Knowledge and Awareness of Breast Self-Examination among Secondary School Girls in Seremban, Negeri Sembilan. Asian Pac. J. Cancer Care 2019, 4, 39–43. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Zhang, H.; Zhao, H.; He, Z.; Shi, L.; He, Y.; Ju, N.; Rong, Y.; Qiu, J. Design and fabrication of a personalized anthropomorphic phantom using 3D printing and tissue equivalent materials. Quant. Imaging Med. Surg. 2019, 9, 94–100. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Belmont, B.; Greve, J.M.; Manders, A.B.; Downey, B.C.; Zhang, X.; Xu, Z.; Guo, D.; Shih, A. Polyvinyl chloride as a multimodal tissue-mimicking material with tuned mechanical and medical imaging properties. Med. Phys. 2016, 43, 5577–5592. [Google Scholar] [CrossRef]
- Adams, F.; Qiu, T.; Mark, A.; Fritz, B.; Kramer, L.; Schlager, D.; Wetterauer, U.; Miernik, A.; Fischer, P. Soft 3D-Printed Phantom of the Human Kidney with Collecting System. Ann. Biomed. Eng. 2017, 45, 963–972. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cropp, R.J.; Seslija, P.; Tso, D.; Thakur, Y. Scanner and kVp dependence of measured CT numbers in the ACR CT phantom. J. Appl. Clin. Med. Phys. 2013, 14, 338–349. [Google Scholar] [CrossRef]
- Mull, R.T. Mass estimates by computed tomography: Physical density from CT numbers. Am. J. Roentgenol. 1984, 143, 1101–1104. [Google Scholar] [CrossRef] [Green Version]
- Umale, S.; Deck, C.; Bourdet, N.; Dhumane, P.; Soler, L.; Marescaux, J.; Willinger, R. Experimental mechanical characterization of abdominal organs: Liver, kidney & spleen. J. Mech. Behav. Biomed. Mater. 2013, 17, 22–33. [Google Scholar] [CrossRef] [PubMed]
- Filippou, V.; Tsoumpas, C. Recent advances on the development of phantoms using 3D printing for imaging with CT, MRI, PET, SPECT, and ultrasound. Med. Phys. 2018, 45, e740–e760. [Google Scholar] [CrossRef]
- Brisbane, W.; Bailey, M.R.; Sorensen, M.D. An overview of kidney stone imaging techniques. Nat. Rev. Urol. 2016, 13, 654–662. [Google Scholar] [CrossRef]
- Izdihar, K.; Rashmizal, H.; Razak, A.; Supion, N.; Khalis, M.; Karim, A.; Osman, N.H.; Norkhairunnisa, M. Structural, Mechanical, and Dielectric Properties of Polydimethylsiloxane and Silicone Elastomer for the Fabrication of Clinical-Grade Kidney Phantom. Appl. Sci. 2021, 11, 1172. [Google Scholar] [CrossRef]
- Klaus, R.; Niyazi, M.; Lange-Sperandio, B. Radiation-induced kidney toxicity: Molecular and cellular pathogenesis. Radiat. Oncol. 2021, 16, 43. [Google Scholar] [CrossRef] [PubMed]
- Kamal, I.; Chelliah, K.K.; Mustafa, N. Estimates of average glandular dose with auto-modes of X-ray exposures in digital breast tomosynthesis. Sultan Qaboos Univ. Med. J. 2015, 15, e292–e296. [Google Scholar] [PubMed]
- Karimi, A.; Shojaei, A. Measurement of the Mechanical Properties of the Human Kidney. IRBM 2017, 38, 292–297. [Google Scholar] [CrossRef]
- Hill, D.J.T.; Preston, C.M.L.; Salisbury, D.J.; Whittaker, A.K. Molecular weight changes and scission and crosslinking in poly(dimethyl siloxane) on gamma radiolysis. Radiat. Phys. Chem. 2001, 62, 11–17. [Google Scholar] [CrossRef]
- Sankır, M.; Küçükyavuz, Z.; Küçükyavuz, S. Synthesis and Characterization of Poly (dimethylsiloxane)–Polythiophene Composites. J. Appl. Polym. Sci. 2003, 87, 2113–2119. [Google Scholar] [CrossRef]
- Dalod, A.R.M.; Grendal, O.G.; Blichfeld, A.B.; Furtula, V.; Pérez, J.; Henriksen, L.; Grande, T.; Einarsrud, M.A. Structure and optical properties of Titania-PDMS hybrid nanocomposites prepared by in situ non-aqueous synthesis. Nanomaterials 2017, 7, 460. [Google Scholar] [CrossRef] [Green Version]
- Şakar, E.; Özpolat, Ö.F.; Alım, B.; Sayyed, M.I.; Kurudirek, M. Phy-X / PSD: Development of a user friendly online software for calculation of parameters relevant to radiation shielding and dosimetry. Radiat. Phys. Chem. 2020, 166, 108496. [Google Scholar] [CrossRef]
- Kamal, I.; Karim, M.K.A.; Harun, H.H.; Abdul Razak, H.R.; Jian, L.Y.; Chyi, J.L.Y.; Kechik, M.M.A. Evaluation of radiation attenuation properties on a various composition of polydimethylsiloxane (PDMS) for fabrication of kidney phantom. Radiat. Phys. Chem. 2021, 189, 109661. [Google Scholar] [CrossRef]
- Harun, H.H.; Abdul Karim, M.K.; Muhammad, N.A.; Awang Kechik, M.M.; Chew, M.T.; Talib, Z.A. Task-based assessment on various optimization protocols of computed tomography Pulmonary Angiography examination. Radiat. Phys. Chem. 2021, 188, 109692. [Google Scholar] [CrossRef]
- Muhammad, N.A.; Kayun, Z.; Abu Hassan, H.; Wong, J.H.D.; Ng, K.H.; Karim, M.K.A. Evaluation of Organ Dose and Image Quality Metrics of Pediatric CT Chest-Abdomen-Pelvis (CAP) Examination: An Anthropomorphic Phantom Study. Appl. Sci. 2021, 11, 2047. [Google Scholar] [CrossRef]
- Harun, H.H.; Abdul Karim, M.K.; Abd Rahman, M.A.; Abdul Razak, H.R.; Che Isa, I.N.; Harun, F. Establishment of CTPA Local Diagnostic Reference Levels with Noise Magnitude as a Quality Indicator in a Tertiary Care Hospital. Diagnostics 2020, 10, 680. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, Z.; Li, Y.; Tang, S. Effect of Cyclic Loading on Surface Instability of Silicone Rubber under Compression. Polymers 2017, 9, 148. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Volinsky, A.A.; Gallant, N.D. Crosslinking effect on polydimethylsiloxane elastic modulus measured by custom-built compression instrument. J. Appl. Polym. Sci. 2014, 131, 41050. [Google Scholar] [CrossRef] [Green Version]
- Johnston, I.D.; McCluskey, D.K.; Tan, C.K.L.; Tracey, M.C. Mechanical characterization of bulk Sylgard 184 for microfluidics and microengineering. J. Micromech. Microeng. 2014, 24, 035017. [Google Scholar] [CrossRef]
- Pan, Y.; Zhu, F.; Fan, J.; Tao, J.; Lin, X.; Wang, F.; Shi, L. Investigation of mechanical properties of silicone/phosphor composite used in light emitting diodes package. Polymers 2018, 10, 195. [Google Scholar] [CrossRef] [Green Version]
- King, B.W.; Landheer, K.A.; Johns, P.C. X-ray coherent scattering form factors of tissues, water and plastics using energy dispersion. Phys. Med. Biol. 2011, 56, 4377–4397. [Google Scholar] [CrossRef] [PubMed]
- Böke, A. Linear attenuation coefficients of tissues from 1 keV to 150 keV. Radiat. Phys. Chem. 2014, 102, 49–59. [Google Scholar] [CrossRef]
- Manjunatha, H. Comparison of effective atomic numbers of the cancerous and normal kidney tissue. Radiat. Prot. Environ. 2015, 38, 83. [Google Scholar] [CrossRef]
- Grantham, K.; Li, H.; Zhao, T.; Klein, E. SU-E-CAMPUS-J-06: The Impact of CT-Scan Energy On Range Uncertainty in Proton Therapy Planning. Med. Phys. 2014, 41, 387. [Google Scholar] [CrossRef]
- In, E. Development of Polymer-Based Gels for Multimodal Medical Imaging Phantoms; ProQuest LLC: Toronto, ON, Canada, 2016; p. 122. [Google Scholar]
- Artikboeva, R.; Yang, M.; Wu, Y.; Jie, C.; Heng, Q. Preparation and Application of the Hydrophilic Amino-Silicone Softener by Emulsion Polymerization. Adv. Chem. Eng. Sci. 2020, 10, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Sombatsompop, N.; Chaochanchaikul, K. Effect of moisture content on mechanical properties, thermal and structural stability and extrudate texture of poly(vinyl chloride)/wood sawdust composites. Polym. Int. 2004, 53, 1210–1218. [Google Scholar] [CrossRef]
- Akça, B.; Erzeneoğlu, S.Z. The mass attenuation coefficients, electronic, atomic, and molecular cross sections, effective atomic numbers, and electron densities for compounds of some biomedically important elements at 59.5 kev. Sci. Technol. Nucl. Install. 2014, 2014, 901465. [Google Scholar] [CrossRef] [Green Version]
- Rashad, M.; Tekin, H.O.; Zakaly, H.M.; Pyshkina, M.; Issa, S.A.M.; Susoy, G. Physical and nuclear shielding properties of newly synthesized magnesium oxide and zinc oxide nanoparticles. Nucl. Eng. Technol. 2020, 52, 2078–2084. [Google Scholar] [CrossRef]
- Kadri, O.; Alfuraih, A. Photon energy absorption and exposure buildup factors for deep penetration in human tissues Photon energy absorption and exposure buildup factors for deep penetration in human tissues. Nucl. Sci. Tech. 2019, 30, 176. [Google Scholar] [CrossRef]
- Manohara, S.R.; Hanagodimath, S.M.; Gerward, L. Energy absorption buildup factors of human organs and tissues at energies and penetration depths relevant for radiotherapy and diagnostics. J. Appl. Clin. Med. Phys. 2011, 12, 296–312. [Google Scholar] [CrossRef] [PubMed]
- He, T.; Qian, X.; Zhai, R.; Yang, Z. Computed tomography number measurement consistency under different beam hardening conditions: Comparison between dual-energy spectral computed tomography and conventional computed tomography imaging in phantom experiment. J. Comput. Assist. Tomogr. 2015, 39, 981–985. [Google Scholar] [CrossRef] [Green Version]
- Abbasova, N.; Yüksel, Z.; Abbasov, E.; Gülbiçim, H.; Ça, M. Investigation of gamma-ray attenuation parameters of some materials used in dental applications. Results Phys. 2019, 12, 2202–2205. [Google Scholar] [CrossRef]
- Kirby, B.J.; Davis, J.R.; Grand, J.A.; Morgan, M.J. Extracting material parameters from x-ray attenuation: A CT feasibility study using kilovoltage synchrotron x-rays incident upon low atomic number absorbers. Phys. Med. Biol. 2003, 48, 3389. [Google Scholar] [CrossRef]



| Samples | Hydrogen Silicone (g) C7H22O2Si3 | H2O (g) | PDMS (g) C2H6Osi |
|---|---|---|---|
| S1 | 0 | 0 | 20 |
| S2 | 4 | 0 | 16 |
| S3 | 0 | 4 | 16 |
| S4 | 4 | 8 | 8 |
| Samples | Hydrogen Silicone C7H22O2Si3 | Water H2O | PDMS C2H6Osi | Compression Testing (MPa) | Young Modulus (MPa) |
|---|---|---|---|---|---|
| PDMS 100% | 0 | 0 | 20 | 2.6–2.8 * | 2.61 * |
| HS/PDMS 20:80 | 4 | 0 | 16 | 4.06 ± 0.62 | 4.17 |
| H2O/PDMS 20:80 | 0 | 4 | 16 | 1.09 ± 0.362 | 1.19 |
| HS/H2O/PDMS 20:40:40 | 4 | 8 | 8 | 0.41 ± 0.05 | 0.516 |
| Energy (MeV) | Attenuation Properties | ||||
|---|---|---|---|---|---|
| MAC (cm2/g) | Zeff | HVL | Zeq | LAC | |
| 1.50 × 10−2 | 4.586 | 11.38 | 0.15661 | 10.33 | 4.568 |
| 2.00 × 10−2 | 2.044 | 10.29 | 0.3514 | 10.43 | 2.037 |
| 3.00 × 10−2 | 0.736 | 7.91 | 0.97565 | 10.55 | 0.735 |
| 4.00 × 10−2 | 0.417 | 6.26 | 1.72455 | 10.62 | 0.416 |
| 5.00 × 10−2 | 0.300 | 5.34 | 2.3926 | 10.67 | 0.300 |
| 6.00 × 10−2 | 0.246 | 4.83 | 2.91631 | 10.7 | 0.247 |
| 8.00 × 10−2 | 0.198 | 4.35 | 3.62052 | 10.75 | 0.199 |
| 1.00 × 10−1 | 0.176 | 4.16 | 4.06981 | 10.78 | 0.177 |
| 1.50 × 10−1 | 0.150 | 4.00 | 4.79128 | 10.83 | 0.15 |
| 2.00 × 10−1 | 0.135 | 3.96 | 5.31868 | 10.85 | 0.136 |
| 3.00 × 10−1 | 0.116 | 3.93 | 6.18157 | 10.88 | 0.117 |
| 4.00 × 10−1 | 0.104 | 3.92 | 6.92316 | 10.89 | 0.104 |
| 5.00 × 10−1 | 0.095 | 3.92 | 7.59245 | 10.9 | 0.095 |
| 6.00 × 10−1 | 0.087 | 3.92 | 8.21515 | 10.91 | 0.088 |
| 8.00 × 10−1 | 0.077 | 3.91 | 9.35973 | 10.91 | 0.077 |
| 1.00 | 0.069 | 3.91 | 10.41402 | 10.91 | 0.069 |
| 1.50 | 0.056 | 3.92 | 12.79181 | 8.76 | 0.056 |
| 2.00 | 0.048 | 3.93 | 14.87477 | 8.48 | 0.048 |
| 3.00 | 0.039 | 3.99 | 18.42066 | 8.42 | 0.039 |
| 4.00 | 0.034 | 4.05 | 21.3392 | 8.39 | 0.034 |
| 5.00 | 0.030 | 4.13 | 23.78665 | 8.38 | 0.03 |
| 6.00 | 0.028 | 4.21 | 25.84345 | 8.38 | 0.028 |
| 8.00 | 0.025 | 4.37 | 29.07043 | 8.37 | 0.025 |
| 1.00 | 0.023 | 4.52 | 31.42182 | 8.37 | 0.023 |
| 1.50 | 0.021 | 4.87 | 35.01704 | 8.36 | 0.021 |
| Energy (keV) | HS/PDMS 20:80 | King et al. (2011) [27] | Aysun Böke (2014) [28] | Manjunath et al. (2015) [29] |
|---|---|---|---|---|
| 30 | 0.710 | 0.389 | 0.383 | 0.384 |
| 40 | 0.402 | 0.279 | 0.277 | 0.278 |
| 50 | 0.290 | 0.246 | 0.233 | 0.241 |
| 60 | 0.238 | 0.218 | 0.213 | 0.215 |
| 80 | 0.191 | 0.201 | 0.191 | 0.196 |
| kVp | Average CT Number | SD ROI | HU Background | SD Background | SNR | CNR |
|---|---|---|---|---|---|---|
| 80 | 71 | 7.5 | −802 | 10.3 | 15.12 | 87.11 |
| 100 | 63.7 | 6 | −792 | 9.5 | 14.66 | 96.18 |
| 120 | 45 | 5.6 | −789 | 8.2 | 2.56 | 100.9 |
| 140 | 30 | 8.3 | −830 | 84.7 | 1.1 | 9.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamal, I.; Razak, H.R.A.; Abdul Karim, M.K.; Mashohor, S.; Liew, J.Y.C.; Low, Y.J.; Zaaba, N.A.; Norkhairunnisa, M.; Rafi, N.A.S.M. Mechanical and Imaging Properties of a Clinical-Grade Kidney Phantom Based on Polydimethylsiloxane and Elastomer. Polymers 2022, 14, 535. https://doi.org/10.3390/polym14030535
Kamal I, Razak HRA, Abdul Karim MK, Mashohor S, Liew JYC, Low YJ, Zaaba NA, Norkhairunnisa M, Rafi NASM. Mechanical and Imaging Properties of a Clinical-Grade Kidney Phantom Based on Polydimethylsiloxane and Elastomer. Polymers. 2022; 14(3):535. https://doi.org/10.3390/polym14030535
Chicago/Turabian StyleKamal, Izdihar, Hairil Rashmizal Abdul Razak, Muhammad Khalis Abdul Karim, Syamsiah Mashohor, Josephine Ying Chyi Liew, Yiin Jian Low, Nur Atiqah Zaaba, Mazlan Norkhairunnisa, and Nur Athirah Syima Mohd Rafi. 2022. "Mechanical and Imaging Properties of a Clinical-Grade Kidney Phantom Based on Polydimethylsiloxane and Elastomer" Polymers 14, no. 3: 535. https://doi.org/10.3390/polym14030535
APA StyleKamal, I., Razak, H. R. A., Abdul Karim, M. K., Mashohor, S., Liew, J. Y. C., Low, Y. J., Zaaba, N. A., Norkhairunnisa, M., & Rafi, N. A. S. M. (2022). Mechanical and Imaging Properties of a Clinical-Grade Kidney Phantom Based on Polydimethylsiloxane and Elastomer. Polymers, 14(3), 535. https://doi.org/10.3390/polym14030535