Prospect of DFT Utilization in Polymer-Graphene Composites for Electromagnetic Interference Shielding Application: A Review
Abstract
:1. Introduction
2. Crystallography Basics
2.1. Bloch’s Theorem
2.2. Kohn–Sham Theorem
Kohn–Sham Equations Reformulation
3. DFT Concept in Graphene/Graphene-Based (Polymer)Composite Materials (GPM or GPCM)
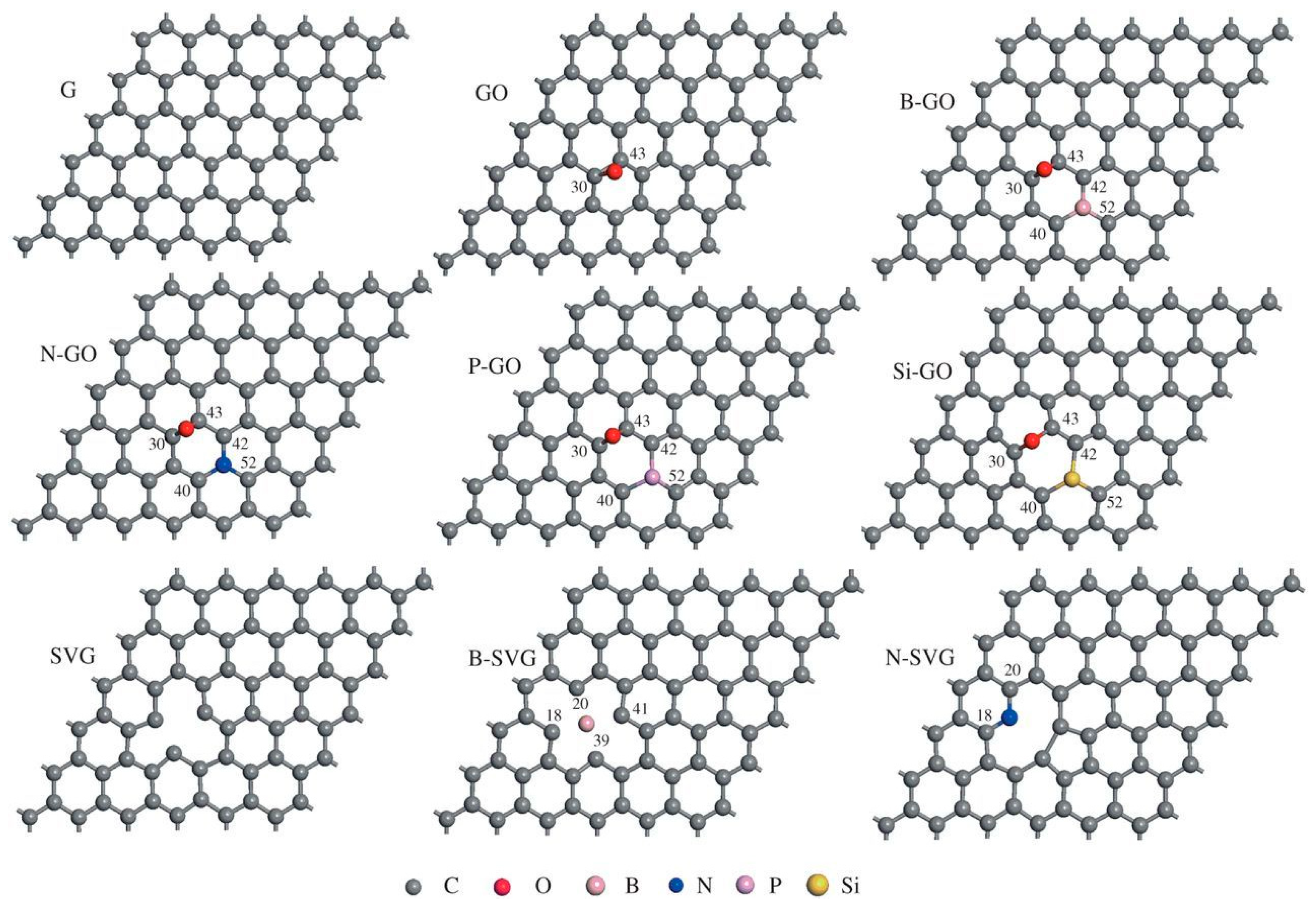
3.1. (Electronic)Structures and Atom Projected Density State of Graphene and/or GPM
3.2. Band Gap, Band Structures and Atom Projected Density States of GPM
3.3. Effects of the Electric Field upon the Properties of Graphene-Based Composites: EMI Shielding Focus
4. Application of DFT in GPM as per Literature
4.1. General Application to/in Atoms
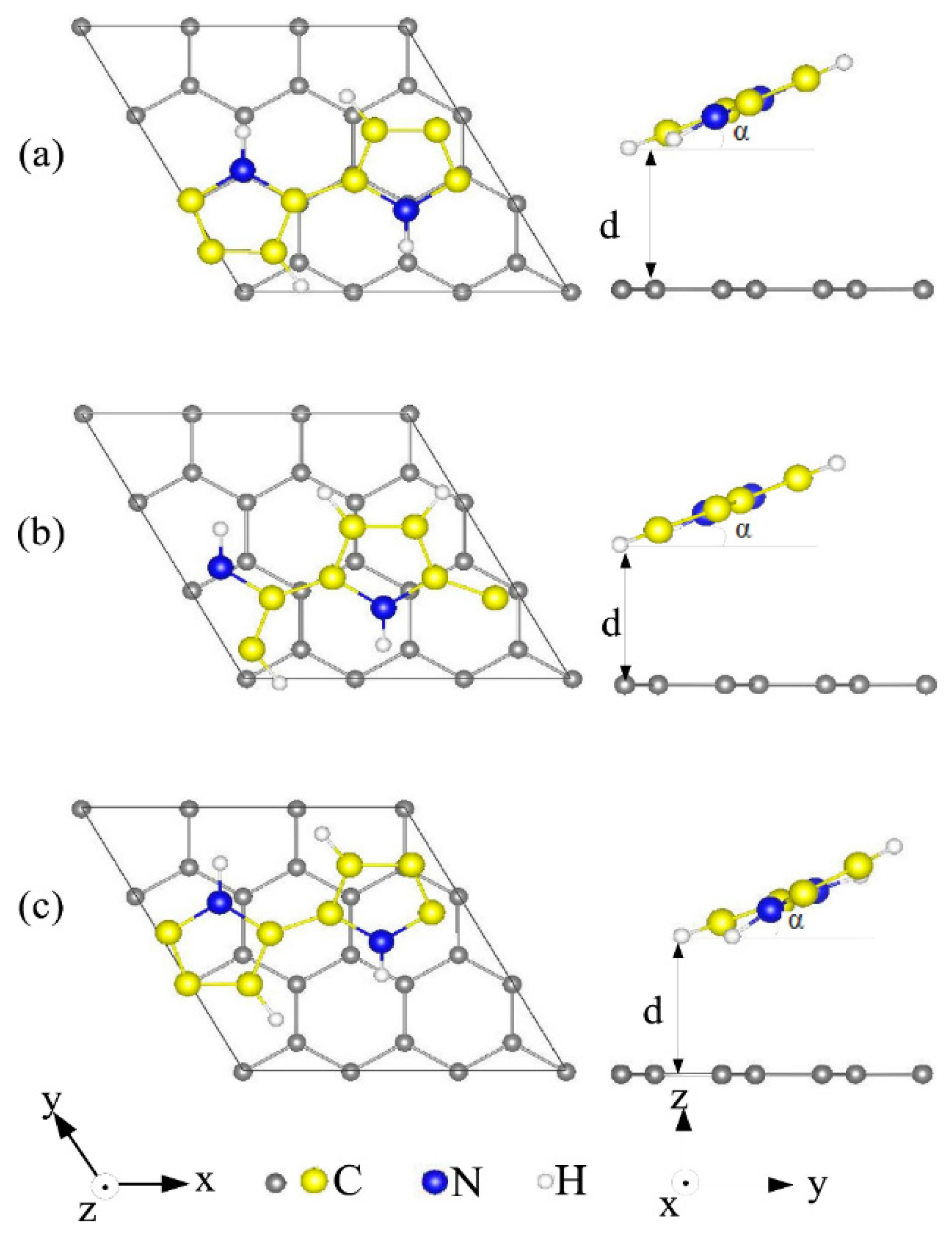
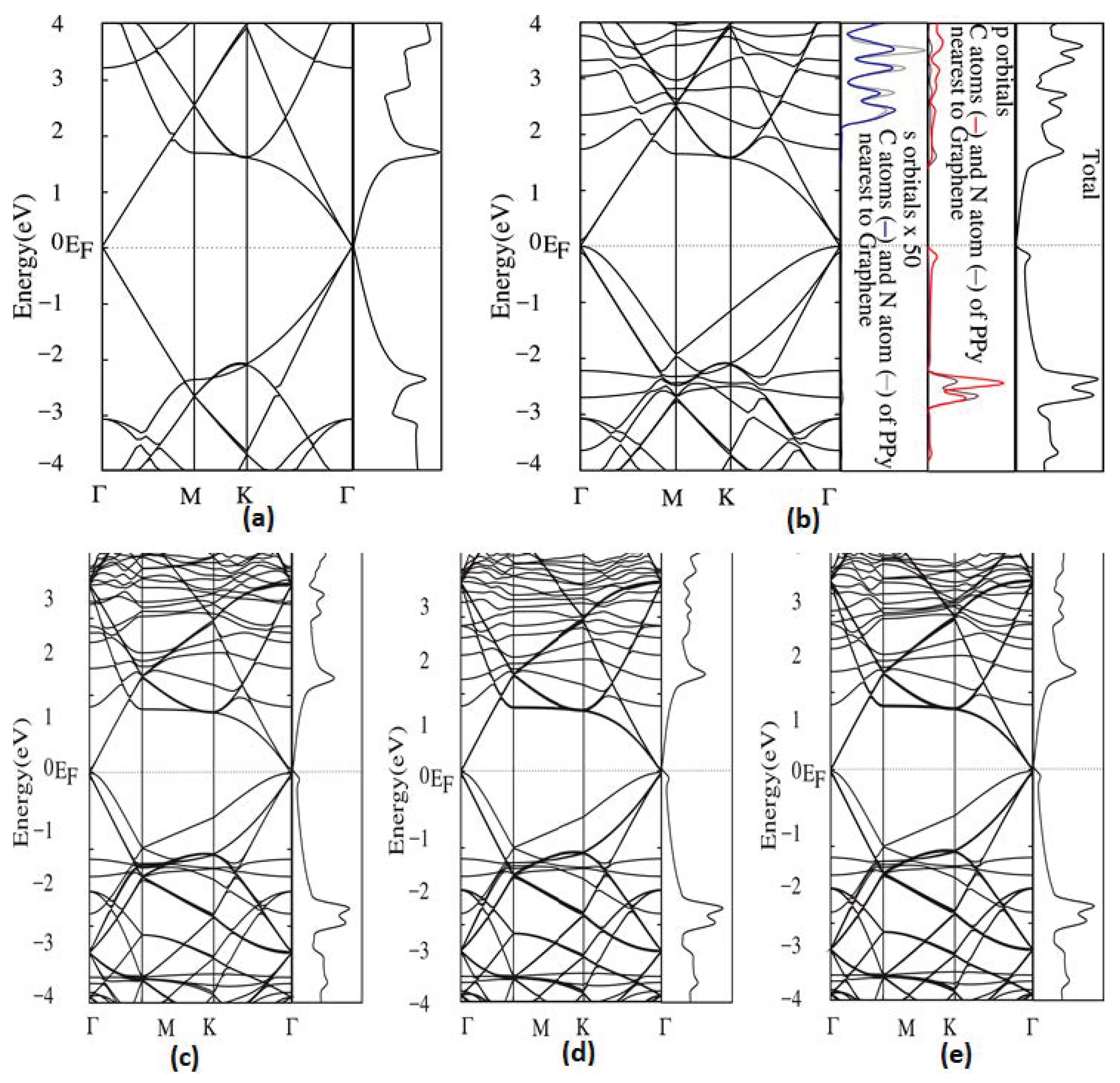
4.2. Molecules
5. Challenges and Future Outlook
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef] [Green Version]
- Sommerfeld, A.; Bethe, H. Elektronentheorie der Metalle. In Handbuch der Physik, 2nd ed.; Springer International Publishing: Cham, Switzerland, 1933; pp. 333–622. [Google Scholar]
- Jepsen, O.; Andersen, O.K. Linear tetrahedron methods for Brillouin zone integration. Solid State Commun. 1971, 9, 1763. [Google Scholar]
- Baldereschi, A. Mean-value point in the Brillouin zone. Phys. Rev. B 1973, 7, 5212. [Google Scholar] [CrossRef]
- Chadi, D.J.; Cohen, M.L. Special points in the brillouin zone. Phys. Rev. B 1973, 8, 5747. [Google Scholar] [CrossRef]
- Cunningham, S.L. Special points in the two-dimensional Brillouin zone. Phys. Rev. B 1974, 10, 4988. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Martin, R.M. Electronic Structure-Basic Theory and Practical Methods; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Chadi, D.J. Special points for Brillouin-zone integrations. Phy. Rev. B 1977, 16, 1746. [Google Scholar] [CrossRef]
- Grabowksi, B.; Hickel, T.; Neugebauer, J. Ab initio study of the thermodynamic properties of nonmagnetic elementary fcc metals: Exchangecorrelation-related error bars and chemical trends. Phys. Rev. B 2007, 76, 024309. [Google Scholar]
- Grabowski, B.; Söderlind, P.; Hickel, T.; Neugebauer, J. Temperature driven phase transitions from first principles including all relevant excitations: The fcc-to-bcc transition in Ca. Phys. Rev. B 2011, 84, 214107. [Google Scholar] [CrossRef] [Green Version]
- Morgan, W.S.; Jorgensen, J.J.; Hess, B.C.; Hart, G.L.W. Efficiency of generalized regular k-point grids. Comp. Mater. Sci. 2018, 153, 424–430. [Google Scholar] [CrossRef] [Green Version]
- Gruber, T.; Liao, K.; Tsatsoulis, T.; Hummel, F.; Grüneis, A. Applying the coupled-cluster ansatz to solids and surfaces in the thermodynamic limit. Phys. Rev. X 2018, 8, 021043. [Google Scholar] [CrossRef] [Green Version]
- Paulus, B. The method of increments-a wavefunction-based ab initio correlation method for solids. Phys. Rep. 2006, 428, 1–52. [Google Scholar] [CrossRef]
- Bloch, F. Über die Quantenmechanik der Elektronen in Kristallgittern. Z. Physik 1928, 52, 555. [Google Scholar] [CrossRef]
- Foulkes, W.M.C.; Mitas, L.; Needs, R.J.; Rajagopal, G. Quantum Monte Carlo simulations of solids. Rev. Mod. Phys. 2001, 73, 33–83. [Google Scholar] [CrossRef] [Green Version]
- Parr, R.G.; Weitao, Y. Density-Functional Theory of Atoms and Molecules. In International Series of Monographs on Chemistry; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Koch, W.; Holthausen, M.C.A. Chemist’s Guide to Density Functional Theory; Wiley-VCH: Weinheim, Germany, 2001. [Google Scholar]
- Sholl, D.S.; Steckel, J.A. Density Functional Theory—A Practical Introduction. Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15. [Google Scholar] [CrossRef]
- Blum, V.; Gehrke, R.; Hanke, F.; Havu, P.; Havu, V.; Ren, X.; Reuter, K.; Scheffler, M. Ab initio molecular simulations with numeric atom-centered orbitals: FHI-aims. Comp. Phys. Commun. 2009, 180, 2175–2196. [Google Scholar] [CrossRef] [Green Version]
- Daniel, A.B.; Martin, J.M.L.; Nicholas, C.H. The role of the basis set: Assessing density functional theory. J. Chem. Phys. 2003, 119, 3005. [Google Scholar]
- Streitwolf, H.W. Group Theory in Solid State Physics; University Physics Series; Macdonald and Co.: London, UK, 1971. [Google Scholar]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Osaka, Y. Formal Theory of an Inhomogeneous Electron Gas. J. Phys. Soc. Japan 1974, 36, 376–385. [Google Scholar] [CrossRef]
- Talman, J.D.; Shadwick, W.F. Optimized effective atomic central potential. Phys. Rev. A 1976, 14, 36. [Google Scholar] [CrossRef]
- Kümmel, S.; Kronik, L. Orbital-dependent density functionals: Theory and applications. Rev. Mod. Phys. 2008, 80, 3–60. [Google Scholar] [CrossRef] [Green Version]
- Gonis, A.; Däne, M.; Nicholson, D.; Stocks, G. Computationally simple, analytic, closed form solution of the Coulomb self-interaction problem in Kohn–Sham density functional theory. Solid State Commun. 2012, 152, 771–774. [Google Scholar] [CrossRef]
- Däne, M.; Gonis, A.; Nicholson, D.; Stocks, G. On a solution of the self-interaction problem in Kohn-Sham density functional theory. J. Phys. Chem. Sol. 2014, 75, 1160–1178. [Google Scholar] [CrossRef] [Green Version]
- Harriman, J.E. Orthonormal orbitals for the representation of an arbitrary density. Phys. Rev. A 1981, 24, 680–682. [Google Scholar] [CrossRef]
- Sahni, V.; Li, Y.; Harbola, M.K. Atomic structure in the Pauli-correlated approximation. Phys. Rev. A 1992, 45, 1434–1448. [Google Scholar] [CrossRef] [PubMed]
- Salmankhani, A.; Karami, Z.; Mashhadzadeh, A.H.; Ganjali, M.R.; Vatanpour, V.; Esmaeili, A.; Habibzadeh, S.; Saeb, M.R.; Fierro, V.; Celzard, A. New Insights into H2S Adsorption on Graphene and Graphene-Like Structures: A Comparative DFT Study. C 2020, 6, 74. [Google Scholar] [CrossRef]
- Xu, W.; EA Kelly, R.; Otero, R.; Schöck, M.; Lægsgaard, E.; Stensgaard, I.; Kantorovich, L.N.; Besenbacher, F. Probing the Hierarchy of Thymine–Thymine Interactions in Self-Assembled Structures by Manipulation with Scanning Tunneling Microscopy. Small 2007, 3, 2011–2014. [Google Scholar] [CrossRef]
- Lu, S.; Hummel, M.; Kang, S.; Pathak, R.; He, W.; Qi, X.; Gu, Z. Density Functional Theory Investigation of the NiO@Graphene Composite as a Urea Oxidation Catalyst in the Alkaline Electrolyte. ACS Omega 2021, 6, 14648–14654. [Google Scholar]
- Mashhadzadeh, A.H.; Fereidoon, A.; Ahangari, M.G. Experimental and multiscale quantum mechanics modeling of the mechanical properties of PVC/graphene nanocomposite. J. Comp. Mat. 2020, 54, 4575–4590. [Google Scholar] [CrossRef]
- Mashhadzadeh, A.H.; Fereidoon, A.; Ahangari, M.G. Combining density functional theory-finite element multi-scale method to predict mechanical properties of polypropylene/graphene nanocomposites: Experimental study. Mat. Chem. Phys. 2017, 201, 214–223. [Google Scholar] [CrossRef]
- Xu, M.; Paci, J.T.; Oswald, J.; Belytschko, T. A constitutive equation for graphene based on density functional theory. Int. J. Sol. Struct. 2012, 49, 2582–2589. [Google Scholar] [CrossRef] [Green Version]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Eect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Avouris, P.; Dimitrakopoulos, C. Graphene: Synthesis and applications. Mater. Tod. 2012, 15, 86–97. [Google Scholar] [CrossRef]
- Park, S.; An, J.; Jung, I.; Piner, R.D.; An, S.J.; Li, X.; Velamakanni, A.; Ruo, R.S. Colloidal Suspensions of Highly Reduced Graphene Oxide in a Wide Variety of Organic Solvents. Nano Lett. 2009, 9, 1593–1597. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Cote, L.J.; Kim, F.; Yuan, W.; Shull, K.R.; Huang, J. Graphene Oxide Sheets at Interfaces. J. Am. Chem. Soc. 2010, 132, 8180–8186. [Google Scholar] [CrossRef]
- Kim, F.; Cote, L.J.; Huang, J. Graphene Oxide: Surface Activity and Two-Dimensional Assembly. Adv. Mater. 2010, 22, 1954–1958. [Google Scholar] [CrossRef] [PubMed]
- Veclani, D.; Tolazzi, M.; Melchior, A. Molecular Interpretation of Pharmaceuticals’ Adsorption on Carbon Nanomaterials: Theory Meets Experiments. Processes 2020, 8, 642. [Google Scholar] [CrossRef]
- Smalley, R.E.; Yakobson, B.I. The future of the fullerenes. Solid State Commun. 1998, 107, 597–606. [Google Scholar] [CrossRef]
- Li, X.; Zhi, L. Graphene hybridization for energy storage applications. Chem. Soc. Rev. 2018, 47, 3189–3216. [Google Scholar] [CrossRef]
- Kharissova, O.V.; Kharisov, B.I.; Oliva González, C.M. Carbon-Carbon Allotropic Hybrids and Composites: Synthesis, Properties, and Applications. Ind. Eng. Chem. Res. 2019, 58, 3921–3948. [Google Scholar] [CrossRef]
- Song, S.; Zhao, H.; Zheng, X.; Zhang, H.; Liu, Y.; Wang, Y.; Han, B. A density functional theory study of the role of functionalized graphene particles as effective additives in power cable insulation. R. Soc. Open Sci. 2018, 5, 170772. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Yu, L.; Wu, X.; Hu, W. Experimental Sensing and Density Functional Theory Study of H 2 S and SOF 2 Adsorption on Au-Modified Graphene. Adv. Sci. 2015, 2, 1500101. [Google Scholar] [CrossRef] [PubMed]
- Ahangari, M.G.; Salmankhani, A.; Imani, A.H.; Shahab, N.; Mashhadzadeh, A.H. Density Functional Theory Study on the Mechanical Properties and Interlayer Interactions of Multi-layer Graphene: Carbonic, Silicon-Carbide and Silicene Graphene-like Structures. Silicon 2019, 11, 1235–1246. [Google Scholar] [CrossRef]
- Özkaya, S.; Blaisten-Barojas, E. Polypyrrole on graphene: A density functional theory study. Surf. Sci. 2018, 674, 1–5. [Google Scholar] [CrossRef]
- Chi, M.; Zhao, Y.-P. First principle study of the interaction and charge transfer between graphene and organic molecules. Comput. Mat. Sci. 2012, 56, 79–84. [Google Scholar] [CrossRef] [Green Version]
- Yafei, D.; Blaisten-Barojas, E. Energetics, structure, and charge distribution of reduced and oxidized n-pyrrole oligomers: A density functional approach. J Chem. Phys. 2008, 129, 164903. [Google Scholar]
- Wu, H.Z.; Zhong, Q.H.; Bandaru, S.; Liu, J.; Lau, W.M.; Li, L.L.; Wang, Z. Exploring the formation and electronic structure properties of the g-C3N4 nanoribbon with density functional theory. J. Phys. Cond. Mat. 2018, 30, 155303. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Antonietti, M. Polymeric Graphitic Carbon Nitride as a Heterogeneous Organocatalyst: From Photochemistry to Multipurpose Catalysis to Sustainable Chemistry. Angew. Chem. Int. Ed. 2012, 51, 68–89. [Google Scholar] [CrossRef]
- Merschjann, C.; Tschierlei, S.; Tyborski, T.; Kailasam, K.; Orthmann, S.; Hollmann, D.; Schedel-Niedrig, T.; Thomas, A.; Lochbrunner, S. Complementing Graphenes: 1D Interplanar Charge Transport in Polymeric Graphitic Carbon Nitrides. Adv. Mater. 2015, 27, 7993–7999. [Google Scholar] [CrossRef]
- Baqi, S.; Deng, B.; Guo, Y.; Zhang, R.Q. Novel Two-Step Surface Boron Decoration of Graphitic Carbon Nitride Photoelectrodes for Efficient Charge Transport and Separation. J. Phys. Chem. C 2021, 125, 25207–25216. [Google Scholar] [CrossRef]
- Torad, N.L.; El-Hosainy, H.; Esmat, M.; El-Kelany, K.E.; Tahawy, R.; Na, J.; Ide, Y.; Fukata, N.; Chaikittisilp, W.; Hill, J.P.; et al. Phenyl-Modified Carbon Nitride Quantum Nanoflakes for Ultra-Highly Selective Sensing of Formic Acid: A Combined Experimental by QCM and Density Functional Theory Study. ACS Appl. Mat. Interf. 2021, 13, 48595–48610. [Google Scholar] [CrossRef] [PubMed]
- Niu, L.; Du, J.; Jiang, D.; Du, H.; Lin, X.; Xu, J.; Li, Z.; Zhu, C.; Gu, L.; Bi, H.; et al. Carbon Defects Induced Delocalization of π Electrons Enables Efficient Charge Separation in Graphitic Carbon Nitride for Increased Photocatalytic H2 Generation. Catal. Lett. 2021, 27, 1–10. [Google Scholar] [CrossRef]
- Gecim, G.; Ozekmekci, M.A. Density functional theory study of molecular H2S adsorption on (4, 0) SWCNT doped with Ge, Ga and B. Surf. Sci. 2021, 711, 121876. [Google Scholar] [CrossRef]
- Kamedulski, P.; Kaczmarek-Kedziera, A.; Lukaszewicz, J.P. Influence of intermolecular interactions on the properties of carbon nanotubes. Bull. Mat. Sci. 2018, 41, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Ostovari, F.; Hasanpoori, M.; Abbasnejad, M.; Salehi, M.A. DFT calculations of graphene monolayer in presence of Fe dopant and vacancy. Phys. B Cond. Mat. 2018, 541, 6–13. [Google Scholar] [CrossRef]
- Oostinga, J.B.; Heersche, H.B.; Liu, X.; Morpurgo, A.F.; Vandersypen, L.M. Gate-induced insulating state in bilayer graphene devices. Nat. Mat. 2008, 7, 151–157. [Google Scholar] [CrossRef] [Green Version]
- Geng, W.; Zhao, X.; Zan, W.; Liu, H.; Yao, X. Effects of the electric field on the properties of ZnO-graphene composites: A density functional theory study. Phys. Chem. Chem. Phys. 2014, 16, 3542–3548. [Google Scholar] [CrossRef]
- Sadhukhan, S.; Ghosh, T.K.; Rana, D.; Roy, I.; Bhattacharyya, A.; Sarkar, G.; Chakraborty, M.; Chattopadhyay, D. Studies on synthesis of reduced graphene oxide (RGO) via green route and its electrical property. Mat. Res. Bul. 2016, 79, 41–51. [Google Scholar] [CrossRef]
- Roy, I.; Rana, D.; Sarkar, G.; Bhattacharyya, A.; Saha, N.R.; Mondal, S.; Pattanayak, S.; Chattopadhyay, S.; Chattopadhyay, D. Physical and electrochemical characterization of reduced graphene oxide/silver nanocomposites synthesized by adopting a green approach. RSC Adv. 2015, 5, 25357–25364. [Google Scholar] [CrossRef]
- Kausar, N.; Roy, I.; Chattopadhyay, D.; Das, A.R. Synthesis of 2,3-dihydroquinazolinones and quinazolin-4(3H)-ones catalyzed by graphene oxide nanosheets in an aqueous medium: “on-water” synthesis accompanied by carbocatalysis and selective C–C bond cleavage. RSC Adv. 2016, 6, 22320–22330. [Google Scholar] [CrossRef]
- Sadhukhan, S.; Bhattacharyya, A.; Rana, D.; Ghosh, T.K.; Orasugh, J.T.; Khatua, S.; Acharya, K.; Chattopadhyay, D. Synthesis of RGO/NiO nanocomposites adopting a green approach and its photocatalytic and antibacterial properties. Mat. Chem. Phy. 2020, 247, 122906. [Google Scholar] [CrossRef]
- Zaman, A.; Orasugh, J.T.; Banerjee, P.; Dutta, S.; Ali, M.S.; Das, D.; Bhattacharya, A.; Chattopadhyay, D. Facile one-pot in-situ synthesis of novel graphene oxide-cellulose nanocomposite for enhanced azo dye adsorption at optimized conditions. Carbohydr. Polym. 2020, 246, 116661. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharyya, A.; Ghorai, S.; Rana, D.; Roy, I.; Sarkar, G.; Saha, N.R.; Orasugh, J.T.; De, S.; Sadhukhan, S.; Chattopadhyay, D. Design of an efficient and selective adsorbent of cationic dye through activated carbon—Graphene oxide nanocomposite: Study on mechanism and synergy. Mat. Chem. Phy. 2020, 260, 124090. [Google Scholar] [CrossRef]
- Hussain, A.; Basit, A. A comparative density functional theory study of oxygen doping versus adsorption on graphene to tune its band gap. J. Mol. Graph. Model. 2021, 107, 107982. [Google Scholar] [CrossRef]
- Kozlov, S.M.; Viñes, F.; Görling, A. Bandgap engineering of graphene by physisorbed adsorbates. Adv. Mater. 2011, 23, 2638–2643. [Google Scholar] [CrossRef] [PubMed]
- Ito, J.; Nakamura, J.; Natori, A. Semiconducting nature of the oxygen-adsorbed graphene sheet. J. Appl. Phys. 2008, 103, 113712. [Google Scholar] [CrossRef]
- Yoo, S.; Lee, B.; Kang, K. Density functional theory study of the mechanical behavior of silicene and development of a Tersoff interatomic potential model tailored for elastic behavior. Nanotechnology 2021, 32, 295702. [Google Scholar] [CrossRef]
- Sachdeva, G.; Lobato, A.; Pandey, R.; Odegard, G.M. Mechanical Response of Polymer Epoxy/BMI Composites with Graphene and a Boron Nitride Monolayer from First Principles. ACS Appl. Polym. Mat. 2021, 3, 1052–1059. [Google Scholar] [CrossRef]
- Moon, J.; Yang, S.; Cho, M. Interfacial strengthening between graphene and polymer through Stone-Thrower-Wales defects: Ab initio and molecular dynamics simulations. Carbon 2017, 118, 66–77. [Google Scholar] [CrossRef]
- Jawaid, M.; Bouhfid, R.; El Kacem Qaiss, A. Functionalized Graphene Nanocomposites and Their Derivatives: Synthesis, Processing and Applications; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Dewhurst, K.; Sharma, S. Development of the elk lapw code. Max Planck Institute of Microstructure Physics. Available online: https://elk.sourceforge.io (accessed on 16 September 2021).
- Peng, B.; Lu, Y.; Luo, J.; Zhang, Z.; Zhu, X.; Tang, L.; Wang, L.; Deng, Y.; Ouyang, X.; Tan, J.; et al. Visible light-activated self-powered photoelectrochemical aptasensor for ultrasensitive chloramphenicol detection based on DFT-proved Z-scheme Ag2CrO4/g-C3N4/graphene oxide. J. Hazar. Mat. 2020, 401, 123395. [Google Scholar] [CrossRef]
- Krieger, J.B.; Li, Y.; Iafrate, G.J. Derivation and application of an accurate Kohn-Sham potential with integer discontinuity. Phys. Lett. A 1990, 146, 256. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef] [PubMed]
- Engel, E.; Chevary, J.A.; Macdonald, L.D.; Vosko, S.H. Asymptotic properties of the exchange energy density and the exchange potential of finite systems: Relevance for generalized gradient approximations. Zeitschrift für Physik D Atoms. Molec. Clust. 1992, 23, 7–14. [Google Scholar] [CrossRef]
- Nagy, Á. Density functional. Theory and application to atoms and molecules. Phys. Repor. 1998, 298, 1–79. [Google Scholar] [CrossRef]
- Gross, E.K.U.; Dobson, J.F.; Petersilka, M. Density functional theory of time-dependent phenomena. Density Funct. Theory II 1996, 181, 81–172. [Google Scholar]
- Gross, E.K.U.; Petersilka, M.; Grabo, T. Density Functional Methods; Ziegler, T., Ed.; American Chemical Society: Washington, DC, USA, 1996. [Google Scholar]
- Wilson, L.C.; Levy, M. Nonlocal Wigner-like correlation-energy density functional through coordinate scaling. Phys. Rev. B 1990, 41, 12930. [Google Scholar] [CrossRef]
- Perdew, J.P. Electronic Structure of Solids ’91; Academic Press: Berlin, Germany, 1991. [Google Scholar]
- Wang, Y.; Perdew, J.P. Correlation hole of the spin-polarized electron gas, with exact small-wave-vector and high-density scaling. Phys. Rev. B 1991, 44, 13298. [Google Scholar] [CrossRef]
- Süle, P.; Gritsenko, O.V.; Nagy, A.; Baerends, E.J. Correlation energy density from ab initio first-and second-order density matrices: A benchmark for approximate functionals. J. Chem. Phys. 1995, 103, 10085–10094. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef] [Green Version]
- Oliphant, N.; Bartlett, R.J. A systematic comparison of molecular properties obtained using Hartree–Fock, a hybrid Hartree–Fock density-functional-theory, and coupled-cluster methods. J. Chem. Phys. 1994, 100, 6550–6561. [Google Scholar] [CrossRef]
- Johnson, B.G.; Gill, P.M.; Pople, J.A. The performance of a family of density functional methods. J. Chem. Phys. 1993, 98, 5612–5626. [Google Scholar] [CrossRef]
- Neumann, R.; Nobes, R.H.; Handy, N.C. Exchange functionals and potentials. Molecul. Phys. 1996, 87, 1–36. [Google Scholar] [CrossRef]
- Baer, R.; Neuhauser, D. Density functional theory with correct long-range asymptotic behavior. Phys. Rev. Lett. 2005, 94, 043002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Görling, A.; Levy, M. Hybrid schemes combining the Hartree–Fock method and density-functional theory: Underlying formalism and properties of correlation functionals. J. Chem. Phys. 1997, 106, 2675–2680. [Google Scholar] [CrossRef]
- Deng, Y.-X.; Chen, S.-Z.; Zhang, Y.; Yu, X.; Xie, Z.-X.; Tang, L.-M.; Chen, K.-Q. Penta-Hexa-Graphene Nanoribbons: Intrinsic Magnetism and Edge Effect Induce Spin-Gapless Semiconducting and Half-Metallic Properties. ACS Appl. Mater. Interf. 2020, 12, 53088–53095. [Google Scholar] [CrossRef]
- Dos Santos, R.M.; de Sousa, L.E.; Galvão, D.S.; Ribeiro, L.A. Tuning penta-Graphene electronic properties through engineered Line Defects. Sci. Repor. 2020, 10, 8014. [Google Scholar] [CrossRef]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Insights into current limitations of density functional theory. Science 2008, 321, 792–794. [Google Scholar] [CrossRef] [Green Version]
- Shekaari, A. QUANTUM ESPRESSO: Decomposing exchange and correlation contributions. J. Phys. Condens. Matter. 2021, 21, 395502. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, D.J.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745. [Google Scholar] [CrossRef] [Green Version]
- Schwarz, K.; Blaha, P. Solid state calculations using WIEN2k. Comput. Mat. Sci. 2003, 28, 259–273. [Google Scholar] [CrossRef]
| Atom | HF | Optimized Potential Method (OPM) | LDA | B |
|---|---|---|---|---|
| He | −1.026 | −1.026 | −0.884 | −1.025 |
| Be | −2.667 | −2.666 | −2.312 | −2.658 |
| Ne | −12.108 | −12.105 | −11.03 | −12.14 |
| Mg | −15.994 | −15.988 | −14.61 | −16.00 |
| Ar | −30.185 | −30.175 | −27.86 | −30.15 |
| Atom | Exp. | HF | OPM | LDA | GGA |
|---|---|---|---|---|---|
| He | −2.9037 | −2.8617 | −2.975 | −2.8989 | |
| C | −37.8450 | −37.6886 | −37.6865 | −38.0522 | −37.8243 |
| Ne | −128.939 | −128.547 | −128.546 | −129.317 | −128.945 |
| Si | −289.383 | −288.854 | −288.850 | −289.912 | −289.368 |
| Cl | −460.217 | −459.482 | −459.477 | −460.838 | −460.162 |
| DFT | QC | Δ (|Ec,exactQC − Ec,exactDFT|/Ec,exactDFT) | Δ% ((|Ec,exactQC − Ec,exactDFT|/Ec,exactDFT)100) | |
|---|---|---|---|---|
| H− | −0.041995 | −0.039821 | +0.002174 | 5.20 |
| He | −0.042107 | −0.042044 | +0.000063 | 0.20 |
| Be+2 | −0.044274 | −0.044267 | +0.000007 | 0.02 |
| Ne+8 | −0.045694 | −0.045693 | +0.000001 | 0.002 |
| Be | −0.096200 | −0.094300 | +0.001900 | 2.00 |
| Ne | −0.394000 | −0.390000 | +0.004000 | 1.00 |
| WL | LYP | GGA | LW | LDA | Exp | |
|---|---|---|---|---|---|---|
| He | 0.042 | 0.043 | 0.046 | 0.042 | 0.112 | 0.042 |
| Be | 0.094 | 0.094 | 0.094 | 0.094 | 0.223 | 0.094 |
| Ne | 0.383 | 0.383 | 0.383 | 0.374 | 0.743 | 0.392 |
| Mg | 0.444 | 0.459 | 0.451 | 0.462 | 0.888 | 0.444 |
| Ar | 0.788 | 0.750 | 0.771 | 0.771 | 1.426 | 0.787 |
| Kr | 1.909 | 1.748 | 1.916 | 1.948 | 3.267 | |
| Xe | 3.156 | 2.742 | 3.150 | 3.174 | 5.173 | |
| Li+ | 0.044 | 0.047 | 0.051 | 0.060 | 0.134 | 0.044 |
| Be2+ | 0.045 | 0.049 | 0.053 | 0.075 | 0.150 | 0.044 |
| Ne6+ | 0.109 | 0.129 | 0.123 | 0.187 | 0.334 | 0.187 |
| B+ | 0.101 | 0.106 | 0.103 | 0.114 | 0.252 | 0.111 |
| Li− | 0.0805 | 0.0732 | 0.078 | 0.069 | 0.182 | 0.073 |
| F− | 0.368 | 0.362 | 0.362 | 0.332 | 0.696 | 0.400 |
| Molecule | WL | LYP | LW | PW | Exp |
|---|---|---|---|---|---|
| H2 | 0.049 | 0.038 | 0.029 | 0.046 | 0.041 |
| Li2 | 0.136 | 0.133 | 0.134 | 0.137 | 0.122 |
| Be2 | 0.231 | 0.200 | 0.193 | 0.205 | 0.205 |
| B2 | 0.336 | 0.289 | 0.265 | 0.296 | 0.330 |
| C2 | 0.446 | 0.384 | 0.344 | 0.391 | 0.514 |
| N2 | 0.532 | 0.483 | 0.435 | 0.490 | 0.546 |
| O2 | 0.621 | 0.583 | 0.533 | 0.588 | 0.657 |
| F2 | 0.683 | 0.675 | 0.633 | 0.671 | 0.746 |
| H2O | 0.386 | 0.340 | 0.314 | 0.347 | 0.367 |
| NH3 | 0.376 | 0.318 | 0.268 | 0.338 | 0.338 |
| CH4 | 0.369 | 0.294 | 0.241 | 0.320 | 0.293 |
| HF | 0.377 | 0.363 | 0.335 | 0.367 | 0.387 |
| LiH | 0.088 | 0.089 | 0.083 | 0.092 | 0.083 |
| LiF | 0.417 | 0.418 | 0.343 | 0.415 | 0.447 |
| HCN | 0.525 | 0.464 | 0.410 | 0.478 | 0.527 |
| CO | 0.516 | 0.484 | 0.440 | 0.488 | 0.550 |
| H2O2 | 0.690 | 0.638 | 0.569 | 0.652 | 0.691 |
| C2H2 | 0.504 | 0.443 | 0.386 | 0.466 | 0.476 |
| C2H6 | 0.678 | 0.551 | 0.426 | 0.577 | 0.553 |
| C2H4 | 0.593 | 0.497 | 0.417 | 0.529 | 0.528 |
| CO2 | 0.865 | 0.791 | 0.720 | 0.807 | 0.829 |
| HF | MP2 | LDA | BLYP | BP | BRP | Exp | |
|---|---|---|---|---|---|---|---|
| H2 | 75.9 | 86.6 | 100.2 | 103.2 | 107.8 | 106.9 | 103.3 |
| LiH | 30.4 | 39.8 | 57.5 | 54.9 | 55.8 | 58.9 | 56.0 |
| NH3 | 170.2 | 232.4 | 306.0 | 270.1 | 289.5 | 286.7 | 276.7 |
| C2H2 | 271.9 | 365.6 | 438.6 | 383.4 | 398.6 | 404.0 | 388.9 |
| H2CO | 237.8 | 335.5 | 417.6 | 361.8 | 371.5 | 372.5 | 357.2 |
| F2 | −34.3 | 36.8 | 83.6 | 54.4 | 49.6 | 47.1 | 36.9 |
| HF | MP2 | LDA | BLYP | BP | BRP | Exp | |
|---|---|---|---|---|---|---|---|
| H2 | 0.730 | 0.738 | 0.765 | 0.748 | 0.747 | 0.741 | 0.741 |
| BeH | 1.348 | 1.348 | 1.370 | 1.355 | 1.356 | 1.353 | 1.343 |
| LiF | 1.555 | 1.567 | 1.544 | 1.561 | 1.580 | 1.582 | 1.564 |
| CO | 1.114 | 1.150 | 1.142 | 1.150 | 1.135 | 1.130 | 1.128 |
| N2 | 1.078 | 1.130 | 1.111 | 1.118 | 1.103 | 1.101 | 1.098 |
| NO | 1.127 | 1.143 | 1.161 | 1.176 | 1.160 | 1.158 | 1.151 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orasugh, J.T.; Ray, S.S. Prospect of DFT Utilization in Polymer-Graphene Composites for Electromagnetic Interference Shielding Application: A Review. Polymers 2022, 14, 704. https://doi.org/10.3390/polym14040704
Orasugh JT, Ray SS. Prospect of DFT Utilization in Polymer-Graphene Composites for Electromagnetic Interference Shielding Application: A Review. Polymers. 2022; 14(4):704. https://doi.org/10.3390/polym14040704
Chicago/Turabian StyleOrasugh, Jonathan Tersur, and Suprakash Sinha Ray. 2022. "Prospect of DFT Utilization in Polymer-Graphene Composites for Electromagnetic Interference Shielding Application: A Review" Polymers 14, no. 4: 704. https://doi.org/10.3390/polym14040704
APA StyleOrasugh, J. T., & Ray, S. S. (2022). Prospect of DFT Utilization in Polymer-Graphene Composites for Electromagnetic Interference Shielding Application: A Review. Polymers, 14(4), 704. https://doi.org/10.3390/polym14040704