Ductility Estimation for Flexural Concrete Beams Longitudinally Reinforced with Hybrid FRP–Steel Bars
Abstract
:1. Introduction
2. Experimental Study
3. Analytical Study
4. Results and Discussion
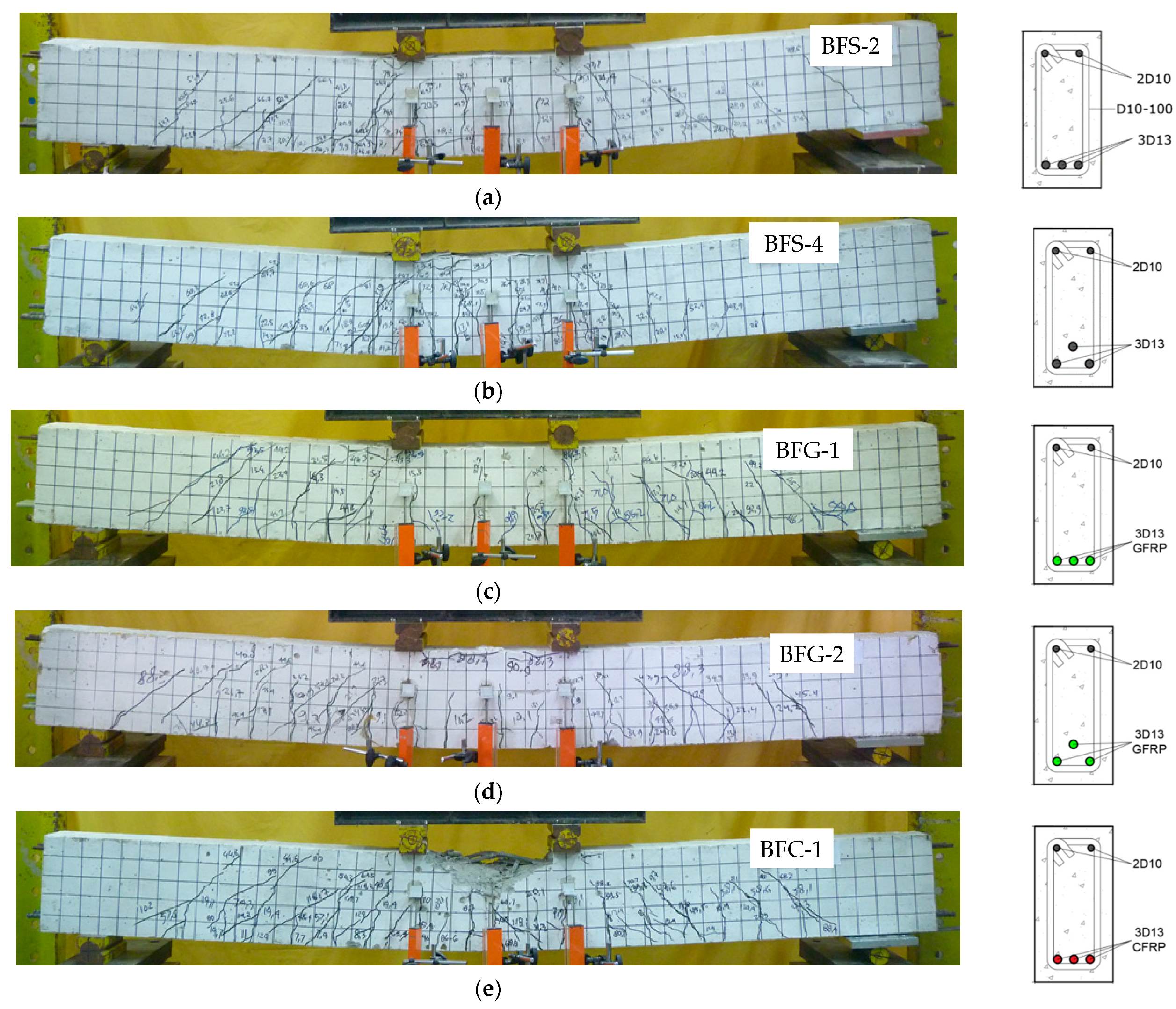
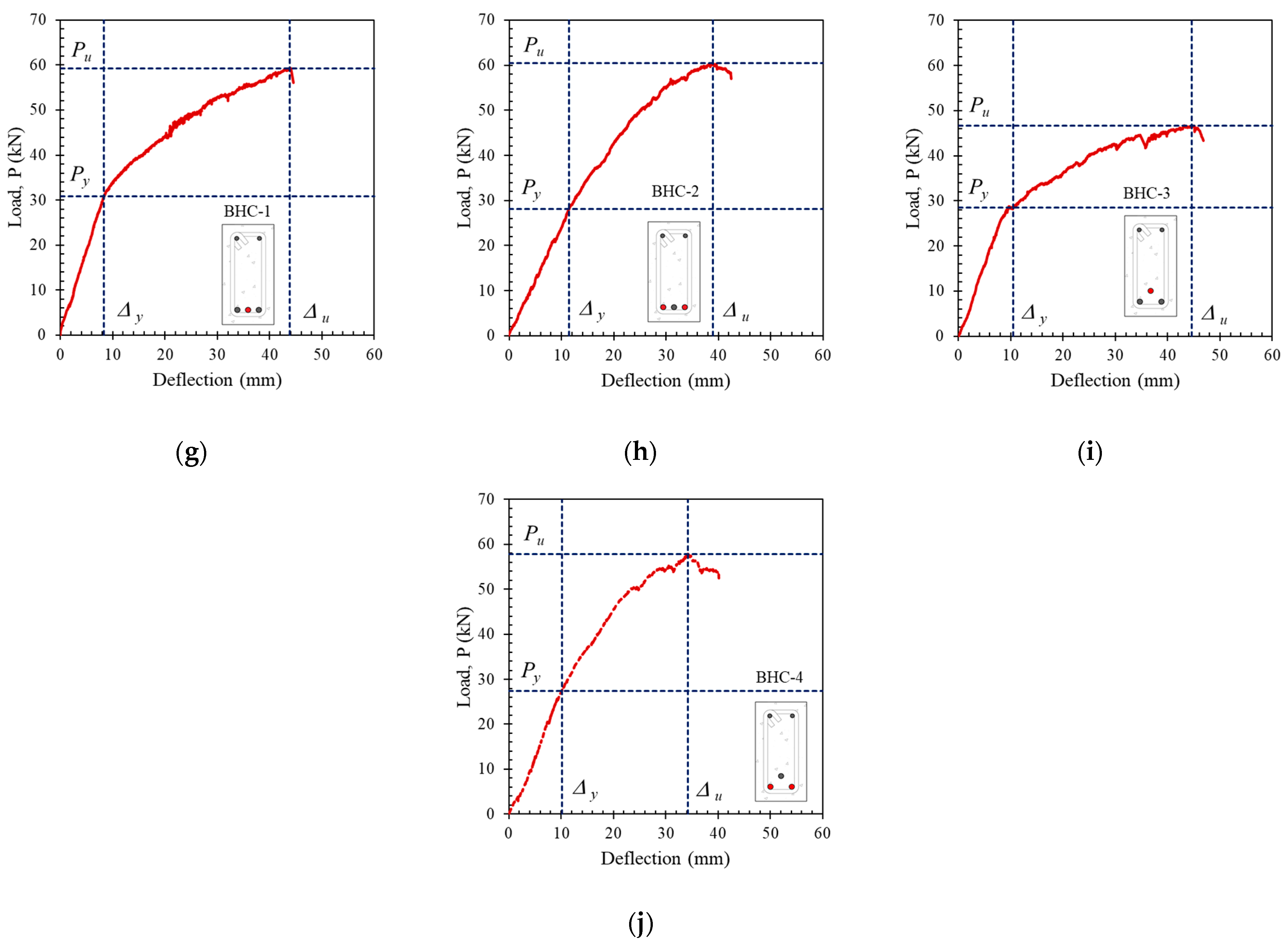
4.1. Crack Patterns and Failure Modes of the Tested Beams
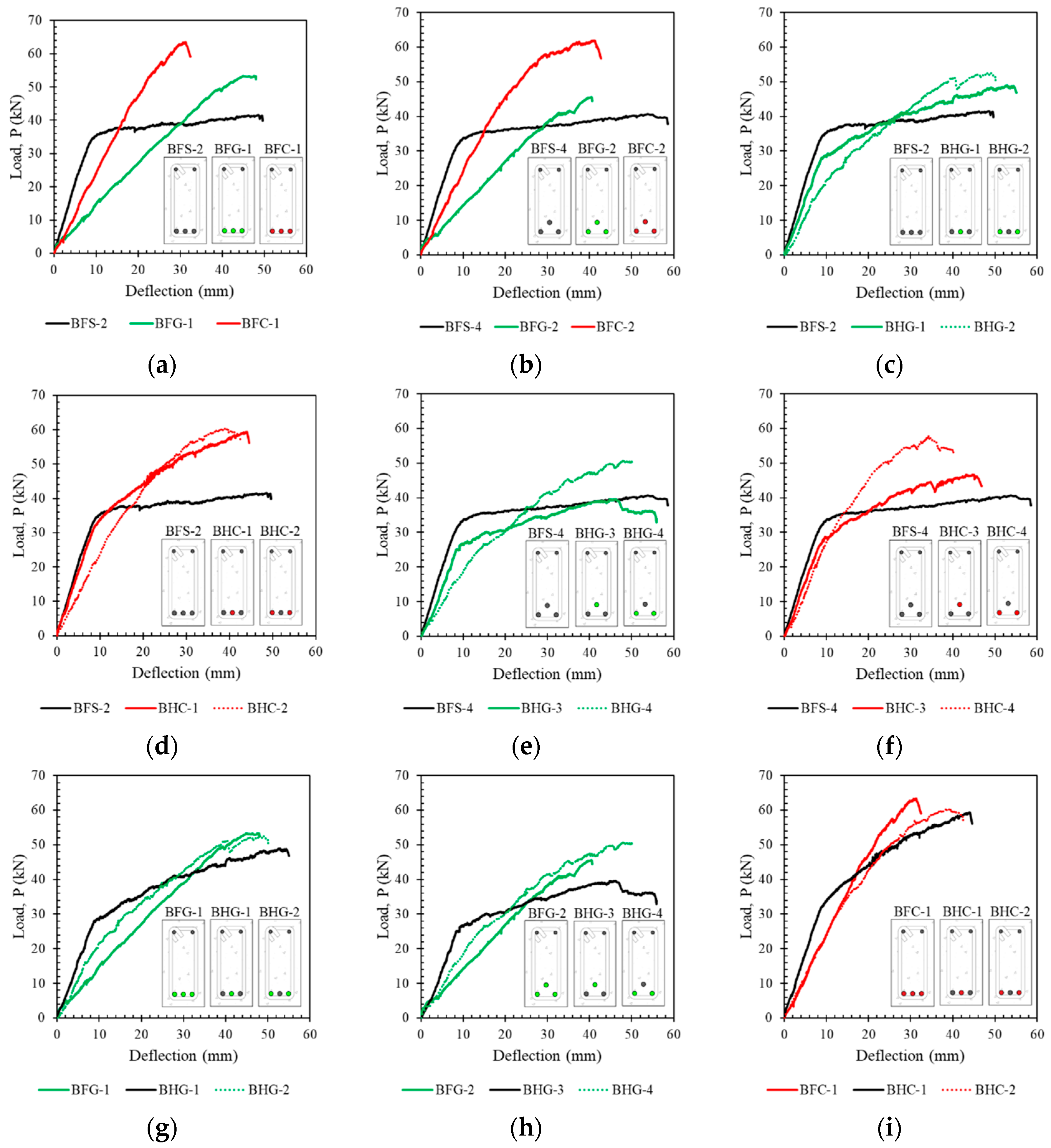
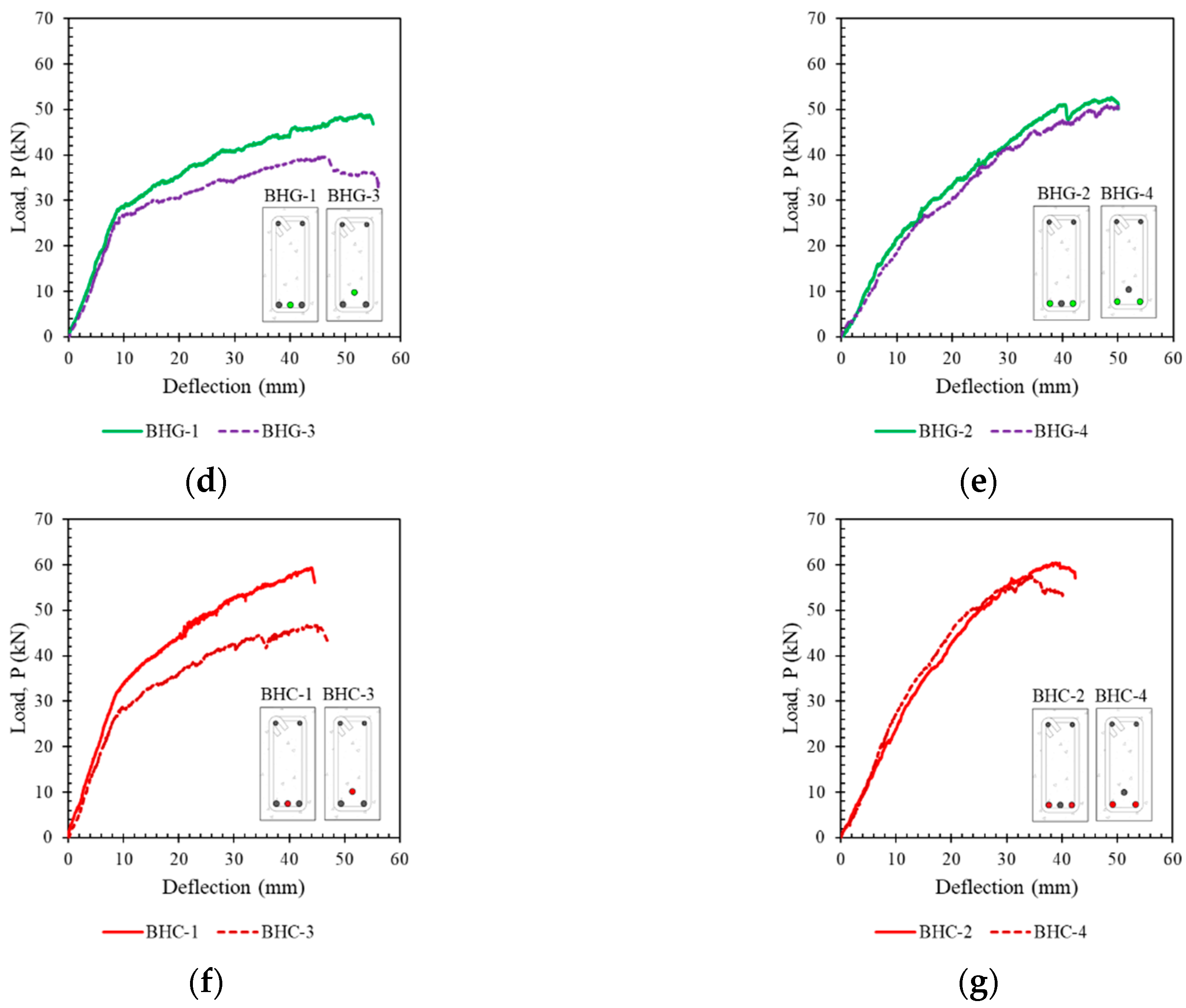
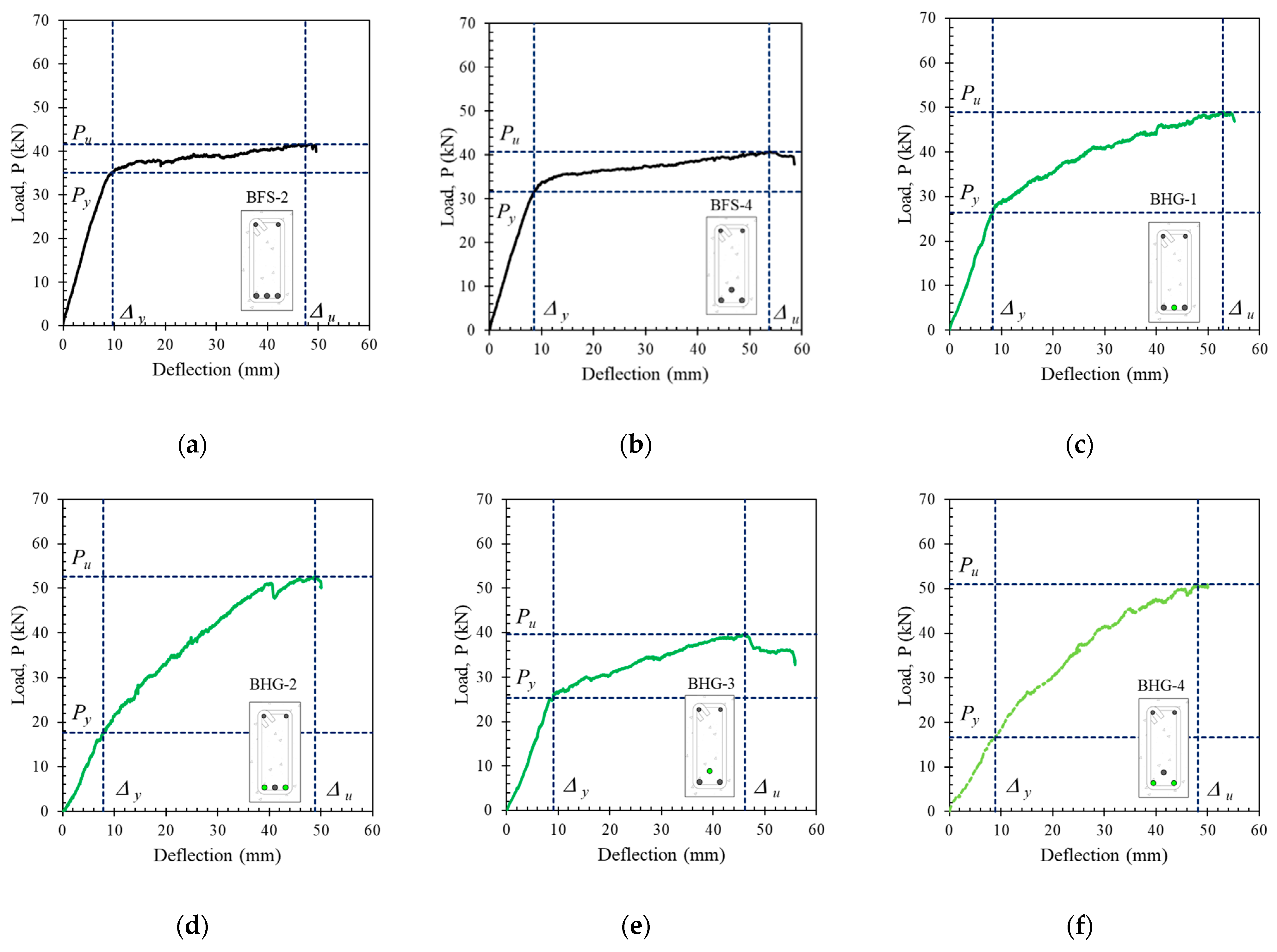
4.2. Effect of Longitudinal Hybrid Reinforcement Ratio (Af/As)
4.3. Effect of Reinforcement Position
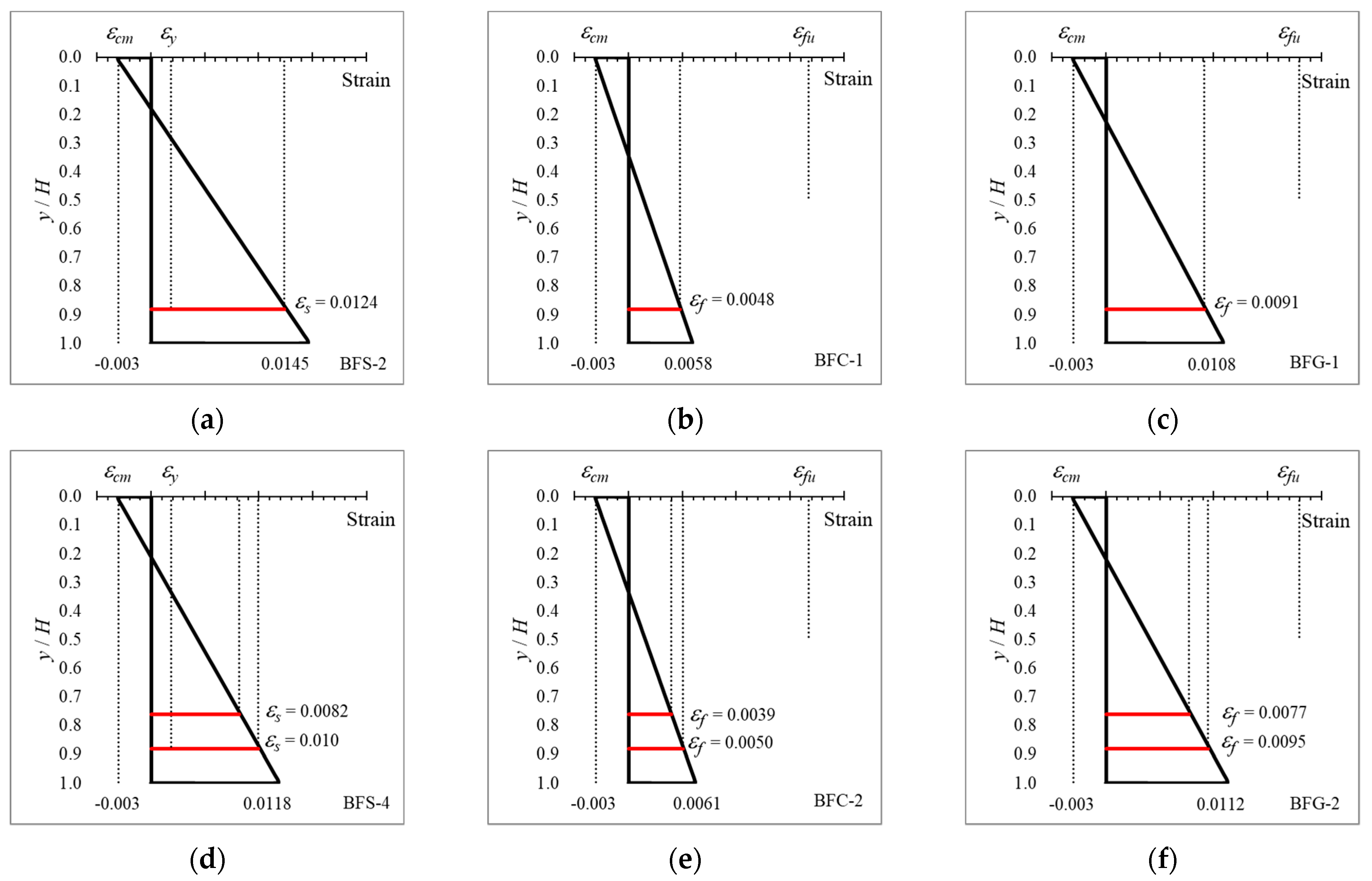
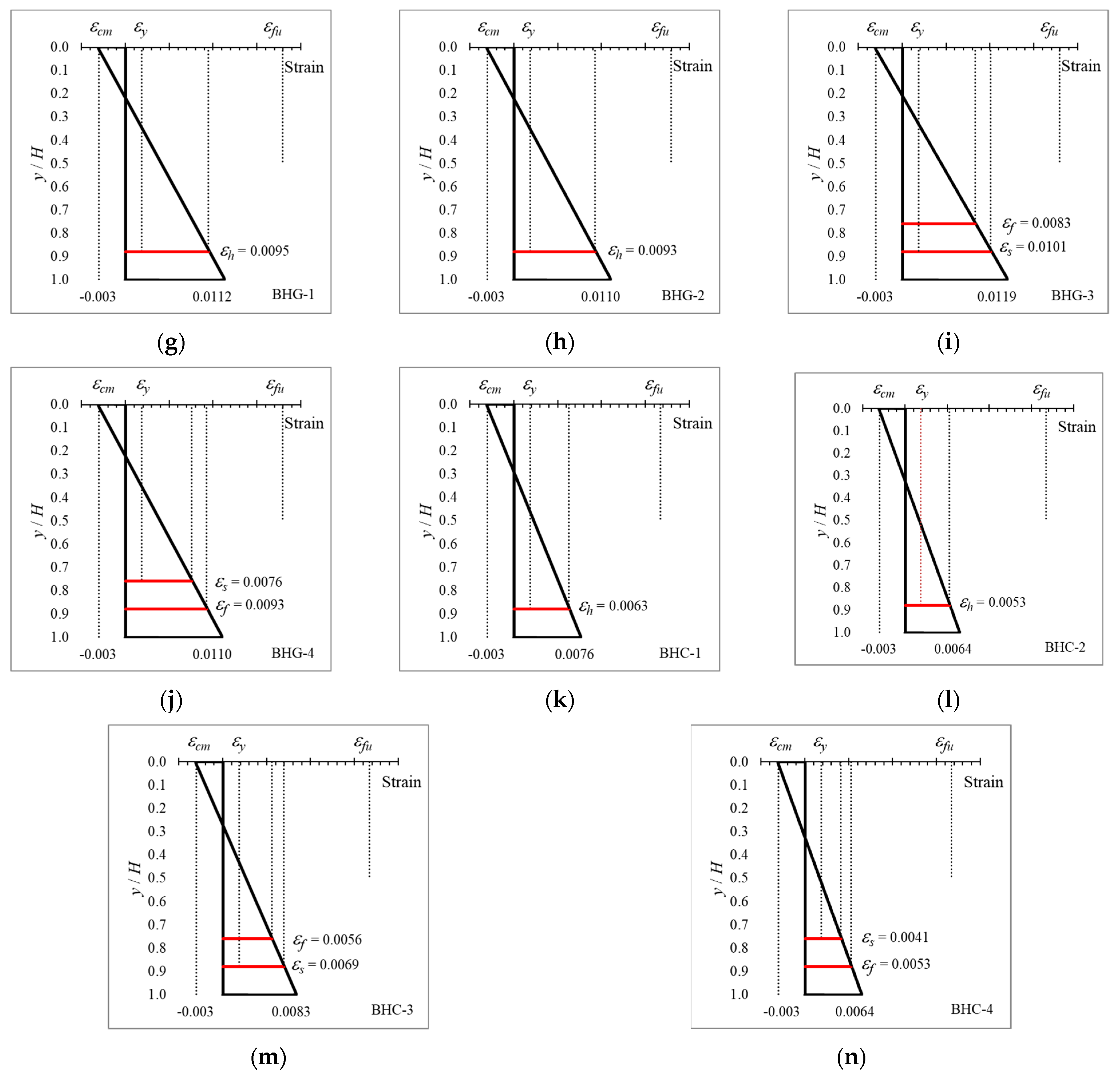
4.4. Strain Distribution in Cross-Sections with Hybrid Reinforcement
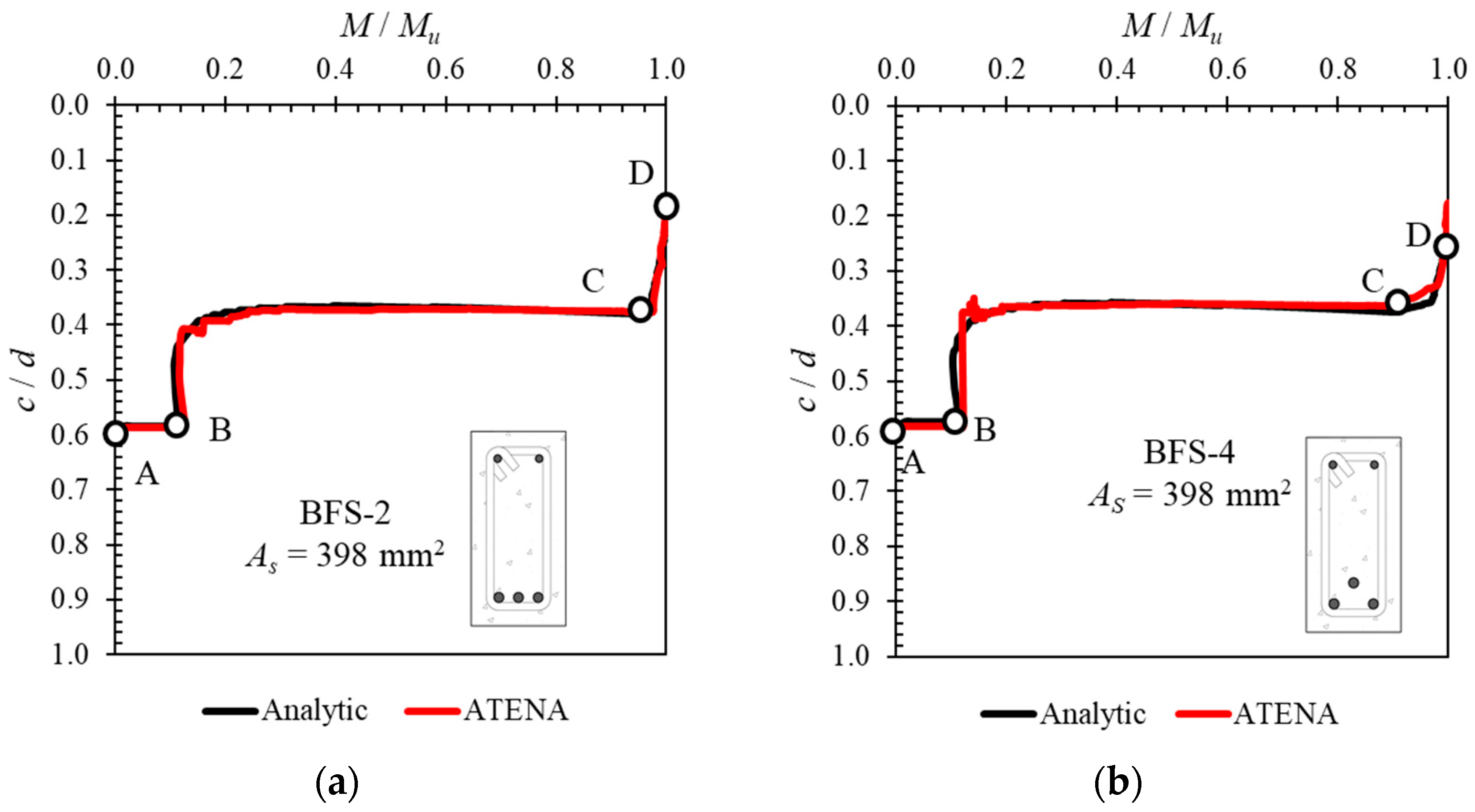
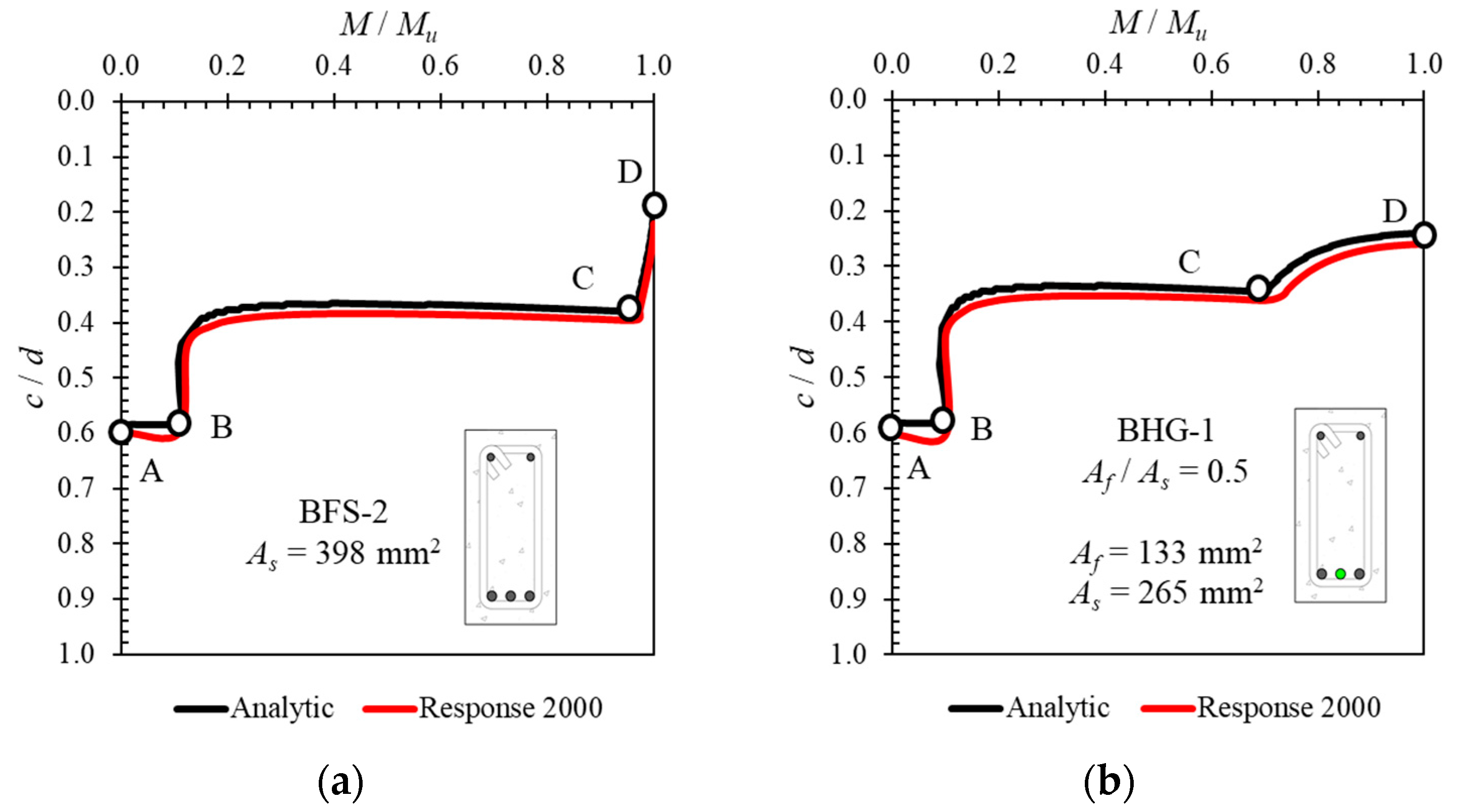
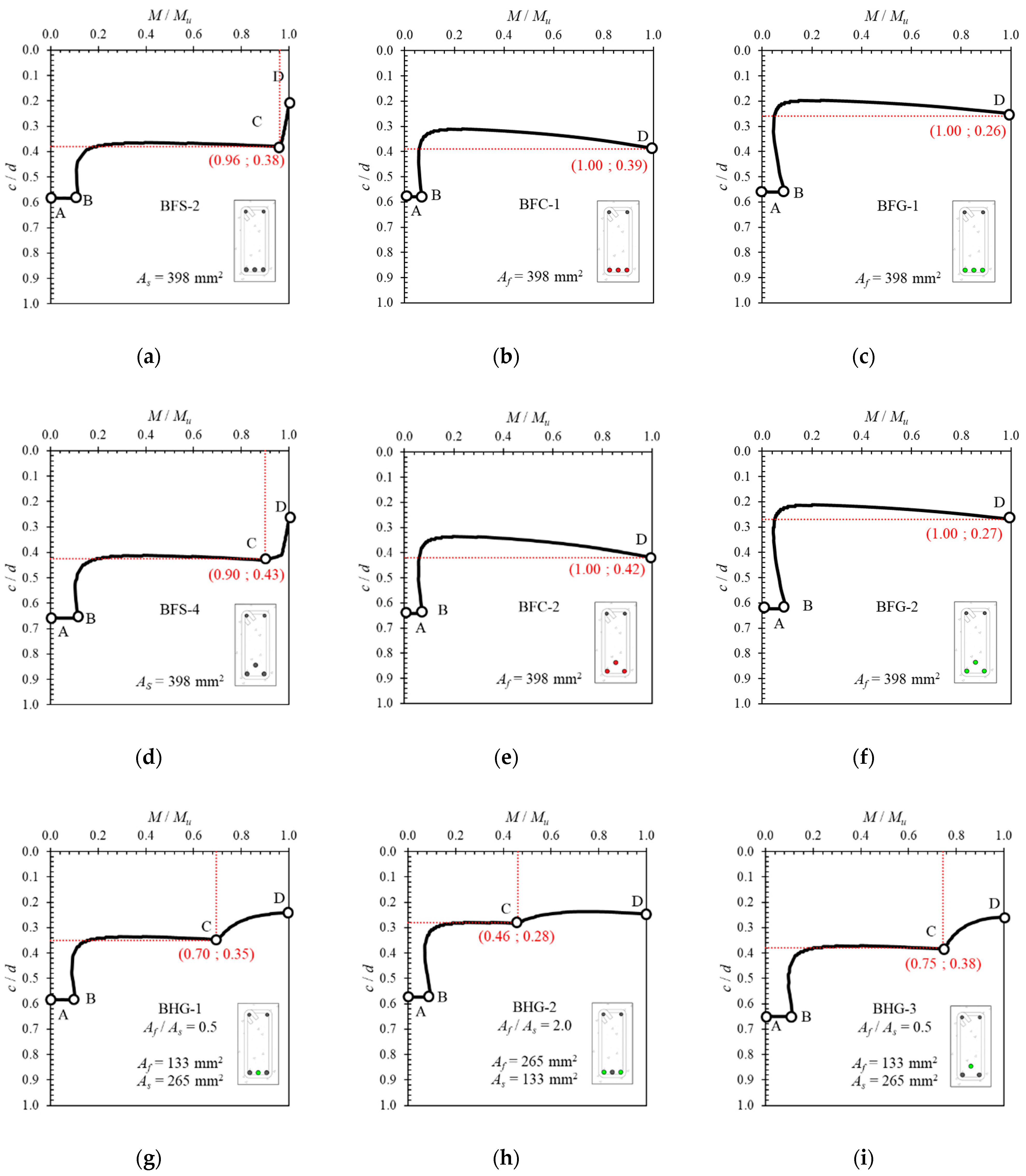
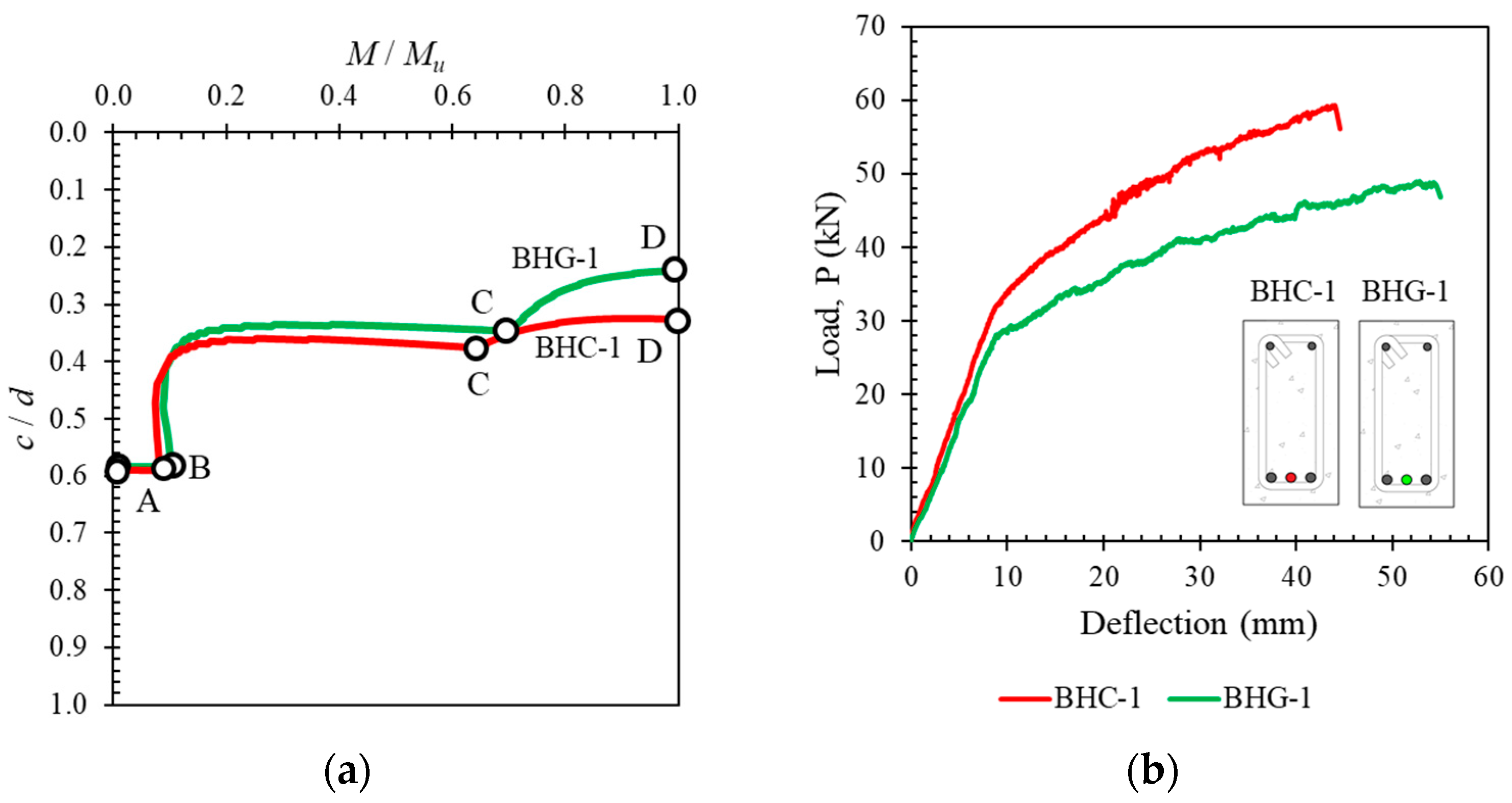
4.5. Neutral Axis Growth in Cross-Sections with Hybrid Reinforcement
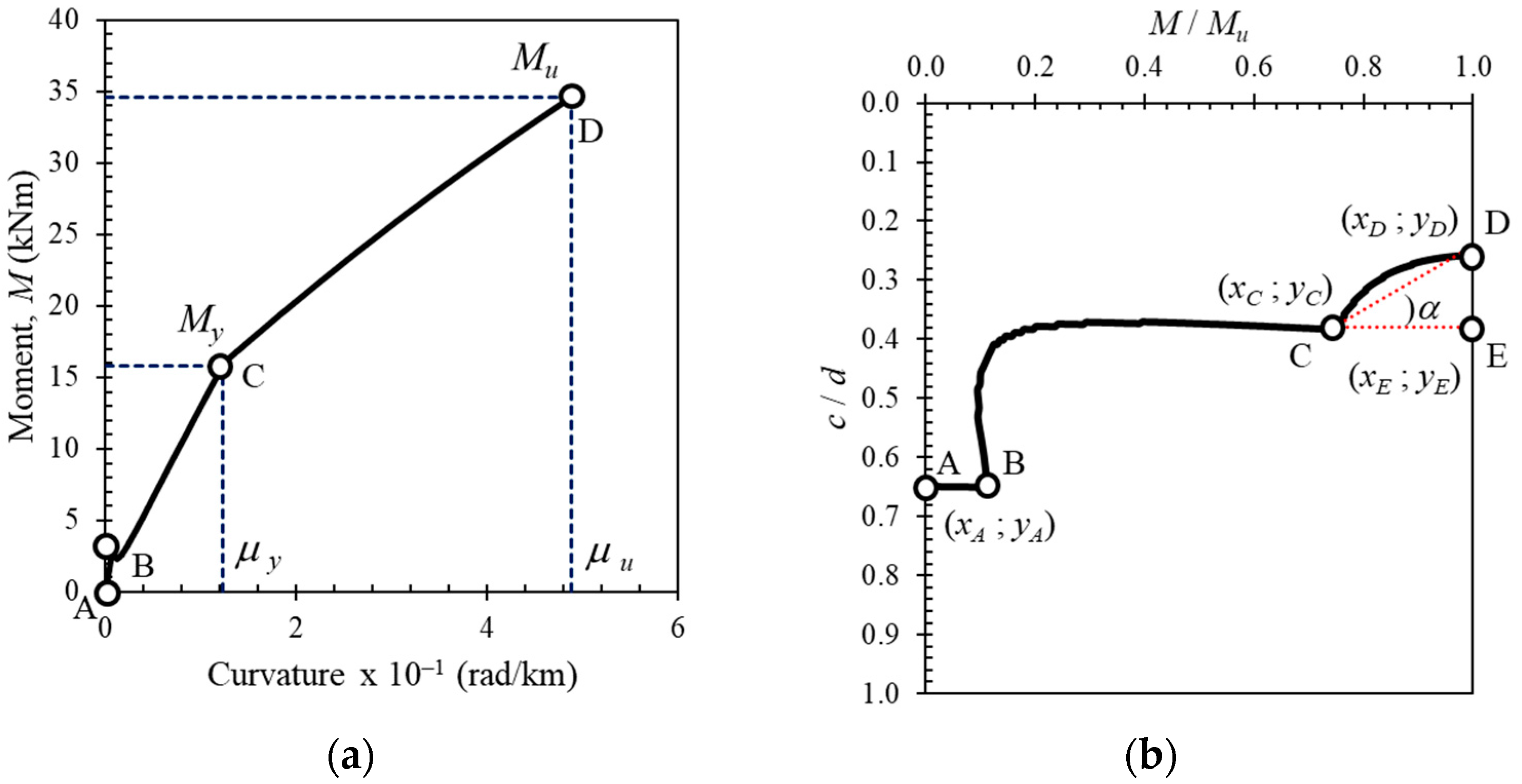
4.6. Ductility of Cross-Sections with Hybrid Reinforcement
4.7. Effect of FRP Type
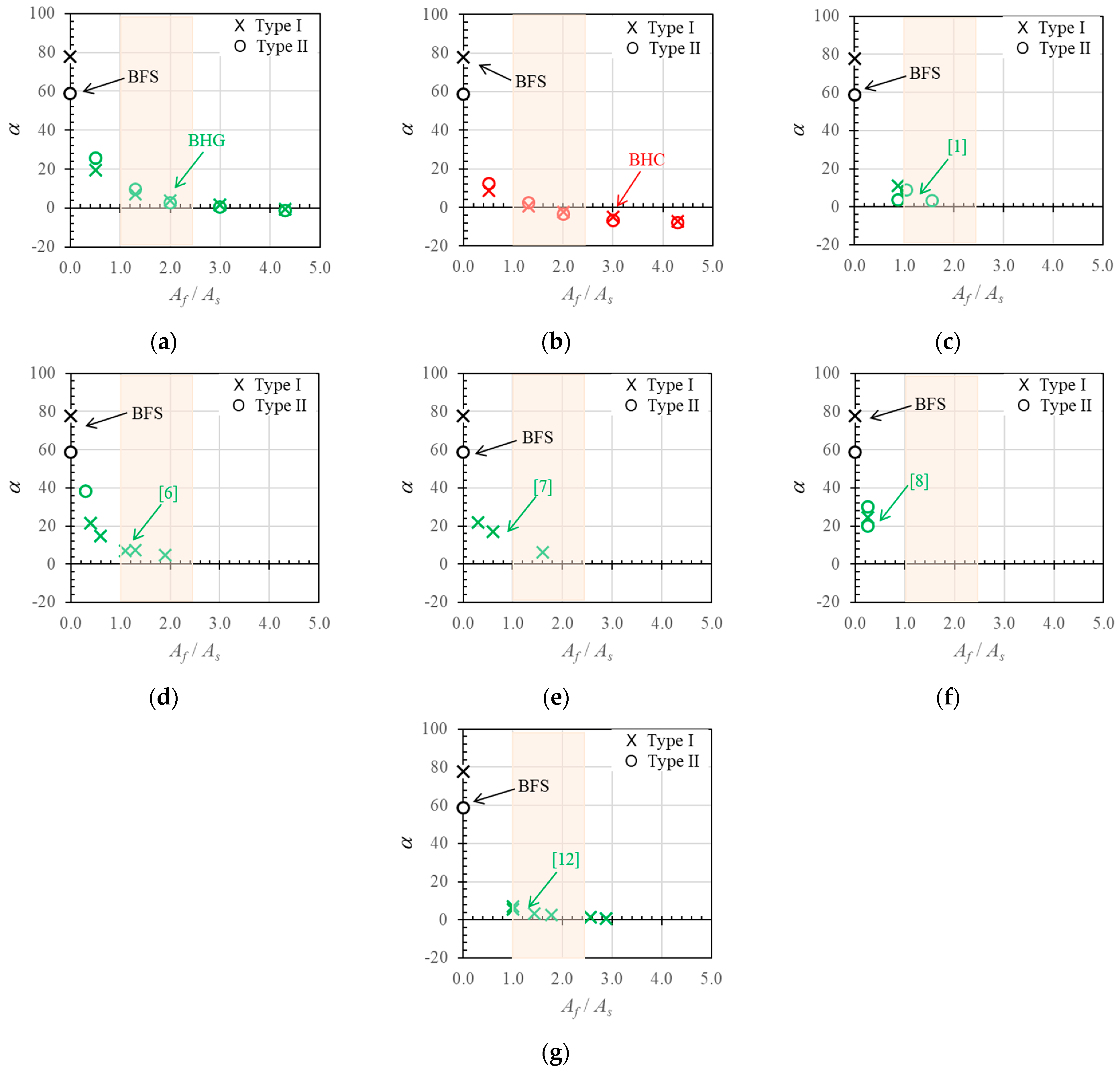
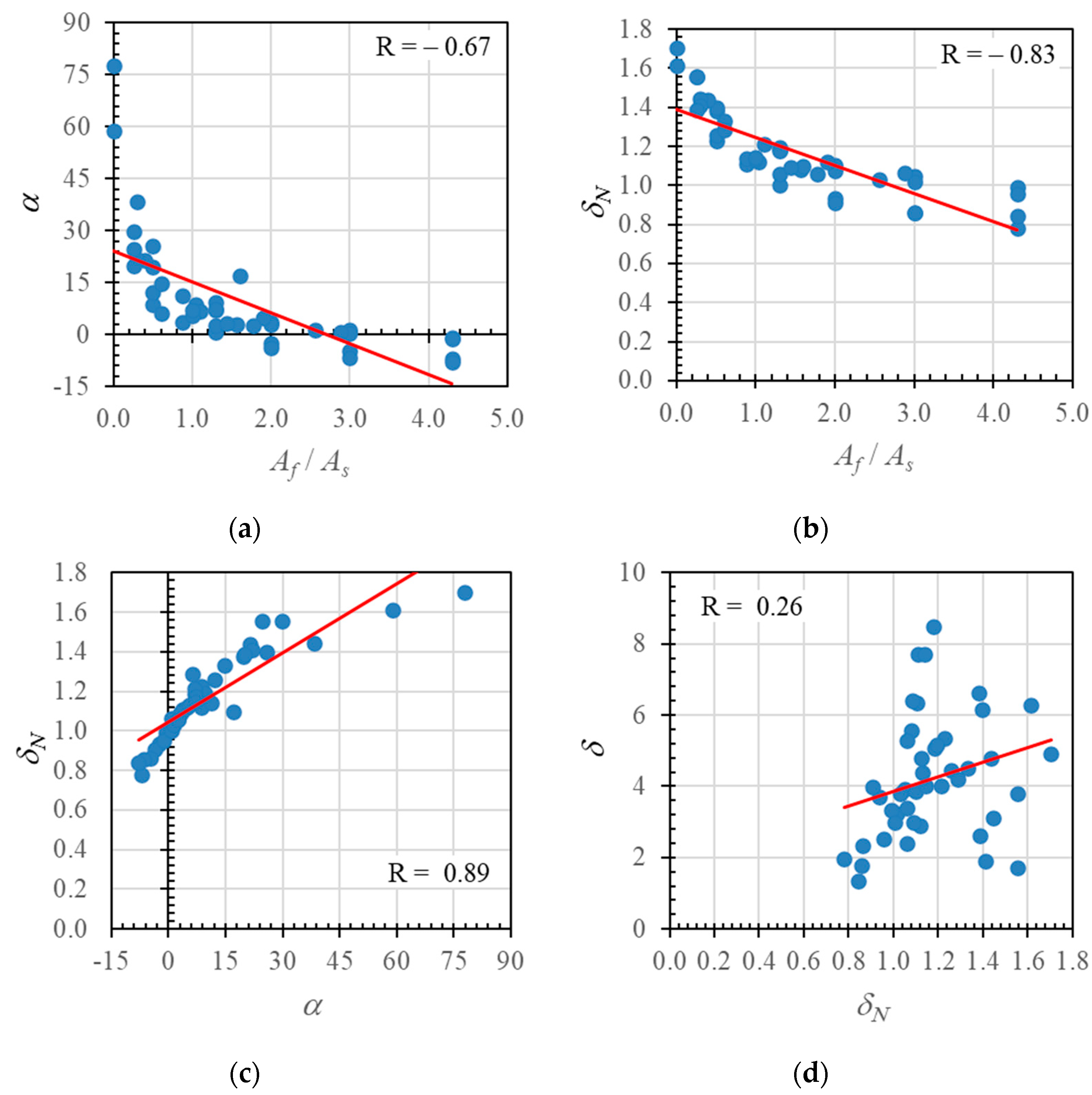
4.8. Neutral Axis Angle (α) and Displacement Index (δN)
5. Conclusions
- (1).
- The reinforcement ratio (Af/As) strongly influenced the capacity and cross-sectional ductility of hybrid reinforced concrete. The higher the hybrid reinforcement ratio, the greater the capacity, but at the cost of ductility, which decreased with increases in the hybrid reinforcement ratio.
- (2).
- The position of the reinforcement slightly affected the capacity and ductility of the beam. Differences in slope in the post-elastic area were seen in beams with lower hybrid reinforcement ratios. However, beams with higher hybrid reinforcement ratios did not show a significant difference in the slope of the load–deflection curve in the post-elastic region.
- (3).
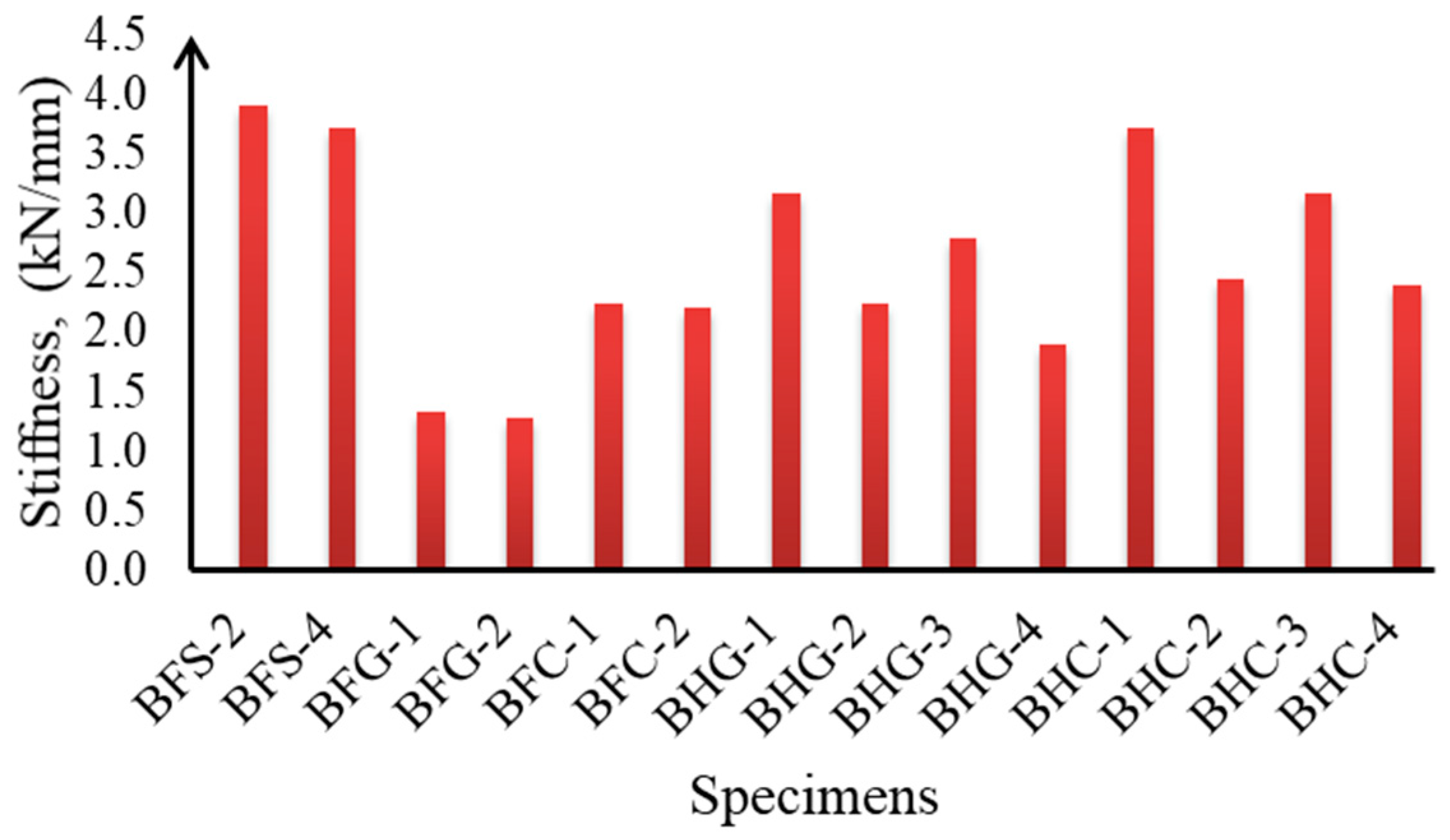
- Cross-sections with Type I reinforcement positions showed higher flexural stiffness values than with Type II positions. A smaller hybrid reinforcement ratio resulted in a higher flexural stiffness value. Moreover, cross-sections with hybrid reinforcement using CFRP exhibited higher flexural stiffness values than those using GFRP.
- (4).
- The type of material used for FRP reinforcement (GFRP or CFRP) significantly affected the profile of the neutral axis curve, capacity, and ductility of hybrid reinforced cross-sections.
- (5).
- There were three regions on the neutral axis curve for cross-sections with hybrid reinforcement, i.e., the region before cracking, the region after cracking, and the region after yielding. The inclination of the neutral axis angle (α) after reinforcement yield depended on the type of FRP and the hybrid reinforcement ratio used.
- (6).
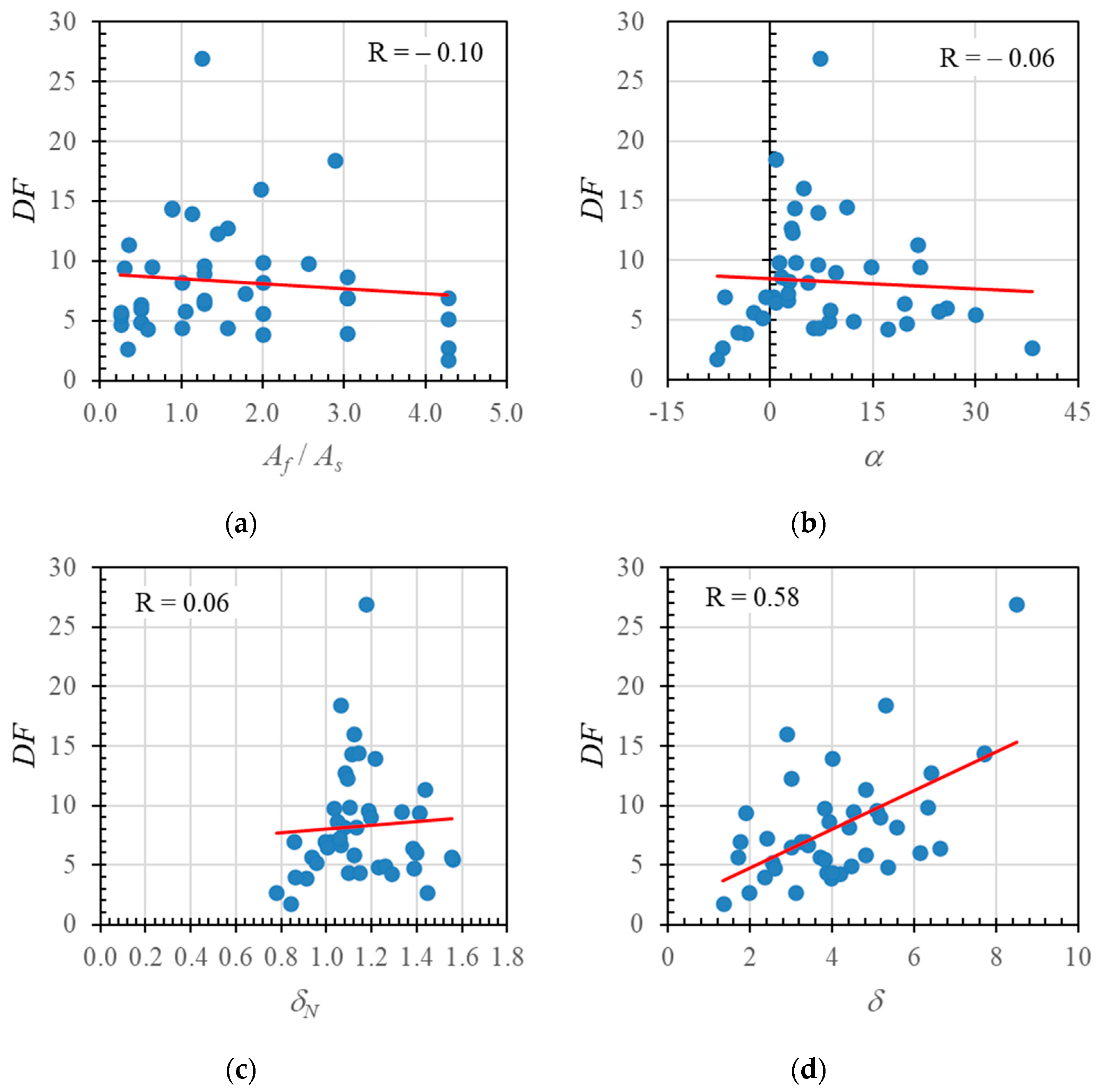
- The ductility of hybrid reinforced beams increased as the neutral axis angle increased. There were significant correlations between the neutral axis angle, neutral axis deformation index value, ductility, and deformation factor. The deformation factor increased with increasing neutral axis angles and deformation index values.
- (7).
- This result suggests that the neutral axis angle (α) and the deformation index value (δN) proposed in this paper can be used to evaluate the ductility of cross-sections with hybrid reinforcement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aiello, M.A.; Ombres, L. Structural performances of concrete beams with hybrid (Fiber-reinforced polymer-steel) reinforcements. J. Compos. Constr. 2002, 6, 133–140. [Google Scholar] [CrossRef]
- Nadjai, A.; Talamona, D.; Ali, F. Fire performance of concrete beams reinforced with FRP bars. In Proceeding of the International Sympsium on Bond Behaviour of FRP in Structures, Hong Kong, China, 7–9 December 2005; pp. 401–410. [Google Scholar]
- Firmo, J.P.; Correia, J.R.; Bisby, L. Fire behavior of FRP-strengthened reinforced concrete structural elements: A state-of-the-art review. Compos. Part B Eng. 2015, 80, 198–216. [Google Scholar] [CrossRef]
- Hajiloo, H.; Green, M.F.; Noel, M.; Benichou, N.; Sultan, M. Fire tests on full-scale FRP reinforced concrete slabs. Compos. Struct. 2017, 179, 705–719. [Google Scholar] [CrossRef]
- Reichenbach, S.; Preinstorfer, P.; Hammerl, M.; Kromoser, B. A review on embedded fiber reinforced polymer reinforcement in structural concrete in Europe. Constr. Build. Mater. 2021, 307, 124946. [Google Scholar] [CrossRef]
- Qu, W.; Zhang, X.; Huang, H. Flexural behavior of concrete beams reinforced with hybrid (GFRP and steel) bars. J. Compos. Constr. 2009, 13, 350–359. [Google Scholar] [CrossRef]
- Lau, D.; Pam, H.J. Experimental study of hybrid FRP reinforced concrete beams. Eng. Struct. 2010, 32, 3857–3865. [Google Scholar] [CrossRef]
- Yinghao, L.; Yong, Y. Arrangement of hybrid rebars on flexural behavior of HSC beams. Compos. Part B 2013, 45, 22–31. [Google Scholar] [CrossRef]
- El-Helou, R.G.; Aboutaha, R.S. Analysis of rectangular hybrid steel-GFRP reinforced concrete beam-columns. Comput. Concr. 2015, 16, 245–260. [Google Scholar] [CrossRef]
- Ge, W.; Zhang, J.; Cao, D.; Tu, Y. Flexural behaviors of hybrid concrete beams reinforced with BFRP bars and steel bars. Constr. Build. Mater. 2015, 87, 28–37. [Google Scholar] [CrossRef]
- Kara, L.F.; Ashour, A.F.; Köroglu, M.A. Flexural behavior of hybrid FRP/steel reinforced concrete beams. Compos. Struct. 2015, 129, 111–121. [Google Scholar] [CrossRef]
- El Refai, A.; Abed, F.; Al-Rahmani, A. Structural performance and serviceability of concrete beams reinforced with hybrid (GFRP and steel) bars. Constr. Build. Mater. 2015, 96, 518–529. [Google Scholar] [CrossRef]
- Bencardino, F.; Condello, A.; Ombres, L. Numerical and analytical modeling of concrete beams with steel, FRP and hybrid FRP-steel reinforcements. Compos. Struct. 2016, 140, 53–65. [Google Scholar] [CrossRef]
- Qin, R.; Zhou, A.; Lau, D. Effect of reinforcement ratio on the flexural performance of hybrid FRP reinforced concrete beams. Compos. Part B 2017, 108, 200–209. [Google Scholar] [CrossRef]
- Bui, L.V.H.; Stitmannaithum, B.; Ueda, T. Ductility of Concrete Beams Reinforced with Both Fiber-Reinforced Polymer and Steel Tension Bars. J. Adv. Concr. Technol. 2018, 16, 531–548. [Google Scholar] [CrossRef] [Green Version]
- Araba, A.M.; Ashour, A.F. Flexural performance of hybrid GFRP-Steel reinforced concrete continuous beams. Compos. Part B 2018, 154, 321–336. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Fu, L.; Feng, D.C.; Vatuloka, A.R.; Wei, Y.; Wu, G. Experimental study on the flexural behavior of concrete beams reinforced with bundled hybrid steel/FRP bars. Eng. Struct. 2019, 197, 109443. [Google Scholar] [CrossRef]
- Kartal, S.; Kalkan, I.; Beycioglu, A.; Dobiszewska, M. Load-Deflection Behavior of Over and Under-Reinforced Concrete Beams with Hybrid FRP-Steel Reinforcements. Materials 2021, 14, 5341. [Google Scholar] [CrossRef]
- Zaki, A.; Thamrin, R. Parametric study on neutral axis growth of concrete beams reinforced with fiber-reinforced polymer and steel bars. In Proceedings of the Second International Conference of Construction, Infrastructure, and Materials, Jakarta, Indonesia, 26 July 2021; p. 216. [Google Scholar]
- Park, R.; Paulay, T. Reinforced Concrete Structures; Wiley: New York, NY, USA, 1975; p. 769. [Google Scholar]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
- Thamrin, R.; Sari, R.P. Flexural Capacity of Strengthened Reinforced Concrete Beams with Web Bonded Steel Plates. Procedia Eng. 2017, 171, 1129–1136. [Google Scholar] [CrossRef]
- Thamrin, R. Analytical prediction on flexural response of RC beams strengthened with steel plates. In Proceedings of the MATEC Web of Conferences: International Symposium on Civil and Environmental Engineering (ISCEE), Melaka, Malaysia, 6 December 2017; Volume 103, p. 02012. [Google Scholar]
- Kosmidou, P.M.K.; Chalioris, C.E.; Karayannis, C.G. Flexural/shear strength of RC beams with longitudinal FRP bars an analytical approach. Comput. Concr. 2018, 22, 573–592. [Google Scholar]
- Thamrin, R. Effect of Strengthening Method and Anchorage Length on Flexural Capacity of RC Beams with Steel Plates. J. Eng. Sci. Technol. 2018, 13, 3781–3794. [Google Scholar]
- Thamrin, R.; Zaidir, Z.; Desharma, S. Debonding Failure Analysis of Reinforced Concrete Beams Strengthened with CFRP Plates. Polymers 2021, 13, 2738. [Google Scholar] [CrossRef] [PubMed]
- American Concrete Institute (ACI). Committee 440, Guide for the Design and Construction of Structural Concrete Reinforced with Fiber Reinforced Polymer (FRP) Bars, ACI 440.1R-15; American Concrete Institute: Farmington Hills, MI, USA, 2015. [Google Scholar]
- Cervenka, V.; Jendele, L.; Cervenka, J. ATENA Program Documentation-Part 1: Theory. Available online: https://www.cervenka.cz/products/atena/documentation (accessed on 11 March 2020).
- Bentz, E.; Collins, M.P. Response 2000, Version 1.0.5; University of Toronto: Toronto, ON, Canada, 2001. [Google Scholar]

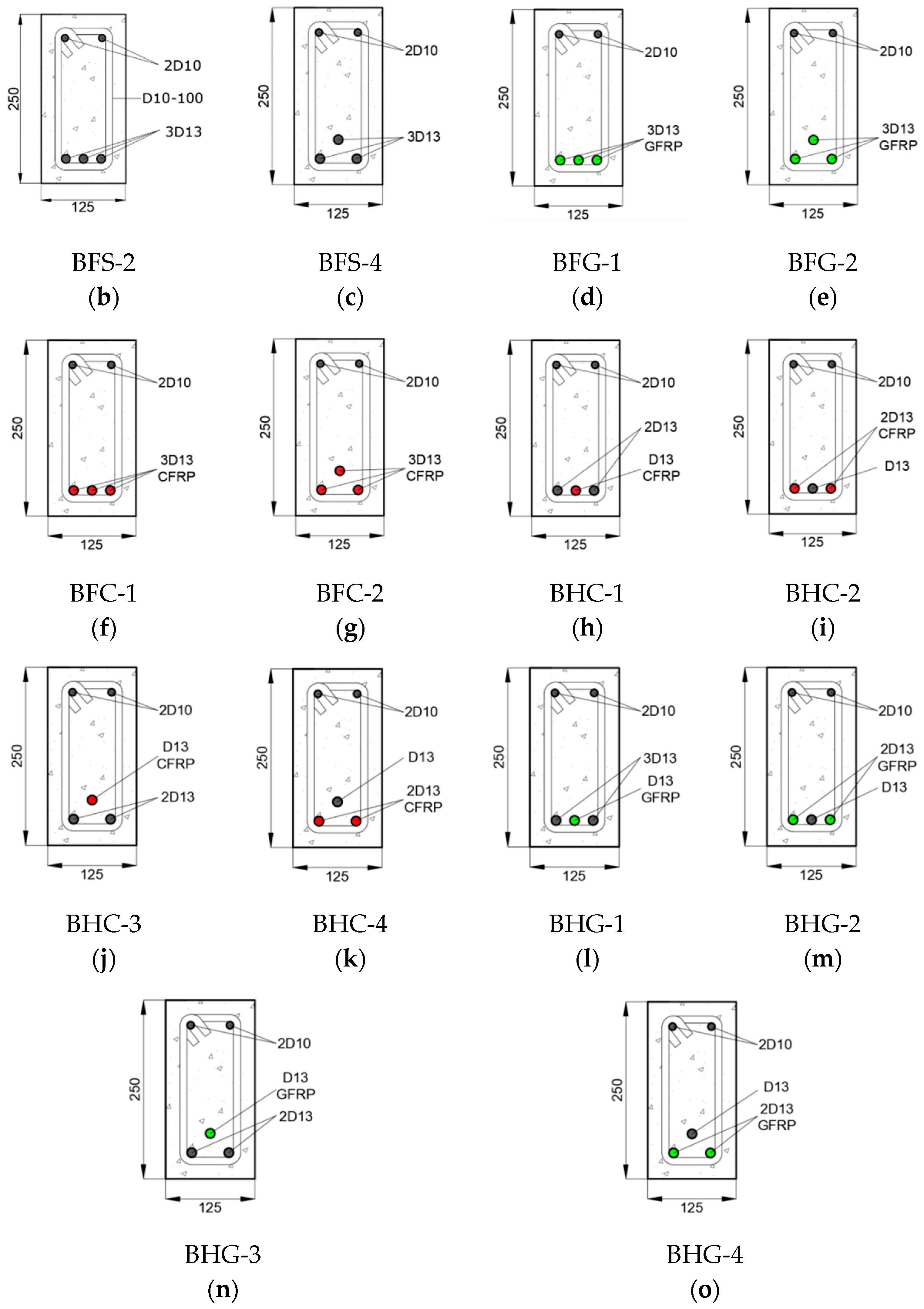


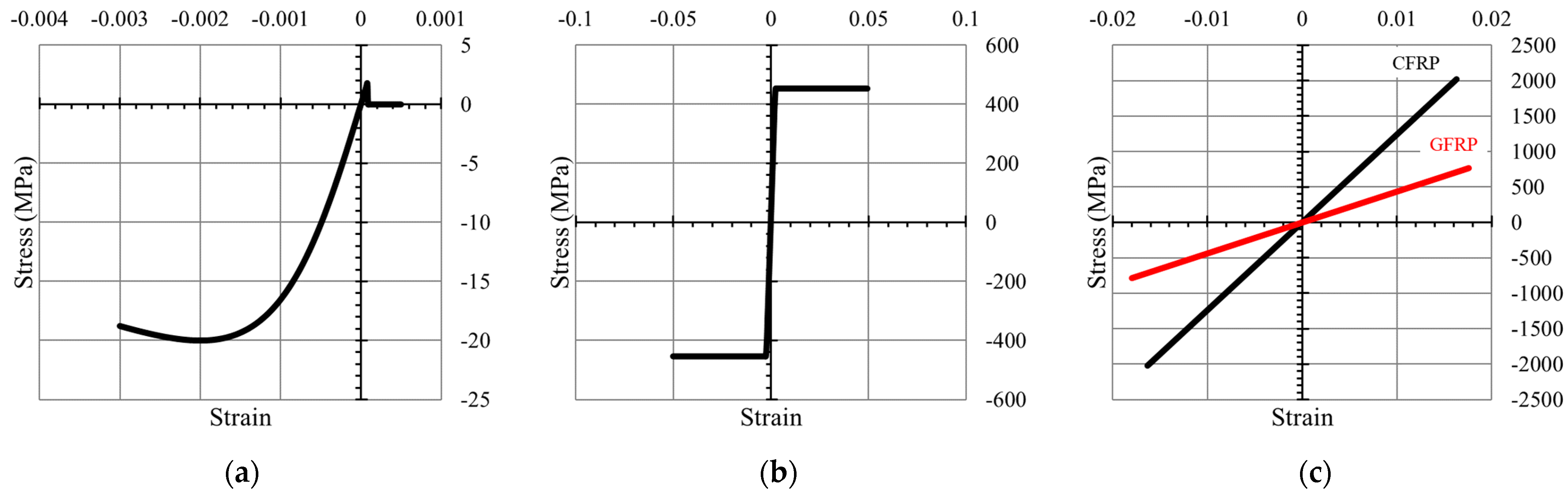








| Beam Notation | Width | Overall Depth | Clear Span Length | fc’ | ffu | fy | df | ds | Ef |
|---|---|---|---|---|---|---|---|---|---|
| (mm) | (mm) | (mm) | (MPa) | (MPa) | (MPa) | (mm) | (mm) | (GPa) | |
| Data from this study [Experimental] | |||||||||
| BFS-2 | 125 | 250 | 2000 | 20 | - | 375 | - | 13 | - |
| BFS-4 | 125 | 250 | 2000 | 20 | - | 375 | - | 13 | - |
| BFG-1 | 125 | 250 | 2000 | 20 | 788 | - | 13 | - | 43.9 |
| BFG-2 | 125 | 250 | 2000 | 20 | 788 | - | 13 | - | 43.9 |
| BFC-1 | 125 | 250 | 2000 | 20 | 2070 | - | 13 | - | 124 |
| BFC-2 | 125 | 250 | 2000 | 20 | 2070 | - | 13 | - | 124 |
| BHG-1 | 125 | 250 | 2000 | 20 | 788 | 375 | 13 | 13 | 43.9 |
| BHG-2 | 125 | 250 | 2000 | 20 | 788 | 375 | 13 | 13 | 43.9 |
| BHG-3 | 125 | 250 | 2000 | 20 | 788 | 375 | 13 | 13 | 43.9 |
| BHG-4 | 125 | 250 | 2000 | 20 | 788 | 375 | 13 | 13 | 43.9 |
| BHC-1 | 125 | 250 | 2000 | 20 | 2070 | 375 | 13 | 13 | 124 |
| BHC-2 | 125 | 250 | 2000 | 20 | 2070 | 375 | 13 | 13 | 124 |
| BHC-3 | 125 | 250 | 2000 | 20 | 2070 | 375 | 13 | 13 | 124 |
| BHC-4 | 125 | 250 | 2000 | 20 | 2070 | 375 | 13 | 13 | 124 |
| Data from this study [Parametric] | |||||||||
| BHG-5 | 125 | 250 | 2000 | 20 | 788 | 375 | 16 | 13 | 43.9 |
| BHG-6 | 125 | 250 | 2000 | 20 | 788 | 375 | 16 | 13 | 43.9 |
| BHG-7 | 125 | 250 | 2000 | 20 | 788 | 375 | 19 | 13 | 43.9 |
| BHG-8 | 125 | 250 | 2000 | 20 | 788 | 375 | 19 | 13 | 43.9 |
| BHG-9 | 125 | 250 | 2000 | 20 | 788 | 375 | 16 | 10 | 43.9 |
| BHG-10 | 125 | 250 | 2000 | 20 | 788 | 375 | 16 | 10 | 43.9 |
| BHC-5 | 125 | 250 | 2000 | 20 | 2070 | 375 | 16 | 13 | 124 |
| BHC-6 | 125 | 250 | 2000 | 20 | 2070 | 375 | 16 | 13 | 124 |
| BHC-7 | 125 | 250 | 2000 | 20 | 2070 | 375 | 19 | 13 | 124 |
| BHC-8 | 125 | 250 | 2000 | 20 | 2070 | 375 | 19 | 13 | 124 |
| BHC-9 | 125 | 250 | 2000 | 20 | 2070 | 375 | 16 | 10 | 124 |
| BHC-10 | 125 | 250 | 2000 | 20 | 2070 | 375 | 16 | 10 | 124 |
| Aiello et al. [1] | |||||||||
| A1 | 150 | 200 | 2700 | 45.7 | 1674 | 465 | 7.5 | 8 | 49 |
| A2 | 150 | 200 | 2700 | 45.7 | 1366 | 465 | 10 | 8 | 50.1 |
| A3 | 150 | 200 | 2700 | 45.7 | 1366 | 465 | 10 | 12 | 50.1 |
| C1 | 150 | 200 | 2700 | 45.7 | 1674 | 465 | 7.5 | 8 | 49 |
| Qu et al. [3] | |||||||||
| B3 | 180 | 250 | 1800 | 33.10 | 782 | 363 | 12.7 | 12 | 45 |
| B4 | 180 | 250 | 1800 | 33.10 | 755 | 336 | 15.9 | 16 | 41 |
| B5 | 180 | 250 | 1800 | 34.40 | 778 | 336 | 9.5 | 16 | 37.7 |
| B6 | 180 | 250 | 1800 | 34.40 | 782 | 336 | 12.7 | 16 | 45 |
| B7 | 180 | 250 | 1800 | 40.65 | 778 | 363 | 9.5 | 12 | 37.7 |
| B8 | 180 | 250 | 1800 | 40.65 | 755 | 336 | 15.9 | 16 | 41 |
| Lau & Pam [4] | |||||||||
| G0.3-MD1.0-A90 | 280 | 380 | 4200 | 41.3 | 588 | 336 | 19 | 25 | 39.5 |
| G1.0-T0.7-A90 | 280 | 380 | 4200 | 39.8 | 582 | 597 | 25 | 20 | 38.0 |
| G0.6-T1.0-A90 | 280 | 380 | 4200 | 44.6 | 588 | 550 | 19 | 25 | 39.5 |
| Yinghao & Yong [5] | |||||||||
| S2 | 150 | 250 | 1800 | 80.1 | 1301 | 374.5 | 12 | 24 | 75.98 |
| S3 | 150 | 250 | 1800 | 80.1 | 1301 | 374.5 | 12 | 24 | 75.98 |
| S4 | 150 | 250 | 1800 | 80.1 | 1301 | 374.5 | 12 | 24 | 75.98 |
| Refai et al. [8] | |||||||||
| 2G12-1S10 | 230 | 300 | 3700 | 40 | 1000 | 520 | 12 | 10 | 50 |
| 2G12-2S10 | 230 | 300 | 3700 | 40 | 1000 | 520 | 12 | 10 | 50 |
| 2G12-2S12 | 230 | 300 | 3700 | 40 | 1000 | 520 | 12 | 12 | 50 |
| 2G16-2S10 | 230 | 300 | 3700 | 40 | 1000 | 520 | 16 | 10 | 50 |
| 2G16-2S12 | 230 | 300 | 3700 | 40 | 1000 | 520 | 16 | 12 | 50 |
| 2G16-2S16 | 230 | 300 | 3700 | 40 | 1000 | 520 | 16 | 16 | 50 |
| Beam Notation | Af/As | First Crack Load | Stiffness | Type of Reinforcement | Reinforcement Ratio | Failure Mode |
|---|---|---|---|---|---|---|
| (kN) | (kN/mm) | |||||
| BFS-2 | - | 3.6 | 3.91 | Steel | Under Reinforced | SY, CC |
| BFS-4 | - | 5.3 | 3.71 | Steel | Under Reinforced | SY, CC |
| BFG-1 | - | 4.6 | 1.33 | GFRP | Over Reinforced | CC |
| BFG-2 | - | 6.2 | 1.27 | GFRP | Over Reinforced | CC |
| BFC-1 | - | 3.7 | 2.24 | CFRP | Over Reinforced | CC |
| BFC-2 | - | 3.9 | 2.21 | CFRP | Over Reinforced | CC |
| BHG-1 | 0.5 | 5.5 | 3.16 | Steel and GFRP | Over Reinforced | SY, CC |
| BHG-2 | 2.0 | 3.5 | 2.23 | Steel and GFRP | Over Reinforced | SY, CC |
| BHG-3 | 0.5 | 5.1 | 2.79 | Steel and GFRP | Over Reinforced | SY, CC |
| BHG-4 | 2.0 | 3.6 | 1.89 | Steel and GFRP | Over Reinforced | SY, CC |
| BHC-1 | 0.5 | 5.3 | 3.71 | Steel and CFRP | Over Reinforced | SY, CC |
| BHC-2 | 2.0 | 3.7 | 2.45 | Steel and CFRP | Over Reinforced | SY, CC |
| BHC-3 | 0.5 | 3.2 | 3.17 | Steel and CFRP | Over Reinforced | SY, CC |
| BHC-4 | 2.0 | 6.3 | 2.39 | Steel and CFRP | Over Reinforced | SY, CC |
| Beam Notation | Af/As | δ | α | δN | My | μy | Mu | μu | DF | Type of FRP | Type of Cross-Section |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (kNm) | (kNm) | ||||||||||
| Data from this study [Experimental] | |||||||||||
| BFS-2 | − | 4.9 | 77.7 | 1.7 | 28.2 | 1.4 | 29.1 | 7.2 | 5.4 | - | Type I |
| BFS-4 | − | 6.3 | 58.8 | 1.6 | 25.1 | 1.4 | 27.4 | 6.0 | 4.8 | - | Type II |
| BHG-1 | 0.5 | 6.6 | 19.6 | 1.4 | 21.2 | 1.3 | 29.9 | 5.8 | 6.4 | GFRP | Type I |
| BHG-2 | 2.0 | 6.3 | 3.6 | 1.1 | 14.2 | 1.2 | 30.4 | 5.7 | 9.9 | GFRP | Type I |
| BHG-3 | 0.5 | 6.1 | 25.7 | 1.4 | 20.6 | 1.3 | 27.2 | 6.1 | 6.0 | GFRP | Type II |
| BHG-4 | 2.0 | 5.6 | 2.8 | 1.1 | 13.6 | 1.5 | 28.9 | 5.7 | 8.2 | GFRP | Type II |
| BHC-1 | 0.5 | 5.4 | 8.5 | 1.2 | 24.4 | 1.4 | 38.1 | 4.3 | 4.9 | CFRP | Type I |
| BHC-2 | 2.0 | 3.7 | −2.4 | 0.9 | 21.2 | 1.3 | 41.4 | 3.9 | 5.7 | CFRP | Type I |
| BHC-3 | 0.5 | 4.5 | 12.2 | 1.3 | 22.7 | 1.4 | 33.4 | 4.6 | 4.9 | CFRP | Type II |
| BHC-4 | 2.0 | 4.0 | −3.6 | 0.9 | 23.1 | 1.7 | 39.9 | 3.9 | 3.9 | CFRP | Type II |
| Data from this study [Parametric] | |||||||||||
| BHG-5 | 3.0 | 3.9 | 1.5 | 1.0 | 15.9 | 1.2 | 34.6 | 4.9 | 8.7 | GFRP | Type I |
| BHG-6 | 3.0 | 3.2 | 0.5 | 1.0 | 15.7 | 1.5 | 33.1 | 4.9 | 6.9 | GFRP | Type II |
| BHG-7 | 4.3 | 3.3 | −0.8 | 1.0 | 18.4 | 1.3 | 38.3 | 4.3 | 7.0 | GFRP | Type I |
| BHG-8 | 4.3 | 2.5 | −1.2 | 1.0 | 19.2 | 1.6 | 36.8 | 4.3 | 5.2 | GFRP | Type II |
| BHG-9 | 1.3 | 5.1 | 7.0 | 1.2 | 14.7 | 1.2 | 28.7 | 6.1 | 9.6 | GFRP | Type I |
| BHG-10 | 1.3 | 5.2 | 9.4 | 1.2 | 13.9 | 1.3 | 24.6 | 6.5 | 9.0 | GFRP | Type II |
| BHC-5 | 3.0 | 2.3 | −4.8 | 0.9 | 26.8 | 1.4 | 45.9 | 3.3 | 4.0 | CFRP | Type I |
| BHC-6 | 3.0 | 1.8 | −6.6 | 0.9 | 15.7 | 1.5 | 33.1 | 4.9 | 6.9 | CFRP | Type II |
| BHC-7 | 4.3 | 2.0 | −7.1 | 0.8 | 33.6 | 1.6 | 49.6 | 2.9 | 2.7 | CFRP | Type I |
| BHC-8 | 4.3 | 1.3 | −7.8 | 0.8 | 38.8 | 2.1 | 48.1 | 2.9 | 1.7 | CFRP | Type II |
| BHC-9 | 1.3 | 3.0 | 0.7 | 1.0 | 19.7 | 1.3 | 38.9 | 4.2 | 6.5 | CFRP | Type I |
| BHC-10 | 1.3 | 3.4 | 2.6 | 1.1 | 17.3 | 1.3 | 32.6 | 4.6 | 6.7 | CFRP | Type II |
| Aiello et al. [1] | |||||||||||
| A1 | 0.9 | 7.7 | 3.6 | 1.1 | 8.8 | 1.9 | 20.2 | 11.9 | 14.4 | AFRP | Type II |
| A2 | 1.6 | 6.4 | 3.1 | 1.1 | 10.4 | 1.9 | 25.8 | 10.0 | 12.7 | AFRP | Type II |
| A3 | 1.0 | 4.8 | 8.7 | 1.1 | 20.0 | 2.2 | 34.1 | 7.6 | 5.8 | AFRP | Type II |
| C1 | 0.9 | 7.7 | 11.2 | 1.1 | 9.7 | 1.8 | 21.2 | 11.9 | 14.5 | AFRP | Type I |
| Qu et al. [3] | |||||||||||
| B3 | 1.1 | 4.0 | 6.9 | 1.2 | 20.7 | 1.2 | 46.0 | 7.5 | 14.0 | GFRP | Type I |
| B4 | 2.0 | 2.9 | 4.9 | 1.1 | 19.5 | 1.1 | 49.9 | 6.7 | 16.0 | GFRP | Type I |
| B5 | 0.4 | 4.8 | 21.5 | 1.4 | 28.4 | 1.1 | 43.4 | 8.4 | 11.4 | GFRP | Type I |
| B6 | 0.6 | 4.5 | 14.7 | 1.3 | 30.4 | 1.2 | 51.9 | 6.6 | 9.5 | GFRP | Type I |
| B7 | 1.3 | 8.5 | 7.3 | 1.2 | 10.7 | 1.1 | 30.8 | 10.5 | 27.0 | GFRP | Type I |
| B8 | 0.3 | 3.1 | 38.3 | 1.4 | 77.6 | 1.6 | 87.3 | 3.7 | 2.7 | GFRP | Type II |
| Lau & Pam [4] | |||||||||||
| G0.3-MD1.0-A90 | 0.3 | 1.9 | 21.9 | 1.4 | 114.9 | 0.8 | 166.3 | 5.0 | 9.4 | GFRP | Type I |
| G1.0-T0.7-A90 | 1.6 | 3.9 | 6.3 | 1.1 | 160.7 | 1.2 | 237.3 | 3.6 | 4.4 | GFRP | Type I |
| G0.6-T1.0-A90 | 0.6 | 4.2 | 17.1 | 1.3 | 195.4 | 1.1 | 250.1 | 3.8 | 4.3 | GFRP | Type I |
| Yinghao & Yong [5] | |||||||||||
| S2 | 0.3 | 2.6 | 19.9 | 1.4 | 66.7 | 1.6 | 93.1 | 5.5 | 4.7 | GFRP | Type II |
| S3 | 0.3 | 3.8 | 29.9 | 1.6 | 72.8 | 1.4 | 95.2 | 5.8 | 5.5 | GFRP | Type II |
| S4 | 0.3 | 1.7 | 24.6 | 1.6 | 75.0 | 1.3 | 103.2 | 5.5 | 5.7 | GFRP | Type I |
| Refai et al. [8] | |||||||||||
| 2G12-1S10 | 2.9 | 5.3 | 0.7 | 1.1 | 15.2 | 1.4 | 47.3 | 8.2 | 18.5 | GFRP | Type I |
| 2G12-2S10 | 1.4 | 3.0 | 3.2 | 1.1 | 25.9 | 1.3 | 58.4 | 7.1 | 12.3 | GFRP | Type I |
| 2G12-2S12 | 1.0 | 4.4 | 5.5 | 1.1 | 31.1 | 1.5 | 55.7 | 6.8 | 8.2 | GFRP | Type I |
| 2G16-2S10 | 2.6 | 3.8 | 1.3 | 1.0 | 31.0 | 1.4 | 71.4 | 5.8 | 9.8 | GFRP | Type I |
| 2G16-2S12 | 1.8 | 2.4 | 2.6 | 1.1 | 37.4 | 1.4 | 70.9 | 5.5 | 7.3 | GFRP | Type I |
| 2G16-2S16 | 1.0 | 4.0 | 7.1 | 1.1 | 56.5 | 1.6 | 81.4 | 4.7 | 4.4 | GFRP | Type I |
| Parameter | Recommended Value |
|---|---|
| α | >0° |
| δN | >1 |
| δ | >4 |
| DF | >6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thamrin, R.; Zaidir, Z.; Iwanda, D. Ductility Estimation for Flexural Concrete Beams Longitudinally Reinforced with Hybrid FRP–Steel Bars. Polymers 2022, 14, 1017. https://doi.org/10.3390/polym14051017
Thamrin R, Zaidir Z, Iwanda D. Ductility Estimation for Flexural Concrete Beams Longitudinally Reinforced with Hybrid FRP–Steel Bars. Polymers. 2022; 14(5):1017. https://doi.org/10.3390/polym14051017
Chicago/Turabian StyleThamrin, Rendy, Zaidir Zaidir, and Devitasari Iwanda. 2022. "Ductility Estimation for Flexural Concrete Beams Longitudinally Reinforced with Hybrid FRP–Steel Bars" Polymers 14, no. 5: 1017. https://doi.org/10.3390/polym14051017







