Experimental and Numerical Study of Downward Flame Spread over Glass-Fiber-Reinforced Epoxy Resin
Abstract
:1. Introduction
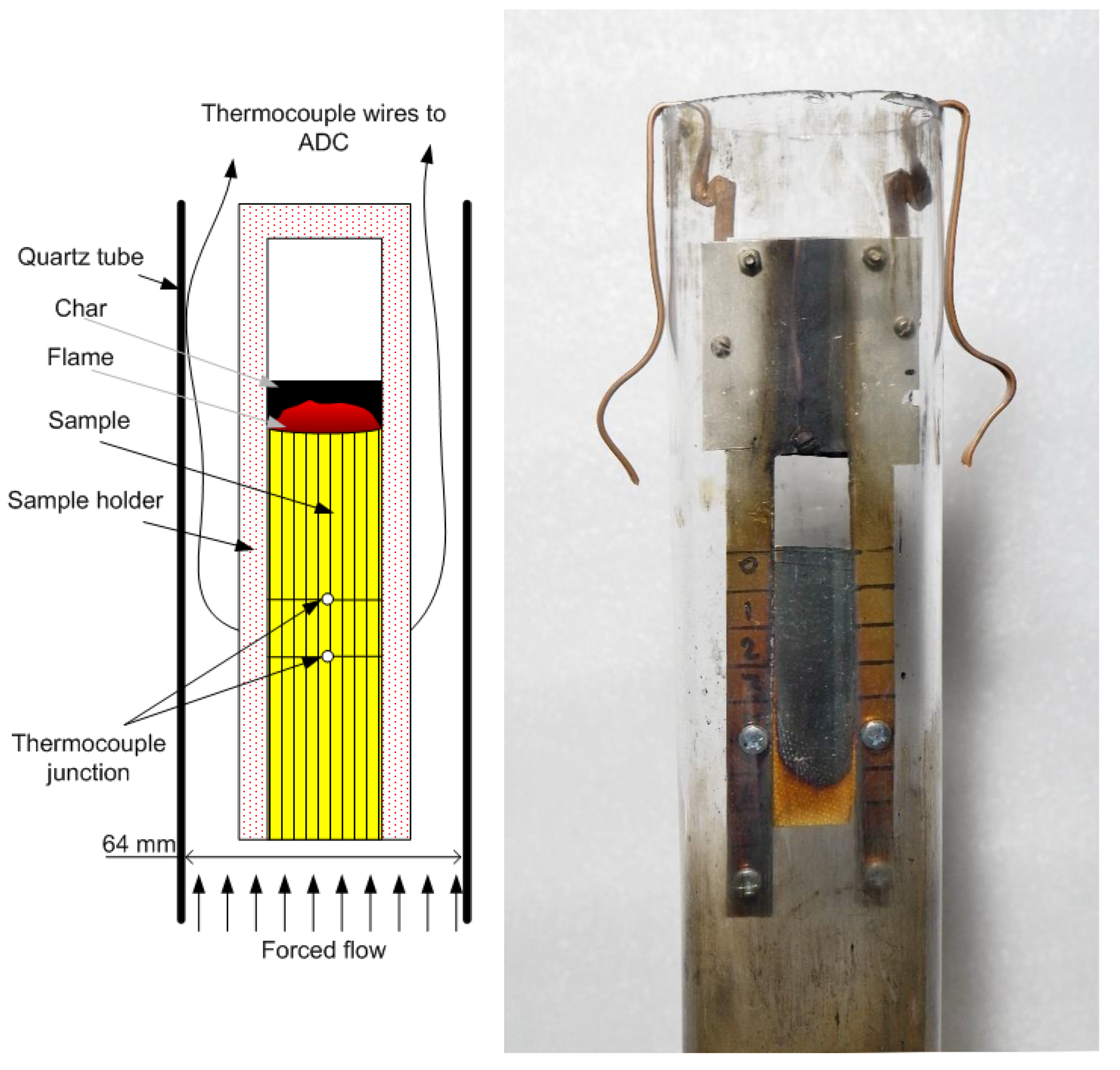
2. Experimental Section
2.1. Materials
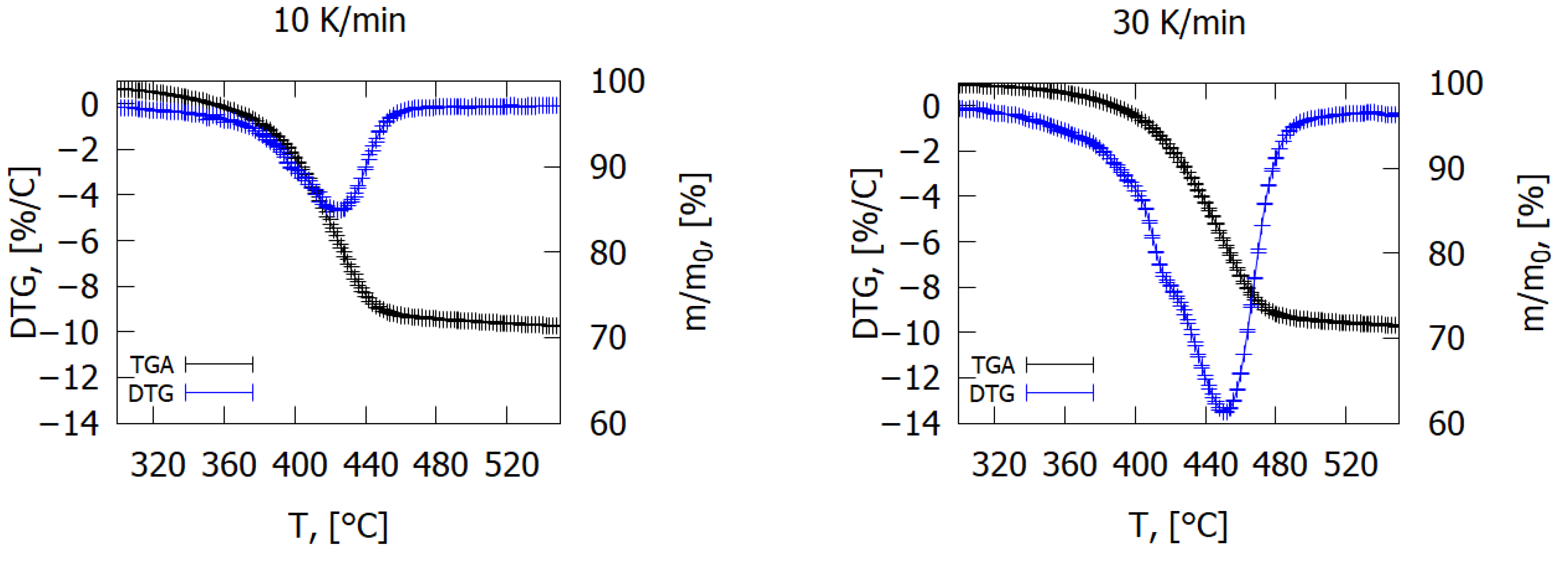
2.2. Thermal Degradation Analysis
2.3. Flame Spread Experiments
3. Numerical Section
3.1. Formulation
3.2. Input Data
4. Results and Discussion
4.1. Pyrolysis Kinetics
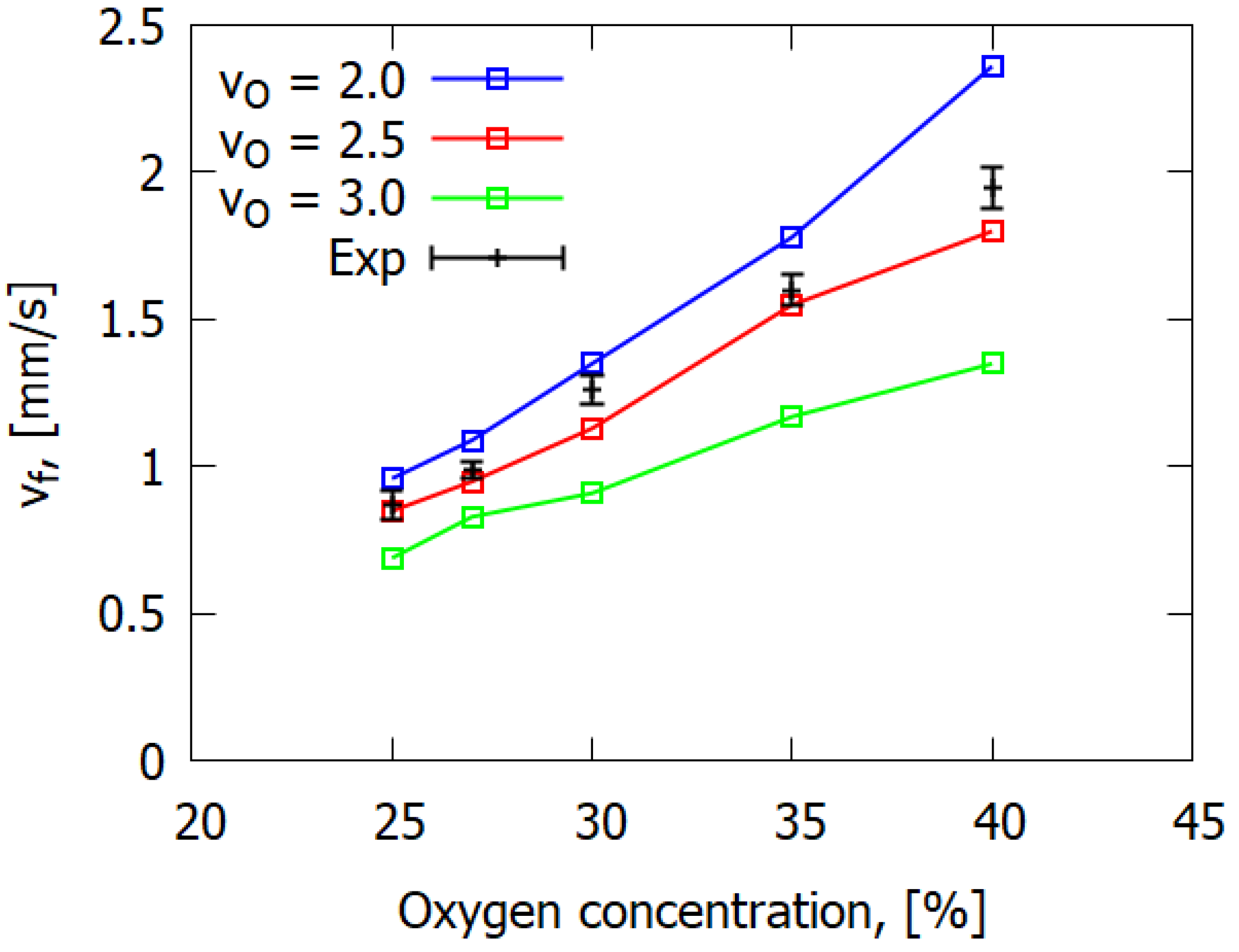
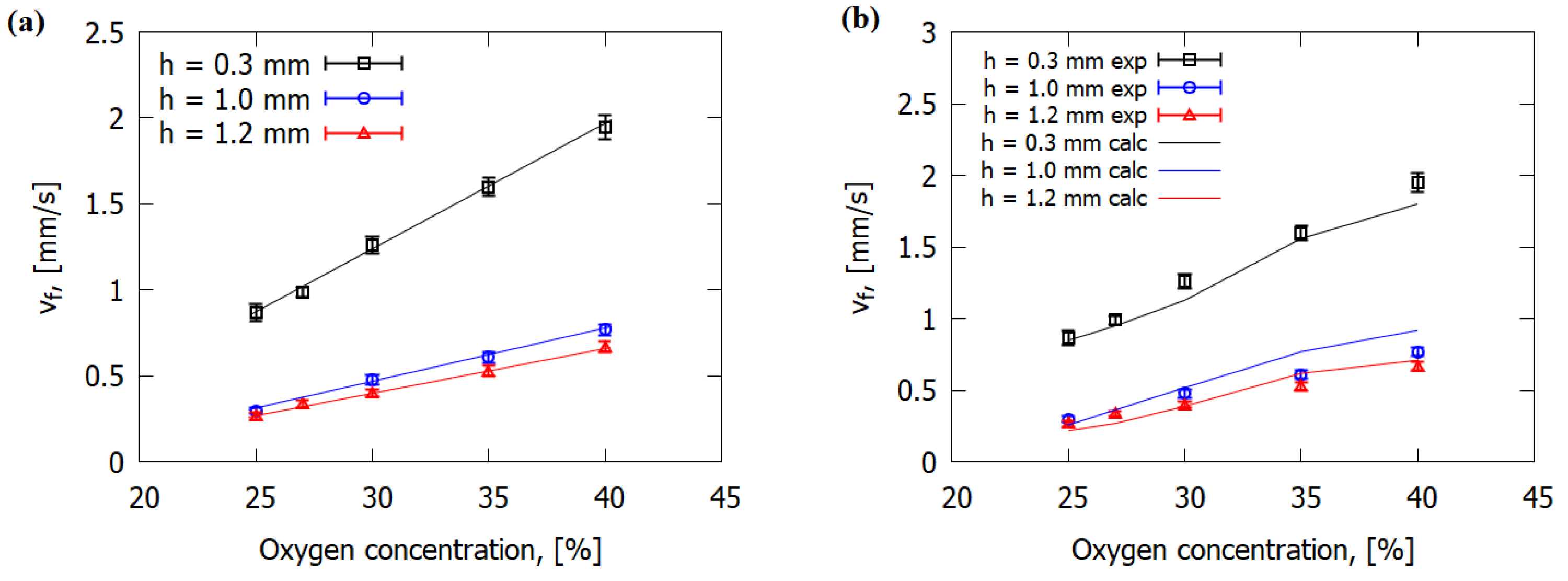
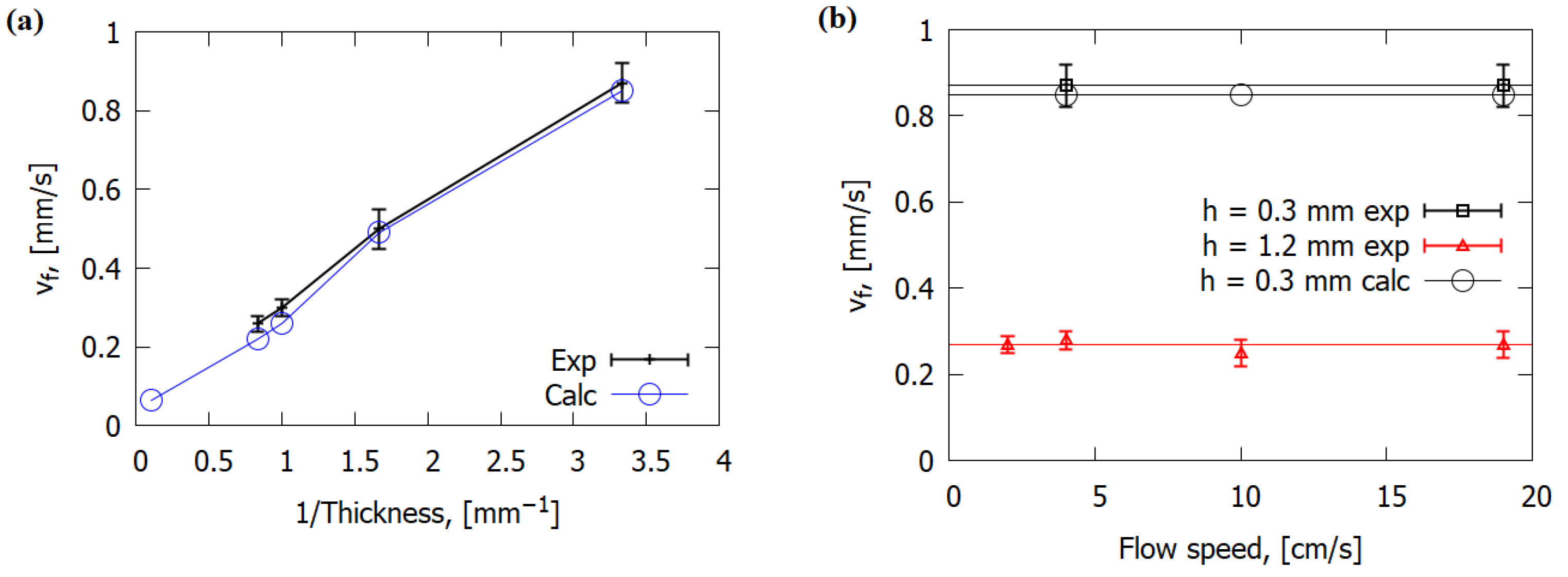
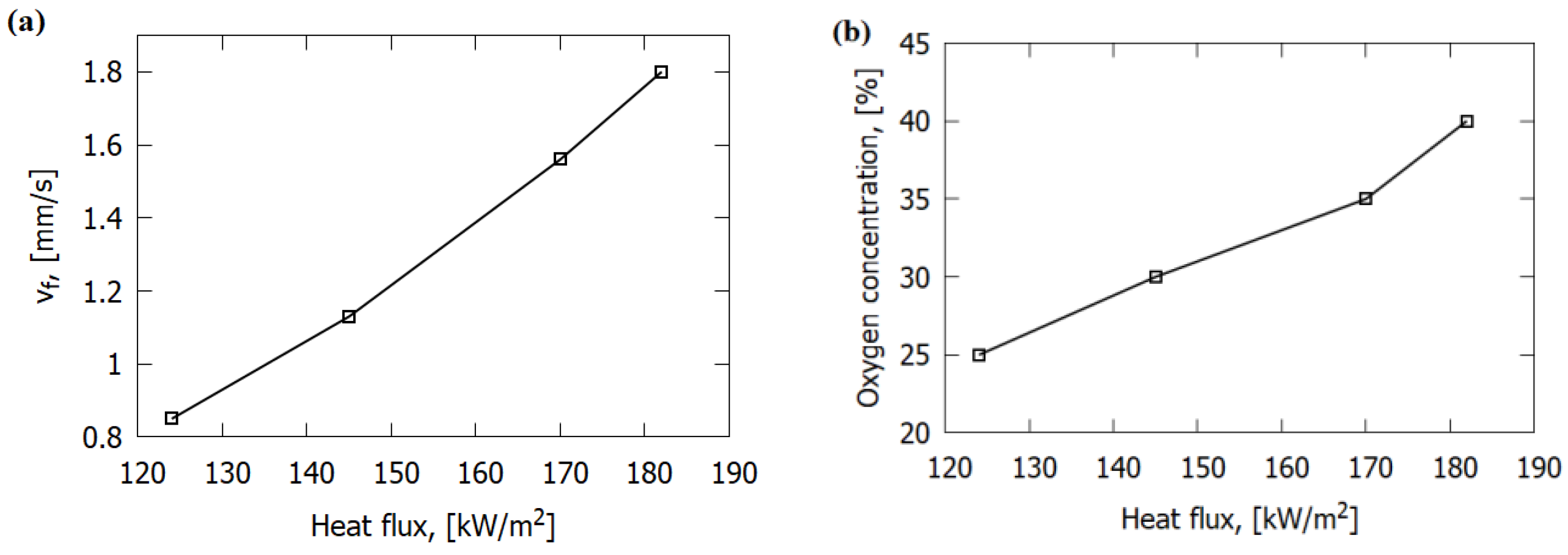
4.2. Dependence of the Flame Propagation Rate over GFRER on the Oxygen Concentration in the Gas Flow and on the Slab Thickness
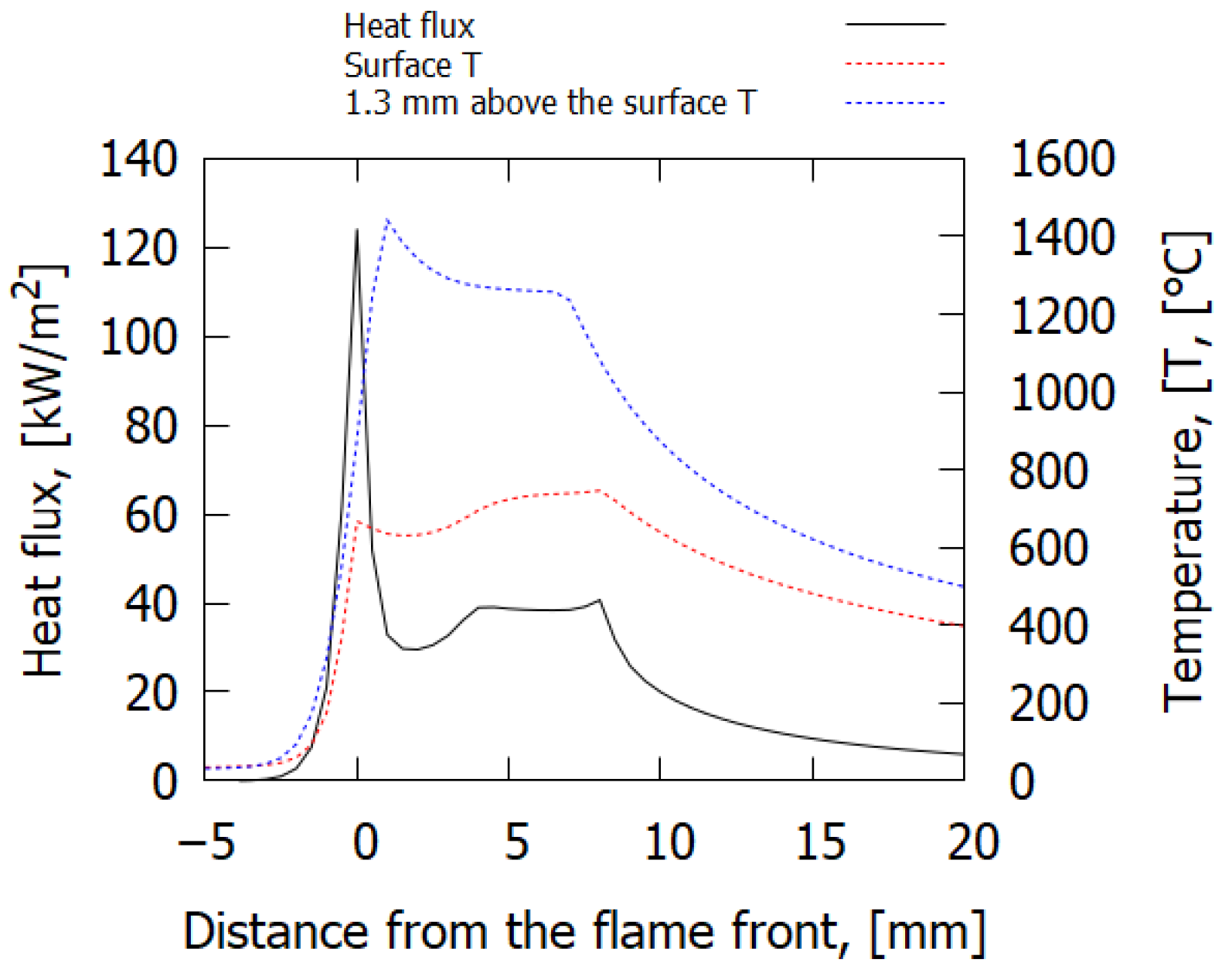
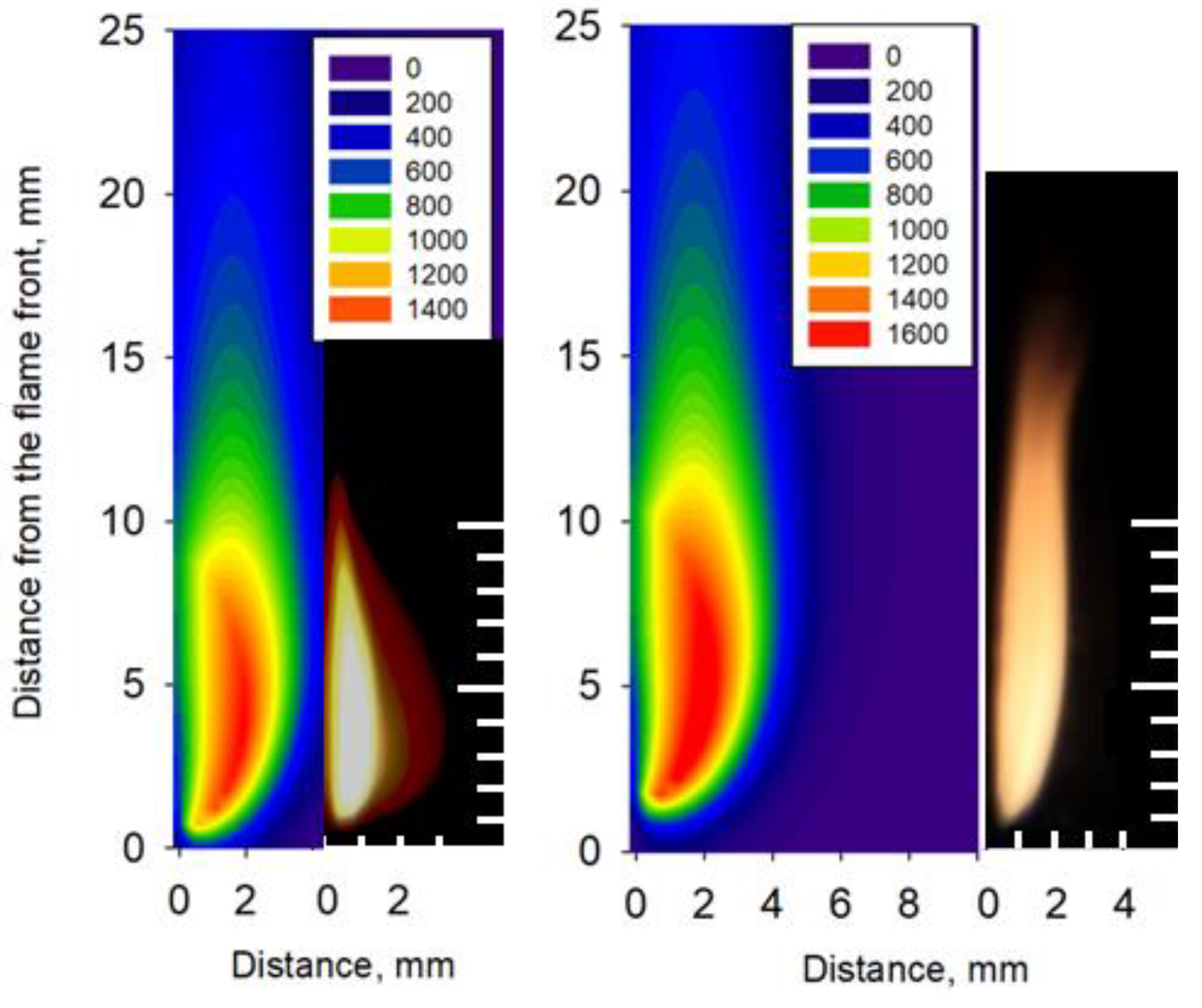
4.3. Thermal Flame Structure
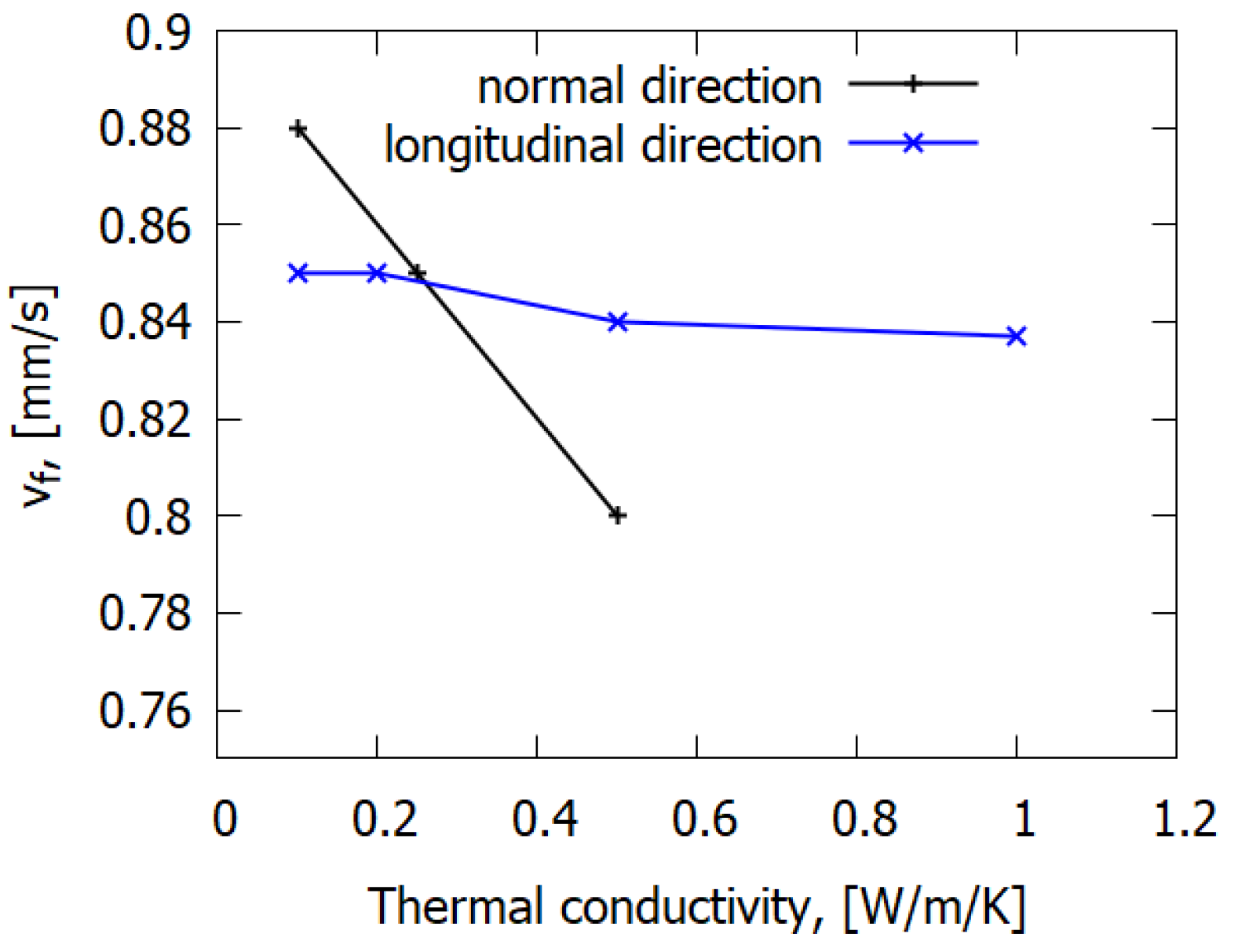
4.4. Sensitivity Analysis of the Model
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFRP | carbon-fiber-reinforced polymer |
| GFRER | glass-fiber-reinforced epoxy resin |
| LOI | limiting oxygen index |
| ROS | rate of flame spread |
| TGA | thermogravimetric analysis |
| DTG | differential thermogravimetric analysis |
| Nomenclature | |
| A | pyrolysis preexponential factor [s−1] |
| C | specific heat capacity [J/kg/K] |
| diffusion coefficient [m2/s] | |
| activation energy [J/mol] | |
| gravity acceleration [m/s2] | |
| sample thickness [mm] | |
| gas-phase preexponential factor [s−1] | |
| molar mass [g/mol] | |
| mass burning rate [g/s] | |
| pyrolysis reaction order [-] | |
| pressure [Pa] | |
| heat release [J/kg] | |
| heat flux [W/m2] | |
| specific gas constant [J/kg/K] | |
| universal gas constant [J/mol/K] | |
| temperature [K] | |
| time [s] | |
| velocity [m/s] | |
| flame spread rate [mm/s] | |
| reaction rate [s−1] | |
| width | |
| coordinate along fuel surface [m] | |
| gas component mass fraction [-] | |
| coordinate normal to fuel surface [m] | |
| Greek symbols | |
| conversion degree [-] | |
| solid component mass fraction [-] | |
| burnout degree [-] | |
| solid component volume fraction [-] | |
| thermal conductivity [W/m/K] | |
| dynamic molecular viscosity [kg/m/s] | |
| stoichiometric coefficient [-] | |
| density [kg/m3] | |
| half-thickness [m] | |
| Subscripts | |
| ambient | |
| binder | |
| fuel | |
| f | fiber |
| gas | |
| inert component | |
| oxidizer | |
| product | |
| pyrolysis | |
| solid | |
| Superscripts | |
| radiative | |
| along fuel surface | |
| normal to fuel surface | |
References
- Wichman, I.S. Theory of Opposed-Flow Flame Spread. Prog. Energy Combust. Sci. 1992, 18, 553–593. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; King, M.D.; Paolini, C. Structure of Downward Spreading Flames: A Comparison of Numerical Simulation, Experimental Results and a Simplified Parabolic Theory. Combust. Theory Model. 2004, 8, 23–39. [Google Scholar] [CrossRef]
- Jiang, L.; Miller, C.H.; Gollner, M.J.; Sun, J.-H. Sample Width and Thickness Effects on Horizontal Flame Spread over a Thin PMMA Surface. Proc. Combust. Inst. 2017, 36, 2987–2994. [Google Scholar] [CrossRef]
- Bhattachariee, S.; King, M.D.; Takahashi, S.; Nagumo, T.; Wakai, K. Downward Flame Spread over Poly(Methyl)Methacrylate. Proc. Combust. Inst. 2000, 28, 2891–2897. [Google Scholar] [CrossRef]
- Pereira, C.M.C.; Martins, M.S.S. Chapter 17—Flame Retardancy of Fiber-Reinforced Polymer Composites Based on Nanoclays and Carbon Nanotubes. In Polymer Green Flame Retardants; Papaspyrides, C.D., Kiliaris, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 551–595. ISBN 978-0-444-53808-6. [Google Scholar]
- Kobayashi, Y.; Terashima, K.; Oiwa, R.; Tokoro, M.; Takahashi, S. Opposed-Flow Flame Spread over Carbon Fiber Reinforced Plastic under Variable Flow Velocity and Oxygen Concentration: The Effect of in-Plane Thermal Isotropy and Anisotropy. Proc. Combust. Inst. 2021, 38, 4857–4866. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Oiwa, R.; Tokoro, M.; Takahashi, S. Buoyant-Flow Downward Flame Spread over Carbon Fiber Reinforced Plastic in Variable Oxygen Atmospheres. Combust. Flame 2021, 232, 111528. [Google Scholar] [CrossRef]
- Kandare, E.; Kandola, B.; Myler, P.; Edwards, G. Thermomechanical Responses of Fiber-Reinforced Epoxy Composites Exposed to High Temperature Environments. Part I: Experimental Data Acquisition. J. Compos. Mater. 2010, 44, 3093–3114. [Google Scholar] [CrossRef]
- Kandare, E.; Kandola, B.K.; McCarthy, E.D.; Myler, P.; Edwards, G.; Yong, J.; Wang, Y.C. Fiber-Reinforced Epoxy Composites Exposed to High Temperature Environments. Part II: Modeling Mechanical Property Degradation. J. Compos. Mater. 2010, 45, 1511–1521. [Google Scholar] [CrossRef]
- Inoue, T.; Hayakawa, K.; Suzuki, Y. Thermal Conductivity Measurement of GFRP at Cryogenic Temperature. In Proceedings of the 19th International Conference on Composite Materials, Montréal, QC, Canada, 28 July–2 August 2013. [Google Scholar]
- Bar, M.; Alagirusamy, R.; Das, A. Flame Retardant Polymer Composites. Fibers Polym. 2015, 16, 705–717. [Google Scholar] [CrossRef]
- Movahedifar, E.; Vahabi, H.; Saeb, M.R.; Thomas, S. Flame Retardant Epoxy Composites on the Road of Innovation: An Analysis with Flame Retardancy Index for Future Development. Molecules 2019, 24, 3964. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; He, C.; Wen, Y.; Ye, Y.; Zhou, X.; Xie, X.; Mai, Y.-W. Improving Thermal and Flame Retardant Properties of Epoxy Resin by Functionalized Graphene Containing Phosphorous, Nitrogen and Silicon Elements. Compos. Part Appl. Sci. Manuf. 2017, 103, 74–83. [Google Scholar] [CrossRef]
- Zhi, M.; Liu, Q.; Chen, H.; Chen, X.; Feng, S.; He, Y. Thermal Stability and Flame Retardancy Properties of Epoxy Resin Modified with Functionalized Graphene Oxide Containing Phosphorus and Silicon Elements. ACS Omega 2019, 4, 10975–10984. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Ma, C.; Wang, P.; Qiu, S.; Cai, W.; Hu, Y. Ultra-Low Phosphorus Loading to Achieve the Superior Flame Retardancy of Epoxy Resin. Polym. Degrad. Stab. 2018, 149, 119–128. [Google Scholar] [CrossRef]
- Zhong, X.; Yang, X.; Ruan, K.; Zhang, J.; Zhang, H.; Gu, J. Discotic Liquid Crystal Epoxy Resins Integrating Intrinsic High Thermal Conductivity and Intrinsic Flame Retardancy. Macromol. Rapid Commun. 2022, 43, 2100580. [Google Scholar] [CrossRef]
- Wang, X.; Song, L.; Pornwannchai, W.; Hu, Y.; Kandola, B. The Effect of Graphene Presence in Flame Retarded Epoxy Resin Matrix on the Mechanical and Flammability Properties of Glass Fiber-Reinforced Composites. Compos. Part Appl. Sci. Manuf. 2013, 53, 88–96. [Google Scholar] [CrossRef]
- Shahari, S.; Fathullah, M.; Abdullah, M.M.A.B.; Shayfull, Z.; Mia, M.; Budi Darmawan, V.E. Recent Developments in Fire Retardant Glass Fibre Reinforced Epoxy Composite and Geopolymer as a Potential Fire-Retardant Material: A Review. Constr. Build. Mater. 2021, 277, 122246. [Google Scholar] [CrossRef]
- Korobeinichev, O.P.; Karpov, A.I.; Bolkisev, A.A.; Shaklein, A.A.; Gonchikzhapov, M.B.; Paletsky, A.A.; Tereshchenko, A.G.; Shmakov, A.G.; Gerasimov, I.E.; Kumar, A. An Experimental and Numerical Study of Thermal and Chemical Structure of Downward Flame Spread over PMMA Surface in Still Air. Proc. Combust. Inst. 2019, 37, 4017–4024. [Google Scholar] [CrossRef]
- Wu, K.K.; Fan, W.F.; Chen, C.H.; Liou, T.M.; Pan, I.J. Downward Flame Spread over a Thick PMMA Slab in an Opposed Flow Environment: Experiment and Modeling. Combust. Flame 2003, 132, 697–707. [Google Scholar] [CrossRef]
- Karpov, A.I.; Korobeinichev, O.P.; Shaklein, A.A.; Bolkisev, A.A.; Kumar, A.; Shmakov, A.G. Numerical Study of Horizontal Flame Spread over PMMA Surface in Still Air. Appl. Therm. Eng. 2018, 144, 937–944. [Google Scholar] [CrossRef]
- Singh, A.V.; Gollner, M.J. Local Burning Rates and Heat Flux for Forced Flow Boundary-Layer Diffusion Flames. AIAA J. 2015, 54, 408–418. [Google Scholar] [CrossRef] [Green Version]
- Shaklein, A.A.; Bolkisev, A.A.; Karpov, A.I.; Korobeinichev, O.P.; Trubachev, S.A. Two-Step Gas-Phase Reaction Model for the Combustion of Polymeric Fuel. Fuel 2019, 255, 115878. [Google Scholar] [CrossRef]
- Korobeinichev, O.; Glaznev, R.; Karpov, A.; Shaklein, A.; Shmakov, A.; Paletsky, A.; Trubachev, S.; Hu, Y.; Wang, X.; Hu, W. An Experimental Study and Numerical Simulation of Horizontal Flame Spread over Polyoxymethylene in Still Air. Fire Saf. J. 2020, 111, 102924. [Google Scholar] [CrossRef]
- Trubachev, S.A.; Korobeinichev, O.P.; Karpov, A.I.; Shaklein, A.A.; Glaznev, R.K.; Gonchikzhapov, M.B.; Paletsky, A.A.; Tereshchenko, A.G.; Shmakov, A.G.; Bespalova, A.S.; et al. The Effect of Triphenyl Phosphate Inhibition on Flame Propagation over Cast PMMA Slabs. Proc. Combust. Inst. 2021, 38, 4635–4644. [Google Scholar] [CrossRef]
- Ma, C.; Sánchez-Rodríguez, D.; Kamo, T. A Comprehensive Study on the Oxidative Pyrolysis of Epoxy Resin from Fiber/Epoxy Composites: Product Characteristics and Kinetics. J. Hazard. Mater. 2021, 412, 125329. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, C.; Liang, R.; Wang, B. Combustion and Thermal Properties of Epoxy/Phenyltrisilanol Polyhedral Oligomeric Silsesquioxane Nanocomposites. J. Therm. Anal. Calorim. 2010, 100, 1009–1015. [Google Scholar] [CrossRef]
- Korobeinichev, O.P.; Paletsky, A.A.; Gonchikzhapov, M.B.; Glaznev, R.K.; Gerasimov, I.E.; Naganovsky, Y.K.; Shundrina, I.K.; Snegirev, A.Y.; Vinu, R. Kinetics of Thermal Decomposition of PMMA at Different Heating Rates and in a Wide Temperature Range. Thermochim. Acta 2019, 671, 17–25. [Google Scholar] [CrossRef]
- Korobeinichev, O.P.; Trubachev, S.A.; Joshi, A.K.; Kumar, A.; Paletsky, A.A.; Tereshchenko, A.G.; Shmakov, A.G.; Glaznev, R.K.; Raghavan, V.; Mebel, A.M. Experimental and Numerical Studies of Downward Flame Spread over PMMA with and without Addition of Tri Phenyl Phosphate. Proc. Combust. Inst. 2021, 38, 4867–4875. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korobeinichev, O.; Karpov, A.; Shaklein, A.; Paletsky, A.; Chernov, A.; Trubachev, S.; Glaznev, R.; Shmakov, A.; Barbot’ko, S. Experimental and Numerical Study of Downward Flame Spread over Glass-Fiber-Reinforced Epoxy Resin. Polymers 2022, 14, 911. https://doi.org/10.3390/polym14050911
Korobeinichev O, Karpov A, Shaklein A, Paletsky A, Chernov A, Trubachev S, Glaznev R, Shmakov A, Barbot’ko S. Experimental and Numerical Study of Downward Flame Spread over Glass-Fiber-Reinforced Epoxy Resin. Polymers. 2022; 14(5):911. https://doi.org/10.3390/polym14050911
Chicago/Turabian StyleKorobeinichev, Oleg, Alexander Karpov, Artem Shaklein, Alexander Paletsky, Anatoliy Chernov, Stanislav Trubachev, Roman Glaznev, Andrey Shmakov, and Sergey Barbot’ko. 2022. "Experimental and Numerical Study of Downward Flame Spread over Glass-Fiber-Reinforced Epoxy Resin" Polymers 14, no. 5: 911. https://doi.org/10.3390/polym14050911
APA StyleKorobeinichev, O., Karpov, A., Shaklein, A., Paletsky, A., Chernov, A., Trubachev, S., Glaznev, R., Shmakov, A., & Barbot’ko, S. (2022). Experimental and Numerical Study of Downward Flame Spread over Glass-Fiber-Reinforced Epoxy Resin. Polymers, 14(5), 911. https://doi.org/10.3390/polym14050911






