Mechanical Behavior of Polyethylene Pipes under Strike-Slip Fault Movements
Abstract
:1. Introduction
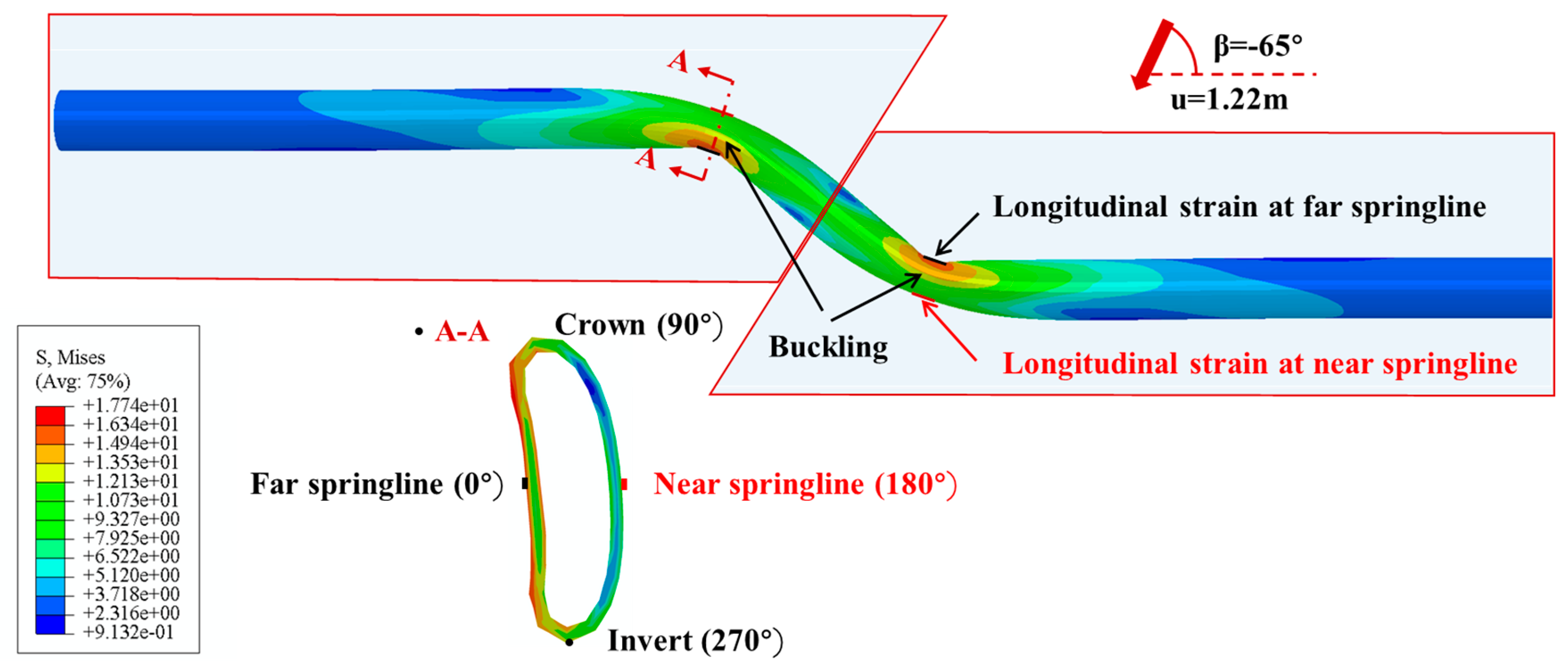
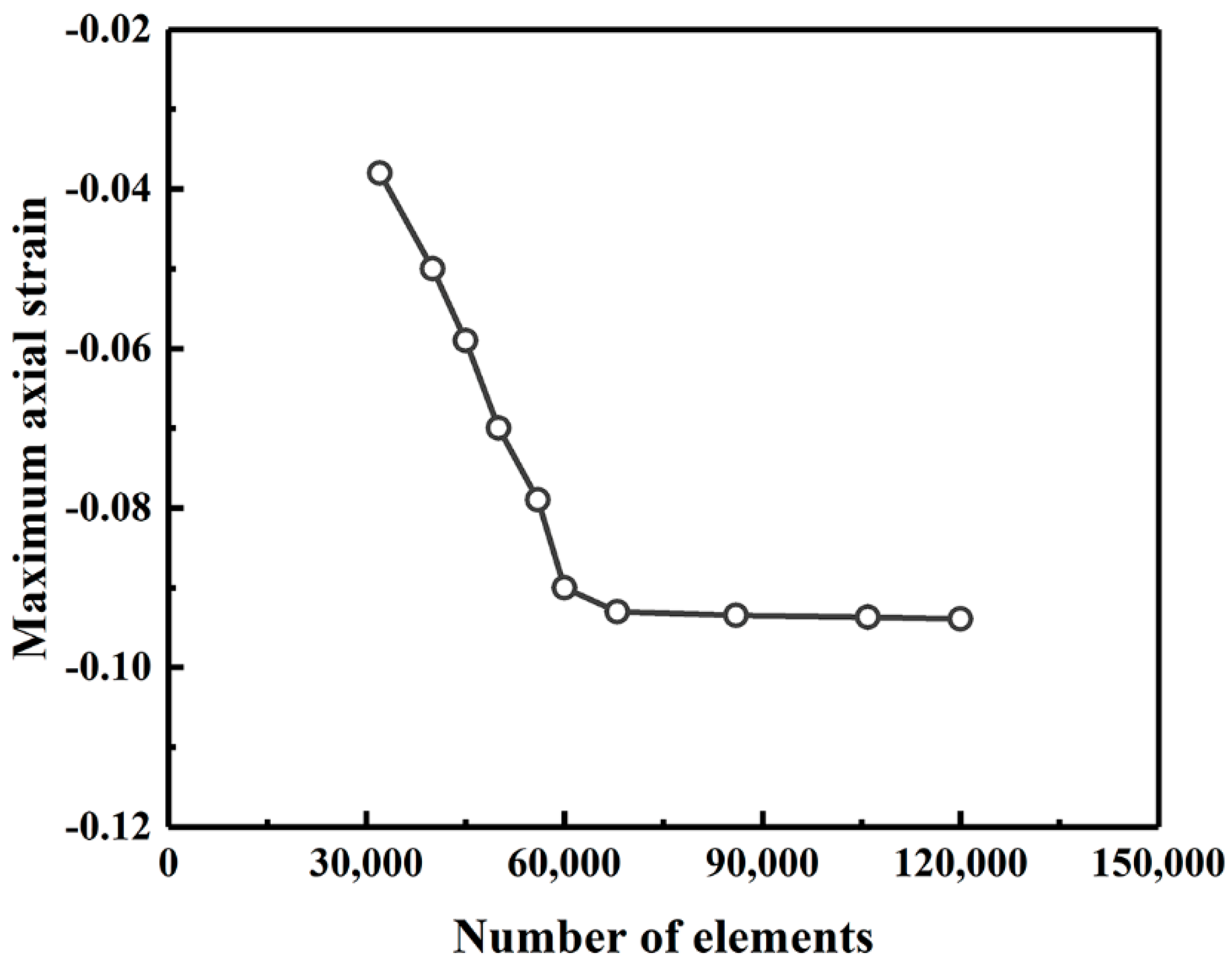
2. Finite Element Model
3. Results and Discussion
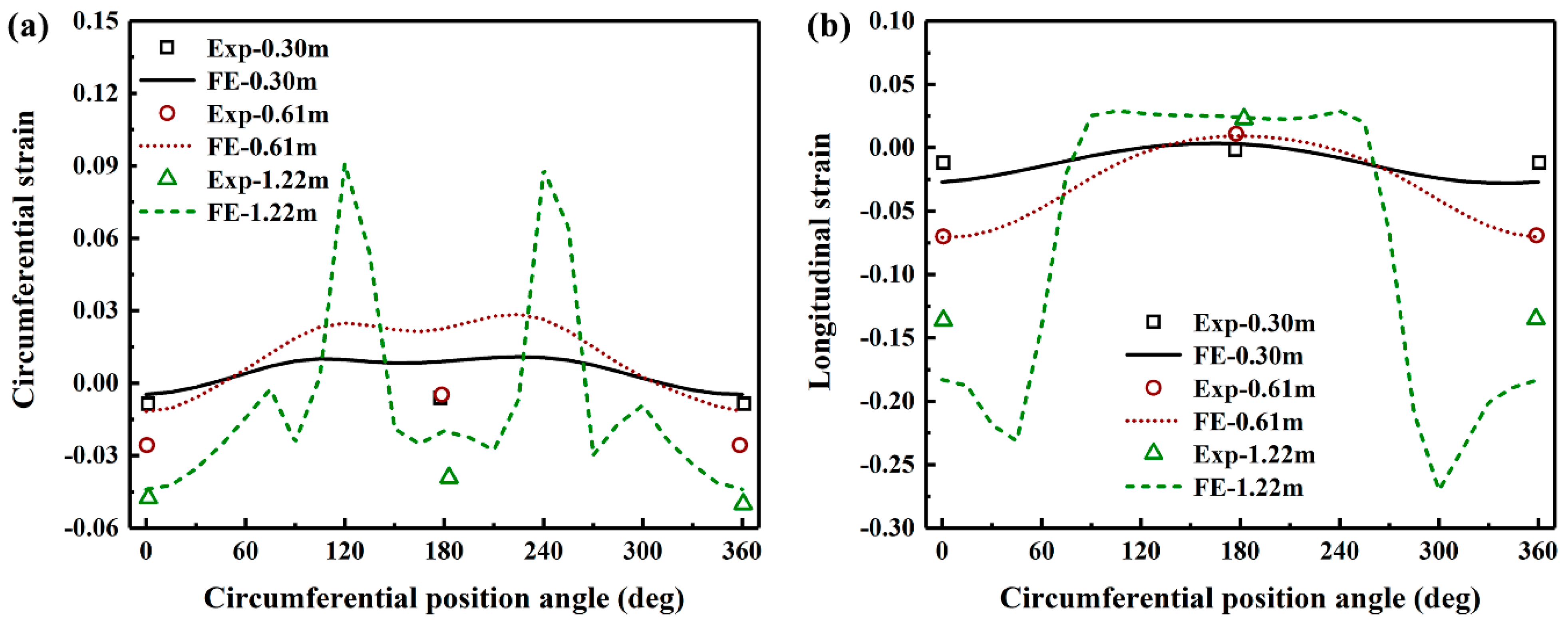
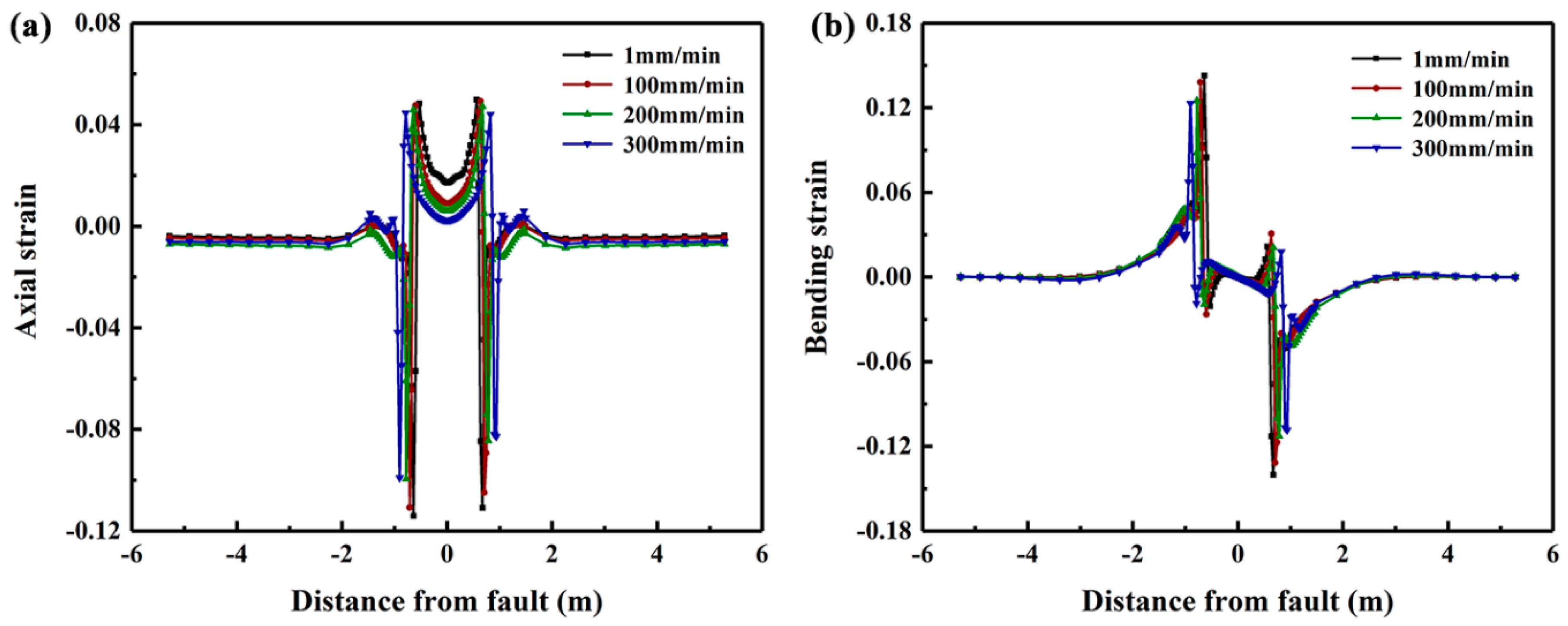
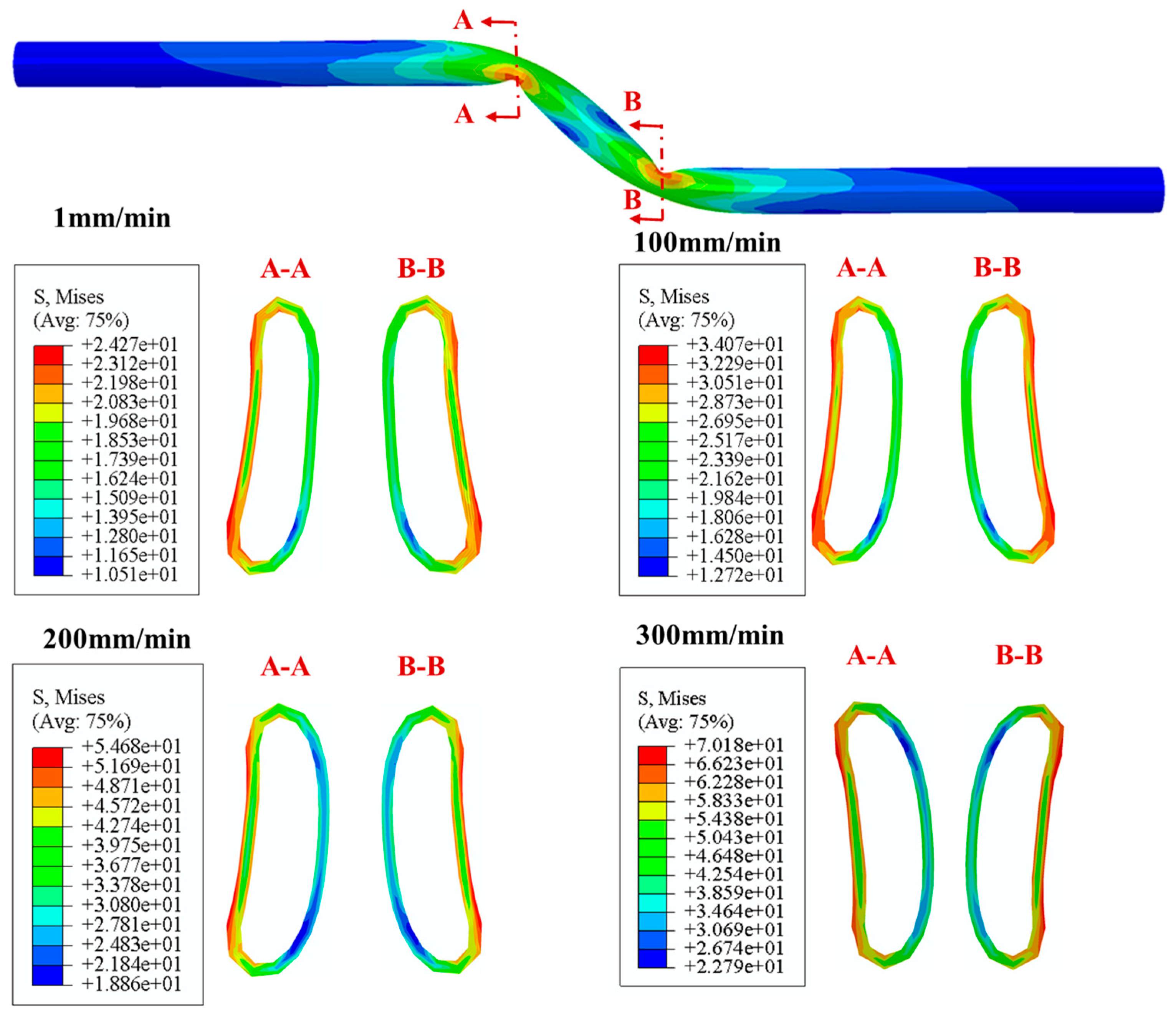
3.1. Comparison with Experimental Results
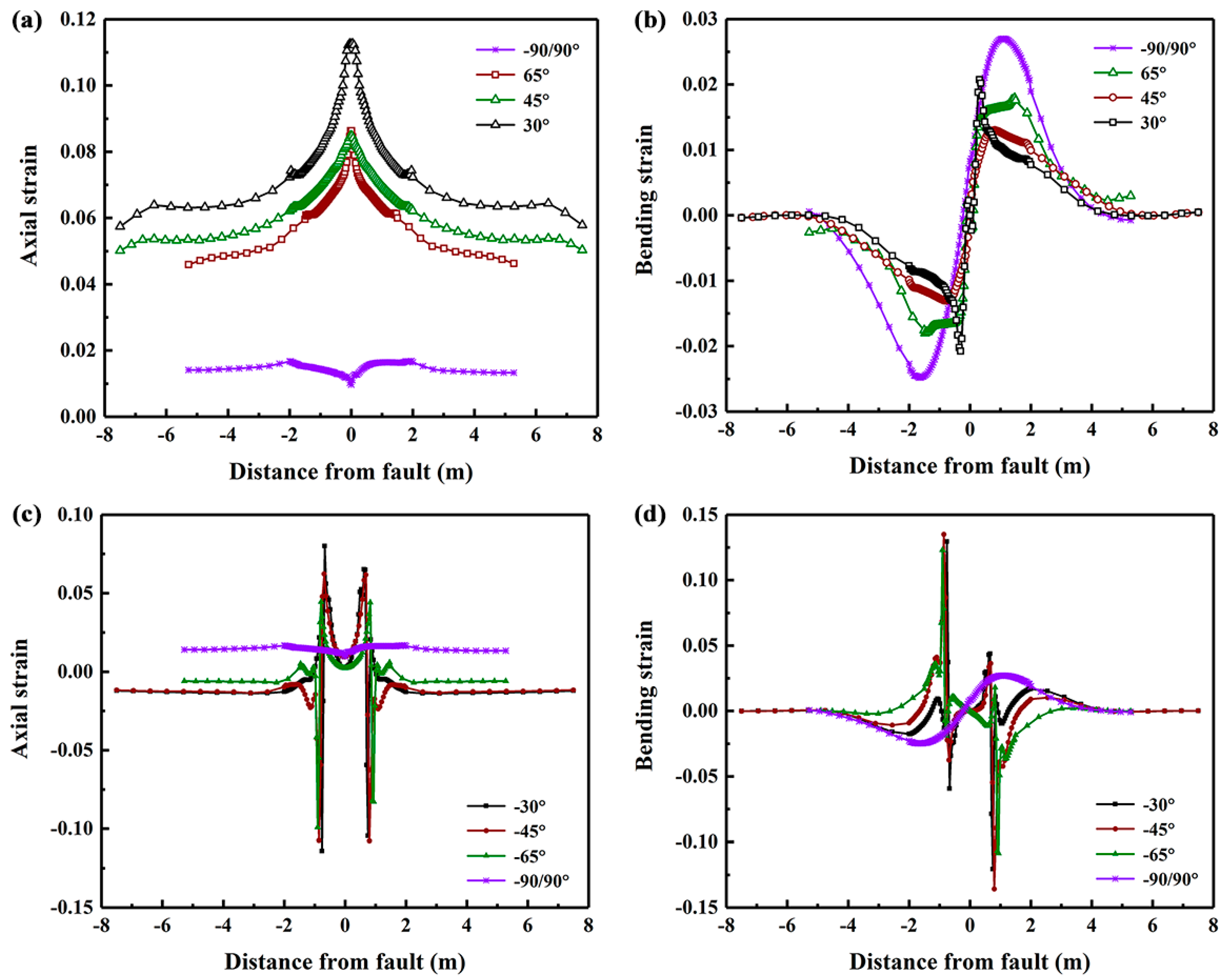
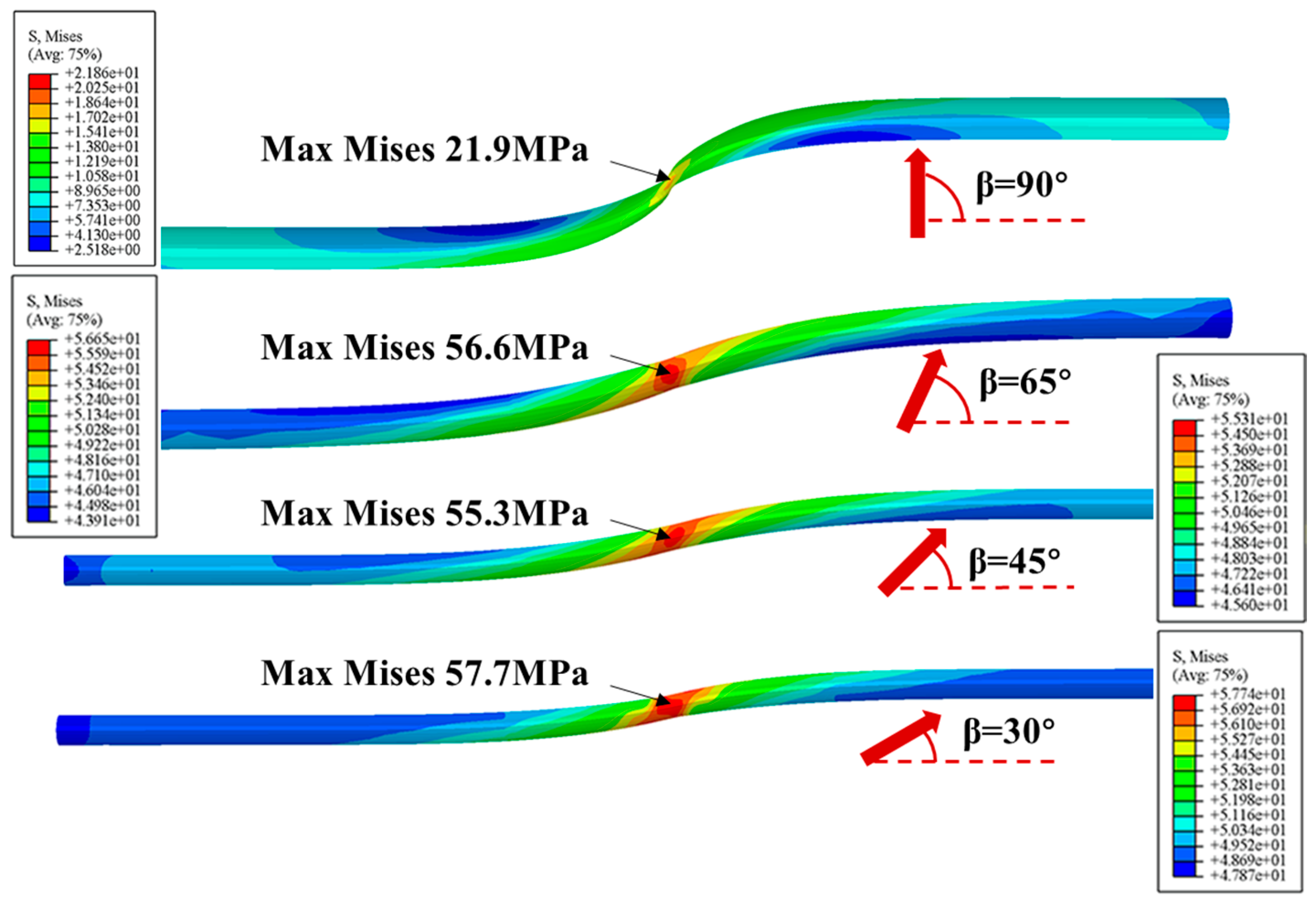
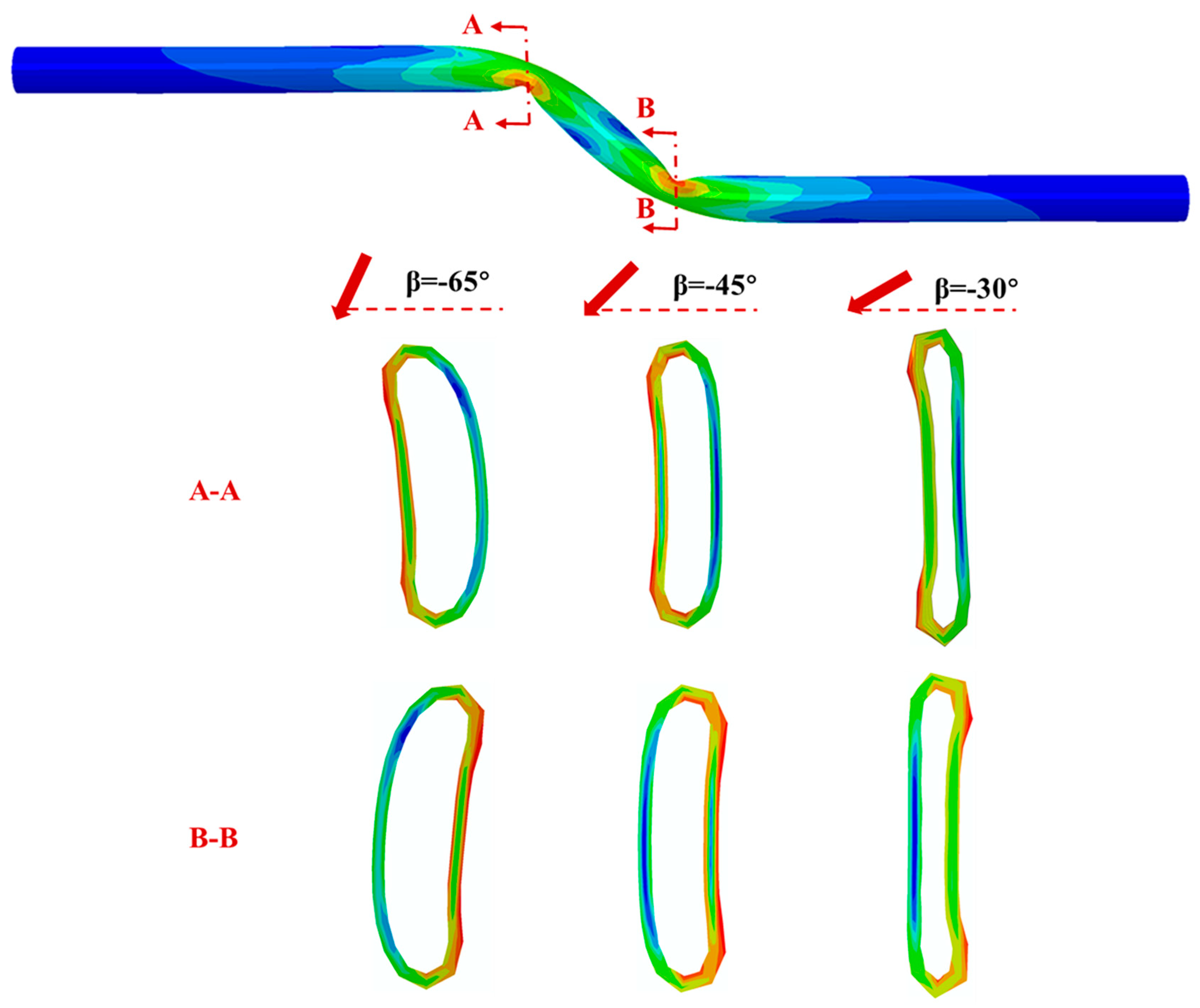
3.2. Effects of Crossing Angle
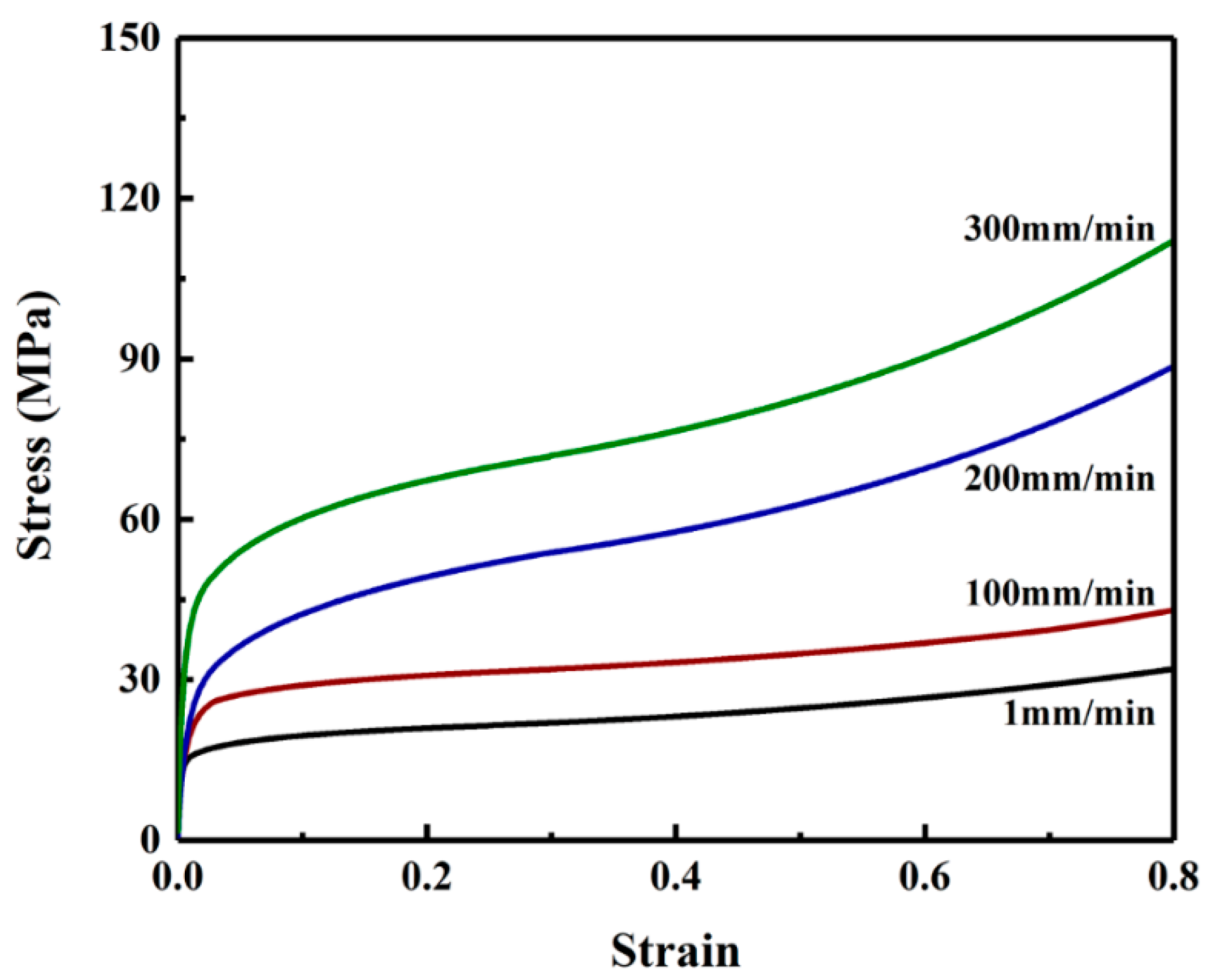
3.3. Effects of Pipe Property
3.4. Effects of Soil Property
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Newmark, N.M.; Hall, W.J. Pipeline Design to Resist Large Fault Displacement. In Proceedings of the US National Conference on Earthquake Engineering, Ann Arbor, MI, USA, 18–20 June 1975; Volume 1975, pp. 416–425. [Google Scholar]
- Kennedy, R.P.; Chow, A.M.; Williamson, R.A. Fault Movement Effects on Buried Oil Pipeline. Transp. Eng. J. Am. Soc. Civ. Eng. 1977, 103, 617–633. [Google Scholar] [CrossRef]
- Vazouras, P.; Karamanos, S.A.; Dakoulas, P. Finite Element Analysis of Buried Steel Pipelines under Strike-Slip Fault Displacements. Soil Dyn. Earthq. Eng. 2010, 30, 1361–1376. [Google Scholar] [CrossRef]
- Vazouras, P.; Karamanos, S.A.; Dakoulas, P. Mechanical Behavior of Buried Steel Pipes Crossing Active Strike-Slip Faults. Soil Dyn. Earthq. Eng. 2012, 41, 164–180. [Google Scholar] [CrossRef]
- Vazouras, P.; Dakoulas, P.; Karamanos, S.A. Pipe–Soil Interaction and Pipeline Performance under Strike–Slip Fault Movements. Soil Dyn. Earthq. Eng. 2015, 72, 48–65. [Google Scholar] [CrossRef]
- Vazouras, P.; Karamanos, S.A. Structural Behavior of Buried Pipe Bends and Their Effect on Pipeline Response in Fault Crossing Areas. Bull. Earthq. Eng. 2017, 15, 4999–5024. [Google Scholar] [CrossRef]
- Kaya, E.S.; Uckan, E.; O’Rourke, M.J.; Karamanos, S.A.; Akbas, B.; Cakir, F.; Cheng, Y. Failure Analysis of a Welded Steel Pipe at Kullar Fault Crossing. Eng. Fail. Anal. 2017, 71, 43–62. [Google Scholar] [CrossRef] [Green Version]
- Demirci, H.E.; Bhattacharya, S.; Karamitros, D.; Alexander, N. Experimental and Numerical Modelling of Buried Pipelines Crossing Reverse Faults. Soil Dyn. Earthq. Eng. 2018, 114, 198–214. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Chen, Y.; Zhang, H. Local Buckling Evolution Mechanism of a Buried Steel Pipe under Fault Movements. Energy Sci. Eng. 2020, 8, 412–425. [Google Scholar] [CrossRef]
- Demirci, H.E.; Karaman, M.; Bhattacharya, S. Behaviour of Buried Continuous Pipelines Crossing Strike-Slip Faults: Experimental and Numerical Study. J. Nat. Gas Sci. Eng. 2021, 92, 103980. [Google Scholar] [CrossRef]
- Cheng, X.; Ma, C.; Huang, R.; Huang, S.; Yang, W. Failure Mode Analysis of X80 Buried Steel Pipeline under Oblique-Reverse Fault. Soil Dyn. Earthq. Eng. 2019, 125, 105723. [Google Scholar] [CrossRef]
- Trifonov, O.V. Numerical Stress-Strain Analysis of Buried Steel Pipelines Crossing Active Strike-Slip Faults with an Emphasis on Fault Modeling Aspects. J. Pipeline Syst. Eng. Pract. 2015, 6, 04014008. [Google Scholar] [CrossRef]
- Trifonov, O.V.; Cherniy, V.P. Application of Composite Wraps for Strengthening of Buried Steel Pipelines Crossing Active Faults. J. Press. Vessel Technol. 2016, 138, 060902. [Google Scholar] [CrossRef]
- Trifonov, O.V.; Cherniy, V.P. Elastoplastic Stress–Strain Analysis of Buried Steel Pipelines Subjected to Fault Displacements with Account for Service Loads. Soil Dyn. Earthq. Eng. 2012, 33, 54–62. [Google Scholar] [CrossRef]
- Uckan, E.; Akbas, B.; Shen, J.; Rou, W.; Paolacci, F.; O’Rourke, M. A Simplified Analysis Model for Determining the Seismic Response of Buried Steel Pipes at Strike-Slip Fault Crossings. Soil Dyn. Earthq. Eng. 2015, 75, 55–65. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Han, Y.; Xia, M.; Zheng, W. A Semi-Empirical Model for Peak Strain Prediction of Buried X80 Steel Pipelines under Compression and Bending at Strike-Slip Fault Crossings. J. Nat. Gas Sci. Eng. 2016, 32, 465–475. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Li, M.; Xia, M.; Zheng, W.; Wu, K.; Han, Y. Effects of Steel Properties on the Local Buckling Response of High Strength Pipelines Subjected to Reverse Faulting. J. Nat. Gas Sci. Eng. 2016, 33, 378–387. [Google Scholar] [CrossRef]
- Trifonov, O.V. The Effect of Variation of Soil Conditions along the Pipeline in the Fault-Crossing Zone. Soil Dyn. Earthq. Eng. 2018, 104, 437–448. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Ndubuaku, O.; Xia, M.; Roger Cheng, J.J.; Li, Y.; Adeeb, S. Effects of Stress–Strain Characteristics on Local Buckling of X80 Pipe Subjected to Strike-Slip Fault Movement. J. Press. Vessel Technol. 2018, 140, 041408. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Wang, B.; Xia, M.; Wu, K.; Zheng, Q.; Han, Y. Local Buckling Behavior and Plastic Deformation Capacity of High-Strength Pipe at Strike-Slip Fault Crossing. Metals 2018, 8, 22. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Symans, M.D.; O’Rourke, M.J.; Abdoun, T.H.; O’Rourke, T.D.; Palmer, M.C.; Stewart, H.E. Numerical Modeling of Buried HDPE Pipelines Subjected to Strike-Slip Faulting. J. Earthq. Eng. 2011, 15, 1273–1296. [Google Scholar] [CrossRef]
- Robert, D.J.; Soga, K.; O’Rourke, T.D. Pipelines Subjected to Fault Movement in Dry and Unsaturated Soils. Int. J. Geomech. 2016, 16, C4016001. [Google Scholar] [CrossRef]
- O’Rourke, T.D.; Jung, J.K.; Argyrou, C. Underground Pipeline Response to Earthquake-Induced Ground Deformation. Soil Dyn. Earthq. Eng. 2016, 91, 272–283. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Xiao, Y.; Liang, Z. Mechanical Behaviors and Failure Mechanisms of Buried Polyethylene Pipes Crossing Active Strike-Slip Faults. Compos. Part B Eng. 2018, 154, 449–466. [Google Scholar] [CrossRef]
- Gu, W.; Wu, K.; Tong, L.; Liu, S. Study of Deflection of Buried HDPE Corrugated Pipeline under the Uneven Settlement of Soil. KSCE J. Civ. Eng. 2022, 26, 221–235. [Google Scholar] [CrossRef]
- Zhou, M.; Moore, I.D.; Lan, H. Experimental Study of Structural Response of Lined-Corrugated HDPE Pipe Subjected to Normal Fault. J. Geotech. Geoenvironmental. Eng. 2019, 145, 04019117. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, F.; Du, Y.-J.; Liu, M.D. Laboratory Evaluation of Buried High-Density Polyethylene Pipes Subjected to Localized Ground Subsidence. Acta Geotech. 2019, 14, 1081–1099. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Symans, M.D.; O’Rourke, M.J.; Abdoun, T.H.; Ha, D.; O’Rourke, T.D.; Palmer, M.C.; Jezerski, J.; Stewart, H.E. Local Buckling of Buried HDPE Pipelines Subjected to Earthquake Faulting: Case Study Via Numerical Simulations and Experimental Testing. J. Earthq. Eng. 2020, 24, 203–225. [Google Scholar] [CrossRef]
- Kwon, H.J.; Jar, P.-Y.B. On the Application of FEM to Deformation of High-Density Polyethylene. Int. J. Solids Struct. 2008, 45, 3521–3543. [Google Scholar] [CrossRef] [Green Version]
- Muhammad, S.; Jar, P.-Y.B. Determining Stress–Strain Relationship for Necking in Polymers Based on Macro Deformation Behavior. Finite Elem. Anal. Des. 2013, 70–71, 36–43. [Google Scholar] [CrossRef]







| FE Model | PE Pipe under Strike-Slip Fault | |||||
|---|---|---|---|---|---|---|
| Fault Moving Speed (mm/Min) | 1 | 100 | 200 | 300 | ||
| Equation (1a) | εy | 0.01 | 0.005 | 0.005 | 0.005 | |
| E (MPa) | 900 | 1200 | 1500 | 1800 | ||
| ν | 0.4 | 0.4 | 0.4 | 0.4 | ||
| Equation (1b) | εn | 0.022 | 0.02 | 0.04 | 0.03 | |
| a | 9.9 | 21 | 69 | 98 | ||
| b | 0.057 | 0.025 | 0.008 | 0.0039 | ||
| c | 0.05 | 0.05 | 0.005 | 0.001 | ||
| d | −23.8 | −23.8 | −23.8 | −23.8 | ||
| e | 15.5 | 15.5 | 18 | 33 | ||
| Equation (1c) | εt | 0.3 | 0.3 | 0.3 | 0.3 | |
| αk | 14.52 | 18.1 | 80.3 | 87 | ||
| N | 0.12 | 0.07 | 0.26 | 0.16 | ||
| Equation (1d) | Section 1 | εt1 | 0.6 | 0.6 | 0.8 | 0.8 |
| K1 | 11.7 | 15.6 | 53.5 | 65.6 | ||
| M1 | 0.68 | 0.59 | 0.8 | 0.8 | ||
| β1 | 1.8 | 1.8 | 1.8 | 1.8 | ||
| Section 2 | εt2 | 0.8 | 0.8 | 1.0 | 1.0 | |
| K2 | 11.6 | 14.6 | 57.5 | 71 | ||
| M2 | 0.72 | 0.71 | 0.69 | 0.68 | ||
| β2 | 1.8 | 1.8 | 1.8 | 1.8 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Qiao, L.; Fan, J.; Zhang, Y. Mechanical Behavior of Polyethylene Pipes under Strike-Slip Fault Movements. Polymers 2022, 14, 987. https://doi.org/10.3390/polym14050987
Li L, Qiao L, Fan J, Zhang Y. Mechanical Behavior of Polyethylene Pipes under Strike-Slip Fault Movements. Polymers. 2022; 14(5):987. https://doi.org/10.3390/polym14050987
Chicago/Turabian StyleLi, Lin, Liang Qiao, Junming Fan, and Yi Zhang. 2022. "Mechanical Behavior of Polyethylene Pipes under Strike-Slip Fault Movements" Polymers 14, no. 5: 987. https://doi.org/10.3390/polym14050987
APA StyleLi, L., Qiao, L., Fan, J., & Zhang, Y. (2022). Mechanical Behavior of Polyethylene Pipes under Strike-Slip Fault Movements. Polymers, 14(5), 987. https://doi.org/10.3390/polym14050987





