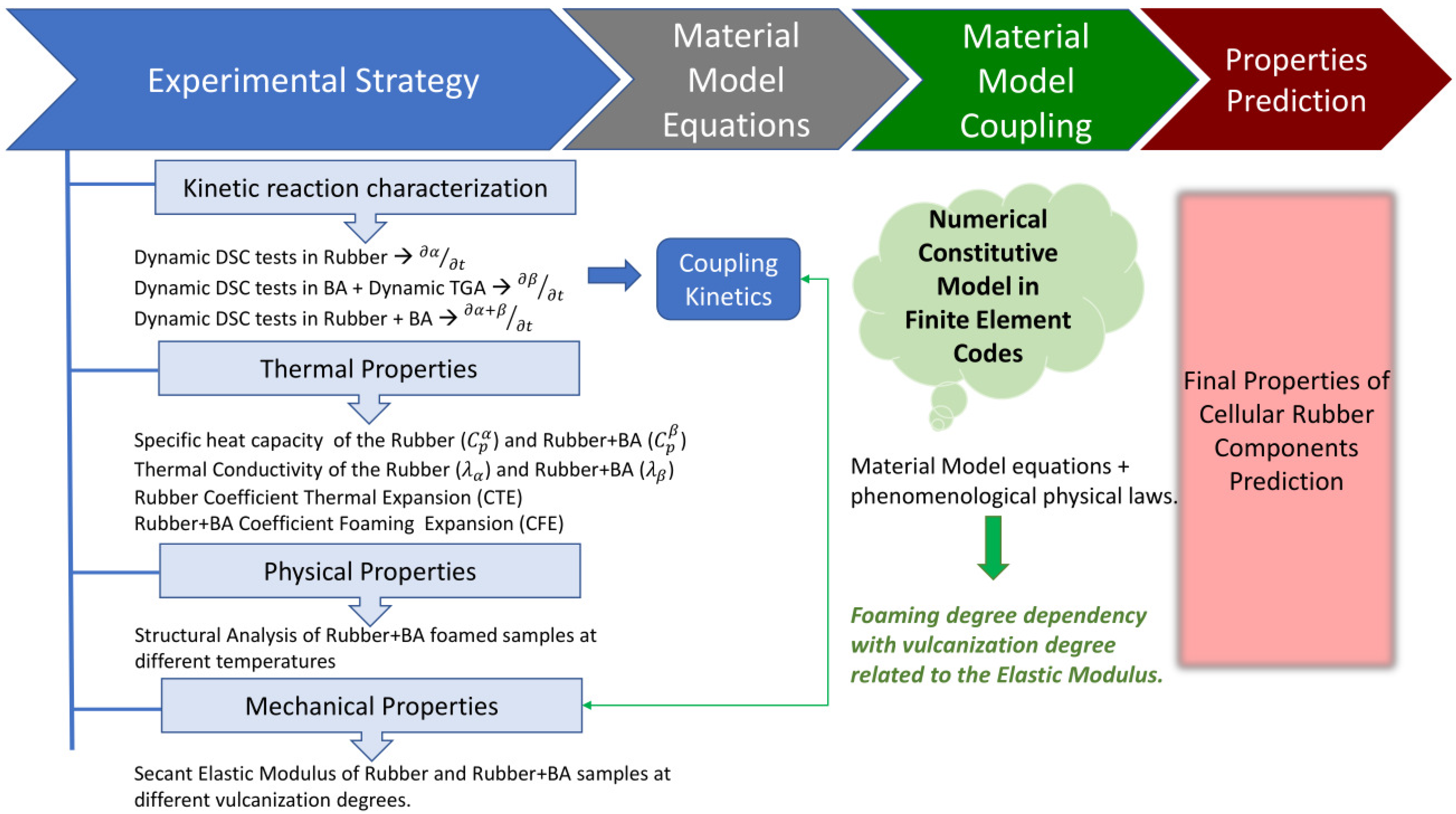
This section details the experimental strategy designed to obtain results for modelling the parameters involved in the vulcanization and foaming processes of the rubber+BA used in this study.
3.1. Vulcanization Reaction
DSC measurements at a constant temperature rate are carried out to obtain the energy necessary to achieve a complete vulcanization reaction and the vulcanization degree of dependence with time. These dynamic DSC tests are performed according to ISO 11357-1 recommendations with a Perkin Elmer DSC6 device. A nitrogen flow rate of about 50 mL/min passes through the cell and an empty pan is used as the reference material. The mass of the sample is between 35 and 40 mg. Three different heating rates are used for the dynamic measurements: 7, 10 and 20 °C/min and the temperature is controlled in the range from 10 °C to 260 °C.
Figure 2 shows that as the heating rate increases the vulcanization temperature peak moves to higher temperatures from 183.29 °C at 7 °C/min to 197.25 °C at 20 °C/min. The exothermic enthalpy related to the vulcanization is obtained from the area enclosed between the first and the second heating step (once the rubber is completely vulcanized) of the DSC thermogram represented in function of time instead of temperature. Thus, the vulcanization enthalpy obtained is between 4–5 J/g.
The vulcanization mechanism of an EPDM rubber consists of a series of parallel and sequential reactions, and, by assuming that the heat generated during the process is only due to the crosslinking reaction, the rubber vulcanization degree and vulcanization kinetic can be determined by means of a DSC test. This technique is especially appropriate due to its high sensitivity in heat determination and the small sample size required [
16]. Curing rubber state can be obtained as the ratio of the instantaneous heat and the total heat of the reaction [
2,
14] in an equivalent way to that described in the standard ISO 11357-5. The heat generation associated with the vulcanization degree,
, that indicates the degree (from 0 to 1) of completion of the vulcanization reaction, is then modeled according to Equation (
1):
where
is the total heat of the reaction associated with the rubber, in W/m
3 and
is the vulcanization kinetic.
The vulcanization kinetic is commonly defined as a Kamal–Sourour semi-empirical auto-catalytic reaction model [
17,
18]. In this work, this model is modified as follows:
where
is the vulcanization degree (dimensionless),
m and
n are the reaction orders,
is the additional parameter to lock the maximum value of
and
K coefficients are defined in Arrhenius-type temperature dependence:
where
E is the activation energy in J × mol
−1, A is the pre-exponential factor, R the universal gas constant in J × mol
−1 × K
−1 and
T is the absolute temperature in Kelvin.
3.2. Foaming and Foaming Evolution Reaction
Dynamic DSC tests are performed on BA material to determine the decomposition reaction as a function of temperature [
2,
14] with independence of its combination with rubber. For this purpose, a power compensation Perkin Elmer DSC Diamond instrument is used. The BA reaction is extremely fast, and a power compensation DSC provides better resolution for sharp events. The DSC is operated with a nitrogen flow rate of about 50 mL/min through the cell and an empty pan is used as the reference material. The mass of the sample is between 5 and 6 mg and the temperature change is controlled from 10 °C to 220 °C at 2.5, 5, 7 and 10 °C/min.
Dynamic DSC results in
Figure 3 show two decomposition peaks of the BA. The first one, much smaller, appears at around 135–150 °C and generates an insignificant enthalpy energy of 5–6 J/g. The second one, which begins to arise from 150 °C at the minimum heating rate of 2.5 °C/min, reaches its maximum decomposition reaction rate at 163.44 °C. The peak temperature at the different heating rates of this second decomposition is included in
Table 1. The second exothermic peak, at higher heating rates, is sharper and appears in a narrower range of the reaction duration, i.e., between the beginning and the end of the reaction there is only 10–20 °C, which would suggests that the reaction is almost explosive. As the heating rate increases, the exothermic reaction takes place at higher temperatures. Please note that at 10 °C/min the DSC device is not able to record accurately the variation in the heat flow (see
Figure 3b, green line). This fact can be recognized in the lower enthalpy value (432.96 J/g) obtained at 10 °C/min (see
Table 1) compared with the enthalpy value obtained at 7 °C/min. The enthalpy associated with the exothermic decomposition reaction of the BA corresponds to the area enclosed by the peak curve of the DSC thermogram represented in function of time instead of temperature, which includes the total energy of both peaks. Therefore, the enthalpy of decomposition reaction selected corresponds with the maximum value obtained of 511.93 J/g (being 5.37 J/g the enthalpy of the first peak and 506.56 J/g the one of the second peak).
The exothermic foaming process and the heat generation rate to be included in the numerical model is defined by Equation (
4):
where
is the total heat of the reaction associated with the foaming agent or BA, expressed in W/m
3 and
is the foaming kinetic,
being the foaming degree ranging from 0 to 1, when the foaming reaction is complete.
The foaming reaction can be, as in the case of the vulcanization reaction, defined by the Kamal–Sourour model:
where
is the foaming degree (dimensionless),
m and
n are the reaction orders,
is the additional parameter to lock the maximum
reachable and
are defined in Arrhenius-type temperature dependence in the form of Equation (
2).
After the decomposition reaction of the BA, a residue remains in the pan. Consequently, the change in mass during the decomposition reaction is measured using a Perkin Elmer thermogravimetric analyzer (TGA). This device detects the mass loss with a resolution of 0.1 μg as a function of the temperature. The samples are evenly and loosely distributed in an open sample pan with an initial weight of 10–11 mg. The BA powder is heated at two different heating rates of 5 °C/min and 10 °C/min from 30 °C to 600 °C in a nitrogen atmosphere, which passes continuously through into the furnace at a flow rate of 50 mL/min.
Figure 4 presents the thermogravimetric decomposition process of the BA. The decomposition reaction of the BA occurs abruptly in the range from 150 °C to 190 °C, where the slope of the weight curve resulting from the TGA experiment, expressed as the weight loss in percentage regarding the initial BA weight introduced in the pan, is more pronounced. Approximately only the 30–33% of the BA material decomposes and almost of 67–69% of the initial weight remains in the pan as residue. The maximum decomposition reaction takes place at 168.98 °C and 173.16 °C at 5 °C/min and 10 °C/min, respectively, according the derivative weight curve. The peak temperatures are extremely close to those obtained in the DSC tests performed in BA samples at both heating rates, despite using two different measuring devices. This fact shows the robustness and reproducibility of the BA decomposition results.
3.3. Rubber Coupled Vulcanization-Foaming Kinetics
Dynamic DSC tests are performed in the rubber+BA to determine and confirm whether the BA decomposition reaction and/or rubber curing is affected by the presence of one or both [
2,
4,
14].
DSC tests are conducted in a Perkin Elmer DSC6 instrument using empty pans for the reference material and rubber+BA samples following the same procedure as already explained for the rubber (see
Section 3.1). The mass of the sample is between 35 and 40 mg. Four different heating rates are used for the dynamic measurements: 5, 7, 10 and 20 °C/min. The temperature change is controlled from 10 °C to 260 °C. A high-purity nitrogen stream passes continuously through into the furnace at a flow rate of 50 mL/min. DSC thermogram curves resulting from these measurements are depicted in
Figure 5.
Table 2 shows numerical values for enthalpy and predominant peak temperature (T peak) for the rubber+BA sample at the different heating rates, but a second peak can also be appreciated at higher temperatures; both peaks are tagged in
Figure 5 in a DSC curve at 20 °C/min but they appear at the different heating rates tested. Attending to the T peak values, the foaming-vulcanization reaction moves to lower temperatures with respect to the vulcanization and foaming reactions separately (
Figure 2 and
Figure 3, respectively).
The DSC results for the vulcanization and foaming reactions and for the coupled one are compared in terms of the kinetic reaction rate. The comparison for the case of 10 °C/min is shown in
Figure 6, being similar for the rest of conditions. The kinetic reaction rate is defined as the vulcanization or foaming degree rate scaled by the enthalpy of the reaction and the mass fraction of each material that are included in the elastomer compound. For the specific case of the rubber+BA, the experimental coupled kinetic reaction rate (green curve in
Figure 6) should result from Equation (
6):
where
is the rubber mass fraction present in the elastomer compound,
is the quantity of BA in mass fraction added to the rubber,
is the coupled vulcanization-foaming reaction rate,
is the rubber vulcanization reaction rate and
is the BA reaction rate,
corresponds to the enthalpy value obtained for the rubber in
Section 3.1,
is the foaming enthalpy from
Table 1 in
Section 3.2 and
is the coupling enthalpy obtained in this Section.
In this compound, only a small percentage of BA is mixed with the rubber, approximately 1–3% in weight (
). Therefore, the rubber mass fraction in the elastomer compound is
= 1 −
. When the BA is mixed with the rubber, an exothermic peak composed of the overlapping of two exothermic peaks can be observed in the green curve of the
Figure 6 for the rubber+BA, one corresponding to the BA reaction at approximately 155–160 °C and the second one to the rubber vulcanization reaction at approximately 190–195 °C (see
Figure 5). The second peak of the rubber+BA sample represented in the green curve in
Figure 6 fits perfectly with the reaction of the rubber (blue curve) in the same figure. However, the first peak is completely different from the reaction of the isolated BA (compare the green curve with the yellow one in
Figure 6). The BA decomposition reaction is produced at lower temperatures when it is mixed with the rubber, and its kinetic reaction rate is completely different from the kinetic observed in the decomposition reaction when it is alone. Therefore, it is assumed that the vulcanization process is not affected by the addition of BA and the vulcanization kinetic can be directly obtained from the experimental data presented in
Section 3.1. Furthermore, to obtain the foaming rate
, it is considered that the heat generated from the foaming reaction (called
in
Figure 6) is the difference of the heat produced in the coupled vulcanization and foaming reactions and the rubber vulcanization heat obtained at the same test conditions.
Once the data are in the format of foaming rate
vs temperature for each heating rate, the parameters of the kinetic reaction for the foaming mechanism in Equation (
5) are obtained by solving a non-linear least-square problem.
3.6. Material Model Coupling
The previous characterization is used to develop a numerical material model able to reproduce the vulcanization and foaming behaviour of the rubber aimed for use in FE codes. As demonstrated by experimental evidence in former sections, the model must include the coupling of the different fields: chemical (vulcanization and foaming kinetics), thermal and mechanical.
The proposed model includes the equations that are defined in previous sections for the individual behaviour of each material property. However, the interaction between the vulcanization and foaming reactions themselves and with other elastomer properties must be also taken into account, as explained in
Section 1.3 and
Section 3.3.
The foaming process is, essentially, a bubble growth process. This bubble growth mechanism has been introduced in the literature by several authors [
10,
11,
12,
13], its fundamental principle being coupled mass and momentum conservation. In the literature, it is normally defined in terms of viscosity, surface tension and pressure inside the bubble [
13]. However, this paper approaches the foaming mechanism in a different way, since most FE codes use the displacement variable as degree of freedom (DoF) instead of velocity. For that reason, the foaming mechanism cannot be implemented as a function of viscosity, which is a velocity-dependent property, but as function of a displacement-dependent property related to the elasticity of the elastomer. In this work, the elasticity property chosen to establish this relationship is the elastic modulus. Previously, it was noticed that the secant elastic modulus at 10% strain is related to the vulcanization degree (
Figure 12). Therefore, the foaming mechanism dependence with vulcanization degree is introduced considering that bubble growth depends on viscosity through the elastic modulus of the material. As the vulcanization reaction progresses, the viscosity of the elastomer increases and so its elastic modulus does. Hence, we propose to introduce the dependency between the foaming and vulcanization degrees using a function
inside Equation (
5), which allows the consideration of the dependence of the vulcanization and foaming degree with the elasticity (elastic modulus) of the elastomer. This function is proposed as stated by Equation (
23):
where
h is a parameter calculated from the fitting of an exponential equation for the data in
Figure 12, expressed as
.
This model, called from this point onwards the initial model, is proved for the test of rubber+BA in
Section 3.4.3 (
Figure 11). A comparison is made in terms of strain,
, or equivalent elastomer thickness expansion,
, which depends on the rubber thermal expansion and the thickness increase produced due to the foaming reaction. Then, the strain can be computed through Equation (
24).
The results from the comparison between the model and test results are shown in
Figure 16a. The parameters used for this model are summarized in
Table 4 (the authors remark that
is expressed as a function of the instantaneous density of the rubber+BA,
).
As can be concluded from
Figure 16a, this model is able to reproduce neither the measured behaviour nor the trends of the strain overtime or the maximum strain reached with the maximum temperature.
Due to the observed mismatch, a different approach is proved for modelling the foaming mechanism in the rubber+BA. For this purpose, the Equation (
5) is replaced by an approach given by Wang et al. [
13] with minor changes. The amount of gas evolved is expressed with Equation (
25) and the amount of bubble volume is expressed according to Equation (
26).
where
N is the quantity of BA in moles of the total amount introduced that in fact decomposes or reacts,
is the initial amount of BA, and
and
E are parameters of the Arrhenius-type equation.
where
V is the volume of bubbles in m
3,
is the viscosity in N × s/m
2 and
is the pressure far from the bubble in Pascals. Both the rubber viscosity and the bubble pressure depend on the vulcanization degree, and they are considered in the model by means of two linear regression Equations (
27) and (
28).
where
is the value that takes
when the rubber is uncured, and
is the slope of the linear regression.
where
is the value that takes
when the rubber is uncured and
is the slope of the linear regression.
In this case, the strain is calculated according to Equation (
29).
The model is implemented using Jupyter notebooks to analyze the effects of some parameters such as
,
,
,
,
,
and
E. There are multiple combinations of parameters available to capture the experimental behaviour. One of the best fits is shown in
Figure 16b. The ‘relaxing’ effect observed in the test can be introduced by means of Equations (
27) and (
28); however, the Wang model is not able to capture the behaviour observed experimentally.
Then, a combination of both approaches, called the Wang–Beta model, is implemented. The foaming law is obtained using Equation (
5) without the function
and the volume of bubbles with Equation (
26), with
. Parameters for the best fit are searched for with Jupyter notebooks, resulting in the one shown in
Figure 16c. Although this model reproduces a global trend, the maximal strain rate observed in the experimental test is reached at a lower temperature in comparison with the model in which it is reached at higher temperature. Additionally, the maximum strain predicted by the model for the case of 140 °C is significantly higher than the one expected according to the experimental measurements. Both facts leave room for model improvement.
For this purpose, a new model based on the Wang–Beta model with a change in the value of the parameter
E of term
in Equations (
2) and (
5) is implemented to prove its predictive goodness. Hence, the values stated for the Wang–Beta model with the variable of the parameter
E are compiled in
Table 5 and results are depicted in
Figure 16d. The best approximation to the experimental results are obtained considering the bubble volume and the amount of gas evolved in the foaming reaction in combination with Equation (
2) for the foaming kinetic and fitting parameter E in the best way, changing the term
in Equations (
2) and (
5).
The Wang–Beta model with modified E-parameter significantly improves the prediction of the experimental measurements of the thickness expansion (
, also referred as “strain” in
Figure 16) since it is able to catch main tendencies as well as the dependency between the maximum temperature and strain. It must be highlighted that this rheometer experiment is a specific case in which the heating mechanism is generated mainly by conductive heat transference, while the model was fitted with experimental data from a DSC experiment, where the heating mechanism is mainly governed by convective heat transference. The different heating mechanisms in the rheometer and the DSC device can impact the accuracy of the developed model, but does not make invalid its prediction capability, which in fact is very significant.
Moreover, the material model is defined from an analytical model, which considers material behaviour to be isotropic, i.e., the model does not take into account any specific dimension, just one, while conducted experiments are three-dimensional, since properties in real samples are measured. This fact, far from being a drawback, makes the developed model even more powerful for its practical application, since, despite being a source of inaccuracy, it seems not to be so outstanding when observing the obtained results.