Investigation of the Polymer Coextrusion Process: A Review
Abstract
:1. The Coextrusion Processes: Interest, Technology and Limiting Problems
1.1. The Different Coextrusion Processes
1.2. Problems Encountered
1.3. Coextrusion Modeling: A Tool for Understanding the Process
2. Poiseuille Coextrusion Flow
2.1. Stationary Isothermal Coextrusion Flow of Two Newtonian Fluids
2.2. Generalization to Shear-Thinning Polymer Fluids
2.3. Transitory Phenomena at the Coextrusion Die Inlet
3. Miscellaneous Applications of Poiseuille Coextrusion Computations
3.1. Multilayer Non-Isothermal Coextrusion Flows
3.2. Investigation of Coextrusion Instabilities
- (a)
- Asymptotic stability analysis
- (b)
- Convective Stability Analysis
- (c)
- Direct Numerical Modeling
4. Coextrusion in a Coat-Hanger Die
4.1. Bilayer 2D Coextrusion Flow
4.2. Comparison with Experiments
5. Encapsulation in Coextrusion
5.1. Experiments
5.2. Modeling
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pinsolle, F. Coextrusion de feuilles et de plaques. Tech. De L’ingénieur 2010, AM3659. [Google Scholar] [CrossRef]
- Agassant, J.F.; Avenas, P.; Carreau, P.J.; Vergnes, B.; Vincent, M. Polymer Processing: Principles and Modeling; Hanser: Munich, Germany, 2017. [Google Scholar]
- Agassant, J.F.; Fortin, A.; Demay, Y. Prediction of stationary interfaces in coextrusion flows. Polym. Eng. Sci. 1994, 34, 1101–1108. [Google Scholar] [CrossRef]
- Puissant, S. Lignes d’extrusion de tubes, Etapes de Fabrication. Tech. De L’ingénieur 2009, AM 3642. [Google Scholar] [CrossRef]
- Mauffrey, J. Etude Numérique et Expérimentale du Phénomène D’enrobage Dans les Écoulements de Coextrusion. Ph.D. Thesis, Ecole des Mines de Paris, Paris, France, 2000. [Google Scholar]
- Han, C.D.; Shetty, R. Studies of multilayer flat film coextrusion 1: The rheology of flat film coextrusion. Polym. Eng. Sci. 1976, 16, 697–705. [Google Scholar] [CrossRef]
- Han, C.D.; Shetty, R. Studies on multilayer film coextrusion II: Interfacial instability in flat film coextrusion. Polym. Eng. Sci. 1978, 18, 180–186. [Google Scholar] [CrossRef]
- Han, C.D.; Chin, H.B. Theoretical prediction of the pressure gradients in coextrusion of non-Newtonian fluids. Polym. Eng. Sci. 1979, 19, 1156–1162. [Google Scholar] [CrossRef]
- Nordberg, M.E., III; Winter, H.H. Fully developed multilayer polymer flows in slits and annuli. Polym. Eng. Sci. 1988, 28, 444–452. [Google Scholar] [CrossRef]
- Uhland, E. Stratified two phase flow of molten polymers in circular dies. Polym. Eng. Sci. 1977, 17, 671–681. [Google Scholar] [CrossRef]
- Basu, S. A theoretical analysis of non-isothermal flow in wire coating coextrusion dies. Polym. Eng. Sci. 1981, 21, 1128–1138. [Google Scholar] [CrossRef]
- Sornberger, G.; Vergnes, B.; Agassant, J.F. Coextrusion flow of two molten polymers between parallel plates: Non-isothermal computation and experimental study. Polym. Eng. Sci. 1986, 26, 682–689. [Google Scholar] [CrossRef]
- Strauch, T. Ein Beitrag zur Rheologischen Auslegung von Coextrusionwerzeugen; PhD, I.K.V.; RWTH: Aachen, Germany, 1986. [Google Scholar]
- Puissant, S. Etude Numérique et Expérimentale de la Coextrusion des Polymères dans une Filière Plate. Ph.D. Thesis, Ecole des Mines de Paris, Paris, France, 1992. [Google Scholar]
- Puissant, S.; Vergnes, B.; Demay, Y.; Agassant, J.F. A general non-isothermal model for one-dimensional multilayer coextrusion flow. Polym. Eng. Sci. 1992, 32, 213–220. [Google Scholar] [CrossRef]
- Sornberger, G. La Coextrusion en Filière Plate: Etude théorique et Expérimentale de L’écoulement en Filière Plate. Ph.D. Thesis, Ecole des Mines de Paris, Paris, France, 1985. [Google Scholar]
- Carreau, P.J. Rheological equations from molecular network theories. Trans. Soc. Rheo. 1972, 16, 99–127. [Google Scholar] [CrossRef]
- Everage, A.E. Theory of stratified bicomponent flow of polymer melts; II Interface motion in transient flow. Trans. Soc. Rheol. 1975, 19, 509–522. [Google Scholar] [CrossRef]
- White, J.L.; Lee, B.L. Theory of interface distortion in stratified two-phase flow. Trans. Soc. Rheol. 1975, 19, 457–479. [Google Scholar] [CrossRef]
- Fortin, A.; Demay, Y.; Agassant, J.F. Computation of stationary interfaces between generalized Newton fluids. J. Eur. Elem. Finis 1992, 1, 191–196. [Google Scholar]
- Han, C.D.; Kim, Y.J.; Chin, H.B. Rheological investigation of interfacial instability in two-layer flat-film coextrusion. Polym. Eng. Rev. 1984, 4, 177–217. [Google Scholar] [CrossRef]
- Schrenk, W.J.; Bradley, N.L.; Alfrey, T.; Maack, H. Interfacial flow instability in multilayer coextrusion. Polym. Eng. Sci. 1978, 18, 620–623. [Google Scholar] [CrossRef]
- Agassant, J.F.; Arda, D.; Combeaud, C.; Merten, A.; Münstedt, H.; Mackley, M.R.; Robert, L.; Vergnes, B. Polymer processing extrusion instabilities and methods for their elimination or minimisation. Int. Polym. Process. 2006, 21, 239–255. [Google Scholar] [CrossRef] [Green Version]
- Southern, J.H.; Ballmann, R.L. Stratified bicomponent flow of molten polymers in a tube. Appl. Polym. Sci. 1973, 20, 175–189. [Google Scholar]
- Southern, J.H.; Ballmann, R.L. Additional observations on stratified bicomponent flow of polymer melts in a tube. J. Polym. Sci. Polym. Phys. Ed. 1975, 13, 863–869. [Google Scholar] [CrossRef]
- Wilson, G.M.; Khomani, B. An experimental investigation of interfacial instabilities in multilayer flow of viscoelastic fluids; Part I: Incompatible polymer systems. J. Non-Newtonian Fluid Mech. 1992, 45, 355–384. [Google Scholar] [CrossRef]
- Khomami, B.; Ranjbaran, M.M. Experimental studies of interfacial instabilities in multilayer pressure-driven flow of polymeric melts. Rheol. Acta 1997, 36, 345–366. [Google Scholar] [CrossRef]
- Valette, R.; Laure, P.; Demay, Y.; Agassant, J.F. Experimental investigation of the development of interfacial instabilities in two-layer coextrusion flow. Int. Polym. Process. 2004, 19, 118–128. [Google Scholar] [CrossRef]
- Chen, K.P. Interfacial instability due to elastic stratification in concentric coextrusion of two viscoelastic fluids. J. Non-Newtonian. Fluid Mech. 1991, 40, 155–175. [Google Scholar] [CrossRef]
- Su, Y.Y.; Khomani, B. Interfacial stability of multilayer viscoelastic fluids in slit and converging channel dies geometries. J. Rheol. 1992, 36, 357–387. [Google Scholar] [CrossRef]
- Laure, P.; Le Meur, H.; Demay, Y.; Saut, J.C. Linear stability of multilayer plane Poiseuille flows of Oldroyd-B fluid. J. Non-Newtonian Fluid Mech. 1997, 71, 1–23. [Google Scholar] [CrossRef]
- Valette, R.; Laure, P.; Demay, Y.; Fortin, A. Convective instabilities in coextrusion process. Int. Polym. Process. 2001, 16, 192–197. [Google Scholar] [CrossRef]
- Ganpule, H.K.; Khomami, B. An investigation of interfacial instabilities in the superposed channel flow of viscoelastic fluids. J. Non-Newtonian Fluid Mech. 1999, 81, 27–69. [Google Scholar] [CrossRef]
- Valette, R.; Laure, P.; Demay, Y.; Agassant, J.F. Convective linear stability analysis of two-layer coextrusion flow for molten polymers. J. Non-Newtonian Fluid Mech. 2004, 121, 41–53. [Google Scholar] [CrossRef]
- Valette, R. Etude de la Stabilité de L’écoulement de Poiseuille de Fluides Viscoélastiques. Application au Procédé de Coextrusion des Polymères. Ph.D. Thesis, Ecole des Mines de Paris, Paris, France, 2001. [Google Scholar]
- Yamaguchi, H.; Mishima, A.; Yasumoto, T.; Ishikawa, T. An arbitrary Lagrangian-Eulerian approach for simulating viscoelastic fluids. J. Non-Newtonian Fluid Mech. 1999, 80, 251–272. [Google Scholar] [CrossRef]
- Zatloukal, M.; Tzoganakis, C.; Vleck, J.; Saha, P. Numerical simulation of polymer coextrusion flows. Int. Polym. Process. 2001, 16, 198–207. [Google Scholar] [CrossRef]
- Mahdaoui, O.; Laure, P.; Agassant, J.F. Numerical investigations of polyester coextrusion instabilities. J. Non-Newtonian Fluid Mech. 2013, 195, 67–76. [Google Scholar] [CrossRef] [Green Version]
- Sornberger, G.; Vergnes, B.; Agassant, J.F. Two directional coextrusion flow of two molten polymers in flat dies. Polym. Eng. Sci. 1986, 26, 451–457. [Google Scholar] [CrossRef]
- Puissant, S.; Demay, Y.; Vergnes, B.; Agassant, J.F. Two dimensional multilayer coextrusion flow in a coat-hanger die. Part 1: Modeling. Polym. Eng. Sci. 1994, 34, 201–208. [Google Scholar] [CrossRef]
- Puissant, S.; Vergnes, B.; Demay, Y.; Agassant, J.F.; Labaig, J.J. Two-dimensional multilayer coextrusion flow in a flat coat-hanger die. Part 2: Experimentation and theoretical validation. Polym. Eng. Sci. 1996, 36, 936–942. [Google Scholar] [CrossRef]
- Minagawa, N.; White, J.L. Co-extrusion of unfilled and TiO2-filled polyethylene: Influence of viscosity and die cross-section on interface shape. Polym. Eng. Sci. 1975, 15, 825–830. [Google Scholar] [CrossRef]
- Han, C.D. Multiphase Flow in Polymer Processing; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Teixera-Pires, J. Etude Expérimentale et Numérique du Phénomène D’enrobage Dans les Écoulements de Coextrusion. Ph.D. Thesis, Ecole des Mines de Paris, Paris, France, 1996. [Google Scholar]
- Anderson, P.D.; Dooley, J.; Meijer, H.E.H. Viscoelastic effects in multilayer polymer extrusion. Appl. Rheol. 2006, 16, 198–205. [Google Scholar] [CrossRef]
- Dooley, J.; Hyun, K.S.; Hughes, K. An experimental study on the effect of polymer viscoelasticity on layer rearrangement in coextruded structures. Polym. Eng. Sci. 1998, 38, 1060–1071. [Google Scholar] [CrossRef]
- Borzacchiello, D.; Leriche, E.; Blottière, B. On the mechanism of viscoelastic encapsulation of fluid layers in polymer coextrusion. J. Rheol. 2014, 58, 493–512. [Google Scholar] [CrossRef]
- Korteweg, D. On a general theorem of the stability of the motion of a viscous fluid, London, Edinburg, Dublin. Philos. J. Sci. 1883, 16, 112. [Google Scholar]
- Han, C.D. A study of coextrusion in a circular die. J. Appl. Polym. Sci. 1975, 19, 1875–1883. [Google Scholar] [CrossRef]
- Léger, L.; Hervet, H.; Massey, G. Slip at the wall. In Rheology for Polymer Processing; Piau, J.M., Agassant, J.F., Eds.; Elsevier: Amsterdam, The Netherlands, 1996; pp. 337–355. [Google Scholar]
- Karagiannis, A.; Mavridis, H.; Htymak, A.N.; Vlachopolos, J. Interface determination in bicomponent extrusion. Polym. Eng. Sci. 1988, 28, 982–988. [Google Scholar] [CrossRef]
- Hesheng, L.; Xiaozhen, D.; Yibin, H.; Xingyuan, H.; Mengshan, L. Three-dimensional viscoelastic simulation of the effect of wall slip on encapsulation in the coextrusion process. J. Polym. Eng. 2013, 33, 625–632. [Google Scholar]
- Dooley, J.; Debbaut, B.; Avalosse, T.; Hughes, K. On the development of secondary motions in straight channels induced by the second normal stress difference: Experiments and Simulations. J. Non-Newtonian Fluid Mech. 1997, 69, 255. [Google Scholar]
- Takase, M.; Kihara, S.I.; Funatsu, K. Three-dimensional viscoelastic numerical analysis of the encapsulation phenomena in coextrusion. Rheol. Acta 1998, 37, 624–634. [Google Scholar] [CrossRef]
- Yue, P.; Zhou, C.; Dooley, J.; Feng, J.J. Elastic encapsulation in bicomponent stratified flow of viscoelastic fluids. J. Rheol. 2008, 52, 1027–1042. [Google Scholar] [CrossRef]
- Borzacchiello, D. Three-Dimensional Numerical Simulation of Encapsulation in Polymer Coextrusion. Ph.D. Thesis, Université Jean Monnet, Saint Etienne, France, 2012. [Google Scholar]
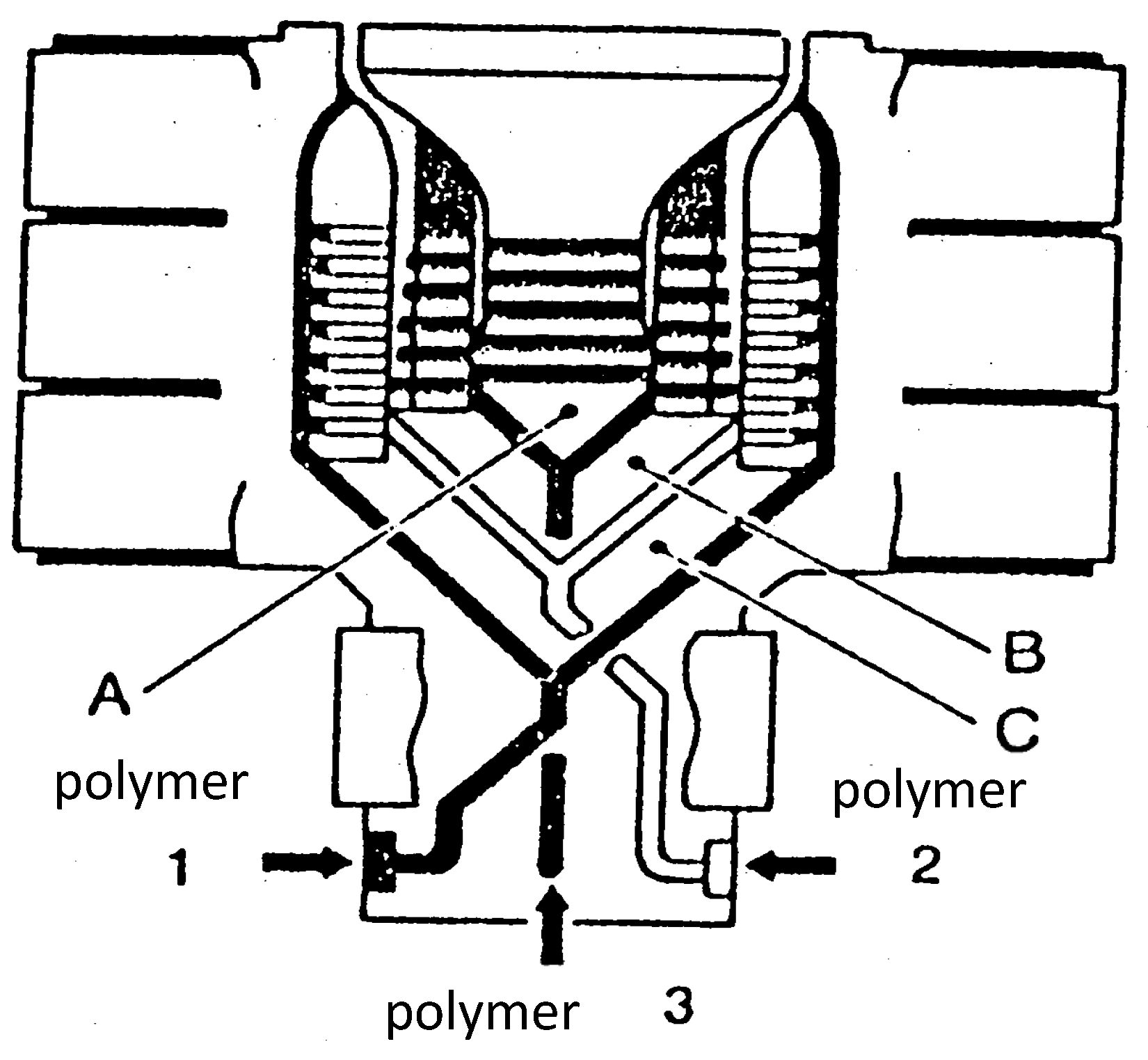









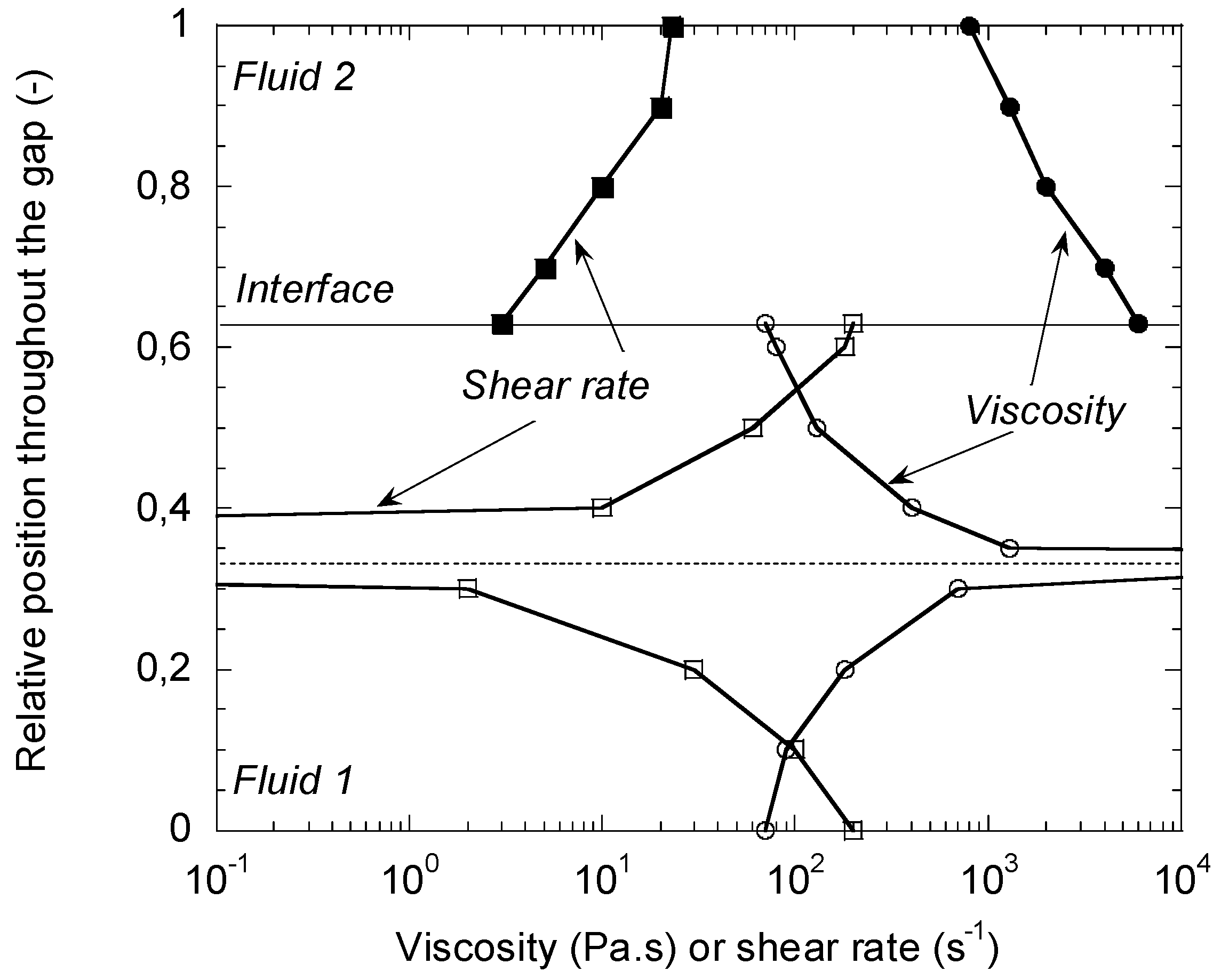



















| PS A | PS B | |
|---|---|---|
| (Pa.s) | 6750 | 6050 |
| (s) | 0.45 | 0.34 |
| m | 0.43 | 0.39 |
| a | 0.87 | 0.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agassant, J.-F.; Demay, Y. Investigation of the Polymer Coextrusion Process: A Review. Polymers 2022, 14, 1309. https://doi.org/10.3390/polym14071309
Agassant J-F, Demay Y. Investigation of the Polymer Coextrusion Process: A Review. Polymers. 2022; 14(7):1309. https://doi.org/10.3390/polym14071309
Chicago/Turabian StyleAgassant, Jean-François, and Yves Demay. 2022. "Investigation of the Polymer Coextrusion Process: A Review" Polymers 14, no. 7: 1309. https://doi.org/10.3390/polym14071309





