Soft Tissue Hybrid Model for Real-Time Simulations
Abstract
:1. Introduction
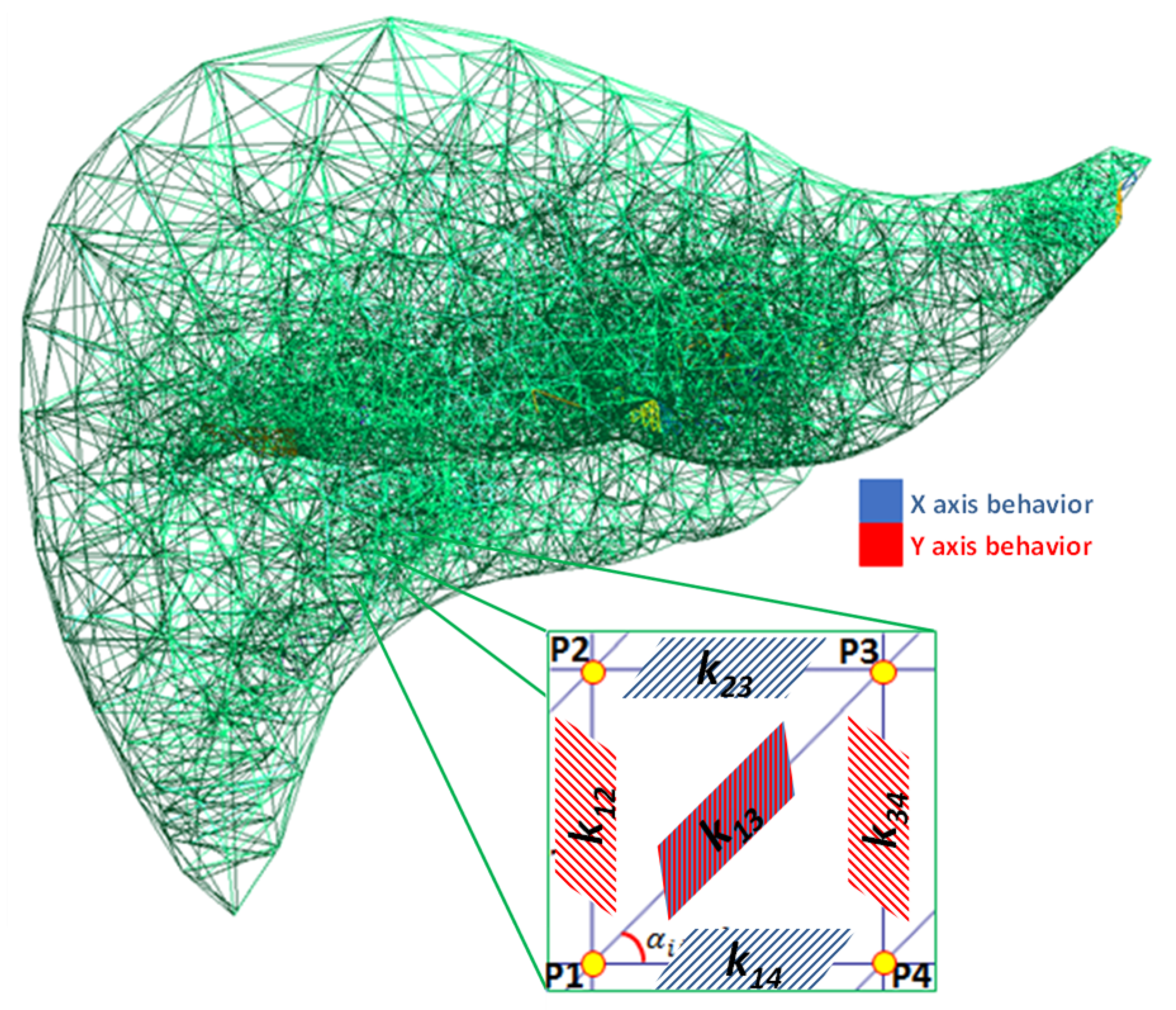
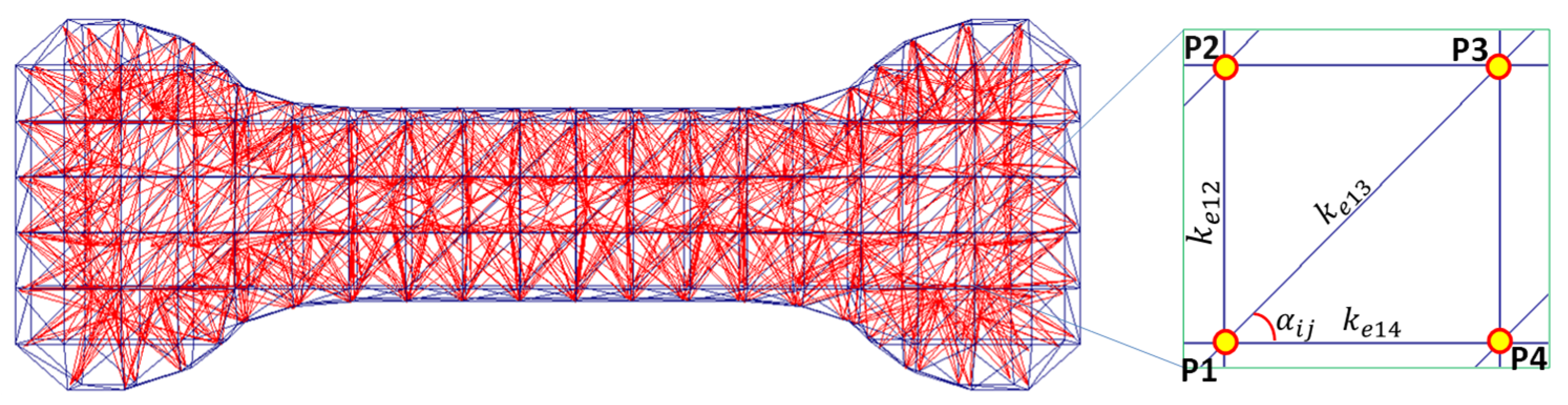
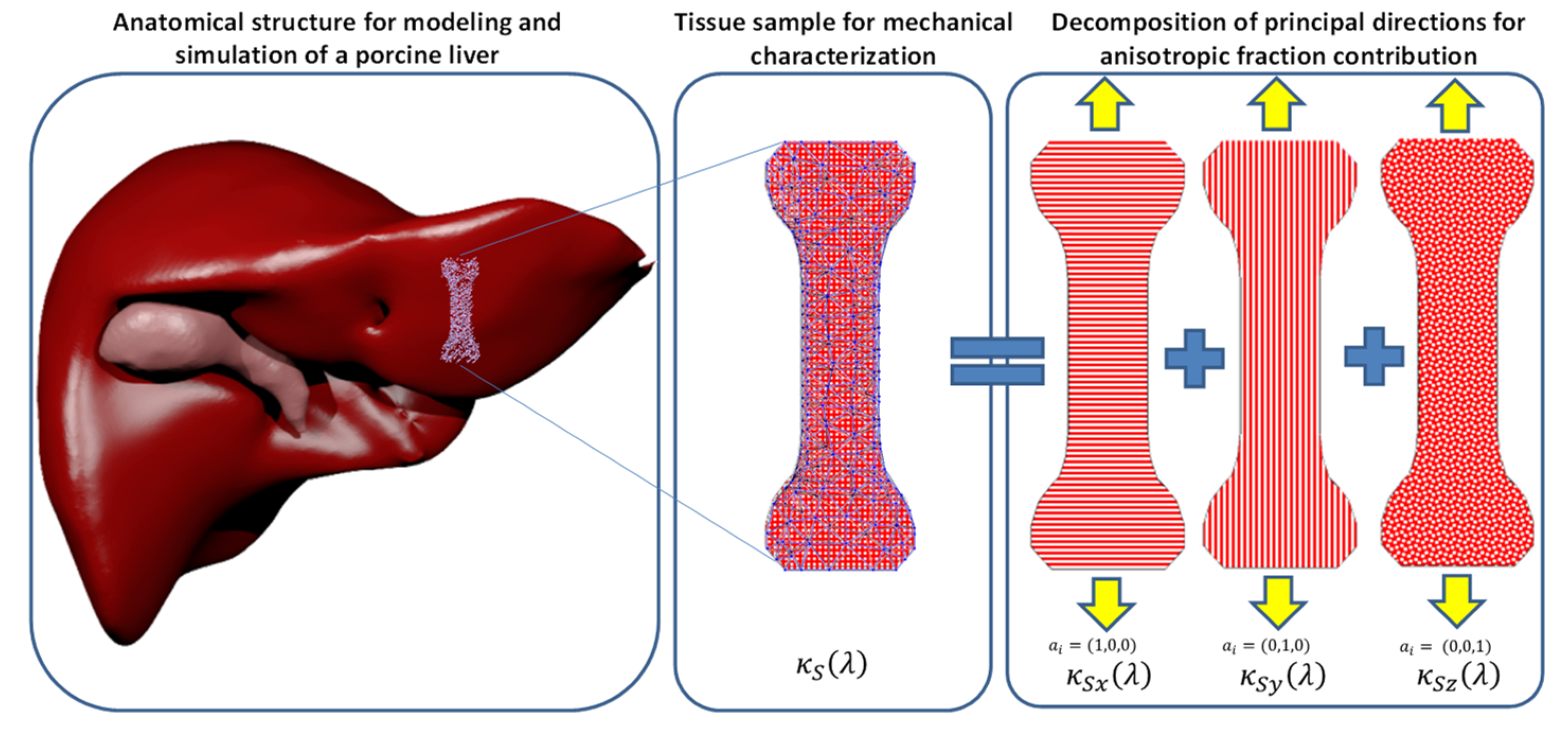
2. Hybrid Material Model
Mathematical Formulation
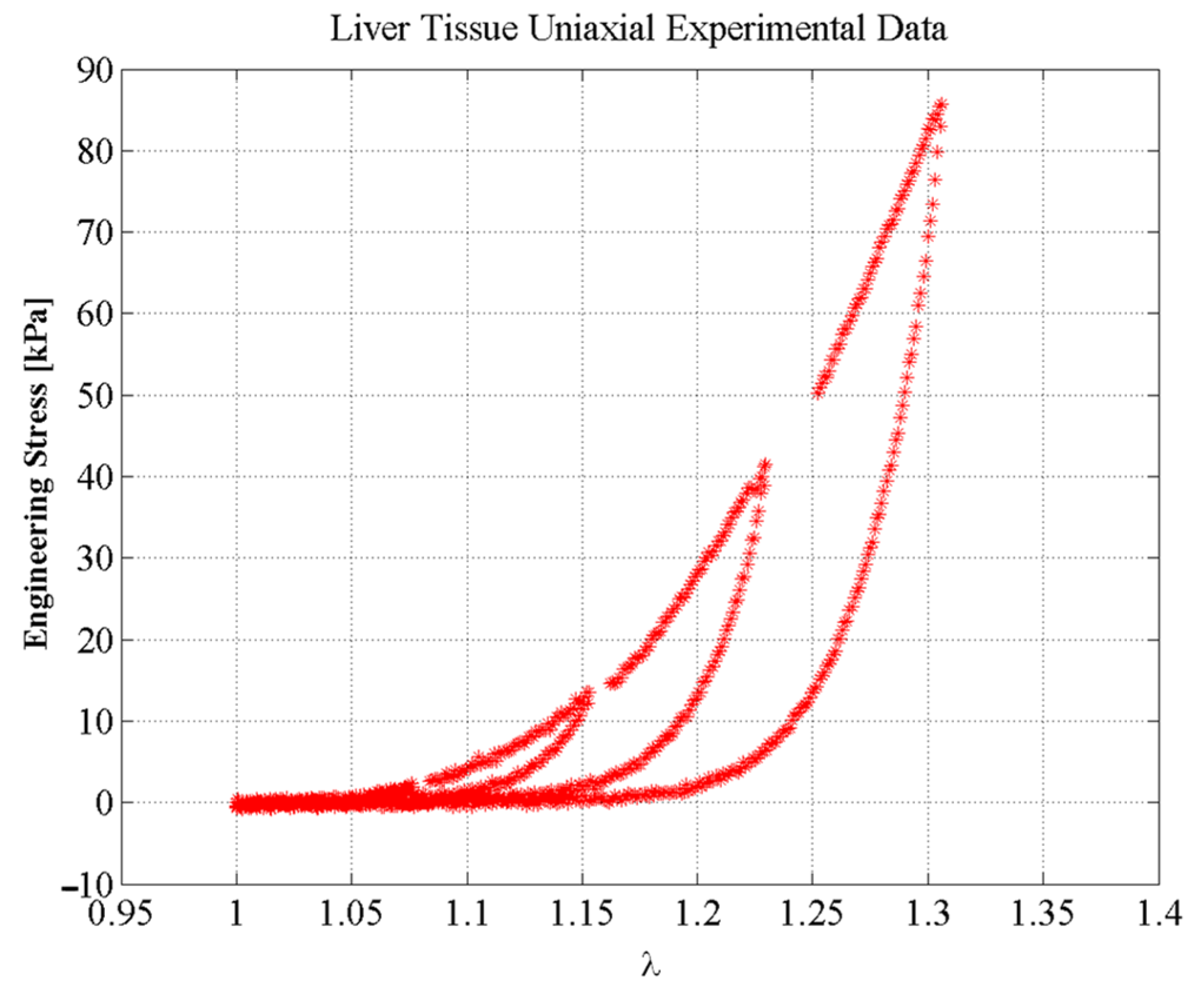
3. Experimental Tests
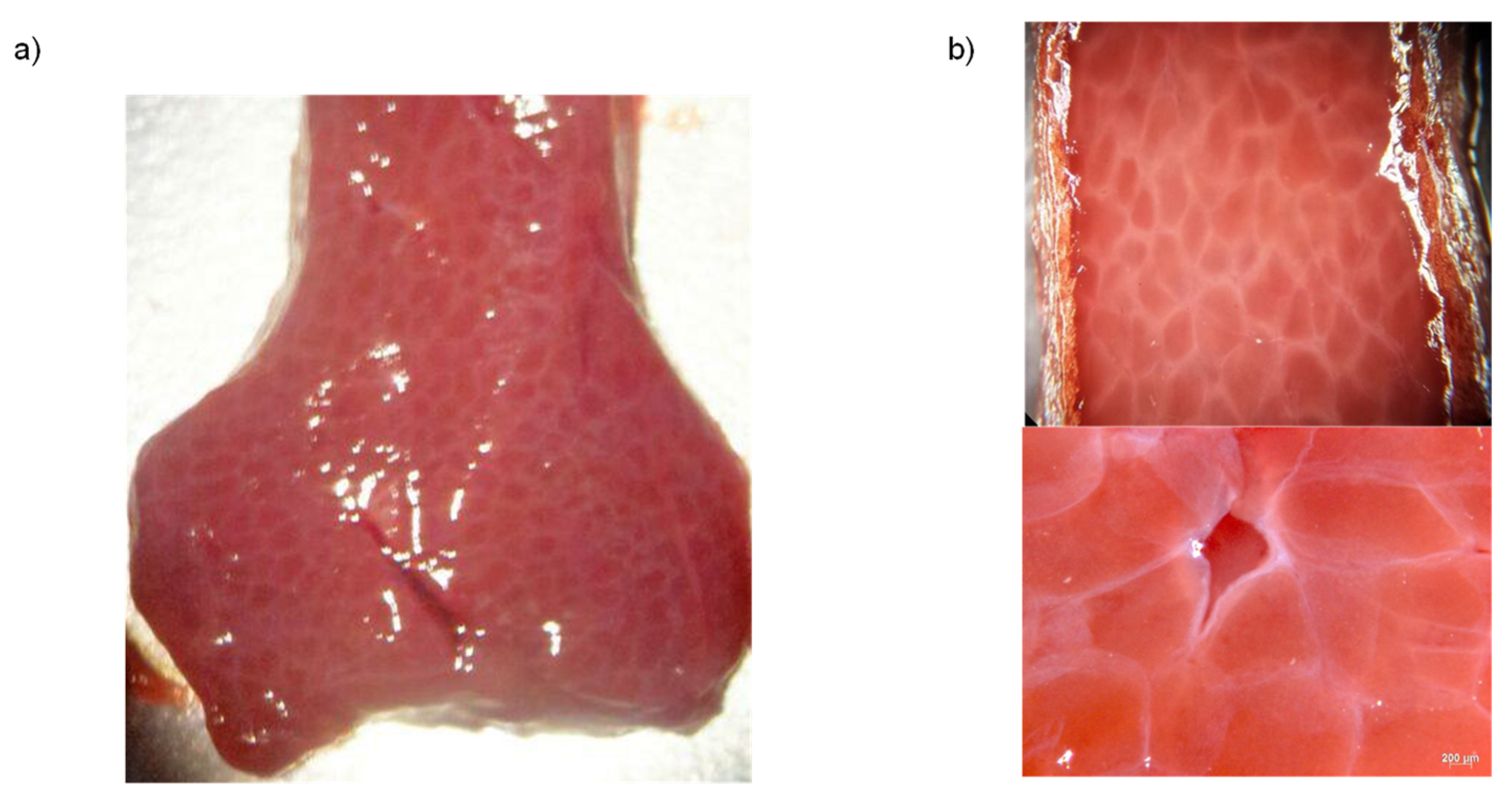
3.1. Sample Preparation
3.2. Experimental Setup
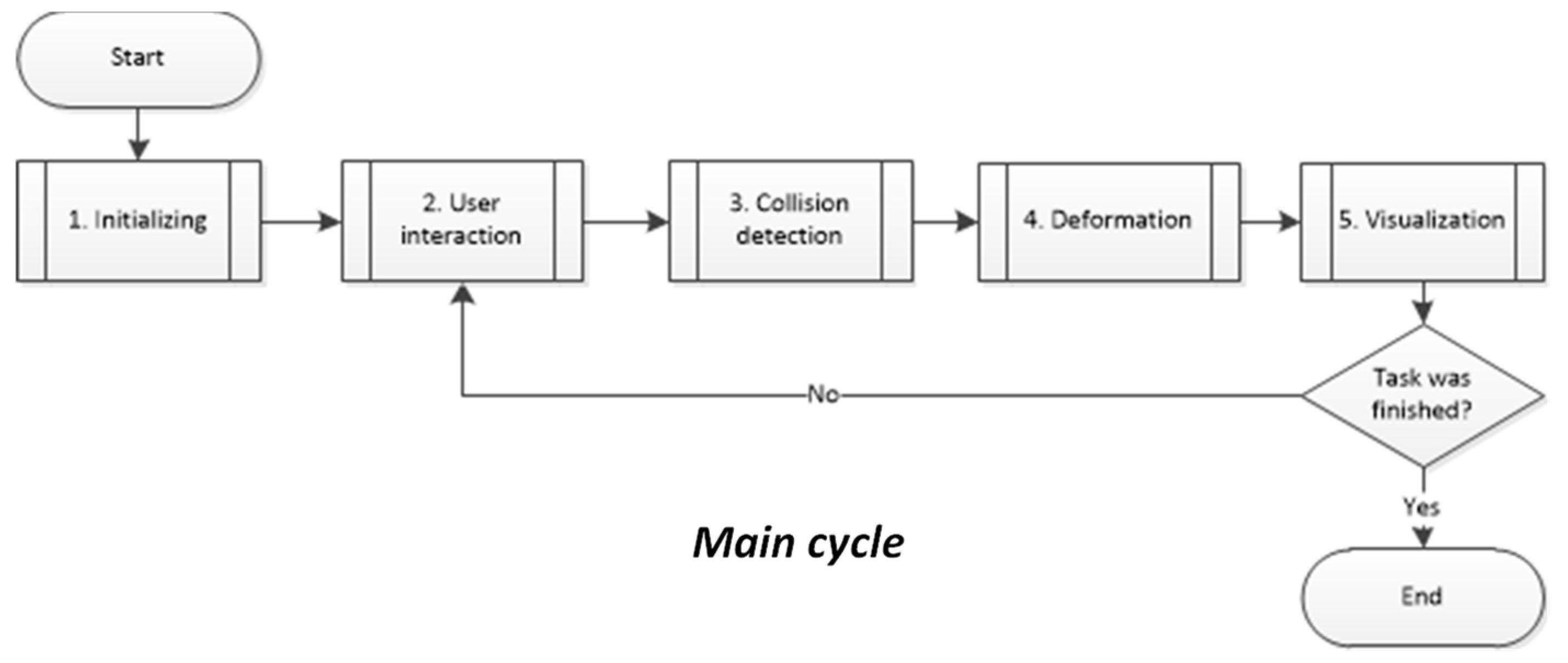
4. Computational Implementation
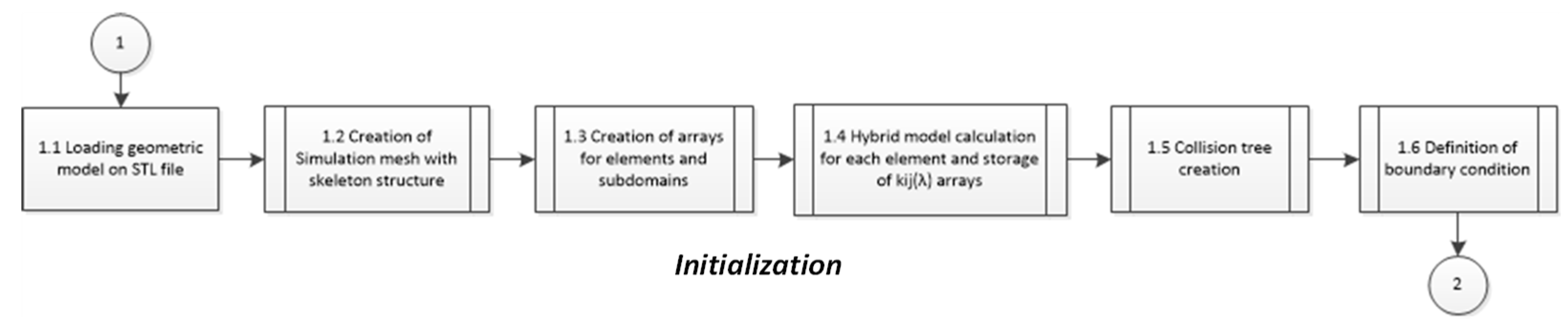
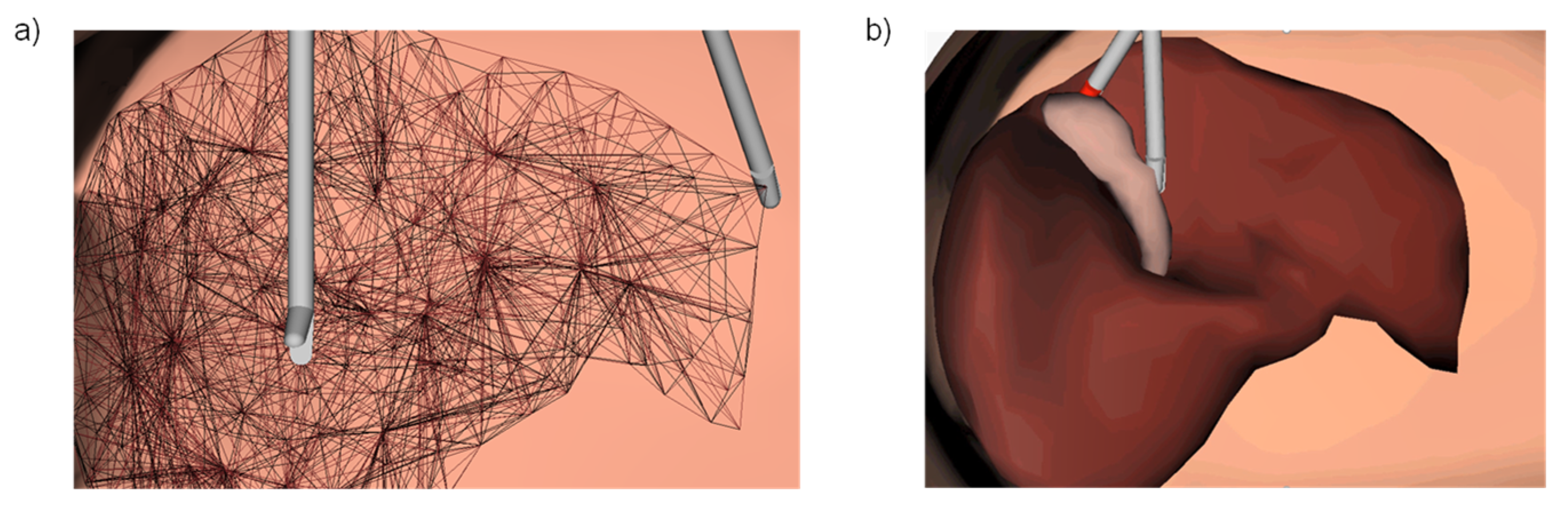
4.1. Simulation Setup
4.2. Model Integration
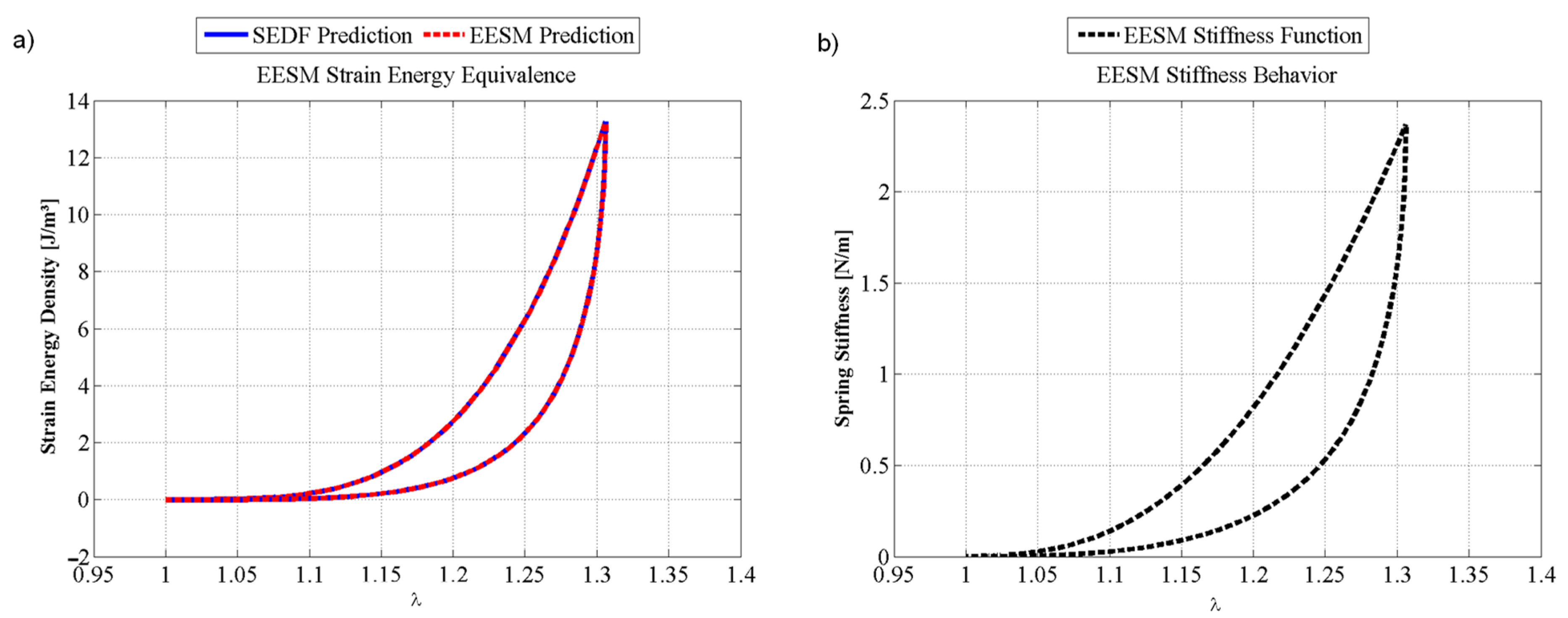
5. Material Constitutive Equation
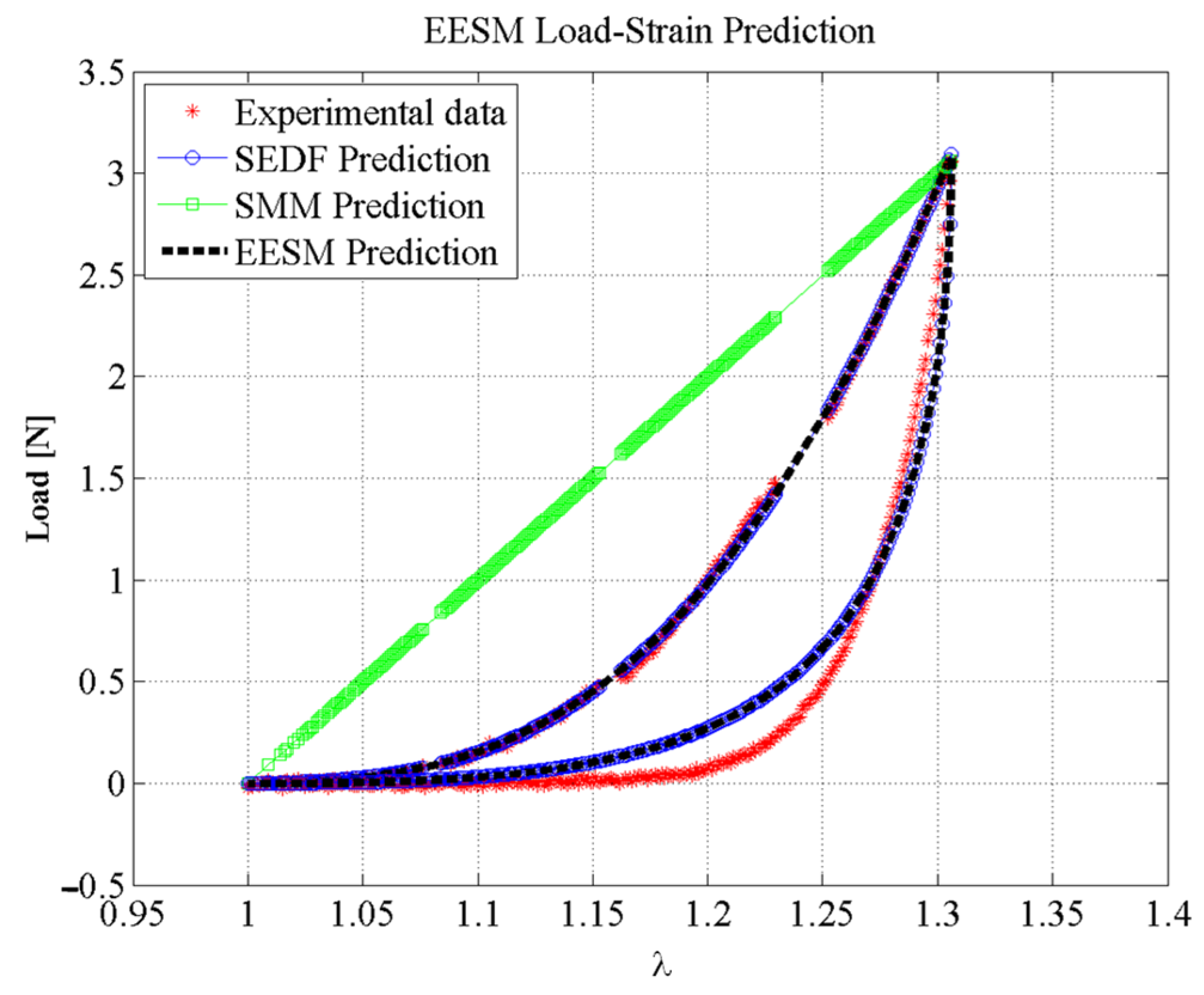
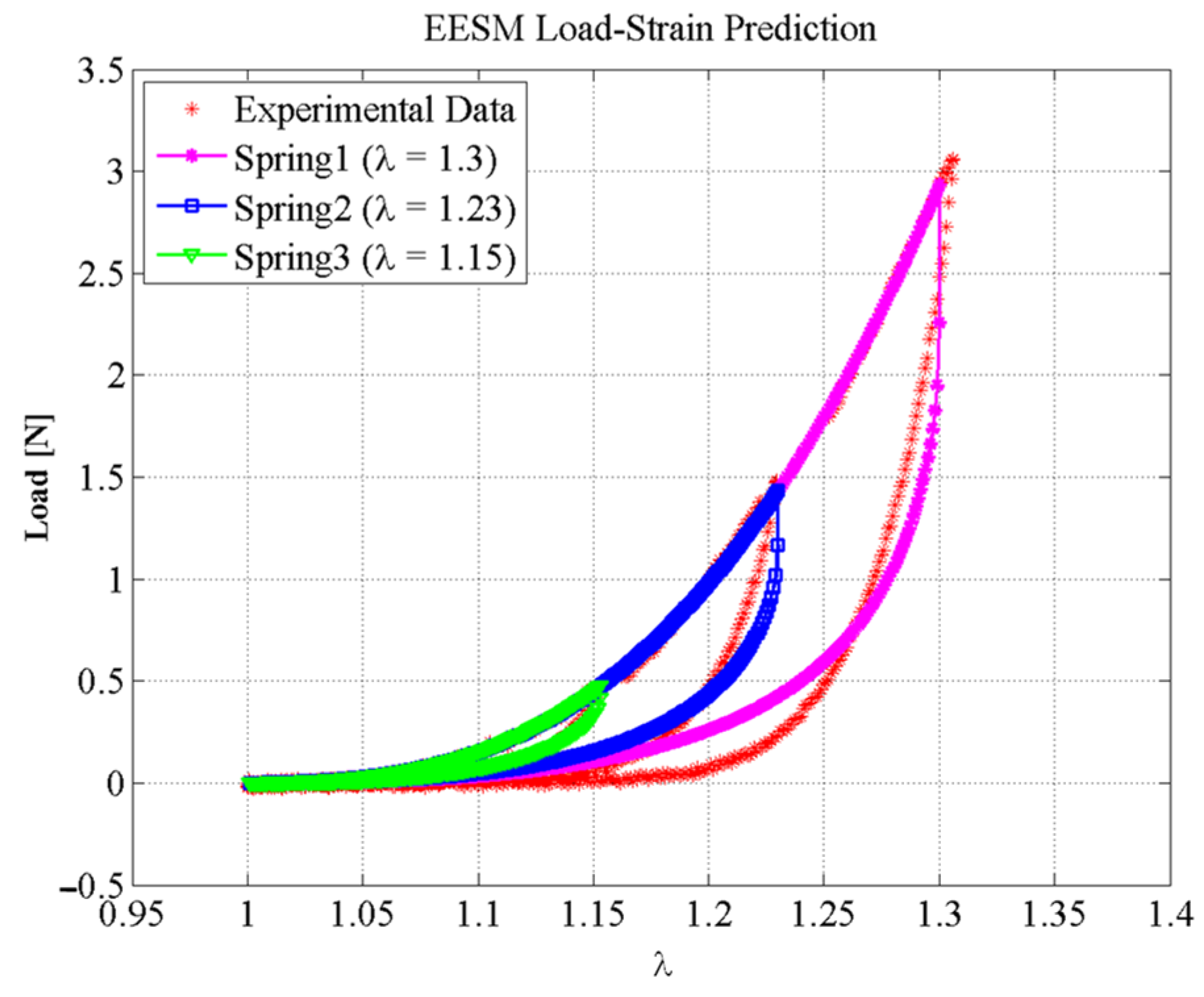
6. Results
Simulation Performance
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dorfmann, A.; Ogden, R.W. A constitutive model for the Mullins effect with permanent set in particle-reinforced rubber. Int. J. Solids Struct. 2004, 41, 1855–1878. [Google Scholar] [CrossRef]
- Holzapfel, G.A. Biomecanics of Soft Tissue. In Handbook of Material Behavior: Nonlinear Models and Properties; Academic Press: Cambridge, MA, USA, 2001; Chapter 10; Volume 3, pp. 1057–1071. [Google Scholar]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. Comparison of a multi-layer structural model for arterial walls with a Fung-type model, and issues of material stability. J. Biomech. Eng. 2004, 126, 264–275. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A.; Ogden, R.W. Constitutive modelling of arteries. Proc. R. Soc. Lond. A 2008, 466, 1551–1597. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A Three-Dimensional Constitutive Model of the Large Stretch Behavior of Rubber Elastic Materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef] [Green Version]
- Cantournet, S.; Boyce, M.C.; Tsou, A.H. Micromechanics and macro- mechanics of carbon nanotube-enhanced elastomers. J. Mech. Phys. Solids 2007, 55, 1321–1339. [Google Scholar] [CrossRef] [Green Version]
- Elías-Zúñiga, A.; Baylon, K.; Ferrer, I.; Sereno, L.; Garcia-Romeu, M.L.; Bagudanch, I.; Grabalosa, J.; Pérez-Recio, T.; Martinez-Romero, O.; Ortega, W.; et al. On the Rule of Mixtures for Predicting Stress-Softening and Residual Strain Effects in Biological Tissues and Biocompatible Materials. Materials 2014, 7, 441–456. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A New Constitutive Frame- work for Arterial Wall Mechanics and a Comparative Study of Material Models. J. Elast. 2000, 61, 1–48. [Google Scholar] [CrossRef]
- Humphrey, J.D. Continuum biomechanics of soft biological tissues. Proc. R. Soc. Lond. A 2003, 459, 3–46. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Gu, L.; Huang, P.; Zhang, J.; Xu, J. Soft Tissue Modeling using Nonlinear Mass Spring and Simplified Medial Reprsentation. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 5083–5086. [Google Scholar] [CrossRef]
- Zhu, B.; Gu, L. A hybrid deformable model for real-time surgical simulation. Comput. Med. Imaging Graph. 2012, 36, 356–365. [Google Scholar] [CrossRef]
- Patete, P.; Iaconoa, M.I.; Spadea, M.F.; Trecate, G.; Vergnaghi, D.; Mainardi, L.M.; Baroni, G. A multi-tissue mass-spring model for computer assisted breast surgery. Med. Eng. Phys. 2013, 35, 47–53. [Google Scholar] [CrossRef]
- Duan, Y.; Huang, W.; Chang, H.; Chen, W.; Zhuo, J.; Teo, S.K.; Su, Y.; Chui, C.K.; Chang, S. Volume Preserved Mass-Spring Model with Novel Con- straints for Soft Tissue Deformation. IEEE J. Biomed. Health Inform. 2016, 20, 268–280. [Google Scholar] [CrossRef] [PubMed]
- Natsupakpong, S.; Çavusoglu, M.C. Determination of elasticity parameters in lumped element (mass-spring) models of deformable objects. Graph. Models 2010, 72, 61–73. [Google Scholar] [CrossRef]
- Delingette, H.; Cotin, S.; Ayache, N. A hybrid elastic model allowing real- time cutting, deformations and force-feedback for surgery training and simulation. In Proceedings of the Computer Animation 1999, Geneva, Switzerland, 26–29 May 1999; pp. 70–81. [Google Scholar]
- Picinbono, G.; Delingette, H.; Ayache, N. Non-linear anisotropic elasticity for real-time surgery simulation. Graph. Models 2000, 65, 305–321. [Google Scholar] [CrossRef] [Green Version]
- Holzapfel, G.A.; Gasser, T.C.; Stadler, M. A Structural Model for the Viscoelastic Behavior of Arterial Walls: Continuum Formulation and Finite Element Analysis. Eur. J. Mech. A Solids 2002, 21, 441–463. [Google Scholar] [CrossRef]
- Ostoja-Starzewski, M. Lattice models in micromechanics. Appl. Mech. Rev. 2002, 55, 35–60. [Google Scholar] [CrossRef]
- Meier, U.; López, O.; Monserrat, C.; Juan, M.C.; Alcañiz, M. Real-time deformable models for surgery simulation: A survey. Comput. Methods Prog. Biomed. 2005, 77, 183–197. [Google Scholar] [CrossRef] [PubMed]
- Nealen, A.; Müller, M.; Keiser, R.; Boxerman, E.; Carlson, M.; Ageia, N. Physically based deformable models in computer graphics. Comput. Graph. Forum 2006, 25, 809–836. [Google Scholar] [CrossRef]
- Luo, Q.; Xiao, J. Contact and Deformation Modeling for Interactive Environments. IEEE Trans. Robot. 2007, 23, 416–430. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, S.; Zhang, Y.; Yin, L.; Zheng, W. An improved method for soft tissue modeling. Biomed. Signal Process. Control 2021, 65, 102367. [Google Scholar] [CrossRef]
- Liu, X.P.; Xu, S.; Zhang, H. A New Hybrid Soft Tissue Model for Visio-Haptic Simulation. IEEE Trans. Instrum. Meas. 2011, 60, 3570–3581. [Google Scholar] [CrossRef]
- San-Vicente, G.; Aguinaga, I.; Celigueta, J.T. Cubical mass-spring model design based on a tensile deformation test and nonlinear material model. IEEE Trans. Vis. Comput. Graph. 2012, 18, 228–241. [Google Scholar] [CrossRef] [PubMed]
- Del-Castillo, E.; Basañez, L.; Gil, E. Modeling non-linear viscoelastic behavior under large deformations. Int. J. Non-Linear Mech. 2013, 57, 54–162. [Google Scholar] [CrossRef]
- Nikolaev, S. Non-linear mass-spring system for large soft tissue deformations modeling. Sci. Tech. J. Inf. Technol. Mech. Opt. 2013, 5, 88–94. [Google Scholar]
- Kot, M.; Nagahashi, H.; Szymezak, P. Elastic moduli of simple mass spring models. Vis. Comput. 2015, 31, 1339–1350. [Google Scholar] [CrossRef]
- Lloyd, J.; Sánchez, A.; Widing, E.; Stavness, I.; Fels, S.; Niroomandi, S.; Perrier, A.; Payan, Y.; Perrier, P. New Techniques for Combined FEM-Multibody Anatomical Simulation. In New Developments on Computational Methods and Imaging in Biomechanics and Biomedical Engineering; Tavares, J.M.R.S., Fernandes, P.R., Eds.; Springer: Cham, Switzerland, 2019; pp. 75–92. [Google Scholar]
- Lloyd, J.E.; Stavness, I.; Fels, S. ArtiSynth: A Fast Interactive Biomechanical Modeling Toolkit Combining Multibody and Finite Element Simulation. Stud. Mechanobiol. Tissue Eng. Biomater. 2012, 11, 355–394. [Google Scholar]
- Omar, M.N.; Zhong, Y. Flexible Mass Spring Method for Modelling Soft Tissue Deformation. Int. J. Eng. Sci. Technol. 2020, 7, 24–41. [Google Scholar] [CrossRef]
- Omar, M.N.; Zhong, Y. A Review of Mass Spring Method Improvements for Modeling Soft Tissue Deformation. In Human-Centered Technology for a Better Tomorrow; Hassan, M.H.A., Manap, Z.A., Baharom, M.Z., Johari, N.H., Jamaludin, U.K., Jalil, M.H., Sahat, I.M., Omar, M.N., Eds.; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Nguyen, T.-N.; Ho Ba Tho, M.-C.; Dao, T.-T. A Systematic Review of Real-Time Medical Simulations with Soft-Tissue Deformation: Computational Approaches, Interaction Devices, System Architectures, and Clinical Validations. Appl. Bionics Biomech. 2020, 2020, 5039329. [Google Scholar] [CrossRef]
- Zhang, J.; Zhong, Y.; Gu, C. Deformable Models for Surgical Simulation: A Survey. IEEE Rev. Biomed. Eng. 2017, 11, 143–164. [Google Scholar] [CrossRef] [Green Version]
- Dong, B.; Li, J.; Yang, G.; Cheng, X.; Gang, Q. A Multi-Component Conical Spring Model of Soft Tissue in Virtual Surgery. IEEE Access 2020, 8, 146093–146104. [Google Scholar] [CrossRef]
- Va, H.; Choi, M.-H.; Hong, M. Real-Time Cloth Simulation Using Compute Shader in Unity3D for AR/VR Contents. Appl. Sci. 2021, 11, 8255. [Google Scholar] [CrossRef]
- Aryeetey, O.; Frank, M.; Lorenz, A.; Estermann, S.J.; Reisinger, A.; Pahr, D. A parameter reduced adaptive quasi-linear viscoelastic model for soft biological tissue in uniaxial tension. J. Mech. Behav. Biomed. Mater. 2021, 126, 104999. [Google Scholar] [CrossRef]
- Tripicchio, P.; D’Avella, S.; Ruffaldi, E. Real-Time Numerical Simulation for Accurate Soft Tissues Modeling during Haptic Interaction. Actuators 2022, 11, 17. [Google Scholar] [CrossRef]
- Ballit, A.; Dao, T.T. HyperMSM: A new MSM variant for efficient simulation of dynamic soft-tissue deformations. Comput. Methods Programs Biomed. 2022, 216, 106659. [Google Scholar] [CrossRef] [PubMed]
- Córdova, R.K.; Elías-Zúñiga, A.; Elizalde, L.E.; Siller, H.R.; Sánchez, J.A.; Rodríguez, C.A.; Ortega, W. Polymeric Materials Reinforced with Multiwall Carbon Nanotubes: A Constitutive Material Model. Materials 2013, 6, 2873–2891. [Google Scholar] [CrossRef] [PubMed]
- Elías-Zúñiga, A.; Montoya, B.; Ortega-Lara, W.; Flores-Villalba, E.; Rodríguez, C.A.; Siller, H.R.; Díaz-Elizondo, J.A.; Martínez-Romero, O. Stress-Softening and Residual Strain Effects in Suture Materials. Adv. Mater. Sci. Eng. 2013, 2013, 249512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elías-Zúñiga, A.; Palacios-Pineda, L.M.; Perales-Martínez, I.A.; Martínez-Romero, O.; Olvera-Trejo, D.; Jiménez-Cedeño, I.H. Investigating the Mullins effect and energy dissipation in magnetorheological polyurethane elastomers. Int. J. Mol. Sci. 2020, 21, 5318. [Google Scholar] [CrossRef] [PubMed]
- Qi, H.J.; Boyce, M.C. Constitutive model for stretch-induced softening of the stress-stretch behavior of elastomeric materials. J. Mech. Phys. Solids 2004, 52, 2187–2205. [Google Scholar] [CrossRef]
- Elías-Zúñiga, A.; Beatty, M.F. Constitutive equations for amended non-Gaussian network models of rubber elasticity. Int. J. Eng. Sci. 2002, 40, 2265–2294. [Google Scholar] [CrossRef]
- Beatty, M.F. An Average-Stretch Full-Network Model for Rubber Elasticity. J. Elast. 2003, 70, 65–86. [Google Scholar] [CrossRef]
- Elías-Zúñiga, A. A non-Gaussian network model for rubber elasticity. Polymer 2006, 47, 907–914. [Google Scholar] [CrossRef]
- Puso, M. Mechanistic Constitutive Models for Rubber Elasticity and Viscoelasticity. Ph.D. Thesis, University of California, Davis, CA, USA, 2003. [Google Scholar]
- Umale, S.; Deck, C.; Bourdet, N.; Dhumane, P.; Soler, L.; Marescaux, J.; Willinger, R. Experimental Mechanical Characterization of Abdominal Organs: Liver, Kidney & Spleen. J. Mech. Behav. Biomed. Mater. 2013, 17, 22–33. [Google Scholar]
- Brunon, A.; Bruyere-Garnier, K.; Coret, M. Mechanical Characterization of Liver Capsule Through Uniaxial Quasi-Static TensileTests Until Failure. J. Biomech. 2010, 43, 2221–2227. [Google Scholar] [CrossRef] [PubMed]
- Moreno Guerra, M.R.; Junqueira Amorin, P.H.; Frnaco de Moraes, T.; Lopes da Silva, J.V.; Rodríguez-González, A.C.; Elías-Zúñiga, A.; Martínez-Romero, O. A Hybrid formulation for soft tissue modeling on real-time surgery simulation. In Proceedings of the XXXVI Iberian Latin-American Congress on Computational Methods in Engineering, Rio de Janeiro, Brazil, 22–25 November 2015. [Google Scholar]
- Elías-Zúñiga, A. A phenomenological energy-based model to characterize stress-softening effect in elastomers. Polymer 2005, 46, 3496–3506. [Google Scholar] [CrossRef]
- Elías-Zúñiga, A.; Rodríguez, C.A. A non-monotonous damage function to characterize stress-softening effects with permanent set during inflation and deflation of rubber balloons. Int. J. Eng. Sci. 2010, 48, 1937–1943. [Google Scholar] [CrossRef]
- Palacios-Pineda, L.M.; Perales-Martínez, I.A.; Moreno-Guerra, M.R.; Elías-Zúñiga, A. An Optimum Specimen Geometry for Equibiaxial Experimental Tests of Reinforced Magnetorheological Elastomers with Iron Micro- and Nanoparticles. Nanomaterials 2017, 7, 254. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Guo, J.; Posnansky, O.; Hirsch, S.; Scheel, M.; Taupitz, M.; Braun, J.; Sack, I. Fractal network dimension and viscoelastic powerlaw behavior: II. An experimental study of structure-mimicking phantoms by magnetic resonance elastography. Phys. Med. Biol. 2012, 57, 4041–4053. [Google Scholar] [CrossRef]
- Leggett, S.E.; Neronhaa, Z.J.; Bhaskara, D.; Sima, J.Y.; Perdikaria, T.M.; Wonga, I.Y. Motility-limited aggregation of mammary epithelial cells into fractal-like clusters. Proc. Natl. Acad. Sci. USA 2019, 116, 7298–17306. [Google Scholar] [CrossRef] [Green Version]
- West, B.J. Fractal physiology and the fractional calculus: A perspective. Front. Physiol. 2010, 1, 12. [Google Scholar] [CrossRef] [Green Version]
- Baleanu, D.; Mohammadi, H.; Rezapour, S. Analysis of the model of HIV-1 infection of CD4+ T-cell with a new approach of fractional derivative. Adv. Differ. Equ. 2020, 2020, 71. [Google Scholar] [CrossRef] [Green Version]
- Baleanu, D.; Jajarmi, A.; Mohammadi, H.; Rezapour, S. A new study on the mathematical modelling of human liver with Caputo–Fabrizio fractional derivative. Chaos Solit. Fractals 2020, 134, 109705. [Google Scholar] [CrossRef]
- Ameen, I.G.; Sweilam, N.H.; Ali, H.M. A fractional-order model of human liver: Analytic-approximate and numerical solutions comparing with clinical data. Alex. Eng. J. 2021, 60, 4797–4808. [Google Scholar] [CrossRef]
- Kurakin, A. The self-organizing fractal theory as a universal discovery method: The phenomenon of life. Theor. Biol. Med. Model 2011, 8, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, J.-H. A tutorial review on fractal spacetime and fractional calculus. Int. J. Theor. Phys. 2014, 53, 3698–3718. [Google Scholar] [CrossRef]
- He, J.-H. Fractal calculus and its geometrical explanation. Res. Phys. 2018, 10, 272–276. [Google Scholar] [CrossRef]
- Elías-Zúñiga, A.; Martínez-Romero, O.; Olvera-Trejo, D.; Palacios-Pineda, L.M. Exact steady-state solution of fractals damped, and forced systems. Res. Phys. 2021, 28, 104580. [Google Scholar] [CrossRef]
- Elías-Zúñiga, A.; Martínez-Romero, O.; Palacios-Pineda, L.M.; Olvera-Trejo, D. New analytical solution of the fractal anharmonic oscillator using an ancient Chinese algorithm: Investigating how plasma frequency changes with fractal parameter values. J. Low Freq. Noise Vib. Act. Control 2022. [Google Scholar] [CrossRef]
- Estrada-Díaz, J.A.; Martínez-Romero, O.; Olvera-Trejo, D.; Elías-Zúñiga, A. Elucidating the Fractal Nature of Powder bed in Selective Laser Melting of Metallic Components. Fractals 2022, 1. [Google Scholar] [CrossRef]
- Elías-Zúñiga, A.; Martínez-Romero, O.; Olvera-Trejo, D.; Palacios-Pineda, L.M. Fractal equation of motion of a non-Gaussian polymer chain: Investigating its dynamic fractal response using an ancient Chinese algorithm. J. Math. Chem. 2022, 60, 461–473. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno-Guerra, M.R.; Martínez-Romero, O.; Palacios-Pineda, L.M.; Olvera-Trejo, D.; Diaz-Elizondo, J.A.; Flores-Villalba, E.; da Silva, J.V.L.; Elías-Zúñiga, A.; Rodriguez, C.A. Soft Tissue Hybrid Model for Real-Time Simulations. Polymers 2022, 14, 1407. https://doi.org/10.3390/polym14071407
Moreno-Guerra MR, Martínez-Romero O, Palacios-Pineda LM, Olvera-Trejo D, Diaz-Elizondo JA, Flores-Villalba E, da Silva JVL, Elías-Zúñiga A, Rodriguez CA. Soft Tissue Hybrid Model for Real-Time Simulations. Polymers. 2022; 14(7):1407. https://doi.org/10.3390/polym14071407
Chicago/Turabian StyleMoreno-Guerra, Mario R., Oscar Martínez-Romero, Luis Manuel Palacios-Pineda, Daniel Olvera-Trejo, José A. Diaz-Elizondo, Eduardo Flores-Villalba, Jorge V. L. da Silva, Alex Elías-Zúñiga, and Ciro A. Rodriguez. 2022. "Soft Tissue Hybrid Model for Real-Time Simulations" Polymers 14, no. 7: 1407. https://doi.org/10.3390/polym14071407








