Approaching Polymer Dynamics Combining Artificial Neural Networks and Elastically Collective Nonlinear Langevin Equation
Abstract
:1. Introduction
2. Methods and Theoretical Background
2.1. Dataset
2.2. Chemical Structure Encoding
2.3. ANN’s Architecture and Optimization
2.4. Nonlinear Langevin Equation
3. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nakajima, H.; Dijkstra, P.; Loos, K. The Recent Developments in Biobased Polymers toward General and Engineering Applications: Polymers That Are Upgraded from Biodegradable Polymers, Analogous to Petroleum-Derived Polymers, and Newly Developed. Polymers 2017, 9, 523. [Google Scholar] [CrossRef] [PubMed]
- Umoren, S.A.; Solomon, M.M. Protective Polymeric Films for Industrial Substrates: A Critical Review on Past and Recent Applications with Conducting Polymers and Polymer Composites/Nanocomposites. Prog. Mater. Sci. 2019, 104, 380–450. [Google Scholar] [CrossRef]
- de Leon, A.C.C.; da Silva, Í.G.M.; Pangilinan, K.D.; Chen, Q.; Caldona, E.B.; Advincula, R.C. High Performance Polymers for Oil and Gas Applications. React. Funct. Polym. 2021, 162, 104878. [Google Scholar] [CrossRef]
- Wu, X.; Chen, X.; Zhang, Q.M.; Tan, D.Q. Advanced Dielectric Polymers for Energy Storage. Energy Storage Mater. 2022, 44, 29–47. [Google Scholar] [CrossRef]
- Wang, Y.; Ghanem, B.S.; Han, Y.; Pinnau, I. State of the Art Polymers of Intrinsic Microporosity for High-Performance Gas Separation Membranes. Curr. Opin. Chem. Eng. 2022, 35, 100755. [Google Scholar] [CrossRef]
- Devaraju, S.; Alagar, M. Polymer Matrix Composite Materials for Aerospace Applications. Encycl. Mater. Compos. 2021, 1, 947–969. [Google Scholar] [CrossRef]
- Vidya; Mandal, L.; Verma, B.; Patel, P.K. Review on Polymer Nanocomposite for Ballistic & Aerospace Applications. Mater. Today Proc. 2020, 26, 3161–3166. [Google Scholar] [CrossRef]
- Gambino, T.; Alegría, A.; Arbe, A.; Colmenero, J.; Malicki, N.; Dronet, S. Modeling the High Frequency Mechanical Relaxation of Simplified Industrial Polymer Mixtures Using Dielectric Relaxation Results. Polymer 2020, 187, 122051. [Google Scholar] [CrossRef]
- Menard, K.P.; Menard, N.R. Dynamic Mechanical Analysis in the Analysis of Polymers and Rubbers. Encycl. Polym. Sci. Technol. 2015, 1–33. [Google Scholar] [CrossRef]
- Capiel, G.; Miccio, L.A.; Montemartini, P.E.; Schwartz, G.A. Water Diffusion and Hydrolysis Effect on the Structure and Dynamics of Epoxy-Anhydride Networks. Polym. Degrad. Stab. 2017, 143, 57–63. [Google Scholar] [CrossRef]
- Otegui, J.; Miccio, L.A.; Arbe, A.; Schwartz, G.A.; Meyer, M.; Westermann, S. Determination of Filler Structure in Silica-Filled SBR Compounds by Means of SAXS and AFM. Rubber Chem. Technol. 2015, 88, 690–710. [Google Scholar] [CrossRef] [Green Version]
- Phan, A.D.; Schweizer, K.S. Elastically Collective Nonlinear Langevin Equation Theory of Glass-Forming Liquids: Transient Localization, Thermodynamic Mapping, and Cooperativity. J. Phys. Chem. B 2018, 122, 8451–8461. [Google Scholar] [CrossRef] [PubMed]
- Phan, A.D.; Wakabayashi, K. Effects of Cooling Rate on Structural Relaxation in Amorphous Drugs: Elastically Collective Nonlinear Langevin Equation Theory and Machine Learning Study. RSC Adv. 2019, 9, 40214–40221. [Google Scholar] [CrossRef] [Green Version]
- Phan, A.D.; Knapik-Kowalczuk, J.; Paluch, M.; Hoang, T.X.; Wakabayashi, K. Theoretical Model for the Structural Relaxation Time in Coamorphous Drugs. Mol. Pharm. 2019, 16, 2992–2998. [Google Scholar] [CrossRef]
- Miccio, L.A.; Schwartz, G.A. From Chemical Structure to Quantitative Polymer Properties Prediction through Convolutional Neural Networks. Polymer. 2020, 193, 122341. [Google Scholar] [CrossRef]
- Miccio, L.A.; Schwartz, G.A. Localizing and Quantifying the Intra-Monomer Contributions to the Glass Transition Temperature Using Artificial Neural Networks. Polymer. 2020, 203, 122786. [Google Scholar] [CrossRef]
- Miccio, L.A.; Schwartz, G.A. Mapping Chemical Structure-Glass Transition Temperature Relationship through Artificial Intelligence. Macromolecules 2021, 54, 1811–1817. [Google Scholar] [CrossRef]
- Weininger, D. SMILES, a Chemical Language and Information System. 1. Introduction to Methodology and Encoding Rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- O’Boyle, N.M. Towards a Universal SMILES Representation-A Standard Method to Generate Canonical SMILES Based on the InChI. J. Cheminform. 2012, 4, 22. [Google Scholar] [CrossRef] [Green Version]
- Plazek, D.J.; Ngai, K.L. The Glass Temperature. In Physical Properties of Polymers Handbook; Mark, J.E., Ed.; Springer: New York, NY, USA, 2007; pp. 187–215. ISBN 978-0-387-69002-5. [Google Scholar]
- Plastic Library, Chemical Retrieval on the Web, Crow. Available online: https://polymerdatabase.com (accessed on 19 April 2019).
- Bertinetto, C.; Duce, C.; Micheli, A.; Solaro, R.; Starita, A.; Tine, M.R. Prediction of the Glass Transition Temperature of (Meth)Acrylic Polymers Containing Phenyl Groups by Recursive Neural Network. Polymer 2007, 48, 7121–7129. [Google Scholar] [CrossRef]
- Wypych, G. Handbook of Polymers, 2nd ed.; ChemTec Publishing: Toronto, ON, Canada, 2016; ISBN 978-1-895198-92-8. [Google Scholar]
- Alkharusi, H. Categorical Variables in Regression Analysis: A Comparison of Dummy and Effect Coding. Int. J. Educ. 2012, 4, 202–210. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- He, X.; Wu, J.; Huang, G.; Wang, X. Effect of Alkyl Side Chain Length on Relaxation Behaviors in Poly(n-Alkyl Acrylates) and Poly(n-Alkyl Methacrylates). J. Macromol. Sci. Part B Phys. 2010, 50, 188–200. [Google Scholar] [CrossRef]
- Qin, Q.; McKenna, G.B. Correlation between Dynamic Fragility and Glass Transition Temperature for Different Classes of Glass Forming Liquids. J. Non-Cryst. Solids 2006, 352, 2977–2985. [Google Scholar] [CrossRef]
- Menissez, C.; Sixou, B.; David, L.; Vigier, G. Dielectric and Mechanical Relaxation Behavior in Poly(Butyl Methacrylate) Isomers. J. Non-Cryst. Solids 2005, 351, 595–603. [Google Scholar] [CrossRef]
- Sato, A.; Sasaki, T. Cooperativity of Dynamics in Supercooled Polymeric Materials and Its Temperature Dependence Predicted from a Surface Controlled Model. Eur. Polym. J. 2018, 99, 485–494. [Google Scholar] [CrossRef]
- Merino, E.G.; Atlas, S.; Raihane, M.; Belfkira, A.; Lahcini, M.; Hult, A.; Dionísio, M.; Correia, N.T. Molecular Dynamics of Poly(ATRIF) Homopolymer and Poly(AN-Co-ATRIF) Copolymer Investigated by Dielectric Relaxation Spectroscopy. Eur. Polym. J. 2011, 47, 1429–1446. [Google Scholar] [CrossRef]
- Xie, S.J.; Schweizer, K.S. Nonuniversal Coupling of Cage Scale Hopping and Collective Elastic Distortion as the Origin of Dynamic Fragility Diversity in Glass-Forming Polymer Liquids. Macromolecules 2016, 49, 9655–9664. [Google Scholar] [CrossRef]
- Godard, M.; Saiter, J. Fragility and Non-Linearity in Polymethyl (n-Alkyl) Acrylates. J. Non-Cryst. Solids 1998, 237, 635–639. [Google Scholar] [CrossRef]
- Calleja, R.D.; Jaime, C.; Sanchis, M.J.; Romcin, J.S.; Gargallo, L. Dynamic Mechanical and Dielectric Relaxations in Poly(Pentachloropheny1 Methacrylate). Macromol. Chem. Phys. 1998, 581, 575–581. [Google Scholar] [CrossRef]
- Calleja, R.D.; Jaime’s, C.; Sanchis-Sanchez, M.J.; Martinez-Piña, F.; Gargallo, L.; Radic, D. Mechanical and Dielectric Properties of Bulky Side Chain Poly(Methacry1ates). Analysis of the Low Frequency Phenomena. 1: Poly(5-Lndanyl Methacrylate). Polym. Eng. Sci. 1997, 37, 882–887. [Google Scholar] [CrossRef]
- Fredrickson, G.H.; Bates, F.S. Dynamics of Block Copolymers: Theory and Experiment. Annu. Rev. Mater. Sci. 1996, 26, 501–550. [Google Scholar] [CrossRef]
- Böhmer, R.; Ngai, K.L.; Angell, C.A.; Plazek, D.J. Nonexponential Relaxations in Strong and Fragile Glass Formers. J. Chem. Phys. 1993, 99, 4201–4209. [Google Scholar] [CrossRef]
- Diaz-Calleja, R. Dielectric Relaxation Studies on Phenyl and Chlorophenyl Esters of Poly(Acry1ic Acid). Macromolecules 1991, 24, 264–269. [Google Scholar] [CrossRef]
- Floudas, G.; Štepánek, P. Structure and Dynamics of Poly(n-Decyl Methacrylate) below and above the Glass Transition. Macromolecules 1998, 31, 6951–6957. [Google Scholar] [CrossRef]
- Garci, A.; Di, R.; Guzma, J. Relaxation Behavior of Acrylate and Methacrylate Polymers Containing Dioxacyclopentane Rings in the Side Chains. J. Polym. Sci. Part B Polym. Phys. 2000, 39, 286–299. [Google Scholar] [CrossRef]
- Sanchis, M.J.; Saiz, E.; Marti, F. Dynamic Mechanical and Dielectric Relaxations of Poly (Difluorobenzyl Methacrylates). J. Polym. Sci. Part B Polym. Phys. 2000, 38, 2179–2188. [Google Scholar]
- García, N.; Compañ, V.; Díaz-Calleja, R.; Guzmán, J.; Riande, E. Comparative Study of the Relaxation Behaviour of Acrylic Polymers with Flexible Cyclic Groups in Their Structure. Polymer 2000, 41, 6603–6611. [Google Scholar] [CrossRef]
- Balabin, R.M. Enthalpy Difference between Conformations of Normal Alkanes: Raman Spectroscopy Study of n-Pentane and n-Butane. J. Phys. Chem. A 2009, 113, 1012–1019. [Google Scholar] [CrossRef]
- Wind, M.; Graf, R.; Renker, S.; Spiess, H.W.; Steffen, W. Structure of Amorphous Poly-(Ethylmethacrylate): A Wide-Angle x-Ray Scattering Study. J. Chem. Phys. 2004, 122, 014906. [Google Scholar] [CrossRef] [PubMed]
- Wind, M.; Graf, R.; Renker, S.; Spiess, H.W. Structural Reasons for Restricted Backbone Motion in Poly(n-Alkyl Methacrylates): Degree of Polymerization, Tacticity and Side-Chain Length. Macromol. Chem. Phys. 2005, 206, 142–156. [Google Scholar] [CrossRef]
- Beiner, M.; Schröter, K.; Hempel, E.; Reissig, S.; Donth, E. Multiple Glass Transition and Nanophase Separation in Poly(n-Alkyl Methacrylate) Homopolymers. Macromolecules 1999, 32, 6278–6282. [Google Scholar] [CrossRef]
- Beiner, M.; Kabisch, O.; Reichl, S.; Huth, H. Structural and Dynamic Nanoheterogeneities in Higher Poly (Alkyl Methacrylate). J. Non-Cryst. Solids 2002, 310, 658–666. [Google Scholar] [CrossRef]
- Beiner, M.; Huth, H. Nanophase Separation and Hindered Glass Transition in Side-Chain Polymers. Nat. Mater. 2003, 2, 595–599. [Google Scholar] [CrossRef] [PubMed]
- Arbe, A.; Genix, A.; Arrese-Igor, S.; Colmenero, J.; Richter, D. Dynamics in Poly (n-Alkyl Methacrylates): A Neutron Scattering, Calorimetric, and Dielectric Study. Macromolecules 2010, 43, 3107–3119. [Google Scholar] [CrossRef] [Green Version]
- Qazvini, N.T.; Mohammadi, N. Segmental Dynamics in Net-Poly(Methyl Methacrylate)-Co-Poly(n-Butyl Acrylate) Copolymer Networks. J. Macromol. Sci. Part B Phys. 2008, 47, 1161–1175. [Google Scholar] [CrossRef]
- Cangialosi, D.; Schwartz, G.A.; Alegría, A.; Colmenero, J. Combining Configurational Entropy and Self-Concentration to Describe the Component Dynamics in Miscible Polymer Blends. J. Chem. Phys. 2005, 123, 144908. [Google Scholar] [CrossRef]
- Schwartz, G.A.; Alegría, Á.; Colmenero, J. Adam-Gibbs Based Model to Describe the Single Component Dynamics in Miscible Polymer Blends under Hydrostatic Pressure. J. Chem. Phys. 2007, 127, 154907. [Google Scholar] [CrossRef] [Green Version]
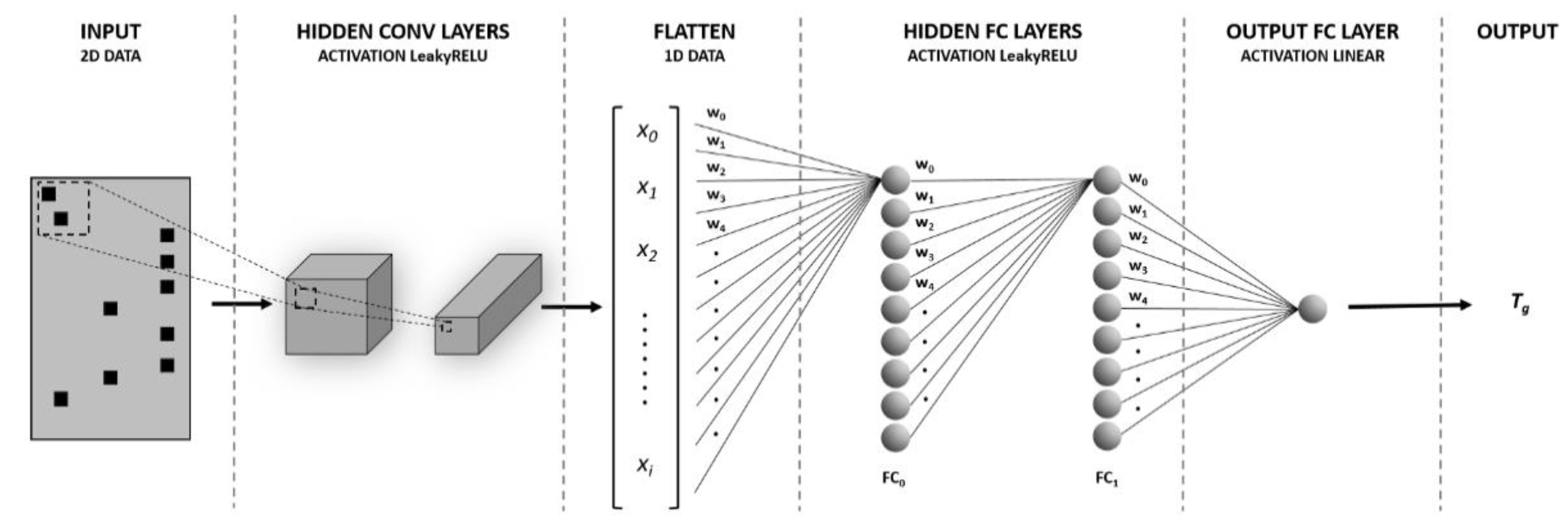
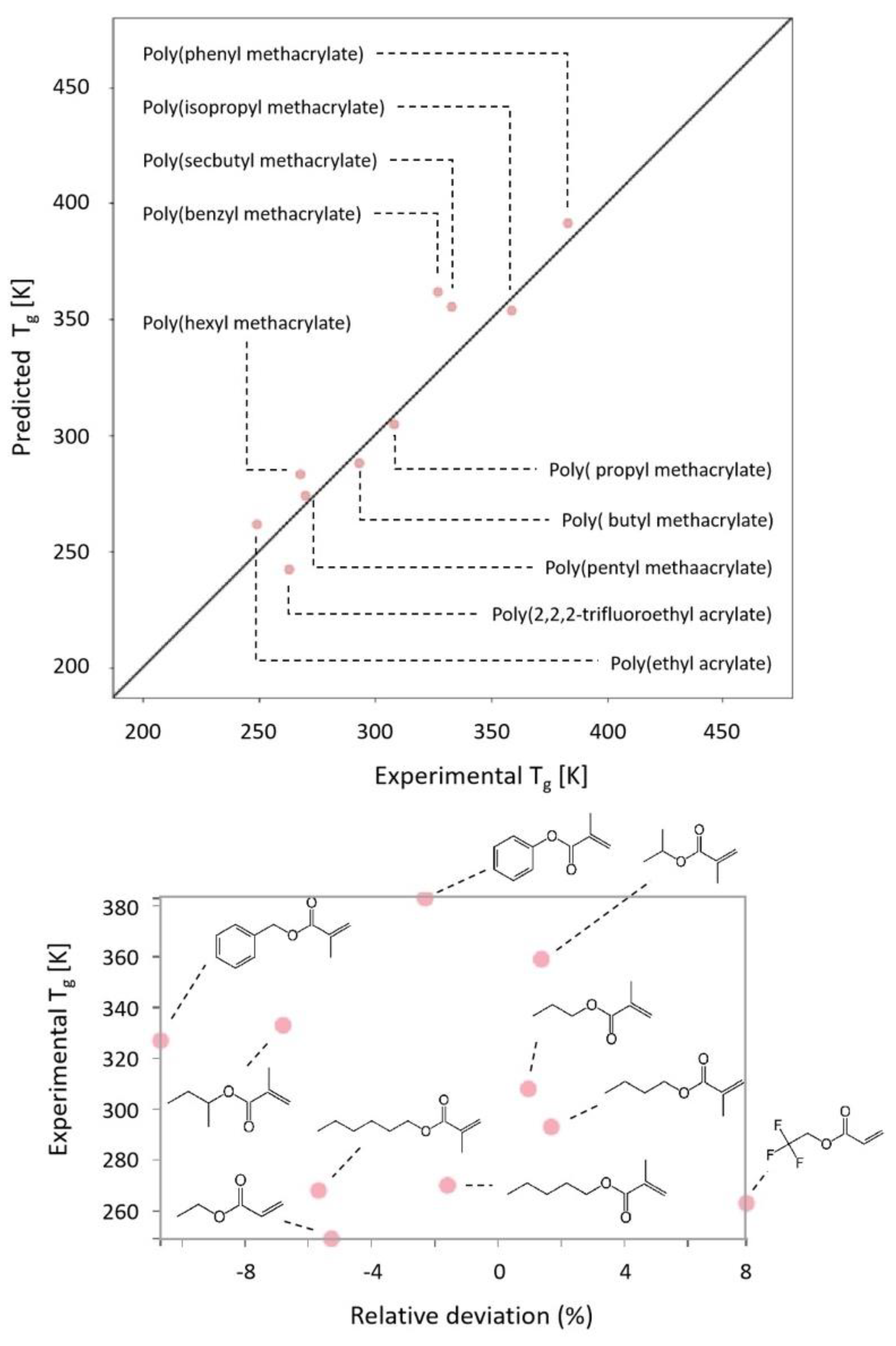


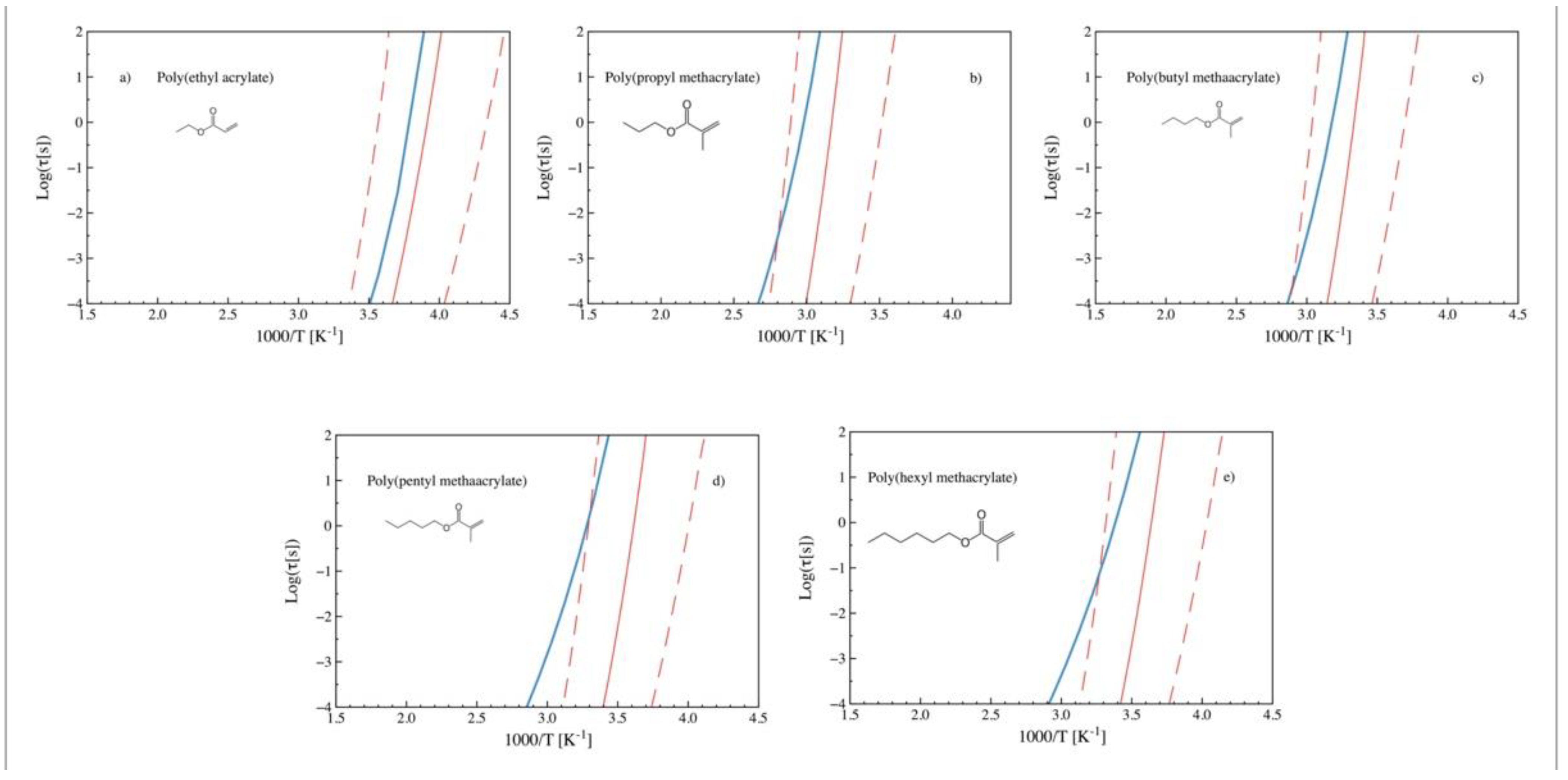

| Item | Value |
|---|---|
| Data split ratio (train/test) | 80/20 |
| Dropout probability | 0 to 0.3 |
| Mini batch size | 20 |
| Learning rate | 0.0001 |
| Beta1 (Beta2) | 0.99 (0.999) |
| # Hidden neurons (FC0–FC1) | 30–20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miccio, L.A.; Borredon, C.; Casado, U.; Phan, A.D.; Schwartz, G.A. Approaching Polymer Dynamics Combining Artificial Neural Networks and Elastically Collective Nonlinear Langevin Equation. Polymers 2022, 14, 1573. https://doi.org/10.3390/polym14081573
Miccio LA, Borredon C, Casado U, Phan AD, Schwartz GA. Approaching Polymer Dynamics Combining Artificial Neural Networks and Elastically Collective Nonlinear Langevin Equation. Polymers. 2022; 14(8):1573. https://doi.org/10.3390/polym14081573
Chicago/Turabian StyleMiccio, Luis A., Claudia Borredon, Ulises Casado, Anh D. Phan, and Gustavo A. Schwartz. 2022. "Approaching Polymer Dynamics Combining Artificial Neural Networks and Elastically Collective Nonlinear Langevin Equation" Polymers 14, no. 8: 1573. https://doi.org/10.3390/polym14081573
APA StyleMiccio, L. A., Borredon, C., Casado, U., Phan, A. D., & Schwartz, G. A. (2022). Approaching Polymer Dynamics Combining Artificial Neural Networks and Elastically Collective Nonlinear Langevin Equation. Polymers, 14(8), 1573. https://doi.org/10.3390/polym14081573






