Experimental and Theoretical Analysis of Mechanical Properties of Graphite/Polyethylene Terephthalate Nanocomposites
Abstract
:1. Introduction
2. Experimental Work
2.1. Materials
2.2. Preparation of PET-GNP Composites
2.3. Characterization of PET-GNP Composites
3. Results and Discussions
3.1. Tensile Properties of PET-GNP Nanocomposites
3.2. DMTA of PET-GNP Nanocomposites
4. Constitutive Modelling of Filled Polymers
4.1. Small Strain-Based Particle-Filled Polymer Models
4.2. Large Strain-Based Particle-Filled Polymer Models
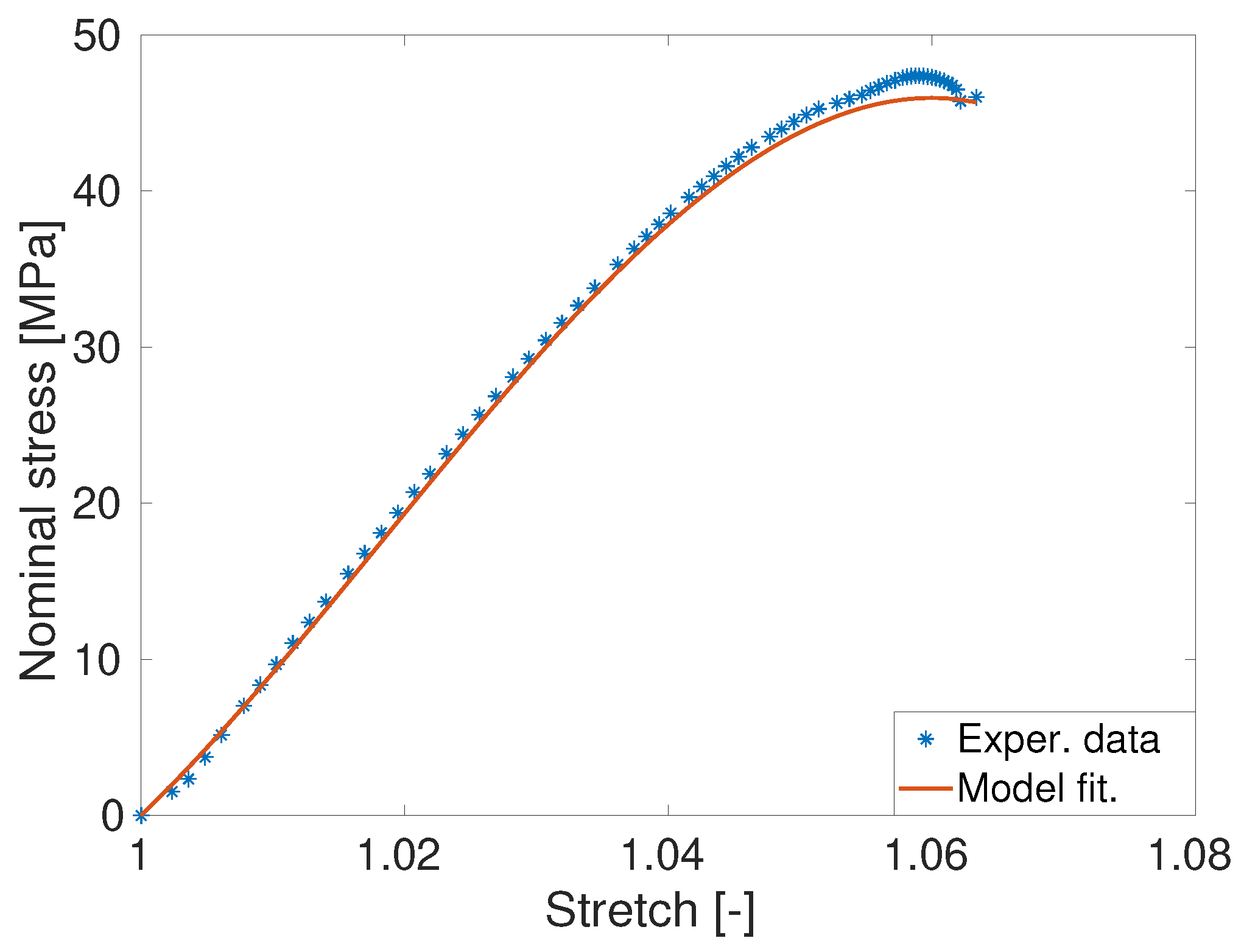
4.3. Parameter Identification and Model Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ahmad, D.; Ajaj, R.M. Multiaxial mechanical characterization of latex skin for morphing wing application. Polym. Test. 2022, 106, 107408. [Google Scholar] [CrossRef]
- Collins, I.; Hossain, M.; Dettmer, W.; Masters, I. Flexible membrane structures for wave energy harvesting: A review of the developments, materials and computational modelling approaches. Renew. Sustain. Energy Rev. 2021, 151, 111478. [Google Scholar] [CrossRef]
- Sun, X.; Sun, H.; Li, H.; Peng, H. Developing Polymer Composite Materials: Carbon Nanotubes or Graphene? Adv. Mater. 2013, 25, 5153–5176. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.L.; Zhang, M.Q.; Rong, M.Z.; Friedrich, K. Tensile performance improvement of low nanoparticles filled-polypropylene composites. Compos. Sci. Technol. 2002, 62, 1327–1340. [Google Scholar] [CrossRef]
- Magaraphan, R.; Lilayuthalert, W.; Sirivat, A.; Schwank, J.W. Preparation, structure, properties and thermal behavior of rigid-rod polyimide/montmorillonite nanocomposites. Compos. Sci. Technol. 2001, 61, 1253–1264. [Google Scholar] [CrossRef]
- Pang, H.; Xu, L.; Yan, D.-X.; Li, Z.-M. Conductive polymer composites with segregated structures. Prog. Polym. Sci. 2014, 39, 1908–1933. [Google Scholar] [CrossRef]
- Li, B.; Zhong, W.H. Review on polymer/graphite nanoplatelet nanocomposites. J. Mater. Sci. 2011, 46, 5595–5614. [Google Scholar] [CrossRef]
- Sengupta, R.; Bhattacharya, M.; Bandyopadhyay, S.; Bhowmick, A.K. A review on the mechanical and electrical properties of graphite and modified graphite reinforced polymer composites. Prog. Polym. Sci. 2011, 36, 638–670. [Google Scholar] [CrossRef]
- Bose, S.; Khare, R.A.; Moldenaers, P. Assessing the strengths and weaknesses of various types of pre-treatments of carbon nanotubes on the properties of polymer/carbon nanotubes composites: A critical review. Polymer 2010, 51, 975–993. [Google Scholar] [CrossRef] [Green Version]
- Paran, S.M.R.; Abdorahimi, M.; Shekarabi, A.; Khonakdar, H.A.; Jafari, S.H.; Saeb, M.R. Modeling and analysis of nonlinear elastoplastic behavior of compatibilized polyolefin/polyester/clay nanocomposites with emphasis on interfacial interaction exploration. Compos. Sci. Technol. 2018, 154, 92–103. [Google Scholar] [CrossRef]
- Paran, S.M.R.; Abdorahimi, M.; Naderi, G.; Javadi, F.; Shemshadi, R.; Saeb, M.R. Experimental and theoretical analyses on mechanical properties and stiffness of hybrid graphene/graphene oxide reinforced EPDM/NBR nanocomposites. Mater. Today Commun. 2022, 22, 100763. [Google Scholar] [CrossRef]
- Hussain, F.; Hojjati, M.; Okamoto, M.; Gorga, R.E. Polymer matrix nanocomposites, processing, manufacturing, and application: An overview. J. Compos. Mater. 2006, 40, 1511–1575. [Google Scholar] [CrossRef]
- Ajorloo, M.; Fasihi, M.; Ohshima, M.; Taki, K. How are the thermal properties of polypropylene/graphene nanoplatelet composites affected by polymer chain configuration and size of nanofiller? Mater. Des. 2019, 181, 108068. [Google Scholar] [CrossRef]
- Khanam, P.N.; AlMaadeed, M.A.; Ouederni, M.; Mayoral, B.; Hamilton, A.; Sun, S. Effect of two types of graphene nanoplatelets on the physico-mechanical properties of linear low-density polyethylene composites. Adv. Manuf. Polym. Compos. Sci. 2016, 2, 67–73. [Google Scholar]
- Um, J.G.; Jun, Y.S.; Alhumade, H.; Krithivasan, H.; Luia, G.; Yu, A. Investigation of the size effect of graphene nano-platelets (GnPs) on the anti-corrosion performance of polyurethane/GnP composites. RSC Adv. 2018, 8, 17091–17100. [Google Scholar] [CrossRef] [Green Version]
- Emblem, A.; Emblem, H. Materials and Processes. In Packaging Technology: Fundamentals; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Schneevogt, H.; Stelzner, K.; Yilmaz, B.; Abali, B.E.; Klunker, A.; Voellmecke, C. Sustainability in additive manufacturing: Exploring the mechanical potential of recycled PET filaments. Compos. Adv. Mater. 2021, 30, 1–8. [Google Scholar] [CrossRef]
- Shamsi, R.; Sadeghi, G.M.M.; Vahabi, H.; Seyfi, J.; Sheibani, R.; Zarrintaj, P.; Laoutid, F.; Saeb, M.R. Hopes Beyond PET Recycling: Environmentally Clean and Engineeringly Applicable. J. Polym. Environ. 2019, 27, 2490–2508. [Google Scholar] [CrossRef]
- Jabarin, S. Poly(ethylene terephthalate): Chemistry and preparation. In Polymeric Materials Encyclopedia; Salamone, J., Ed.; CRC Press: Boca Raton, FL, USA, 1996; pp. 6079–6085. ISBN 084932470X. [Google Scholar]
- Yang, B.; Chen, J.; Su, L.F.; Miao, J.B.; Chen, P.; Qian, J.S.; Xia, R.; Jun, Y.S.Y.S.; Alhumade, H.; Krithivasan, H.; et al. Melt crystallization and thermal properties of graphene platelets (GNPs) modified recycled polyethylene terephthalate (RPET) composites: The filler network analysis. Polym. Test. 2019, 77, 105869. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, C.; Wang, B.; Chen, Y.; Wang, H. In situ polymerization and characterization of graphite nanoplatelet/poly (ethylene terephthalate) nanocomposites for construction of melt-spun fibers. RSC Adv. 2017, 53, 33477–33485. [Google Scholar] [CrossRef] [Green Version]
- Chowreddy, R.R.; Varhaug, K.N.; Rapp, F. Recycled polyethylene terephthalate/carbon nanotube composites with improved processability and performance. J. Mater. Sci. 2018, 53, 7017–7029. [Google Scholar] [CrossRef]
- Xie, F.; Liang, H.; Ren, X.J.; Chen, Y.F. Isothermal crystallization of PET/PTT-CNTs composites. Adv. Mater. Res. 2013, 750–752, 191–194. [Google Scholar] [CrossRef]
- Tasic, A.; Rusmirovic, J.D.; Nikolic, J.; Bozic, A.; Pavlovic, V.; Marinkovic, A.D.; Uskokovic, P.S. Effect of the vinyl modification of multi-walled carbon nanotubes on the performances of waste poly (ethylene terephthalate)-based nanocomposites. J. Compos. Mater. 2017, 51, 491–505. [Google Scholar] [CrossRef]
- Zhang, H.B.; Zheng, W.G.; Yan, Q.; Yang, Y.; Wang, J.W.; Lu, Z.H.; Ji, G.Y.; Yu, Z.Z. Electrically conductive polyethylene terephthalate/graphene nanocomposites prepared by melt compounding. Polymer 2010, 51, 1191–1196. [Google Scholar] [CrossRef]
- Mallakpour, S.; Behranvand, V. Recycled PET/MWCNT-ZnO quantum dot nanocomposites: Adsorption of Cd (II) ion, morphology, thermal and electrical conductivity properties. Chem. Eng. J. 2017, 313, 873–881. [Google Scholar] [CrossRef]
- Barbosa, C.N.; Goncalves, F.; Viana, J.C. Nano and hybrid composites based on poly (ethylene terephthalate): Blending and characterization. Adv. Polym. Technol. 2014, 33, 21397. [Google Scholar] [CrossRef]
- Inuwa, I.M.; Arjmandi, R.; Ibrahim, A.N.; Haafiz, A.K.M.; Wong, S.L.; Majeed, K.; Hassan, A. Enhanced mechanical and thermal properties of hybrid graphene nanoplatelets/multiwall carbon nanotubes reinforced polyethylene terephthalate nanocomposites. Fibers Polym. 2016, 17, 1657–1666. [Google Scholar] [CrossRef]
- Mansor, M.R.; Fadzullah, S.H.S.M.; Masripan, N.A.B.; Omar, G.; Akop, M.Z. Comparison Between Functionalized Graphene and Carbon Nanotubes: Effect of Morphology and Surface Group on Mechanical, Electrical, and Thermal Properties of Nanocomposites. In Functionalized Graphene Nanocomposites and Their Derivatives; Elsevier: Amsterdam, The Netherlands, 2019; pp. 177–204. [Google Scholar]
- Alshammari, B.A.; Wilkinson, A.N.; Almutairi, G. Electrical, Thermal, and Morphological Properties of Poly (ethylene terephthalate)-Graphite Nanoplatelets Nanocomposites. Int. J. Polym. Sci. 2017, 6758127. [Google Scholar] [CrossRef] [Green Version]
- Yasmin, A.; Daniel, I.M. Mechanical and thermal properties of graphite platelet/epoxy composites. Polymer 2004, 45, 8211–8219. [Google Scholar] [CrossRef]
- Al-Jabareen, A.; Al-Bustami, H.; Harel, H.; Marom, G. Improving the oxygen barrier properties of polyethylene terephthalate by graphite nanoplatelets. J. Appl. Polym. Sci. 2013, 128, 1534–1539. [Google Scholar] [CrossRef]
- King, J.A.; Klimek, D.R.; Miskioglu, I.; Odegard, G.M. Mechanical properties of graphene nanoplatelet/epoxy composites. J. Appl. Polym. Sci. 2013, 128, 4217–4223. [Google Scholar] [CrossRef]
- Alshammari, B.A.; Al-Mubaddel, F.S.; Karim, M.R.; Hossain, M.; Al-Mutairi, A.S.; Wilkinson, A.N. Addition of Graphite Filler to Enhance Electrical, Morphological, Thermal, and Mechanical Properties in Poly (Ethylene Terephthalate): Experimental Characterization and Material Modeling. Polymers 2019, 11, 1411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramanathan, T.; Stankovich, S.; Dikin, D.; Liu, H.; Shen, H.; Nguyen, S.; Brinson, L. Graphitic nanofillers in PMMA nanocomposites-an investigation of particle size and dispersion and their influence on nanocomposite properties. J. Polym. Sci. Part B Polym. Phys. 2007, 45, 2097–2112. [Google Scholar] [CrossRef]
- Li, M.; Jeong, Y.G. Poly (ethylene terephthalate)/exfoliated graphite nanocomposites with improved thermal stability, mechanical and electrical properties. Compos. Part A Appl. Sci. Manuf. 2011, 42, 560–566. [Google Scholar] [CrossRef]
- Li, M.; Jeong, Y.G. Preparation and Characterization of High Performance Poly (trimethylene terephthalate) Nanocomposites Reinforced with Exfoliated Graphite. Macromol. Mater. Eng. 2011, 296, 159–167. [Google Scholar] [CrossRef]
- Li, M.; Jeong, Y.G. Influences of exfoliated graphite on structures, thermal stability, mechanical modulus, and electrical resistivity of poly (butylene terephthalate). J. Appl. Polym. Sci. 2012, 125, 532–540. [Google Scholar] [CrossRef]
- Zheng, W.; Lu, X.; Wong, S.C. Electrical and mechanical properties of expanded graphite-reinforced high-density polyethylene. J. Appl. Polym. Sci. 2004, 91, 2781–2788. [Google Scholar] [CrossRef]
- Zheng, W.; Wong, S.C. Electrical conductivity and dielectric properties of PMMA/expanded graphite composites. Compos. Sci. Technol. 2003, 63, 225–235. [Google Scholar] [CrossRef]
- Zhang, M.; Li, D.J.; Wu, D.F.; Yan, C.H.; Lu, P.; Qiu, G.M. Poly (ethylene terephthalate)/expanded graphite conductive composites: Structure, properties, and transport behavior. J. Appl. Polym. Sci. 2008, 108, 1482–1489. [Google Scholar] [CrossRef]
- Guth, L. Theory of filler reinforcement. J. Appl. Phys. 1945, 16, 20–25. [Google Scholar] [CrossRef]
- Guth, L.; Gold, O. On the hydrodynamical theory of the viscosity of suspensions. Phys. Rev. 1938, 53, 322. [Google Scholar]
- Bergstroem, J.; Boyce, M.C. Mechanical behaviour of particle filled elastomers. Rubber Chem. Technol. 1999, 72, 633. [Google Scholar] [CrossRef]
- Possart, P.S.M.H.G. Hyperelastic models for rubber-like materials: Consistent tangent operators and suitability for Treloar’s data. Arch. Appl. Mech. 2012, 82, 1183–1217. [Google Scholar]
- Hossain, M.; Steinmann, P. More hyperelastic models for rubber-like materials: Consistent tangent operator and comparative study. J. Mech. Behav. Mater. 2013, 22, 27–50. [Google Scholar] [CrossRef]
- Hossain, M.; Kabir, N.; Amin, A.F.M.S. Eight-chain and full-network models and their modified versions for rubber hyperelasticity: A comparative study. J. Mech. Behav. Mater. 2015, 24, 11–24. [Google Scholar] [CrossRef] [Green Version]
- Shen, S.; Zhong, D.; Qu, S.; Xiao, R. A hyperelastic-damage model based on the strain invariants. Extrem. Mech. Lett. 2022, 52, 101641. [Google Scholar] [CrossRef]
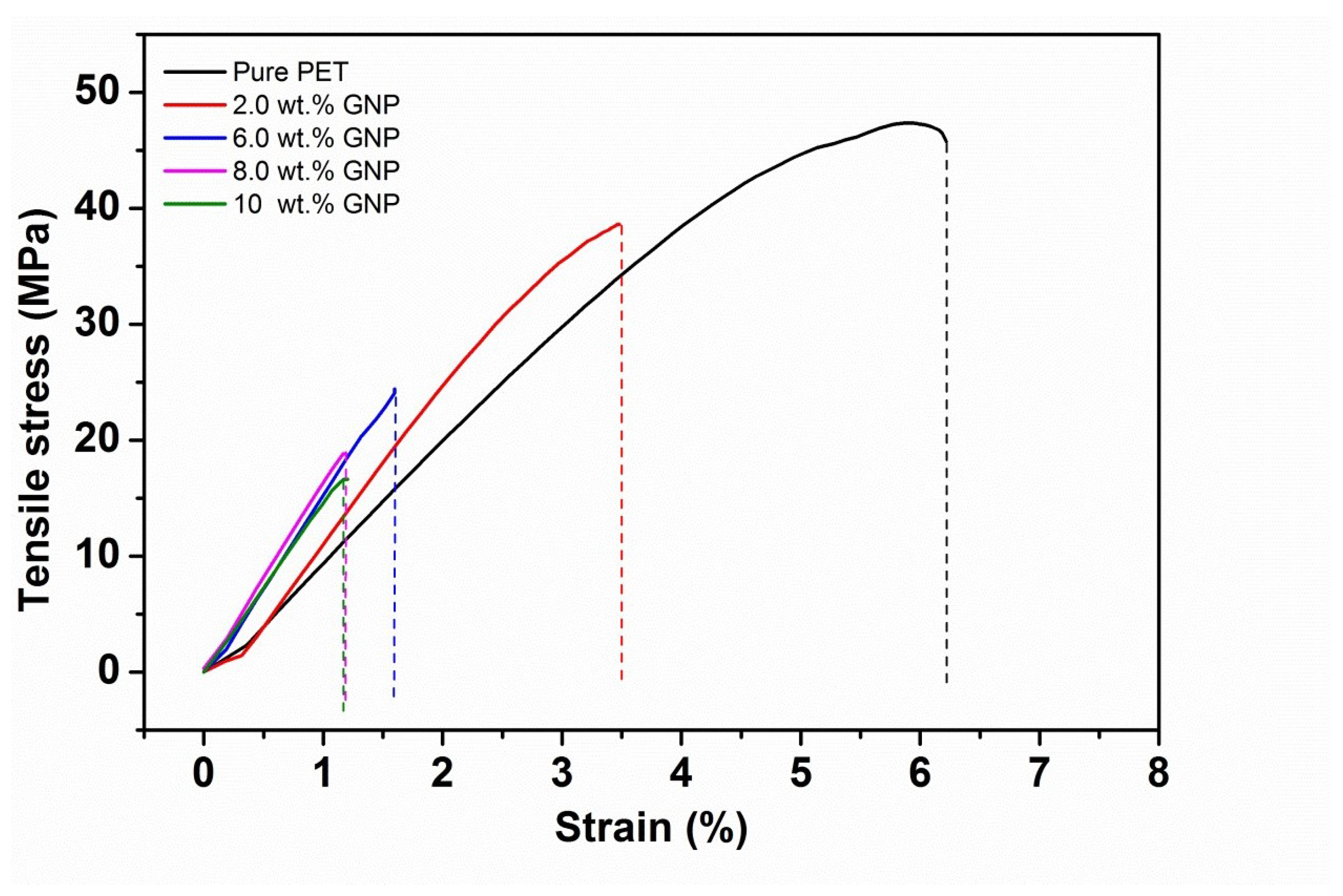
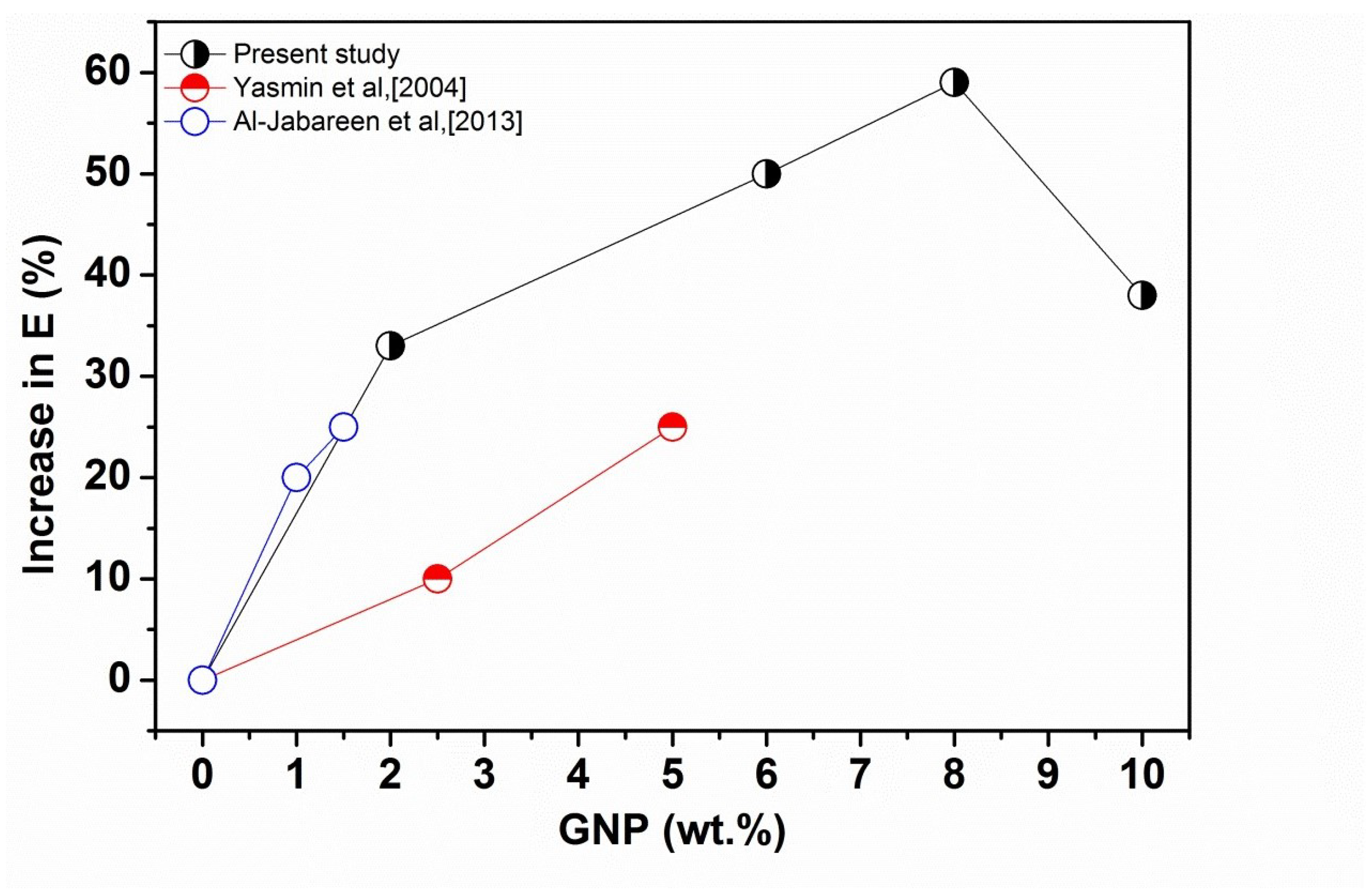
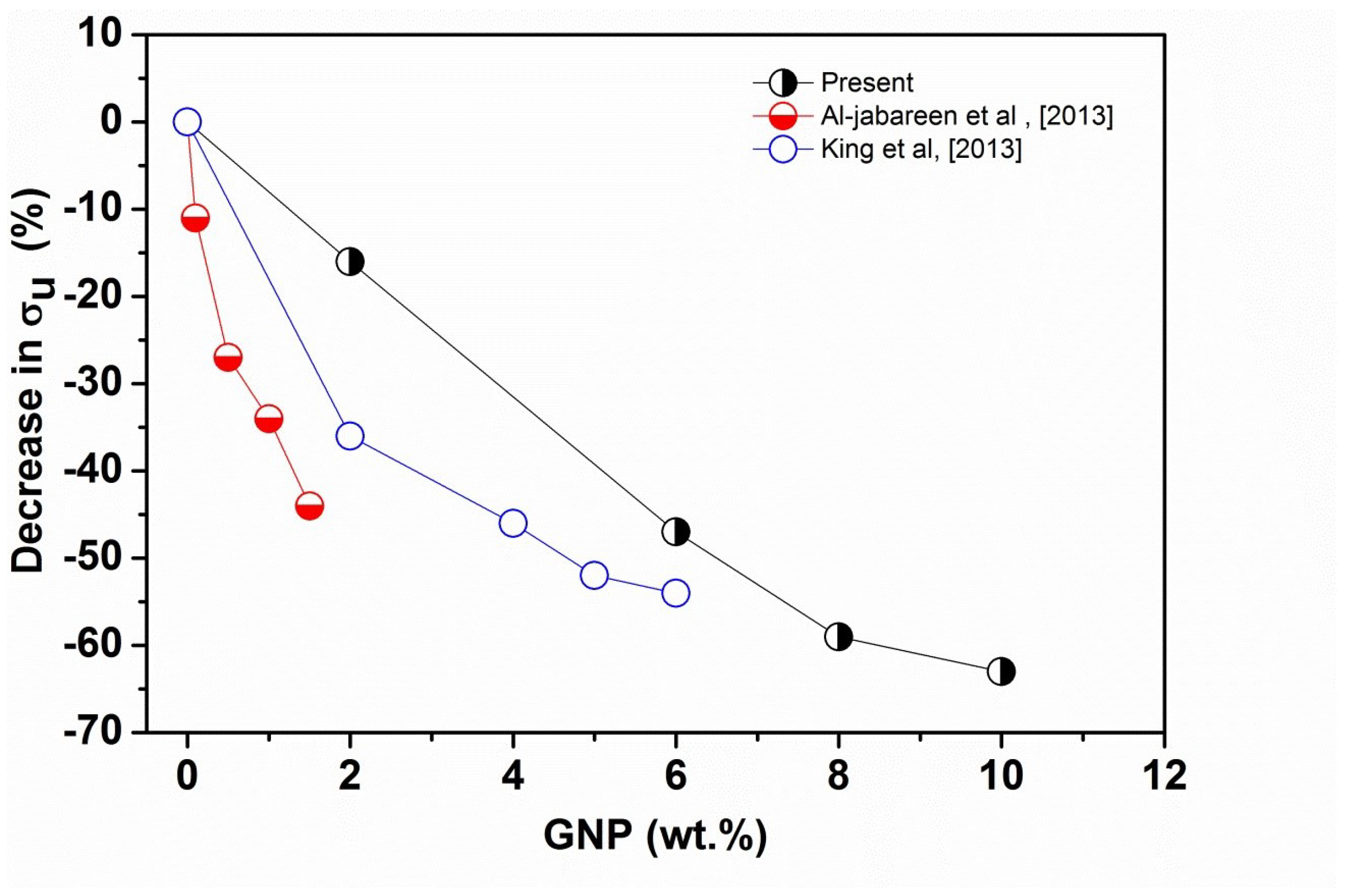
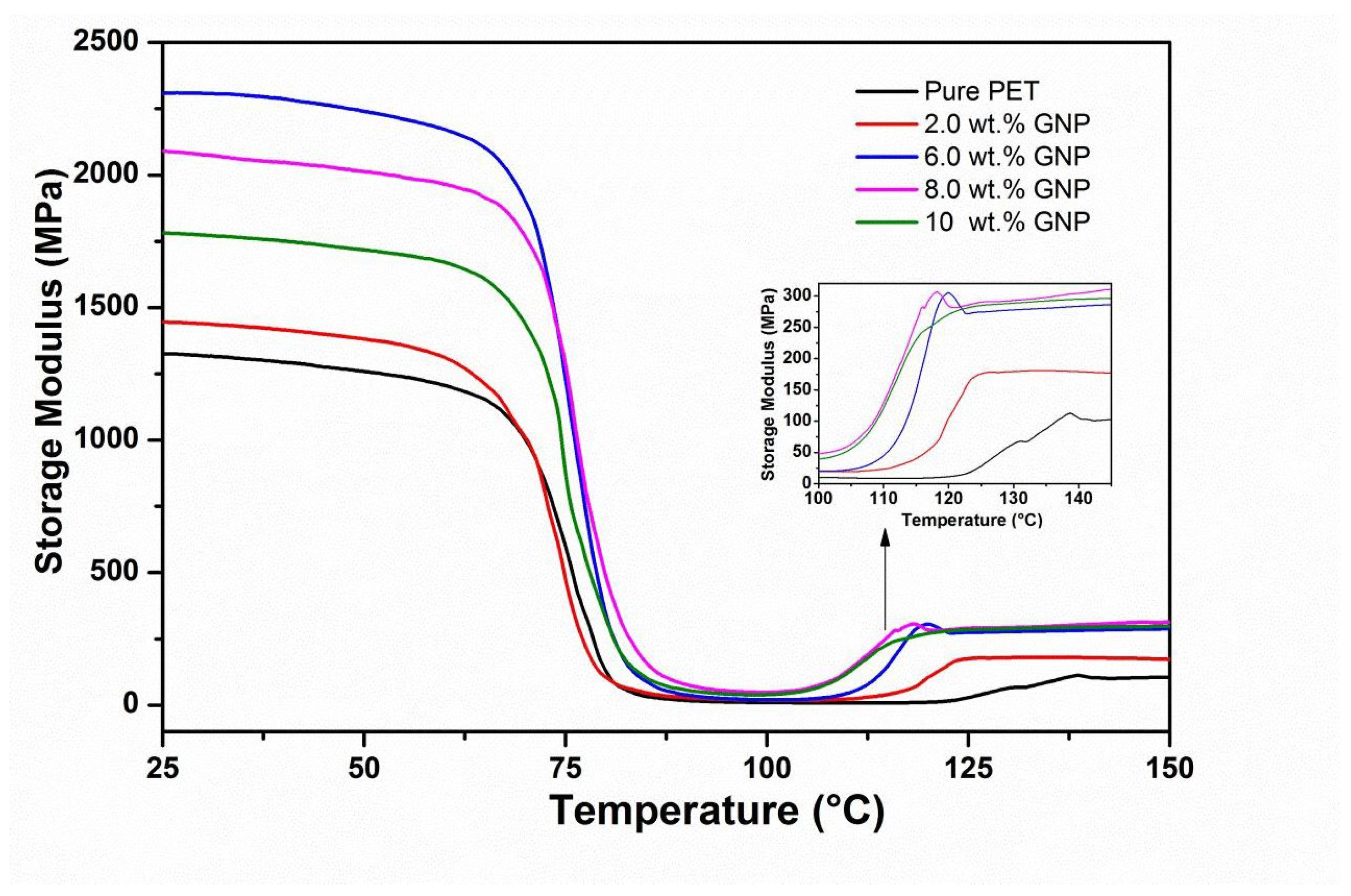
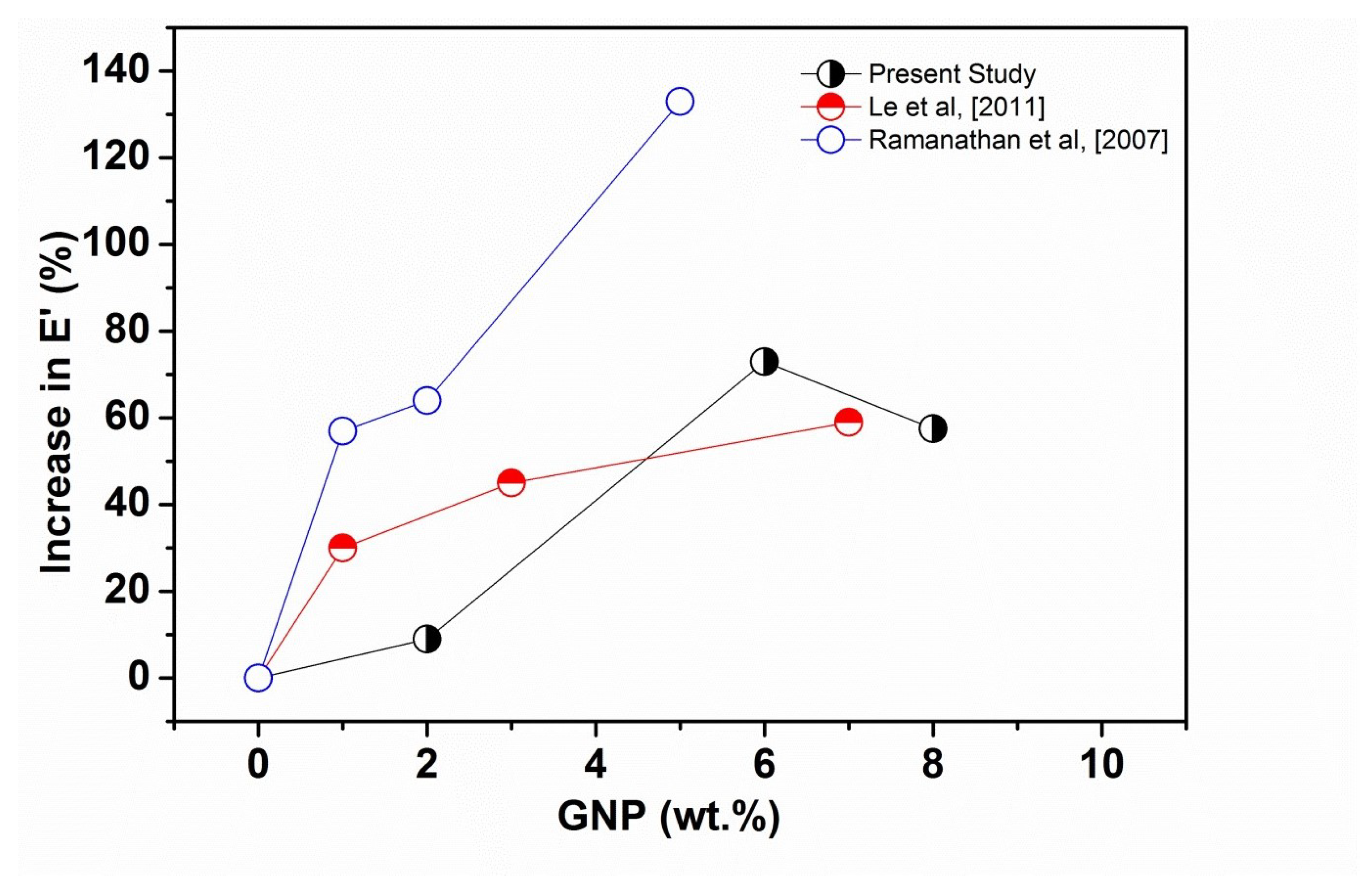
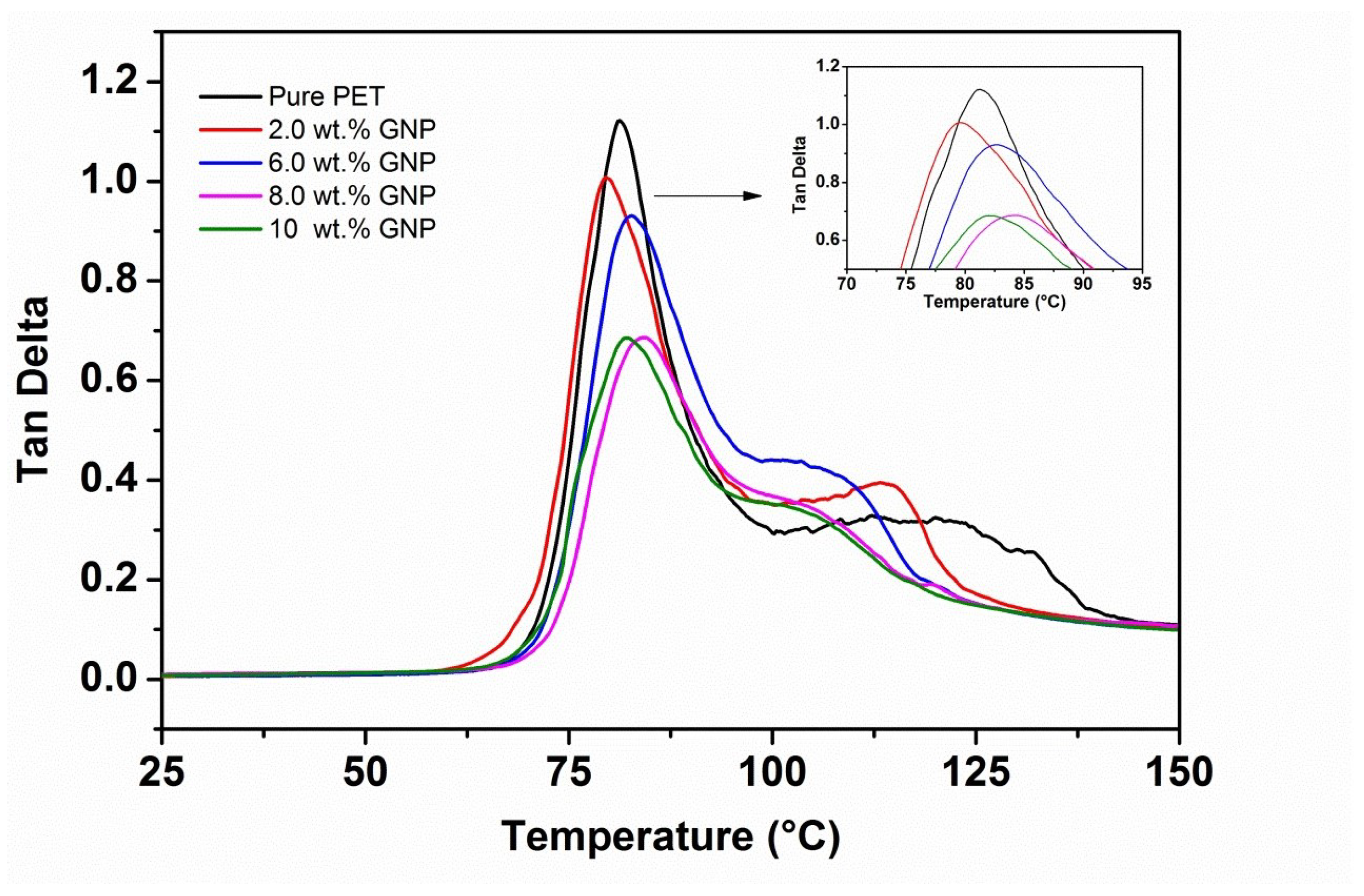


| GNP (wt.%) | Tensile Modulus (MPa) | Tensile Strength (MPa) | Elongation at Break % |
|---|---|---|---|
| 0 | 1073.3 ± 15.7 | 45.8 ± 2.3 | 6.3 ± 1.9 |
| 2 | 1429.5 ± 42.0 | 38.6 ± 4.7 | 3.4 ± 0.6 |
| 6 | 1611.3 ± 53.0 | 24.4 ± 3.4 | 1.6 ± 0.1 |
| 8 | 1708.7 ± 65.0 | 18.8 ± 1.3 | 1.2 ± 0.1 |
| 10 | 1443.2 ± 71.9 | 16.8 ± 2.5 | 1.2 ± 0.3 |
| GNP (wt.%) | E (MPa) at 25 °C (MPa) | E (MPa) at 100 °C (MPa) | (°C) | at |
|---|---|---|---|---|
| 0 | 1330 ± 92 | 10.0 ± 2.5 | 80.5 ± 1.3 | 1.15 ± 0.10 |
| 2 | 1447 ± 88 | 22.9 ± 2.2 | 80.7 ± 0.5 | 0.93 ± 0.02 |
| 6 | 2308 ± 62 | 44.6 ± 5.2 | 82.7 ± 0.5 | 0.93 ± 0.02 |
| 8 | 2095 ± 84 | 129.4 ± 14 | 83.5 ± 0.7 | 0.69 ± 0.04 |
| 10 | 1782 ± 33 | 120.0 ± 44 | 82.1 ± 0.9 | 0.69 ± 0.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshammari, B.A.; Hossain, M.; Alenad, A.M.; Alharbi, A.G.; AlOtaibi, B.M. Experimental and Theoretical Analysis of Mechanical Properties of Graphite/Polyethylene Terephthalate Nanocomposites. Polymers 2022, 14, 1718. https://doi.org/10.3390/polym14091718
Alshammari BA, Hossain M, Alenad AM, Alharbi AG, AlOtaibi BM. Experimental and Theoretical Analysis of Mechanical Properties of Graphite/Polyethylene Terephthalate Nanocomposites. Polymers. 2022; 14(9):1718. https://doi.org/10.3390/polym14091718
Chicago/Turabian StyleAlshammari, Basheer A., Mokarram Hossain, Asma M. Alenad, Abdullah G. Alharbi, and Bandar M. AlOtaibi. 2022. "Experimental and Theoretical Analysis of Mechanical Properties of Graphite/Polyethylene Terephthalate Nanocomposites" Polymers 14, no. 9: 1718. https://doi.org/10.3390/polym14091718
APA StyleAlshammari, B. A., Hossain, M., Alenad, A. M., Alharbi, A. G., & AlOtaibi, B. M. (2022). Experimental and Theoretical Analysis of Mechanical Properties of Graphite/Polyethylene Terephthalate Nanocomposites. Polymers, 14(9), 1718. https://doi.org/10.3390/polym14091718







