Experimental and Numerical Investigation on Fatigue Properties of Carbon Fiber Cross-Ply Laminates in Hygrothermal Environments
Abstract
:1. Introduction
2. Specimens and Tests
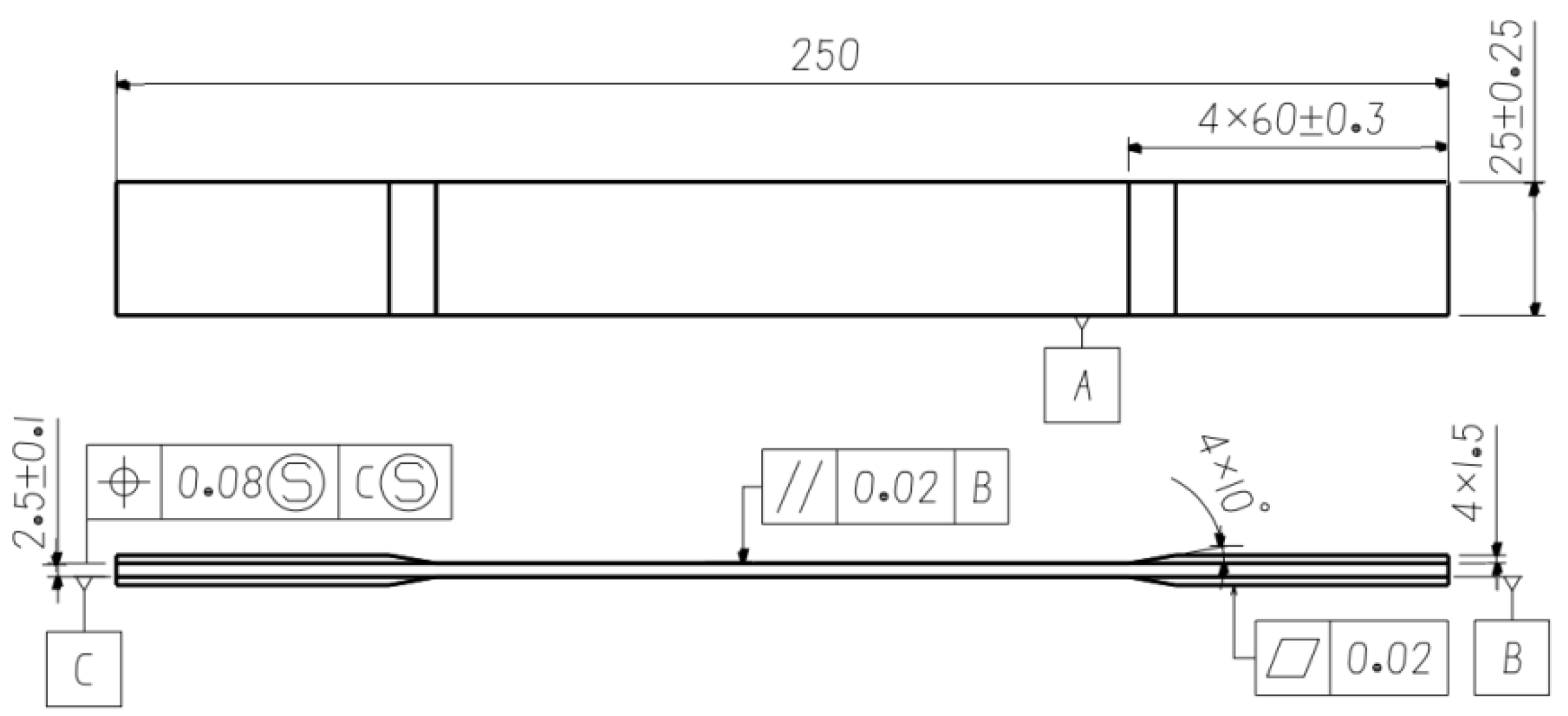
2.1. Specimen Design and Manufacture
2.2. Experimental Procedures
2.2.1. Moisture Absorption
2.2.2. Tensile Fatigue Tests
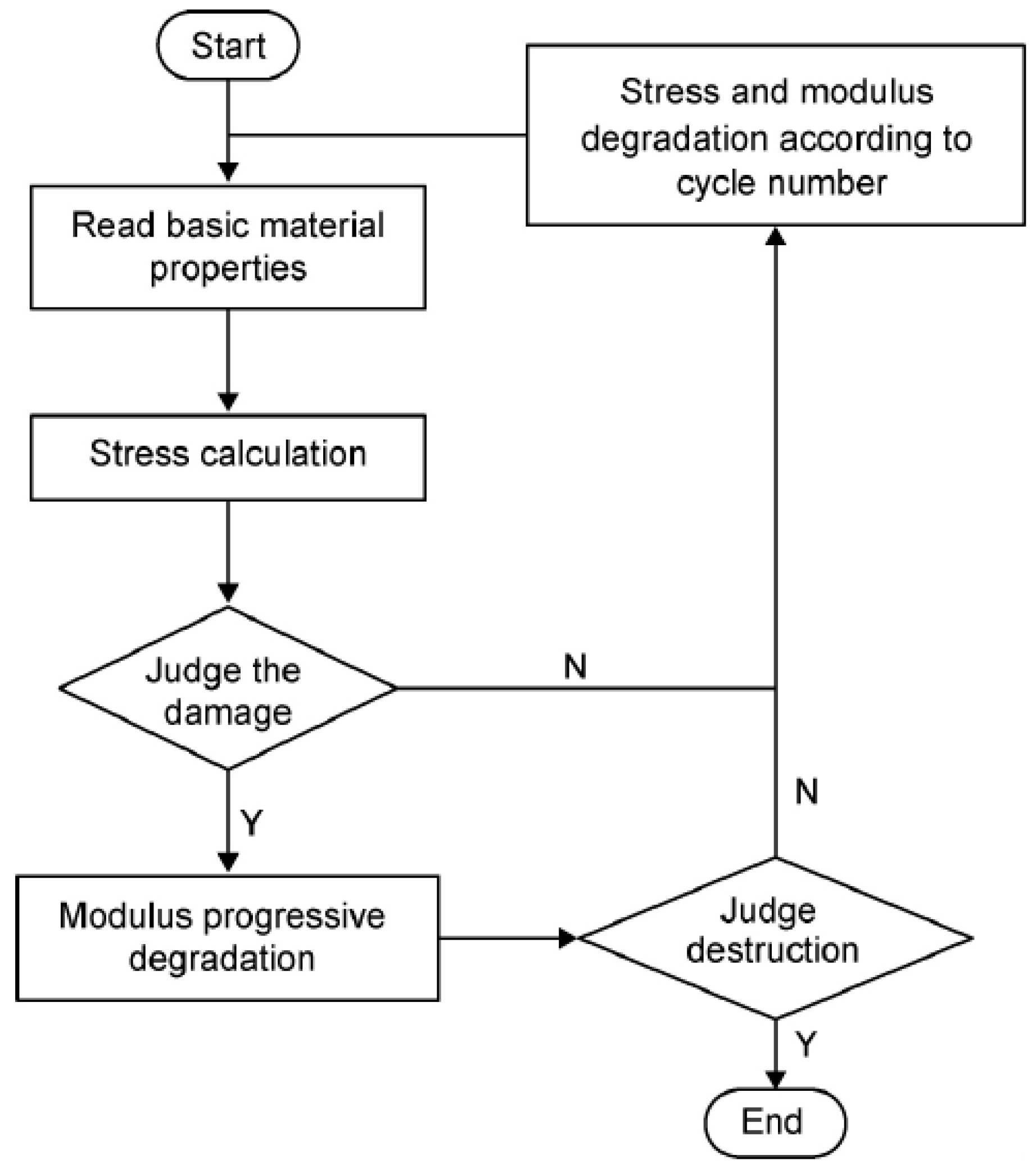
3. Numerical Study
3.1. Basic Property Degradation
3.2. Fatigue Failure Criterion and Property Degradation Model
- Longitudinal fiber tensile failure:
- Longitudinal fiber compressive failure:
- Transverse fiber tensile failure:
- Transverse fiber compressive failure:
- Fiber-matrix shear failure:where and are the components of normal and shear stress. and are the ris1ual shear strength in the 1-3 and 2-3 planes after n cycles.
3.3. Fatigue Finite Element Model
4. Results and Discussion
4.1. Tensile Tests
4.2. Fatigue Test
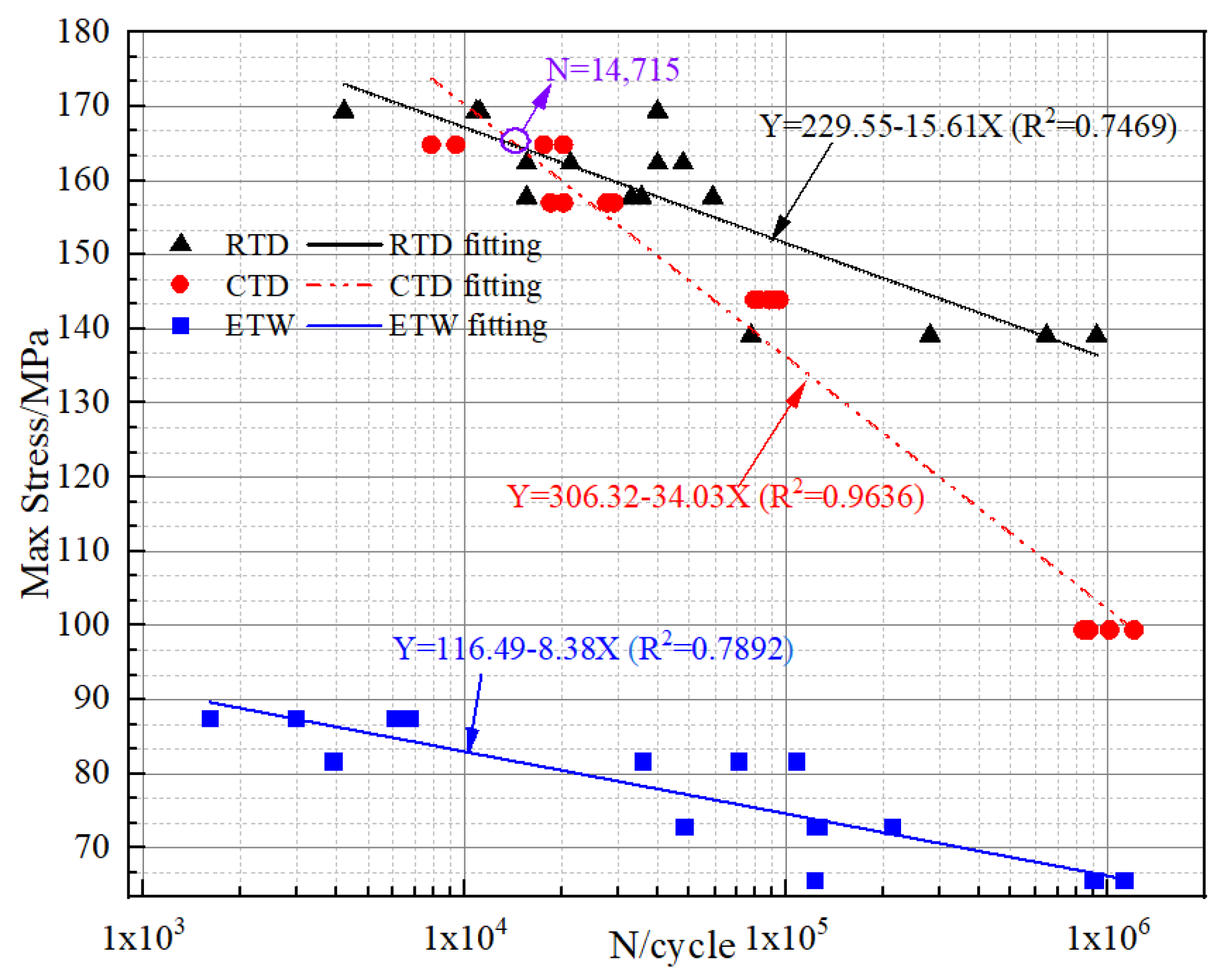
4.2.1. Hygrothermal Environment on the Fatigue Properties
4.2.2. Failure Mode Analysis
4.3. Finite Element Results
4.3.1. Model Verification
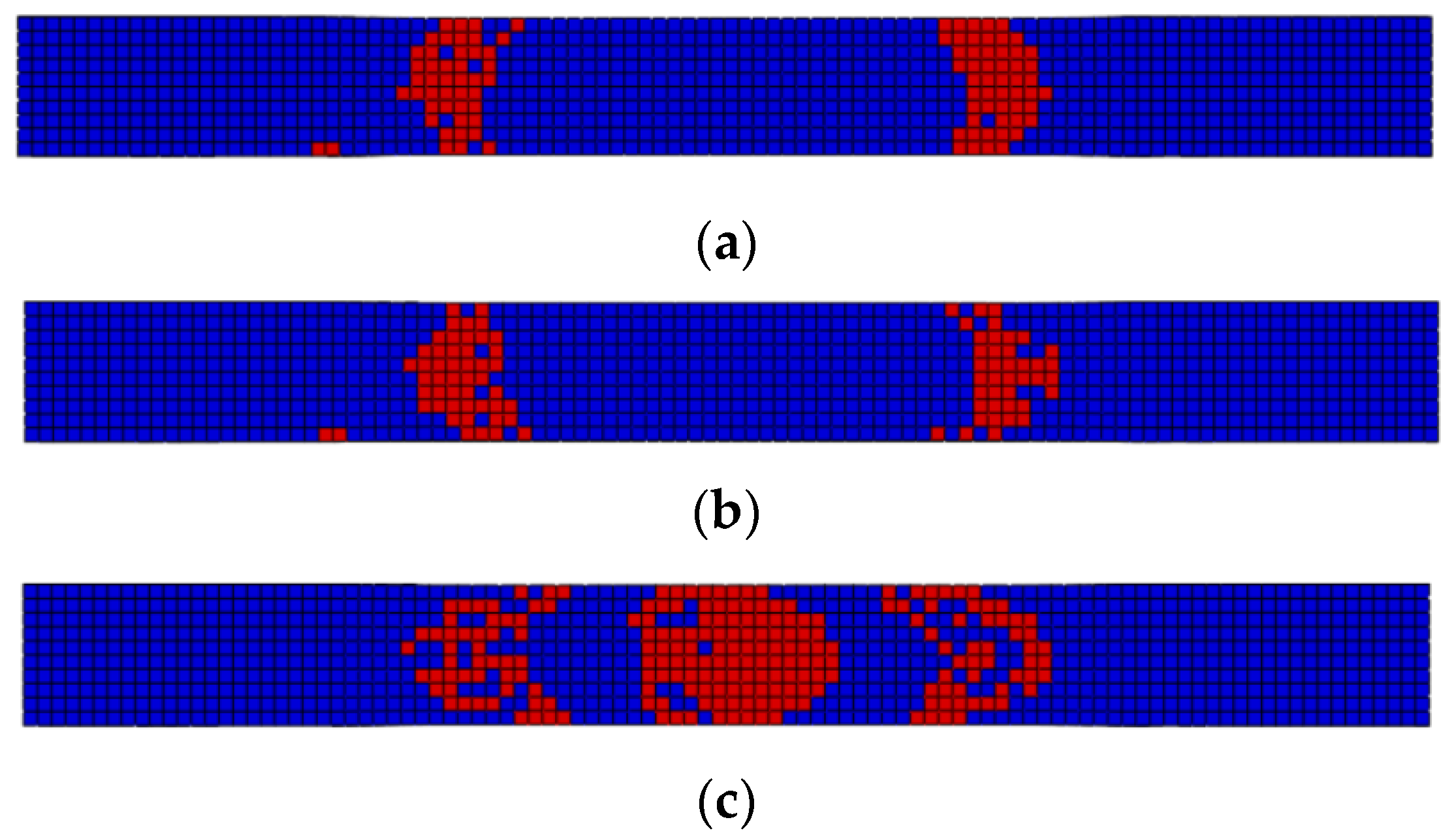
4.3.2. Failure Process Analysis
4.3.3. Effect of Different Environments on Fatigue Life
5. Conclusions
- Compared with the RTD environment, the tensile strength in CTD and ETW increased by 12.84% and decreased by −37.11%, and the tensile modulus increased by 12.67% and decreased by −8.54%, respectively.
- Only cool temperatures have obvious negative effects on the fatigue life dispersion of the test specimens, and high temperature and high moisture have no effect on that.
- The decline rate of the S–N curve is the largest in CTD and the smallest in ETW. Cool temperature has a positive effect on low-cycle fatigue but has a negative effect on high-cycle fatigue.
- When N = 106, the fatigue limit in CTD and ETW is, respectively, decreased by 24.88% and 51.28% of that in RTD. The temperature plays a large role on the fatigue limit and the combination of high temperature and moisture has a much larger effect on that.
- The failure morphology in three environments is similar, including fiber fracture, matrix cracking and delamination damage. However, the severity of failure is different, the failure of specimens in ETW is the most significant as well as the least in CTD. The fatigue morphology in ETW shows the obvious necking phenomenon since the matrix was seriously weakened.
- Numerical analysis shows that the effect of temperature on fatigue property is significantly stronger than that of moisture absorption, and when the temperature exceeds 40 °C, the effects of moisture absorption are great.
- A method for determining the environmental factors of fatigue life of angle-ply composite materials is proposed, which can be used for the life prediction of that in different environmental conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.; Cheng, X.Q.; Zhang, J.; Wang, S.; Cheng, Y.; Zhang, T. Experimental and numerical investigation of composite box joint under tensile load. Compos. B Eng. 2016, 107, 75–83. [Google Scholar] [CrossRef]
- Liu, S.F.; Zhang, J.; Zhang, Q.; Guo, X.; Cheng, X.Q.; Bao, J.W. An investigation of hygrothermal effects on adhesive materials and double lap shear joints of CFRP composite laminates. Compos. B Eng. 2016, 91, 431–440. [Google Scholar] [CrossRef]
- Cheng, X.Q.; Zhang, J.; Bao, J.W.; Zeng, B.Y.; Cheng, Y.J.; Hu, R.W. Low-velocity impact performance and effect factor analysis of scarf-repaired composite laminates. Int. J. Impact Eng. 2018, 111, 85–93. [Google Scholar] [CrossRef]
- Jin, H. Study on the fatigue properties of carbon fiber composite laminates under environmental conditions. Sci. Technol. Innov. Her. 2014, 1, 76–77. [Google Scholar]
- Cheng, X.Q.; Yang, M.M.; Zhang, J.; Zhang, Q.; Zhang, J.K. Thermal behavior and tensile properties of composite joints with bonded embedded metal plate under thermal circumstance. Compos. B Eng. 2016, 99, 340–347. [Google Scholar]
- Sousa, J.M.; Correia, J.R.; Cabral-Fonseca, S. Some permanent effects of hygrothermal and outdoor ageing on a structural polyurethane adhesive used in civil engineering applications. Int. J. Adhes. Adhes. 2018, 84, 406–419. [Google Scholar] [CrossRef]
- Du, Y.; Ma, Y.E. Fatigue performance of fiber reinforced polymer composites under hygrothermal environment—A review. Acta Mater. Compos. Sin. 2021, 19, 1–15. [Google Scholar]
- Venkatesha, B.K.; Saravanan, K.; Anand, B. Effect of moisture absorption on woven bamboo/glass fiber reinforced epoxy hybrid composites. Mater. Today Proc. 2021, 45, 216–221. [Google Scholar] [CrossRef]
- Bachchan, A.A.; Das, P.P.; Chaudhary, V. Effect of moisture absorption on the properties of natural fiber reinforced polymer composites: A review. Mater. Today Proc. 2021, 49, 3403–3408. [Google Scholar] [CrossRef]
- Bao, L.R.; Yee, A.F. Moisture diffusion and hygrothermal aging in bismaleimide matrix carbon fiber composites—Part I: Uni-weave composites. Compos. Sci. Technol. 2002, 62, 2099–2110. [Google Scholar] [CrossRef]
- Wu, F.Q.; Yao, W.X. Residual strength degradation model of fiber reinforced plastic. J. Nanjing Univ. Aeronaut. Astronaut. 2008, 40, 517–520. [Google Scholar]
- Meziere, Y.; Bunsell, A.R.; Favrya, Y.; Teissedrea, J.C.; Dob, A.T. Large strain cyclic fatigue testing of unidirectional carbon fiber reinforced epoxy resin. Compos. Part A Appl. Sci. Manuf. 2005, 36, 1627–1636. [Google Scholar] [CrossRef]
- Karad, S.K.; Jones, F.R.; Attwood, D. Moisture absorption by cyanate ester modified epoxy resin matrices. Part II. The reverse thermal effect. Polymer 2002, 43, 5643–5649. [Google Scholar] [CrossRef]
- Guo, F.-L.; Guo, P.; Huang, Y.L.; Hu, N.; Fu, S.-Y. Multiscale modeling of mechanical behaviors of carbon fiber reinforced epoxy composites subjected to hygrothermal aging. Compos. Struct. 2021, 256, 113098. [Google Scholar] [CrossRef]
- Guo, F.; Yan, Y.; Hong, Y.; Tian, Z.; Li, J. Prediction and optimization design for thermal expansion coefficients of three dimensional directional braided composites. Polym. Compos. 2019, 40, 2495–2509. [Google Scholar] [CrossRef]
- Ray, B.C. Temperature effect during humid ageing on interfaces of glass an carbon fibers reinforced epoxy composites. J. Colloid Interface Sci. 2006, 298, 111–117. [Google Scholar] [CrossRef]
- Yu, Z.G.; Yang, S.C.; Song, B.F. Comparison of wet and hot aging resistance of T700 and T300 carbon fiber strengthened epoxy resin composites. Mater. Mech. Eng. 2009, 33, 48–51. [Google Scholar]
- Sha, M.; Xiong, X.; Xu, M.R.; Zeng, B.Y.; Cheng, X.Q. Effect of hygrothermal environment on fatigue properties of composite materials. Hi Tech Fiber Appl. 2017, 42, 37–43. [Google Scholar]
- Chen, H.R.; Xi, Z.C.; He, X.D. Non-linear analysis of thermal deformations of composite laminates under transient thermal loading. J. Dalian Univ. Technol. 1994, 34, 280–286. [Google Scholar]
- Sethi, S.; Ray, B.C. Environmental effects on fiber reinforced polymeric composites: Evolving reasons and remarks on interfacial strength and stability. Adv. Colloid Interface Sci. 2015, 217, 43–67. [Google Scholar] [CrossRef]
- Kawai, M.; Yagihashi, Y.; Hoshi, H.; Iwahori, Y. Anisomorphic constant fatigue life diagrams for quasi-isotropic woven fabric carbon/epoxy laminates under different hygrothermal environments. Adv. Compos. Mater. 2013, 22, 79–98. [Google Scholar] [CrossRef]
- Mcbagonluri, F.; Garcia, K.; Hayes, M.; Verghese, K.N.E.; Lesko, J.J. The Characterization of fatigue and combined environment on durability performance of glass/vinyl ester composite for a new method for the processing of multifunction applications. Int. J. Fatigue 2000, 22, 53–64. [Google Scholar] [CrossRef]
- Malpot, A.; Touchard, S.; Bergamo. An investigation of the influence of moisture on fatigue damage mechanisms in a woven glass-fibre-reinforced PA66 composite using acoustic emission and infrared thermography. Compos. Part B Eng. 2017, 130, 11–20. [Google Scholar] [CrossRef]
- Kawai, M.; Yajima, S.; Hachinohe, A. High-temperature off-axis fatigue behavior of unidirectional carbon-fiber-reinforced composites with different resin matrices. Compos. Sci. Technol. 2001, 61, 1285–1302. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Lessard, L.B. Progressive fatigue damage modeling of composite materials, Part I: Modeling. J. Compos. Mater. 2000, 34, 1056–1080. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Lessard, L.B. Progressive fatigue damage modeling of composite materials, Part II: Material characterization and model verification. J. Compos. Mater. 2000, 34, 1081–1116. [Google Scholar] [CrossRef]
- Harper, P.W.; Hallett, S.R. A fatigue degradation law for cohesive interface elements-Development and application to composite materials. Int. J. Fatigue 2010, 32, 1774–1787. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.L.; Meng, Q.C.; Xu, M.R.; Zeng, B.Y.; Cheng, X.Q.; Sun, W. Tensile fatigue properties of carbon fiber reinforced composite orthogonal laminates after moisture absorption. J. Mater. Eng. 2021, 49, 169–177. [Google Scholar]
- D3479/D3479M-2012; Standard Test Method for Tension-Tension Fatigue of Polymer Matrix Composite Materials. American Society of Testing Materials International: West Conshehoken, PA, USA, 2012; pp. 1–6.
- HB7401-1996; People’s Republic of China Aviation Industry Standard. Moisture Absorption Test Method for Resin Matrix Composite Laminates under Hygrothermal Environment. Aviation Industry Corporation of China: Beijing, China, 1996.
- ASTM D5229/D5229M-2014; Standard Test Method for Moisture Absorption Properties and Equilibrium Conditioning of Polymer Matrix Composite Materials. American Society of Testing Materials International: West Conshehoken, PA, USA, 2014; pp. 1–6.
- Shan, M.; Zhao, L.; Hong, H.; Liu, F.; Zhang, J. A progressive fatigue damage model for composite structures in hygrothermal environments. Int. J. Fatigue 2018, 111, 299–307. [Google Scholar] [CrossRef]
- Spindel, J.; Haibach, E. Some considerations in the statistical determination of the slope of SN curves. In Statistical Analysis of Fatigue Data; American Society of Testing Materials International: West Conshehoken, PA, USA, 1981. [Google Scholar]





| Test Category | RTD | CTD | ETW |
|---|---|---|---|
| Moisture absorption | 3 | ||
| Static tensile | 3 | 3 | 3 |
| Tension fatigue | 16 | 16 | 16 |
| 54.3 | 54.3 | 680 | 680 | 3.26 | 116 | 1.42 | 1.23 | 45 |
| Tg0/°C | T0/°C | g/°C/c | a | b | c | d |
|---|---|---|---|---|---|---|
| 120 | 20 | 5 | 0.05 | 0.15 | 0.22 | 0.56 |
| E1/GPa | E2/GPa | E3/GPa | G12/GPa | G13/GPa | G23/GPa | ν12 | ν13 |
|---|---|---|---|---|---|---|---|
| 54.3 | 54.3 | 3.3 | 3.26 | 2.17 | 2.17 | 0.04 | 0.01 |
| ν23 | XT/MPa | XC/MPa | YT/MPa | YC/MPa | S12/MPa | S13/MPa | S23/MPa |
| 0.01 | 680 | 614.29 | 680 | 614.29 | 115.98 | 73.5 | 73.5 |
| Static Properties | RTD | CTD | ETW |
|---|---|---|---|
| Maximum load/kN | 16.85 | 19.02 | 10.75 |
| Elastic modulus/GPa | 12.10 | 13.63 | 11.07 |
| Tensile strength/MPa | 231.86 | 261.63 | 145.82 |
| Environments | Stress Level /% | Max Stress /MPa | Fatigue Life /Cycle |
|---|---|---|---|
| RTD | 60 | 139.1 | 645,427, 77,795, 280,167, 925,905 |
| 68 | 157.7 | 59,040, 15,576, 35,494, 33,051 | |
| 70 | 162.3 | 21,348, 15,576, 47,731, 39,773 | |
| 73 | 169.3 | 4213, 10,871, 11,142, 399,891 | |
| CTD | 38 | 99.4 | 874,358, 1,207,366, 1,015,576, 840,721 |
| 55 | 143.9 | 79,826, 88,424, 95,197, 82,243 | |
| 60 | 157 | 18,463, 29,169, 27,646, 20,312 | |
| 63 | 164.8 | 7866, 17,618, 9382, 20,316 | |
| ETW | 45 | 65.6 | 1,124,138, 122,504, 917,306, 895,576 |
| 50 | 72.9 | 213,125, 125,555, 123,153, 48,097 | |
| 56 | 81.7 | 70,968, 107,692, 35,724, 3890 | |
| 60 | 87.5 | 1608, 2988, 6730, 6038 |
| Stress Level | Life Cycle Number/Cycle | Logarithmic Life Number | ||||
|---|---|---|---|---|---|---|
| Test | Simulation | Error | Simulation | Test | Error | |
| RTD-60% | 482,324 | 546,000 | 13.2% | 5.53 | 5.74 | 3.8% |
| RTD-68% | 35,790 | 36,500 | 2.0% | 4.51 | 4.56 | 1.1% |
| RTD-70% | 31,107 | 17,500 | −43.7% | 4.45 | 4.24 | −4.72% |
| RTD-73% | 16,500 | 6800 | −58.8% | 4.08 | 3.83 | −6.1% |
| CTD-38% | 984,505 | 1,014,000 | 3.0% | 5.99 | 6.01 | 0.3% |
| CTD-55% | 86,423 | 50,000 | −42.1% | 4.94 | 4.70 | −4.9% |
| CTD-60% | 23,898 | 27,000 | 13.0% | 4.37 | 4.43 | 1.4% |
| CTD-63% | 13,796 | 12,000 | −13.0% | 4.11 | 4.08 | −0.7% |
| ETW-45% | 764,881 | 780,000 | 2.0% | 5.76 | 5.89 | 2.3% |
| ETW-50% | 127,483 | 123,750 | −3.0% | 5.05 | 5.09 | 0.8% |
| ETW-56% | 54,569 | 16,000 | −70.7% | 4.51 | 4.20 | −6.9% |
| ETW-60% | 4341 | 3400 | −21.7% | 3.57 | 3.53 | −1.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Zeng, B.; An, Z.; Xiong, X.; Cheng, X. Experimental and Numerical Investigation on Fatigue Properties of Carbon Fiber Cross-Ply Laminates in Hygrothermal Environments. Polymers 2022, 14, 1857. https://doi.org/10.3390/polym14091857
Xu M, Zeng B, An Z, Xiong X, Cheng X. Experimental and Numerical Investigation on Fatigue Properties of Carbon Fiber Cross-Ply Laminates in Hygrothermal Environments. Polymers. 2022; 14(9):1857. https://doi.org/10.3390/polym14091857
Chicago/Turabian StyleXu, Mingrui, Benyin Zeng, Ziqian An, Xin Xiong, and Xiaoquan Cheng. 2022. "Experimental and Numerical Investigation on Fatigue Properties of Carbon Fiber Cross-Ply Laminates in Hygrothermal Environments" Polymers 14, no. 9: 1857. https://doi.org/10.3390/polym14091857
APA StyleXu, M., Zeng, B., An, Z., Xiong, X., & Cheng, X. (2022). Experimental and Numerical Investigation on Fatigue Properties of Carbon Fiber Cross-Ply Laminates in Hygrothermal Environments. Polymers, 14(9), 1857. https://doi.org/10.3390/polym14091857







