Development of Fatigue Life Model for Rubber Materials Based on Fracture Mechanics
Abstract
1. Introduction
1.1. Theory of Fatigue Research
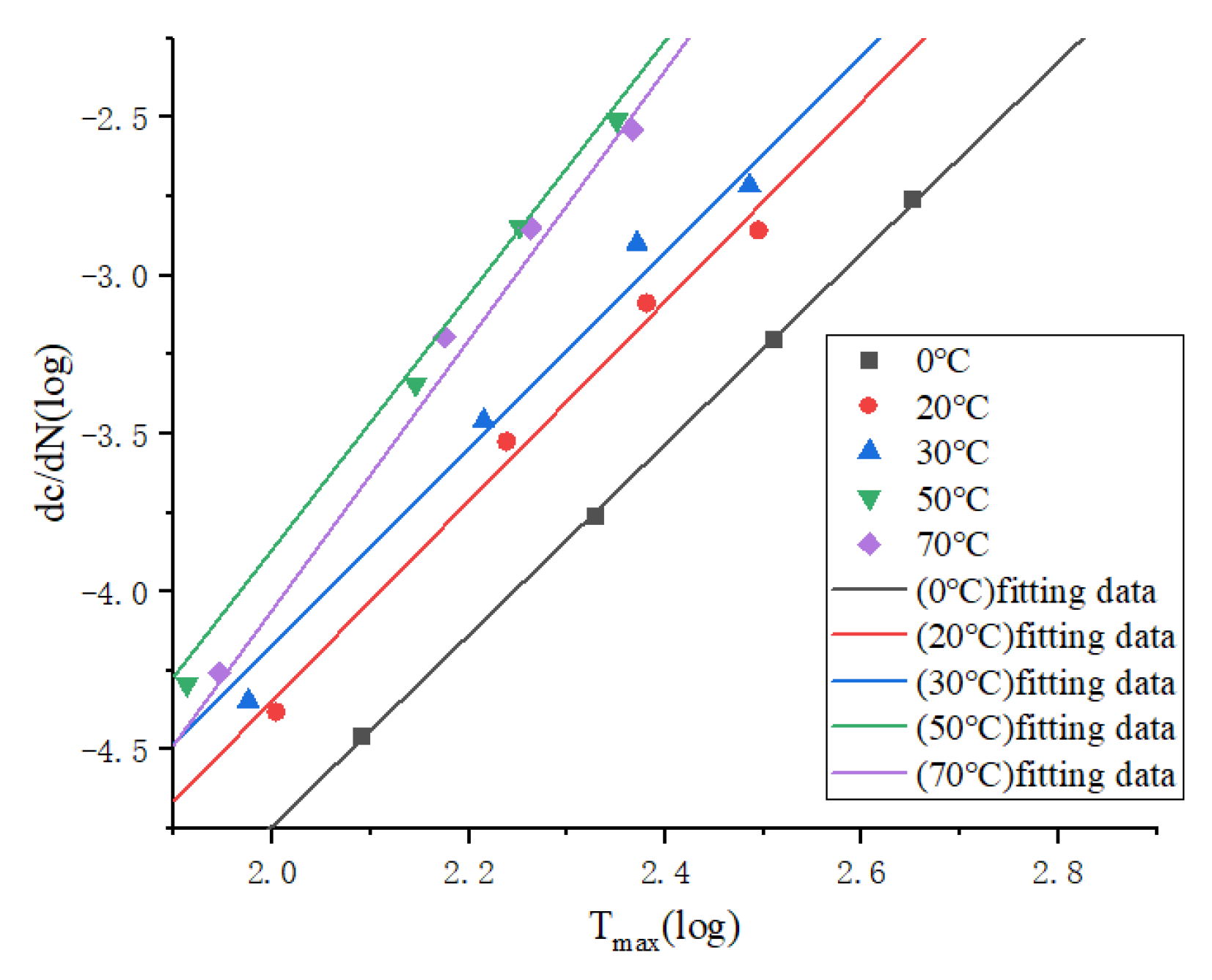
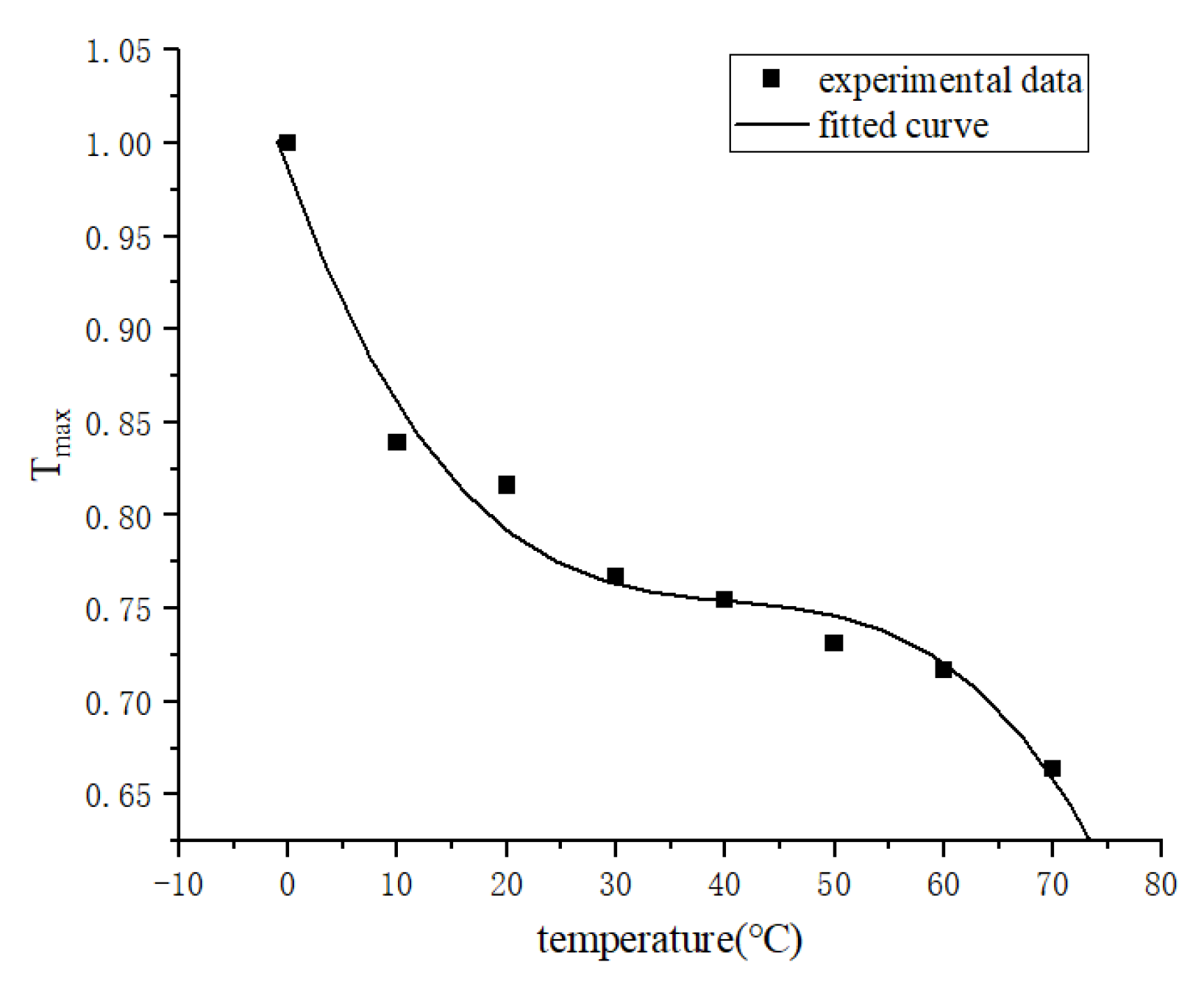
1.2. The Effect of Temperature on Rubber Fatigue
1.3. Research Significance
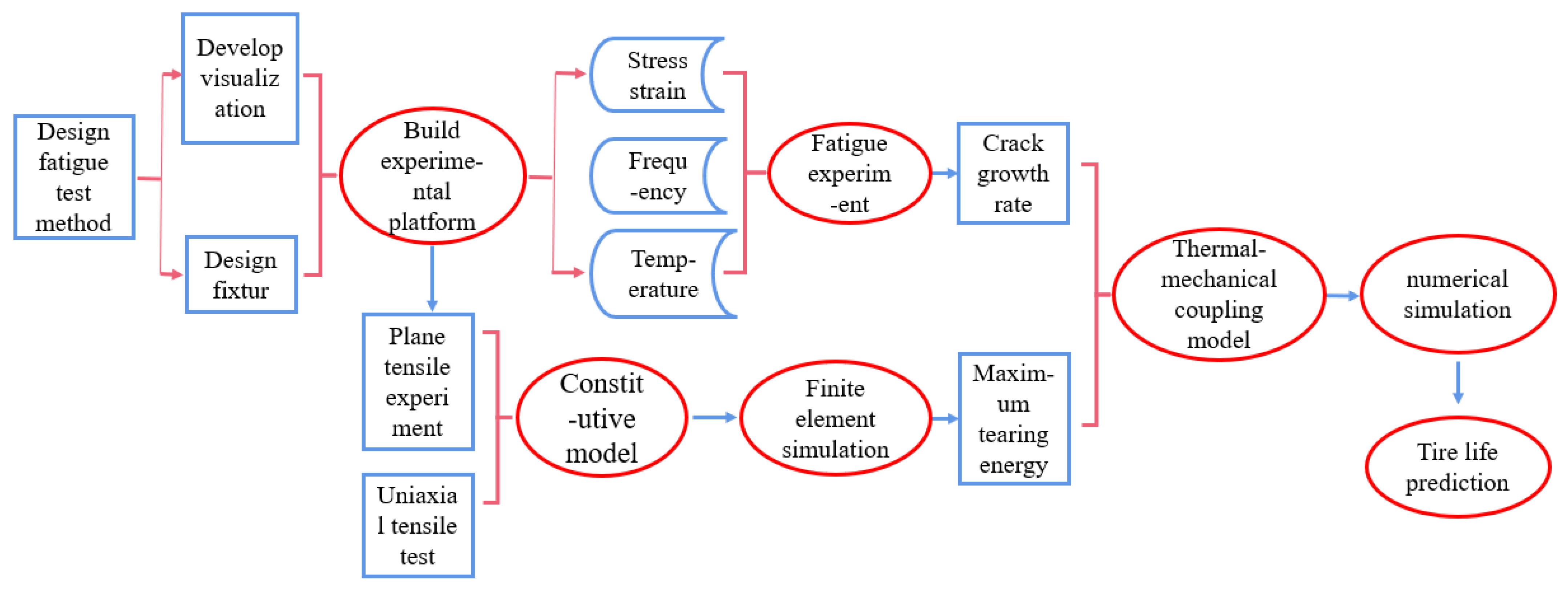
2. Construction of Fatigue Test Rig and Parameter Acquisition
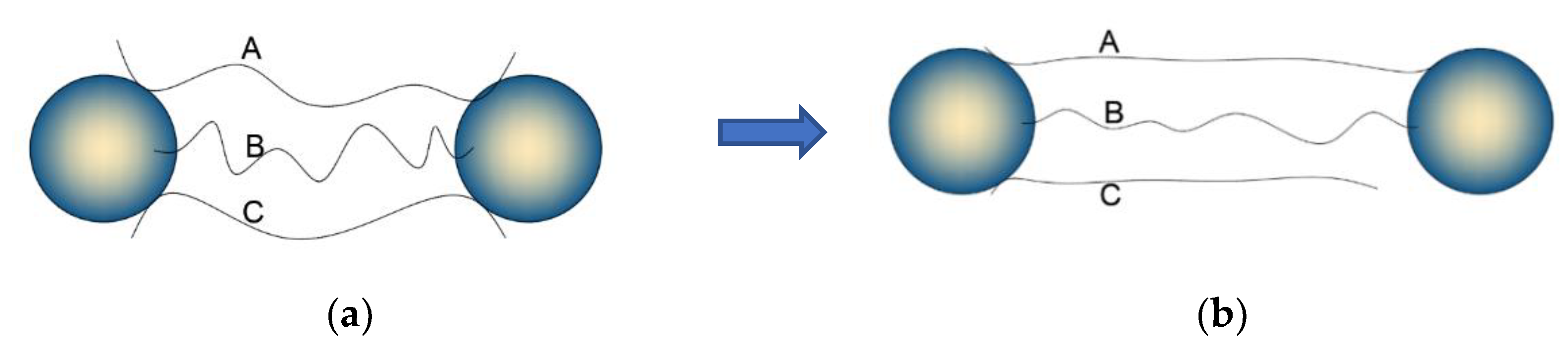
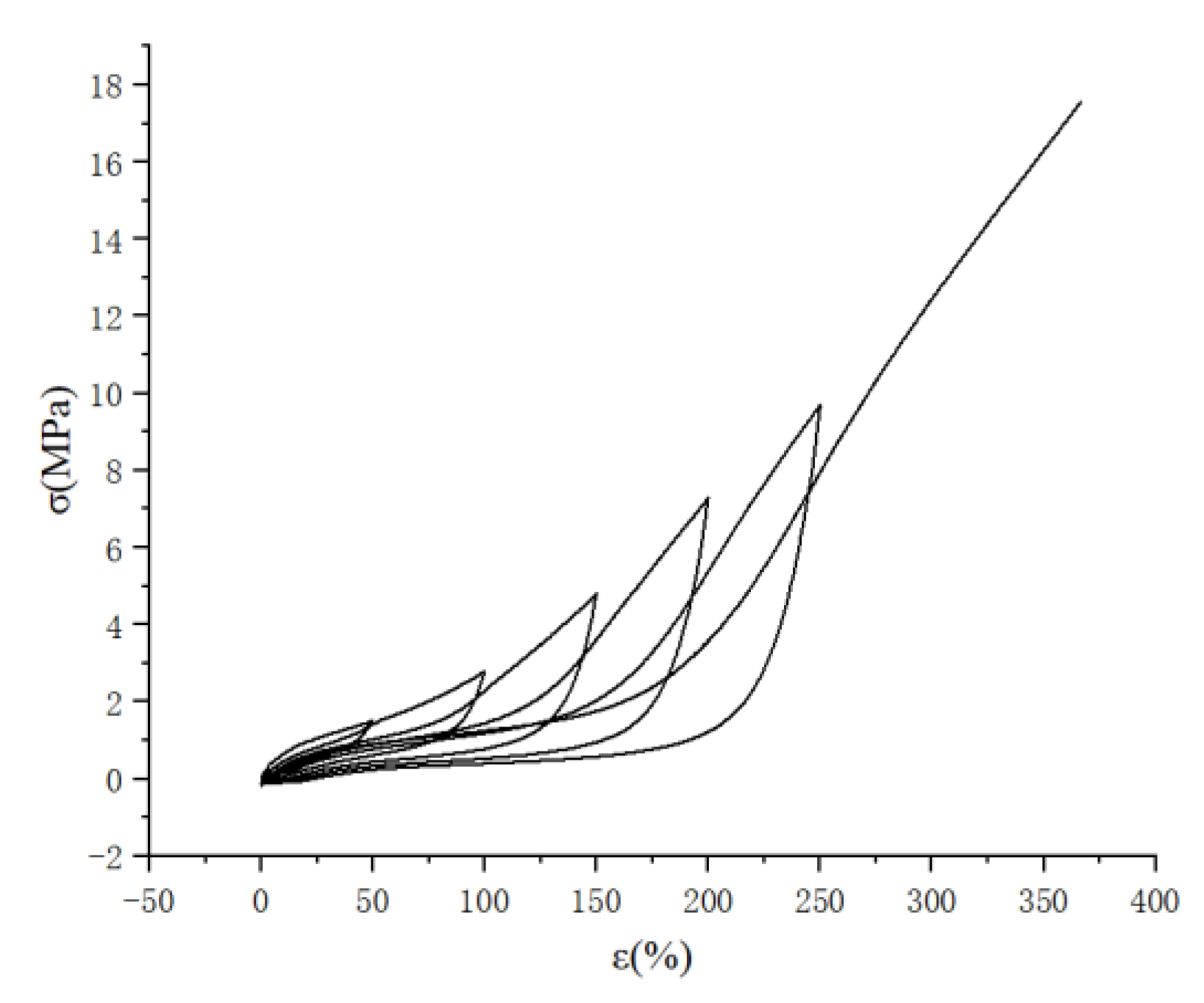
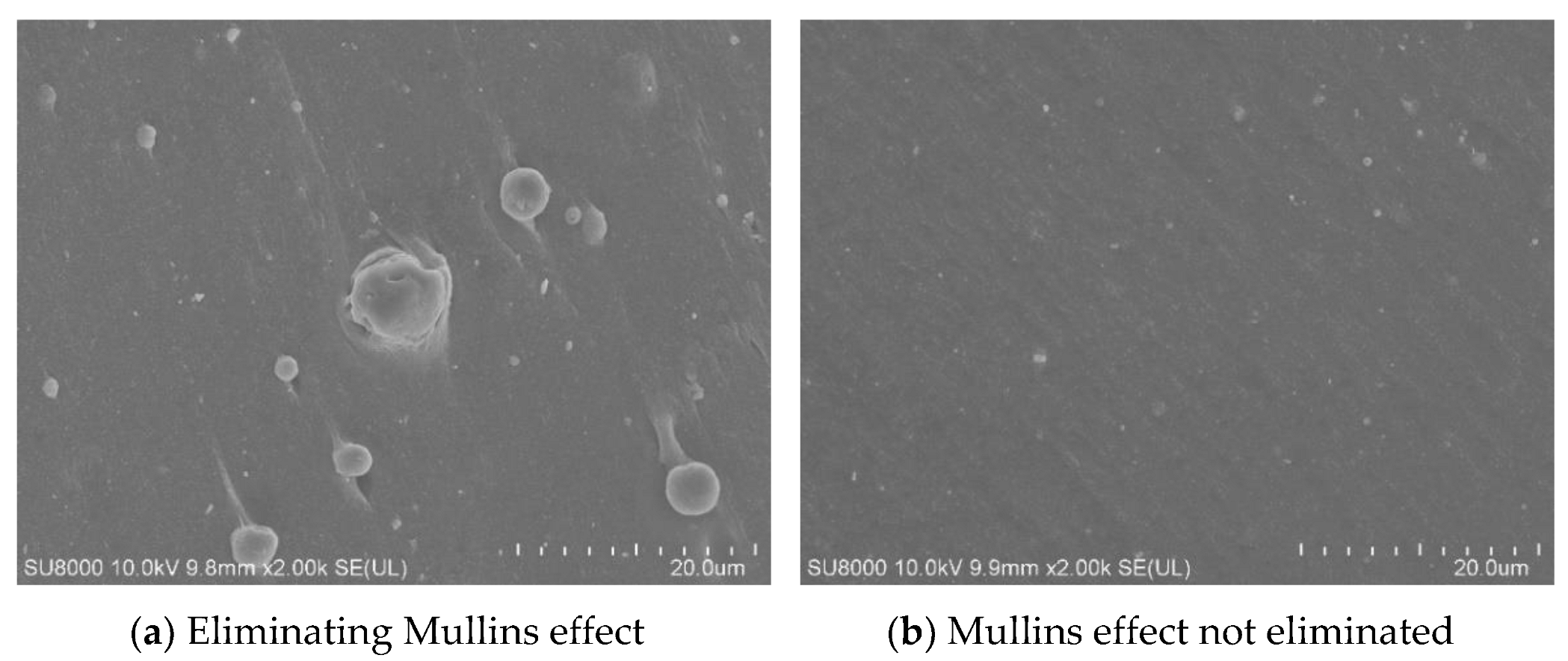
2.1. Mullins Effect Study
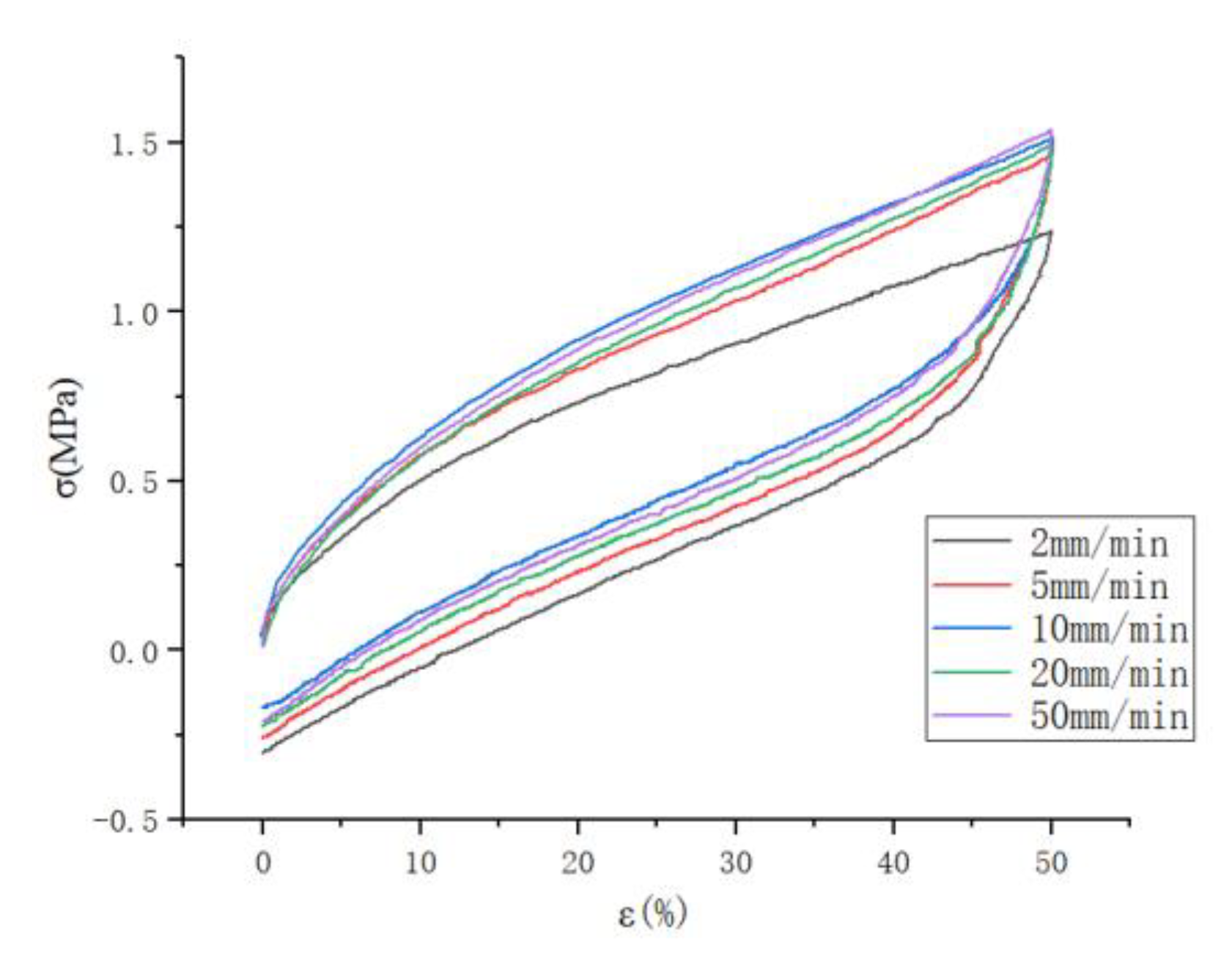
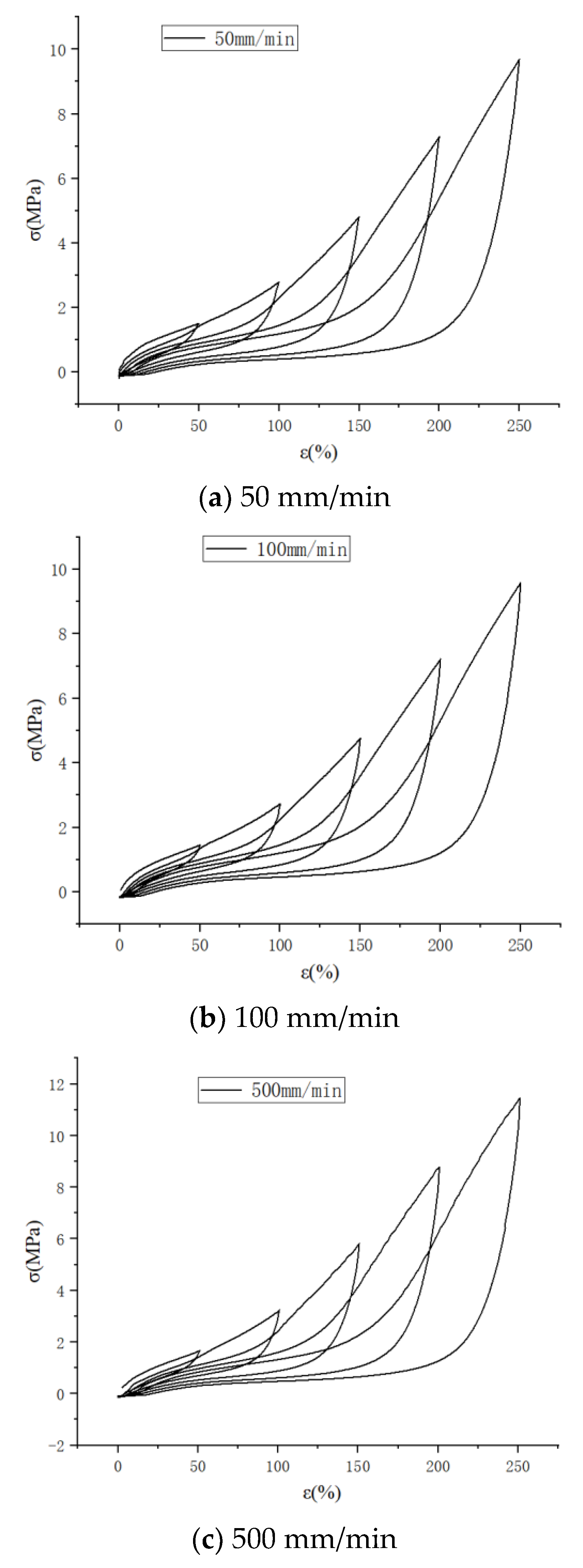
2.1.1. Low-Speed Stretching (≤50 mm/min), the Effect of Stretching Speed on the Mullins Effect
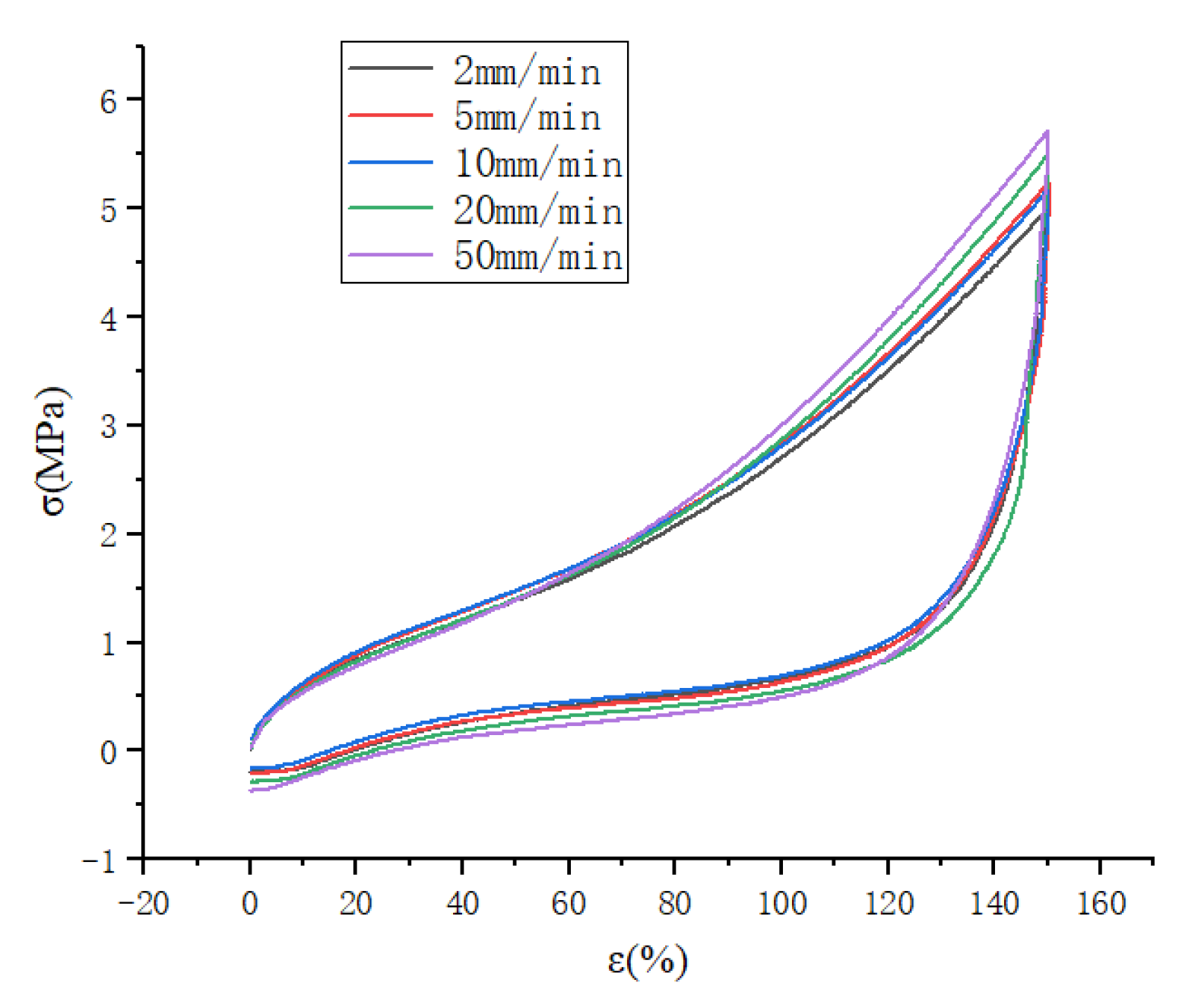
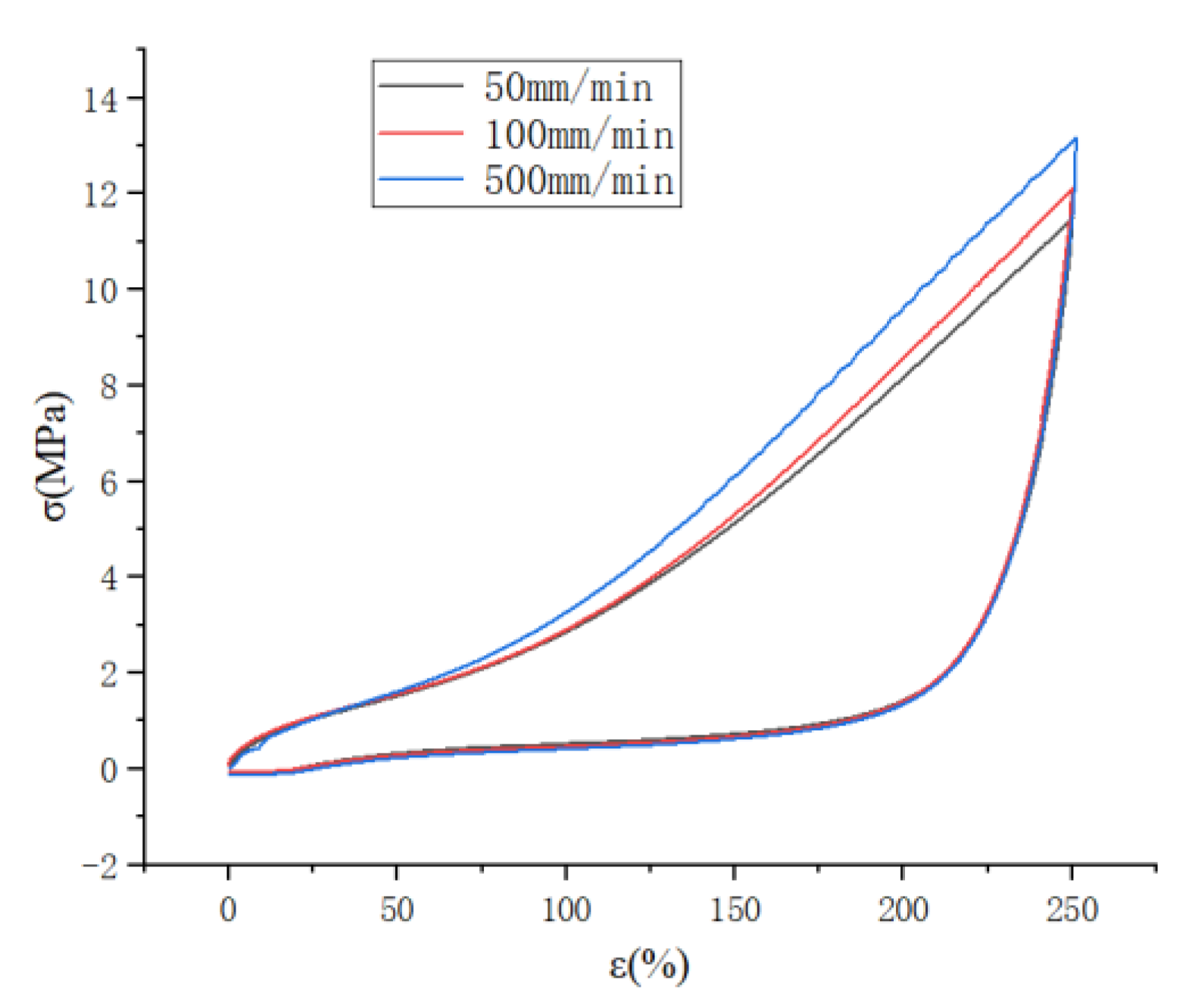
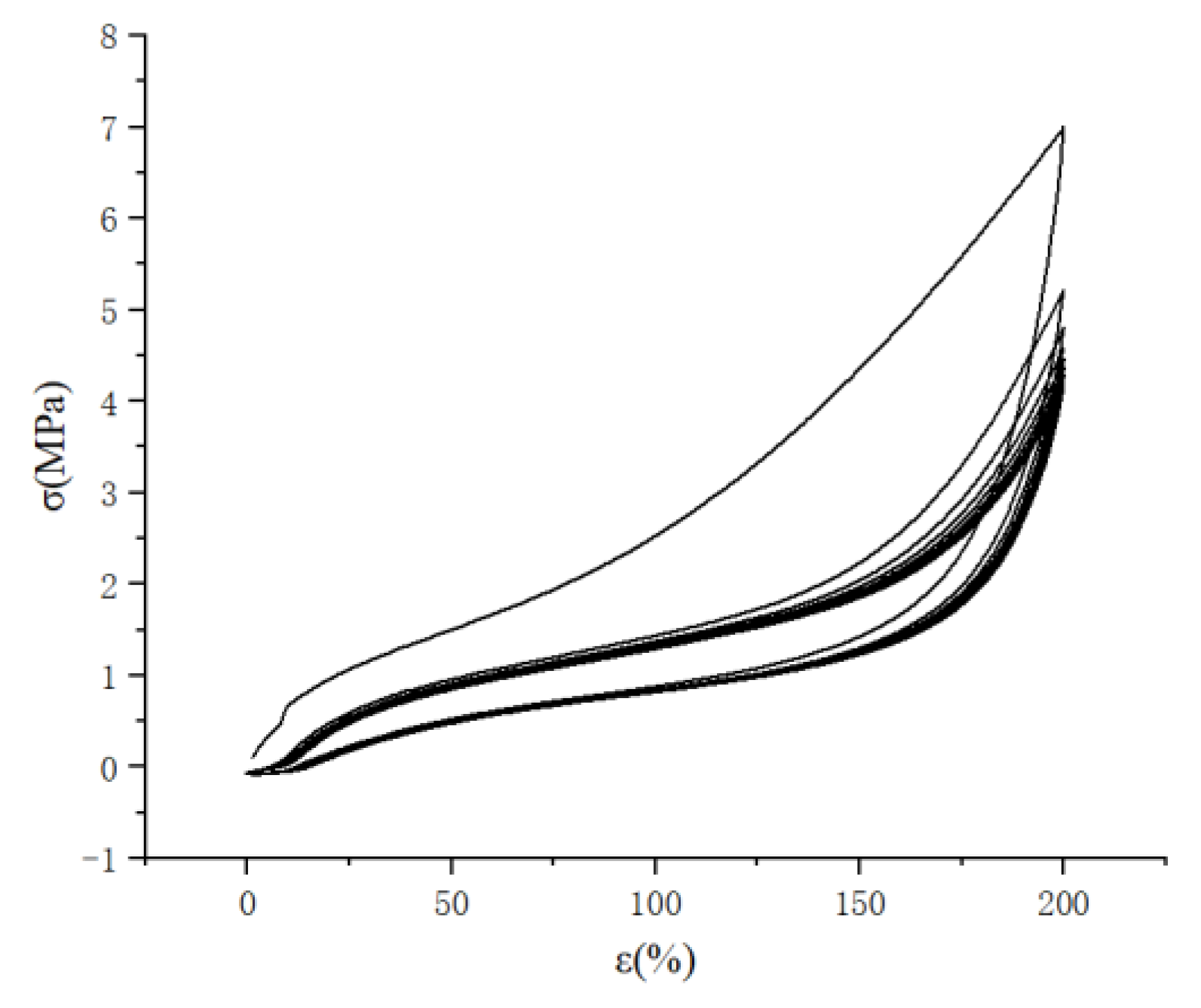
2.1.2. High-Speed Stretching (≥50 mm/min), the Effect of Stretching Speed on the Mullins Effect
2.2. Fatigue Test Bench Construction
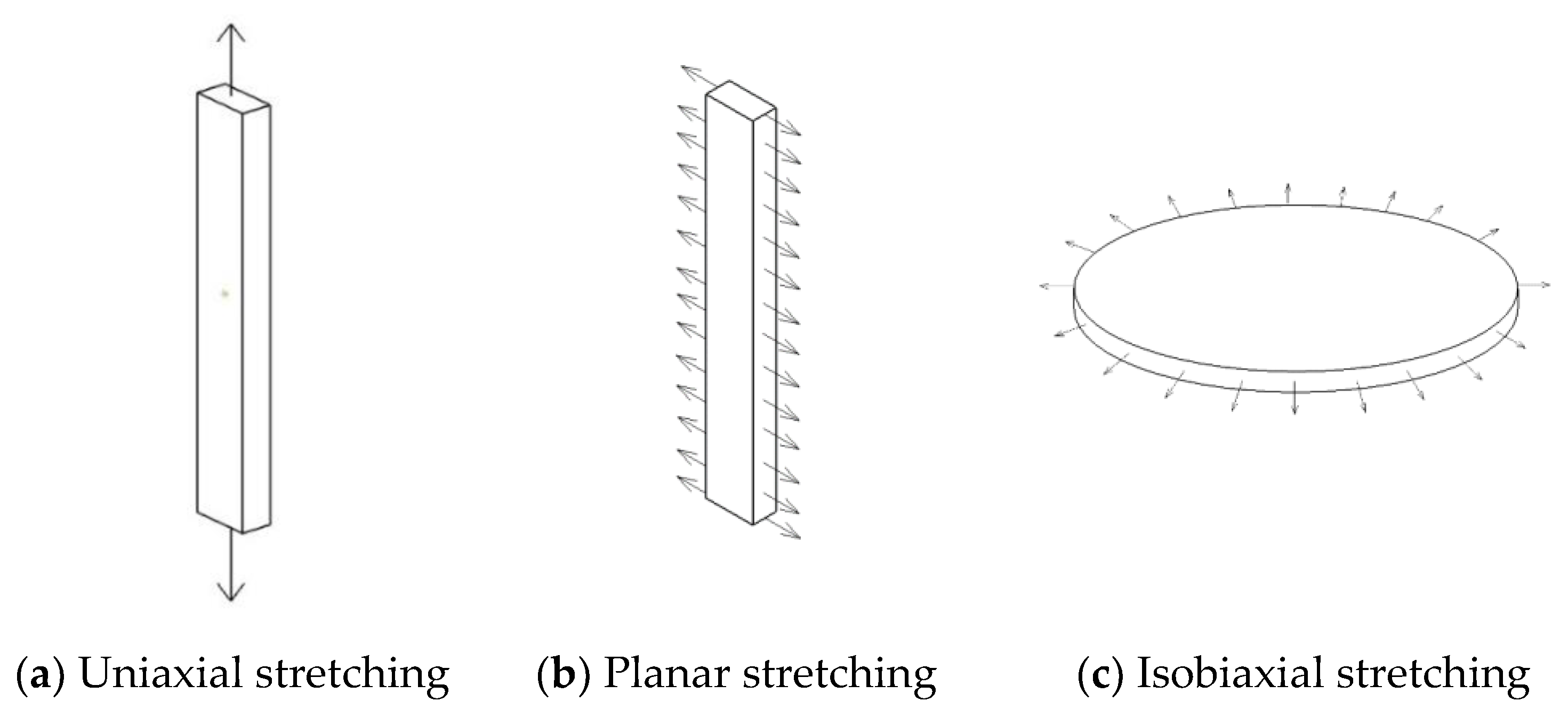
2.3. Selection of Constitutive Model
3. The Relationship between Fatigue and the Variables
3.1. Stress Ratio
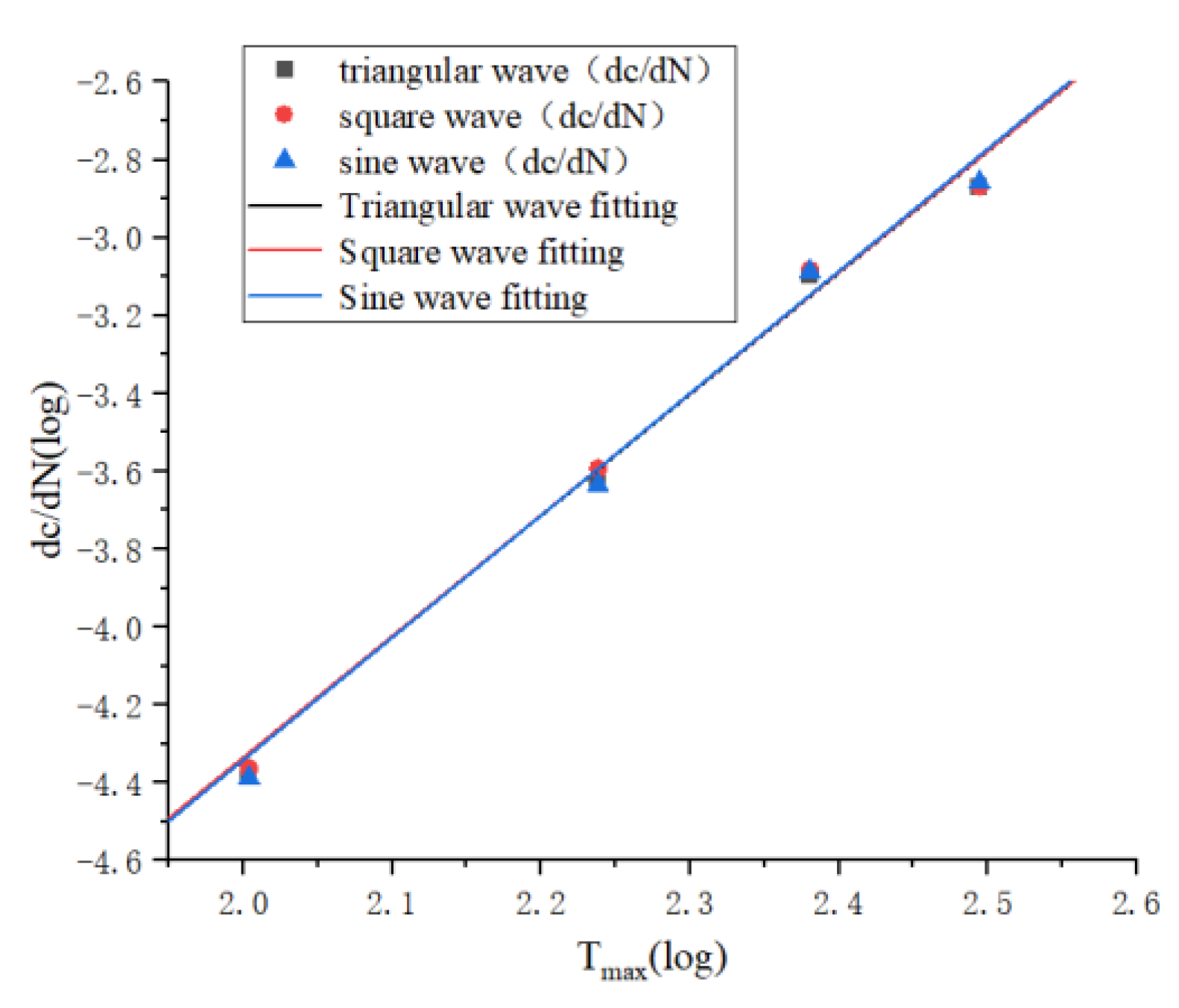
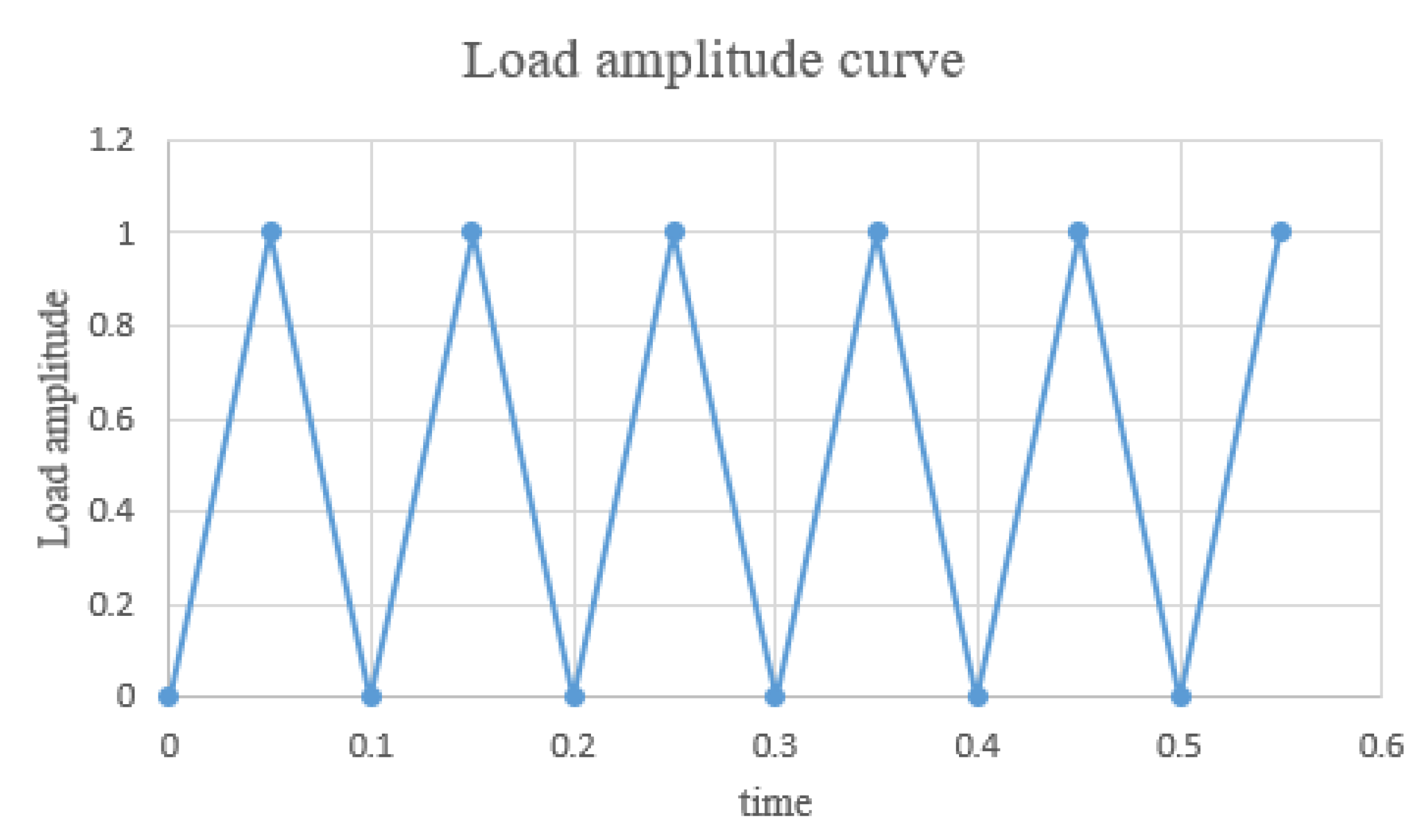
3.2. Loading Method
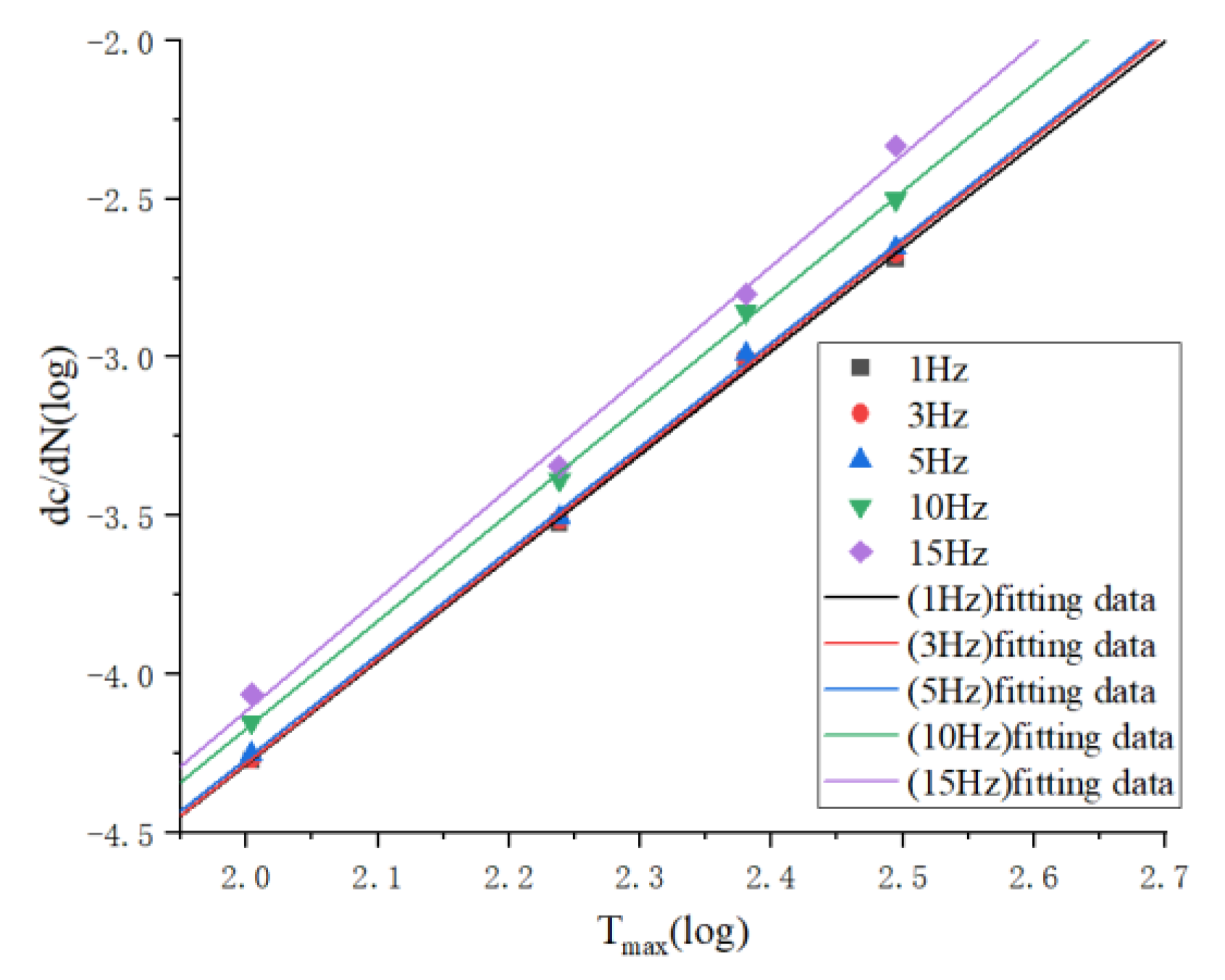
3.3. Frequency
3.4. Effect of Orientation on Fatigue Life
3.5. Effect of Mullins Effect on Fatigue Life
3.6. Construction of a Thermodynamic Coupling Model for Fatigue Life of Rubber
3.7. Validation of Fatigue-Thermal Coupling Model
4. Study of Fatigue Micromechanisms in Rubber
4.1. Experiments and Discussion of Results
4.1.1. Experiment
4.1.2. Discussion of the Results
4.2. Micromechanism of Rubber Fatigue
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Tee, Y.L.; Loo, M.S.; Andriyana, A. Recent advances on fatigue of rubber after the literature survey by Mars and Fatemi in 2002 and 2004. Int. J. Fatigue 2018, 110, 115–129. [Google Scholar] [CrossRef]
- Glanowski, T.; Huneau, B.; Marco, Y.; Le Saux, V.; Champy, C.; Charrier, P. Fatigue initiation mechanisms in elastomers: A microtomography-based analysis. MATEC Web Conf. 2018, 165, 08005. [Google Scholar] [CrossRef]
- Huneau, B.; Masquelier, I.; Marco, Y.; Le Saux, V.; Noizet, S.; Schiel, C.; Charrier, P. Fatigue crack initiation in a carbon black–filled natural rubbe. Rubber Chem. Technol. 2016, 89, 126–141. [Google Scholar] [CrossRef]
- Gent, A.N.; Lindley, P.B.; Thomas, A.G. Cut growth and fatigue of rubbers. I. The relationship between cut growth and fatigue. J. Appl. Polym. Sci. 1964, 8, 455–466. [Google Scholar] [CrossRef]
- Mars, W.; Fatemi, A. A literature survey on fatigue analysis approaches for rubber. Int. J. Fatigue 2002, 24, 949–961. [Google Scholar] [CrossRef]
- Cadwell, S.M.; Merrill, R.A.; Sloman, C.M.; Yost, F.L. Dynamic Fatigue Life of Rubber. Rubber Chem. Technol. 1940, 13, 304–315. [Google Scholar] [CrossRef]
- Thomas, A.G. Rupture of rubber. V. Cut growth in natural rubber vulcanizates. J. Polym. Sci. 1958, 31, 467–480. [Google Scholar] [CrossRef]
- Lake, G.J.; Lindley, P.B. Cut growth and fatigue of rubbers. II. Experiments on a noncrystallizing rubber. J. Appl. Polym. Sci. 1964, 8, 707–721. [Google Scholar] [CrossRef]
- Lindley, P.B. Energy for crack growth in model rubber components. J. Strain Anal. 1972, 7, 132–140. [Google Scholar] [CrossRef]
- Rivlin, R.S.; Thomas, A.G. Rupture of rubber. I. Characteristic energy for tearing. J. Polym. Sci. 1953, 10, 291–318. [Google Scholar]
- Mars, W.V.; Fatemi, A. Fatigue crack nucleation and growth in filled natural rubber subjected to multiaxial stress states. Fatigue Fract. Eng. Mater. Struct. 2003, 26, 779–789. [Google Scholar] [CrossRef]
- Lindley, P.B. Relation between hysteresis and the dynamic crack growth resistance of natural rubber. Int. J. Fatigue 1973, 9, 449–462. [Google Scholar] [CrossRef]
- Legorju-Jago, K.; Bathias, C. Fatigue initiation and propagation in natural and synthetic rubbers. Int. J. Fatigue 2002, 24, 85–92. [Google Scholar] [CrossRef]
- Xin, R. Study on fatigue failure mechanism of rubber. Sci.-Tech. Wind 2019, 143. [Google Scholar]
- Ruellan, B.; Le Cam, J.B.; Robin, E.; Jeanneau, I.; Canevet, F.; Mortier, F. Influence of the Temperature on Lifetime Reinforcement of a Filled NR. In Fracture, Fatigue, Failure and Damage Evolution, Volume 6: Proceedings of the 2018 Annual Conference on Experimental and Applied Mechanics; Springer International Publishing: Cham, Switzerland, 2019; pp. 45–50. [Google Scholar]
- Ngolemasango, F.E.; Bennett, M.; Clarke, J. Degradation and life prediction of a natural rubber engine mount compound. J. Appl. Polym. Sci. 2008, 110, 348–355. [Google Scholar] [CrossRef]
- Rey, T.; Chagnon, G.; Le Cam, J.-B.; Favier, D. Influence of the temperature on the mechanical behaviour of filled and unfilled silicone rubbers. Polym. Test. 2013, 32, 492–501. [Google Scholar] [CrossRef]
- Haroonabadi, L.; Dashti, A.; Najipour, M. Investigation of the effect of thermal aging on rapid gas decompression (RGD) resistance of nitrile rubber. Polym. Test. 2018, 67, 37–45. [Google Scholar] [CrossRef]
- Chou, H.-W.; Huang, J.-S.; Lin, S.-T. Effects of thermal aging on fatigue of carbon black–reinforced EPDM rubber. J. Appl. Polym. Sci. 2007, 103, 1244–1251. [Google Scholar] [CrossRef]
- Neuhaus, C.; Lion, A.; Johlitz, M.; Heuler, P.; Barkhoff, M.; Duisen, F. Fatigue behaviour of an elastomer under consideration of ageing effects. Int. J. Fatigue 2017, 104, 72–80. [Google Scholar] [CrossRef]
- Luo, W.; Huang, Y.; Yin, B.; Jiang, X.; Hu, X. Fatigue Life Assessment of Filled Rubber by Hysteresis Induced Self-Heating Temperature. Polymers 2020, 12, 846. [Google Scholar] [CrossRef]
- Ruellan, B.; Le Cam, J.-B.; Jeanneau, I.; Canévet, F.; Mortier, F.; Robin, E. Fatigue of natural rubber under different temperatures. Int. J. Fatigue 2019, 124, 544–557. [Google Scholar] [CrossRef]
- Federico, C.E.; Padmanathan, H.R.; Kotecky, O.; Rommel, R.; Rauchs, G.; Fleming, Y.; Addiego, F.; Westermann, S. Cavitation Micro-mechanisms in Silica-Filled Styrene-Butadiene Rubber Upon Fatigue and Cyclic Tensile Testing. In Fatigue Crack Growth in Rubber Materials: Experiments and Modelling; Springer: Berlin/Heidelberg, Germany, 2021; pp. 109–129. [Google Scholar]
- Schieppati, J.; Schrittesser, B.; Wondracek, A.; Robin, S.; Holzner, A.; Pinter, G. Temperature impact on the mechanical and fatigue behavior of a non-crystallizing rubber. Int. J. Fatigue 2021, 144, 106050. [Google Scholar] [CrossRef]
- Liu, X.; Shangguan, W.-B.; Zhao, X. Probabilistic fatigue life prediction model of natural rubber components based on the expanded sample data. Int. J. Fatigue 2022, 163, 107034. [Google Scholar] [CrossRef]
- Demiral, M.; Mamedov, A. Fatigue Performance of a Step-Lap Joint under Tensile Load: A Numerical Study. Polymers 2023, 15, 1949. [Google Scholar] [CrossRef]
- Fang, Y.; Zhang, H. High-temperature fatigue life prediction method for rubber bushing of new-energy vehicles based on modified fatigue damage theory. Mater. Res. Express 2020, 7, 015346. [Google Scholar]
- Weng, G.; Huang, G.; Lei, H.; Qu, L.; Zhang, P.; Nie, Y.; Wu, J. Crack initiation of natural rubber under high temperature fatigue loading. J. Appl. Polym. Sci. 2012, 124, 4274–4280. [Google Scholar] [CrossRef]
- Zhang, J.; Xue, F.; Wang, Y.; Zhang, X.; Han, S. Strain energy-based rubber fatigue life prediction under the influence of temperature. R. Soc. Open Sci. 2018, 5, 180951. [Google Scholar] [CrossRef]
- Luo, W.; Li, M.; Huang, Y.; Yin, B.; Hu, X. Effect of temperature on the tear fracture and fatigue life of carbon-black-filled rubber. Polymers 2019, 11, 768. [Google Scholar] [CrossRef]
- Seichter, S.; Archodoulaki, V.M.; Koch, T.; Holzner, A.; Wondracek, A. Investigation of different influences on the fatigue behaviour of industrial rubbers. Polym. Test. 2017, 59, 99–106. [Google Scholar] [CrossRef]
- Grandcoin, J.; Boukamel, A.; Lejeunes, S. A micro-mechanically based continuum damage model for fatigue life prediction of filled rubbers. Int. J. Solids Struct. 2014, 51, 1274–1286. [Google Scholar] [CrossRef]
- Aït-Bachir, M.; Mars, W.; Verron, E. Energy release rate of small cracks in hyperelastic materials. Int. J. Non-linear Mech. 2012, 47, 22–29. [Google Scholar] [CrossRef]
- Julie, D.; Fayolle, B.; Gilormini, P. A review on the Mullins effect. Eur. Polym. J. 2009, 45, 601–612. [Google Scholar]
- Marckmann, G.; Verron, E.; Gornet, L.; Chagnon, G.; Charrier, P.; Fort, P. A theory of network alteration for the Mullins effect. J. Mech. Phys. Solids 2002, 50, 2011–2028. [Google Scholar] [CrossRef]
- Martinez, J.R.S.; Le Cam, J.-B.; Balandraud, X.; Toussaint, E.; Caillard, J. New elements concerning the Mullins effect: A thermomechanical analysis. Eur. Polym. J. 2014, 55, 98–107. [Google Scholar] [CrossRef]
- Li, M. Thermal dissipation and fatigue performance of carbon black filled rubber. Ph.D. Thesis, Xiangtan University, Xiangtan, China, 2019. [Google Scholar]
- Ghoreishy, M.H.R.; Sourki, F.A. Development of a new combined numerical/experimental approach for the modeling of the nonlinear hyper-viscoelastic behavior of highly carbon black filled rubber compound. Polym. Test. 2018, 70, 135–143. [Google Scholar] [CrossRef]
- Poisson, J.L.; Méo, S.; Lacroix, F.; Berton, G.; Hosséini, M.; Ranganathan, N. Comparison of Fatigue Criteria under Proportional and Non-Proportional Multiaxial Loading. Rubber Chem. Technol. 2018, 91, 320–338. [Google Scholar] [CrossRef]
- Yong, Z. Preparation of Magnetorheological Elastomer and Study on Fatigue Fracture Mechanism. Doctoral Dissertation, University of Science and Technology, Qingdao, China, 2018. [Google Scholar]
- Beatty, J.R. Fatigue of rubber. Rubber Chem. Technol. 1964, 37, 1341–1364. [Google Scholar] [CrossRef]
- Champy, C.; Le Saux, V.; Marco, Y.; Glanowski, T.; Charrier, P.; Hervouet, W. Fatigue of crystallizable rubber: Generation of a Haigh diagram over a wide range of positive load ratios. Int. J. Fatigue 2021, 150, 106313. [Google Scholar] [CrossRef]
- Le Cam, J.B.; Pérocheau, F.; Huneau, B.; Verron, E.; Gornet, L. Cavitation influence on fatigue crack growth in filled natural rubber. Mec. Ind. 2006, 7, 123–129. [Google Scholar]
- Euchler, E.; Schneider, K.; Wiessner, S.; Bernhardt, R.; Heinrich, G.; Roth, S.V.; Tada, T. Cavitation damage in tire rubber materials. In Constitutive Models for Rubber XI; CRC Press: Boca Raton, FL, USA, 2019; pp. 87–91. [Google Scholar]


















| No. | MU1 | MU2 | MU3 | ALPHA1 | ALPHA2 | ALPHA3 |
|---|---|---|---|---|---|---|
| Parameters | 1.485 | −5.016 | 10.038 | 1.704 | 12.501 | −24.999 |
| Strain | 30% | 50% | 80% | 100% |
|---|---|---|---|---|
| strain energy density | 0.745 | 1.385 | 2.311 | 3.370 |
| Tearing energy | 102.637 | 177.633 | 270.572 | 374.313 |
| No. | R | Frequency | Waveform | Strain | dc/dN |
|---|---|---|---|---|---|
| 1 | 0 | 4 Hz | Sine wave | 80% | 6.143 × 10−4 |
| 2 | 1/3 | 4 Hz | Sine wave | 80% | 6.944 × 10−5 |
| 3 | 1/2 | 4 Hz | Sine wave | 80% | 3.472 × 10−5 |
| No. | Orientation | Strain | Waveform | dc/dN |
|---|---|---|---|---|
| 1 | Vertical | 50% | Sine wave | 2.778 × 10−4 |
| 2 | Parallel | 50% | Sine wave | 3.543 × 10−4 |
| No. | Mullins Effect | Strain | Waveform | dc/dN |
|---|---|---|---|---|
| 1 | Eliminated | 50% | Sine wave | 2.454 × 10−4 |
| 2 | Not eliminated | 50% | Sine wave | 2.315 × 10−4 |
| Different Models | Thomas Model | Thermodynamic Coupling Model | Experimental Results |
|---|---|---|---|
| Fatigue life | 8.315 × 105 | 6.588 × 105 | 6.42 × 105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, X.; Yin, H.; Xing, Q.; Jin, Q. Development of Fatigue Life Model for Rubber Materials Based on Fracture Mechanics. Polymers 2023, 15, 2746. https://doi.org/10.3390/polym15122746
Qiu X, Yin H, Xing Q, Jin Q. Development of Fatigue Life Model for Rubber Materials Based on Fracture Mechanics. Polymers. 2023; 15(12):2746. https://doi.org/10.3390/polym15122746
Chicago/Turabian StyleQiu, Xingwen, Haishan Yin, Qicheng Xing, and Qi Jin. 2023. "Development of Fatigue Life Model for Rubber Materials Based on Fracture Mechanics" Polymers 15, no. 12: 2746. https://doi.org/10.3390/polym15122746
APA StyleQiu, X., Yin, H., Xing, Q., & Jin, Q. (2023). Development of Fatigue Life Model for Rubber Materials Based on Fracture Mechanics. Polymers, 15(12), 2746. https://doi.org/10.3390/polym15122746






