Hybrid Finite Element–Smoothed Particle Hydrodynamics Modelling for Optimizing Cutting Parameters in CFRP Composites
Abstract
:1. Introduction
2. Modelling and Experimental
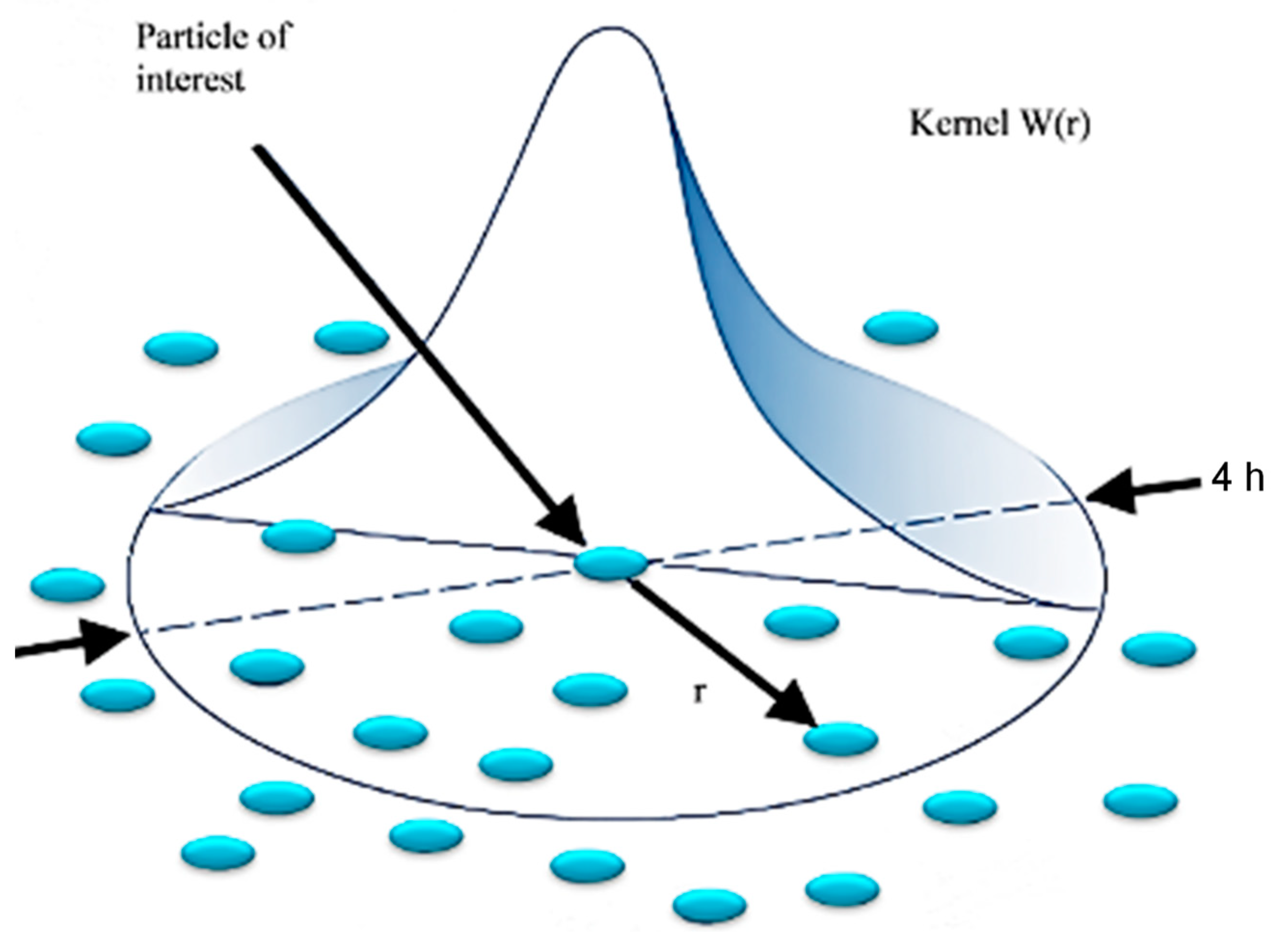
2.1. Smoothed Particle Hydrodynamic Model
2.2. Hybrid Model Development
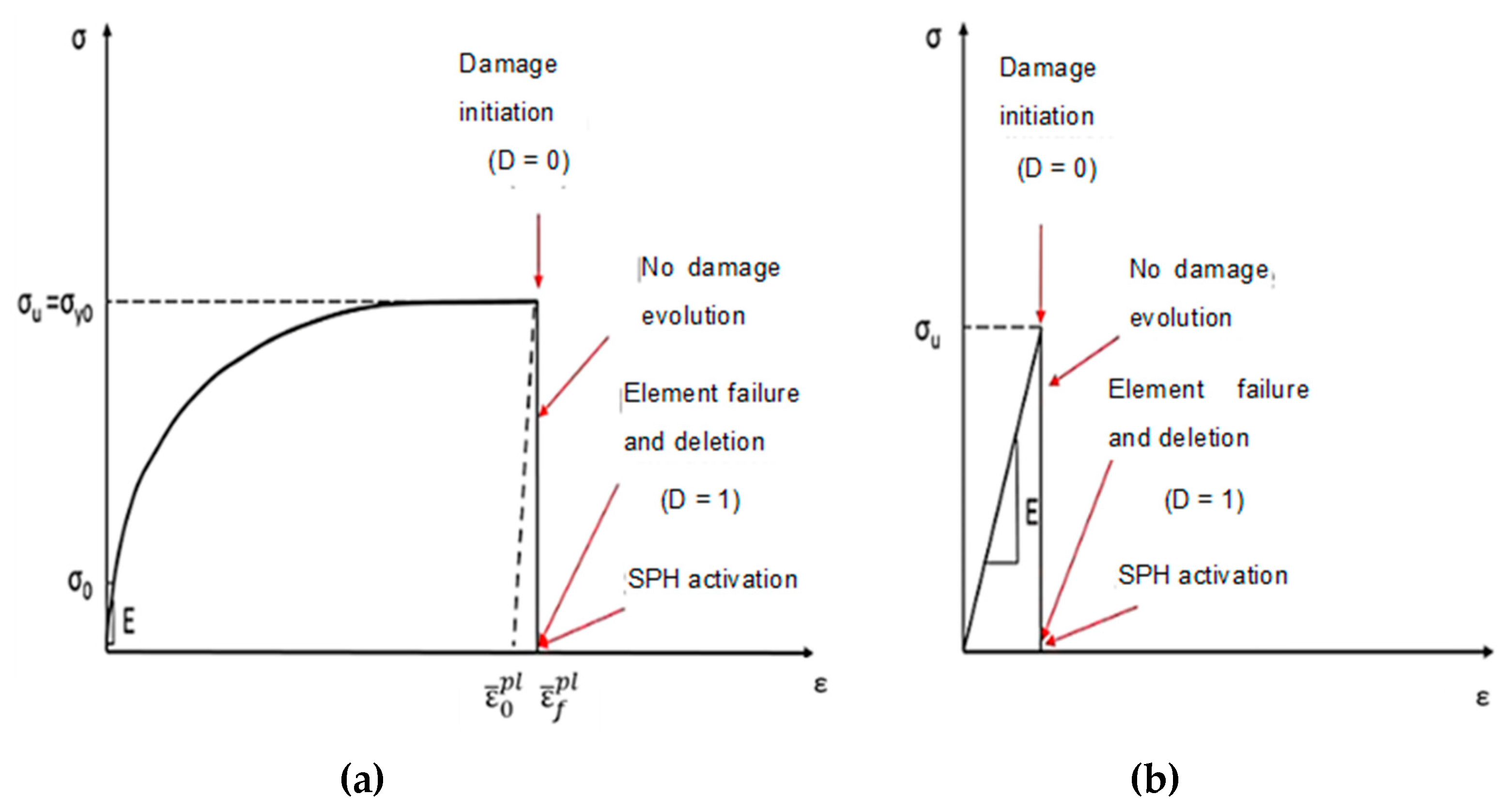
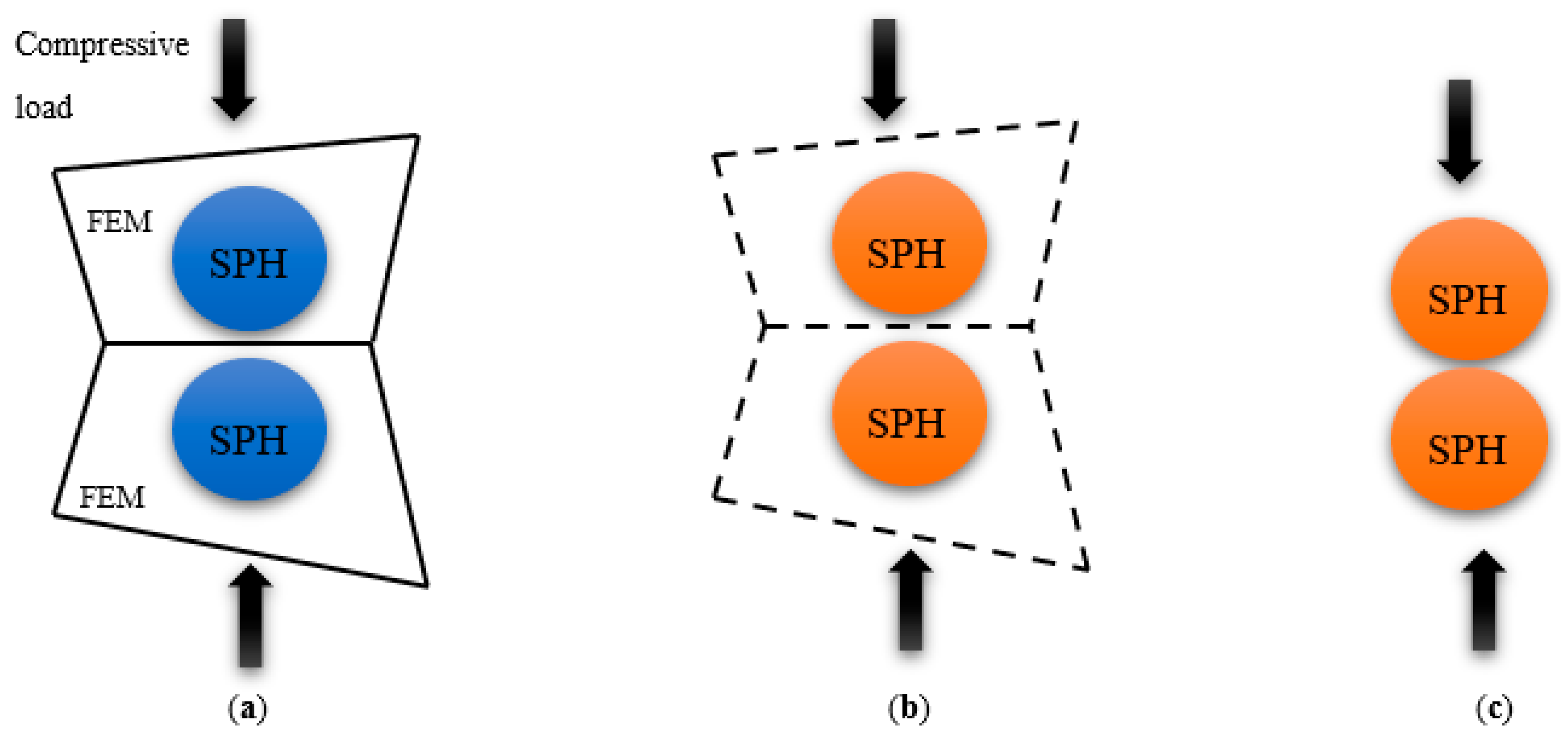
2.2.1. The FEM-SPH Hybrid Subroutine
2.2.2. SPH Particle Dimensions
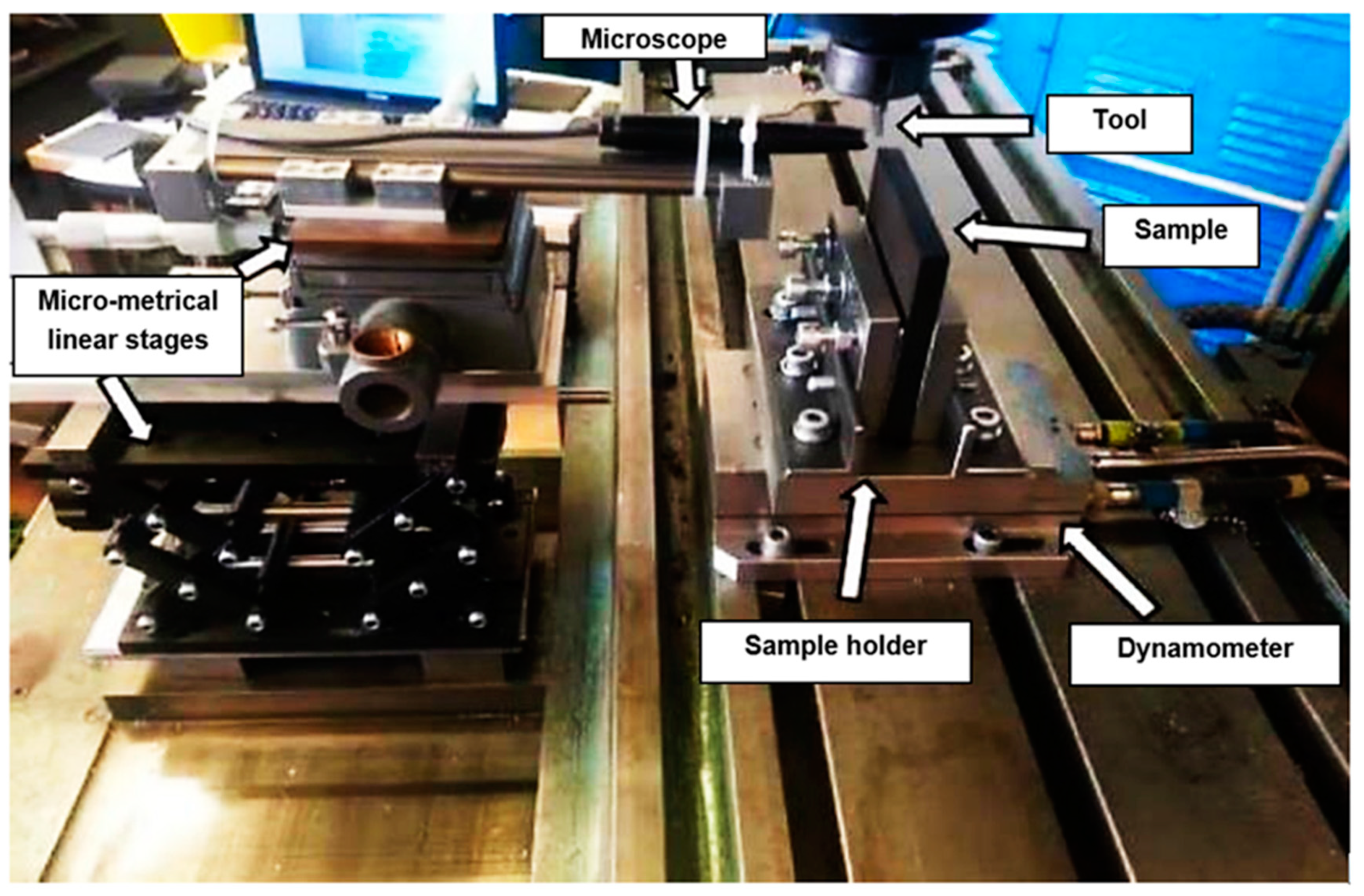
2.3. Experimental
3. Results and Discussion
3.1. Damage and Chip Formation
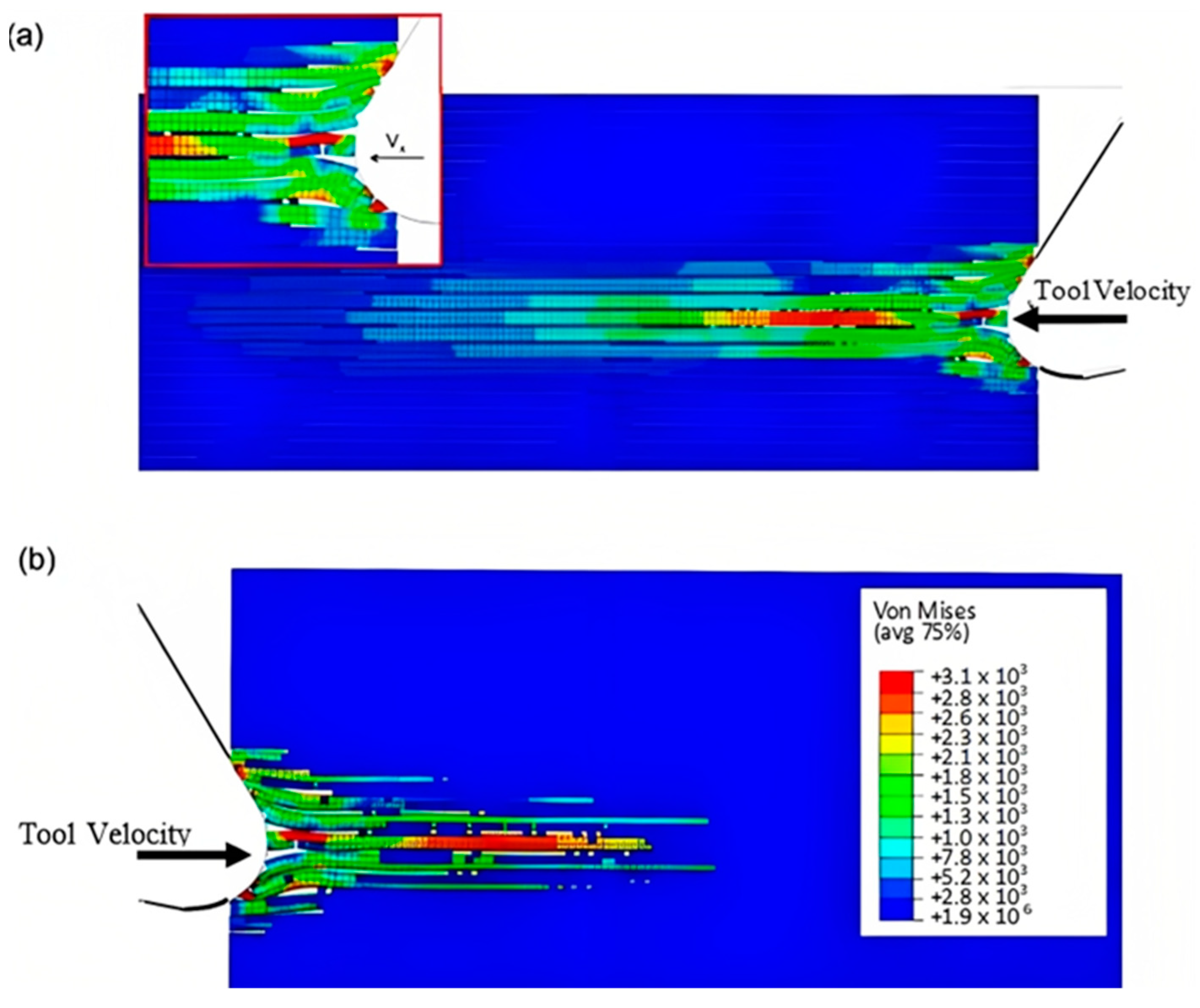
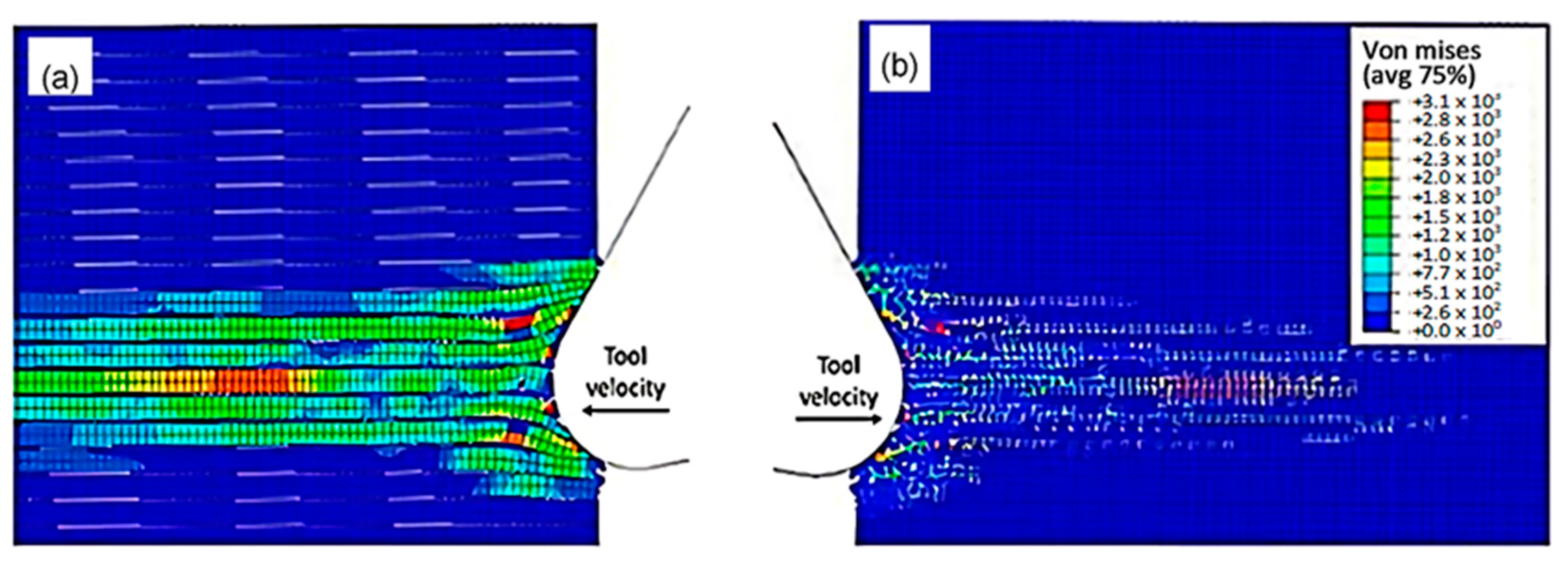
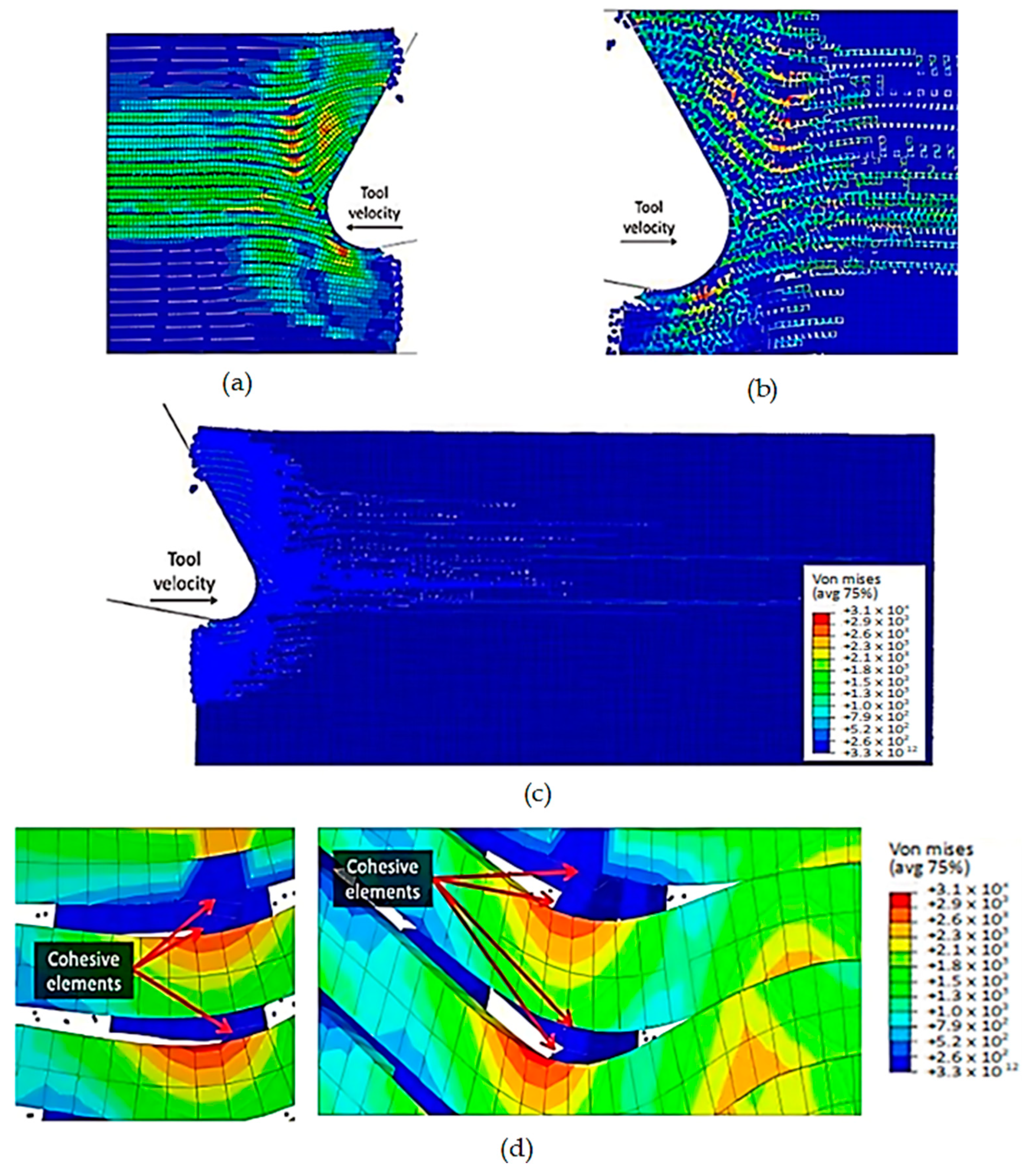
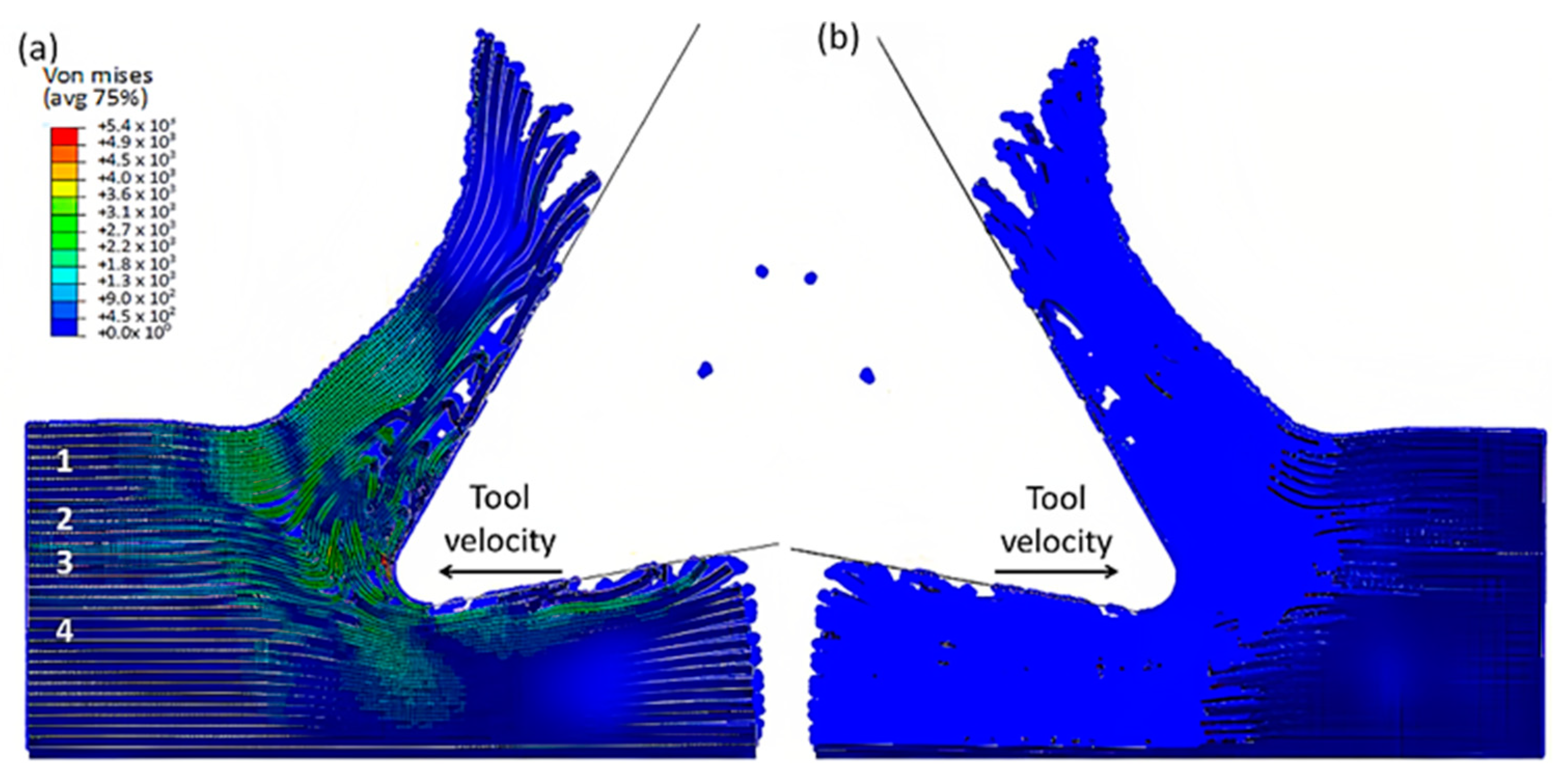
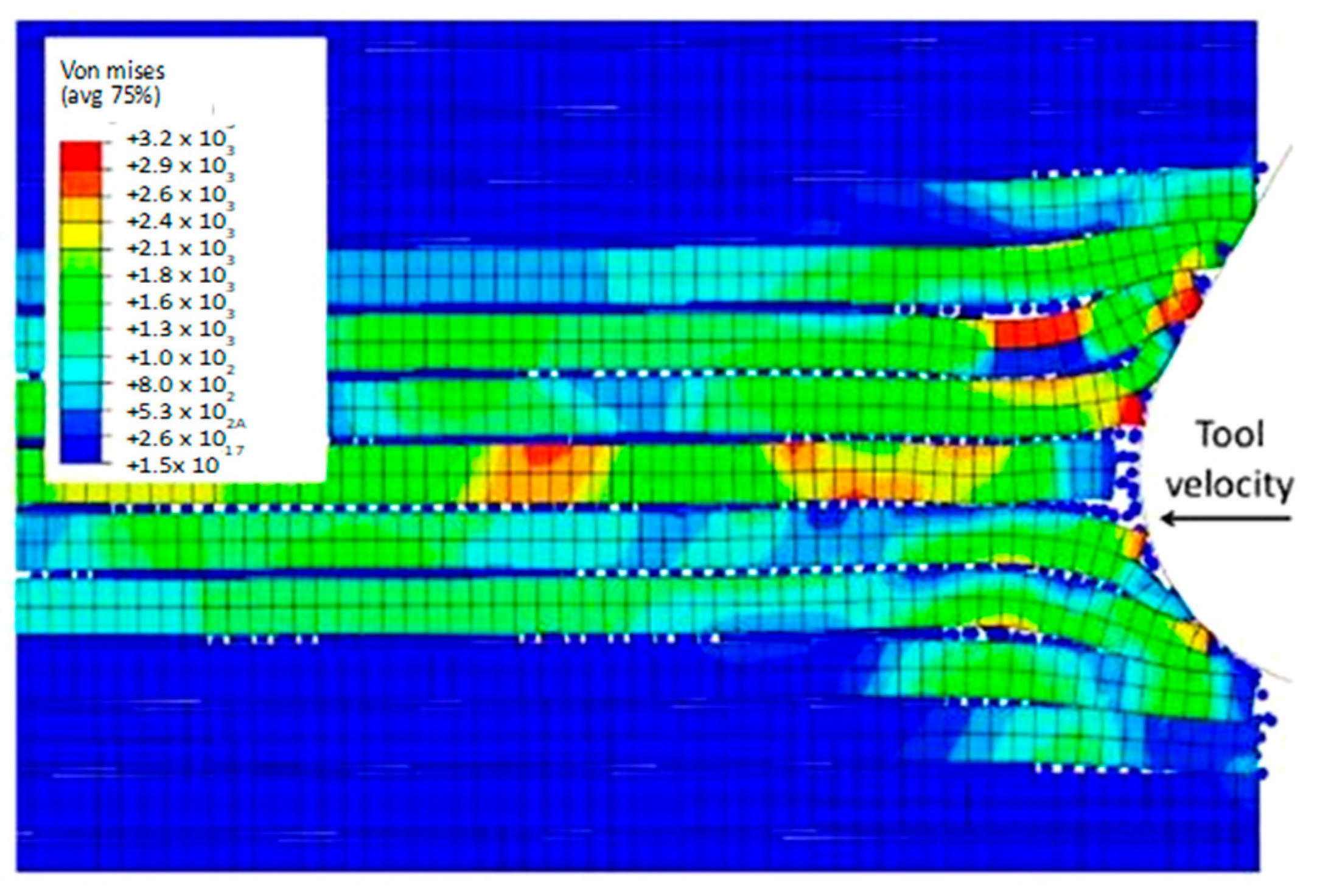
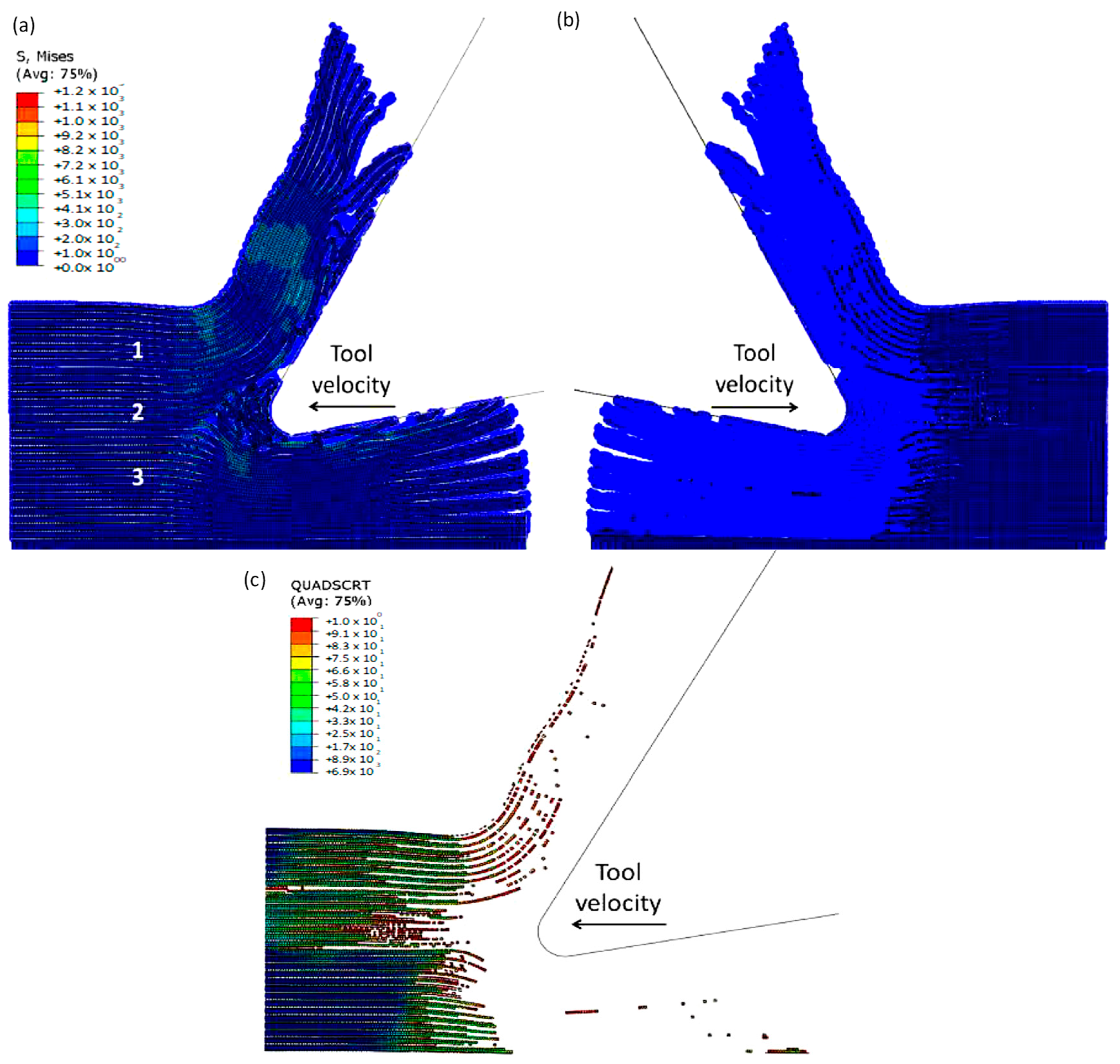
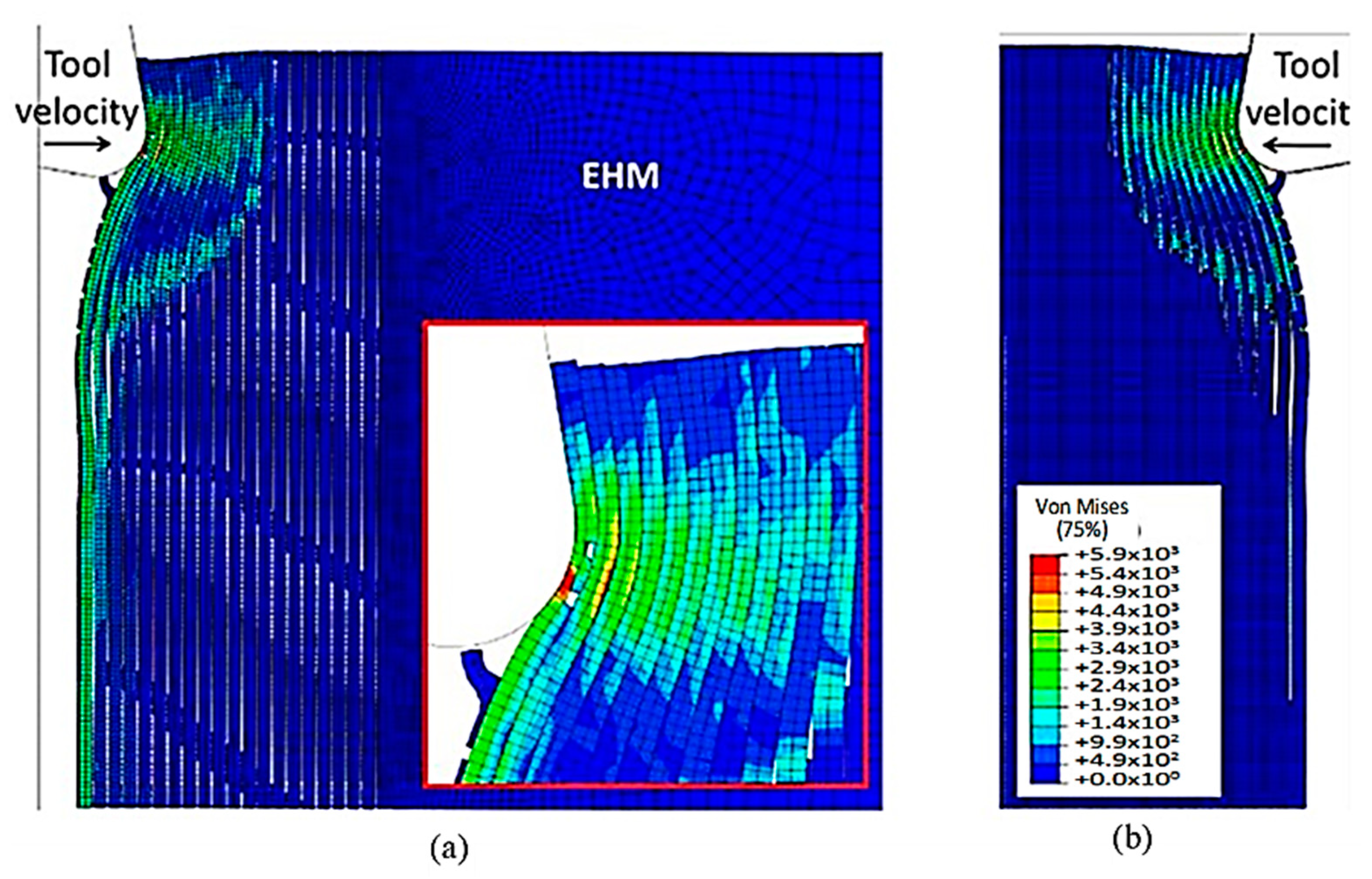
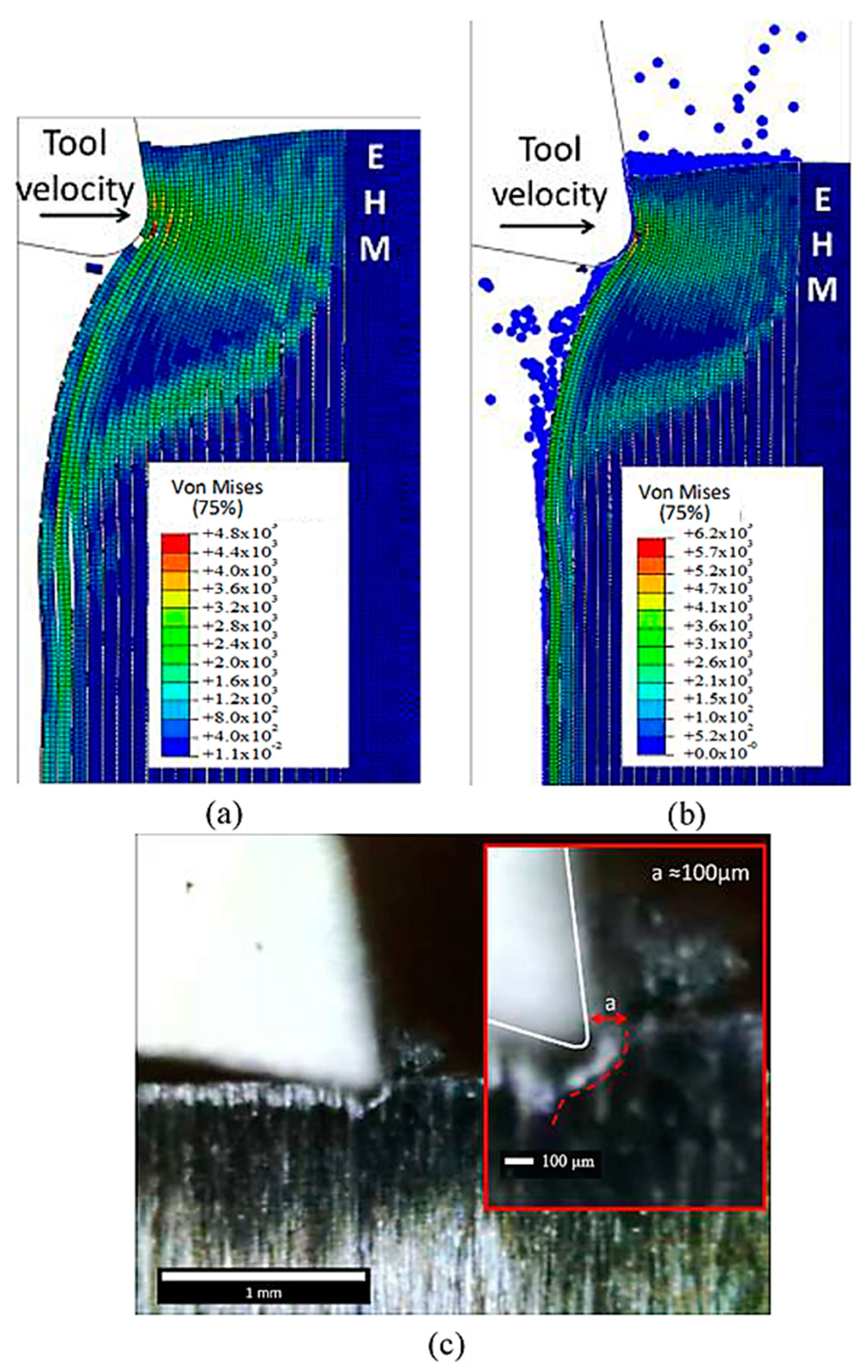
3.1.1. FEM for 0° Finite Fibre Orientation
3.1.2. FEM-SPH Model for 0° Fibre Orientation
- a
- At damage variable (D) of =0.8.
- b
- At damage variable (D) of 0.1.
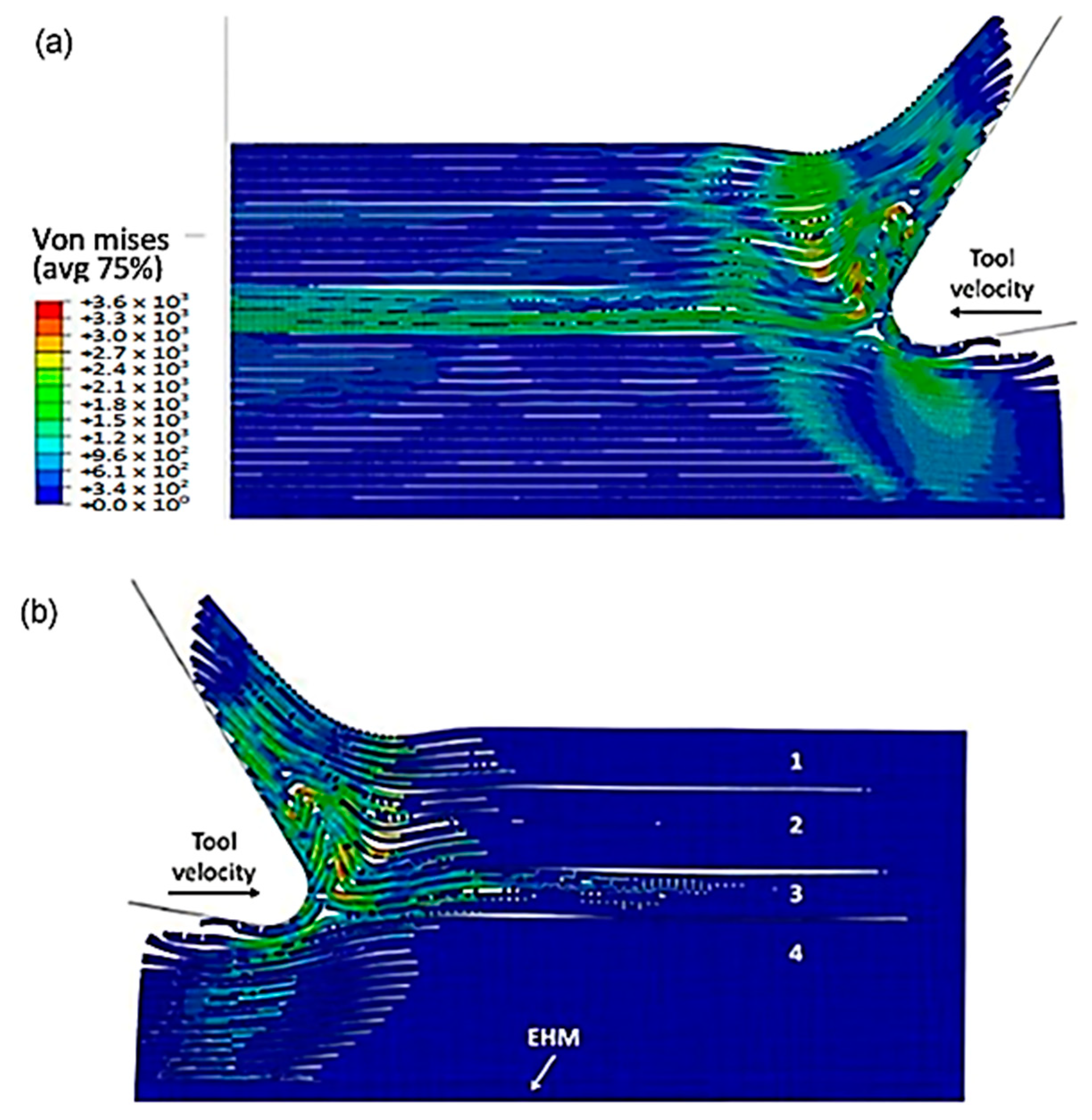
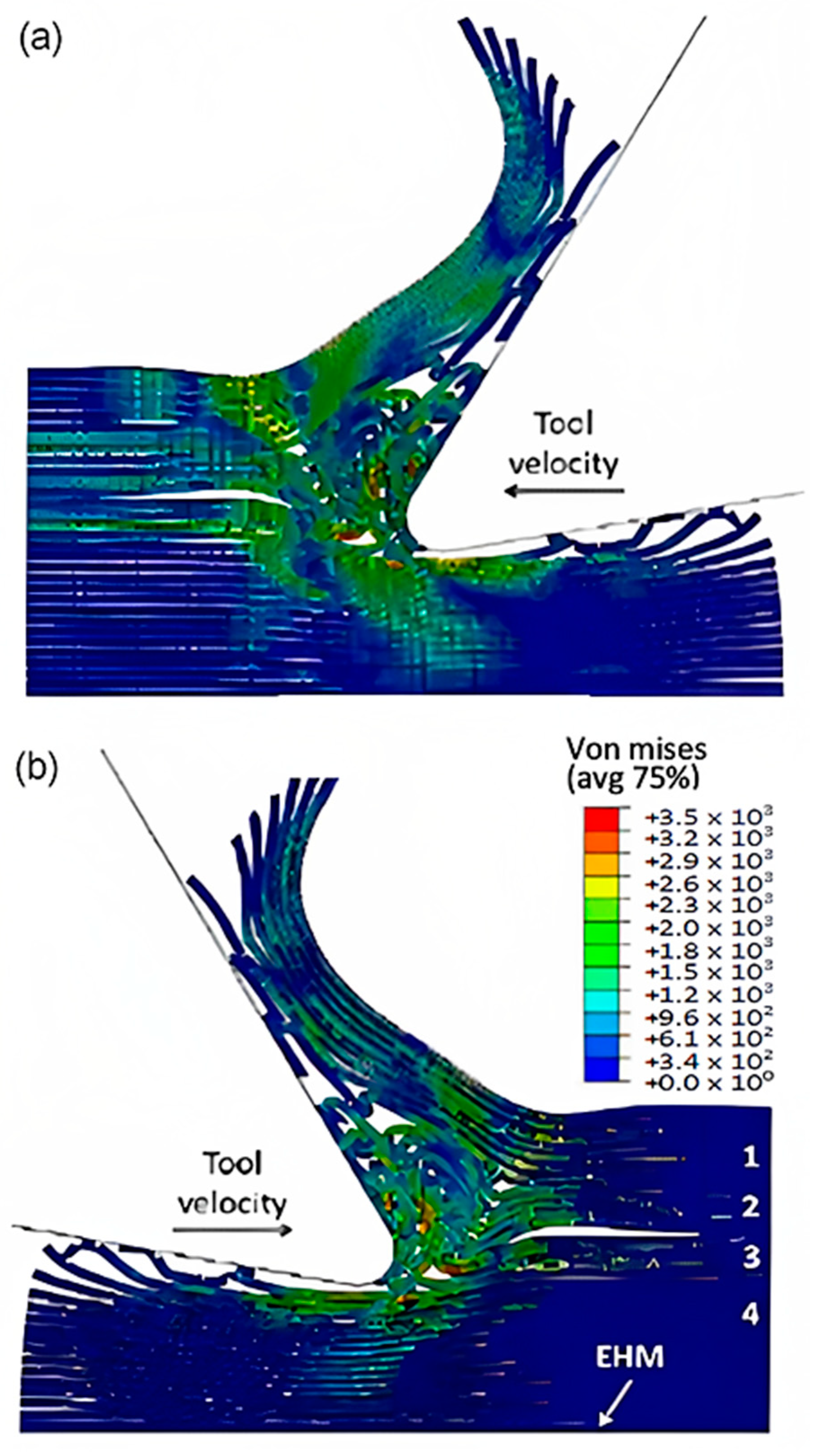
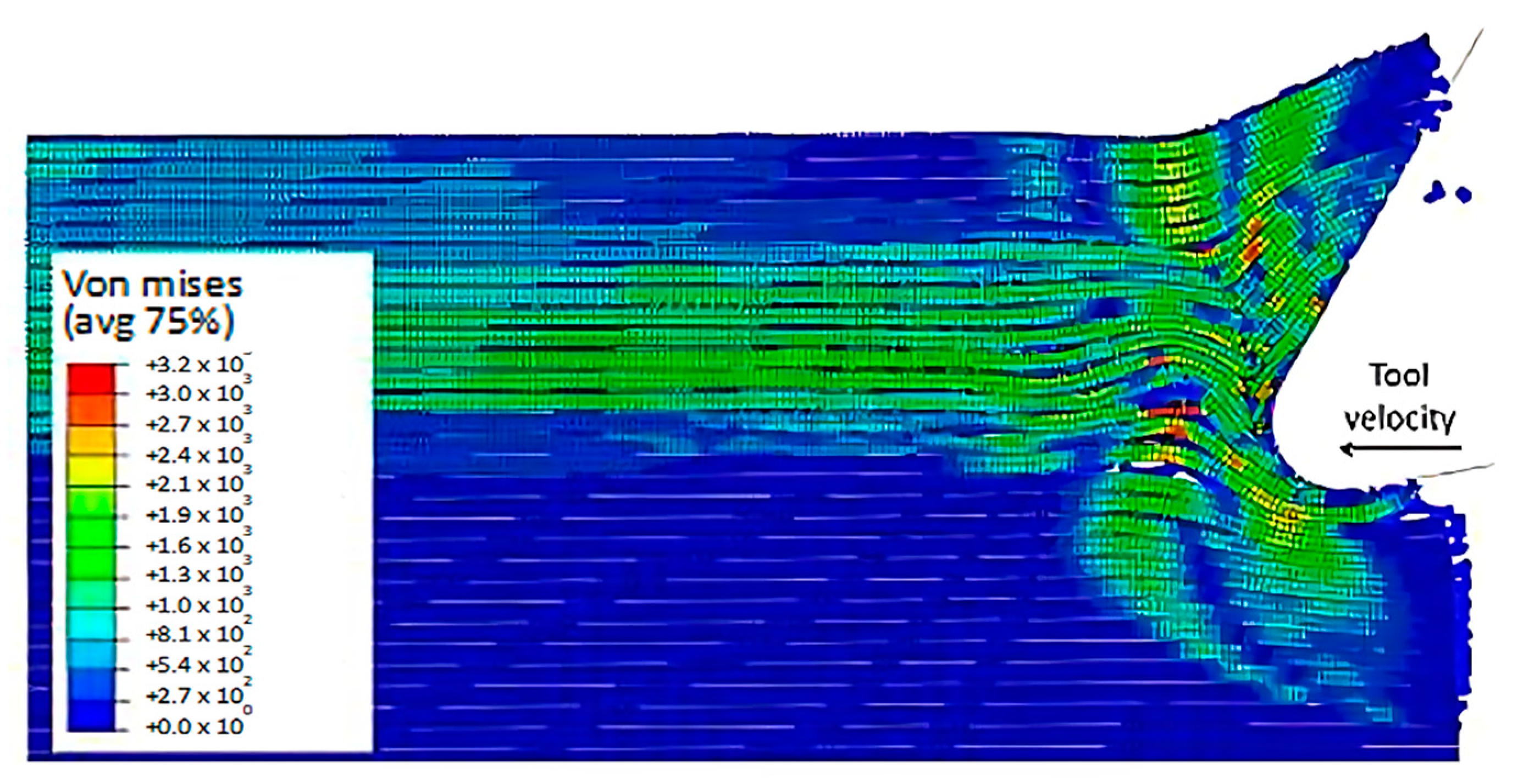
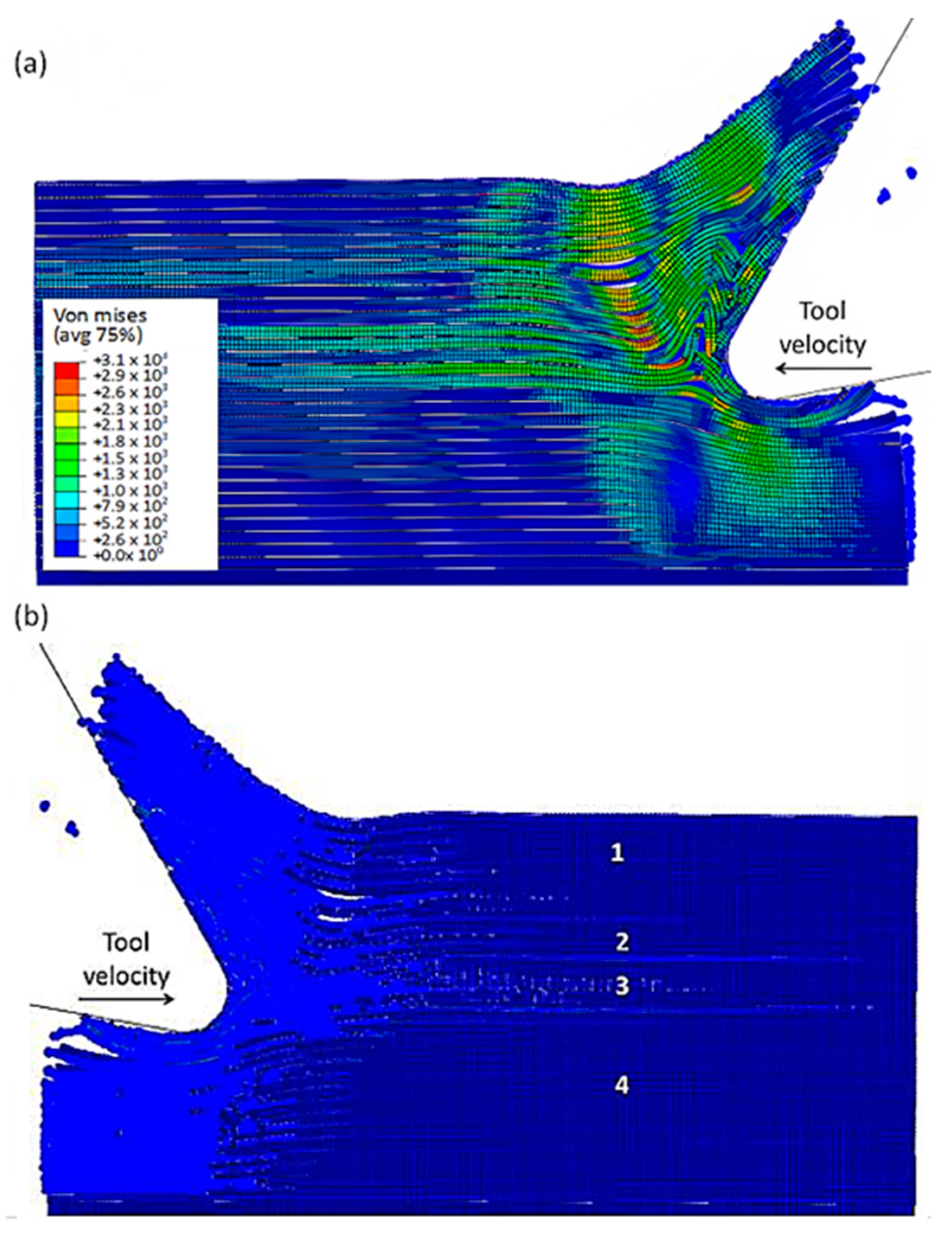
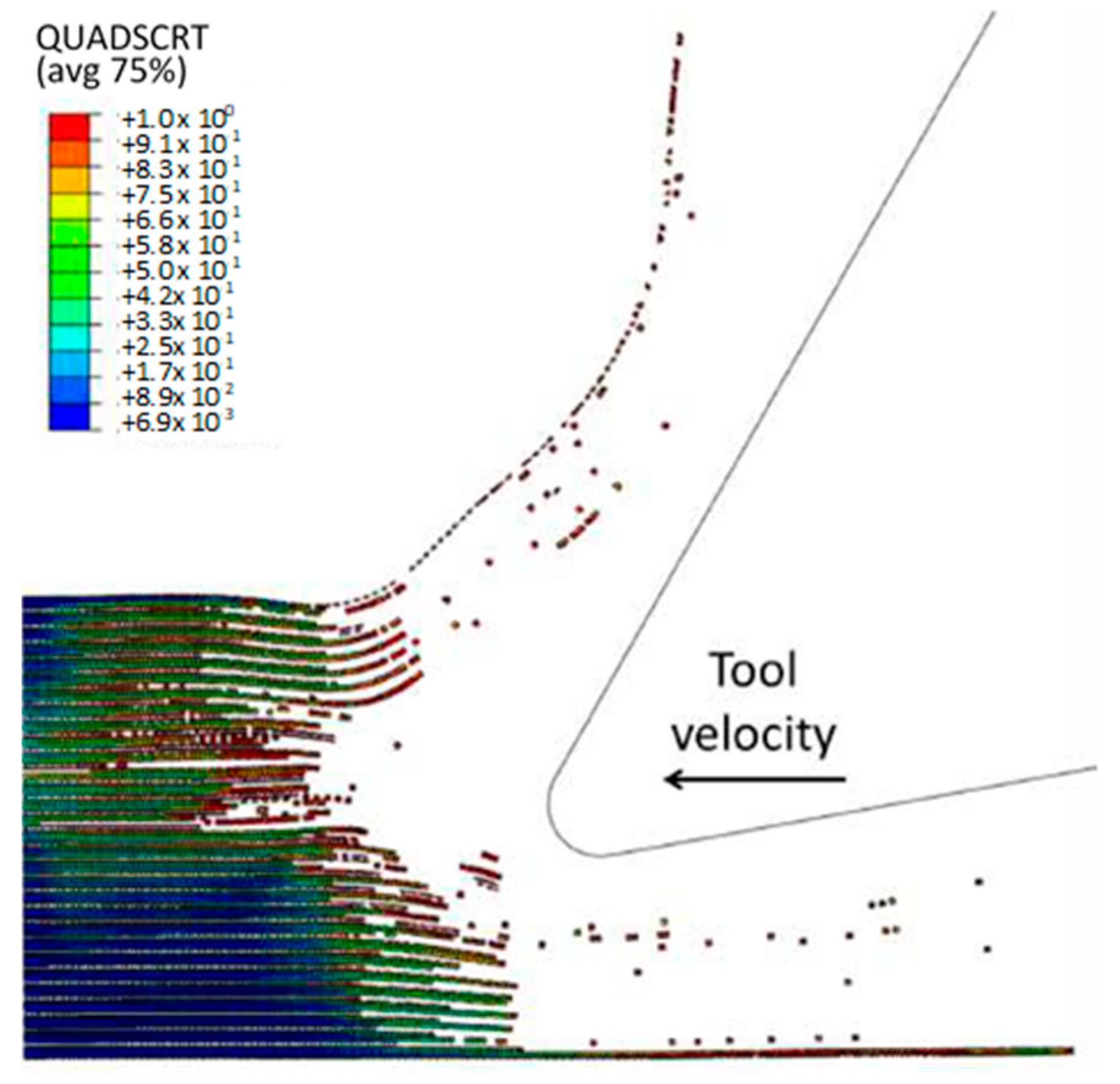
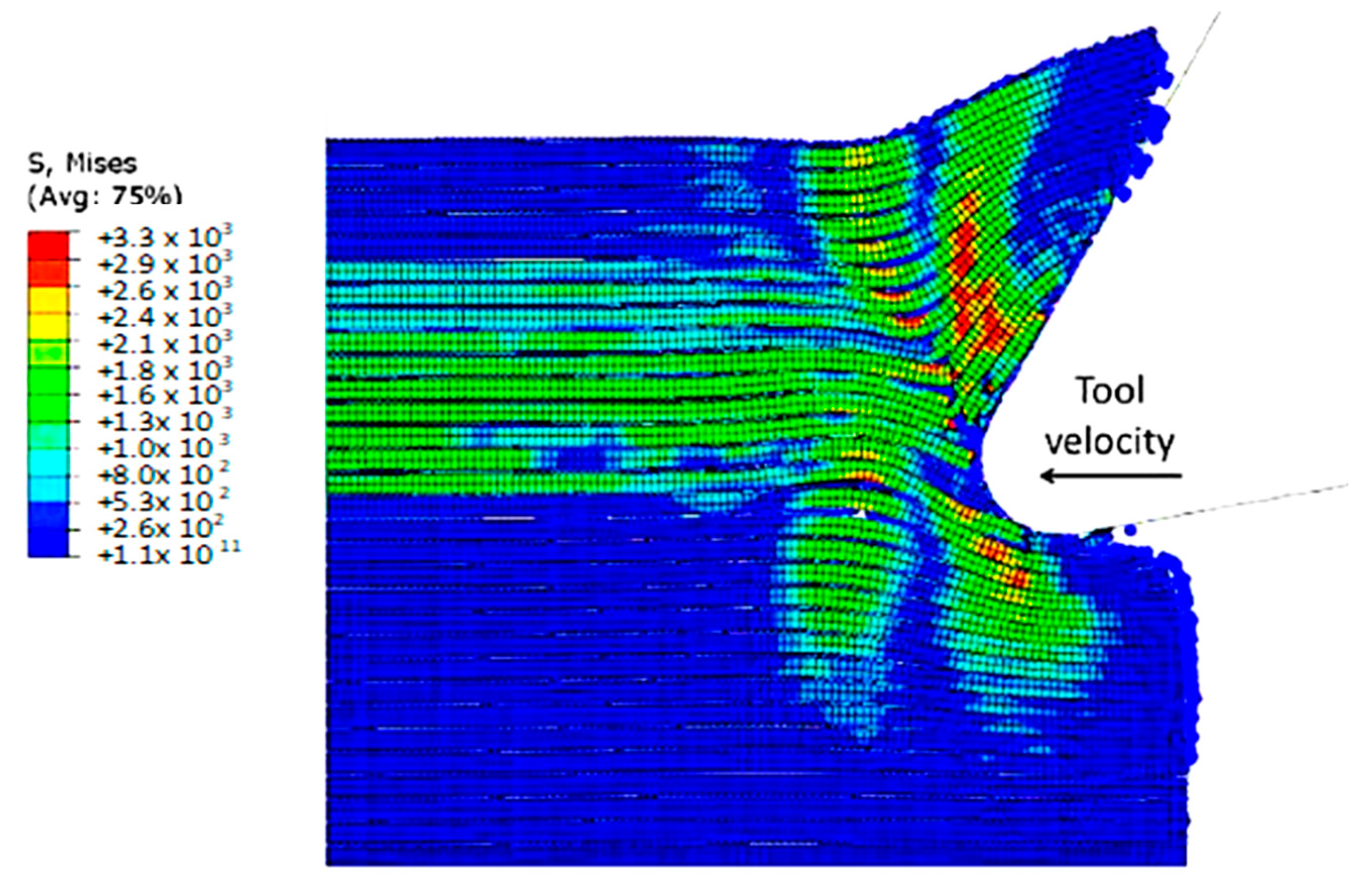
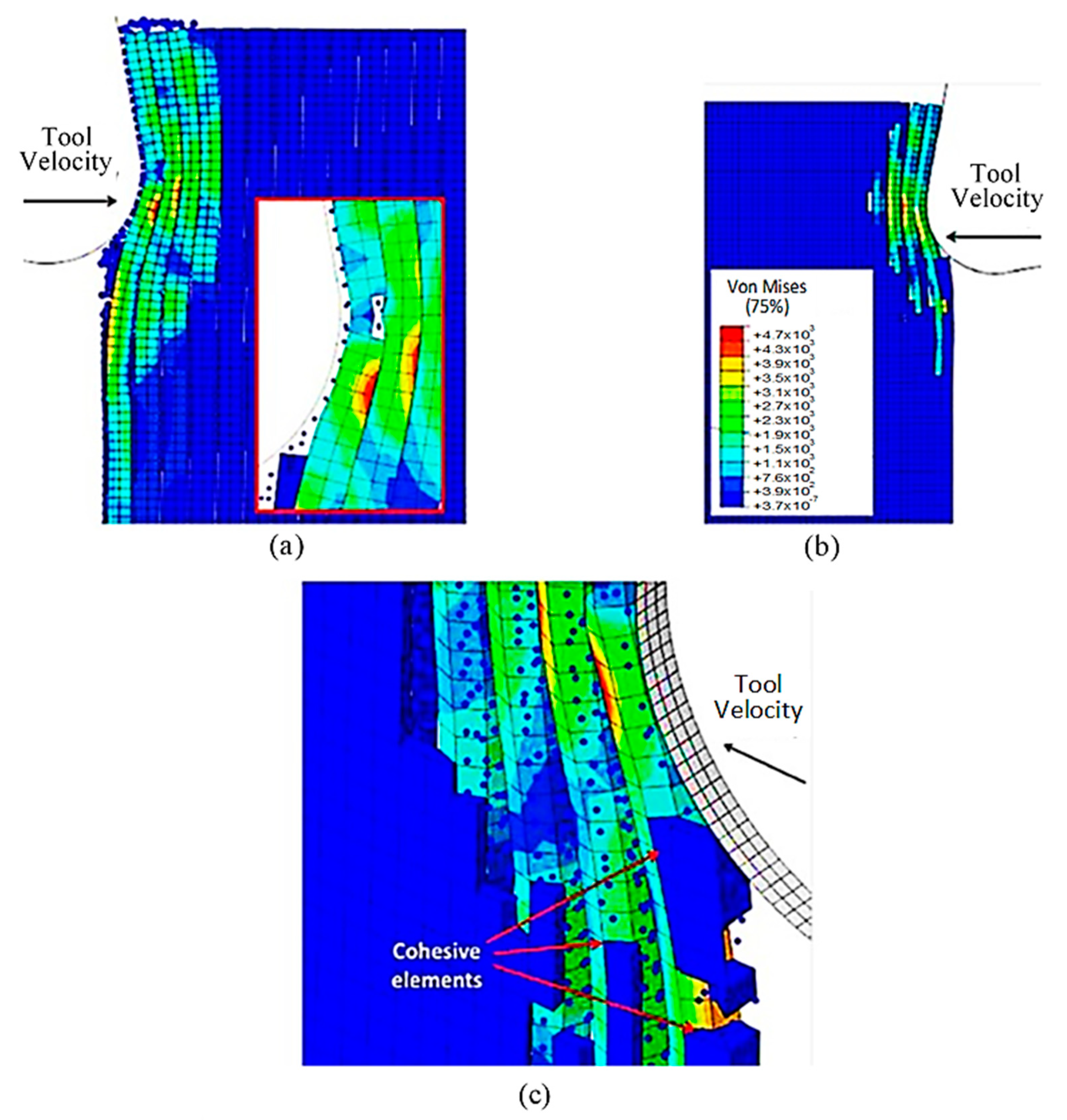
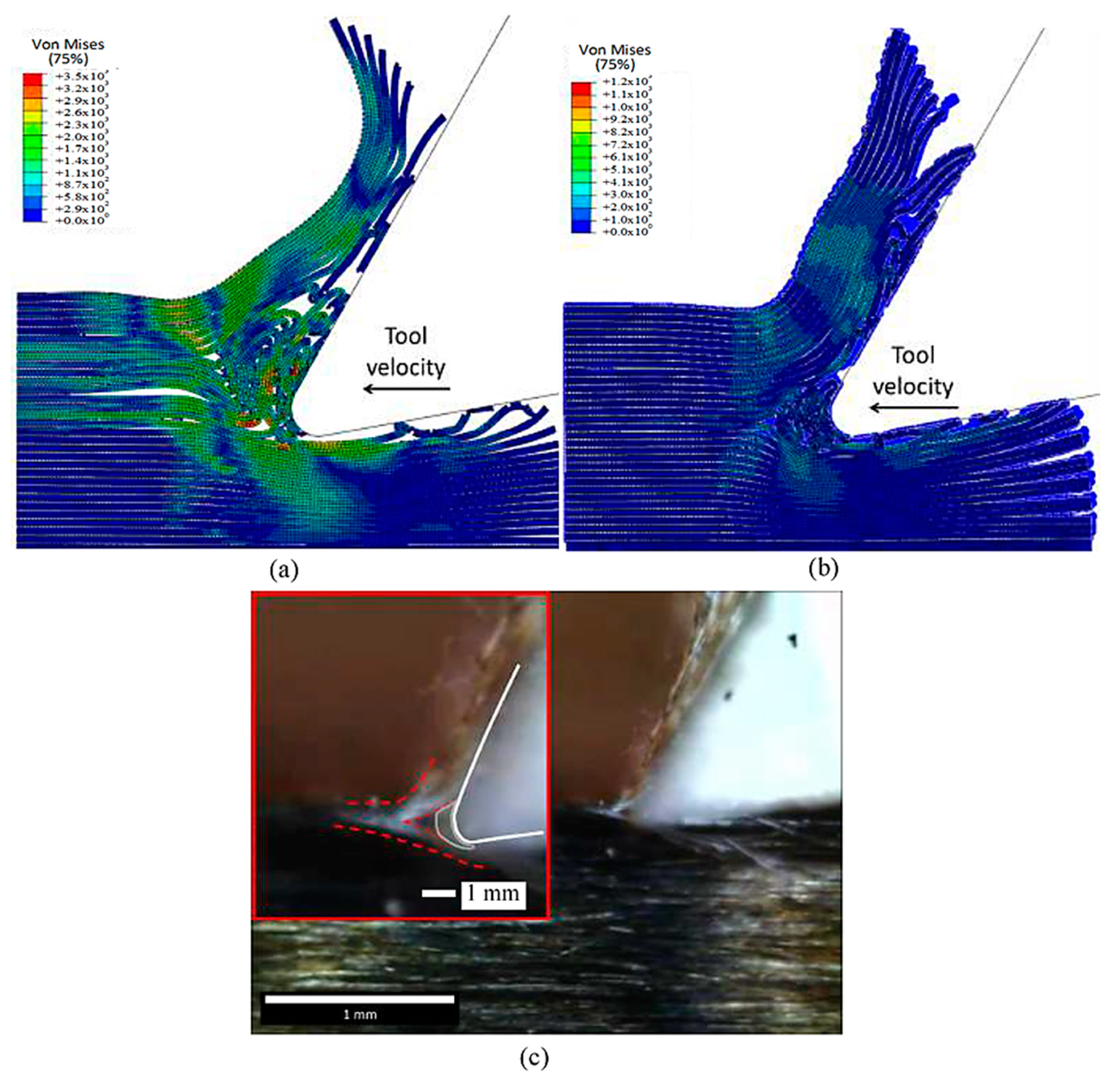
3.1.3. FEM for 90º Fibre Orientation
3.1.4. FEM-SPH for 90º Finite Orientation
3.2. Experimental Validation
3.2.1. The Cutting Forces
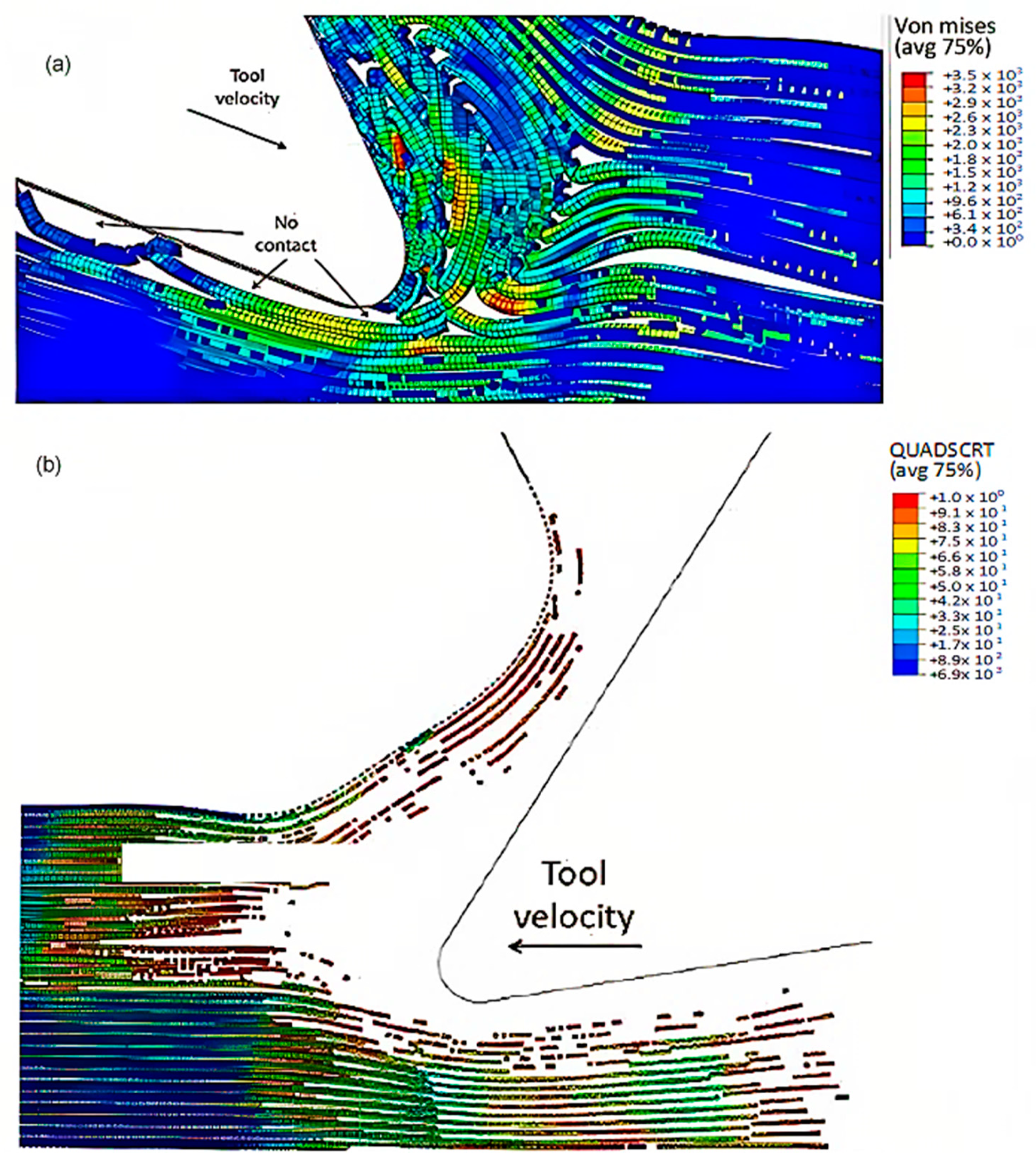
3.2.2. Chip Formation and Type
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahmad, H.; Markina, A.A.; Porotnikov, M.V.; Ahmad, F. A review of carbon fiber materials in automotive industry. IOP Con-Ference Ser. Mater. Sci. Eng. 2020, 971, 032011. [Google Scholar] [CrossRef]
- Caggiano, A. Machining of fibre reinforced plastic composite materials. Materials 2018, 11, 442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Galatas, A.; Hassanin, H.; Zweiri, Y.; Seneviratne, L. Additive Manufactured Sandwich Composite/ABS Parts for Unmanned Aerial Vehicle Applications. Polymers 2018, 10, 1262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Teti, R. Machining of Composite Materials. CIRP Ann. 2002, 51, 611–634. [Google Scholar] [CrossRef]
- Poór, D.I.; Geier, N.; Pereszlai, C.; Xu, J. A critical review of the drilling of CFRP composites: Burr formation, characterisation and challenges. Compos. Part B Eng. 2021, 223, 109155. [Google Scholar] [CrossRef]
- Rawal, S.; Sidpara, A.M.; Paul, J. A review on micro machining of polymer composites. J. Manuf. Process. 2022, 77, 87–113. [Google Scholar] [CrossRef]
- Alarifi, I.M. A Review on Factors Affecting Machinability and Properties of Fiber-Reinforced Polymer Composites. J. Nat. Fibers 2023, 20, 2154304. [Google Scholar] [CrossRef]
- Shetty, N.; Shahabaz, S.M.; Sharma, S.S.; Shetty, S.D. A review on finite element method for machining of composite materials. Compos. Struct. 2017, 176, 790–802. [Google Scholar] [CrossRef]
- Takeyama, H.; Iijima, N. Machinability of Glassfiber Reinforced Plastics and Application of Ultrasonic Machining. CIRP Ann. 1988, 37, 93–96. [Google Scholar] [CrossRef]
- Zhang, L.C.; Zhang, H.J.; Wang, X.M. A force prediction model for cutting unidirectional fibre-reinforced plastics. Mach. Sci. Technol. 2001, 5, 293–305. [Google Scholar] [CrossRef]
- Cantero, J.L.; Santiuste, C.; Marín, N.; Soldani, X.; Miguélez, H. 2D and 3D approaches to simulation of metal and composite cutting. AIP Conf. Proc. 2012, 1431, 651–659. [Google Scholar]
- Santiuste, C.; Olmedo, A.; Soldani, X.; Miguélez, H. Delamination prediction in orthogonal machining of carbon long fi-ber-reinforced polymer composites. J. Reinf. Plast. Compos. 2012, 31, 875–885. [Google Scholar] [CrossRef] [Green Version]
- Santiuste, C.; Soldani, X.; Miguélez, M.H. Machining FEM model of long fiber composites for aeronautical components. Compos. Struct. 2010, 92, 691–698. [Google Scholar] [CrossRef] [Green Version]
- Nayak, D.; Singh, I.; Bhatnagar, N.; Mahajan, P. An Analysis of Machining Induced Damages in FRP Composites—A Micro-mechanics Finite Element Approach. AIP Conf. Proc. 2004, 712, 327–331. [Google Scholar]
- Palani, V.; Bahr, B. Finite Element Simulation of 3D Drilling in Unidirectional CFRP Composite. Master’s Thesis, Wichita State University, Wichita, KS, USA, 2006. [Google Scholar]
- Isbilir, O.; Ghassemieh, E. Numerical investigation of the effects of drill geometry on drilling induced delamination of carbon fiber reinforced composites. Compos. Struct. 2013, 105, 126–133. [Google Scholar] [CrossRef]
- Phadnis, V.A.; Roy, A.; Silberschmidt, V.V. A Finite Element Model of Ultrasonically Assisted Drilling in Carbon/Epoxy Com-posites. Procedia CIRP 2013, 8, 141–146. [Google Scholar] [CrossRef] [Green Version]
- Hale, P.; Ng, E.-G. 3D Finite Element Model on Drilling of CFRP with Numerical Optimization and Experimental Validation. Materials 2021, 14, 1161. [Google Scholar] [CrossRef]
- Orifici, A.; Herszberg, I.; Thomson, R.S. Review of methodologies for composite material modelling incorporating failure. Compos. Struct. 2008, 86, 194–210. [Google Scholar] [CrossRef]
- Altenbach, H.; Tushtev, K. A New Static Failure Criterion for Isotropic Polymers. Mech. Compos. Mater. 2001, 37, 475–482. [Google Scholar] [CrossRef]
- Rao, G.V.G.; Mahajan, P.; Bhatnagar, N. Micro-mechanical modeling of machining of FRP composites—Cutting force analysis. Compos. Sci. Technol. 2007, 67, 579–593. [Google Scholar] [CrossRef]
- Rao, G.V.G.; Mahajan, P.; Bhatnagar, N. Machining of UD-GFRP composites chip formation mechanism. Compos. Sci. Technol. 2007, 67, 2271–2281. [Google Scholar]
- Rentsch, R.; Pecat, O.; Brinksmeier, E. Macro and micro process modeling of the cutting of carbon fiber reinforced plastics using FEM. Procedia Eng. 2011, 10, 1823–1828. [Google Scholar] [CrossRef] [Green Version]
- Abena, A.; Soo, S.; Essa, K. A Finite Element Simulation for Orthogonal Cutting of UD-CFRP Incorporating a Novel Fibre-matrix Interface Model. Procedia CIRP 2015, 31, 539–544. [Google Scholar] [CrossRef] [Green Version]
- Beklemysheva, K.; Vasyukov, A.; Ermakov, A.; Petrov, I. Numerical simulation of the failure of composite materials by using the grid-characteristic method. Mathematical Models and Computer Simulations. 2016, 8, 557–567. [Google Scholar] [CrossRef]
- Hu, Y.; Xia, Z.; Ellyin, F. The Failure Behavior of an Epoxy Resin Subject to Multiaxial Loading. Pipelines 2006, 2006, 1–8. [Google Scholar]
- Zhou, Y.; Wang, Y.; Xia, Y.; Jeelani, S. Tensile behavior of carbon fiber bundles at different strain rates. Mater. Lett. 2010, 64, 246–248. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Y.; Jeelani, S.; Xia, Y. Experimental Study on Tensile Behavior of Carbon Fiber and Carbon Fiber Reinforced Aluminum at Different Strain Rate. Appl. Compos. Mater. 2007, 14, 17–31. [Google Scholar] [CrossRef]
- Honjo, K. Fracture toughness of PAN-based carbon fibers estimated from strength–mirror size relation. Carbon 2003, 41, 979–984. [Google Scholar] [CrossRef]
- Oya, N.; Johnson, D. Longitudinal compressive behaviour and microstructure of PAN-based carbon fibres. Carbon 2001, 39, 635–645. [Google Scholar] [CrossRef]
- Ueda, M.; Saito, W.; Imahori, R.; Kanazawa, D.; Jeong, T.-K. Longitudinal direct compression test of a single carbon fiber in a scanning electron microscope. Compos. Part A Appl. Sci. Manuf. 2014, 67, 96–101. [Google Scholar] [CrossRef]
- Dandekar, C.R.; Shin, Y.C. Multiphase Finite Element Modeling of Machining Unidirectional Composites: Prediction of Debonding and Fiber Damage. J. Manuf. Sci. Eng. -Trans. Asme 2008, 130, 051016. [Google Scholar] [CrossRef]
- Phadnis, V.A.; Makhdum, F.; Roy, A.; Silberschmidt, V.V. Drilling in carbon/epoxy composites: Experimental investigations and finite element implementation. Compos. Part A Appl. Sci. Manuf. 2013, 47, 41–51. [Google Scholar] [CrossRef] [Green Version]
- Feito, N.; López-Puente, J.; Santiuste, C.; Miguélez, M.H. Numerical prediction of delamination in CFRP drilling. Compos. Struct. 2014, 108, 677–683. [Google Scholar] [CrossRef] [Green Version]
- Shinde, A.S.; Siva, I.; Munde, Y.; Sultan, M.T.H.; Hua, L.S.; Shahar, F.S. Numerical modelling of drilling of fiber reinforced polymer matrix composite: A review. J. Mater. Res. Technol. 2022, 20, 3561–3578. [Google Scholar] [CrossRef]
- Camanho, P.; Dávila, C. Mixed-mode dechoesion finite elements for the simulation of delamination in composite materials. NTRS 2002, 1, NASA/TM-2002-211737. [Google Scholar]
- May, M. Numerical evaluation of cohesive zone models for modeling impact induced delamination in composite materials. Compos. Struct. 2015, 133, 16–21. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Zahedi, A.; Li, S.; Roy, A.; Babitsky, V.; Silberschmidt, V.V. Application of Smooth-Particle Hydrodynamics in Metal Machining. J. Phys. Conf. Ser. 2012, 382, 012017. [Google Scholar] [CrossRef] [Green Version]
- Spreng, F.; Eberhard, P. Machining Process Simulations with Smoothed Particle Hydrodynamics. Procedia CIRP 2015, 31, 94–99. [Google Scholar] [CrossRef] [Green Version]
- Madaj, M.; Píška, M. On the SPH Orthogonal Cutting Simulation of A2024-T351 Alloy. Procedia CIRP 2013, 8, 152–157. [Google Scholar] [CrossRef] [Green Version]
- Zetterberg, M. A critical overview of machining simulations in ABAQUS. Master’s Thesis, KTH Royal Institute Of Technology, Stockholm, Switzerland, 2014. [Google Scholar]
- Limido, J.; Espinosa, C.; Salaün, M.; Mabru, C.; Chieragatti, R. High speed machining modelling: SPH method capabilities. In Proceedings of the 4th Smoothed Particle Hydrodynamics European Research Interest Community (SPHERIC) Workshop, Nantes, France, 27–29 May 2009. [Google Scholar]
- Villumsen, M.; Fauerholdt, T.G. Simulation of Metal Cutting using Smooth Particle Hydrodynamics. LS-DYNA Anwend. 2008, C-III, 17–36. [Google Scholar]
- Avachat, C.S.; Cherukuri, H.P. A Parametric Study of the Modeling of Orthogonal Machining Using the Smoothed Particle Hydrodynamics Method. Am. Soc. Mech. Eng. 2015, 57571, V014T06A005. [Google Scholar]
- Xi, Y.; Bermingham, M.; Wang, G.; Dargusch, M. SPH/FE modeling of cutting force and chip formation during thermally assisted machining of Ti6Al4V alloy. Comput. Mater. Sci. 2014, 84, 188–197. [Google Scholar] [CrossRef]
- Llanos, I.; Villar, J.; Urresti, I.; Arrazola, P. Finite element modeling of oblique machining using an arbitrary Lagrangian–Eulerian formulation. Mach. Sci. Technol. 2009, 13, 385–406. [Google Scholar] [CrossRef]
- Calzada, K.; Kapoor, S.; DeVor, R.; Samuel, J.; Srivastava, A. Modeling and interpretation of fiber orientation-based failure mechanisms in machining of carbon fiber-reinforced polymer composites. J. Manuf. Process. 2012, 14, 141–149. [Google Scholar] [CrossRef]
- Littell, J.D.; Ruggeri, C.R.; Goldberg, R.K.; Roberts, G.D.; Arnold, W.A.; Binienda, W.K. Measurement of Epoxy Resin Tension, Compression, and Shear Stress–Strain Curves over a Wide Range of Strain Rates Using Small Test Specimens. J. Aerosp. Eng. 2008, 21, 162–173. [Google Scholar]
- Zitoune, R.; Collombet, F.; Lachaud, F.; Piquet, R.; Pasquet, P. Experiment–calculation comparison of the cutting conditions rep-resentative of the long fiber composite drilling phase. Compos. Sci. Technol. 2005, 65, 455–466. [Google Scholar] [CrossRef]
- Bhatnagar, N.; Ramakrishnan, N.; Naik, N.K.; Komanduri, R. On the machining of fiber reinforced plastic (FRP) composite laminates. Int. J. Mach. Tools Manuf. 1995, 35, 701–716. [Google Scholar] [CrossRef]
- Li, H.; Qin, X.; He, G.; Jin, Y.; Sun, D.; Price, M. Investigation of chip formation and fracture toughness in orthogonal cutting of UD-CFRP. Int. J. Adv. Manuf. Technol. 2016, 82, 1079–1088. [Google Scholar] [CrossRef] [Green Version]
- Wei, Y.; An, Q.; Cai, X.; Chen, M.; Ming, W. Influence of Fiber Orientation on Single-Point Cutting Fracture Behavior of Car-bon-Fiber/Epoxy Prepreg Sheets. Materials 2015, 8, 6738–6751. [Google Scholar] [CrossRef] [Green Version]
- Kahwash, F.; Shyha, I.; Maheri, A. Machining Unidirectional Composites using Single-Point Tools: Analysis of Cutting Forces, Chip Formation and Surface Integrity. Procedia Eng. 2015, 132, 569–576. [Google Scholar] [CrossRef] [Green Version]
- Abena, A.; Soo, S.; Essa, K. Modelling the orthogonal cutting of UD-CFRP composites: Development of a novel cohesive zone model. Compos. Struct. 2017, 168, 65–83. [Google Scholar] [CrossRef] [Green Version]
- Abena, A.; Soo, S.L.; Ataya, S.; Hassanin, H.; El-Sayed, M.A.; Ahmadein, M.; Alsaleh, N.A.; Ahmed, M.M.Z.; Essa, K. Chip Formation and Orthogonal Cutting Optimisation of Unidirectional Carbon Fibre Composites. Polymers 2023, 15, 1897. [Google Scholar] [CrossRef] [PubMed]
- Abena, A.; Essa, K. 3D micro-mechanical modelling of orthogonal cutting of UD-CFRP using smoothed particle hydrodynamics and finite element methods. Compos. Struct. 2019, 218, 174. [Google Scholar] [CrossRef]
- Liu, T.; Qiu, F.; Yang, H.; Liu, S.; Jiang, Q.; Zhang, L. Exploring the potential of FSW-ed Al–Zn–Mg–Cu-based composite reinforced by trace in-situ nanoparticles in manufacturing workpiece with customizable size and high mechanical performances. Compos. Part B Eng. 2023, 250, 110425. [Google Scholar] [CrossRef]
- Yang, H.; Yan, Y.; Liu, T.; Dong, B.; Chen, L.; Shu, S.; Qiu, F.; Jiang, Q.; Zhang, L. Unprecedented enhancement in strength-plasticity synergy of (TiC+Al6MoTi+Mo)/Al cermet by multiple length-scale microstructure stimulated synergistic deformation. Compos. Part B Eng. 2021, 225, 109265. [Google Scholar] [CrossRef]
- Dong, B.; Li, Q.; Wang, Z.; Liu, T.; Yang, H.; Shu, S.; Chen, L.; Qiu, F.; Jiang, Q.; Zhang, L. Enhancing strength-ductility synergy and mechanisms of Al-based composites by size-tunable in-situ TiB2 particles with specific spatial distribution. Compos. Part B Eng. 2021, 217, 108912. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Z.; Chen, L.; Shu, S.; Qiu, F.; Zhang, L. Interface formation and bonding control in high-volume-fraction (TiC+TiB2)/Al composites and their roles in enhancing properties. Compos. Part B Eng. 2021, 209, 108605. [Google Scholar] [CrossRef]









| Material | Property | Value |
|---|---|---|
| Carbon fibre | Elastic constants Longitudinal strength | E1 = 294 GPa, E2 = E3 = 14 GPa GPa, G23 = 5.5 GPaν12 = ν13 = 0.2, ν23 = 0.25G12 = G13 = 28 GPa Xt= 5.88 GPa, Xc= 3.288 GPa |
| Compressive strain failure | 0.155 | |
| Compressive yield | 594.5 MPa | |
| Epoxy matrix | Elastic constants | E = 2.96 GPa, ν = 0.4 |
| Interface | Failure strength fracture Normal strength shear energy | σu = 74.7 MPa τmax = 25 MPa Gc= 0.05 σmax = 167.5 MPa N/mm2 |
| Trust Force at Samples with Fibre Orientation of 0° | Trust Force at Samples with Fibre Orientation of 90° | |
|---|---|---|
| Measured experimentally | 35.68 N/mm | 59.29 N/mm |
| Calculated using the FEM model | −3.03 N/mm | −4.28 N/mm |
| Calculated using the hybrid model with D = 0.8 | 14.2 N/mm | N/A |
| Calculated using the hybrid model with D = 0.1 | 16.1 N/mm | 24.9 N/mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abena, A.; Ataya, S.; Hassanin, H.; El-Sayed, M.A.; Ahmadein, M.; Alsaleh, N.A.; Ahmed, M.M.Z.; Essa, K. Hybrid Finite Element–Smoothed Particle Hydrodynamics Modelling for Optimizing Cutting Parameters in CFRP Composites. Polymers 2023, 15, 2789. https://doi.org/10.3390/polym15132789
Abena A, Ataya S, Hassanin H, El-Sayed MA, Ahmadein M, Alsaleh NA, Ahmed MMZ, Essa K. Hybrid Finite Element–Smoothed Particle Hydrodynamics Modelling for Optimizing Cutting Parameters in CFRP Composites. Polymers. 2023; 15(13):2789. https://doi.org/10.3390/polym15132789
Chicago/Turabian StyleAbena, Alessandro, Sabbah Ataya, Hany Hassanin, Mahmoud Ahmed El-Sayed, Mahmoud Ahmadein, Naser A. Alsaleh, Mohamed M. Z. Ahmed, and Khamis Essa. 2023. "Hybrid Finite Element–Smoothed Particle Hydrodynamics Modelling for Optimizing Cutting Parameters in CFRP Composites" Polymers 15, no. 13: 2789. https://doi.org/10.3390/polym15132789










