Conformal Cooling Channel Design for Improving Temperature Distribution on the Cavity Surface in the Injection Molding Process
Abstract
:1. Introduction
- Unleashing creative design possibilities: WAAM facilitates the construction of intricate geometries that traditional methods find challenging or impossible. Once these complex structures are erected, milling steps in to refine and perfect the part. This collaborative effort results in delivering precision and enhancing the quality of the meticulously designed shapes.
- Material and cost efficiency: WAAM, a form of directed energy deposition (DED) technology, provides stellar material usage efficiency. Since it primarily engages the deposition of wire-fed materials, the resultant waste is negligible, leading to a significant reduction in raw material costs. Further, the subtractive nature of milling is carefully regulated to cut down waste, fostering even greater cost-efficiency.
- Time-efficient production: The impressive deposition rates of WAAM facilitate a swift production of large components or molds. Subsequently, milling refines these products rapidly and accurately. This amalgamation of processes potentially leads to substantial time savings, especially when compared to the utilization of either technique in isolation.
- Enhancement of mechanical properties: The layer-by-layer additive procedure inherent to WAAM can culminate in the refinement of mechanical properties, brought about by rapid cooling and grain refinement. This enhancement can be especially observable in the case of alloyed materials.
- Repair and remanufacturing capabilities: The synergy of WAAM and milling also proves beneficial for mold repair or remanufacturing. It adds material precisely where required and mills it to achieve the perfect, final shape. This strategy prolongs the lifecycle of molds or parts, eliminating the need for a complete overhaul.
- Hybrid flexibility: The integration of both additive and subtractive methods within a single setup paves the way for remarkable flexibility. By transitioning between processes as required, manufacturers can fine-tune different aspects of production, such as material usage, surface finish, and dimensional accuracy.
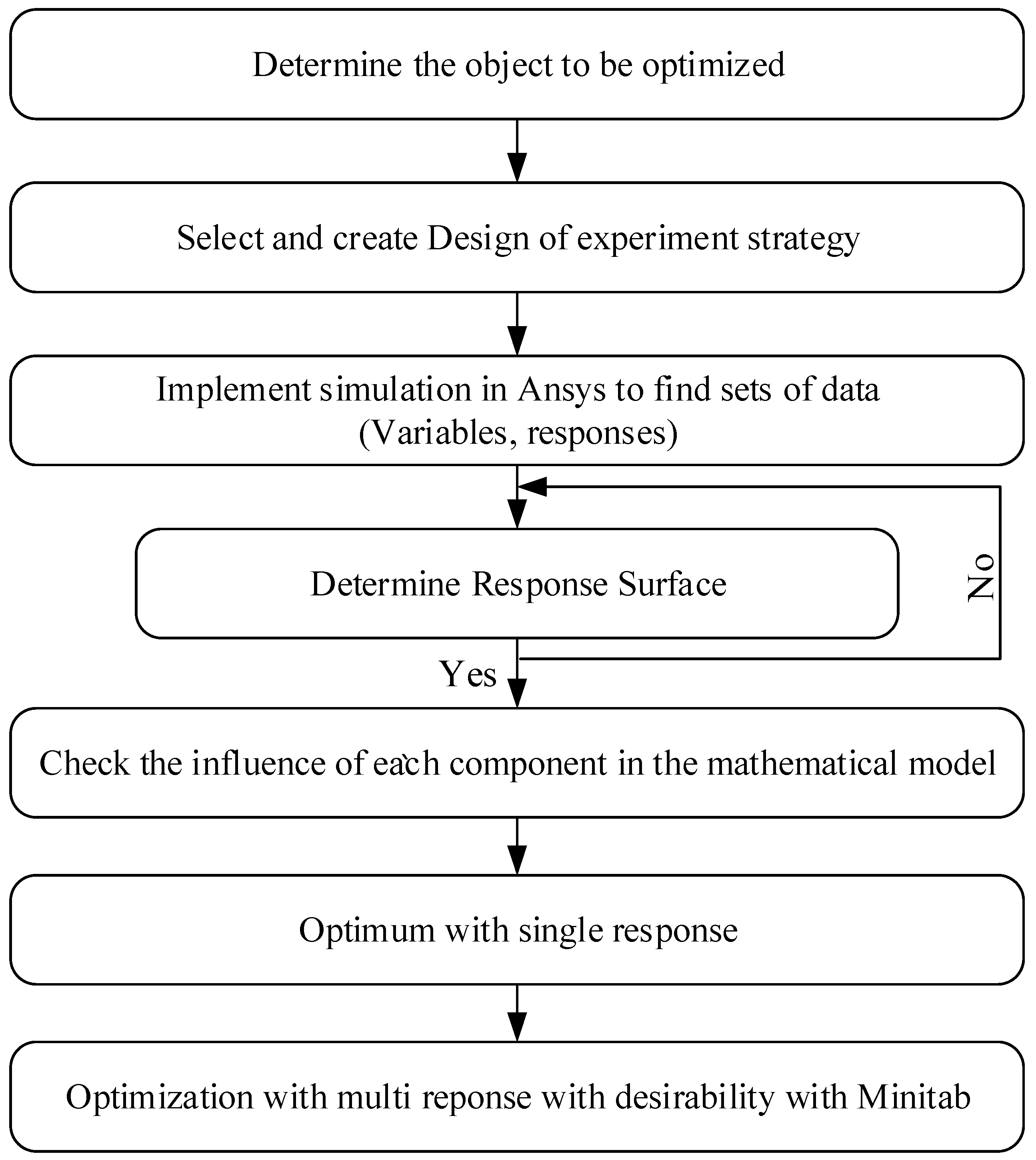
2. Simulation and Experimental Methods
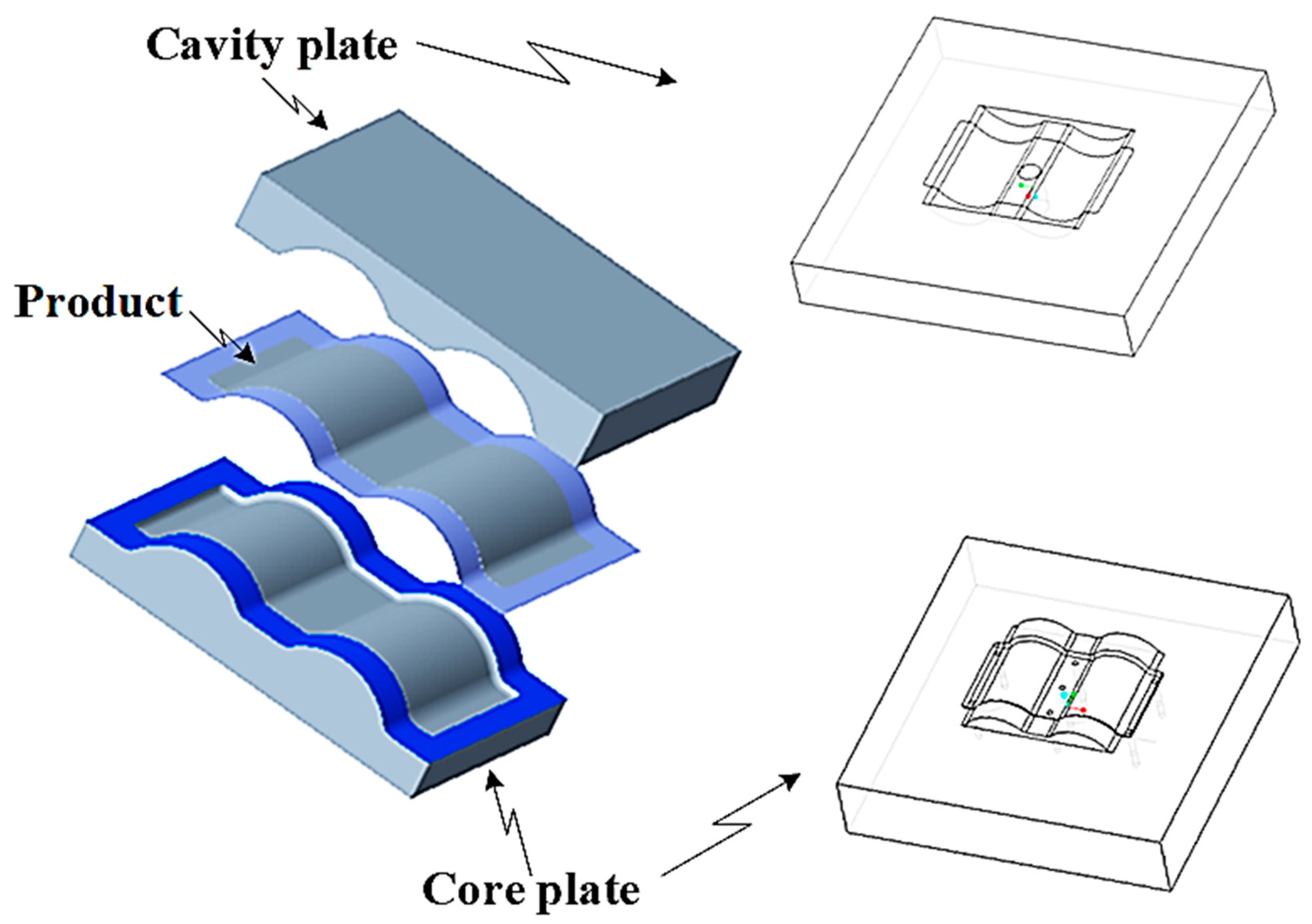
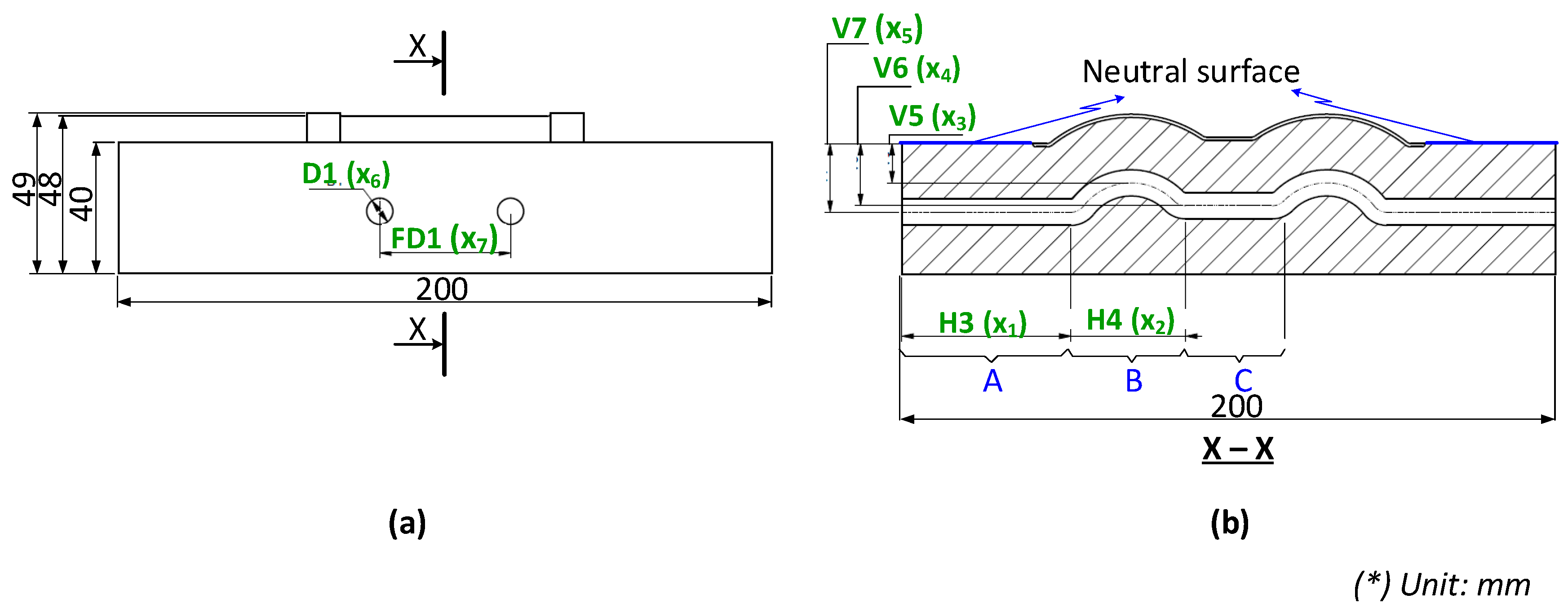
2.1. Design Products for Experiments
2.2. Mold Design
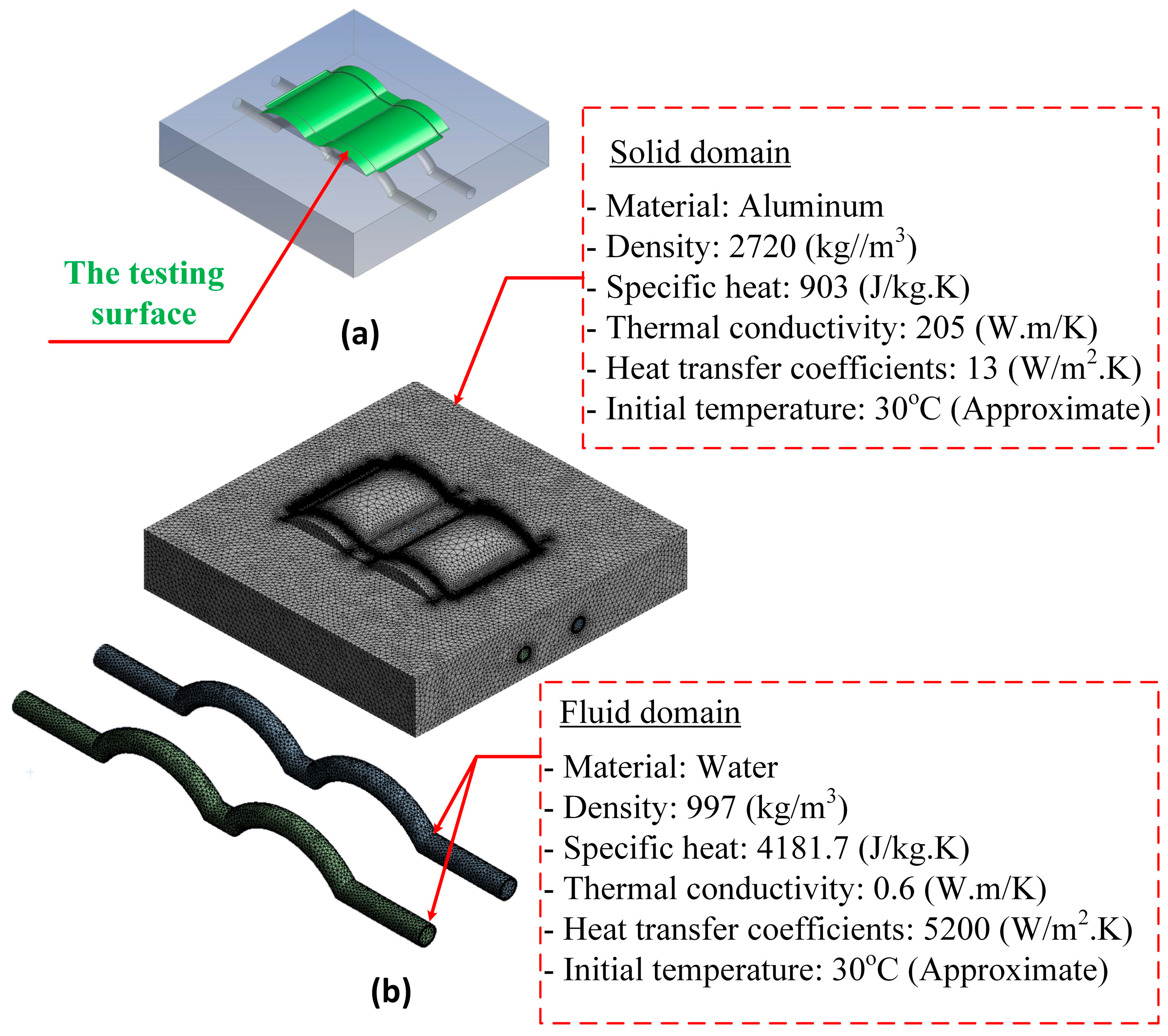
2.3. Simulation Setup
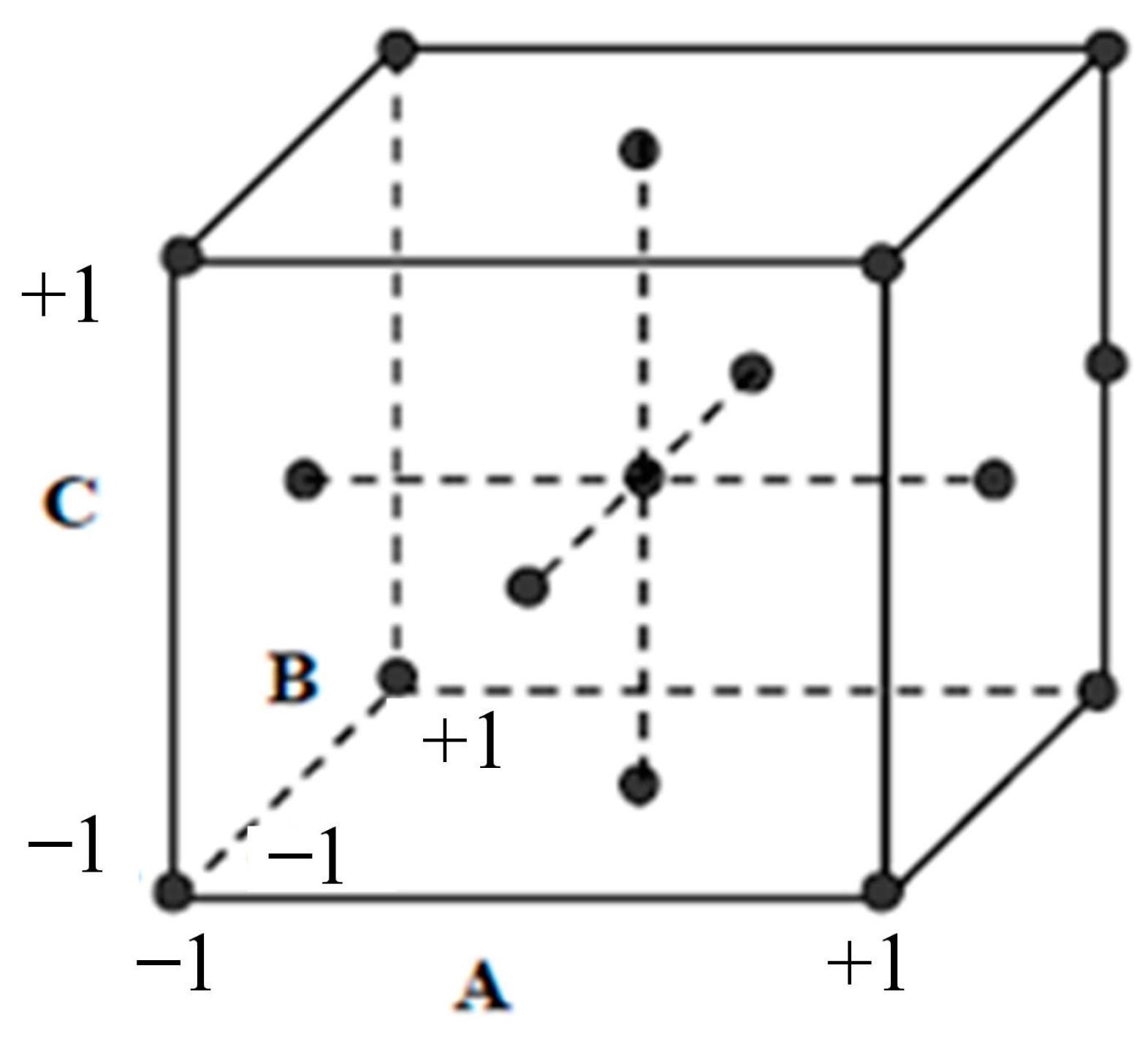
2.4. Response Surface Methodology
- Y: response;
- : linear component of the equation;
- : quadratic component of the equation;
- : interaction between variables;
- : constant;
- : error.
2.5. Multi-Response Optimization
- di: desirability function of response i;
- ki: the importance coefficient of response i.
- Li: the upper bound value;
- Ui: the lower bound value;
- Ti: the desirability value;
- wi: weight of each response.
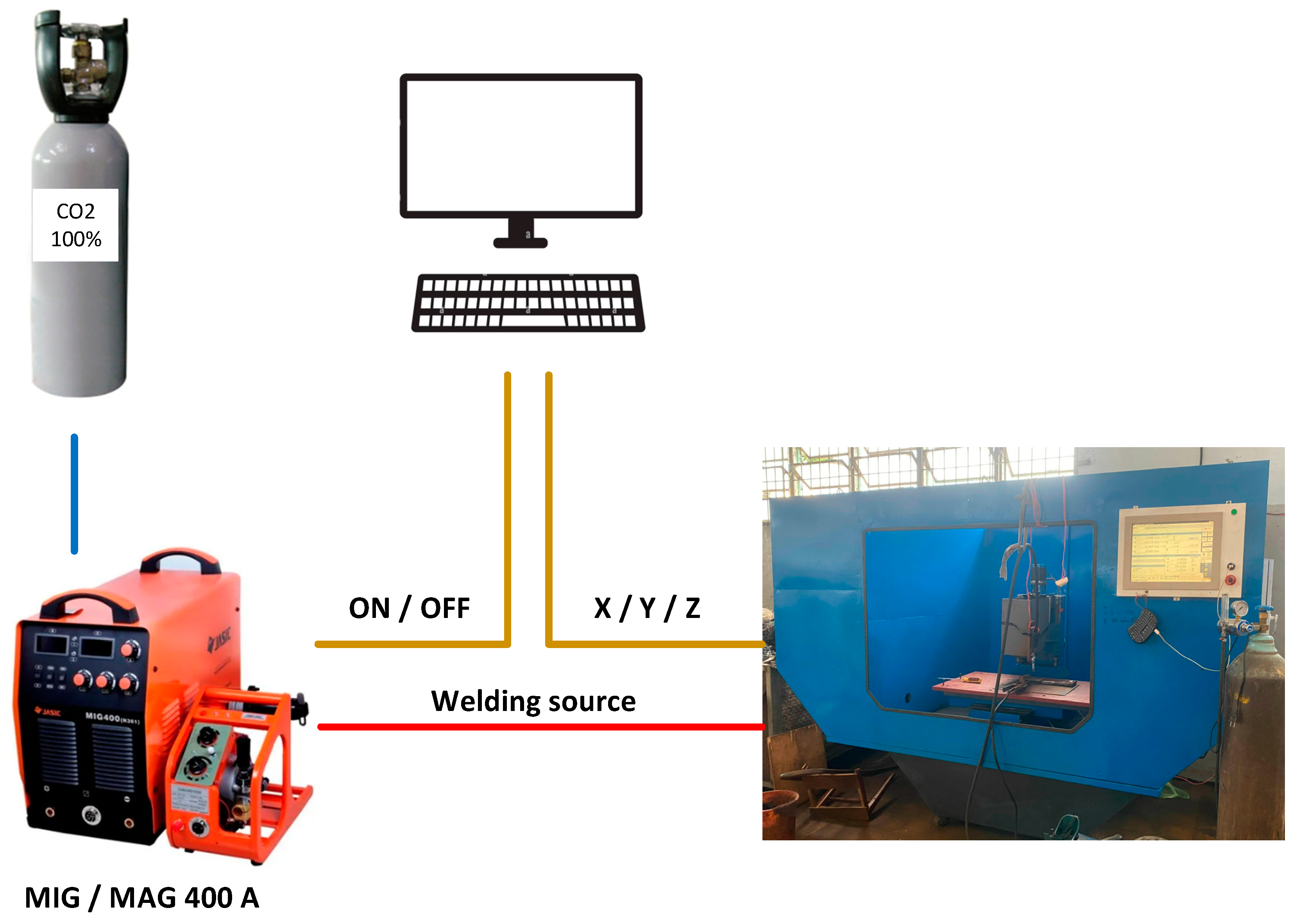
2.6. Experimental Verification
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nian, S.-C.; Li, M.-H.; Huang, M.-S. Warpage control of headlight lampshades fabricated using external gas-assisted injection molding. Int. J. Heat Mass Transf. 2015, 86, 358–368. [Google Scholar] [CrossRef]
- Ravikiran, B.; Pradhan, D.K.; Jeet, S.; Bagal, D.K.; Barua, A.; Nayak, S. Parametric optimization of plastic injection moulding for FMCG polymer moulding (PMMA) using hybrid Taguchi-WASPAS-Ant Lion optimization algorithm. Mater. Today Proc. 2021, 56, 2411–2420. [Google Scholar] [CrossRef]
- Sreedharan, J.; Jeevanantham, A. Optimization of Injection Molding Process to Minimize Weld-line and Sink-mark Defects Using Taguchi based Grey Relational Analysis. Mater. Today Proc. 2018, 5, 12615–12622. [Google Scholar] [CrossRef]
- Minh, P.S.; Le, M.-T. Improving the Melt Flow Length of Acrylonitrile Butadiene Styrene in Thin-Wall Injection Molding by External Induction Heating with the Assistance of a Rotation Device. Polymers 2021, 13, 2288. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Sharma, S.; Muniappan, A.; Pimenov, D.Y.; Wojciechowski, S.; Jha, K.; Dwivedi, S.P.; Li, C.; Królczyk, J.B.; Walczak, D.; et al. In Situ Micro-Observation of Surface Roughness and Fracture Mechanism in Metal Microforming of Thin Copper Sheets with Newly Developed Compact Testing Apparatus. Materials 2022, 15, 1368. [Google Scholar] [CrossRef]
- Nhan, P.T.; Do, T.T.; Anh Son, T.; Son Minh, P. Study on External Gas-Assisted Mold Temperature Control for Improving the Melt Flow Length of Thin Rib Products in the Injection Molding Process. Adv. Polym. Technol. 2019, 5973403. [Google Scholar] [CrossRef]
- Chen, S.-C.; Lin, C.-Y.; Chang, J.-A.; Minh, P.S. Gas-Assisted Heating Technology for High Aspect Ratio Microstructure Injection Molding. Adv. Mech. Eng. 2013, 5, 282906. [Google Scholar] [CrossRef] [Green Version]
- Minh, P.S.; Do, T.T.; Uyen, T.M.T. The feasibility of external gas-assisted mold-temperature control for thin-wall injection molding. Adv. Mech. Eng. 2018, 10, 1687814018806102. [Google Scholar] [CrossRef] [Green Version]
- Park, H.-S.; Dang, X.-P. Optimization of conformal cooling channels with array of baffles for plastic injection mold. Int. J. Precis. Eng. Manuf. 2010, 11, 879–890. [Google Scholar] [CrossRef]
- Mazur, M.; Brincat, P.; Leary, M.; Brandt, M. Numerical and experimental evaluation of a conformally cooled H13 steel injection mould manufactured with selective laser melting. Int. J. Adv. Manuf. Technol. 2017, 93, 881–900. [Google Scholar] [CrossRef]
- Meckley, R.J. Edwards, A Study on the Design and Effectiveness of Conformal Cooling Channels in Rapid Tooling Inserts. Technol. Interface J. 2009, 10, 1–28. Available online: https://www.academia.edu/download/32648037/RT_with_cc.pdf (accessed on 10 March 2023).
- Shayfull, Z.; Sharif, S.; Zain, A.M.; Ghazali, M.F.; Saad, R.M. Potential of Conformal Cooling Channels in Rapid Heat Cycle Molding: A Review. Adv. Polym. Technol. 2013, 33, 21381. [Google Scholar] [CrossRef]
- Vojnová, E. The Benefits of a Conforming Cooling Systems the Molds in Injection Moulding Process. Procedia Eng. 2016, 149, 535–543. [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; Gu, J.; Ruan, S.; Shen, C.; Lyu, Y.; Zhao, Y. Topology Optimization for the Design of Conformal Cooling System in Thin-wall Injection Molding Based on BEM. Int. J. Adv. Manuf. Technol. 2018, 94, 1041–1059. [Google Scholar] [CrossRef]
- Sachs, E.; Wylonis, E.; Allen, S.; Cima, M.; Guo, H. Production of Injection Molding Tooling with Conformal Cooling Channels Using the Three Dimensional Printing Process; Massachusetts Institute of Technology: Cambridge, MA, USA, 1995; Available online: https://dspace.mit.edu/bitstream/handle/1721.1/10727/36829909-MIT.pdf?sequence=2 (accessed on 15 March 2023).
- Song, Y.A.; Park, S.; Jee, H.; Choi, D.; Shin, B. 3D welding and milling—A direct approach for fabrication of injection molds. In Proceedings of the Solid Freeform Fabrication Symposium; University of Texas at Austin: Austin, TX, USA, 1999; pp. 793–800. [Google Scholar]
- Song, Y.A.; Park, S.; Hwang, K.; Choi, D.; Jee, H. 3D welding and milling for direct prototyping of metallic parts. In 1998 International Solid Freeform Fabrication Symposium; The University of Texas at Austin: Austin, TX, USA, 1998; pp. 495–502. [Google Scholar] [CrossRef]
- Kuo, C.-C.; Chen, B.-C. Development of hot embossing stamps with conformal cooling channels for microreplication. Int. J. Adv. Manuf. Technol. 2016, 88, 2603–2608. [Google Scholar] [CrossRef]
- Cheng, R.; Wu, X.Y.; Zheng, J.P. Indirect rapid manufacture of injection mould with conformal cooling channels based on SLS. Die Mould Ind. 2011, 37, 70–75. [Google Scholar]
- Yang, Y.; Hannula, S.-P. Development of precision spray forming for rapid tooling. Mater. Sci. Eng. A 2008, 477, 63–68. [Google Scholar] [CrossRef]
- Dang, X.-P.; Park, H.-S. Design of U-shape milled groove conformal cooling channels for plastic injection mold. Int. J. Precis. Eng. Manuf. 2011, 12, 73–84. [Google Scholar] [CrossRef]
- Shayfull, Z.; Sharif, S.; MohdZain, A.; MohdSaad, R.; Fairuz, M.A. Milled Groove Square Shape Conformal Cooling Channels in Injection Moulding Process. Mater. Manuf. Process. 2013, 28, 884–891. [Google Scholar] [CrossRef]
- Saifullah, A.B.M.; Masood, S.H.; Sbarski, I. New cooling channel design for injection moulding. In Proceedings of the World Congress on Engineering, London, UK, 1–3 July 2009. [Google Scholar]
- Huang, J.; Lu, Y.; Wang, Q.; Lin, F. Design and Fabrication of Conformal Cooling Channels with Vacuum Diffusion Bonding. Recent Patents Chem. Eng. 2014, 6, 176–183. [Google Scholar] [CrossRef]
- Hughes, A. Method of Manufacturing a Mold with Conformal Cooling Passages and Mold Manufactured According to Said Method. US Patent Application US 13/679,318, 21 March 2013. [Google Scholar]
- Ahari, H.; Khajepour, A.; Bedi, S. Manufacturing optimization of laminated tooling with conformal cooling channels. Rapid Prototyp. J. 2011, 17, 429–440. [Google Scholar] [CrossRef]
- Ahari, H.; Khajepour, A.; Bedi, S. Laminated injection mould with conformal cooling channels: Optimization, fabrication and testing. J. Mach. Manuf. Autom. 2013, 2, 16–24. [Google Scholar]
- Hölker, R.; Haase, M.; Ben Khalifa, N.; Tekkaya, A.E. Hot Extrusion Dies with Conformal Cooling Channels Produced by Additive Manufacturing. Mater. Today Proc. 2015, 2, 4838–4846. [Google Scholar] [CrossRef]
- Yoo, S. Design of Conformal Cooling/Heating Channels for Layered Tooling. In Proceedings of the 2008 International Conference on Smart Manufacturing Application, Goyang-Si, Republic of Korea, 9–11 April 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 126–129. [Google Scholar] [CrossRef]
- Williams, R.E.; Walczyk, D.F.; Dang, H.T. Using abrasive flow machining to seal and finish conformal channels in laminated tooling. Rapid Prototyp. J. 2007, 13, 64–75. [Google Scholar] [CrossRef]
- Dimitrov, D.; Moammer, A. Investigation of the impact of conformal cooling on the performance of injection moulds for the packaging industry. J. New Gener. Sci. 2003, 8, 29–46. [Google Scholar]
- Wang, L.; Wei, Q.S.; Xue, P.J.; Shi, Y.S. Fabricate Mould Insert with Conformal Cooling Channel Using Selective Laser Melting. Adv. Mater. Res. 2012, 502, 67–71. [Google Scholar] [CrossRef]
- Klingaa, C.G.; Technical University of Denmark (DTU); Bjerre, M.K.; Baier, S.; De Chiffre, L.; Mohanty, S.; Hattel, J.H. Roughness Investigation of SLM Manufactured Conformal Cooling Channels Using X-ray Computed Tomography. In Proceedings of the 9th Conference on Industrial Computed Tomography (ICT 2019), Padova, Italy, 13–15 February 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Feng, S.; Chen, S.; Kamat, A.M.; Zhang, R.; Huang, M.; Hu, L. Investigation on shape deviation of horizontal interior circular channels fabricated by laser powder bed fusion. Addit. Manuf. 2020, 36, 101585. [Google Scholar] [CrossRef]
- Legesse, F.; Karunakaran, K.P. Additive manufacturing of tooling element with conformal cooling channel. J. Def. Technol. 2015, 10, 82–89. [Google Scholar]
- Karunakaran, K.; Kapil, S.; Vithasth, H.; Legesse, F. Additive manufacturing of H13 tooling element with conformal cooling channel using MIG cladding. Int. J. Rapid Manuf. 2018, 7, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Soshi, M.; Ring, J.; Young, C.; Oda, Y.; Mori, M. Innovative grid molding and cooling using an additive and subtractive hybrid CNC machine tool. CIRP Ann. 2017, 66, 401–404. [Google Scholar] [CrossRef]
- Eiamsa-Ard, K.; Wannissorn, K. Conformal bubbler cooling for molds by metal deposition process. Comput. Des. 2015, 69, 126–133. [Google Scholar] [CrossRef]
- Park, H.-S.; Dang, X.-P. Development of a Smart Plastic Injection Mold with Conformal Cooling Channels. Procedia Manuf. 2017, 10, 48–59. [Google Scholar] [CrossRef]
- Jahan, S.A.; Wu, T.; Zhang, Y.; Zhang, J.; Tovar, A.; Elmounayri, H. Thermo-mechanical Design Optimization of Conformal Cooling Channels using Design of Experiments Approach. Procedia Manuf. 2017, 10, 898–911. [Google Scholar] [CrossRef]
- Venkatesh, G.; Kumar, Y.R. Thermal Analysis for Conformal Cooling Channel. Mater. Today Proc. 2017, 4, 2592–2598. [Google Scholar] [CrossRef]
- Barbeiro, S.; Enguiça, R.; Lobo, D. Automatic Generation of Conformal Cooling Channels in Injection Moulding. Comput. Des. 2022, 150, 103312. [Google Scholar] [CrossRef]
- Minh, P.S.; Nguyen, V.-T.; Nguyen, V.T.; Uyen, T.M.T.; Do, T.T.; Nguyen, V.T.T. Study on the Fatigue Strength of Welding Line in Injection Molding Products under Different Tensile Conditions. Micromachines 2022, 13, 1890. [Google Scholar] [CrossRef]
- Shen, S.; Kanbur, B.B.; Zhou, Y.; Duan, F. Thermal and mechanical analysis for conformal cooling channel in plastic injection molding. Mater. Today Proc. 2020, 28, 396–401. [Google Scholar] [CrossRef]
- Jahan, S.A.; El-Mounayri, H. Optimal Conformal Cooling Channels in 3D Printed Dies for Plastic Injection Molding. Procedia Manuf. 2016, 5, 888–900. [Google Scholar] [CrossRef] [Green Version]
- Venkatesh, G.; Kumar, Y.R.; Raghavendra, G. Comparison of Straight Line to Conformal Cooling Channel in Injection Molding. Mater. Today Proc. 2017, 4, 1167–1173. [Google Scholar] [CrossRef]
- Kitayama, S.; Tamada, K.; Takano, M.; Aiba, S. Numerical optimization of process parameters in plastic injection molding for minimizing weldlines and clamping force using conformal cooling channel. J. Manuf. Process. 2018, 32, 782–790. [Google Scholar] [CrossRef]
- Khuri, I.A.; Cornell, A.J. Response Surfaces: Designs and Analyses, 2nd ed.; Marcel Dekker Inc.: New York, NY, USA, 1996. [Google Scholar]
- Şimşek, B.; Iç, Y.T.; Şimşek, E.H. A RSM-Based Multi-Response Optimization Application for Determining Optimal Mix Proportions of Standard Ready-Mixed Concrete. Arab. J. Sci. Eng. 2015, 41, 1435–1450. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Tran, V.T.; Pham, T.H.N.; Nguyen, V.-T.; Thanh, N.C.; Thi, H.M.N.; Duy, N.V.A.; Thanh, D.N.; Nguyen, V.T.T. Influences of Material Selection, Infill Ratio, and Layer Height in the 3D Printing Cavity Process on the Surface Roughness of Printed Patterns and Casted Products in Investment Casting. Micromachines 2023, 14, 395. [Google Scholar] [CrossRef]
- The Mould Design Guide; Smithers Rapra Technology: Shawbury, UK, 2008.
- Harrington, E.C., Jr. The desirability function industrial. Qual. Control 1965, 21, 494–498. [Google Scholar]
- Derringer, G.; Suich, R. Simultaneous Optimization of Several Response Variables. J. Qual. Technol. 1980, 12, 214–219. [Google Scholar] [CrossRef]
- Cheng, C.-D.; Liao, Y.-L.; Tsai, H.-H. Investigation of the Warpage of a High-Density Polyethylene Pallet by Plastic Injection Compression Molding: Part I—Numerical Approach. Polymers 2022, 14, 1437. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Lin, L.; Jiang, J.; Li, Q.; Hwang, S.-S. Effect of Gas Counter Pressure on the Surface Roughness, Morphology, and Tensile Strength between Microcellular and Conventional Injection-Molded PP Parts. Polymers 2022, 14, 1078. [Google Scholar] [CrossRef]
- Turek, P.; Budzik, G.; Sęp, J.; Oleksy, M.; Józwik, J.; Przeszłowski, Ł.; Paszkiewicz, A.; Kochmański, Ł.; Żelechowski, D. An Analysis of the Casting Polymer Mold Wear Manufactured Using PolyJet Method Based on the Measurement of the Surface Topography. Polymers 2020, 12, 3029. [Google Scholar] [CrossRef] [PubMed]





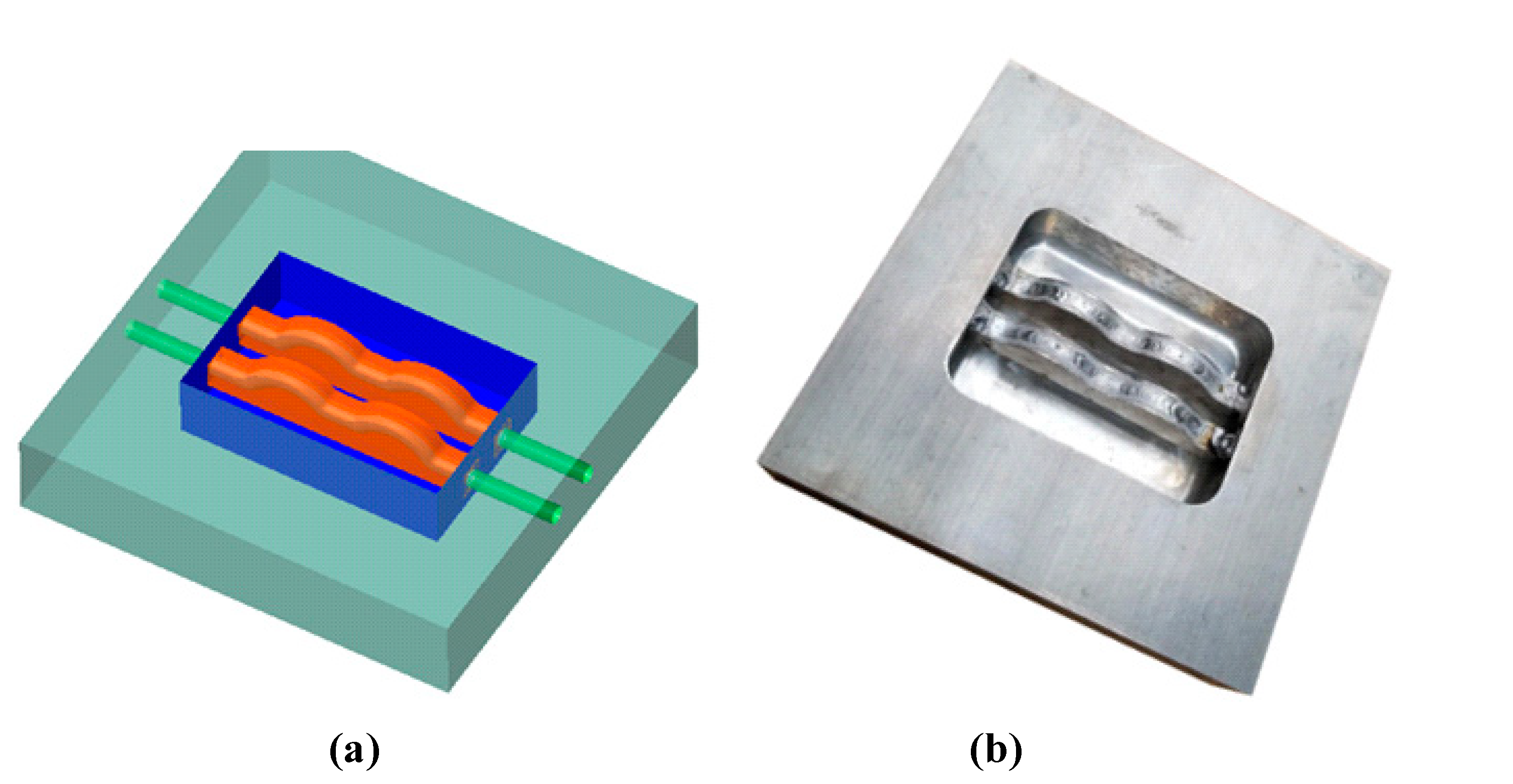







| Product Thickness | Channel Diameter | Distance between Two Channels | Distance from the Channel Centerline to the Mold Surface |
|---|---|---|---|
| 2 mm | 8–10 mm | 24~40 mm | 16~30 mm |
| 4 mm | 10–12 mm | 30~48 mm | 20~36 mm |
| 6 mm | 12–15 mm | 36~60 mm | 24~45 mm |
| Lower Bound (mm) | Upper Bound (mm) | |
|---|---|---|
| H3 (x1) | 35 | 40 |
| H4 (x2) | 50 | 55 |
| V5 (x3) | 5 | 15 |
| V6 (x4) | 15 | 23 |
| V7 (x5) | 16 | 24 |
| D1 (x6) | 8 | 10 |
| FD1 (x7) | 24 | 40 |
| Density (kg·m−3) | Specific Heat (J·kg−1·K−1) | Thermal Conductivity (W·m−1·K) | Heat Transfer Coefficients (W·m−2·K) | |
|---|---|---|---|---|
| Water | 997.0 | 4181.7 | 0.6 | 5200 |
| Aluminum | 2720 | 903 | 205.00 | 13 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 17 | 3941.18 | 231.83 | 617.16 | 0.000 |
| Linear | 7 | 3802 | 543.14 | 1445.89 | 0.000 |
| H3 | 1 | 13.84 | 13.84 | 36.84 | 0.000 |
| H4 | 1 | 2.12 | 2.12 | 5.64 | 0.019 |
| V5 | 1 | 1018.71 | 1018.71 | 2711.9 | 0.000 |
| V6 | 1 | 2.08 | 2.08 | 5.55 | 0.020 |
| V7 | 1 | 32.54 | 32.54 | 86.62 | 0.000 |
| D1 | 1 | 77.98 | 77.98 | 207.59 | 0.000 |
| FD1 | 1 | 2654.73 | 2654.73 | 7067.12 | 0.000 |
| Square | 1 | 42.39 | 42.39 | 112.84 | 0.000 |
| V5*V5 | 1 | 42.39 | 42.39 | 112.84 | 0.000 |
| Two-Way Interaction | 9 | 96.79 | 10.75 | 28.63 | 0.000 |
| H3*H4 | 1 | 1.82 | 1.82 | 4.85 | 0.030 |
| H3*V5 | 1 | 8.08 | 8.08 | 21.51 | 0.000 |
| H3*V6 | 1 | 1.62 | 1.62 | 4.3 | 0.040 |
| H3*V7 | 1 | 6.18 | 6.18 | 16.44 | 0.000 |
| V5*V6 | 1 | 28.2 | 28.2 | 75.07 | 0.000 |
| V5*V7 | 1 | 3.51 | 3.51 | 9.35 | 0.003 |
| V5*FD1 | 1 | 3.86 | 3.86 | 10.29 | 0.002 |
| V6*V7 | 1 | 40.57 | 40.57 | 108 | 0.000 |
| V6*FD1 | 1 | 2.96 | 2.96 | 7.88 | 0.006 |
| Error | 125 | 46.96 | 0.38 | ||
| Total | 142 | 3988.14 | |||
| S | R-sq | R-sq (adj) | |||
| 0.612889 | 98.82% | 98.66% | |||
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 21 | 1889.03 | 89.95 | 2861.98 | 0.000 |
| Linear | 7 | 1824.79 | 260.68 | 8293.95 | 0.000 |
| H3 | 1 | 0.43 | 0.43 | 13.64 | 0.000 |
| H4 | 1 | 0.15 | 0.15 | 4.67 | 0.033 |
| V5 | 1 | 1151.52 | 1151.52 | 36,636.8 | 0.000 |
| V6 | 1 | 1.32 | 1.32 | 42.13 | 0.000 |
| V7 | 1 | 16.31 | 16.31 | 519.04 | 0.000 |
| D1 | 1 | 313.69 | 313.69 | 9980.47 | 0.000 |
| FD1 | 1 | 341.37 | 341.37 | 10,860.9 | 0.000 |
| Square | 1 | 0.57 | 0.57 | 18.04 | 0.000 |
| FD1*FD1 | 1 | 0.57 | 0.57 | 18.04 | 0.000 |
| Two-Way Interaction | 13 | 63.67 | 4.9 | 155.83 | 0.000 |
| H3*V5 | 1 | 0.18 | 0.18 | 5.74 | 0.018 |
| H3*V6 | 1 | 0.57 | 0.57 | 18 | 0.000 |
| H3*V7 | 1 | 0.71 | 0.71 | 22.45 | 0.000 |
| H4*V5 | 1 | 0.24 | 0.24 | 7.53 | 0.007 |
| H4*V6 | 1 | 0.13 | 0.13 | 4.02 | 0.047 |
| H4*V7 | 1 | 0.23 | 0.23 | 7.21 | 0.008 |
| V5*V6 | 1 | 7.25 | 7.25 | 230.55 | 0.000 |
| V5*V7 | 1 | 20.88 | 20.88 | 664.29 | 0.000 |
| V5*FD1 | 1 | 25.12 | 25.12 | 799.21 | 0.000 |
| V6*V7 | 1 | 5.31 | 5.31 | 168.9 | 0.000 |
| V6*FD1 | 1 | 0.14 | 0.14 | 4.47 | 0.036 |
| V7*FD1 | 1 | 0.12 | 0.12 | 3.73 | 0.056 |
| D1*FD1 | 1 | 2.82 | 2.82 | 89.74 | 0.000 |
| Error | 121 | 3.8 | 0.03 | ||
| Total | 142 | 1892.83 | |||
| S | R-sq | R-sq (adj) | |||
| 0.177287 | 99.80% | 99.76% | |||
| H3 | H4 | V5 | V6 | V7 | D1 | FD1 | P8 | P9 |
|---|---|---|---|---|---|---|---|---|
| 35 | 50 | 5 | 23 | 24 | 8 | 24 | 13.08 | 62.94 |
| 35 | 50 | 5 | 23 | 16 | 8 | 40 | 10.03 | 62.64 |
| Solution | H3 | H4 | V5 | V6 | V7 | D1 | FD1 | P9 Fit | P8 Fit | Composite Desirability |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 40 | 50 | 7.53 | 15 | 16 | 10 | 40 | 67.2494 | 13.2292 | 0.802845 |
| H3 | H4 | V5 | V6 | V7 | D1 | FD1 | P9 | P8 | |
|---|---|---|---|---|---|---|---|---|---|
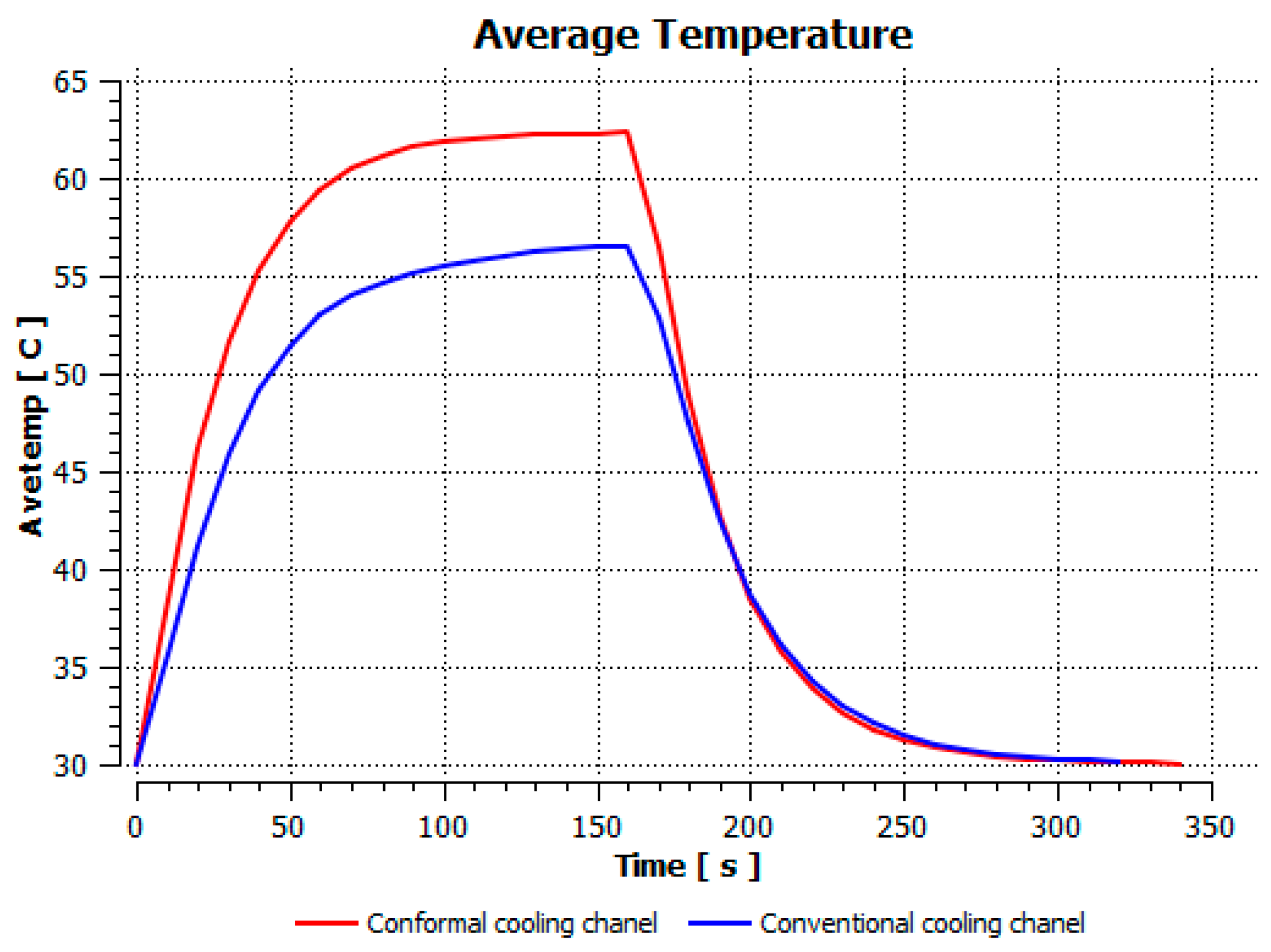
| Prediction | 40 | 50 | 7.5 | 15 | 16 | 10 | 40 | 67.25 °C | 13.23 °C |
| Simulation | 62.34 °C | 12.59 °C |
| Conformal Cooling Channel | Conventional Cooling Channel | |
|---|---|---|
| Heating process | 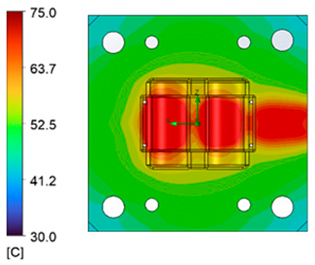 | 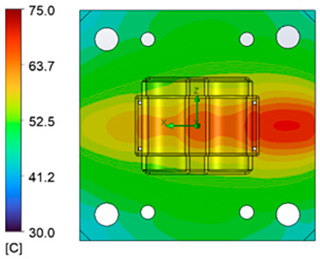 |
| Conformal Cooling Channel | Conventional Cooling Channel | |
|---|---|---|
| Cooling process |  | 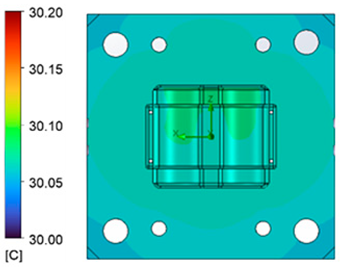 |
| Conformal Cooling Channel | Conventional Cooling Channel | |
|---|---|---|
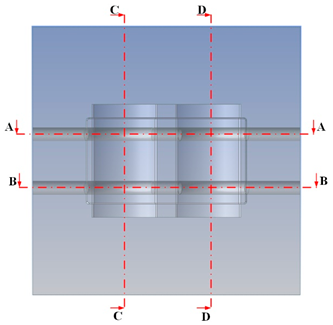 |  | |
| A-A | 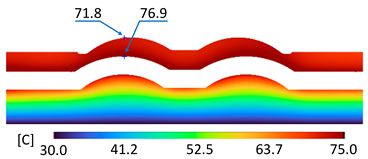 |  |
| B-B |  | 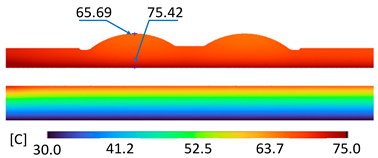 |
| C-C |  | 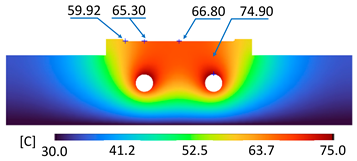 |
| D-D | 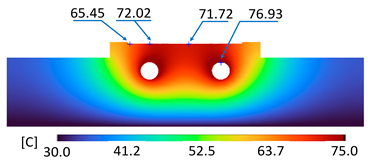 | 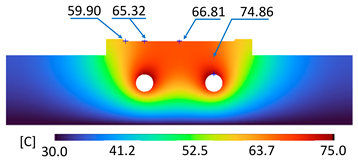 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, V.-T.; Minh, P.S.; Uyen, T.M.T.; Do, T.T.; Ha, N.C.; Nguyen, V.T.T. Conformal Cooling Channel Design for Improving Temperature Distribution on the Cavity Surface in the Injection Molding Process. Polymers 2023, 15, 2793. https://doi.org/10.3390/polym15132793
Nguyen V-T, Minh PS, Uyen TMT, Do TT, Ha NC, Nguyen VTT. Conformal Cooling Channel Design for Improving Temperature Distribution on the Cavity Surface in the Injection Molding Process. Polymers. 2023; 15(13):2793. https://doi.org/10.3390/polym15132793
Chicago/Turabian StyleNguyen, Van-Thuc, Pham Son Minh, Tran Minh The Uyen, Thanh Trung Do, Nguyen Canh Ha, and Van Thanh Tien Nguyen. 2023. "Conformal Cooling Channel Design for Improving Temperature Distribution on the Cavity Surface in the Injection Molding Process" Polymers 15, no. 13: 2793. https://doi.org/10.3390/polym15132793
APA StyleNguyen, V.-T., Minh, P. S., Uyen, T. M. T., Do, T. T., Ha, N. C., & Nguyen, V. T. T. (2023). Conformal Cooling Channel Design for Improving Temperature Distribution on the Cavity Surface in the Injection Molding Process. Polymers, 15(13), 2793. https://doi.org/10.3390/polym15132793






