Textured Polyester Fiber in Three-Dimensional (3D) Carpet Structure Application: Experimental Characterizations under Compression–Bending–Abrasion–Rubbing Loading
Abstract
1. Introduction
2. Materials and Methods
2.1. Carpet Structure
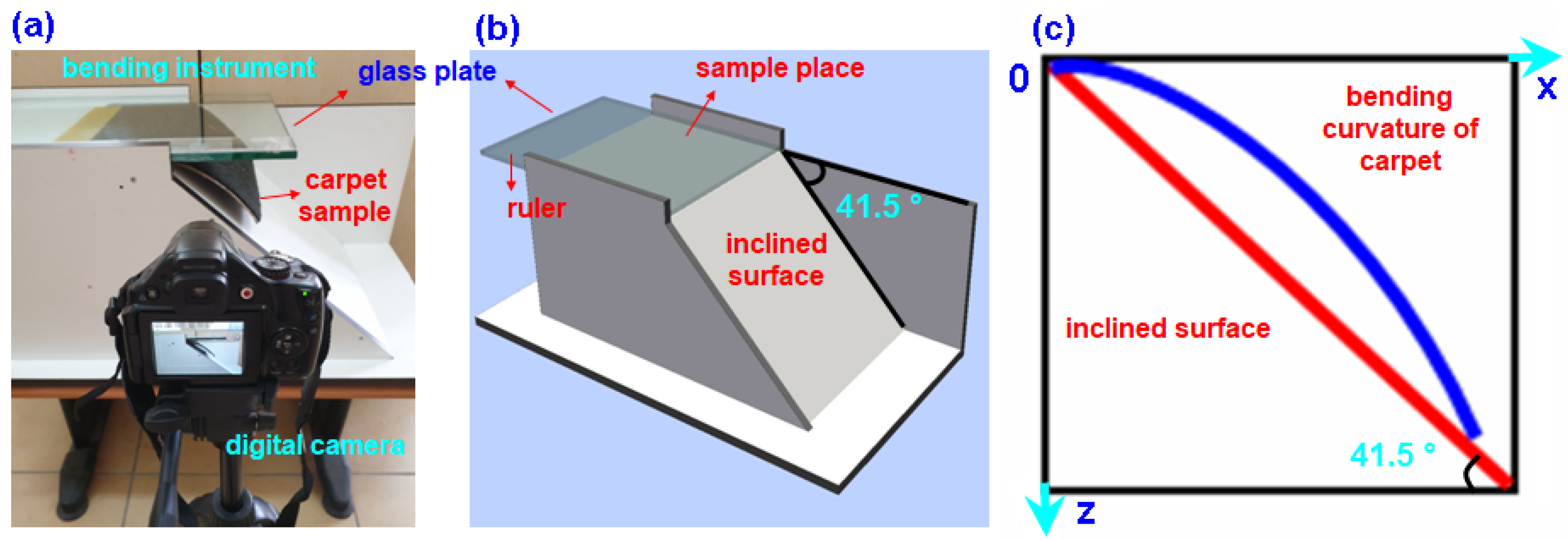
2.1.1. Bending (Flexure) Test
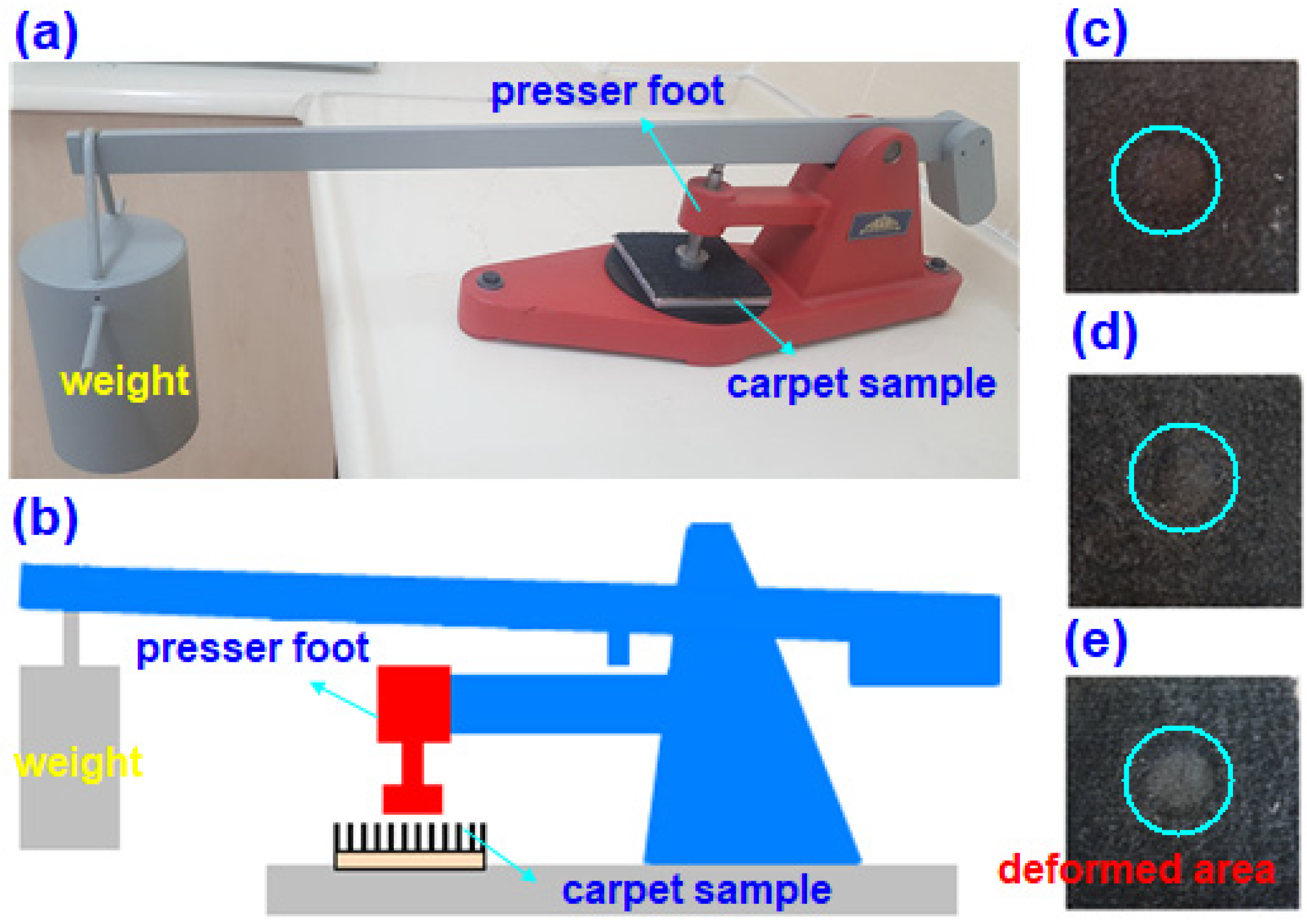
2.1.2. Static Loading Test
2.1.3. Abrasion (Martindale) Test
2.1.4. Rubbing (Token) Test
2.2. Statistical Model
3. Results and Discussion
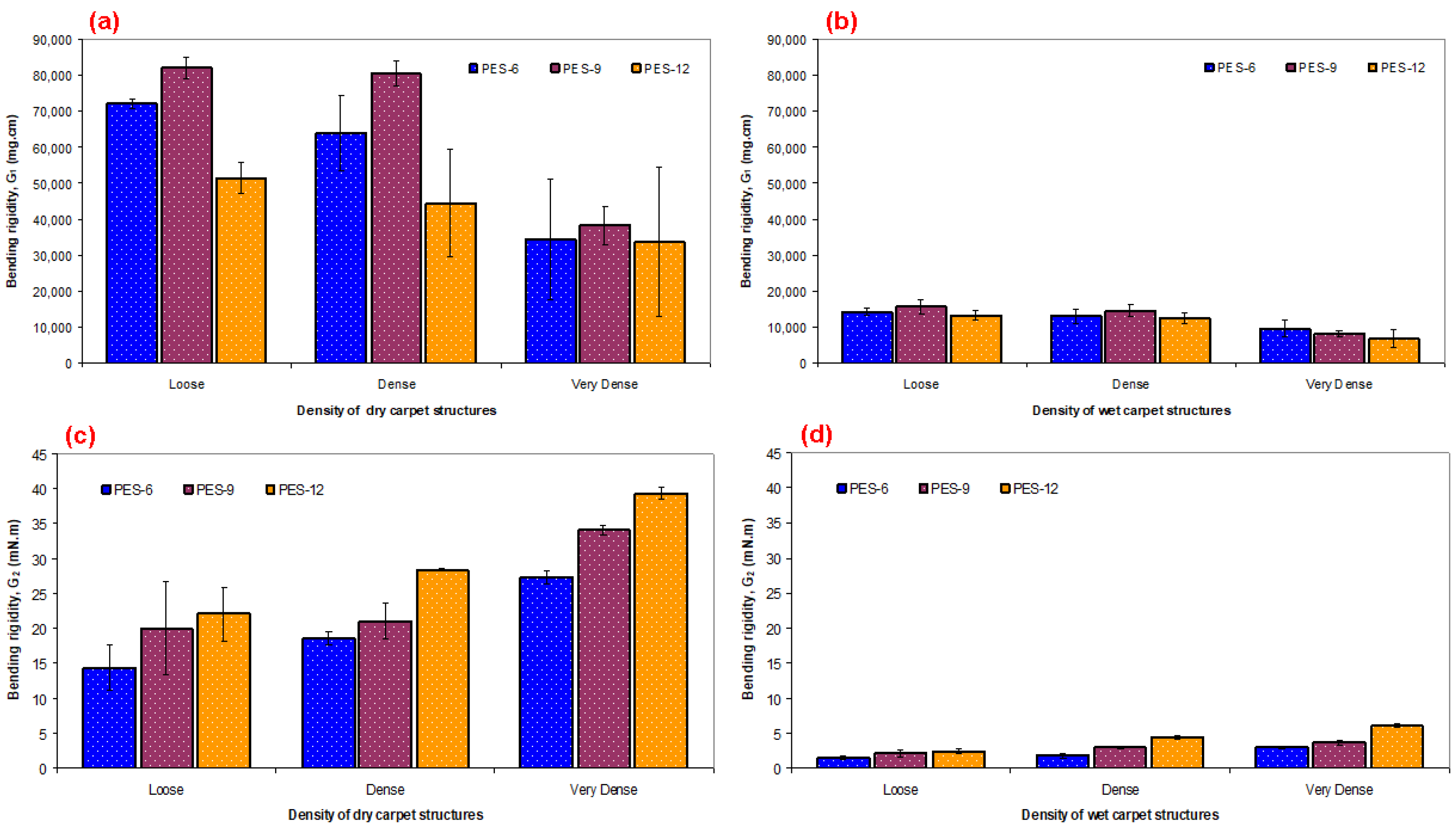
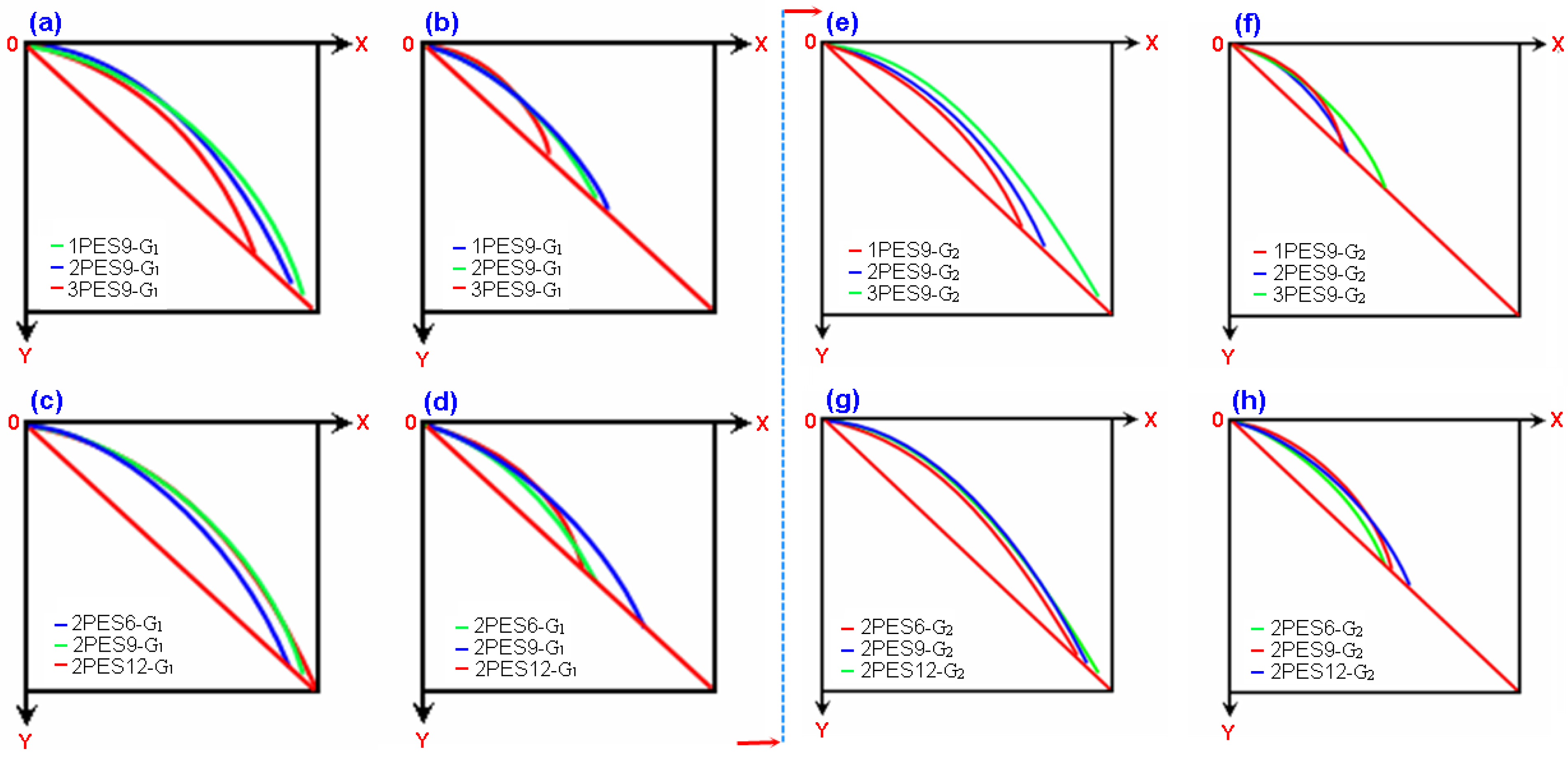
3.1. Carpet Structure Bending Results
Carpet Structure Curvature Results
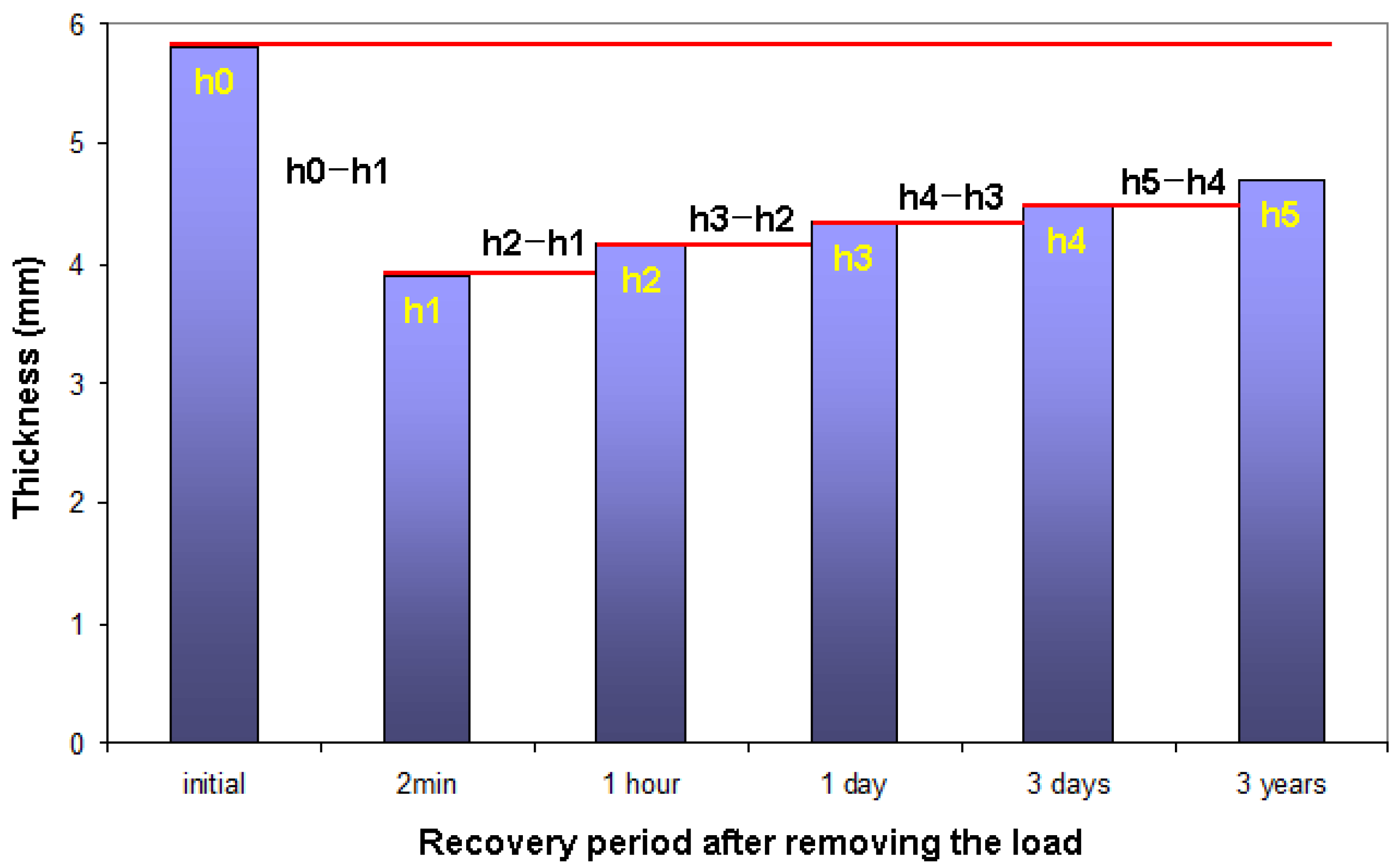
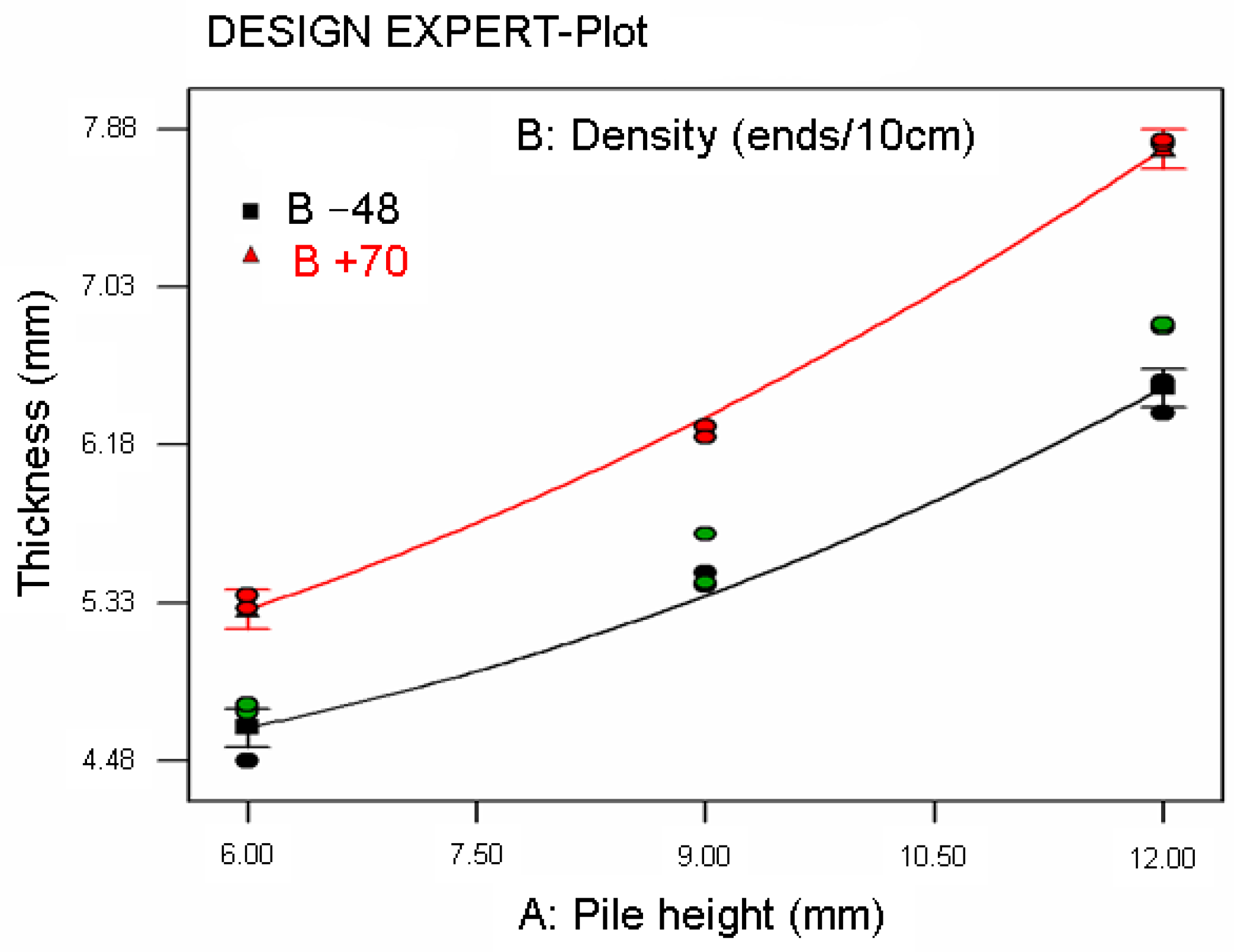
3.2. Carpet Structure Static Loading Results
3.3. Martindale Abrasion Results
3.4. Token Rubbing Results
3.5. Statistical Modelling Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chaudhuri, S.K.; Bandyopadyay, S. Structure and properties of carpet fibres and yarns. In Advances in Carpet Manufacture; Woodhead Publishing: Sawston, UK, 2017; pp. 19–43. [Google Scholar] [CrossRef]
- Gupta, S.K.; Goswami, K.K.; Majumdar, A. Durability of handmade wool carpets: A review. J. Nat. Fibers 2015, 12, 399–418. [Google Scholar] [CrossRef]
- Militki, J. Tensile failure of polyester fibers. In Handbook of Properties of Textile and Technical Fibres, 2nd ed.; The Textile Institute Book Series; Bunsell, A.R., Ed.; Woodhead Publishing: Sawston, UK, 2018; pp. 421–514. [Google Scholar] [CrossRef]
- Jaffe, M.; Easts, A.J.; Feng, X. Polyester fibers. In Thermal Analysis of Textiles and Fibers; Jaffe, M., Menczel, J.D., Eds.; Woodhead Publishing: Sawston, UK, 2020; pp. 133–149. [Google Scholar] [CrossRef]
- Rwei, S.P.; Lin, Y.T.; Su, Y.Y. Study of self-crimp polyester fibers. Polym. Eng. Sci. 2005, 45, 838–845. [Google Scholar] [CrossRef]
- Hsieh, Y.-L. Surface Characteristics of Fibers and Textiles; Pastore, C.M., Kiekens, P., Eds.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Abingdon, UK, 2018; pp. 34–55. [Google Scholar] [CrossRef]
- Tufail, M.R.; Jamshaid, H.; Mishra, R.; Hussain, U.; Tichy, M.; Muller, M. Characterization of hybrid composites with polyester waste fibers, olive root fibers and coir pith micro-particles using mixture design analysis for structural applications. Polymers 2021, 13, 2291. [Google Scholar] [CrossRef] [PubMed]
- East, A.J. The structure of polyester fibers. In Handbook of Textile Fiber Structure; Fundamentals and Manufactured Polymer Fibers; Eichhorn, S.J., Hearle, J.W.S., Jaffe, M., Kikutani, T., Eds.; Woodhead Publishing: Sawston, UK; CRC Press LLC: Cambridge, UK, 2009; Volume 1, pp. 81–225. [Google Scholar]
- Mandell, J.F.; Steckel, M.G.; Chung, S.S.; Kenney, M.C. Fatigue and environmental resistance of polyester and nylon fibers. Polym. Eng. Sci. 1987, 27, 1121–1127. [Google Scholar] [CrossRef]
- Karaca, E.; Ozcelik, F. Influence of the cross-sectional shape on the structure and properties of polyester fibers. J. Appl. Polym. Sci. 2007, 103, 2615–2621. [Google Scholar] [CrossRef]
- Mendelson, C. Home Comforts: The Art and Science of Keeping House; Simon and Schuster: New York, NY, USA, 2005; p. 896. [Google Scholar]
- Kale, P.D.; Lokhande, H.T. Grafting on polyester fibers. J. Appl. Polym. Sci. 1975, 19, 461–480. [Google Scholar] [CrossRef]
- Presley, A.B. Evaluation of carpet appearance loss: Structural factors. Text. Res. J. 1997, 67, 174–180. [Google Scholar] [CrossRef]
- Wang, J.; Wood, E.J. A new method for measuring carpet texture change. Text. Res. J. 1994, 64, 215–224. [Google Scholar] [CrossRef]
- Wilding, M.A.; Lomas, B.; Woodhouse, A.K. Changes due to wear in tufted pile carpets. Text. Res. J. 1990, 60, 627–640. [Google Scholar] [CrossRef]
- Xu, B. Quantifying surface roughness of carpets by fractal dimension. Cloth. Text. Res. J. 1997, 15, 155–161. [Google Scholar] [CrossRef]
- Postle, R.; Carnaby, G.A.; de-Jong, S. The Mechanics of Wool Structures; John Wiley: New York, NY, USA, 1988. [Google Scholar]
- Beil, N.B.; Roberts, W.W. Modeling and computer simulation of the compressional behavior of fiber assemblies: Part 1: Comparison to van wyk’s theory. Text. Res. J. 2002, 72, 341–351. [Google Scholar] [CrossRef]
- Vangheluwe, L.; Kiekens, P. Resilience properties of polypropylene carpets. Text. Res. J. 1997, 67, 671–676. [Google Scholar] [CrossRef]
- Laughlin, K.C.; Cusick, G.E. Carpet performance evaluation, Part II: Stress-strain behavior. Text. Res. J. 1968, 38, 72–80. [Google Scholar] [CrossRef]
- Wood, E.J. Description and measurement of carpet appearance. Text. Res. J. 1993, 63, 580–594. [Google Scholar] [CrossRef]
- Savilla, B.P. Physical Testing of Textiles; The Textile Institute: Manchester, UK; Woodhead Publishing: Sawston, UK, 1999. [Google Scholar]
- Goswami, K.K. Advances in Carpet Manufacture; Elseviere Ltd.: Cambridge, MA, USA, 2018; p. 323. [Google Scholar]
- Wu, J.; Pan, N.; Williams, K.R. Mechanical, biomechanical and psychophysical study of carpet performance. Text. Res. J. 2007, 77, 172–178. [Google Scholar] [CrossRef]
- McNeil, S.J.; Tapp, L.S. The design and initial evaluation of visual cues in carpets to assist walking. J. Text. Inst. 2016, 107, 376–385. [Google Scholar] [CrossRef]
- Kucuk, M.; Korkmaz, Y. Sound absorption properties of acrylic carpets. J. Text. Inst. 2017, 108, 1398–1405. [Google Scholar] [CrossRef]
- Kucuk, M.; Korkmaz, Y. Acoustic and thermal properties of polypropylene carpets: Effect of pile length and loop density. Fibers Polym. 2019, 20, 1519–1525. [Google Scholar] [CrossRef]
- Grosberg, P. The mechanical properties of woven fabrics part II: The bending of woven fabrics. Text. Res. J. 1966, 36, 205–214. [Google Scholar] [CrossRef]
- Abbott, N.J. Part II: A study of the peirce cantilever test for stiffness of textile fabrics. Text. Res. J. 1951, 21, 441–444. [Google Scholar] [CrossRef]
- Skelton, J. The bending behavior of fabrics at high curvatures. Text. Res. J. 1971, 41, 174–181. [Google Scholar] [CrossRef]
- Gibson, V.L.; Postle, R. An analysis of the bending and shear properties of woven, double-knitted and warp-knitted outerwear fabrics. Text. Res. J. 1978, 48, 14–27. [Google Scholar] [CrossRef]
- Matsuo, T. Bending of woven fabrics. J. Text. Mach. Soc. Jpn. 1969, 15, 19–33. [Google Scholar] [CrossRef]
- Cooper, D.N.E. The stiffness of woven textiles. J. Text. Inst. 1960, 51, P547. [Google Scholar] [CrossRef]
- Ghosh, T.K.; Batra, S.K.; Barker, R.L. The bending behaviour of plain-woven fabrics part I: A critical review. J. Text. Inst. 1990, 81, 245–254. [Google Scholar] [CrossRef]
- Hu, J. Structure and Mechanics of Woven Fabrics; Woodhead Publishing Ltd.: Cambridge, UK, 2004. [Google Scholar]
- Park, J.-W.; Oh, A.-G. Bending rigidity of yarns. Text. Res. J. 2006, 76, 478–485. [Google Scholar] [CrossRef]
- Bilisik, K. Bending behavior of multilayered and multidirectional stitched aramid woven fabric structures. Text. Res. J. 2011, 81, 1748–1761. [Google Scholar] [CrossRef]
- Dolatabadi, M.K.; Montazer, M.; Latifi, M. The effect of polyester fibres on quality of hand-knotted carpets. J. Text. Inst. 2005, 96, 1–9. [Google Scholar] [CrossRef]
- Yu, W.; Du, Z. Determination of the bending characteristic parameters of the bending evaluation system of fabric and yarn. Text. Res. J. 2006, 76, 702–711. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Plaut, R.H. Formulas to determine fabric bending rigidity from simple tests. Text. Res. J. 2015, 85, 884–894. [Google Scholar] [CrossRef]
- Kimura, K.; Kawabata, S.; Kawai, H. Compressive deformation theory of carpets. J. Text. Mach. Soc. Jpn. 1970, 23, T67–T76. [Google Scholar] [CrossRef]
- Kimura, K.; Kawabata, S. Improvement of the compressive deformation theory of carpets and its application to the carpet woven from compressible yarn. J. Text. Mach. Soc. Jpn. 1971, 24, T207–T214. [Google Scholar]
- Celik, N.; Koc, E. An experimental study on thickness loss of wilton type carpets produced with different pile materials after prolonged heavy static loading. part 2: Energy absorption and hysteresis effect. Fibres Text. East. Eur. 2007, 15, 87–92. [Google Scholar]
- Celik, N.; Koc, E. Study on the thickness loss of wilton-type carpets under dynamic loading. Fibres Text. East. Eur. 2010, 18, 54–59. [Google Scholar]
- Koc, E.; Celik, N.; Tekin, M. An experimental study on thickness loss of wilton-type carpets produced with different pile materials after prolonged heavy static loading. part-I: Characteristic parameters and carpet behaviour. Fibres Text. East. Eur. 2005, 13, 56–62. [Google Scholar]
- Dubinskaite, K.; Langenhove, L.V.; Milasius, R. Influence of pile height and density on the end-use properties of carpets. Fibres Text. East. Eur. 2008, 16, 68. [Google Scholar]
- Javidpanah, M.; Najar, S.S.; Dayiary, M. Study on thickness loss of cut-pile carpet produced with heat process-modified polyester pile yarn. Part I: Static loading. J. Text. Inst. 2014, 105, 1265–1271. [Google Scholar] [CrossRef]
- Javidpanah, M.; Najar, S.S.; Dayiary, M. Study on thickness loss of cut-pile carpet produced with heat process modified polyester pile yarn. Part II: Dynamic loading. J. Text. Inst. 2015, 106, 236–241. [Google Scholar] [CrossRef]
- Sarıoğlu, E.; Kaynak, H.K.; Çelik, H.İ.; Vuruşkan, D. Effects of structural parameters on compressibility and soiling properties of machine woven carpets. J. Text. Inst. 2019, 110, 1263–1270. [Google Scholar] [CrossRef]
- Tabatabaei, S.M.; Ghane, M. Effect of traffic exposure on toughness characteristics of hand-knotted carpets. Fibres Text. East. Eur. 2015, 23, 64–68. [Google Scholar] [CrossRef]
- Jafari, S.; Ghane, M.; Moezzi, M. The effect of UV degradation on the recovery behavior of cut-pile carpets after static loading. J. Text. Inst. 2017, 108, 256–259. [Google Scholar] [CrossRef]
- Liu, H.; Tandon, S.K.; Wood, E.J. Probability fracture mechanics of wear in wool carpet, Part I: Wear model of cut pile carpet. Text. Res. J. 2002, 72, 954–958. [Google Scholar] [CrossRef]
- Liu, H.; Tandon, S.K.; Wood, E.J. Part II: Wear model of loop pile carpet. Text. Res. J. 2002, 72, 958–962. [Google Scholar] [CrossRef]
- Hearle, J.W.S.; Liu, H.; Tandon, S.K.; Wood, E.J. Computational model of wool carpet wear. J. Text. Inst. 2005, 96, 137–142. [Google Scholar] [CrossRef]
- Carnaby, G.A. The mechanics of carpet wear. Text. Res. J. 1981, 51, 514–519. [Google Scholar] [CrossRef]
- Carnaby, G.A.; Wood, E.J. The physics of carpets. J. Text. Inst. 1989, 80, 71–90. [Google Scholar] [CrossRef]
- Hearle, J.W.S.; Lomas, B.; Goodman, P.J.; Camaby, G.A. Microscopic Examination of Worn Carpets, Part I: Comparison of the Modes of Fibre Failure in Floor Trials; WRONZ Communication C79; Wool Research Organisation of New Zealand: Christchurch, New Zealand, 1983. [Google Scholar]
- Hearle, J.W.S.; Mukhopadyay, S.K.; Sengonul, A. A Study of Fatigue Types and Distribution in a Controlled Damaged Wool Carpet, Part I: Straight-Walk Worn Carpet; WRONZ Report R212; Wool Research Organisation of New Zealand: Christchurch, New Zealand, 1997. [Google Scholar]
- Dayiary, M. Study on compressional energy contribution into total energy of pile deformation in cut-pile carpet. J. Text. Inst. 2015, 106, 1315–1321. [Google Scholar] [CrossRef]
- Dayiary, M.; Najar, S.S.; Shamsi, M. An experimental verification of cut-pile carpet compression behaviour. J. Text. Inst. 2010, 101, 488–494. [Google Scholar] [CrossRef]
- Hersh, S.P.; El-Shiekh, A. Energy consideration in the recovery of carpets. J. Text. Inst. 1972, 63, 660–663. [Google Scholar]
- Dayiary, M.; Najar, S.S.; Shamsi, M. A new theoretical approach to cut-pile carpet compression based on elastic-stored bending energy. J. Text. Inst. 2009, 100, 688–694. [Google Scholar] [CrossRef]
- Jafari, S.; Ghane, M. An analytical approach for the recovery behavior of cut pile carpet after static loading by mechanical models. Fibers Polym. 2016, 17, 651–655. [Google Scholar] [CrossRef]
- Khavari, S.; Ghane, M. An analytical approach for the compression and recovery behavior of cut pile carpets under constant rate of compression by mechanical models. Fibers Polym. 2017, 18, 190–195. [Google Scholar] [CrossRef]
- Mehta, P.V. An Introduction to Quality Control for the Apparel Industry; ASQC Quality Press: Milwaukee, WI, USA, 1992. [Google Scholar]
- Collier, B.J.; Epps, H.H. Textile Testing and Analysis; Prentice Hall Publishing: Englewood Cliffs, NJ, USA, 1999; Volume 7, p. 374. [Google Scholar]
- Manich, A.M.; Castellar, M.D.D.; Sauri, R.M.; Miguel, R.A.; Barella, A. Abrasion kinetics of wool and blended fabric. Text. Res. J. 2001, 71, 469–474. [Google Scholar] [CrossRef]
- Ozdil, N.; Kayseri, G.O.; Menguc, G.S. Analysis of abrasion characteristics in textiles. In Abrasion Resistance of Materials; Adamiak, M., Ed.; IntechOpen: London, UK, 2012; pp. 119–146. [Google Scholar] [CrossRef]
- Onder, E.; Berkalp, O.B. Effects of different structural parameters on carpet physical properties. Text. Res. J. 2001, 71, 549–555. [Google Scholar] [CrossRef]
- Bilisik, K.; Yolacan, G. Abrasion propertiesof upholstery flocked fabrics. Text. Res. J. 2009, 79, 1625–1632. [Google Scholar] [CrossRef]
- Gupta, N.P.; Shakyawar, D.B.; Sinha, R.D. Influence of fibre diameter and medullation on woollen spun yarns and their products. Indian J. Fibre Text. Res. 1998, 23, 32–37. [Google Scholar]
- Bilisik, K.; Turhan, Y.; Demiryurek, O. Tearing properties of upholstery flocked fabrics. Text. Res. J. 2011, 81, 290–300. [Google Scholar] [CrossRef]
- Bilisik, K.; Turhan, Y.; Demiryurek, O. Analysis and tensile characterization of flocked fabric after rubbing. J. Text. Inst. 2011, 102, 808–822. [Google Scholar] [CrossRef]
- Zhou, C.E.; Zhang, Q.; Kan, C.W. Some properties of a thickener for preparing inkjet printing ink for nylon carpet. Color. Technol. 2017, 133, 116–121. [Google Scholar] [CrossRef]
- Vandewiele, N.V. Carpet Weaving: Face-to-Face Carpet Weaving. Available online: http://www.vandewiele.be/carpetlooms.htm (accessed on 1 January 2022).
- ISO 4604; Textiles Glass–Woven Fabrics–Determination of Conventional Flexural Stiffness–Fixed Angle Flexometer Method. International Organization for Standardization: Geneva, Switzerland, 1978.
- Peirce, F.T. The handle of cloth as a measurable quantity. J. Text. Inst. 1937, 21, 377–416. [Google Scholar] [CrossRef]
- Peirce, F.T. The geometry of cloth structure. J. Text. Inst. 1937, 28, 45–96. [Google Scholar] [CrossRef]
- BS 3356; Method for Determination of Bending Length and Flexural Rigidity of Fabrics. British Standards Institution: London, UK, 1990.
- TS 1409; Method for Determination of Flexural Rigidity of Woven Fabrics. Turkish Standards Institution: Ankara, Turkey, 1974.
- Bilisik, K.; Yolacan, G. Experimental determination of bending behavior of multilayered and multidirectionally-stitched E-glass fabric structures for composites. Text. Res. J. 2012, 82, 1038–1049. [Google Scholar] [CrossRef]
- Matlab, R. MATLAB R2016a; The MathWorks Inc.: Natick, MA, USA, 2016. [Google Scholar]
- BS 4939; Method for Determination of Thickness Loss of Textile Floor Coverings after Prolonged Heavy Static Loading. British Standards Institution: London, UK, 2007.
- ISO 3416; Textile Floor Coverings; Determination of Thickness Loss after Prolonged Heavy Static Loading. International Organization for Standardization: Geneva, Switzerland, 1986.
- ISO 12947-3; Determination of the Abrasion Resistance of Fabrics by the Martindale Method Part 3: Determination of Mass Loss. International Organization for Standardization: Geneva, Switzerland, 1998.
- BS 2543; Upholstery Fabrics for End Use Applications. British Standards Institution: London, UK, 2004.
- TS 251 (ISO 3801:1977); Determination of Mass per Unit Length and Mass per Unit Area of Woven Fabrics. International Organization for Standardization: Geneva, Switzerland, 1991.
- TS 7125 (ISO 1766); Textile Floor Coverings-Determination of Thickness of Pile above the Substrate. International Organization for Standardization: Geneva, Switzerland, 2003.
- TS 3374 (ISO 1765); Machine Made Textile Floor Coverings-Determination of Thickness. International Organization for Standardization: Geneva, Switzerland, 1991.
- ISO 139; Textiles-Standard Atmospheres for Conditioning and Testing. International Organization for Standardization: Geneva, Switzerland, 2005.
- Hearle, J.W.S.; Grosberg, P.; Backer, S. Structural Mechanics of Fibres, Yarn and Fabrics; Wiley Interscience, Inc.: New York, NY, USA, 1969. [Google Scholar]
- State-Ease, Inc. Design Expert 6.0.1; State-Ease, Inc.: Minneapolis, MN, USA, 1985. [Google Scholar]










| Sample | Sample Codes | Yarn Linear Density (Tex) | Yarn Composition (%) | Density (Ends/10 cm) | Substrate Weight (Warp + Weft) (g/m2) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Warp | Weft | Warp | Weft | Warp | Weft | |||||
| Stuffer | Chain | Stuffer | Chain | |||||||
 | 1PES6 1PES9 1PES12 | 211 | 118 | 556 | 80% Pes/20% Co | 80% Pes/20% Co | Jute | 48 | 48 | 843 |
 | 2PES6 2PES9 2PES12 | 211 | 118 | 556 | 80% Pes/20% Co | 80% Pes/20% Co | Jute | 48 | 55 | 925 |
 | 3PES6 3PES9 3PES12 | 211 | 118 | 556 | 80% Pes/20% Co | 80% Pes/20% Co | Jute | 48 | 70 | 896 |
| Sample Codes | Pile | Carpet | ||||||
|---|---|---|---|---|---|---|---|---|
| Fiber Type | Yarn Linear Density (Tex) | Substrate Thickness (mm) | Pile Height (mm) | Pile Density (Knots/m2) | Pile Weight (g/m2) | Carpet Thickness (mm) | Carpet Weight (g/m2) | |
| 1PES6 | Polyester | 165 | 2.57 | 6 (3.34) | 230,400 | 954 | 5.91 | 1797 (1890) |
| 1PES9 | Polyester | 165 | 2.62 | 9 (4.21) | 230,400 | 1223 | 6.82 | 2066 (2142) |
| 1PES12 | Polyester | 165 | 2.59 | 12 (5.88) | 230,400 | 1453 | 8.47 | 2297 (2219) |
| 2PES6 | Polyester | 165 | 2.63 | 6 (3.36) | 264,000 | 1049 | 5.99 | 1974 (2098) |
| 2PES9 | Polyester | 165 | 2.59 | 9 (4.83) | 264,000 | 1357 | 7.42 | 2282 (2121) |
| 2PES12 | Polyester | 165 | 2.65 | 12 (5.88) | 264,000 | 1621 | 8.53 | 2546 (2650) |
| 3PES6 | Polyester | 165 | 3.05 | 6 (3.54) | 336,000 | 1253 | 6.58 | 2149 (2343) |
| 3PES9 | Polyester | 165 | 3.16 | 9 (4.46) | 336,000 | 1645 | 7.61 | 2541 (2477) |
| 3PES12 | Polyester | 165 | 3.19 | 12 (6.46) | 336,000 | 1981 | 9.65 | 2877 (2875) |
| Bending for Apparel Fabric | ||||
| Sample | Dry | Wet | ||
| Length of Overhang l (cm) | Bending Rigidity G1 (mg.cm) | Length of Overhang l (cm) | Bending Rigidity G1 (mg.cm) | |
| 1PES6-G1 | 14.50 ± 0.08 | 72,028.90 ± 1216.73 | 8.48 ± 0.19 | 14,397.10 ± 946.09 |
| 1PES9-G1 | 14.53 ± 0.17 | 82,075.36 ± 2881.66 | 8.38 ± 0.34 | 15,786.35 ± 1873.15 |
| 1PES12-G1 | 12.28 ± 0.36 | 51,400.23 ± 4449.87 | 7.83 ± 0.25 | 13,320.29 ± 1263.42 |
| 2PES6-G1 | 13.43 ± 0.78 | 63,929.32 ± 10,601.42 | 7.93 ± 0.38 | 13,119.76 ± 1869.14 |
| 2PES9-G1 | 14.48 ± 0.21 | 80,446.04 ± 3440.73 | 8.20 ± 0.34 | 14,672.87 ± 1732.53 |
| 2PES12-G1 | 10.90 ± 1.42 | 44,462.45 ± 14,881.99 | 7.23 ± 0.31 | 12,544.26 ± 1568.66 |
| 3PES6-G1 | 10.33 ± 1.85 | 34,524.16 ± 16,745.18 | 6.90 ± 0.50 | 9735.21 ± 2186.97 |
| 3PES9-G1 | 10.73 ± 0.51 | 38,387.64 ± 5379.77 | 6.45 ± 0.19 | 8324.76 ± 730.94 |
| 3PES12-G1 | 9.38 ± 2.39 | 33,774.07 ± 20,862.79 | 5.68 ± 0.66 | 6767.60 ± 2376.14 |
| Bending for technical fabric | ||||
| Sample | Dry | Wet | ||
| Length of Overhang l (cm) | Bending Rigidity G2 (mN.m) | Length of Overhang l (cm) | Bending Rigidity G2 (mN.m) | |
| 1PES6-G2 | 18.40 ± 16.26 | 14.44 ± 3.25 | 8.60 ± 4.25 | 1.47 ± 0.22 |
| 1PES9-G2 | 19.70 ± 28.99 | 20.08 ± 6.67 | 9.30 ± 9.19 | 2.11 ± 0.49 |
| 1PES12-G2 | 20.10 ± 16.97 | 22.10 ± 3.78 | 9.60 ± 6.36 | 2.41 ± 0.22 |
| 2PES6-G2 | 19.30 ± 3.54 | 18.50 ± 0.92 | 8.90 ± 2.83 | 1.81 ± 0.30 |
| 2PES9-G2 | 20.10 ± 9.90 | 21.12 ± 2.56 | 10.40 ± 3.54 | 2.93 ± 0.20 |
| 2PES12-G2 | 20.60 ± 0.71 | 28.41 ± 0.20 | 11.10 ± 2.83 | 4.44 ± 0.26 |
| 3PES6-G2 | 21.20 ± 4.95 | 27.38 ± 0.88 | 10.10 ± 4.24 | 2.96 ± 0.18 |
| 3PES9-G2 | 22.40 ± 4.24 | 34.14 ± 0.64 | 10.60 ± 4.95 | 3.62 ± 0.26 |
| 3PES12-G2 | 22.35 ± 4.95 | 39.36 ± 0.76 | 12.00 ± 6.36 | 6.09 ± 0.25 |
| Bending for Apparel Fabric | ||||
| Sample Codes | Dry | Wet | ||
| Equation of Regression Curve | Coefficient of Regression (R2) | Equation of Regression Curve | Coefficient of Regression (R2) | |
| 1PES6-G1 | y = 4.404x0.7361 − 1.238x + 0.04107 | R2 = 0.9995 | y = 4.553x0.8316 − 2.146x + 0.01205 | R2 = 0.9993 |
| 1PES9-G1 | y = 53.88x0.9864 − 51.03x − 0.1173 | R2 = 0.9993 | y = 36.58x0.9857 − 34.47x − 0.03946 | R2 = 0.9989 |
| 1PES12-G1 | y = 36.5x0.9799 − 33.72x − 0.08238 | R2 = 0.9992 | y = 15.87x0.9718 − 14.02x − 0.01899 | R2 = 0.9998 |
| 2PES6-G1 | y = − 21.89x1.029 + 24.56x + 0.2938 | R2 = 0.9980 | y = 45.24x0.9906 − 43.24x − 0.1656 | R2 = 0.9964 |
| 2PES9-G1 | y = 39.7x0.9813 − 36.83x − 0.3762 | R2 = 0.9954 | y = 23.71x0.9741 − 21.48x − 0.003374 | R2 = 0.9999 |
| 2PES12-G1 | y = −26.88x1.025 + 29.57x − 0.05452 | R2 = 0.9989 | y = 101.5x0.9941 − 99.26x − 0.1659 | R2 = 0.9902 |
| 3PES6-G1 | y = 5.598x0.7809 − 2.351x − 0.03235 | R2 = 0.9985 | y = 5.323x0.8408 − 2.866x − 0.008245 | R2 = 0.9998 |
| 3PES9-G1 | y = 28.67x0.9749 − 26.02x − 0.000902 | R2 = 0.9995 | y = 17.04x0.9506 − 14.53x − 0.01272 | R2 = 0.9998 |
| 3PES12-G1 | y = −7.888x1.072 + 10.3x − 0.01667 | R2 = 0.9994 | y = −0.3296x1.763 + 2.383x − 0.008711 | R2 = 0.9998 |
| Bending for technical fabric | ||||
| Sample Codes | Dry | Wet | ||
| Equation of Regression Curve | Coefficient of Regression (R2) | Equation of Regression Curve | Coefficient of Regression (R2) | |
| 1PES6-G2 | y = 45.62x0.9883 − 43.11x − 0.2136 | R2 = 0.9988 | y = 39.03x0.9894 − 37.06x − 0.2257 | R2 = 0.9914 |
| 1PES9-G2 | y = 13.55x0.9445 − 10.68x − 0.02309 | R2 = 0.9997 | y = 41.66x0.9857 − 39.51x − 0.09046 | R2 = 0.9968 |
| 1PES12-G2 | y = 4.758x0.8202 − 1.804x − 0.03475 | R2 = 0.9996 | y = 59.4x0.9919 − 57.18x − 0.2335 | R2 = 0.9947 |
| 2PES6-G2 | y = 39.37x0.987 − 37.02x − 0.1696 | R2 = 0.9979 | y = 58.79x0.9907 − 56.82x − 0.1212 | R2 = 0.9870 |
| 2PES9-G2 | y = 27.29x0.9814 − 25.01x − 0.1595 | R2 = 0.9970 | y = 35.46x0.9804 − 32.87x − 0.1126 | R2 = 0.9984 |
| 2PES12-G2 | y = 5.569x0.8483 − 2.619x − 0.0268 | R2 = 0.9997 | y = 76.96x0.9925 − 74.73x − 0.3564 | R2 = 0.9524 |
| 3PES6-G2 | y = 28.98x0.9798 − 26.31x − 0.2785 | R2 = 0.9978 | y = 25.58x0.9801 − 23.53x − 0.09408 | R2 = 0.9969 |
| 3PES9-G2 | y = 4.663x0.757 − 1.286x − 0.02506 | R2 = 0.9999 | y = 59.48x0.9911 − 57.49x − 0.2258 | R2 = 0.9555 |
| 3PES12-G2 | y = 4.675x0.8484 − 2.016x − 0.01012 | R2 = 0.9999 | y = 88.58x0.9898 − 85.61x − 0.2765 | R2 = 0.9649 |
| Sample Codes | Initial Thickness (mm) | Carpet Thickness of Various Recovery Periods (mm) | ||||
| h1 (after 2 min.) | h2 (after 1 h) | h3 (after 1 Day) | h4 (3 Days) | h5 (3 Years) | ||
| 1PES6 | 5.91 | 4.21 ± 0.44 | 4.38 ± 0.28 | 4.51 ± 0.23 | 4.62 ± 0.20 | 5.26 ± 0.79 |
| 1PES9 | 6.82 | 4.68 ± 0.03 | 5.16 ± 0.01 | 5.40 ± 0.02 | 5.46 ± 0.05 | 6.27 ± 0.66 |
| 1PES12 | 8.47 | 5.99 ± 0.05 | 6.17 ± 0.09 | 6.37 ± 0.13 | 6.44 ± 0.12 | 7.54 ± 0.47 |
| 2PES6 | 5.99 | 4.22 ± 0.08 | 4.39 ± 0.11 | 4.52 ± 0.02 | 4.76 ± 0.03 | 5.44 ± 0.54 |
| 2PES9 | 7.42 | 5.04 ± 0.08 | 5.31 ± 0.22 | 5.51 ± 0.18 | 5.57 ± 0.18 | 6.14 ± 0.13 |
| 2PES12 | 8.53 | 6.29 ± 0.03 | 6.41 ± 0.04 | 6.66 ± 0.02 | 6.82 ± 0.01 | 7.03 ± 0.64 |
| 3PES6 | 6.58 | 4.98 ± 0.04 | 5.12 ± 0.04 | 5.25 ± 0.04 | 5.34 ± 0.05 | 5.72 ± 0.20 |
| 3PES9 | 7.61 | 5.74 ± 0.06 | 5.93 ± 0.06 | 6.09 ± 0.04 | 6.25 ± 0.04 | 6.66 ± 0.23 |
| 3PES12 | 9.65 | 7.30 ± 0.07 | 7.53 ± 0.01 | 7.70 ± 0.01 | 7.81 ± 0.01 | 8.69 ± 0.26 |
| Sample Codes | Initial Thickness (mm) | Carpet Thickness Loss of Various Recovery Periods (%) | ||||
| h1 (after 2 min.) | h2 (after 1 h) | h3 (after 1 day) | h4 (3 days) | h5 (3 years) | ||
| 1PES6 | 5.91 | 28.76 ± 7.42 | 25.89 ± 4.79 | 23.69 ± 3.83 | 21.83 ± 3.35 | 11.00 ± 13.40 |
| 1PES9 | 6.82 | 31.38 ± 0.41 | 24.34 ± 0.21 | 20.89 ± 0.31 | 20.01 ± 0.73 | 8.06 ± 9.75 |
| 1PES12 | 8.47 | 29.34 ± 0.58 | 27.21 ± 1.09 | 24.85 ± 1.59 | 24.03 ± 1.42 | 11.04 ± 5.59 |
| 2PES6 | 5.99 | 29.55 ± 1.42 | 26.79 ± 1.77 | 24.62 ± 0.35 | 20.53 ± 0.47 | 9.18 ± 8.97 |
| 2PES9 | 7.42 | 32.08 ± 1.14 | 28.50 ± 2.95 | 25.81 ± 2.38 | 24.93 ± 2.48 | 17.32 ± 1.81 |
| 2PES12 | 8.53 | 26.26 ± 0.33 | 24.91 ± 0.41 | 21.98 ± 0.25 | 20.05 ± 0.17 | 17.64 ± 7.54 |
| 3PES6 | 6.58 | 24.32 ± 0.64 | 22.19 ± 0.64 | 20.29 ± 0.54 | 18.92 ± 0.75 | 13.07 ± 3.01 |
| 3PES9 | 7.61 | 24.57 ± 0.74 | 22.08 ± 0.74 | 19.97 ± 0.56 | 17.87 ± 0.56 | 12.48 ± 2.97 |
| 3PES12 | 9.65 | 24.35 ± 0.73 | 22.02 ± 0.07 | 20.21 ± 0.15 | 19.07 ± 0.15 | 10.00 ± 2.71 |
| Sample Codes | Initial Thickness (mm) | Carpet Resilience of Various Recovery Periods (%) | ||||
| h1 (after 2 min.) | h2 (after 1 h) | h3 (after 1 day) | h4 (3 days) | h5 (3 years) | ||
| 1PES6 | 5.91 | - | 9.12 ± 6.80 | 16.59 ± 8.20 | 23.06 ± 8.20 | 66.66 ± 37.99 |
| 1PES9 | 6.82 | - | 22.43 ± 0.36 | 33.41 ± 1.87 | 36.21 ± 3.16 | 74.30 ± 30.72 |
| 1PES12 | 8.47 | - | 7.24 ± 1.85 | 15.29 ± 3.72 | 18.11 ± 3.21 | 62.37 ± 18.32 |
| 2PES6 | 5.99 | - | 9.32 ± 1.65 | 16.67 ± 2.80 | 30.51 ± 1.74 | 68.93 ± 28.91 |
| 2PES9 | 7.42 | - | 11.13 ± 6.05 | 19.54 ± 4.56 | 22.27 ± 4.96 | 46.01 ± 7.57 |
| 2PES12 | 8.53 | - | 5.13 ± 0.38 | 16.29 ± 0.11 | 23.66 ± 1.60 | 32.81 ± 29.58 |
| 3PES6 | 6.58 | - | 8.75 ± 0.23 | 16.56 ± 4.42 | 22.19 ± 5.16 | 46.25 ± 10.95 |
| 3PES9 | 7.61 | - | 10.16 ± 0.31 | 18.72 ± 0.19 | 27.27 ± 0.07 | 49.20 ± 13.64 |
| 3PES12 | 9.65 | - | 9.57 ± 3.02 | 17.02 ± 1.90 | 21.70 ± 2.96 | 58.94 ± 12.37 |
| Sample Codes | Abrasion Cycles | Carpet Mass (mg) | Carpet mass Loss (mg) | Carpet mass Loss (%) | Carpet Thickness (mm) | Carpet Thickness Loss (mm) | Carpet Thickness Loss (%) |
|---|---|---|---|---|---|---|---|
| 1PES6 | 0 | 2030 | 0.00 ± 0.00 | 0.00 ± 0.00 | 5.91 ± 0.06 | 0.49 ± 0.14 | 8.30 ± 2.47 |
| 5000 | 2015 | 15 ± 7.07 | 0.74 ± 0.37 | - | |||
| 10,000 | 2010 | 20 ± 0.00 | 0.99 ± 0.03 | - | |||
| 20,000 | 2005 | 25 ± 7.07 | 1.23 ± 0.31 | - | |||
| 30,000 | 2005 | 25 ± 7.07 | 1.23 ± 0.31 | - | |||
| 40,000 | 1995 | 35 ± 7.07 | 1.72 ± 0.30 | - | |||
| 50,000 | 1990 | 40 ± 0.00 | 1.97 ± 0.05 | 5.42 ± 0.20 | |||
| 1PES9 | 0 | 2385 | 0.00 ± 0.00 | 0.00 ± 0.00 | 6.82 ± 0.11 | 0.57 ± 0.10 | 9.33 ± 2.70 |
| 5000 | 2380 | 5 ± 7.07 | 0.21 ± 0.30 | - | |||
| 10,000 | 2370 | 15 ± 7.07 | 0.63 ± 0.29 | - | |||
| 20,000 | 2360 | 25 ± 21.21 | 1.05 ± 0.89 | - | |||
| 30,000 | 2350 | 35 ± 21.21 | 1.47 ± 0.89 | - | |||
| 40,000 | 2340 | 45 ± 21.21 | 1.89 ± 0.88 | - | |||
| 50,000 | 2335 | 50 ± 14.41 | 2.10 ± 0.59 | 6.25 ± 0.01 | |||
| 1PES12 | 0 | 2530 | 0.00 ± 0.00 | 0.00 ± 0.00 | 8.47 ± 0.07 | 1.34 ± 0.17 | 15.81 ± 1.87 |
| 5000 | 2525 | 5 ± 7.07 | 0.20 ± 0.28 | - | |||
| 10,000 | 2515 | 15 ± 7.07 | 0.59 ± 0.28 | - | |||
| 20,000 | 2505 | 25 ± 7.07 | 0.99 ± 0.29 | - | |||
| 30,000 | 2485 | 45 ± 7.07 | 1.78 ± 0.27 | - | |||
| 40,000 | 2465 | 65 ± 7.07 | 2.57 ± 0.29 | - | |||
| 50,000 | 2455 | 75 ± 7.07 | 2.97 ± 0.30 | 7.13 ± 0.10 | |||
| 2PES6 | 0 | 2260 | 0.00 ± 0.00 | 0.00 ± 0.00 | 5.99 ± 0.04 | 0.59 ± 0.11 | 9.86 ± 1.95 |
| 5000 | 2225 | 35 ± 21.21 | 1.56 ± 0.97 | - | |||
| 10,000 | 2175 | 85 ± 7.07 | 3.76 ± 0.24 | - | |||
| 20,000 | 2160 | 100 ± 0.00 | 4.43 ± 0.08 | - | |||
| 30,000 | 2150 | 110 ± 0.00 | 4.87 ± 0.09 | - | |||
| 40,000 | 2145 | 115 ± 7.07 | 5.09 ± 0.41 | - | |||
| 50,000 | 2130 | 130 ± 0.00 | 5.75 ± 0.11 | 5.40 ± 0.15 | |||
| 2PES9 | 0 | 2110 | 0.00 ± 0.00 | 0.00 ± 0.00 | 7.42 ± 0.12 | 1.58 ± 0.04 | 21.32 ± 0.92 |
| 5000 | 2090 | 20 ± 0.00 | 0.95 ± 0.07 | - | |||
| 10,000 | 2045 | 65 ± 35.36 | 3.03 ± 1.45 | - | |||
| 20,000 | 2025 | 85 ± 21.21 | 4.00 ± 0.71 | - | |||
| 30,000 | 2015 | 95 ± 21.21 | 4.48 ± 0.68 | - | |||
| 40,000 | 1975 | 135 ± 77.78 | 6.28 ± 3.22 | - | |||
| 50,000 | 1920 | 190 ± 141.42 | 8.78 ± 6.05 | 5.84 ± 0.16 | |||
| 2PES12 | 0 | 2665 | 0.00 ± 0.00 | 0.00 ± 0.00 | 8.53 ± 0.28 | 2.05 ± 0.42 | 23.91 ± 4.10 |
| 5000 | 2655 | 10 ± 0.00 | 0.38 ± 0.00 | - | |||
| 10,000 | 2650 | 15 ± 7.07 | 0.56 ± 0.27 | - | |||
| 20,000 | 2615 | 50 ± 14.14 | 1.87 ± 0.51 | - | |||
| 30,000 | 2585 | 80 ± 28.28 | 3.00 ± 1.02 | - | |||
| 40,000 | 2555 | 110 ± 0.00 | 4.13 ± 0.05 | - | |||
| 50,000 | 2345 | 320 ± 84.85 | 11.99 ± 3.02 | 6.49 ± 0.13 | |||
| 3PES6 | 0 | 2675 | 0.00 ± 0.00 | 0.00 ± 0.00 | 6.58 ± 0.10 | 0.24 ± 0.08 | 3.64 ± 1.23 |
| 5000 | 2665 | 10 ± 0.00 | 0.37 ± 0 | - | |||
| 10,000 | 2660 | 15 ± 7.07 | 0.56 ± 0.26 | - | |||
| 20,000 | 2650 | 25 ± 7.07 | 0.93 ± 0.26 | - | |||
| 30,000 | 2550 | 125 ± 91.92 | 4.69 ± 3.47 | - | |||
| 40,000 | 2535 | 140 ± 113.14 | 5.25 ± 4.27 | - | |||
| 50,000 | 2525 | 150 ± 113.14 | 5.62 ± 4.27 | 6.34 ± 0.01 | |||
| 3PES9 | 0 | 2715 | 0.00 ± 0.00 | 0.00 ± 0.00 | 7.61 ± 0.10 | 1.78 ± 0.36 | 23.30 ± 4.44 |
| 5000 | 2690 | 25 ± 7.07 | 0.92 ± 0.27 | - | |||
| 10,000 | 2440 | 275 ± 35.36 | 10.12 ± 1.22 | - | |||
| 20,000 | 2420 | 295 ± 35.36 | 10.86 ± 1.22 | - | |||
| 30,000 | 2410 | 305 ± 35.36 | 11.23 ± 1.21 | - | |||
| 40,000 | 2395 | 320 ± 42.43 | 11.78 ± 1.47 | - | |||
| 50,000 | 2365 | 350 ± 70.71 | 12.88 ± 2.50 | 5.84 ± 0.26 | |||
| 3PES12 | 0 | 2860 | 0.00 ± 0.00 | 0.00 ± 0.00 | 9.65 ± 0.13 | 2.39 ± 0.10 | 24.79 ± 1.37 |
| 5000 | 2850 | 10 ± 0.00 | 0.35 ± 0.00 | - | |||
| 10,000 | 2835 | 25 ± 7.07 | 0.87 ± 0.25 | - | |||
| 20,000 | 2820 | 40 ± 14.14 | 1.40 ± 0.50 | - | |||
| 30,000 | 2795 | 65 ± 21.21 | 2.27 ± 0.73 | - | |||
| 40,000 | 2770 | 90 ± 56.57 | 3.14 ± 1.96 | - | |||
| 50,000 | 2740 | 120 ± 98.99 | 4.19 ± 3.44 | 7.26 ± 0.23 |
| Sample Codes | Stroke Number at the Beginning of Fractured Pile Yarns | Stroke Number after Complete Fractured Pile Yarns |
|---|---|---|
| 1PES6 | 1125 | 11,000 |
| 1PES9 | 1250 | 19,750 |
| 1PES12 | 1750 | 23,750 |
| 2PES6 | 1750 | 14,750 |
| 2PES9 | 1750 | 20,000 |
| 2PES12 | 2000 | 32,250 |
| 3PES6 | 2250 | 7000 |
| 3PES9 | 1750 | 18,250 |
| 3PES12 | 1750 | 23,000 |
| Carpet Thickness | |||||||
| Source | Sum of Squares | Contribution (%) | DF | Mean Square | F Value | Prob > F | Significance |
| Model | 16.89 | 99.19 | 5 | 3.38 | 293.23 | <0.0001 | significant |
| A | 13.66 | 80.21 | 1 | 13.66 | 1185.60 | <0.0001 | significant |
| B | 2.77 | 16.29 | 1 | 2.77 | 240.82 | <0.0001 | significant |
| A2 | 0.17 | 0.99 | 1 | 0.17 | 14.59 | 0.0024 | significant |
| B2 | 0.03 | 0.19 | 1 | 0.03 | 2.85 | 0.1169 | |
| AB | 0.22 | 1.30 | 1 | 0.22 | 19.26 | 0.0009 | significant |
| Residual | 0.14 | 0.81 | 12 | 0.01 | |||
| Lack of Fit | 0.04 | 0.25 | 3 | 0.01 | 1.35 | 0.3188 | not significant |
| Pure Error | 0.10 | 0.56 | 9 | 0.01 | |||
| Cor Total | 17.03 | 100.00 | 17 | ||||
| Resilience | |||||||
| Source | Sum of Squares | Contribution (%) | DF | Mean Square | F Value | Prob > F | Significance |
| Model | 2646.52 | 71.44 | 9 | 294.06 | 12.23 | <0.0001 | significant |
| A | 35.75 | 0.97 | 1 | 35.75 | 1.49 | 0.2292 | |
| B | 93.52 | 2.52 | 1 | 93.52 | 3.89 | 0.0549 | |
| C | 1910.68 | 51.58 | 1 | 1910.68 | 79.46 | <0.0001 | significant |
| A2 | 501.43 | 13.54 | 1 | 501.43 | 20.85 | <0.0001 | significant |
| B2 | 42.05 | 1.14 | 1 | 42.05 | 1.75 | 0.1929 | |
| C2 | 168.31 | 4.54 | 1 | 168.31 | 7.00 | 0.0113 | significant |
| AB | 18.80 | 0.51 | 1 | 18.80 | 0.78 | 0.3813 | |
| AC | 11.71 | 0.32 | 1 | 11.71 | 0.49 | 0.4889 | |
| BC | 0.86 | 0.02 | 1 | 0.86 | 0.04 | 0.8508 | |
| Residual | 1058.04 | 28.56 | 44 | 24.05 | |||
| Lack of Fit | 669.36 | 18.07 | 17 | 39.37 | 2.74 | 0.0095 | significant |
| Pure Error | 388.67 | 10.49 | 27 | 14.40 | |||
| Cor Total | 3704.55 | 100.00 | 53 | ||||
| Abrasion thickness loss | |||||||
| Source | Sum of Squares | Contribution (%) | DF | Mean Square | F Value | Prob > F | Significance |
| Model | 9.09 | 91.99 | 4 | 2.27 | 37.31 | <0.0001 | significant |
| A | 7.16 | 72.47 | 1 | 7.16 | 117.57 | <0.0001 | significant |
| B | 1.35 | 13.62 | 1 | 1.35 | 22.10 | 0.0004 | significant |
| B2 | 0.60 | 6.05 | 1 | 0.60 | 9.82 | 0.0079 | |
| AB | 0.83 | 8.41 | 1 | 0.83 | 13.65 | 0.0027 | significant |
| Residual | 0.79 | 8.01 | 13 | 0.06 | |||
| Lack of Fit | 0.55 | 5.60 | 4 | 0.14 | 5.21 | 0.0188 | significant |
| Pure Error | 0.24 | 2.42 | 9 | 0.03 | |||
| Cor Total | 9.88 | 100.00 | 17 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erdogan, G.; Yucel, S.; Bilisik, K. Textured Polyester Fiber in Three-Dimensional (3D) Carpet Structure Application: Experimental Characterizations under Compression–Bending–Abrasion–Rubbing Loading. Polymers 2023, 15, 3006. https://doi.org/10.3390/polym15143006
Erdogan G, Yucel S, Bilisik K. Textured Polyester Fiber in Three-Dimensional (3D) Carpet Structure Application: Experimental Characterizations under Compression–Bending–Abrasion–Rubbing Loading. Polymers. 2023; 15(14):3006. https://doi.org/10.3390/polym15143006
Chicago/Turabian StyleErdogan, Gulhan, Sinem Yucel, and Kadir Bilisik. 2023. "Textured Polyester Fiber in Three-Dimensional (3D) Carpet Structure Application: Experimental Characterizations under Compression–Bending–Abrasion–Rubbing Loading" Polymers 15, no. 14: 3006. https://doi.org/10.3390/polym15143006
APA StyleErdogan, G., Yucel, S., & Bilisik, K. (2023). Textured Polyester Fiber in Three-Dimensional (3D) Carpet Structure Application: Experimental Characterizations under Compression–Bending–Abrasion–Rubbing Loading. Polymers, 15(14), 3006. https://doi.org/10.3390/polym15143006







