Dynamic Crushing Behavior of Ethylene Vinyl Acetate Copolymer Foam Based on Energy Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
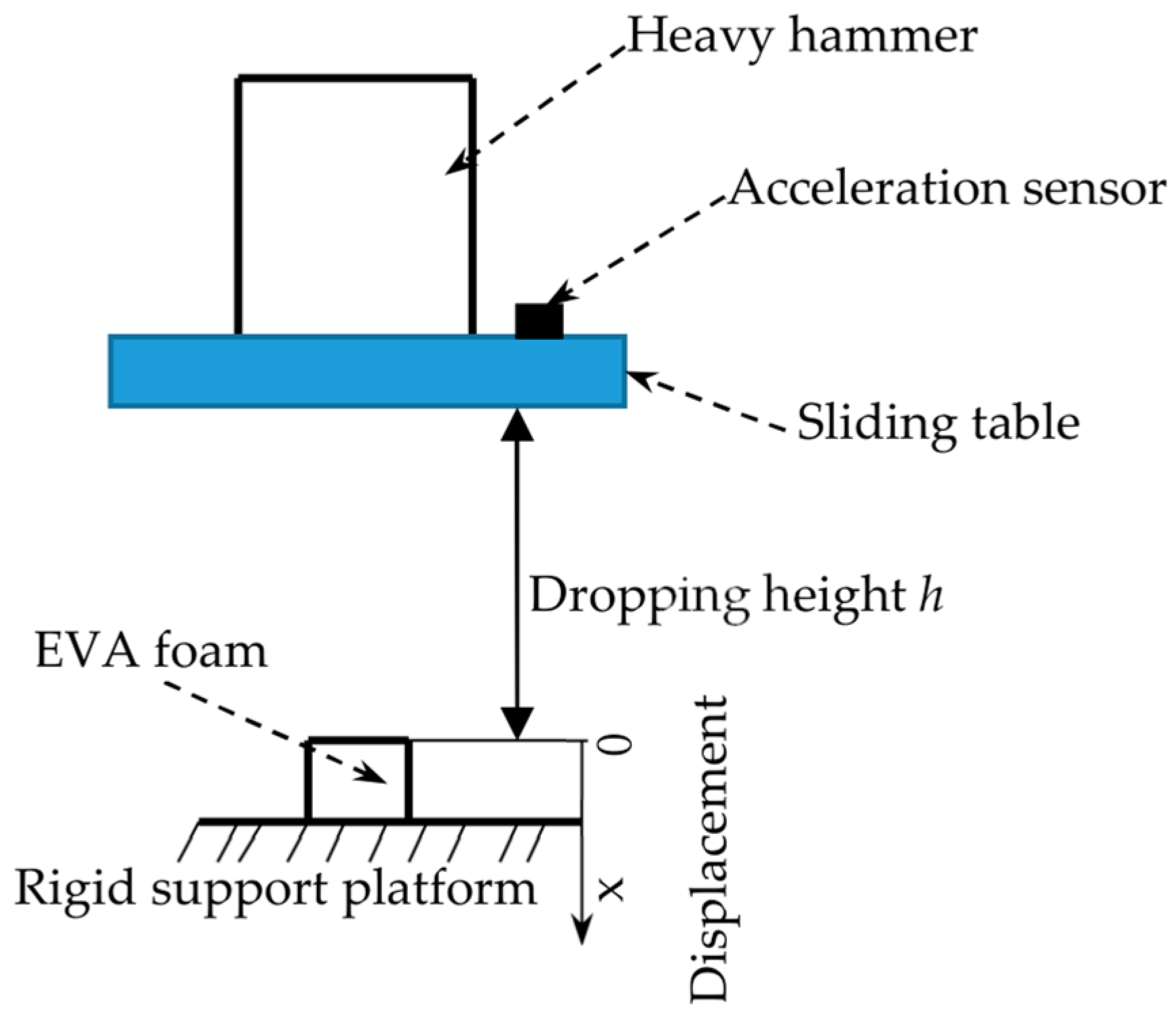
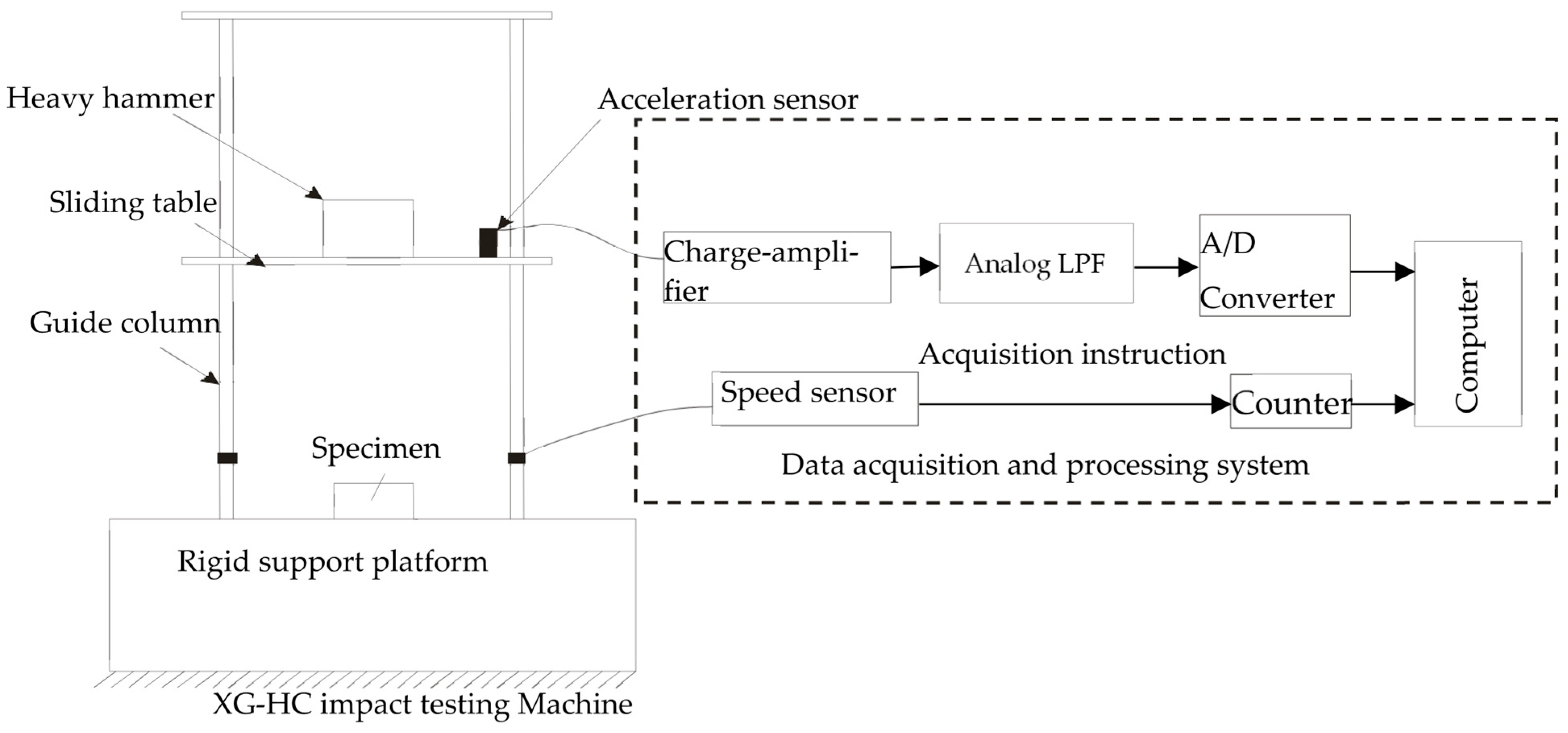
2.2. Impact Test Equipment and Method
2.3. Impact Compression Test Equipment
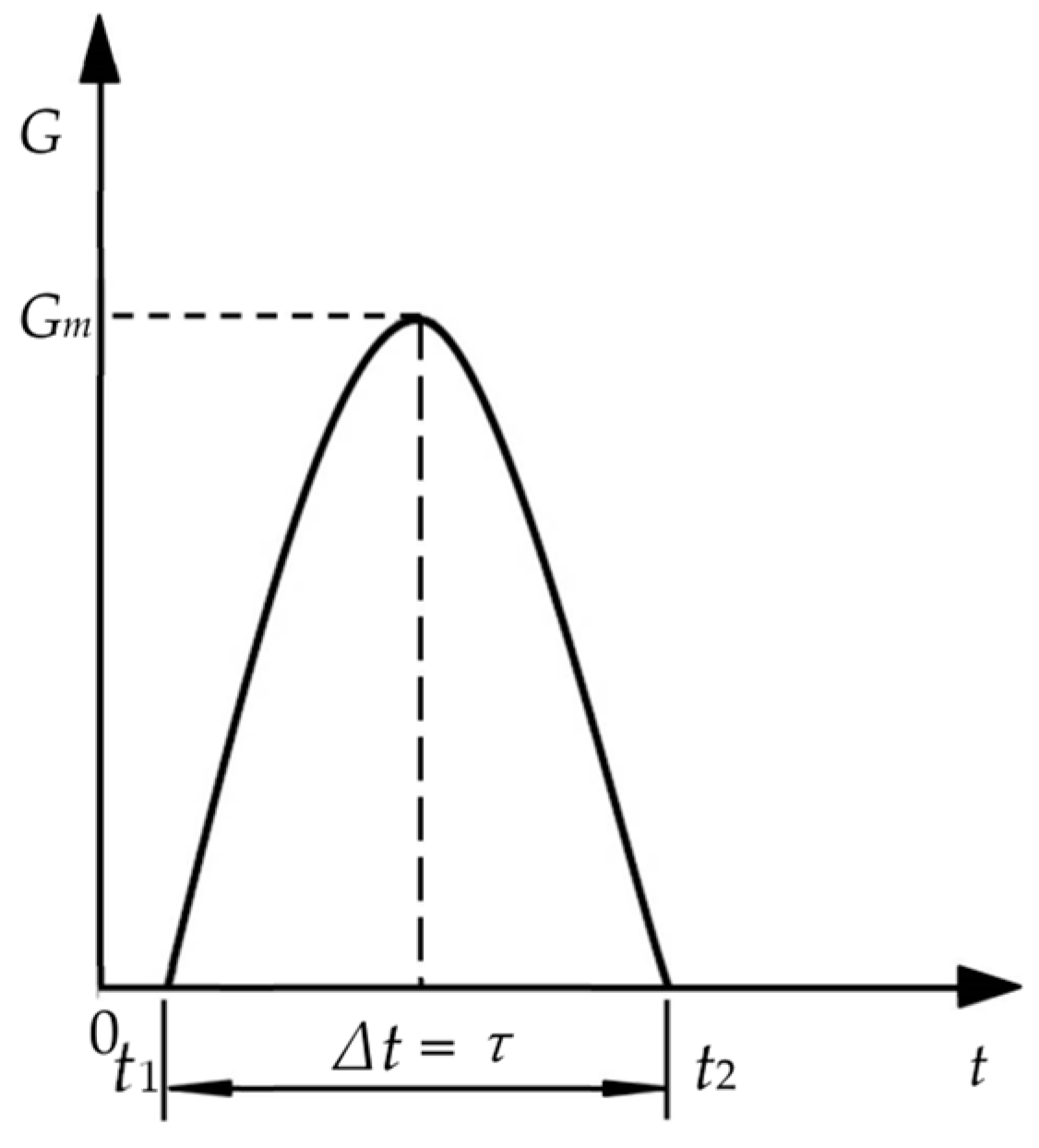
2.4. Impact Characteristic Criteria
3. Results and Discussion
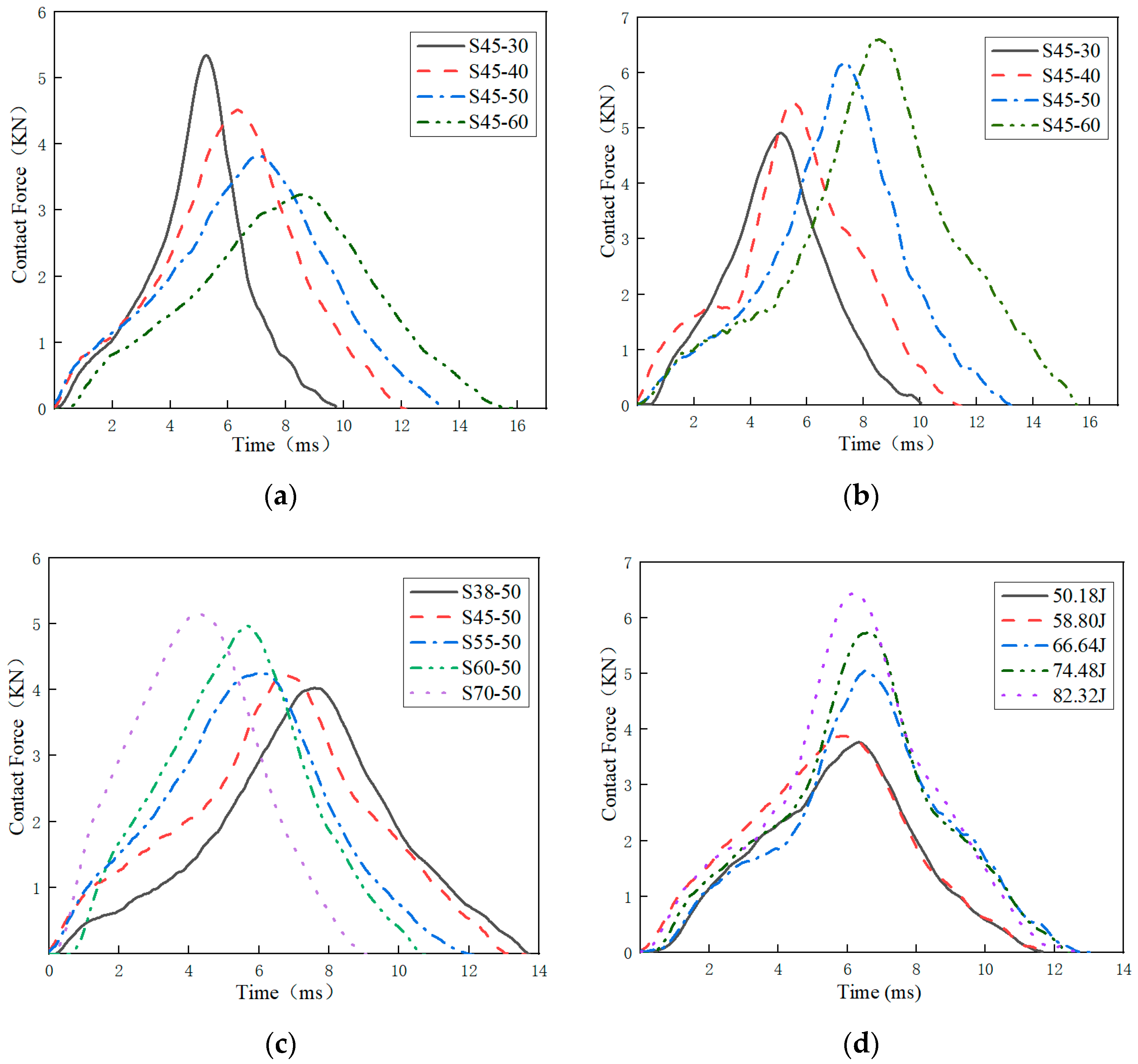
3.1. The Contact Force
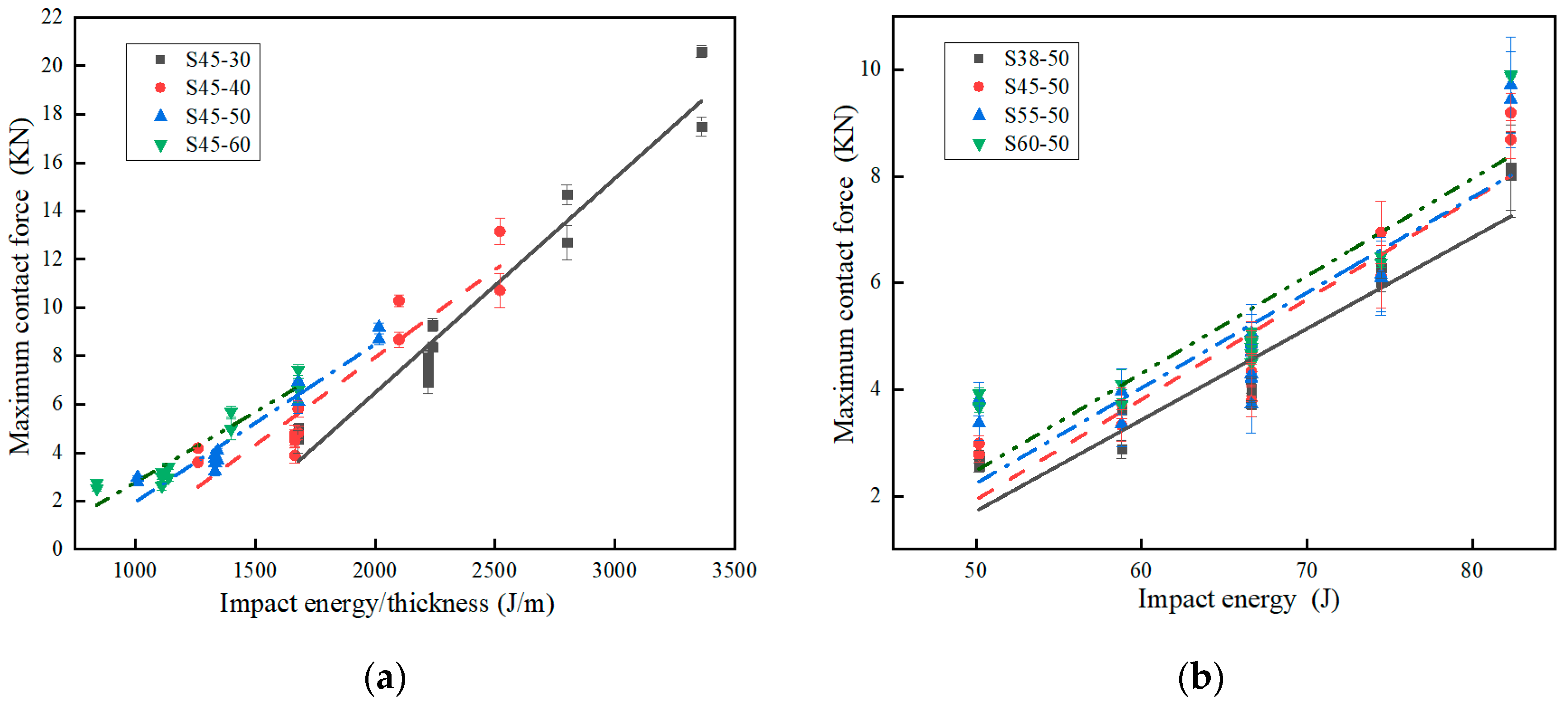
3.2. The Maximum Contact Forces, Displacement and Strain
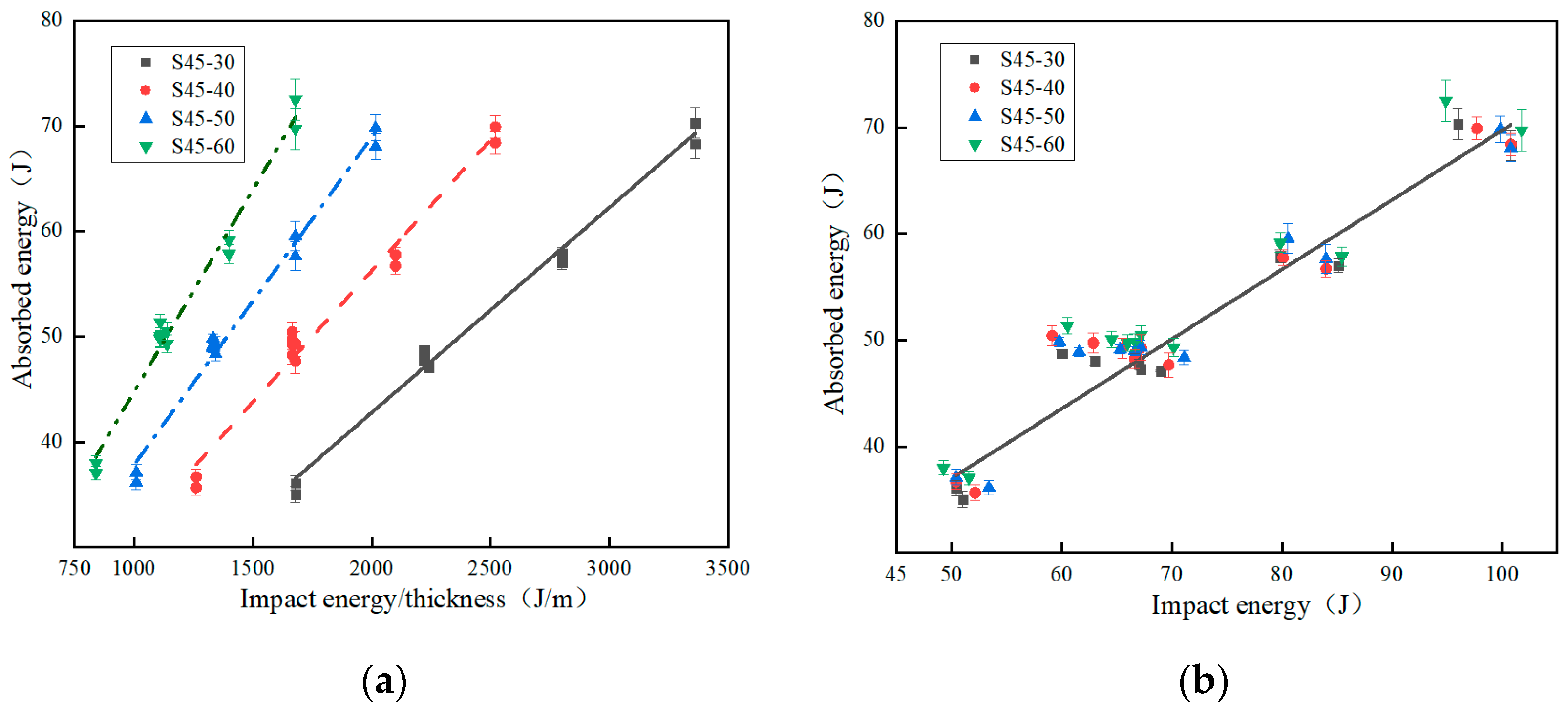
3.3. Absorbed Energy
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, B.S.; Zhang, Z.X.; Lv, X.F.; Lu, B.X.; Xin, Z.X. Properties of chlorinated polyethylene rubber/ethylene vinyl acetate copolymer blend-based foam. Polym. Eng. Sci. 2011, 52, 218–224. [Google Scholar] [CrossRef]
- Liu, F.; Zong, R.; Yan, G.; Xu, H. Research on lightweight EVA sole material. Plast. Ind. 2009, 37, 4. [Google Scholar]
- Deng, F.; Ma, J.; Xue, Z.; Duan, Z. Study on morphology and properties of EVA/OSEP composite foaming Materials. Funct. Mater. 2013, 44, 5. [Google Scholar]
- Riahinezhad, M.; Ghasemi, I.; Karrabi, M.; Azizi, H. An investigation on the correlation between rheology and morphology of nanocomposite foams based on low-density polyethylene and ethylene vinyl acetate blends. Polym. Compos. 2010, 31, 1808–1816. [Google Scholar] [CrossRef]
- Ye, C.; Wang, Z. Characterization of energy absorption properties of EPE and EVA Foaming buffer Materials. Packag. Eng. 2012, 33, 6. [Google Scholar]
- Wang, D.M. Impact behavior and energy absorption of paper honeycomb sandwich panels. Int. J. Impact Eng. 2009, 36, 110–114. [Google Scholar] [CrossRef]
- Zhou, Q.; Mayer, R. Characterization of aluminum honeycomb material failure in large deformation compression, shear, and tearing. J. Eng. Mater. Technol. Trans. ASME 2002, 124, 412–420. [Google Scholar] [CrossRef]
- Cronin, D.S.; Ouellet, S. Low density polyethylene, expanded polystyrene and expanded polypropylene: Strain rate and size effects on mechanical properties. Polym. Test. 2016, 53, 40–50. [Google Scholar] [CrossRef]
- Tan, P.J.; Reid, S.R.; Harrigan, J.J.; Zou, Z.; Li, S. Dynamic compressive strength properties of aluminum foams. Part I-experimental data and observations. J. Mech. Phys. Solids 2005, 53, 2174–2205. [Google Scholar] [CrossRef]
- Petrone, G.; Rao, S.; Rosa, S.D.; Mace, B.R.; Franco, F.; Bhattacharyya, D. Behavior of fiber-reinforced honeycomb core under low velocity impact loading. Compos. Struct. 2013, 100, 356–362. [Google Scholar] [CrossRef] [Green Version]
- Tan, C.Y.; Akil, H.M. Impact response of fiber metal laminate sandwich composite structure with polypropylene honeycomb core. Compos. Part B-Eng. 2012, 43, 1433–1438. [Google Scholar] [CrossRef]
- Wang, Z.; Tian, H.; Lu, Z.; Zhou, W. High-speed axial impact of aluminum honeycomb-Experiments and simulations. Compos. Part B-Eng. 2014, 56, 1–8. [Google Scholar] [CrossRef]
- Sánchez-Sáez, S.; García-Castillo, S.K.; Barbero, E.; Cirne, J. Dynamic crushing behavior of agglomerated cork. Mater. Des. 2015, 65, 743–748. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.-J.; Chen, M.-R.; Sun, D.-Q. Experimental Analysis of Out-of-plane Dynamic Impact Properties of Honeycomb Paperboard. Packag. Eng. 2017, 38, 106–110. [Google Scholar]
- Bouix, R.; VIot, P.; Lataillade, J.L. Polypropylene Foam Behavior under Dynamic Loadings: Strain Rate, Density and Microstructure Effects. Int. J. Impact Eng. 2009, 36, 329–342. [Google Scholar] [CrossRef] [Green Version]
- Gameiro, C.P.; Cirne, J. Dynamic axial crushing of short to long circular aluminum tubes with agglomerate cork filler. Int. J. Mech. Sci. 2007, 49, 1029–1037. [Google Scholar] [CrossRef] [Green Version]
- Alcântara, I.; Teixeira-Dias, F.; Paulino, M. Cork composites for the absorption of impact energy. Compos. Struct. 2013, 95, 16–27. [Google Scholar] [CrossRef]
- Sanchez-Saez, S.; Barbero, E.; Cirne, J. Experimental study of agglomerated-cork cored structures subjected to ballistic impacts. Mater. Lett. 2011, 65, 2152–2154. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.S.; Park, N.H.; Yoon, H.S. Dynamic Mechanical Characteristics of Expanded Polypropylene Foams. J. Cell. Plast. 2010, 46, 43–55. [Google Scholar]
- Anjos, O.; Pereira, H.; Rosa, M.E. Effect of quality, porosity and density on the compression properties of cork. Holz als Roh-und Werkstoff 2008, 66, 295–301. [Google Scholar] [CrossRef]
- Coelho, R.M.; Alves de Sousa, R.J.; Fernandes, F.A.O.; Teixeira-Dias, F. New composite liners for energy absorption purposes. Mater. Des. 2013, 43, 384–392. [Google Scholar] [CrossRef]
- Anjos, O.; Rodrigues, C.; Morais, J.; Pereira, H. Effect of density on the compression behavior of cork. Mater. Des. 2014, 53, 1089–1096. [Google Scholar] [CrossRef]
- Xing, Y.; Sun, D.; Zhang, M.; Shu, G. Crushing responses of expanded polypropylene foam. Polymers 2023, 15, 2059. [Google Scholar] [CrossRef] [PubMed]
- GB/T 8167-2008; Testing Method of Dynamic Compression for Packaging Cushioning Materials. China Standards Press: Beijing, China, 2008.
- Di Landro, L.; Sala, G.; Olivieri, D. Deformation mechanisms and energy absorption of polystyrene foams for protective helmets. Polym. Test. 2002, 21, 17–28. [Google Scholar] [CrossRef]
- Peng, G. Logistics and Transportation Packaging Design; Printing Industry Press: Beijing, China, 2012. [Google Scholar]
- Jin, Q.; Sun, D.; Li, G.; Xing, Y. Effect of density on dynamic impact properties of polypropylene foam materials. Packag. Eng. 2018, 39, 88–92. [Google Scholar]
- Sun, D.; Jin, Q.; Li, G.; Shi, Y.; Li, G.; Li, J.; Hu, X.; Xing, Y. Study on dynamic mechanical behavior of foamed polypropylene materials. Packag. Eng. 2019, 40, 63–68. [Google Scholar]
- Sanchez-Saez, S.; Barbero, E.; Navarro, C. Compressive residual strength at low temperatures of composite laminates subjected to low-velocity impacts. Compos. Struct. 2008, 85, 226–232. [Google Scholar] [CrossRef] [Green Version]
- Castro, O.; Silva, J.M.; Devezas, T.; Silva, A.; Gil, L. Cork agglomerates as an ideal core material in lightweight structures. Mater. Des. 2010, 31, 425–432. [Google Scholar] [CrossRef] [Green Version]




| Specimen | Thickness (mm) | Theoretical Impact Energy (J) | Theoretical Impact Energy-to-Thickness Ratio (J/m) | Number of Specimens |
|---|---|---|---|---|
| S45-30 | 30 | 50.4 | 1680 | 5 |
| 66.64 | 2221 | 5 | ||
| 67.2 | 2240 | 5 | ||
| 84 | 2800 | 6 | ||
| 100.8 | 3360 | 6 | ||
| S45-40 | 40 | 50.4 | 1260 | 5 |
| 66.64 | 1666 | 5 | ||
| 67.2 | 1680 | 5 | ||
| 84 | 2100 | 6 | ||
| 100.8 | 2320 | 6 | ||
| S45-50 | 50 | 50.4 | 1008 | 5 |
| 66.64 | 1333 | 5 | ||
| 67.2 | 1344 | 5 | ||
| 84 | 1680 | 6 | ||
| 100.8 | 2016 | 6 | ||
| S45-60 | 60 | 50.4 | 840 | 5 |
| 66.64 | 1110 | 5 | ||
| 67.2 | 1120 | 5 | ||
| 84 | 1400 | 6 | ||
| 100.8 | 1680 | 6 |
| Specimen | Density (kg/m3) | Theoretical Impact Energy (J) | Theoretical Impact Energy/Thickness Ratio (J/m) | Number of Specimens |
|---|---|---|---|---|
| S38-50 | 70 | 50.18 | 1003 | 5 |
| 58.80 | 1176 | 5 | ||
| 66.64 | 1333 | 5 | ||
| 74.48 | 1489 | 6 | ||
| 83.32 | 1666 | 6 | ||
| S55-50 | 110 | 50.18 | 1003 | 5 |
| 58.80 | 1176 | 5 | ||
| 66.64 | 1333 | 5 | ||
| 74.48 | 1489 | 6 | ||
| 83.32 | 1666 | 6 | ||
| S60-50 | 150 | 50.18 | 1003 | 5 |
| 58.80 | 1176 | 5 | ||
| 66.64 | 1333 | 5 | ||
| 74.48 | 1489 | 6 | ||
| 83.32 | 1666 | 6 | ||
| S70-50 | 175 | 50.18 | 1003 | 5 |
| 58.80 | 1176 | 5 | ||
| 66.64 | 1333 | 5 | ||
| 74.48 | 1489 | 6 | ||
| 83.32 | 1666 | 6 |
| Specimen | Theoretical Impact Energy/Thickness Ratio (J/m) | Maximum Displacement (mm) | Maximum Strain | Maximum Contact Force (KN) |
|---|---|---|---|---|
| S45-30 | 1680 ± 2 | 10.92 ± 0.10 | 0.36 ± 0.02 | 4.91 ± 0.20 |
| 2221 ± 3 | 12.22 ± 0.20 | 0.41 ± 0.02 | 5.63 ± 0.20 | |
| 2240 ± 3 | 14.16 ± 0.20 | 0.47 ± 0.02 | 10.56 ± 0.50 | |
| 2800 ± 4 | 15.36 ± 0.20 | 0.51 ± 0.01 | 13.79 ± 0.50 | |
| 3360 ± 4 | 16.01 ± 0.20 | 0.53 ± 0.02 | 17.75 ± 0.50 | |
| S45-40 | 1260 ± 2 | 15.751 ± 0.20 | 0.41 ± 0.02 | 3.71 ± 0.40 |
| 1666 ± 2 | 17.83 ± 0.20 | 0.45 ± 0.02 | 4.52 ± 0.40 | |
| 1680 ± 2 | 18.83 ± 0.10 | 0.47 ± 0.02 | 5.46 ± 0.40 | |
| 2100 ± 3 | 18.50 ± 0.20 | 0.46 ± 0.01 | 7.03 ± 0.40 | |
| 2520 ± 3 | 19.12 ± 0.20 | 0.48 ± 0.02 | 12.63 ± 0.50 | |
| S45-50 | 1008 ± 2 | 21.69 ± 0.20 | 0.45 ± 0.01 | 2.06 ± 0.20 |
| 1333 ± 2 | 23.06 ± 0.20 | 0.46 ± 0.02 | 3.81 ± 0.30 | |
| 1344 ± 2 | 23.87 ± 0.20 | 0.48 ± 0.03 | 4.68 ± 0.30 | |
| 1680 ± 2 | 24.39 ± 0.20 | 0.49 ± 0.02 | 6.30 ± 0.30 | |
| 2016 ± 3 | 25.07 ± 0.10 | 0.50 ± 0.02 | 8.48 ± 0.40 | |
| S45-60 | 840 ± 2 | 29.46 ± 0.24 | 0.51 ± 0.01 | 2.60 ± 0.20 |
| 1110 ± 2 | 32.20 ± 0.20 | 0.54 ± 0.03 | 3.24 ± 0.20 | |
| 1120 ± 2 | 33.09 ± 0.20 | 0.55 ± 0.01 | 4.39 ± 0.20 | |
| 1400 ± 2 | 33.23 ± 0.20 | 0.55 ± 0.01 | 5.48 ± 0.30 | |
| 1680 ± 3 | 34.01 ± 0.30 | 0.57 ± 0.02 | 6.87 ± 0.40 |
| Specimen | Theoretical Impact Energy (J) | Maximum Displacement (mm) | Maximum Strain | Maximum Contact Force (KN) |
|---|---|---|---|---|
| S60-50 | 50.18 ± 1 | 18.72 ± 0.30 | 0.37 ± 0.01 | 3.79 ± 0.20 |
| 58.80 ± 1 | 19.475 ± 0.40 | 0.39 ± 0.01 | 3.91 ± 0.20 | |
| 66.64 ± 2 | 20.41 ± 0.30 | 0.41 ± 0.01 | 4.73 ± 0.30 | |
| 74.48 ± 2 | 21.27 ± 0.40 | 0.43 ± 0.01 | 6.44 ± 0.40 | |
| 82.32 ± 3 | 22.91 ± 0.50 | 0.46 ± 0.01 | 9.90 ± 0.50 | |
| S55-50 | 50.18 ± 1 | 21.89 ± 0.30 | 0.43 ± 0.01 | 3.59 ± 0.20 |
| 58.80 ± 1 | 22.46 ± 0.30 | 0.45 ± 0.01 | 3.66 ± 0.20 | |
| 66.64 ± 2 | 23.85 ± 0.40 | 0.49 ± 0.01 | 4.49 ± 0.30 | |
| 74.48 ± 2 | 24.76 ± 0.50 | 0.49 ± 0.01 | 6.12 ± 0.40 | |
| 82.32 ± 3 | 26.07 ± 0.50 | 0.52 ± 0.02 | 9.58 ± 0.50 | |
| S45-50 | 50.18 ± 1 | 22.85 ± 0.30 | 0.46 ± 0.01 | 2.88 ± 0.20 |
| 58.80 ± 1 | 24.49 ± 0.30 | 0.49 ± 0.01 | 3.53 ± 0.30 | |
| 66.64 ± 2 | 26.31 ± 0.40 | 0.53 ± 0.02 | 4.57 ± 0.40 | |
| 74.48 ± 2 | 26.78 ± 0.50 | 0.54 ± 0.02 | 6.53 ± 0.40 | |
| 82.32 ± 3 | 27.83 ± 0.50 | 0.56 ± 0.02 | 8.94 ± 0.50 | |
| S38-50 | 50.18 ± 1 | 30.16 ± 0.30 | 0.60 ± 0.03 | 2.66 ± 0.20 |
| 58.80 ± 1 | 32.08 ± 0.30 | 0.64 ± 0.03 | 3.25 ± 0.20 | |
| 66.64 ± 2 | 33.16 ± 0.40 | 0.66 ± 0.03 | 3.94 ± 0.30 | |
| 74.48 ± 2 | 33.24 ± 0.50 | 0.66 ± 0.03 | 6.15 ± 0.40 | |
| 82.32 ± 2 | 33.76 ± 0.50 | 0.67 ± 0.03 | 8.09 ± 0.50 |
| Specimen | Impact Energy (J) | Impact Energy/Thickness (J/m) | Absorbed Energy (J) | SEA (J/g) |
|---|---|---|---|---|
| S45-30 | 50.40 ± 1 | 1680 ± 3 | 36.11 ± 1 | 2.81 ± 0.10 |
| 66.64 ± 2 | 2221 ± 4 | 47.77 ± 1 | 2.81 ± 0.10 | |
| 67.20 ± 2 | 2240 ± 4 | 47.26 ± 1 | 2.76 ± 0.10 | |
| 84.00 ± 3 | 2800 ± 4 | 57.01 ± 2 | 2.66 ± 0.10 | |
| 100.80 ± 3 | 3360 ± 5 | 68.29 ± 3 | 2.66 ± 0.10 | |
| S45-40 | 50.40 ± 1 | 1260 ± 3 | 36.69 ± 1 | 2.85 ± 0.10 |
| 66.64 ± 2 | 1666 ± 3 | 48.27 ± 2 | 2.84 ± 0.10 | |
| 67.20 ± 2 | 1680 ± 3 | 49.32 ± 2 | 2.88 ± 0.10 | |
| 84.00 ± 3 | 2100 ± 4 | 57.78 ± 3 | 2.70 ± 0.10 | |
| 100.80 ± 3 | 2520 ± 4 | 69.92 ± 3 | 2.72 ± 0.10 | |
| S45-50 | 50.40 ± 1 | 1008 ± 3 | 37.12 ± 1 | 2.89 ± 0.10 |
| 66.64 ± 2 | 1333 ± 3 | 48.89 ± 2 | 2.88 ± 0.10 | |
| 67.20 ± 2 | 1344 ± 3 | 49.14 ± 2 | 2.89 ± 0.10 | |
| 84.00 ± 3 | 1680 ± 3 | 57.62 ± 3 | 2.69 ± 0.10 | |
| 100.80 ± 3 | 2016 ± 4 | 69.83 ± 3 | 2.72 ± 0.10 | |
| S45-60 | 50.40 ± 1 | 840 ± 2 | 37.04 ± 2 | 2.88 ± 0.10 |
| 66.64 ± 2 | 1110 ± 2 | 49.74 ± 3 | 2.93 ± 0.10 | |
| 67.20 ± 2 | 1120 ± 3 | 50.51 ± 3 | 2.95 ± 0.10 | |
| 84.00 ± 3 | 1400 ± 3 | 59.16 ± 3 | 2.76 ± 0.10 | |
| 100.80 ± 3 | 1680 ± 3 | 72.52 ± 4 | 2.82 ± 0.10 |
| Specimen | Impact Energy (J) | Absorbed Energy (J) | SEA (J/g) |
|---|---|---|---|
| S38-50 | 50.18 ± 1 | 36.84 ± 1 | 1.05 ± 0.10 |
| 58.80 ± 1 | 40.81 ± 2 | 1.17 ± 0.10 | |
| 66.64 ± 2 | 47.77 ± 2 | 1.36 ± 0.10 | |
| 74.48 ± 2 | 51.64 ± 3 | 1.48 ± 0.10 | |
| 82.32 ± 3 | 53.58 ± 3 | 1.53 ± 0.10 | |
| S45-50 | 50.18 ± 1 | 36.90 ± 1 | 0.88 ± 0.05 |
| 58.80 ± 1 | 42.15 ± 1 | 1.00 ± 0.10 | |
| 66.64 ± 2 | 48.27 ± 1 | 1.15 ± 0.10 | |
| 74.48 ± 2 | 50.04 ± 2 | 1.19 ± 0.10 | |
| 82.32 ± 3 | 51.35 ± 2 | 1.22 ± 0.10 | |
| S55-50 | 50.18 ± 1 | 36.78 ± 1 | 0.67 ± 0.02 |
| 58.80 ± 1 | 44.53 ± 1 | 0.81 ± 0.02 | |
| 66.64 ± 2 | 48.52 ± 1 | 0.88 ± 0.02 | |
| 74.48 ± 3 | 51.99 ± 2 | 0.99 ± 0.02 | |
| 82.32 ± 4 | 53.90 ± 2 | 1.11 ± 0.1 | |
| S60-50 | 50.18 ± 1 | 38.55 ± 1 | 0.51 ± 0.01 |
| 58.80 ± 1 | 43.42 ± 1 | 0.58 ± 0.01 | |
| 66.64 ± 2 | 49.74 ± 2 | 0.66 ± 0.01 | |
| 74.48 ± 3 | 52.72 ± 2 | 0.70 ± 0.01 | |
| 82.32 ± 4 | 55.84 ± 2 | 0.74 ± 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Y.; Guo, X.; Shu, G.; He, X. Dynamic Crushing Behavior of Ethylene Vinyl Acetate Copolymer Foam Based on Energy Method. Polymers 2023, 15, 3016. https://doi.org/10.3390/polym15143016
Xing Y, Guo X, Shu G, He X. Dynamic Crushing Behavior of Ethylene Vinyl Acetate Copolymer Foam Based on Energy Method. Polymers. 2023; 15(14):3016. https://doi.org/10.3390/polym15143016
Chicago/Turabian StyleXing, Yueqing, Xiya Guo, Guowei Shu, and Xiaolong He. 2023. "Dynamic Crushing Behavior of Ethylene Vinyl Acetate Copolymer Foam Based on Energy Method" Polymers 15, no. 14: 3016. https://doi.org/10.3390/polym15143016
APA StyleXing, Y., Guo, X., Shu, G., & He, X. (2023). Dynamic Crushing Behavior of Ethylene Vinyl Acetate Copolymer Foam Based on Energy Method. Polymers, 15(14), 3016. https://doi.org/10.3390/polym15143016






