Numerical Study of the Effect of High Gravity in Material Extrusion System and Polymer Characteristics during Filament Fabrication
Abstract
:1. Introduction
2. High Gravity in Material Extrusion
2.1. Applications of Centrifugal Acceleration and Material Extrusion
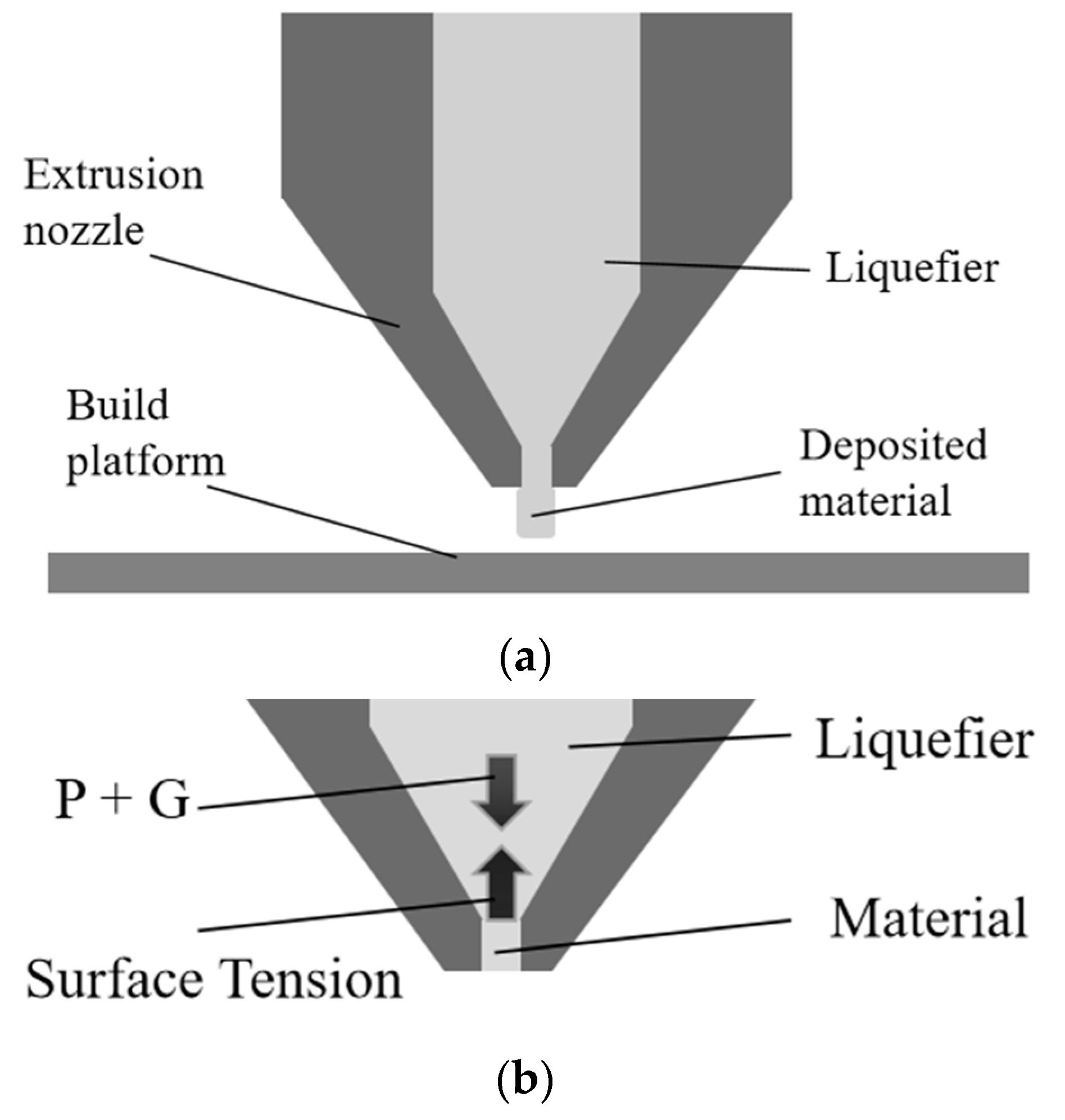
2.2. HG-MEX System
3. Experiment and Numerical Study of High Gravity
3.1. HG-MEX System Development
3.2. Polymer Science and Material Extrusion Conditions
4. Results and Discussion
4.1. Behavior of Material Extrusion
4.2. Filament Fabrication by Different Gravity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rajan, K.; Samykano, M.; Kadirgama, K.; Harun, W.S.W.; Rahman, M.M. Fused Deposition Modeling: Process, Materials, Parameters, Properties, and Applications. Int. J. Adv. Manuf. Technol. 2022, 120, 1531–1570. [Google Scholar] [CrossRef]
- Cleeman, J.; Bogut, A.; Mangrolia, B.; Ripberger, A.; Kate, K.; Zou, Q.; Malhotra, R. Scalable, flexible and Resilient Parallelization of Fused Filament Fabrication: Breaking Endemic Tradeoffs in Material Extrusion Additive Manufacturing. Addit. Manuf. 2022, 56, 102926. [Google Scholar] [CrossRef]
- Jiang, J.; Xu, X.; Stringer, J. Optimization of Process Planning for Reducing Material Waste in Extrusion Based Additive Manufacturing. Robot. Comput.-Integr. Manuf. 2019, 59, 317–325. [Google Scholar] [CrossRef]
- Vyavahare, S.; Teraiya, S.; Panghal, D.; Kumar, S. Fused Deposition Modelling: A Review. Rapid Prototyp. J. 2020, 26, 176–201. [Google Scholar] [CrossRef]
- Goh, G.D.; Yap, Y.L.; Tan, H.K.J.; Sing, S.L.; Goh, G.L.; Yeong, W.Y. Process–Structure–Properties in Polymer Additive Manufacturing via Material Extrusion: A Review. Crit. Rev. Solid State Mater. Sci. 2020, 45, 113–133. [Google Scholar] [CrossRef]
- Romanczuk-Ruszuk, E.; Sztorch, B.; Pakuła, D.; Gabriel, E.; Nowak, K.; Przekop, R.E. 3D Printing Ceramics—Materials for Direct Extrusion Process. Ceramics 2023, 6, 364–385. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive Manufacturing (3D Printing): A Review of Materials, Methods, Applications And Challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Rahim, T.N.A.T.; Abdullah, A.M.; Md Akil, H. Recent Developments in Fused Deposition Modeling-Based 3D Printing of Polymers and their Composites. Polym. Rev. 2019, 59, 589–624. [Google Scholar] [CrossRef]
- Xia, Q.; Sun, G.; Kim, J.; Li, Y. Multi-Scale Modeling and Simulation of Additive Manufacturing Based on Fused Deposition Technique. Phys. Fluids 2023, 35, 034116. [Google Scholar] [CrossRef]
- Phan, D.D.; Horner, J.S.; Swain, Z.R.; Beris, A.N.; Mackay, M.E. Computational Fluid Dynamics Simulation of the Melting Process in the Fused Filament Fabrication Additive Manufacturing Technique. Addit. Manuf. 2020, 33, 101161. [Google Scholar] [CrossRef]
- Xia, H.; Lu, J.; Dabiri, S.; Tryggvason, G. Fully Resolved Numerical Simulations of Fused Deposition Modeling. Part I: Fluid Flow. Rapid Prototyp. J. 2018, 24, 463–476. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Lee, C.; Jadidi, M. An Introduction of Droplet Impact Dynamics to Engineering Students. Fluids 2020, 5, 107. [Google Scholar] [CrossRef]
- Sontti, S.G.; Atta, A. CFD Analysis of Microfluidic Droplet Formation in Non–Newtonian Liquid. Chem. Eng. J. 2017, 330, 245–261. [Google Scholar] [CrossRef]
- Cai, Z.; Song, Y. Implementing Contact Angle Hysteresis in Moving Mesh-Based Two-Phase Flow Numerical Simulations. ACS Omega 2021, 6, 35711–35717. [Google Scholar] [CrossRef]
- Mohammadi-Khanaposhtani, M.; Kazemzadeh, Y.; Daneshfar, R. Positive Coupling Effect in Gas Condensate Flow: Role of Capillary Number, Scheludko Number and Weber Number. J. Pet. Sci. Eng. 2021, 203, 108490. [Google Scholar] [CrossRef]
- Placone, J.K.; Engler, A.J. Recent Advances in Extrusion-Based 3D Printing for Biomedical Applications. Adv. Healthc. Mater. 2018, 7, 1701161. [Google Scholar] [CrossRef] [Green Version]
- Sontti, S.G.; Atta, A. Numerical Insights on Controlled Droplet Formation in a Microfluidic Flow-Focusing Device. Ind. Eng. Chem. Res. 2019, 59, 3702–3716. [Google Scholar] [CrossRef]
- Knoche, S.; Vella, D.; Aumaitre, E.; Degen, P.; Rehage, H.; Cicuta, P.; Kierfeld, J. Elastometry of Deflated Capsules: Elastic Moduli from Shape and Wrinkle Analysis. Langmuir 2013, 29, 12463–12471. [Google Scholar] [CrossRef] [Green Version]
- Lei, M.; Wei, Q.; Li, M.; Zhang, J.; Yang, R.; Wang, Y. Numerical Simulation and Experimental Study the Effects of Process Parameters on Filament Morphology and Mechanical Properties of FDM 3D Printed PLA/GNPs Nanocomposite. Polymers 2022, 14, 3081. [Google Scholar] [CrossRef]
- Keller, J.B.; Miksis, M.J. Surface Tension Driven Flows. SIAM J. Appl. Math. 1983, 43, 268–277. [Google Scholar] [CrossRef]
- Xu, X.; Jagota, A.; Peng, S.; Luo, D.; Wu, M.; Hui, C.Y. Gravity and Surface Tension Effects on the Shape Change of Soft Materials. Langmuir 2013, 29, 8665–8674. [Google Scholar] [CrossRef] [PubMed]
- Koike, R.; Sugiura, Y. Metal Powder Bed Fusion in High Gravity. CIRP Ann. 2021, 70, 191–194. [Google Scholar] [CrossRef]
- Sugiura, Y.; Koike, R. High-Gravitational Effect on Process Stabilization for Metal Powder Bed Fusion. Addit. Manuf. 2021, 46, 102153. [Google Scholar] [CrossRef]
- Mounsey, S.; Hon, B.; Sutcliffe, C. Performance Modelling and Simulation of Metal Powder Bed Fusion Production System. CIRP Ann. 2016, 65, 421–424. [Google Scholar] [CrossRef]
- Li, Z.; Li, H.; Yin, J.; Li, Y.; Nie, Z.; Li, X.; You, D.; Guan, K.; Duan, W.; Cao, L.; et al. A Review of Spatter in Laser Powder Bed Fusion Additive Manufacturing: In Situ Detection, Generation, Effects, and Countermeasures. Micromachines 2022, 13, 1366. [Google Scholar] [CrossRef] [PubMed]
- Ramshaw, C. The Opportunities for Exploiting Centrifugal Fields. Heat Recovery Syst. CHP 1993, 13, 493–513. [Google Scholar] [CrossRef]
- Scott, R.F. Centrifuge Model Testing at Caltech. Int. J. Soil Dyn. Earthq. Eng. 1983, 2, 188–198. [Google Scholar] [CrossRef]
- Koike, R.; Alkhaled, A.; Kashimoto, T. Basic Study for Lunar Regolith Powder bed fusion in High Gravity. CIRP Ann. 2023, 72, 125–128. [Google Scholar] [CrossRef]
- Hua, J.; Lou, J. Numerical Simulation of Bubble Rising in Viscous Liquid. J. Comput. Phys. 2007, 222, 769–795. [Google Scholar] [CrossRef]
- Sharaf, D.M.; Premlata, A.R.; Tripathi, M.K.; Karri, B.; Sahu, K.C. Shapes and Paths of an Air Bubble Rising in Quiescent Liquids. Phys. Fluids 2017, 29, 122104. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, J. Critical Eotvos Numbers for Buoyancy-Induced Oil Drop Detachment Based on Shape Analysis. Adv. Colloid Interface Sci. 2002, 98, 265–283. [Google Scholar] [CrossRef] [PubMed]
- Lecacheux, L.; Sadoudi, A.; Duri, A.; Planchot, V.; Ruiz, T. The Role of Laplace Pressure in the Maximal Weight of Pendant Drops. J. Colloid Interface Sci. 2022, 606, 920–928. [Google Scholar] [CrossRef] [PubMed]
- Arashiro, E.Y.; Demarquette, N.R. Use of the Pendant Drop Method to Measure Interfacial Tension between Molten Polymers. Mater. Res. 1999, 2, 23–32. [Google Scholar] [CrossRef]
- Vafaei, S.; Wen, D. Modification of the Young–Laplace Equation and Prediction of Bubble Interface in the Presence of Nanoparticles. Adv. Colloid Interface Sci. 2015, 225, 1–15. [Google Scholar] [CrossRef]
- Mhatre, S.; Simon, S.; Sjöblom, J. Methodology to Calculate Interfacial Tension Under Electric Field Using Pendent Drop Profile Analysis. Proc. R. Soc. A 2019, 475, 20180852. [Google Scholar] [CrossRef] [Green Version]
- Ghassemi, H.; Panahi, S.; Kohnsal, A.R. Solving the Laplace’s Equation by FDM and BEM Using Mixed Boundary Conditions. Am. J. Appl. Math. Stat. 2016, 4, 37–42. [Google Scholar]
- Mo, J.; Sha, J.; Li, D.; Li, Z.; Chen, Y. Fluid Release Pressure For Nanochannels: The Young–Laplace Equation Using the Effective Contact Angle. Nanoscale 2019, 11, 8408–8415. [Google Scholar] [CrossRef]
- Parulski, C.; Jennotte, O.; Lechanteur, A.; Evrard, B. Challenges of Fused Deposition Modeling 3D Printing in Pharmaceutical Applications: Where are we Now? Adv. Drug Deliv. Rev. 2021, 175, 113810. [Google Scholar] [CrossRef]








| Parameter | Value | Unit |
|---|---|---|
| Diameter | 1.75 | mm |
| Melt temperature | 190–230 | °C |
| Density | 1.24 | g/cm3 |
| Tensile strength | 60 | N/mm3 |
| Tensile modulus | 3600 | MPa |
| Poisson’s ratio | 0.35 | |
| Specific heat | 2040 | J/kg·K |
| Coefficient of thermal conductivity | 0.231 | W/(m·K) |
| Coefficient of thermal expansion | 1.999 × 10−6 | |
| Thermal diffusivity | 0.205 | mm2/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Koike, R. Numerical Study of the Effect of High Gravity in Material Extrusion System and Polymer Characteristics during Filament Fabrication. Polymers 2023, 15, 3037. https://doi.org/10.3390/polym15143037
Jiang X, Koike R. Numerical Study of the Effect of High Gravity in Material Extrusion System and Polymer Characteristics during Filament Fabrication. Polymers. 2023; 15(14):3037. https://doi.org/10.3390/polym15143037
Chicago/Turabian StyleJiang, Xin, and Ryo Koike. 2023. "Numerical Study of the Effect of High Gravity in Material Extrusion System and Polymer Characteristics during Filament Fabrication" Polymers 15, no. 14: 3037. https://doi.org/10.3390/polym15143037
APA StyleJiang, X., & Koike, R. (2023). Numerical Study of the Effect of High Gravity in Material Extrusion System and Polymer Characteristics during Filament Fabrication. Polymers, 15(14), 3037. https://doi.org/10.3390/polym15143037






