A Leakage Prediction Model for Sealing Performance Assessment of EPDM O-Rings under Irradiation Conditions
Abstract
:1. Introduction
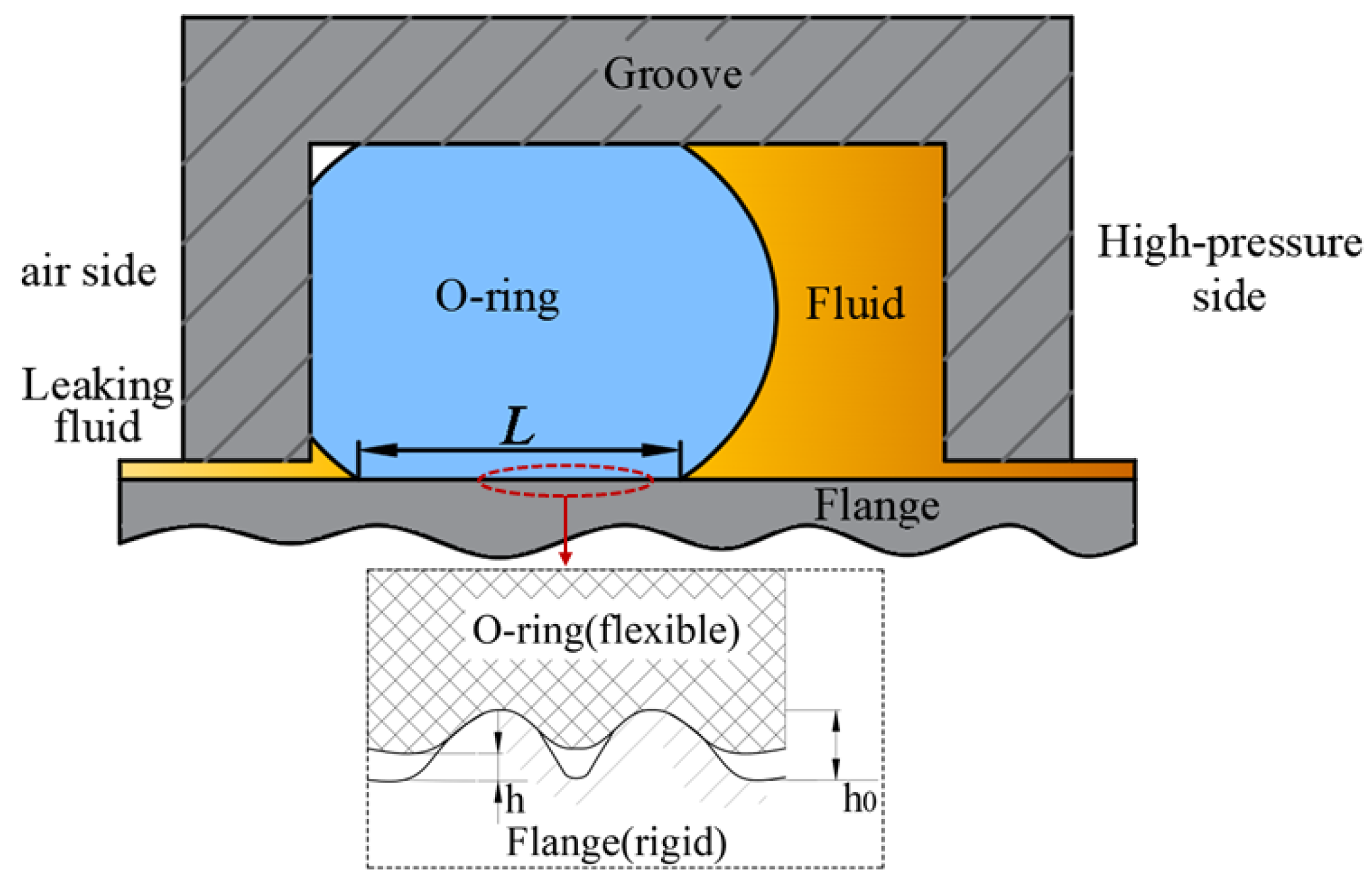
2. Leakage Prediction Model of O-Ring
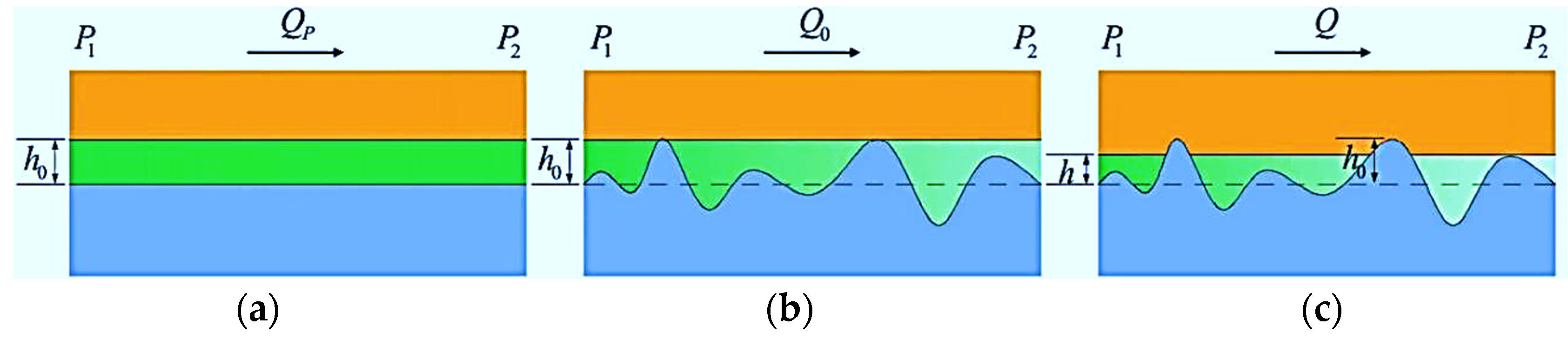
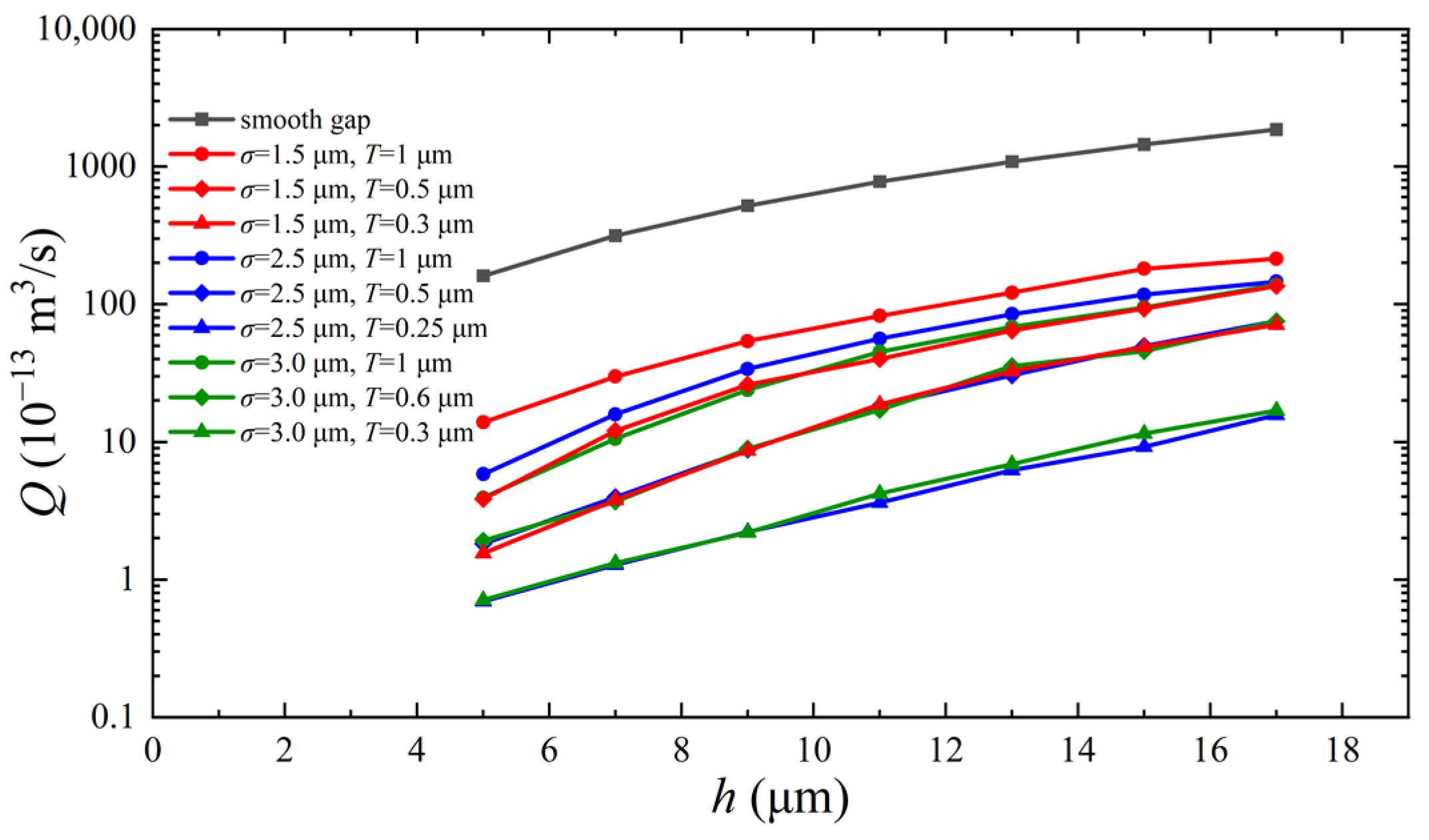
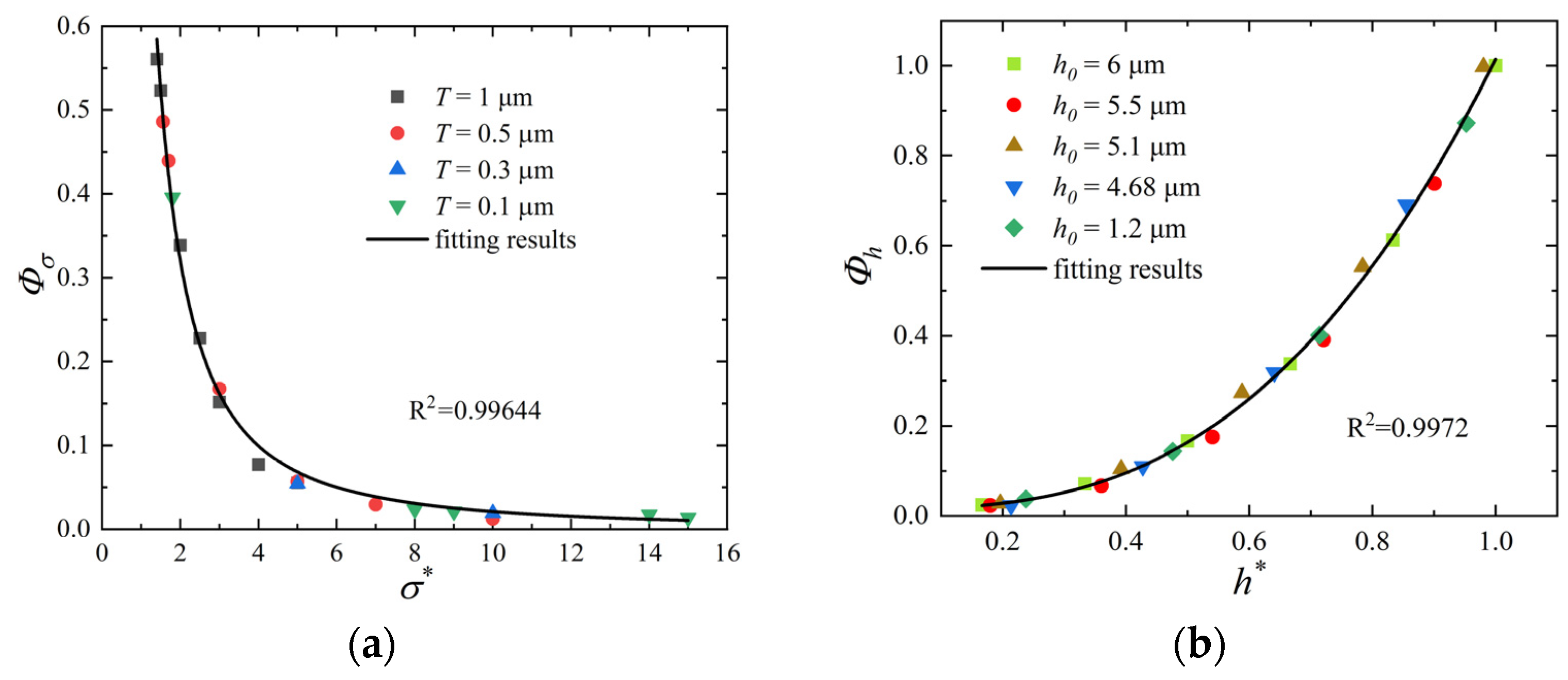
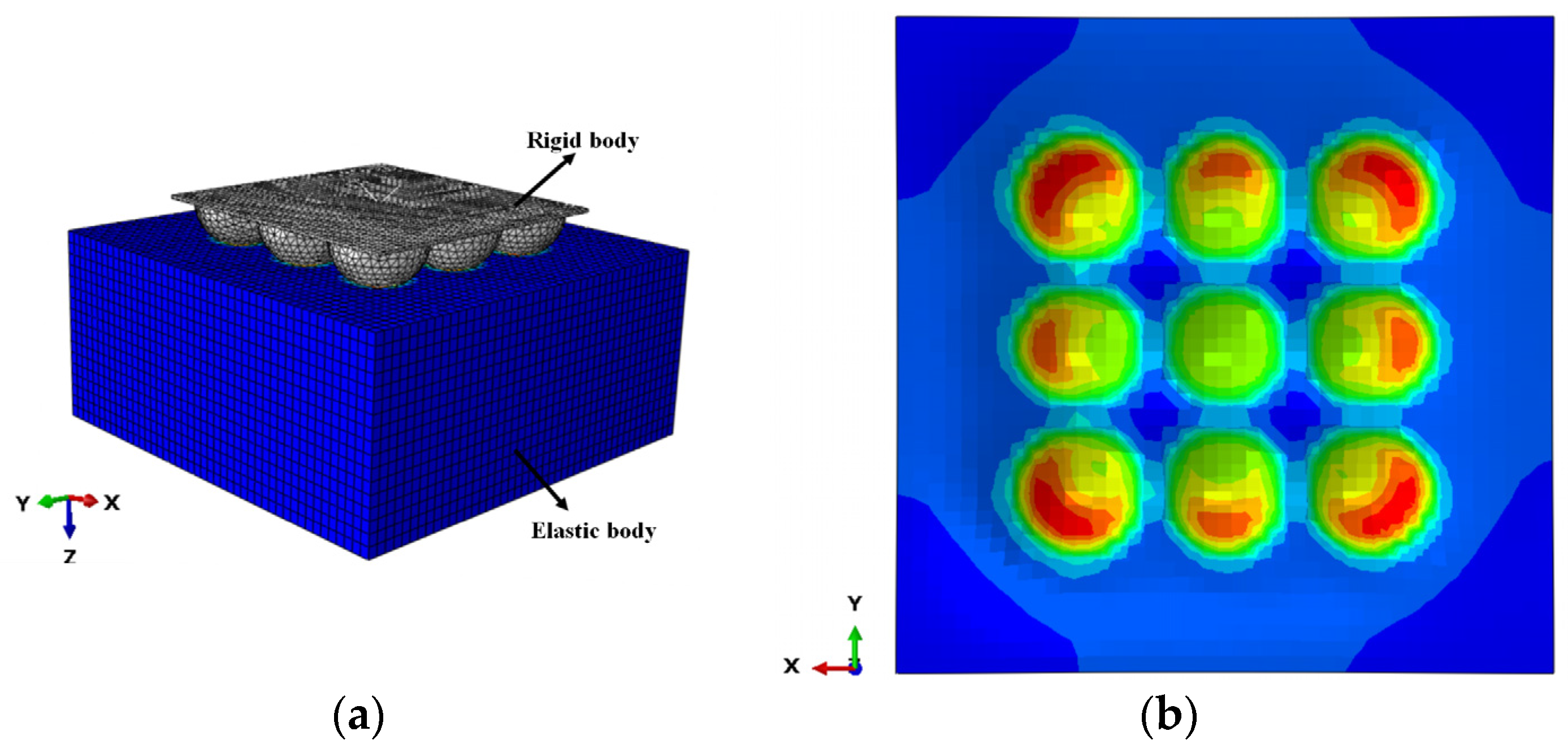
2.1. Mesoscopic Simulation of Interfacial Leakage
2.2. Assessing the Gap Height at the Sealing Interface
3. Numerical Simulation of O-Ring Sealing Performance
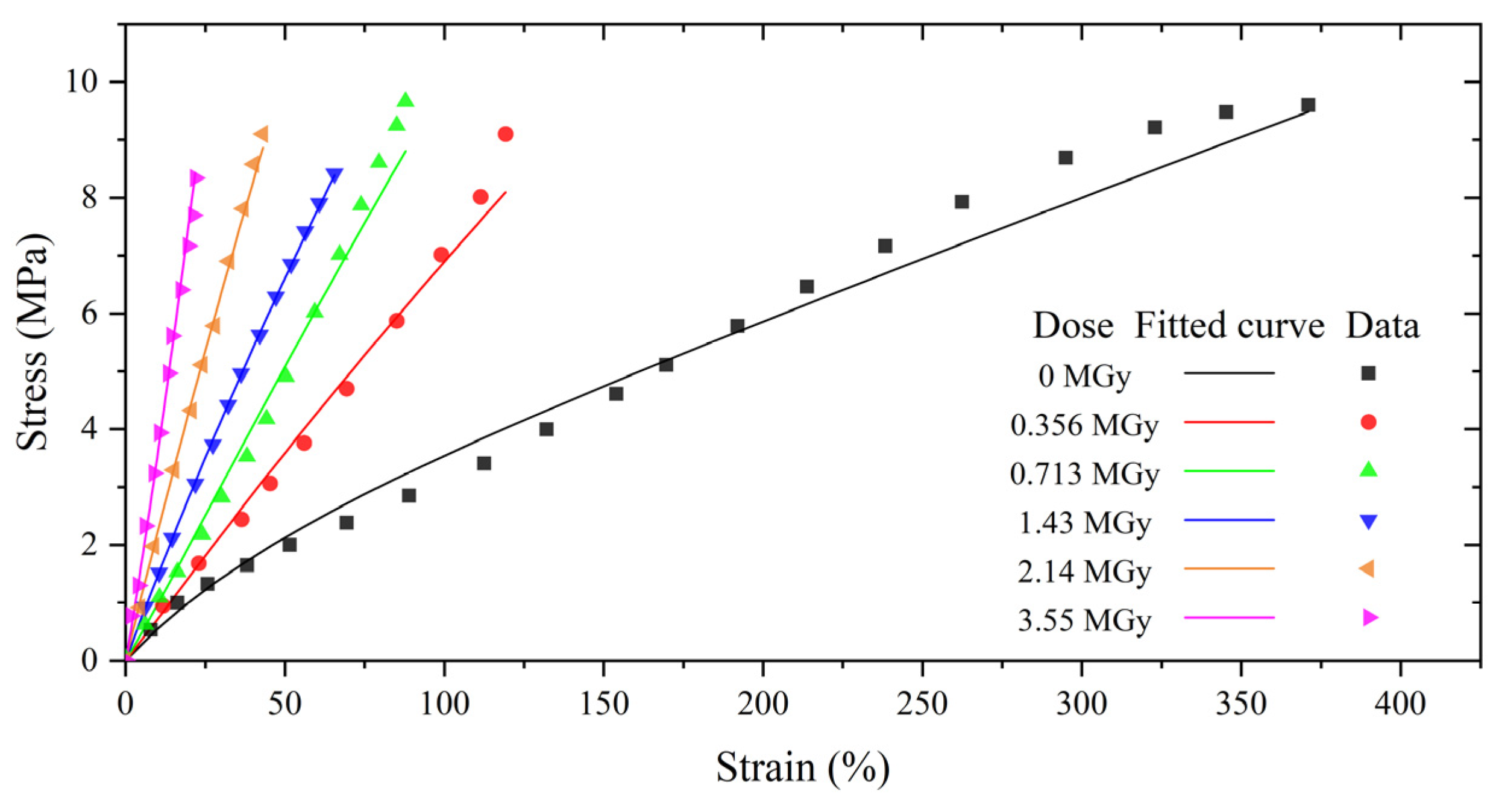
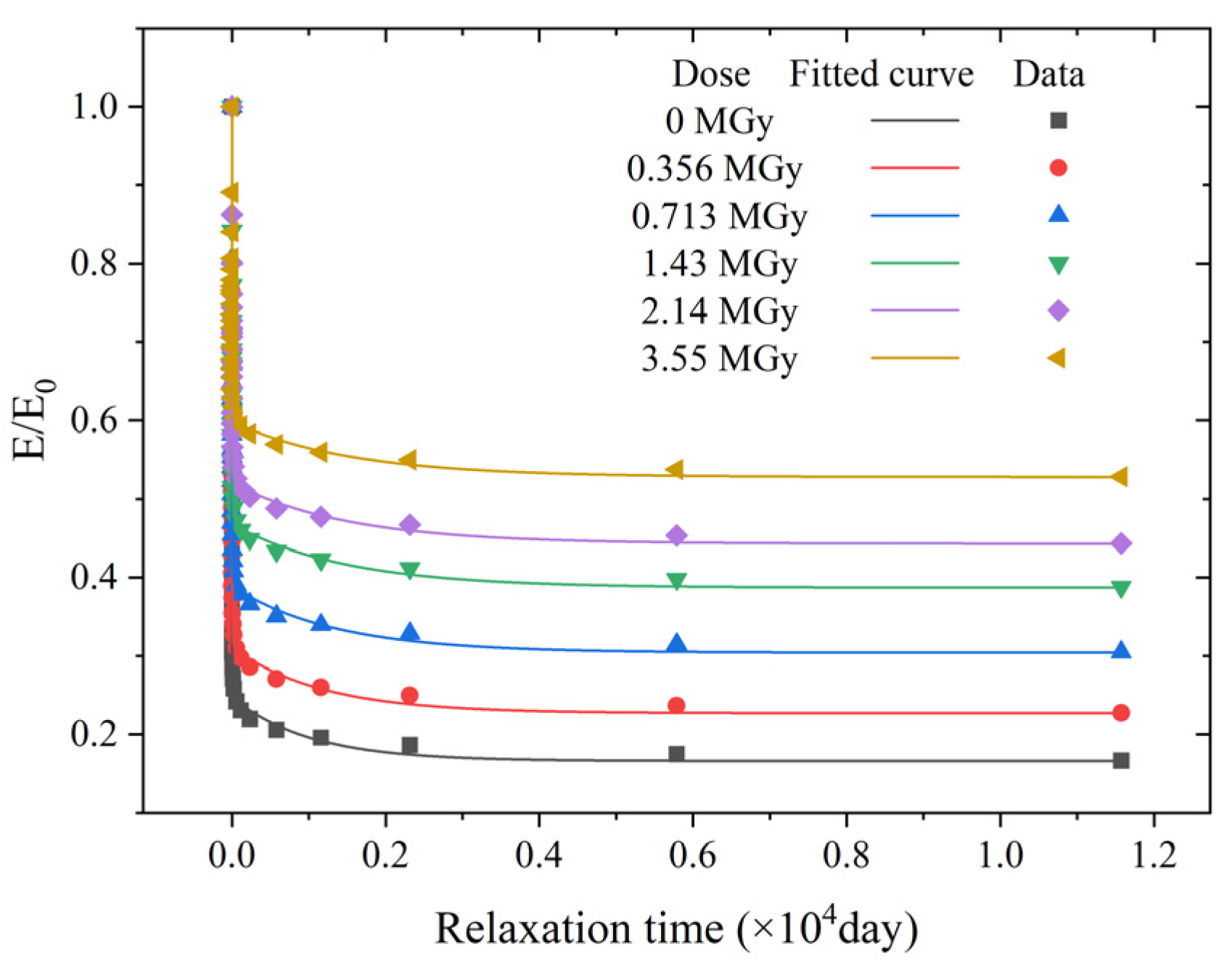
3.1. Irradiation Effects on Material Properties
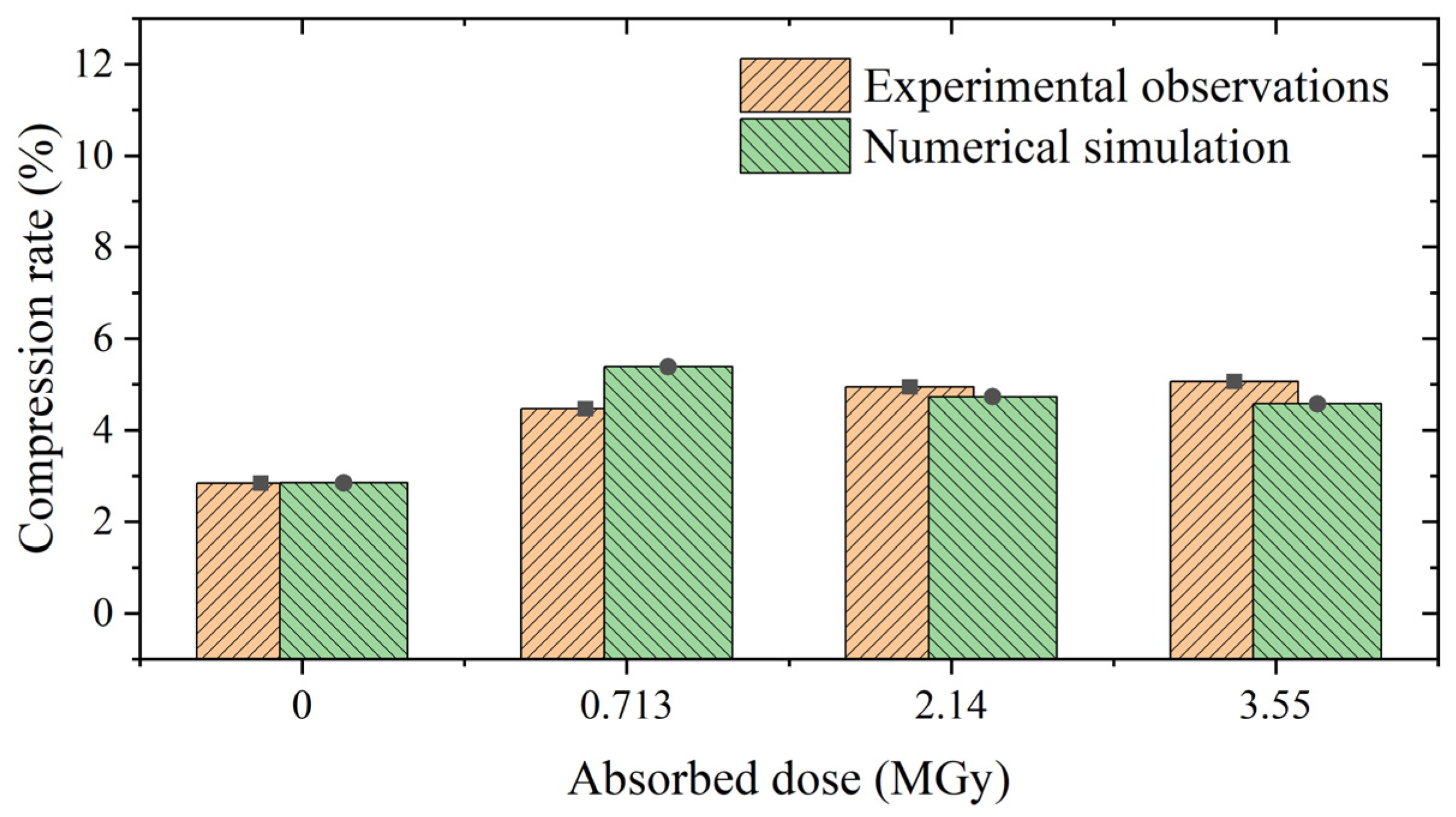
3.2. Simulation and Validation of Vacuum Leak Tests
4. Irradiation Effect on the Sealing Performance of O-Rings at High Pressure
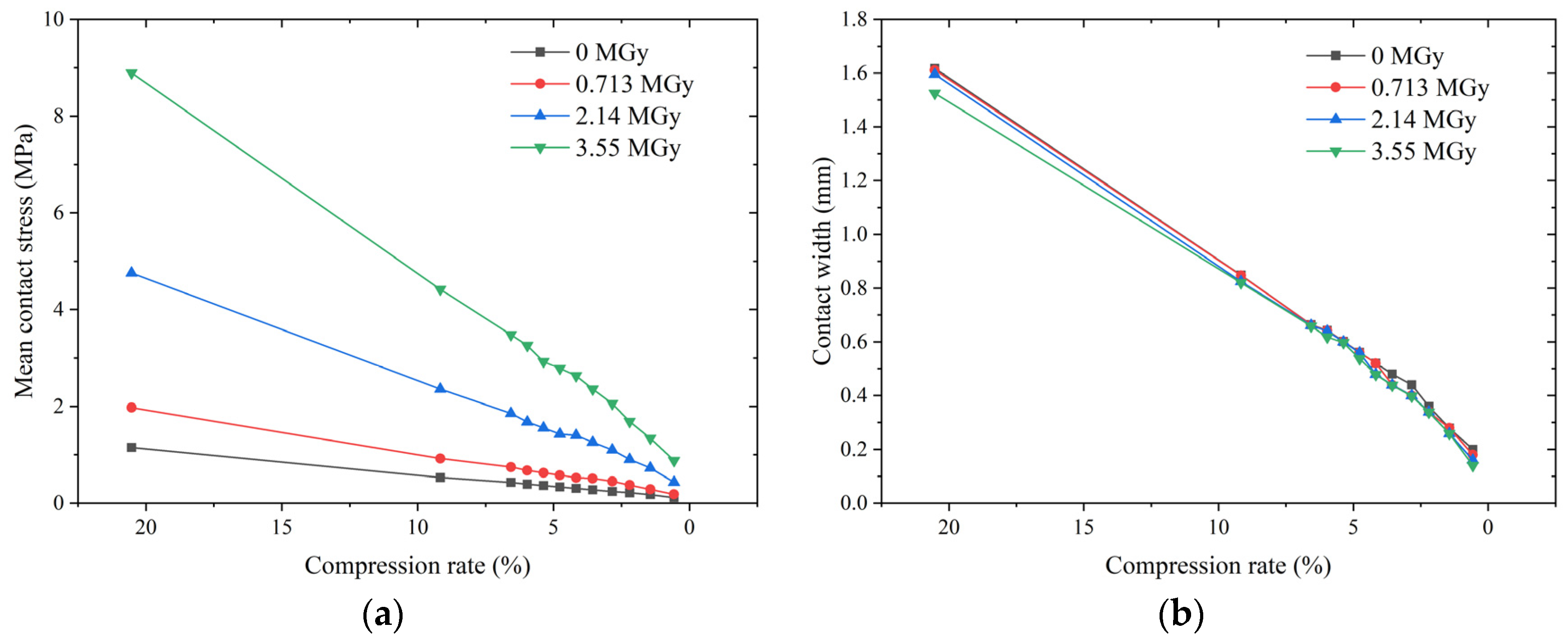
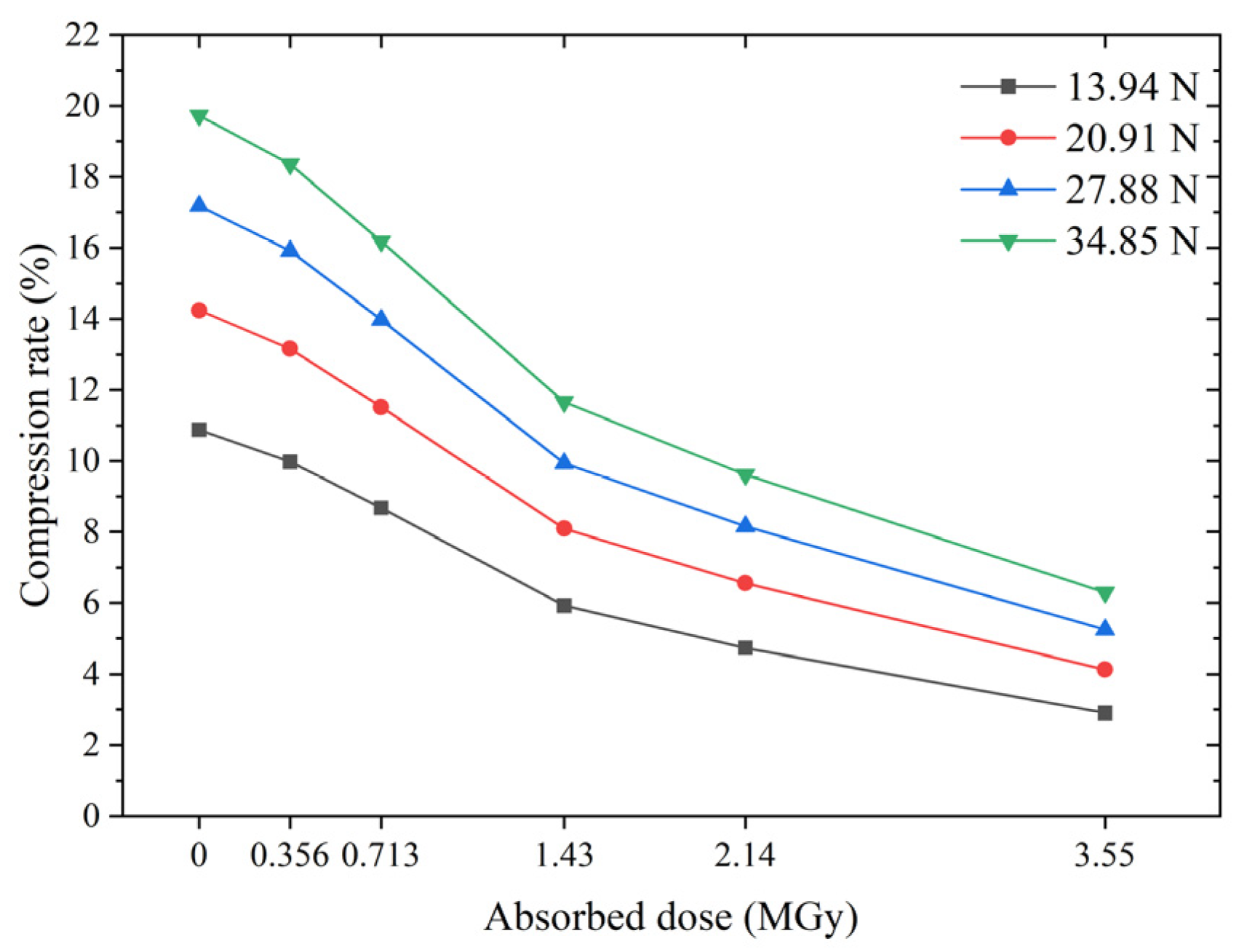
4.1. Analysis of Mechanical Behavior
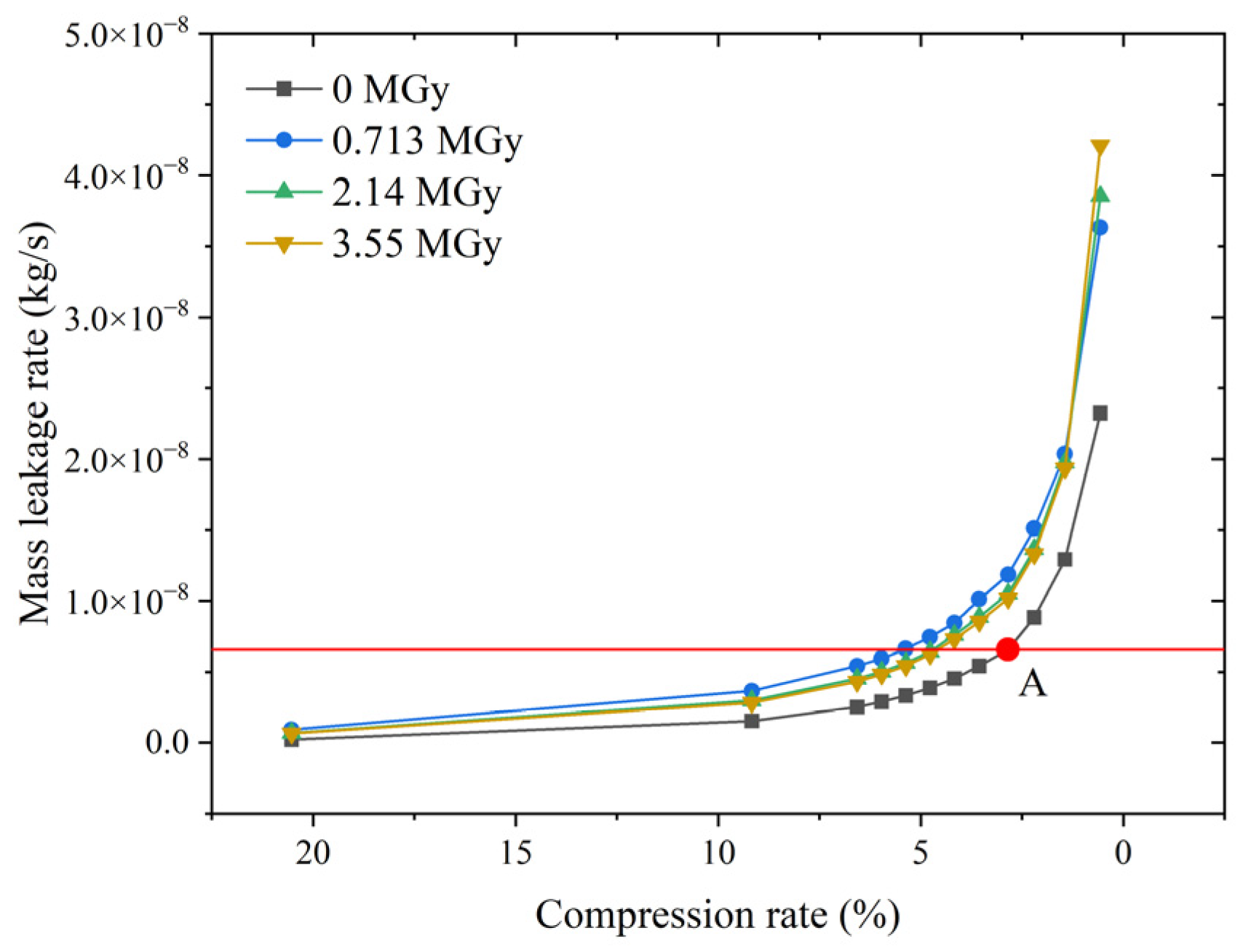
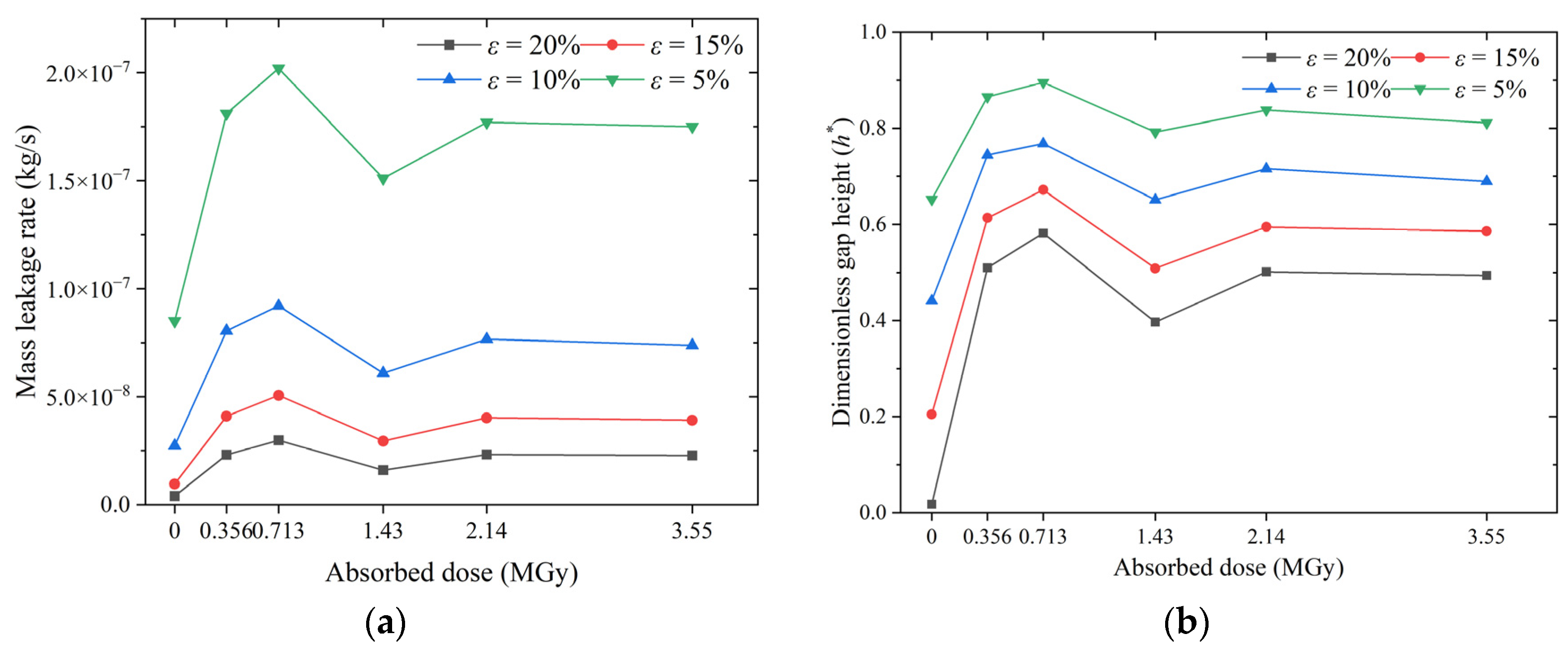
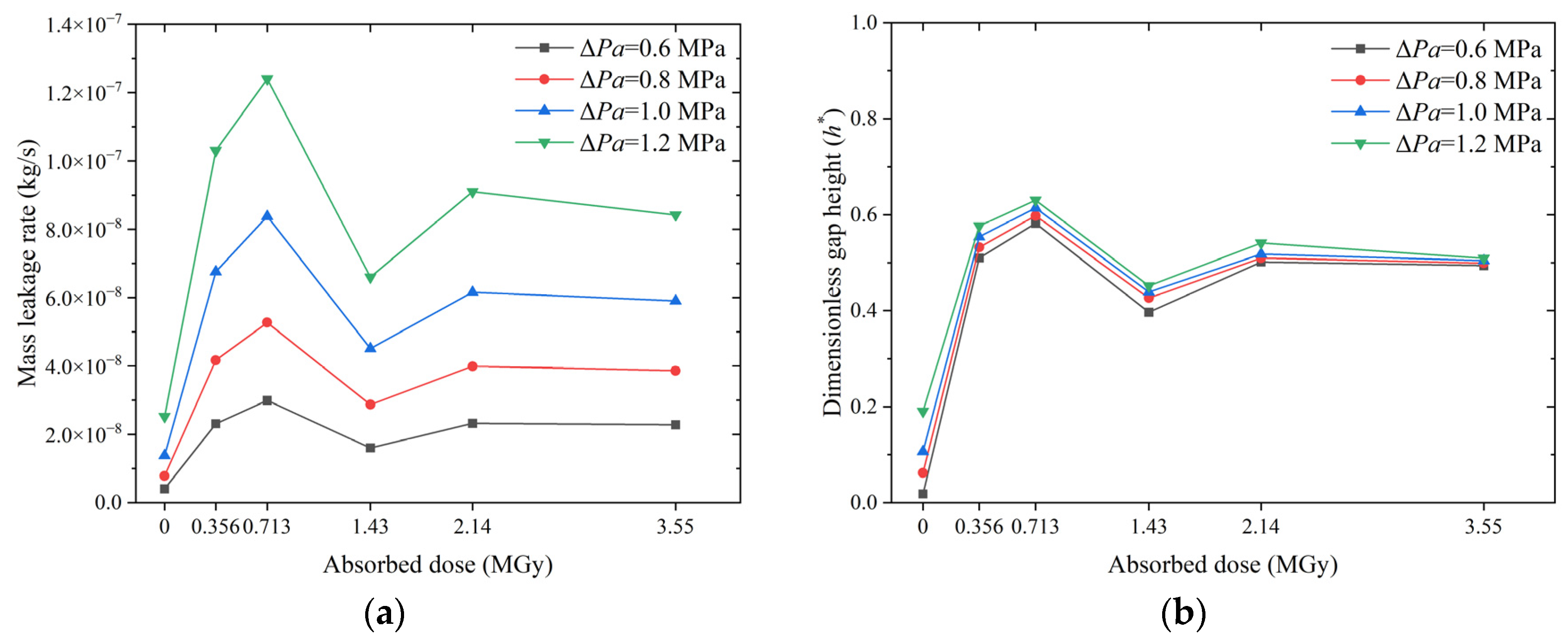
4.2. Analysis of Leakage Behavior
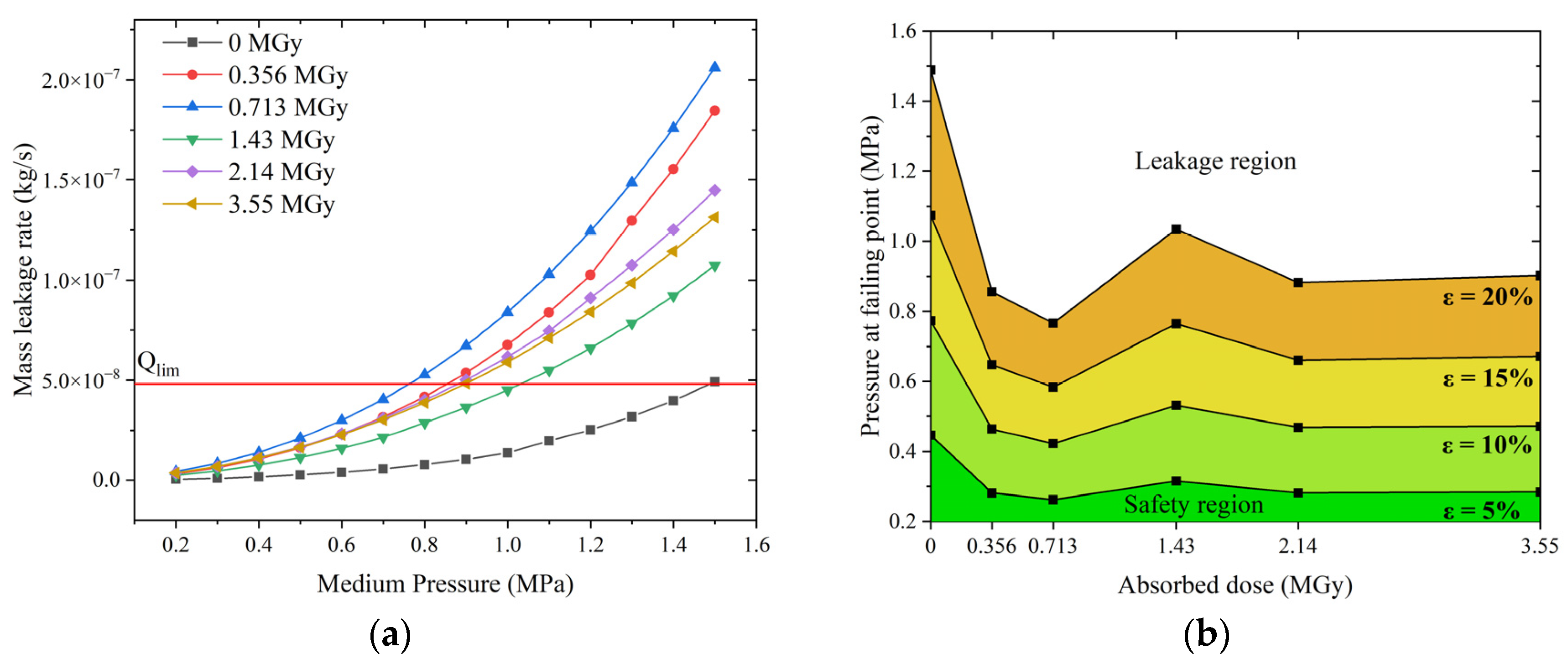
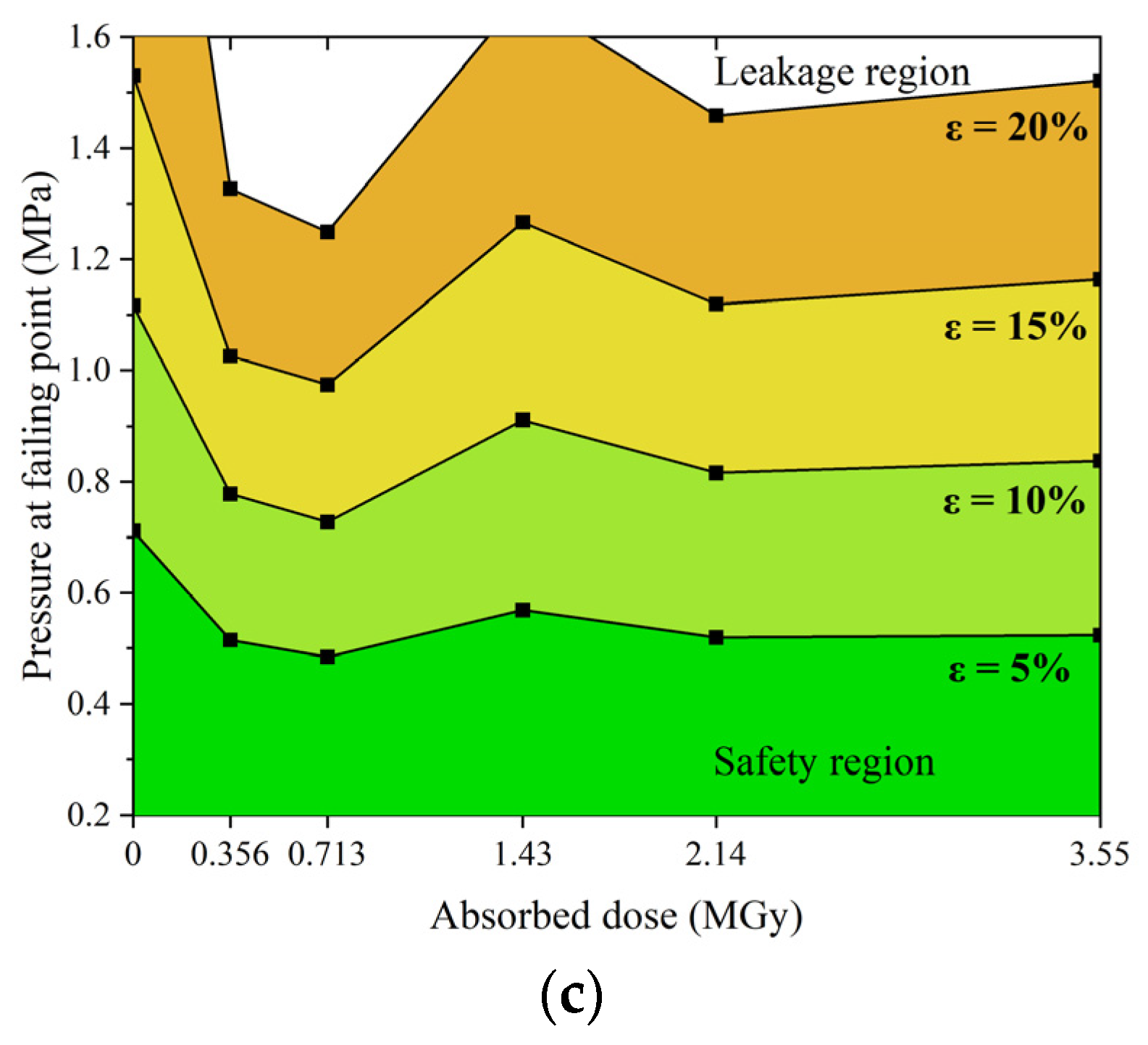
4.3. Assessment of the Sealing Performance
5. Conclusions
- A leakage rate prediction model for O-rings was developed. The model was derived using mesoscopic interfacial gap flow simulations. The gap height was used as a critical parameter to couple the gap flow analysis with the mechanical simulation to predict the leakage rate of the irradiated O-ring under operating conditions. The model was proved to be an accurate predictor of the onset of leakage and was validated by a vacuum test.
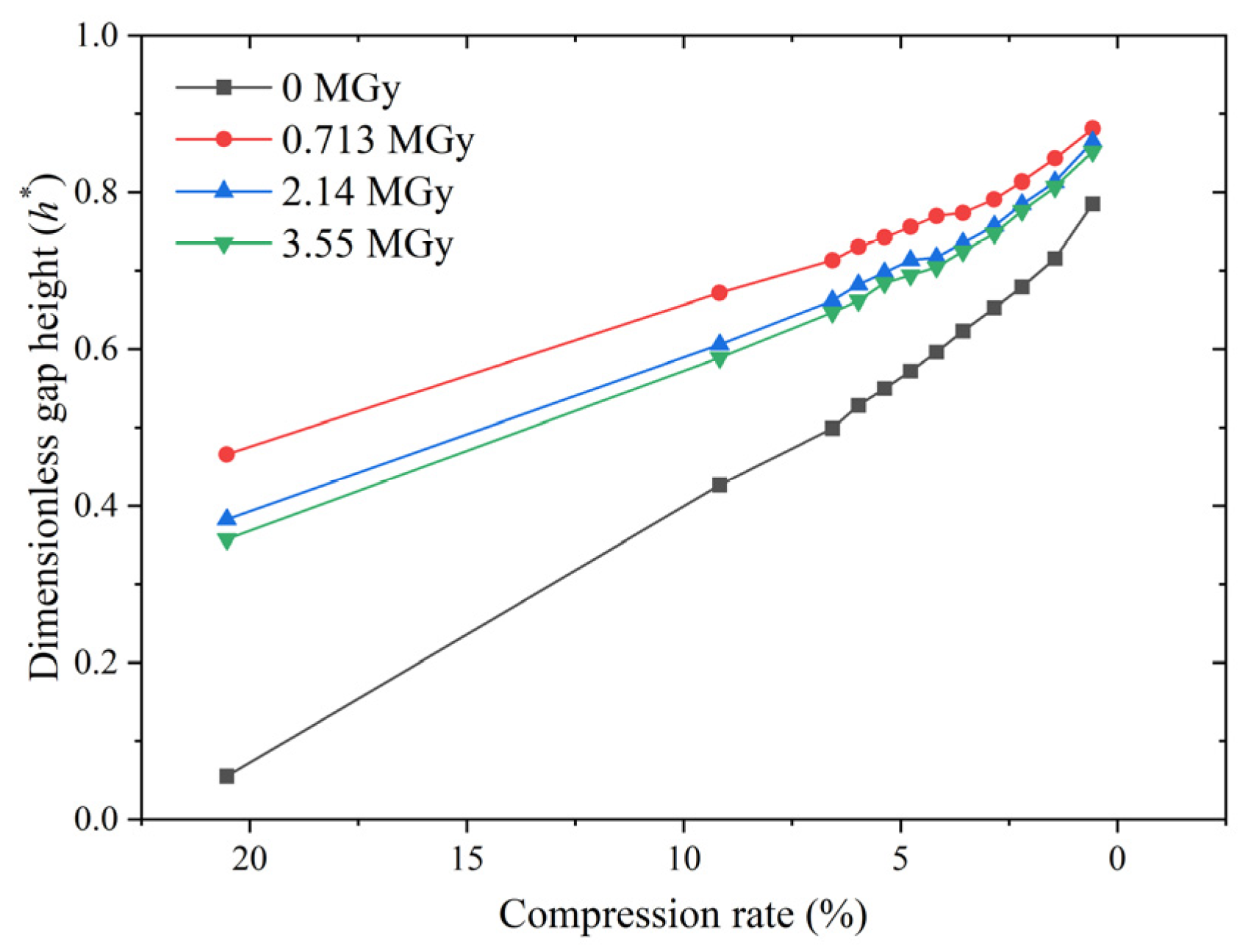
- The proposed model was applied to predict the leakage behavior of O-rings after irradiation. Although the mechanical properties of the material degraded monotonically with an increase in the absorbed dose, the leakage rate increased non-monotonically. The model-based analysis shows that this non-monotonicity can be accurately indicated by the dimensionless gap height, thus revealing that it is the result of the combined effect of contact interface micro-deformation and elastomer macro-deformation.
- When all other factors remained the same, the sealing performance of the O-rings was always the worst at a dose of 0.713 MGy and optimum/best at a dose of 1.43 MGy at all irradiation doses. The high compression rate maintained the seal, even at an irradiation dose of 3.55 MGy, but the O-ring may become brittle. In contrast, the non-irradiated O-ring exhibited a much better sealing performance than the irradiated O-ring.
- A method was developed to classify the sealing performance by using the maximum allowable leakage rate as an indicator. It can be used to determine the appropriate compression rate of an O-ring based on the design requirements of the site (pressure and exposed dose). It can also be used to assess the safety of a seal based on the pressure level under accident conditions.
- The models and methods presented in this paper can be used not only to assess the safety limits of irradiated materials but also their service life. The only difference is that Table 1 needs to be supplemented with data reflecting the effects of ageing. Both the life analysis and safety assessment are topics of great interest for elastomers used in nuclear power plants, and further work can be carried out on the basis of this work.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Holzman, P.M.; Sliter, G.E. Nuclear Power Plant Equipment Qualification Reference Manual; Electric Power Research Institute: Palo Alto, CA, USA, 1992. [Google Scholar] [CrossRef]
- Hirao, K.; Zama, T.; Goto, M.; Naruse, Y.; Saito, K.; Suzuki, T.; Sugino, H. High-Temperature Leak-Characteristics of PCV Hatch Flange Gasket. Nucl. Eng. Des. 1993, 145, 375–386. [Google Scholar] [CrossRef]
- King, D.B. Beta and Gamma Dose Calculations for PWR and BWR Containments; Nuclear Regulatory Commission: Washington, DC, USA, 1989. [CrossRef] [Green Version]
- Plaček, V. Assessment of Parameters for Simulation of Thermal Ageing of Materials in Nuclear Power Plants Using DSC. J. Therm. Anal. Calorim. 2005, 80, 525–528. [Google Scholar] [CrossRef]
- Rodríguez-Prieto, A.; Primera, E.; Frigione, M.; Camacho, A.M. Reliability Prediction of Acrylonitrile O-Ring for Nuclear Power Applications Based on Shore Hardness Measurements. Polymers 2021, 13, 943. [Google Scholar] [CrossRef] [PubMed]
- Porter, C.P.; Edge, R.; Ogden, M.D. Polymeric Seal Degradation in Nuclear Power Plants: Effect of Gamma Radiation on Sealing Properties. J. Appl. Polym. Sci. 2017, 134. [Google Scholar] [CrossRef]
- Maiti, A.; Gee, R.H.; Weisgraber, T.; Chinn, S.; Maxwell, R.S. Constitutive Modeling of Radiation Effects on the Permanent Set in a Silicone Elastomer. Polym. Degrad. Stab. 2008, 93, 2226–2229. [Google Scholar] [CrossRef] [Green Version]
- Jia, D.; Yan, S.; Peng, Y.; Wei, L.; Wang, L.; Gao, Y.; Hao, Z.; Qiu, Y.; Wan, Q. Constitutive Modeling of γ-Irradiated Silicone Rubber Foams under Compression and Shear Loading. Polym. Degrad. Stab. 2021, 183, 109410. [Google Scholar] [CrossRef]
- Le Lay, F. Study on the Lifetime of EPDM Seals in Nuclear-Powered Vessels. Radiat. Phys. Chem. 2013, 84, 210–217. [Google Scholar] [CrossRef]
- Plaček, V.; Kohout, T.; Hnát, V.; Bartoníček, B. Assessment of the EPDM Seal Lifetime in Nuclear Power Plants. Polym. Test. 2009, 28, 209–214. [Google Scholar] [CrossRef]
- Seo, Y.-D.; Lee, H.-S.; Kim, Y.-S.; Song, C.-S. A Study on the Aging Degradation of Ethylene-Propylene-Diene Monomer (EPDM) under LOCA Condition. Nucl. Eng. Technol. 2011, 43, 279–286. [Google Scholar] [CrossRef] [Green Version]
- Nakano, M.; Sasaki, H.; Ono, H. Radiation Resistance of Rubber Compound for Gasket. In Proceedings of the Small Modular Reactors Symposium, Washington, DC, USA, 28–30 September 2011; Volume 54730, pp. 153–160. [Google Scholar] [CrossRef]
- Nakano, M.; Sasaki, H.; Hanashima, K. The Prediction of Long-Term and Emergency Sealability of Silicone and EPDM Gaskets. In Proceedings of the International Conference on Nuclear Engineering, Xi’an, China, 17–21 May 2010; Volume 49330, pp. 309–316. [Google Scholar] [CrossRef]
- Battini, D.; Donzella, G.; Avanzini, A.; Zenoni, A.; Ferrari, M.; Donzella, A.; Pandini, S.; Bignotti, F.; Andrighetto, A.; Monetti, A. Experimental Testing and Numerical Simulations for Life Prediction of Gate Valve O-Rings Exposed to Mixed Neutron and Gamma Fields. Mater. Des. 2018, 156, 514–527. [Google Scholar] [CrossRef]
- Ferrari, M.; Pandini, S.; Zenoni, A.; Donzella, G.; Battini, D.; Avanzini, A.; Salvini, A.; Zelaschi, F.; Andrighetto, A.; Bignotti, F. Degradation of EPDM and FPM Elastomers Irradiated at Very High Dose Rates in Mixed Gamma and Neutron Fields. Polym. Eng. Sci. 2019, 59, 2522–2532. [Google Scholar] [CrossRef]
- Gillen, K.T.; Bernstein, R.; Wilson, M.H. Predicting and Confirming the Lifetime of O-Rings. Polym. Degrad. Stab. 2005, 87, 257–270. [Google Scholar] [CrossRef]
- Chayoukhi, S.; Abid, M.; Gassoumi, B.; Mejri, A.; Boukhachem, A.; Amlouk, M. Experimental and Numerical Studies of the Mechanical Properties of Nitrile-Butadiene Rubber Exposed to Gamma Radiation. Radiat. Phys. Chem. 2023, 208, 110925. [Google Scholar] [CrossRef]
- Bradley, G.L.; Chang, P.C.; Mckenna, G.B. Rubber Modeling Using Uniaxial Test Data. J. Appl. Polym. Sci. 2001, 81, 837–848. [Google Scholar] [CrossRef]
- Gudsoorkar, U.; Bindu, R. Computer Simulation of Hyper Elastic Re-Treaded Tire Rubber with ABAQUS. Mater. Today Proc. 2021, 43, 1992–2001. [Google Scholar] [CrossRef]
- Zaghdoudi, M.; Weber, M.; Kömmling, A.; Jaunich, M.; Wolff, D. Simulation of Compression Set of EPDM O-Rings During Aging. In Proceedings of the Pressure Vessels and Piping Conference, Las Vegas, NV, USA, 17–22 July 2022; American Society of Mechanical Engineers: New York, NY, USA, 2022; Volume 86199, p. V005T07A027. [Google Scholar] [CrossRef]
- Kömmling, A.; Jaunich, M.; Pourmand, P.; Wolff, D.; Hedenqvist, M. Analysis of O-Ring Seal Failure under Static Conditions and Determination of End-of-Lifetime Criterion. Polymers 2019, 11, 1251. [Google Scholar] [CrossRef] [Green Version]
- Kömmling, A.; Jaunich, M.; Goral, M.; Wolff, D. Insights for Lifetime Predictions of O-Ring Seals from Five-Year Long-Term Aging Tests. Polym. Degrad. Stab. 2020, 179, 109278. [Google Scholar] [CrossRef]
- Momon, S.; Garcia, J.; Issard, H. Leak Tightness of O-Rings for Transport of Radioactive Material. Packag. Transp. Storage Secur. Radioact. Mater. 2013, 24, 3–9. [Google Scholar] [CrossRef]
- Kambhammettu, S.K.S.; Chebolu, L.R.; Deshpande, A.P. A Wedge Penetration Model to Estimate Leak through Elastomer–Metal Interface. Int. J. Adv. Eng. Sci. Appl. Math. 2020, 12, 65–72. [Google Scholar] [CrossRef]
- Kambhammettu, S.K.S.; Deshpande, A.P.; Chebolu, L.R. A Compressible Porous Media Model to Estimate Fluid Leak Through a Metal–Elastomer Interface. Transp. Porous Media 2021, 136, 191–215. [Google Scholar] [CrossRef]
- Roth, A. The Influence of the Surface Roughness on the Specific Leak Rate of Gasket Seals. Vacuum 1970, 20, 431–435. [Google Scholar] [CrossRef]
- Zhang, B.; Hong, H.; Yu, M.; Yang, H. Leakage Analysis and Ground Tests of Knife Edge Indium Seal to Lunar Sample Return Devices. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 2010–2022. [Google Scholar] [CrossRef]
- Yang, Z.; Zhu, W.; Dong, R.; Cao, Z. Multi-Scale Dimensionless Prediction Model of PEMFC Sealing Interface Leakage Rate Based on Fractal Geometry. Int. J. Hydrog. Energy 2023, 48, 5276–5287. [Google Scholar] [CrossRef]
- Huang, X.; Yao, B.; Xu, G.; Lü, X. Research on Leakage of Metallic Gasket Based on Fractal Porous Seepage. J. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 2016, 44, 1–5. [Google Scholar] [CrossRef]
- Liang, P.; Qiu, D.; Peng, L.; Yi, P.; Lai, X.; Ni, J. Contact Resistance Prediction of Proton Exchange Membrane Fuel Cell Considering Fabrication Characteristics of Metallic Bipolar Plates. Energy Convers. Manag. 2018, 169, 334–344. [Google Scholar] [CrossRef]
- Huang, X.; Liu, S.; Yu, X.; Liu, Y.; Zhang, Y.; Xu, G. A Mechanism Leakage Model of Metal-Bipolar-Plate PEMFC Seal Structures with Stress Relaxation Effects. Int. J. Hydrog. Energy 2022, 47, 2594–2607. [Google Scholar] [CrossRef]
- Xu, G.; Du, Y.; Zhou, J.; Tian, Y.; Huang, X. Numerical Analysis of Gas Tightness of Seals in PSOFCs Based on Lattice Boltzmann Method Simulation. Int. J. Hydrog. Energy 2019, 44, 21136–21147. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of Nominally Flat Surfaces. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1996, 294, 21. [Google Scholar] [CrossRef]
- Berthe, D.; Vergne, P. An Elastic Approach to Rough Contact with Asperity Interactions. Wear 1987, 117, 211–222. [Google Scholar] [CrossRef]
- Johnson, K.L.; Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987; ISBN 0-521-34796-3. [Google Scholar] [CrossRef]
- ISO 5208:2015; Industrial valves—Pressure testing of metallic valves. ISO: Geneva, Switzerland, 2015.






| Absorbed Dose (MGy) | Young’s Modulus (MPa) | Strain at Break (%) | Tensile Strength (MPa) | Compression Set (%) |
|---|---|---|---|---|
| 3.55 | 37.07 | 23 ± 3 | 8.3 ± 1 | / |
| 2.14 | 21.11 | 43 ± 6 | 9.1 ± 0.7 | 5.4 ± 0.3 |
| 1.43 | 12.68 | 65 ± 6 | 8.4 ± 0.6 | 4.8 ± 0.3 |
| 0.713 | 10.98 | 88 ± 7 | 9.7 ± 1 | 5.2 ± 0.3 |
| 0.356 | 7.30 | 120 ± 7 | 9.1 ± 0.6 | 3.9 ± 0.3 |
| 0 | 2.63 | 370 ± 40 | 9.6 ± 0.9 | 9.0 ± 0.3 |
| Parameters | Values |
|---|---|
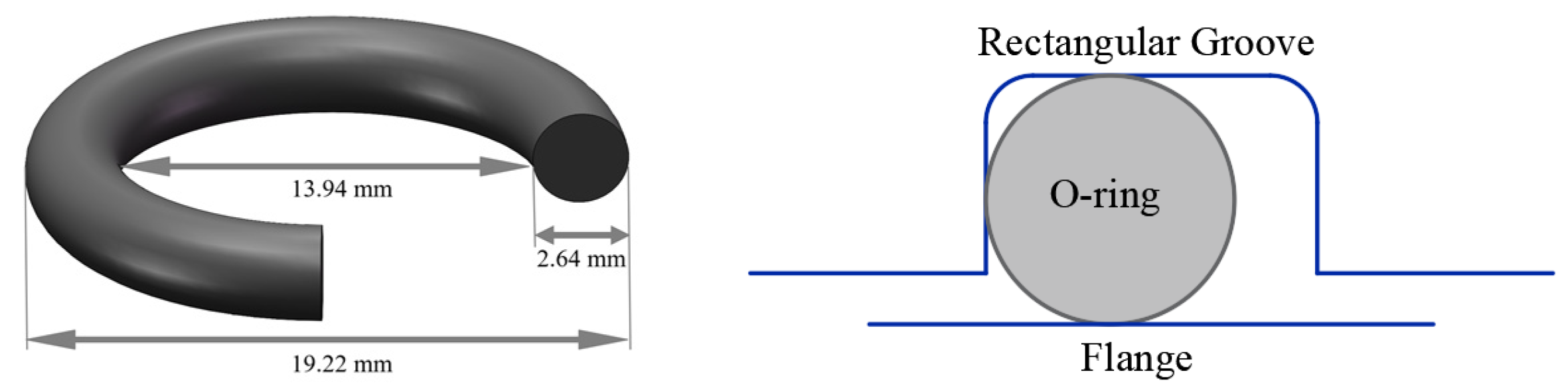
| Cross-sectional diameter (mm) | 2.64 |
| Internal diameter (mm) | 13.94 |
| Irradiation dose (MGy) | 0, 0.356, 0.713, 1.43, 2.14, 3.55 |
| Surface roughness (μm) | 0.8 |
| Compression ratio (%) | 20 |
| Pressure difference (MPa) | 0.6 |
| Absorbed Doses (MGy) | 0 | 0.356 | 0.713 | 1.43 | 2.14 | 3.55 | |
|---|---|---|---|---|---|---|---|
| Compression Rate | |||||||
| ε = 5% | 0.45 | 0.28 | 0.26 | 0.32 | 0.28 | 0.28 | |
| ε = 10% | 0.77 | 0.46 | 0.42 | 0.53 | 0.47 | 0.47 | |
| ε = 15% | 1.07 | 0.64 | 0.58 | 0.76 | 0.66 | 0.67 | |
| ε = 20% | 1.49 | 0.86 | 0.77 | 1.03 | 0.88 | 0.90 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Gu, J.; Li, M.; Yu, X.; Liu, Y.; Xu, G. A Leakage Prediction Model for Sealing Performance Assessment of EPDM O-Rings under Irradiation Conditions. Polymers 2023, 15, 3073. https://doi.org/10.3390/polym15143073
Huang X, Gu J, Li M, Yu X, Liu Y, Xu G. A Leakage Prediction Model for Sealing Performance Assessment of EPDM O-Rings under Irradiation Conditions. Polymers. 2023; 15(14):3073. https://doi.org/10.3390/polym15143073
Chicago/Turabian StyleHuang, Xiaoming, Jimin Gu, Ming Li, Xinli Yu, Yu Liu, and Guoliang Xu. 2023. "A Leakage Prediction Model for Sealing Performance Assessment of EPDM O-Rings under Irradiation Conditions" Polymers 15, no. 14: 3073. https://doi.org/10.3390/polym15143073
APA StyleHuang, X., Gu, J., Li, M., Yu, X., Liu, Y., & Xu, G. (2023). A Leakage Prediction Model for Sealing Performance Assessment of EPDM O-Rings under Irradiation Conditions. Polymers, 15(14), 3073. https://doi.org/10.3390/polym15143073





