Probing the Free Volume in Polymers by Means of Positron Annihilation Lifetime Spectroscopy
Abstract
:1. Introduction
2. Positronium in Polymers
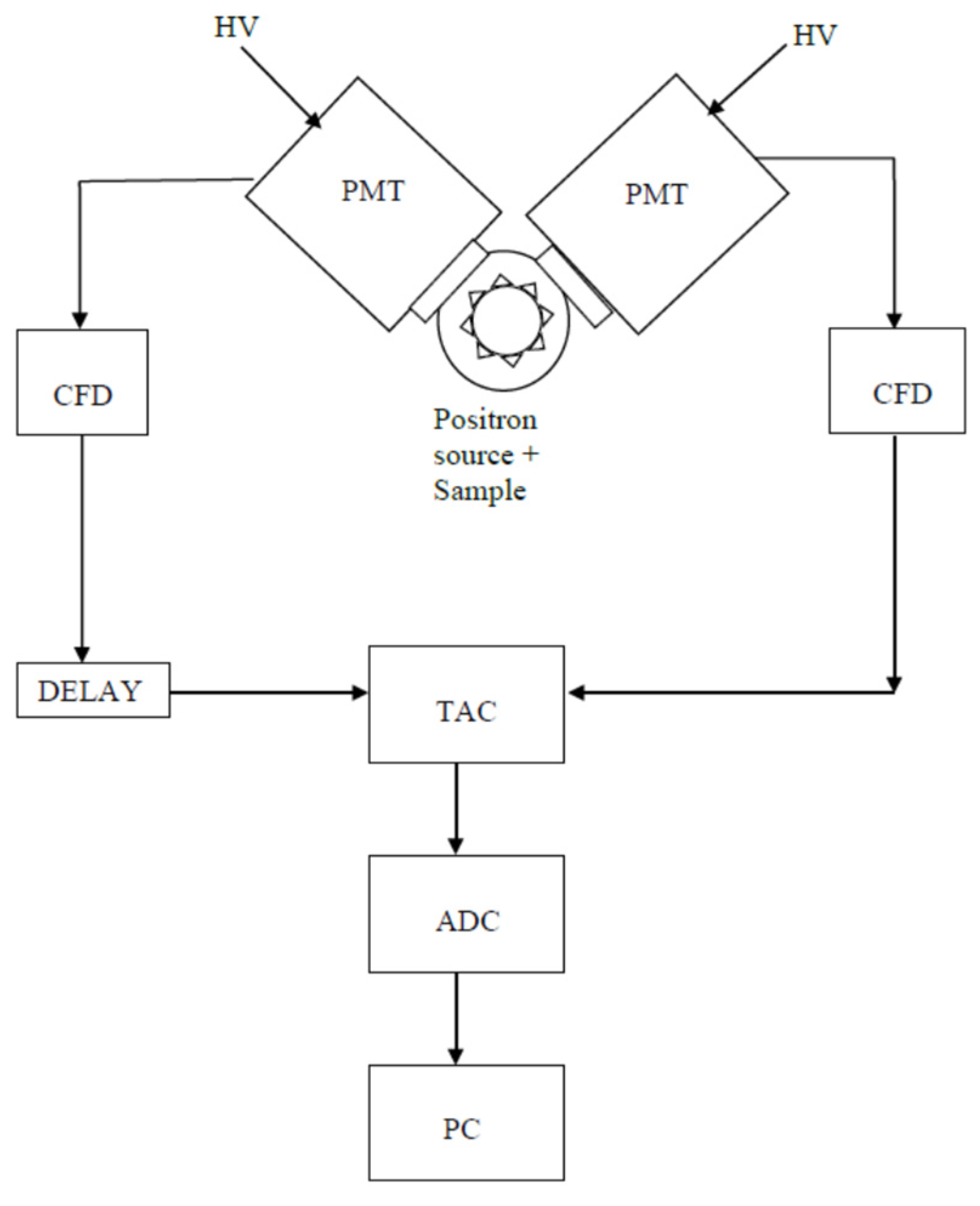
3. Experimental Setup
4. Discussion of Some PALS Results in Polymeric Systems
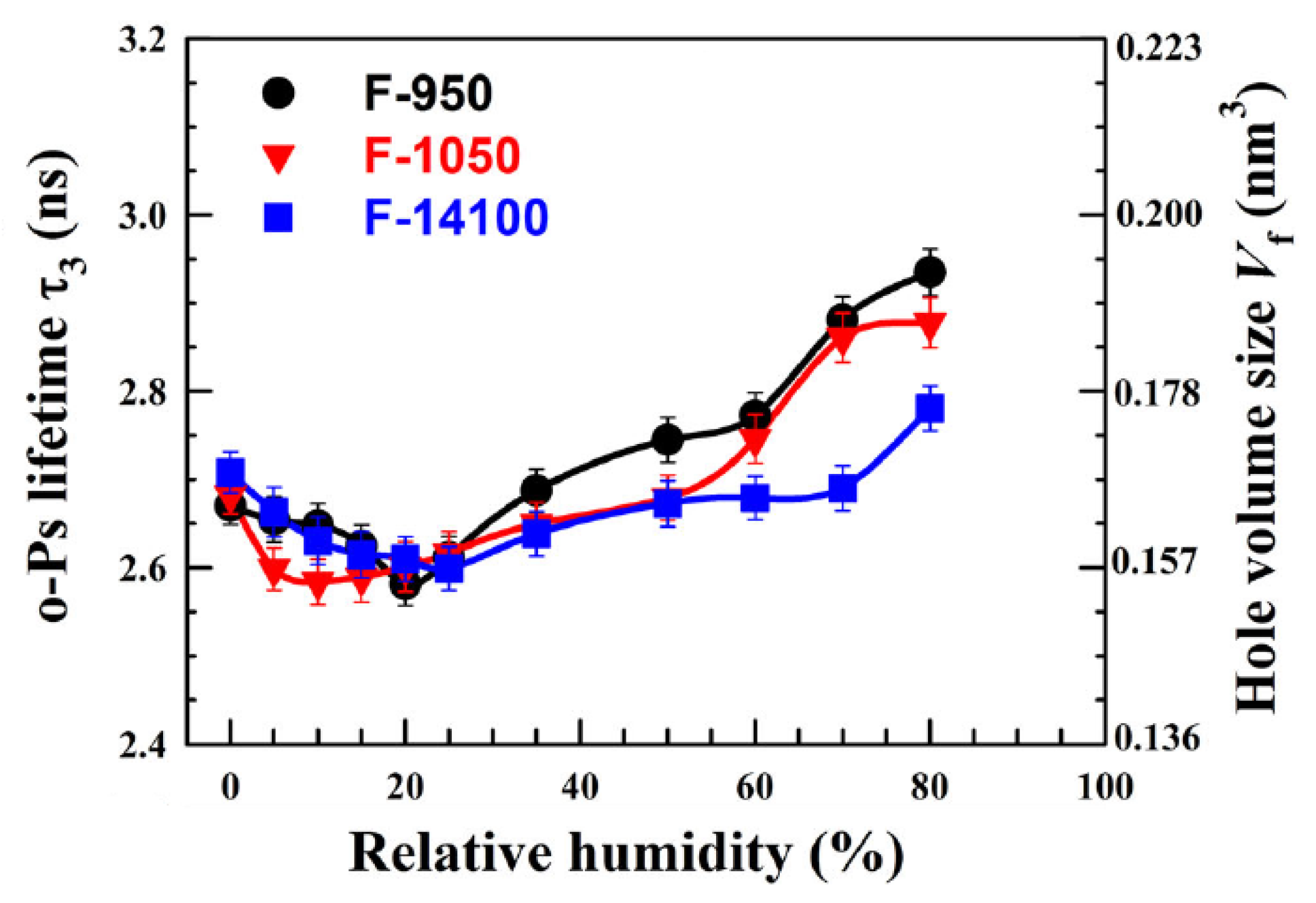
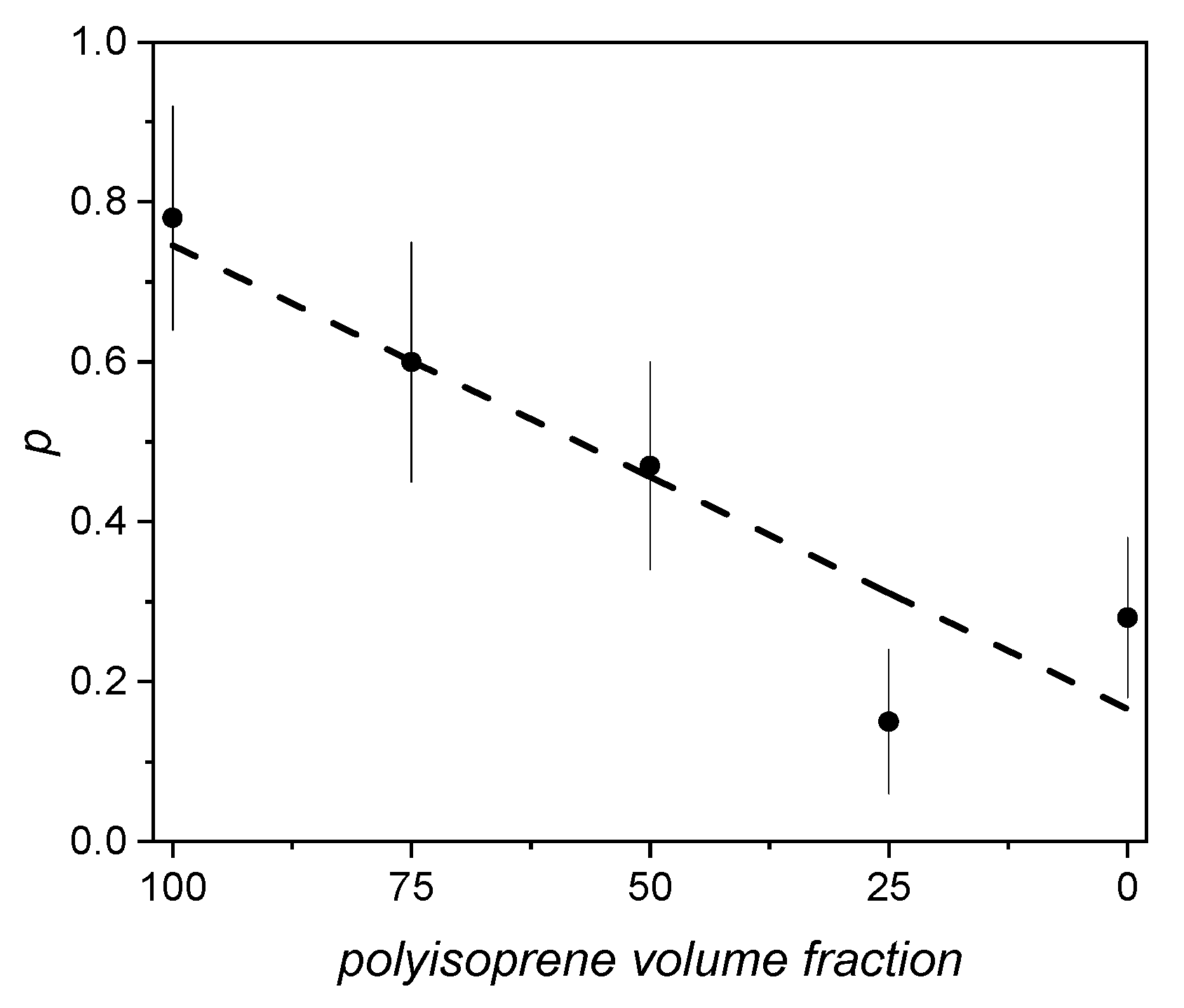
4.1. Membranes
4.2. Composites
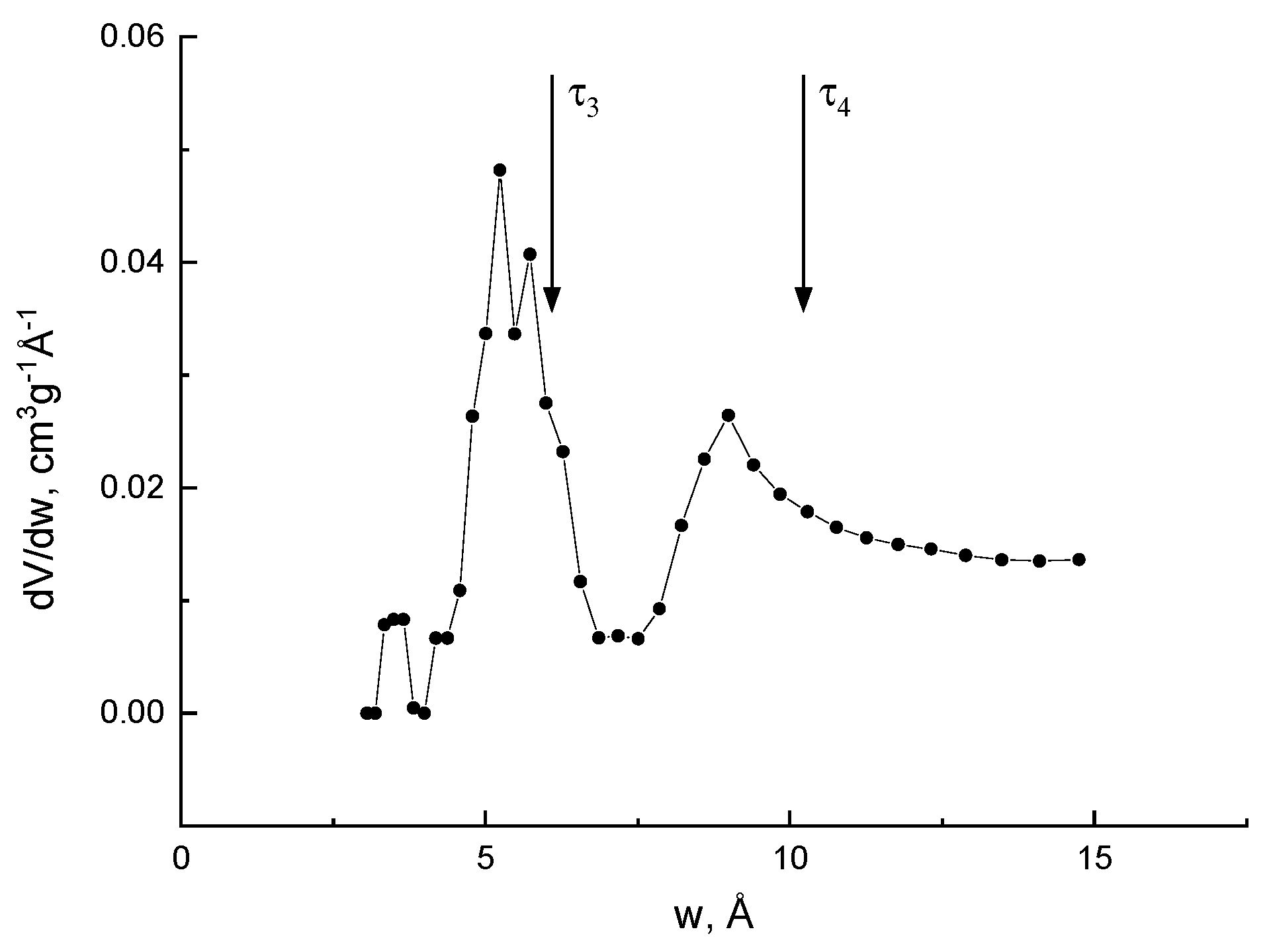
4.3. Porous Polymers
4.4. Bioplastics and Natural Polymers
4.5. Irradiated Polymers
4.6. Photopolymerization
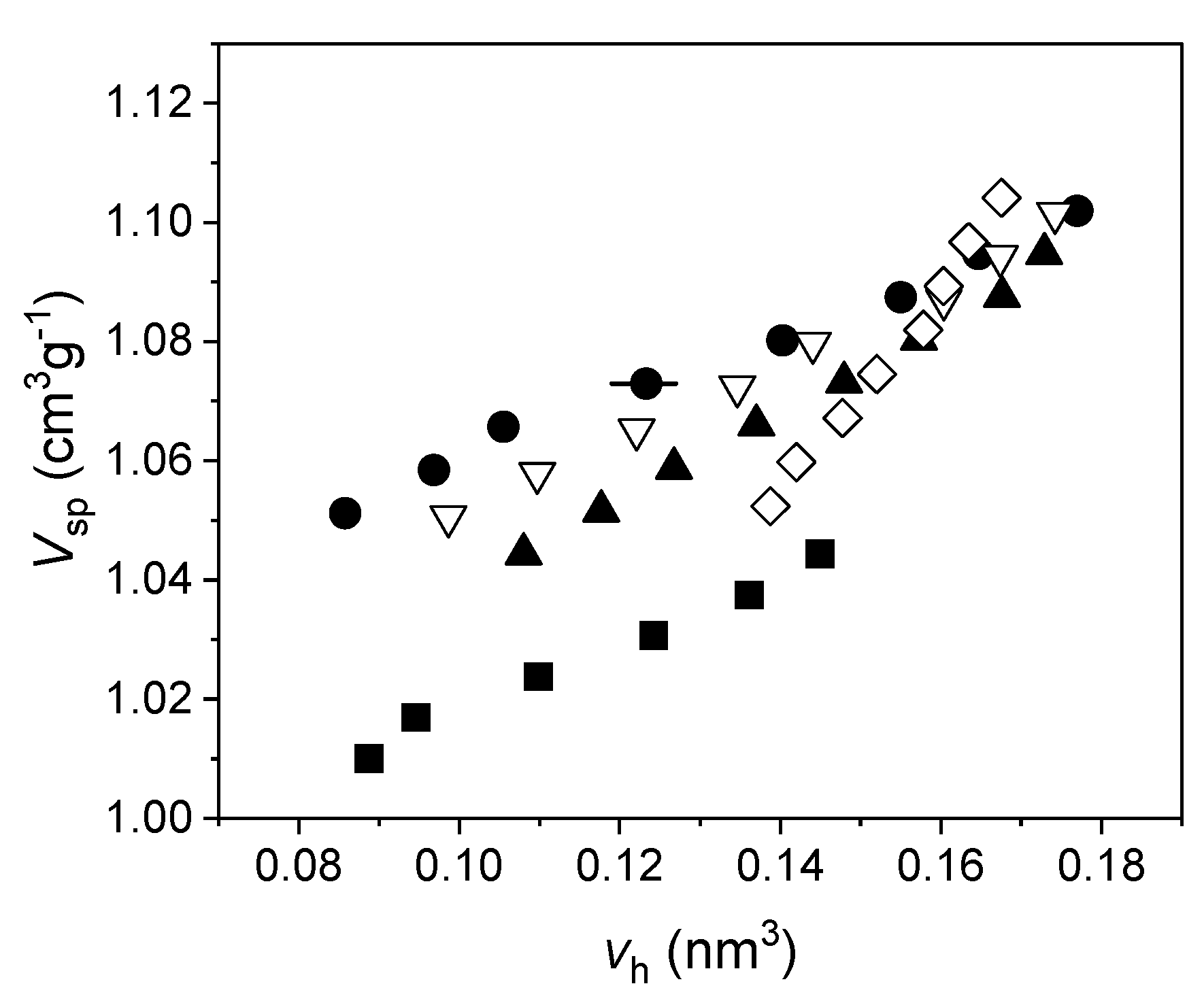
4.7. Coupling PALS and Dilatometry: An Alternative Route to the Free Volume Fraction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- White, R.P.; Lipson, J.L.G. Polymer Free Volume and Its Connection to Glass Transition. Macromolecules 2016, 49, 3987–4007. [Google Scholar] [CrossRef]
- Zhang, H.J.; Sellaiyan, S.; Kakizaki, T.; Uedono, A.; Taniguchi, Y.; Hayashi, K. Effect of Free-Volume Holes on Dynamic Mechanical Properties of Epoxy Resins for Carbon-Fiber-Reinforced Polymers. Macromolecules 2017, 50, 3933–3942. [Google Scholar] [CrossRef]
- Mallon, P.E. Application to polymers. In Principles and Applications of Positron and Positronium Chemistry; Jean, Y.C., Mallon, P.E., Schrader, D.M., Eds.; World Scientific: London, UK, 2003; pp. 253–280. [Google Scholar]
- Sharma, J.; Tewari, K.; Arya, R.K. Diffusion in polymeric systems. A review on free volume theory. Prog. Organ. Coat. 2017, 111, 83–92. [Google Scholar] [CrossRef]
- Merkel, T.C.; Freeman, B.D.; Spontak, R.J.; He, Z.; Pinnau, I.; Meakin, P.; Hill, A.J. Sorption, transport, and structural evidence for enhanced free volume in poly(4-methyl-2-penthyne)/fumed silica nanocomposite membranes. Chem. Mater. 2003, 15, 109–123. [Google Scholar] [CrossRef]
- Odegard, G.M.; Bandyopadhyay, A. Physical aging of epoxy polymers and their composites. J. Polym. Sci. Part B Polym. Phys. 2011, 49, 1695–1716. [Google Scholar] [CrossRef]
- Struik, L.C.E. On the rejuvenation of physically aged polymers by mechanical deformation. Polymer 1997, 38, 4053–4057. [Google Scholar] [CrossRef]
- Zaccone, A.; Terentjev, E.M. Disorder-assisted melting and the glass transition in amorphous solids. Phys. Rev. Lett. 2013, 110, 178002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bondi, A. Free Volumes and free rotation in simple liquids and liquid saturated hydrocarbons. J. Phys. Chem. 1954, 58, 929. [Google Scholar] [CrossRef]
- Fox, T.G.; Flory, P.J. Second-order transition temperatures and related properties of polystyrene. I: Influence of molecular weight. J. Appl. Phys. 1950, 21, 581. [Google Scholar] [CrossRef]
- Simha, R.; Somcynsky, T. On the statistical thermodynamics of spherical and chain molecules fluids. Macromolecules 1969, 2, 342. [Google Scholar] [CrossRef]
- Lamarre, L.; Sung, C.S.P. Studies of physical aging and molecular motion by azochromophoric labels attached to the main chains of amorphous polymers. Macromolecules 1983, 16, 1729. [Google Scholar] [CrossRef]
- Victor, J.G.; Torkelson, J.M. On measuring the distribution of local free volume in glassy polymers by photochromic and fluorescence techniques. Macromolecules 1987, 20, 2241. [Google Scholar] [CrossRef]
- Roe, R.J.; Song, H.H. Isothermal relaxation of volume and density fluctuations of polystyrene glass prepared under pressure. Macromolecules 1985, 18, 1603. [Google Scholar] [CrossRef]
- Berko, S.; Pendleton, H.N. Positronium. Ann. Rev. Nucl. Part. Sci. 1980, 30, 543–581. [Google Scholar] [CrossRef]
- Baugher, A.H.; Kossler, W.J.; Petzinger, K.G. Does quantum mechanical tunneling affect the validity of hole distributions obtained from positron annihilation lifetime measurements? Macromolecules 1996, 29, 7280. [Google Scholar] [CrossRef]
- Krause-Rehberg, R.; Leipner, H.S. Positron Annihilation in Semiconductors; Defect Studies: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Tuomisto, F.; Makkonen, I. Defect identification in semiconductors with positron annihilation: Experiment and theory. Rev. Mod. Phys. 2013, 85, 1583. [Google Scholar] [CrossRef] [Green Version]
- Cízek, J. Characterization of lattice defects in metallic materials by positron annihilation spectroscopy: A review. J. Mater. Sci. Technol. 2018, 34, 577–598. [Google Scholar] [CrossRef]
- Dupasquier, A.; Folegati, P.; De Diego, N.; Somoza, A. Current positron studies of structural modifications in age-hardenable metallic systems. J. Phys. Condens. Matter 1998, 10, 10409. [Google Scholar] [CrossRef]
- Petersen, K.; Thrane, N.; Cotterill, R. A positron annihilation study of the annealing of, and void formation in, neutron-irradiated molybdenum. Philos. Mag. 1974, 29, 9–23. [Google Scholar] [CrossRef]
- Vehanen, A.; Hautojarvi, P.; Johansson, J.; Yli-Kauppila, J.; Moser, P. Vacancies and carbon impurities in α-iron: Electron irradiation. Phys. Rev. B 1982, 25, 762. [Google Scholar] [CrossRef]
- Fujinami, M.; Miyagoe, T.; Sawada, T.; Akahane, T. Improved depth profiling with slow positrons of ion implantation-induced damage in silicon. J. Appl. Phys. 2003, 94, 4382–4388. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, J.; Stepanov, P.; Haseman, M.; Zhou, T.; Winarski, D.; Saadatkia, P.; Agarwal, S.; Selim, F.A.; Yang, H.; et al. Defects and solarization in YAG transparent ceramics. Photonics Res. 2019, 7, 549–557. [Google Scholar] [CrossRef]
- Hugenschmidt, C. Positrons in surface physics. Surf. Sci. Rep. 2016, 71, 547–594. [Google Scholar] [CrossRef] [Green Version]
- Jean, Y.C.; Van Horn, J.D.; Hung, W.S.; Lee, K.R. Perspective of Positron Annihilation Spectroscopy in Polymer. Macromolecules 2013, 46, 7133. [Google Scholar] [CrossRef]
- Sharma, S.K.; Pujari, P.K. Role of free volume characteristics of polymer matrix in bulk physical properties of polymer nanocomposites: A review of positron annihilation lifetime studies. Prog. Polym. Sci. 2017, 75, 31–47. [Google Scholar] [CrossRef]
- Madzarevic, Z.P.; Schut, H.; Cízek, J.; Dingemans, T.J. Free volume in poly(ether imide) membranes measured by positron annihilation lifetime spectroscopy and Doppler broadening of annihilation radiation. Macromolecules 2018, 51, 9925. [Google Scholar] [CrossRef]
- Charlton, M.; Humberston, J.M. Positron Physics; Cambridge Monographs on Atomic, Molecular and Chemical Physics: 11; Cambridge University Press: Cambridge, UK, 2001; Chapter 1. [Google Scholar]
- Jean, Y.C. Characterizing free volumes and holes in polymers by positron annihilation spectroscopy. In Positron Spectroscopy of Solids; Dupasquier, A., Mills, A.P., Jr., Eds.; IOS Press: Amsterdam, The Netherlands, 1995; p. 563. [Google Scholar]
- Tao, S.J. Positronium Annihilation in Molecular Substances. J. Chem. Phys. 1972, 56, 5499–5510. [Google Scholar] [CrossRef]
- Eldrup, M.; Lightbody, D.; Sherwood, N.J. The temperature dependence of positron lifetimes in solid pivalic acid. Chem. Phys. 1981, 63, 51. [Google Scholar] [CrossRef]
- Jean, Y.C.; Shi, H. Positronium lifetime in an ellipsoidal free-volume hole of polymers. J. Non-Cryst. Solids 1994, 172, 806. [Google Scholar] [CrossRef]
- Consolati, G. Positronium trapping in small voids: Influence of their shape on positron annihilation results. J. Chem. Phys. 2002, 117, 7279–7283. [Google Scholar] [CrossRef]
- Nakanishi, H.; Wang, S.J.; Jean, Y.C. Microscopic surface tension studied by positron annihilation. In Positron Annihilation Studies of Fluids; Sharma, S.C., Ed.; World Scientific: Singapore, 1988; p. 292. [Google Scholar]
- Gol’dman, I.I.; Krivchenkov, V.D. Problems in Quantum Mechanics; Dover Publications, Inc.: New York, NY, USA, 1993; pp. 135–136. [Google Scholar]
- Nakanishi, H.; Wang, Y.Y.; Jean, Y.C.; Sandreczki, T.C. Temperature and pressure dependences of free volume in an amine-cured epoxy polymer. In Positron Annihilation Studies of Fluids; Sharma, S.C., Ed.; World Scientific: Singapore, 1988; p. 285. [Google Scholar]
- Han, X.; Chen, T.; Zhao, Y.; Gao, J.; Sang, Y.; Xiong, H.; Chen, Z. Relationship between the Microstructure and Performance of Graphene/Polyethylene Composites Investigated by Positron Annihilation Lifetime Spectroscopy. Nanomaterials 2021, 11, 2990. [Google Scholar] [CrossRef] [PubMed]
- Makarewicz, C.; Safandoska, M.; Idczak, R.; Rozanski, A. Positron annihilation lifetime spectroscopy analysis of plastic deformation of high-density polyethylene. Macromolecules 2021, 54, 9649–9662. [Google Scholar] [CrossRef]
- Lopez-Castanares, R.; Angeles, A.E.; Sanchez, V.; Fendler, J.H. Detection of glass transition in Poly(ethylene terephthalate) and Nylon-6 by positron annihilation. J. Appl. Polym. Sci. 1996, 62, 451–457. [Google Scholar] [CrossRef]
- Qi, N.; Chen, Z.Q.; Uedono, A. Molecular motion and relaxation below glass transition temperature in poly (methyl methacrylate) studied by positron annihilation. Rad. Phys. Chem. 2015, 108, 81–86. [Google Scholar] [CrossRef]
- Buttafava, A.; Consolati, G.; Mariani, M.; Quasso, F.; Ravasio, U. Effects induced by gamma irradiation of different polyesters studied by viscometry, thermal analysis and positron annihilation spectroscopy. Pol. Degr. Stab. 2005, 89, 133–139. [Google Scholar] [CrossRef]
- Bartos, J.; Bandzuch, P.; Sausa, O.; Kristiakova, K.; Kristiak, J.; Kanaya, T.; Jenninger, W. Free Volume Microstructure and Its Relationship to the Chain Dynamics in cis-1,4-Poly(butadiene) As Seen by Positron Annihilation Lifetime Spectroscopy. Macromolecules 1997, 30, 6906–6912. [Google Scholar] [CrossRef]
- Mostafa, M.; Ali, E.A.; Mohsen, M. Dynamic study of free volume properties in Polyethylene/Styrene Butadiene rubber blends by positron annihilation lifetime method. J. Appl. Polym. Sci. 2009, 113, 3228–3235. [Google Scholar] [CrossRef]
- Sui, H.; Liu, X.; Zhong, F.; Li, X.; Wang, B.; Ju, X. Polydimethylsiloxane rubber gamma radiation effect studies by positron annihilation lifetime spectroscopy. Rad. Eff. Defects Solids 2014, 169, 628–635. [Google Scholar] [CrossRef]
- Long, T.H.; Hieu, D.T.T.; Hao, L.H.; Cuong, N.T.; Loan, T.T.H.; Man, T.V.; Tap, T.D. Positron annihilation lifetime spectroscopy of Nafion and grafted-type polymer membranes for fuel cell applications. Polym. Eng. Sci. 2022, 62, 4005–4017. [Google Scholar] [CrossRef]
- Hamdy, F.M.M.; Abdel-Hady, E.E.; Salwa, S.M. Temperature dependence of the free volume in polytetrafluoroethylene studied by positron annihilation spectroscopy. Rad. Phys. Chem. 2007, 76, 160–164. [Google Scholar]
- Consolati, G.; Genco, I.; Pegoraro, M.; Zanderighi, L. Positron annihilation lifetime (PAL) in Poly[1-(trimethyl-silyl)propine] (PTMSP): Free volume determination and time dependence of permeability. J. Polym. Sci. Part B Polym. Phys. 1996, 34, 357–367. [Google Scholar] [CrossRef]
- MacKenzie, I.K. Experimental Methods of Annihilation Time and Energy Spectrometry. In Positron Solid-State Physics; Brandt, W., Dupasquier, A., Eds.; North-Holland: Amsterdam, The Netherlands, 1983; p. 214. [Google Scholar]
- Schrader, D.M.; Jean, Y.C. (Eds.) Introduction. In Positron and Positronium Chemistry; Elsevier: Amsterdam, The Netherlands, 1988; p. 13. [Google Scholar]
- Pujari, P.K.; Sen, D.; Amarendra, G.; Abhaya, S.; Pandey, A.K.; Dutta, D.; Mazumder, S. Study of pore structure in grafted polymer membranes using slow positron beam and small-angle X-ray scattering techniques. Nucl. Instrum. Methods Phys. Res. Sect. B 2007, 254, 278. [Google Scholar] [CrossRef]
- Panzarasa, G.; Aghion, S.; Soliveri, G.; Consolati, G.; Ferragut, R. Positron Annihilation Spectroscopy: A New Frontier for Understanding Nanoparticle- Loaded Polymer Brushes. Nanotechnology 2016, 27, 02LT03. [Google Scholar] [CrossRef] [PubMed]
- Algers, J.; Suzuki, R.; Ohdaira, T.; Maurer, F.H. Characterization of free volume and density gradients of polystyrene surfaces by low-energy positron lifetime measurements. Polymer 2004, 45, 4533. [Google Scholar] [CrossRef]
- Huang, S.H.; Hung, W.S.; Liaw, D.J.; Tsai, H.A.; Jiang, G.J.; Lee, K.R.; Lai, J.Y. Positron annihilation study on thin-film composite pervaporation membranes: Correlation between polyamide fine structure and different interfacial polymerization conditions. Polymer 2010, 51, 1370. [Google Scholar] [CrossRef]
- Panzarasa, G.; Aghion, S.; Marra, G.; Wagner, A.; Liedke, M.O.; Elsayed, M.; Krause-Rehberg, R.; Ferragut, R.; Consolati, G. Probing the Impact of the Initiator Layer on Grafted-from Polymer Brushes: A Positron Annihilation Spectroscopy Study. Macromolecules 2017, 50, 5574. [Google Scholar] [CrossRef]
- Gabriel, F.; Gippner, P.; Grosse, E.; Janssen, D.; Michel, P.; Prade, H.; Schamlott, A.; Seidel, W.; Wolf, A.; Wünsch, R. The Rossendorf Radiation Source ELBE and Its FEL Projects. Nucl. Instrum. Methods Phys. Res. Sect. B 2000, 161, 1143–1147. [Google Scholar] [CrossRef]
- Coleman, G.P. Experimental techniques in positron spectroscopy. In Positron and Positronium Chemistry; Jean, Y.C., Mallon, P.E., Schrader, D.M., Eds.; World Scientific: Singapore, 2003; Chapter 3. [Google Scholar]
- Wang, H.B.; Zhao, Q.H.; Liang, H.; Gu, B.C.; Liu, J.D.; Zhang, H.J.; Ye, B.J. A new SiPM-based positron annihilation lifetime spectrometer using LYSO and LFS-3 scintillators. Nucl. Inst. Meth. Phys. Res. A 2020, 960, 163662. [Google Scholar] [CrossRef]
- Wang, H.B.; Liu, J.D.; Zhang, H.J.; Liang, H.; Ye, B.J. Multiple time-over-threshold readout electronics for fast timing and energy resolving in a SiPM-based positron annihilation lifetime spectrometer. JINST 2020, 15, P11006. [Google Scholar] [CrossRef]
- Saito, H.; Nagashima, Y.; Kurihara, T.; Hyodo, T. A new positron lifetime spectrometer using a fast- digital oscilloscope and BaF2 scintillators. Nucl. Instrum. Methods Phys. Res. Sect. A 2002, 487, 612–617. [Google Scholar] [CrossRef]
- Rytsölä, K.; Nissilä, J.; Kokkonen, J.; Laakso, A.; Aavikko, R.; Saarinen, K. Digital measurement of positron lifetime. Appl. Surf. Sci. 2002, 194, 260–263. [Google Scholar] [CrossRef] [Green Version]
- Becvar, F. Methodology of positron lifetime spectroscopy: Present status and perspectives. Nucl. Instrum. Methods Phys. Res. Sect. B 2007, 261, 871–874. [Google Scholar] [CrossRef]
- Ye, R.; Zhao, Q.H.; Wang, H.B.; Gu, B.C.; Pan, Z.W.; Liu, J.D.; Ye, B.J. Coincidence time resolution investigation of BaF2-based H6610 detectors for a digital positron annihilation lifetime Spectrometer. JINST 2020, 15, P06001. [Google Scholar] [CrossRef]
- Fang, M.; Bartholomew, N.; Di Fulvio, A. Positron annihilation lifetime spectroscopy using fast scintillators and digital Electronics. Nucl. Inst. Meth. Phys. Res. A 2019, 943, 162507. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.H.; Ye, R.; Wang, H.B.; Cong, L.H.; Liu, J.D.; Zhang, H.J.; Ye, B.J. A multi-parameter discrimination digital positron annihilation lifetime spectrometer using a fast-digital oscilloscope. Nucl. Instrum. Meth. Phys. Res. A 2022, 1023, 165974. [Google Scholar] [CrossRef]
- Jean, Y.C.; Schrader, D.M. Experimental Techniques in Positron and Positronium Chemistry. In Positron and Positronium Chemistry; Schrader, D.M., Jean, Y.C., Eds.; Elsevier: Amsterdam, The Netherlands, 1988; p. 103. [Google Scholar]
- Olsen, J.V.; Kirkegaard, P.; Pedersen, N.J.; Eldrup, M. PALSfit: A new program for the evaluation of positron lifetime spectra. Phys. Stat. Sol. 2007, 4, 4004–4006. [Google Scholar] [CrossRef]
- Gregory, R.B. Analysis of positron annihilation lifetime data by numerical Laplace inversion: Corrections for source terms and zero-time shift errors. Nucl. Instrum. Methods Phys. Res. Sect. A 1991, 302, 496–507. [Google Scholar] [CrossRef]
- Shukla, A.; Peter, M.; Hoffmann, L. Analysis of positron lifetime spectra using quantified maximum entropy and a general filter. Nucl. Instrum. Methods Phys. Res. Sect. A 1993, 335, 310–317. [Google Scholar] [CrossRef]
- Kansy, J. Microcomputer program for analysis of positron annihilation lifetime spectra. Nucl. Instrum. Methods Phys. Res. Sect. A 1996, 374, 235–244. [Google Scholar] [CrossRef]
- Yin, C.; Wang, L.; Li, J.; Zhou, Y.; Zhang, H.; Fang, P.; He, C. Positron annihilation characteristics, water uptake and proton conductivity of composite Nafion membranes. Phys. Chem. Chem. Phys 2017, 19, 15953. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, H.F.M.; Abdel-Hady, E.E.; Abdel Hamed, M.O.; Said, M. Microstructure characterization of Nafion HP JP as a proton exchange membrane for fuel cell: Positron annihilation study. Acta Phys. Pol. A 2017, 132, 1543. [Google Scholar] [CrossRef]
- Elsharkawi, M.R.M.; Hassanien, M.H.M.; Mohamed, H.F.M.; Gomaa, M.M. Humidity effect on the transport properties on per-fluorinated sulfonic acid/PTFE proton exchange membranes: Positron annihilation study. Polym. Adv. Technol. 2022, 33, 952. [Google Scholar] [CrossRef]
- Awad, S.; Abdel-Hady, E.E.; Mohamed, H.F.M.; Elsharkawy, Y.S.; Gomaa, M.M. Non-fluorinated PVA/SSA proton exchange membrane studied by positron annihilation technique for fuel cell applications. Polym. Adv. Technol. 2021, 32, 3322. [Google Scholar] [CrossRef]
- Gomaa, M.M.; Hugenschmidt, C.; Dickmann, M.; Abdel-Hady, E.E.; Mohamed, H.F.M.; Abdel-Hamed, M.O. Cross-linked PVA/SSA proton exchange membranes: Correlation between physiochemical properties and free volume determined by positron annihilation spectroscopy. Phys. Chem. Chem. Phys. 2018, 20, 28287. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.J.; Sellaiyan, S.; Sako, K.; Uedono, A.; Taniguchi, Y.; Hayashi, K. Effect of free volume holes on static mechanical properties of epoxy resins studied by positron annihilation and PVT experiments. Polymer 2020, 190, 122225. [Google Scholar] [CrossRef]
- Constantin, F.; Petruneac, M.; Focsaneanu, M. Positron annihilation spectroscopy studies of implanted polymer membranes. Polym. Adv. Technol. 2021, 32, 241. [Google Scholar] [CrossRef]
- Fan, J.; Zhou, W.; Wang, Q.; Chu, Z.; Yang, L.; Yang, L.; Sun, J.; Zhao, L.; Xu, J.; Liang, Y.; et al. Structure dependence of water vapor permeation in polymer nanocomposite membranes investigated by positron annihilation lifetime spectroscopy. J. Membr. Sci. 2018, 549, 581. [Google Scholar] [CrossRef]
- Jo Kim, S.; Kook, S.; O’Rourke, B.E.; Lee, J.; Hwang, M.; Kobayashi, Y.; Suzuki, R.; Kim, I.S. Characterization of pore size distribution (PSD) in cellulose triacetate (CTA) and polyamide (PA) thin active layers by positron annihilation lifetime spectroscopy (PALS) and fractional rejection (FR) method. J. Membr. Sci. 2017, 527, 143. [Google Scholar] [CrossRef]
- Söylemez, M.A. Synthesis and characterization of tetracycline-imprinted membranes: A detailed positron annihilation lifetime spectroscopy investigation. J. Mol. Recognit. 2021, 34, e2895. [Google Scholar]
- Söylemez, M.A.; Güven, O. Detailed positron annihilation lifetime spectroscopic investigation of atrazine imprinted polymers grafted onto PE/PPnon-woven fabrics. J. Mol. Recognit. 2018, 31, e2676. [Google Scholar] [CrossRef]
- El-Gamal, S.; Elsayed, M. Positron annihilation and electrical studies on the influence of loading magnesia nanoribbons on PVA-PVP blend. Polym. Test. 2020, 89, 106681. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, Y.; Peng, X.; Huang, Z.; Qian, L.; He, C.; Fang, P. Water diffusivity transition in fumed silica-filled polydimethylsiloxane composite: Correlation with the interfacial free volumes characterized by positron annihilation lifetime spectroscopy. J. Mater. Sci. 2021, 56, 3095. [Google Scholar] [CrossRef]
- Uedono, A.; Sako, K.; Ueno, W.; Kimura, M. Free volumes introduced by fractures of CFRP probed using positron annihilation. Compos. Part A 2019, 122, 54. [Google Scholar] [CrossRef]
- Winberg, P.; Eldrup, M.; Maurer, F.H.J. Nanoscopic properties of silica filled polydimethylsiloxane by means of positron annihilation lifetime spectroscopy. Polymer 2004, 45, 8253–8264. [Google Scholar] [CrossRef]
- Sharma, S.K.; Prakash, J.; Pujari, P.K. Effects of the molecular level dispersion of graphene oxide on the free volume characteristics of poly(vinyl alcohol) and its impact on the thermal and mechanical properties of their nanocomposites. Phys. Chem. Chem. Phys. 2015, 17, 29201–29209. [Google Scholar] [CrossRef]
- Aly, H. Positron annihilation study on nickel and iron nanoparticles in natural rubber nanocomposites. Am. J. Appl. Sci. 2011, 8, 147–155. [Google Scholar] [CrossRef] [Green Version]
- Awad, S.; Chen, H.; Chen, G.; Gu, X.; Lee, J.L.; Abdel-Hady, E.E.; Jean, Y.C. Free volumes, glass transitions, and cross-links in zinc oxide/waterborne polyurethane nanocomposites. Macromolecules 2011, 44, 29–38. [Google Scholar] [CrossRef]
- Merkel, T.C.; Freeman, B.D.; Spontak, R.J.; He, Z.; Pinnau, I.; Meakin, P.; Hill, A.J. Ultrapermeable, reverse-selective nanocomposite membranes. Science 2002, 296, 519–522. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Sitter, K.; Winberg, P.; D’Haen, J.; Dotremont, C.; Leysen, R.; Martens, J.A.; Mullens, S.; Maurer, F.H.J.; Vankelecom, I.F.J. Silica filled poly(1-trimethylsilyl-1-propyne) nanocomposite membranes: Relation between the transport of gases and structural characteristics. J. Membr. Sci. 2006, 278, 83–91. [Google Scholar] [CrossRef]
- Song, Q.; Nataraj, S.K.; Roussenova, M.V.; Tan, J.C.; Hughes, D.J.; Li, W.; Bourgoin, P.; Alam, M.A.; Cheetham, A.K.; Al-Muhtaseb, S.A.; et al. Zeolitic imidazolate framework (ZIF-8) based polymer nanocomposite membranes for gas separation. Energy Environ. Sci. 2012, 5, 8359–8369. [Google Scholar] [CrossRef]
- Anil Kumar, S.; Yuelong, H.; Yumei, D.; Le, Y.; Kumaran, M.G.; Thomas, S. Gas transport through nano poly(ethylene-co-vinyl acetate) composite membranes. Ind. Eng. Chem. Res. 2008, 47, 4898–4904. [Google Scholar] [CrossRef]
- Sharma, S.K.; Prakash, J.; Sudarshan, K.; Maheshwari, P.; Sathiyamoorthy, D.; Pujari, P.K. Effect of interfacial interaction on free volumes in phenol-formaldehyde resin–carbon nanotube composites: Positron annihilation lifetime and age-momentum correlation studies. Phys. Chem. Chem. Phys. 2012, 14, 10972–10978. [Google Scholar] [CrossRef]
- Sharma, S.K.; Prakash, J.; Sudarshan, K.; Sen, D.; Mazumder, S.; Pujari, P.K. Structure at interphase of poly(vinyl alcohol)-SiC nanofiber composite and its impact on mechanical properties: Positron annihilation and small-angle X-ray scattering studies. Macromolecules 2015, 48, 5706–5713. [Google Scholar] [CrossRef]
- Sharma, S.K.; Bahadur, J.; Patil, P.N.; Maheshwari, P.; Mukherjee, S.; Sudarshan, K.; Mazumder, S.; Pujari, P.K. Revealing the nano-level molecular packing in chitosan–NiO nanocomposite by using positron annihilation spectroscopy and small-angle X-ray scattering. Chem. Phys. Chem. 2013, 14, 1055–1062. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Qi, N.; Zhou, B.; Chen, Z. Exceptionally High CO2 Capture in an Amorphous Polymer with Ultramicropores Studied by Positron Annihilation. ACS Appl. Mater. Interfaces 2019, 11, 30747. [Google Scholar] [CrossRef] [PubMed]
- Shantarovich, V.P.; Bekeshev, V.G.; Bermeshev, M.V.; Alentiev, D.A.; Gustov, V.W.; Belousova, E.V.; Kevdina, I.B.; Novikov, Y.A. Study of Microporosity of Polymer Glasses Using Techniques of Positron Annihilation and Low-Temperature Sorption of Carbon Dioxide. High Energy Chem. 2019, 53, 276. [Google Scholar] [CrossRef]
- Shantarovich, V.P.; Bekeshev, V.G.; Kevdina, I.B.; Yampolskii, Y.P.; Bermeshev, M.V.; Belov, N.A. Nanoporosity of Polymer Membrane Materials and Sorbents According to Positron Annihilation and Low-Temperature Gas Sorption Data. High Energy Chem. 2018, 52, 275. [Google Scholar] [CrossRef]
- Shantarovich, V.P.; Bekeshev, V.G.; Kevdina, I.B.; Bermeshev, M.V.; Wozniak, A.I. Microporosity of Polynorbornenes by Positron Annihilation and Sorption Data. High Energy Chem. 2021, 55, 80. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, M.; Shu, G.; Yang, Z.; Liu, Q.; Zeng, M.; Qi, C.; Cao, X.; Wang, B. Positron annihilation characteristics and catalytic performances of poly (vinyl alcohol) intercalated montmorillonite supported Pd0 nanoparticles composites. Rad. Phys. Chem. 2018, 153, 164. [Google Scholar] [CrossRef]
- Rhim, J.W.; Kuzeci, S.; Roy, S.; Akti, N.; Tav, C.; Yahsi, U. Effect of Free Volume on Curcumin Release from Various Polymer-Based Composite Films Analyzed Using Positron Annihilation Lifetime Spectroscopy. Materials 2021, 14, 5679. [Google Scholar] [CrossRef]
- Anbinder, P.S.; Macchi, C.; Amalvy, J.; Somoza, A. A study of the structural changes in a chitosan matrix produced by the adsorption of copper and chromium ions. Carbohydr. Polym. 2019, 222, 114987. [Google Scholar] [CrossRef] [PubMed]
- Gaydarov, V.; Chen, Z.; Zamfirova, G.; Söylemez, M.A.; Zhang, J.; Djourelov, N.; Zhang, J. Micromechanical and positron annihilation lifetime study of new cellulose esters with different topological structures. Carbohydr. Polym. 2019, 219, 56. [Google Scholar] [CrossRef] [PubMed]
- Nuruddin, M.; Chowdhury, R.A.; Lopez-Perez, N.; Montes, F.J.; Youngblood, J.P.; Howarter, J.A. Influence of Free Volume Determined by Positron Annihilation Lifetime Spectroscopy (PALS) on Gas Permeability of Cellulose Nanocrystal Films. Appl. Mater. Interfaces 2020, 12, 24380. [Google Scholar] [CrossRef]
- Hagihara, H.; Sato, H.; Hara, Y.; Jonai, S.; Masuda, A. Lamination-interface-dependent deacetylation of ethylene vinyl acetate encapsulant in crystalline Si photovoltaic modules evaluated by positron annihilation lifetime spectroscopy. Jpn. J. Appl. Phys. 2018, 57, 082301. [Google Scholar] [CrossRef]
- Utpalla, P.; Sharma, S.K.; Sudarshan, K.; Sahu, M.; Pujari, P.K. Investigation of the free volume characteristics of PEO based solid state polymer electrolyte by means of positron annihilation spectroscopy. Solid State Ion. 2019, 339, 114990. [Google Scholar] [CrossRef]
- Utpalla, P.; Sharma, S.K.; Sudarshan, K.; Deshpande, S.K.; Sahu, M.; Pujari, P.K. Investigating the Correlation of Segmental Dynamics, Free Volume Characteristics, and Ionic Conductivity in Poly(ethylene oxide)-Based Electrolyte: A Broadband Dielectric and Positron Annihilation Spectroscopy Study. J. Phys. Chem. C 2020, 124, 4489. [Google Scholar] [CrossRef]
- Li, J.; Yin, C.; Zhou, Y.; Li, G.; Yeh, Y.; He, C. Positron Annihilation Studies of the Free Volumes in Nylon12/PVA Films Treated by Supercritical Carbon Dioxide. Acta Phys. Pol. A 2017, 132, 1552. [Google Scholar] [CrossRef]
- Onodera, K.; Oka, T.; Kino, Y.; Sekine, T. Degradation of electron-irradiated polyethylene studied by positron annihilation lifetime spectroscopy. J. Phys. Conf. Ser. 2017, 791, 012026. [Google Scholar] [CrossRef]
- Ismayil; Ravindrachary, V.; Sanjeev, G.; Praveena, S.D. Electron beam induced modifications in the microstructure of PVA/Li2B4O7 polymer films: Positron annihilation study. Rad. Chem. Phys. 2018, 151, 69. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, P.; Gupta, S.K.; Gupta, R.; Jaiswal, M.K.; Prasad, M.; Roychowdhury, A.; Chauhan, R.P.; Das, D. Radiation induced nano-scale free volume modifications in amorphous polymeric material: A study using positron annihilation lifetime spectroscopy. J. Radioanal. Nucl. Chem. 2017, 314, 1659. [Google Scholar] [CrossRef]
- Švajdlenková, H.; Šauša, O.; Peer, G.; Gorsche, C. In situ investigation of the kinetics and microstructure during photopolymerization by positron annihilation technique and NIR-photorheology. RCS Adv. 2018, 8, 37085. [Google Scholar]
- Shpotyuk, O.; Ingram, A.; Shpotyuk, O. Photopolymerization shrinkage in dimethacrylate-based dental restorative composites probed by means of positron annihilation lifetime spectroscopy. Polymer 2020, 196, 122485. [Google Scholar] [CrossRef]
- Shantarovich, V.P. On the role of free volume in pick-off annihilation and positronium chemical reactions. J. Radioanal. Nucl. Chem. 1996, 210, 357. [Google Scholar] [CrossRef]
- Wang, C.L.; Hirade, T.; Maurer, F.J.H.; Eldrup, M.; Pedersen, N.J. Free-volume distribution and positronium formation in amorphous polymers: Temperature and positron-irradiation-time dependence. J. Chem. Phys. 1998, 108, 4654. [Google Scholar] [CrossRef]
- Biganeh, A.; Kakuee, O.; Rafi-Kheiri, H.; Lamehi-Rachti, M.; Sheikh, N.; Yahaghi, E. Positron Annihilation Lifetime and Doppler Broadening Spectroscopy of Polymers. Rad. Phys. Chem. 2020, 166, 108461. [Google Scholar] [CrossRef]
- Mogensen, O.E. Positron Annihilation in Chemistry; Goldanskii, V.I., Ed.; Springer Series in Chemical Physics: Berlin/Heidelberg, Germany; New York, NY, USA, 1995; Volume 58. [Google Scholar]
- Hirade, T.; Maurer, F.J.H.; Eldrup, M. Positronium formation at low temperatures: The role of trapped electrons. Rad. Phys. Chem. 2000, 58, 465. [Google Scholar] [CrossRef]
- Shantavovich, V.P.; Hirade, T.; Kevdina, I.B.; Gustov, V.W.; Oleinik, E.F. Comments on the effect of γ-irradiation on positronium formation in polymers at low temperatures. Acta Phys. Pol. A 2001, 99, 497. [Google Scholar] [CrossRef]
- Shantarovich, V.P. Positron annihilation and free volume studies in polymer glasses. J. Polym. Sci. Part B Polym. Phys. 2008, 46, 2485. [Google Scholar] [CrossRef]
- Srithawatpong, R.; Peng, Z.L.; Olson, B.G.; Jamieson, A.M.; Simha, R.; McGervey, J.D.; Maier, T.R.; Halasa, A.F.; Ishida, H. Positron annihilation lifetime studies of changes in free volume on cross-linking cis-polyisoprene, high-vinyl polybutadiene, and their miscible blends. J. Polym. Sci. Part B Polym. Phys. 1999, 37, 2754–2770. [Google Scholar] [CrossRef]
- Dlubek, G. Local Free-Volume Distribution from PALS and Dynamics of Polymers. In Polymer Physics. From Suspensions to Nanocomposites and Beyond; Utracki, L.A., Jamieson, A.M., Eds.; John Wiley & Sons: Singapore, 2010; pp. 421–472. [Google Scholar]
- Simha, R.; Wilson, P.S. Thermal Expansion of Amorphous Polymers at Atmospheric Pressure. II. Theoretical Considerations. Macromolecules 1973, 6, 908. [Google Scholar] [CrossRef]
- Consolati, G.; Mossini, E.; Nichetti, D.; Quasso, F.; Viola, G.M.; Yaynik, E. Shape and Temperature Expansion of Free Volume Holes in Some Cured Polybutadiene-Polyisoprene Rubber Blends. Int. J. Mol. Sci. 2021, 22, 1436. [Google Scholar] [CrossRef] [PubMed]
- Utracki, L.A. Compressibility and thermal expansion coefficients of nanocomposites with amorphous and crystalline polymer matrix. Eur. Polym. J. 2009, 45, 1891–1903. [Google Scholar] [CrossRef]
- Consolati, G.; Quasso, F.; Simha, R.; Olson, G.B. On the relation between positron annihilation lifetime spectroscopy and lattice-hole-theory free volume. J. Pol. Sci. B 2005, 43, 2225–2229. [Google Scholar] [CrossRef]
- Consolati, G. On the Thermal Expansion of Nanohole Free Volume in Perfluoropolyethers. J. Phys. Chem. B 2005, 109, 10096–10099. [Google Scholar] [CrossRef] [PubMed]
- Consolati, G. Temperature dependence of nanoholes free volume in polypropylene glycols. Appl. Phys. Lett. 2006, 88, 111902. [Google Scholar] [CrossRef]
- Bradac, C.; Consolati, G.; Quasso, F. Temperature dependence of free volume in atactic polypropylene. Eur. Polym. J. 2009, 45, 3010–3015. [Google Scholar] [CrossRef]
- Consolati, G.; Mercurio, G.; Quasso, F. Free volume fraction and nanoholes shapes in polyvinyl acetate. Chem. Phys. Lett. 2009, 475, 54–57. [Google Scholar] [CrossRef]
- Consolati, G.; Nichetti, D.; Quasso, F. Constraints and Thermal Expansion of the Free Volume in a Micro-phase Separated Poly(ester-adipate)urethane. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 2104. [Google Scholar] [CrossRef]
- Consolati, G.; Nichetti, D.; Briatico Vangosa, F.; Quasso, F. Beyond the spherical approximation: Elongated free volume holes in rubbers: A positron annihilation study. Rubber Chem. Technol. 2019, 92, 709–721. [Google Scholar] [CrossRef]
- Consolati, G.; Nichetti, D.; Quasso, F. Free volume expansion in some polybutadiene–acrylonitrile rubbers: Comparison between theory and experiments. Polym. Int. 2022, 71, 1287. [Google Scholar] [CrossRef]
- Olson, B.G.; Prodpran, T.; Jamieson, A.M.; Nazarenko, S. Positron annihilation in syndiotactic polystyrene containing α and β crystalline forms. Polymer 2002, 43, 6775–6784. [Google Scholar] [CrossRef]
- Wang, S.Q. On Chain Statistics and Entanglement of Flexible Linear Polymer Melts. Macromolecules 2007, 40, 8684–8694. [Google Scholar] [CrossRef]
- Milner, S.T. Predicting the Tube Diameter in Melts and Solutions. Macromolecules 2005, 38, 4929–4939. [Google Scholar] [CrossRef]
- Sega, M.; Jedlovsky, P.; Medvedev, N.N.; Vallauri, R. Free volume properties of a linear soft polymer: A computer simulation study. J. Chem. Phys. 2004, 121, 2422. [Google Scholar] [CrossRef] [Green Version]
- Don, H.; Jacob, K.I. Effect of Molecular Orientation on Polymer Free Volume Distribution: An Atomistic Approach. Macromolecules 2003, 36, 8881. [Google Scholar]
- Hofmann, D.; Entrialgo-Castano, M.; Lerbret, A.; Heuchel, M.; Yampolskii, Y. Molecular Modeling Investigation of Free Volume Distributions in Stiff Chain Polymers with Conventional and Ultrahigh Free Volume: Comparison between Molecular Modeling and Positron Lifetime Studies. Macromolecules 2003, 36, 8528. [Google Scholar] [CrossRef]
- Račko, D.; Capponi, S.; Alvarez, F.; Colmenero, J.; Bartoš, J. The free-volume structure of a polymer melt, poly(vinyl methylether) from molecular dynamics simulations and cavity analysis. J. Chem. Phys. 2009, 131, 064903. [Google Scholar] [CrossRef]








| Polymer | τ3 (ns) | R3 (nm) | I3 (%) | τ4 (ns) | R4 (nm) | I4 (%) | Ref. |
|---|---|---|---|---|---|---|---|
| LDPE | 2.55 ± 0.01 | 0.33 | 21.1 ± 0.4 | [38] | |||
| HDPE | 2.38 ± 0.04 | 0.32 | 19.7 ± 0.3 | [39] | |||
| Nylon-6 | 1.55 ± 0.02 | 0.24 | 24.5 ± 0.04 | [40] | |||
| PMMA | 1.92 ± 0.01 | 0.28 | 23.6 ± 0.02 | [41] | |||
| PET | 1.66 ± 0.03 | 0.25 | 20.4 ± 0.3 | [42] | |||
| Cis1,4-polybutadiene | 2.614 ± 0.005 | 0.34 | 39.45 ± 0.07 | [43] | |||
| SBR | 2.50 ± 0.02 | 0.33 | 34.2 ± 0.9 | [44] | |||
| PDMS | 3.27 ± 0.03 | 0.39 | 30.3 ± 0.5 | [45] | |||
| Nafion | 3.27 ± 0.01 | 0.39 | 6.33 ± 0.06 | [46] | |||
| PTFE | 1.12 ± 0.09 | 0.19 | 9.6 ± 0.9 | 3.92 ± 0.02 | 0.43 | 13.8 ± 0.2 | [47] |
| PTMSP | 4.7 ± 0.3 | 0.47 | 9.7 ± 0.5 | 13.8 ± 0.1 | 0.79 | 31.1 ± 0.6 | [48] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Consolati, G.; Nichetti, D.; Quasso, F. Probing the Free Volume in Polymers by Means of Positron Annihilation Lifetime Spectroscopy. Polymers 2023, 15, 3128. https://doi.org/10.3390/polym15143128
Consolati G, Nichetti D, Quasso F. Probing the Free Volume in Polymers by Means of Positron Annihilation Lifetime Spectroscopy. Polymers. 2023; 15(14):3128. https://doi.org/10.3390/polym15143128
Chicago/Turabian StyleConsolati, Giovanni, Dario Nichetti, and Fiorenza Quasso. 2023. "Probing the Free Volume in Polymers by Means of Positron Annihilation Lifetime Spectroscopy" Polymers 15, no. 14: 3128. https://doi.org/10.3390/polym15143128
APA StyleConsolati, G., Nichetti, D., & Quasso, F. (2023). Probing the Free Volume in Polymers by Means of Positron Annihilation Lifetime Spectroscopy. Polymers, 15(14), 3128. https://doi.org/10.3390/polym15143128








