Structural Integrity Assessment of an NEPE Propellant Grain Considering the Tension–Compression Asymmetry in Its Mechanical Property
Abstract
:1. Introduction
2. Numerical Method
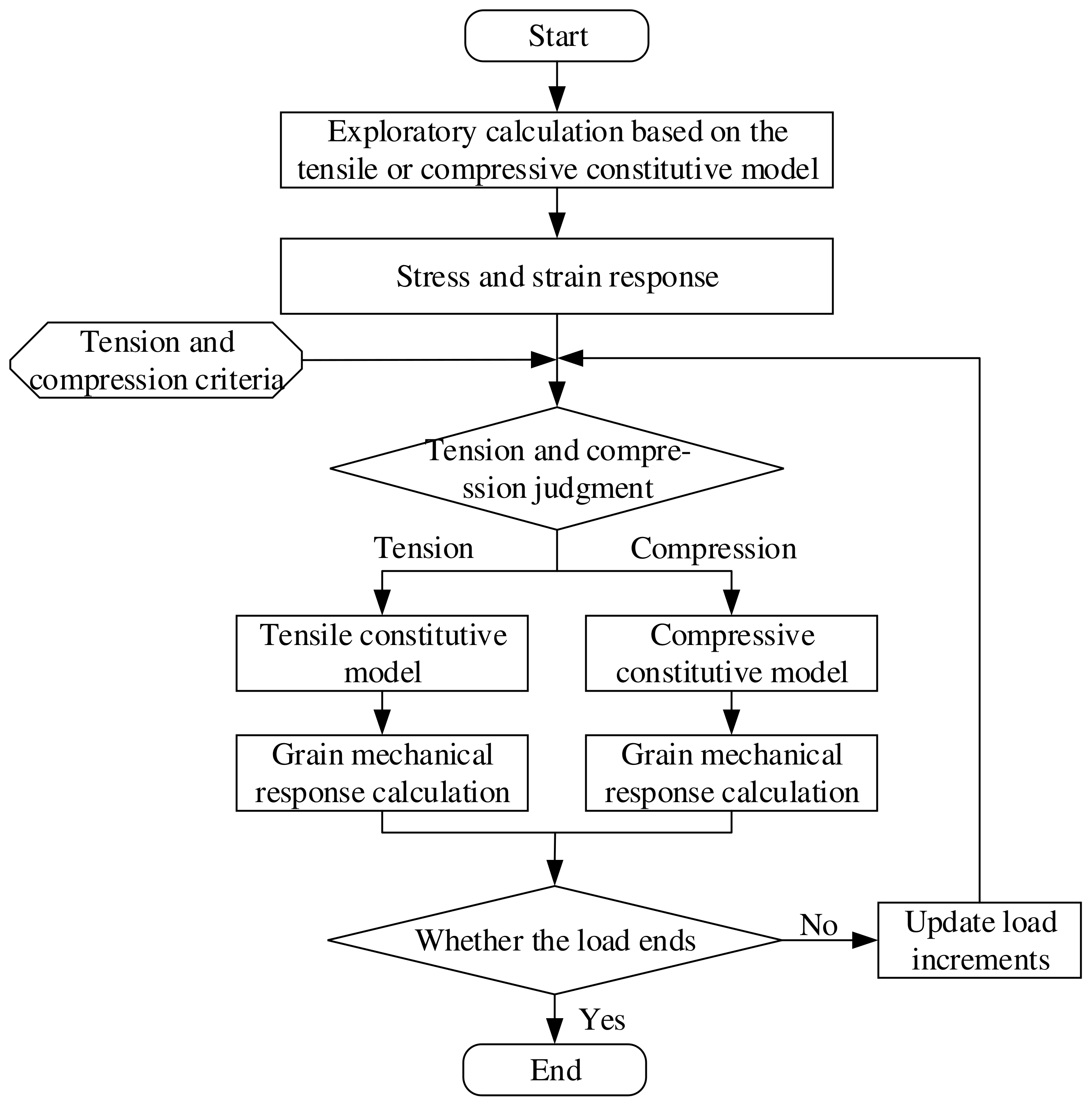
2.1. Numerical Method for Tension–Compression Asymmetry
2.2. Numerical Methods Verification
3. Analysis and Modeling
3.1. Constitutive Model
3.2. Increment Alization of the Constitutive Equations
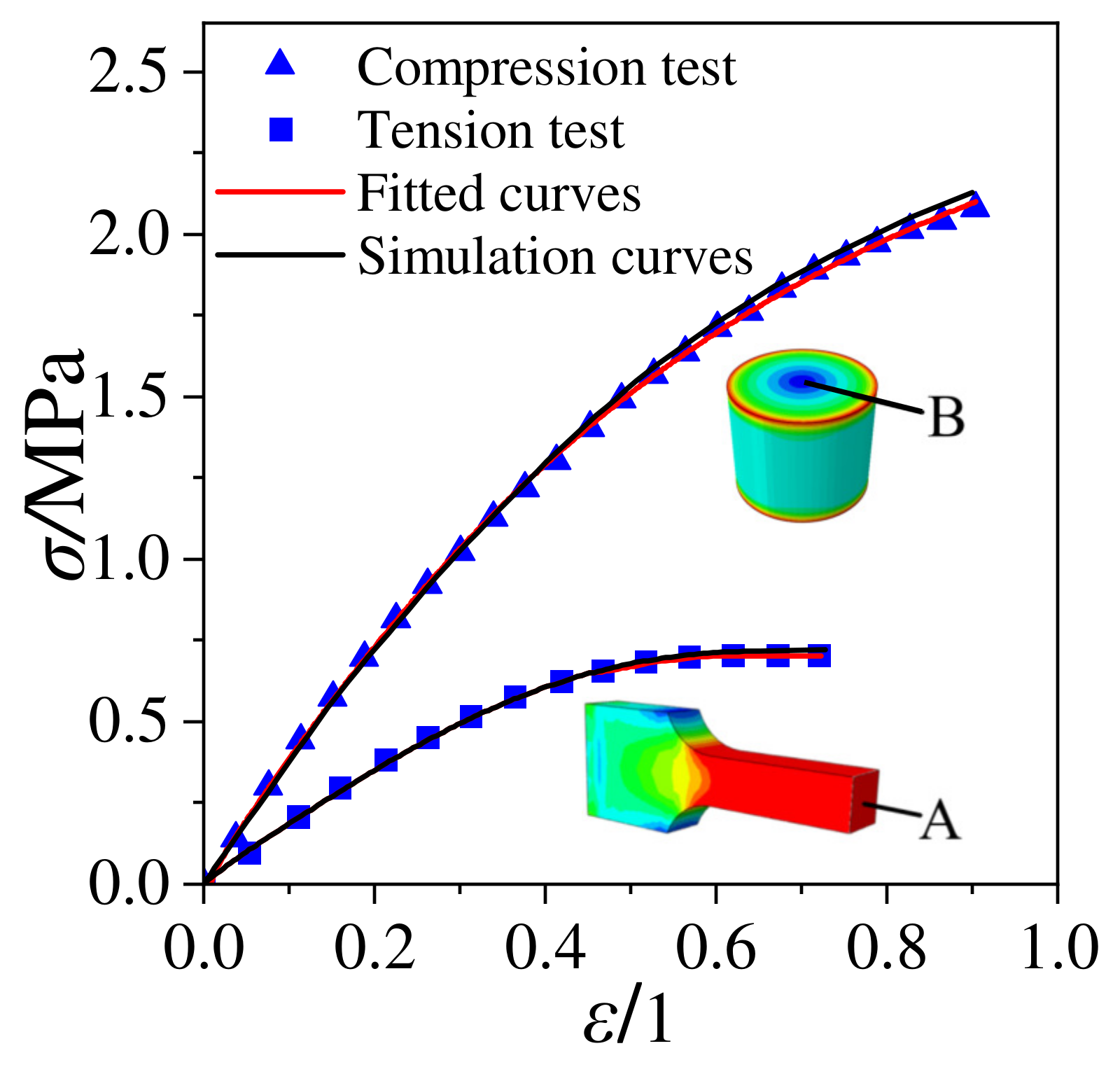
3.3. Model Verification
3.4. Finite Element Modeling
4. Results and Discussion
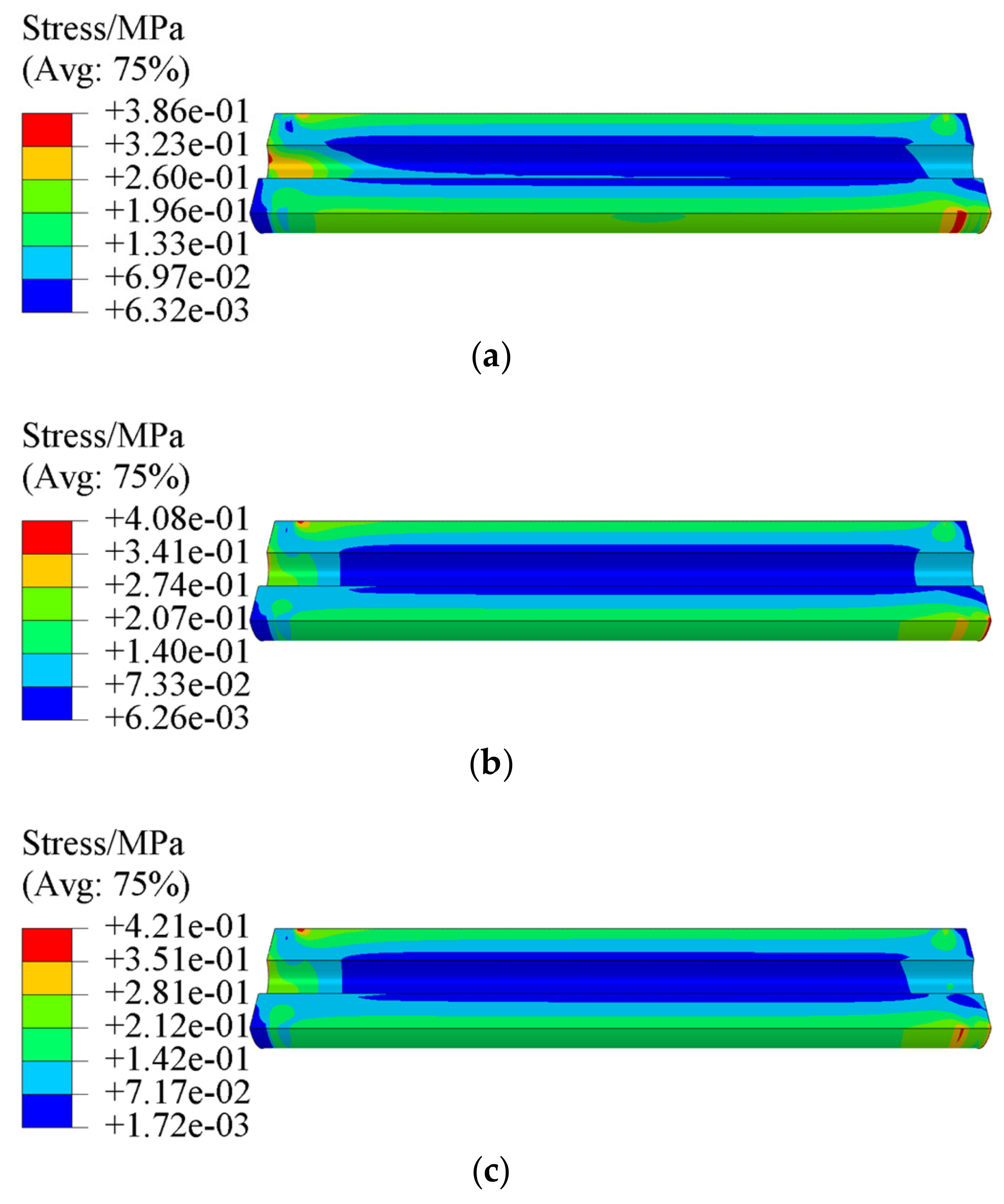
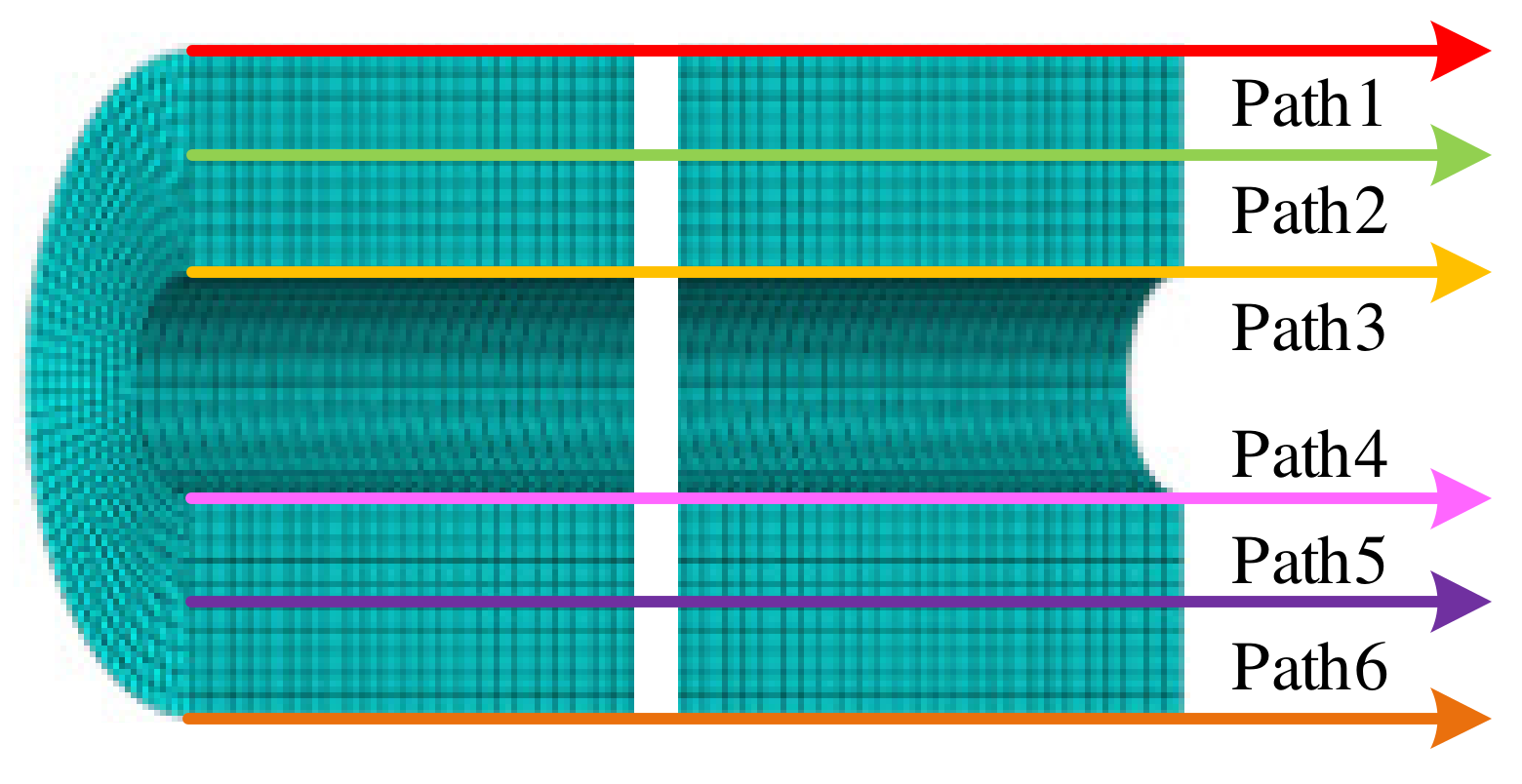
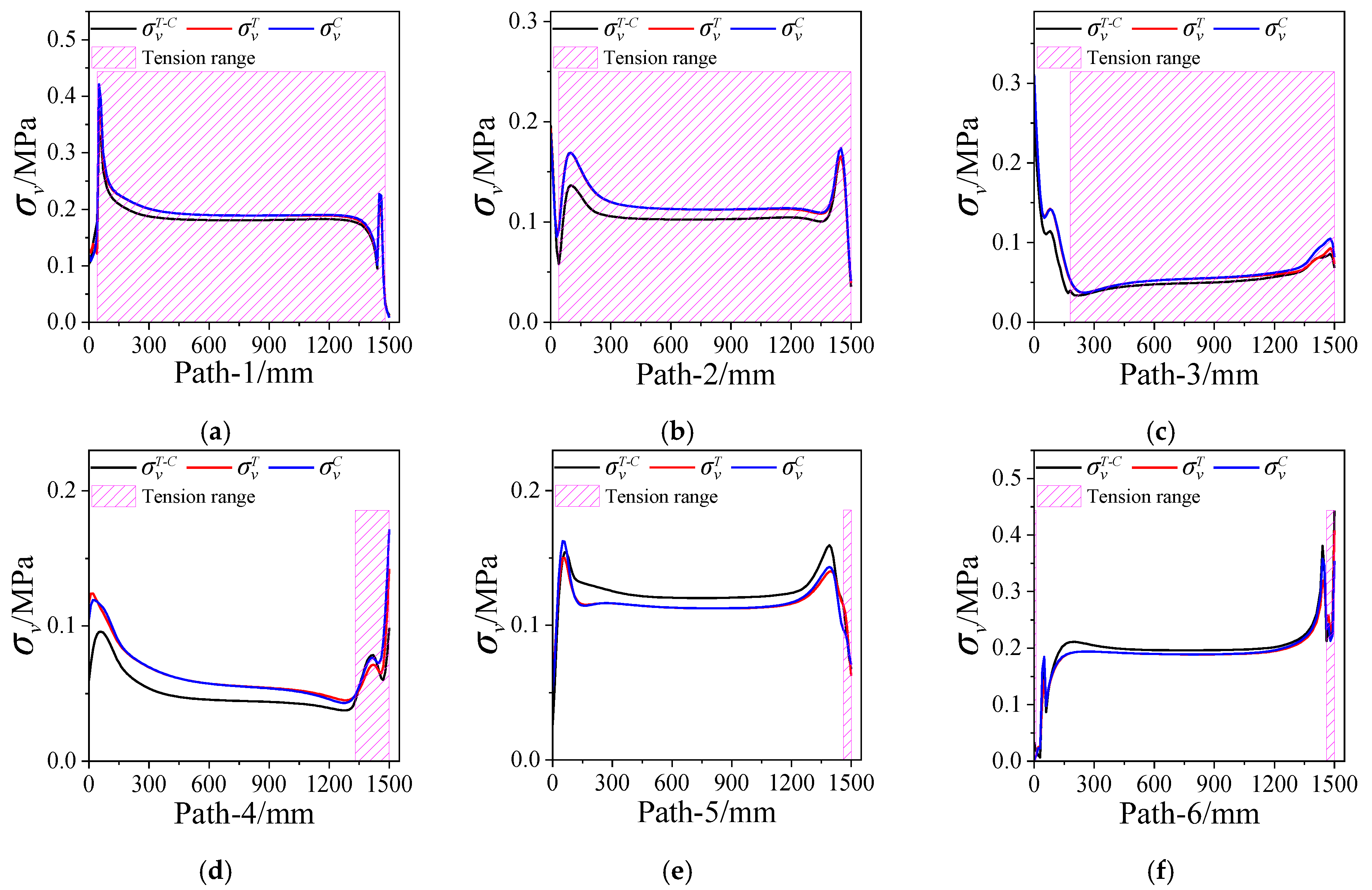
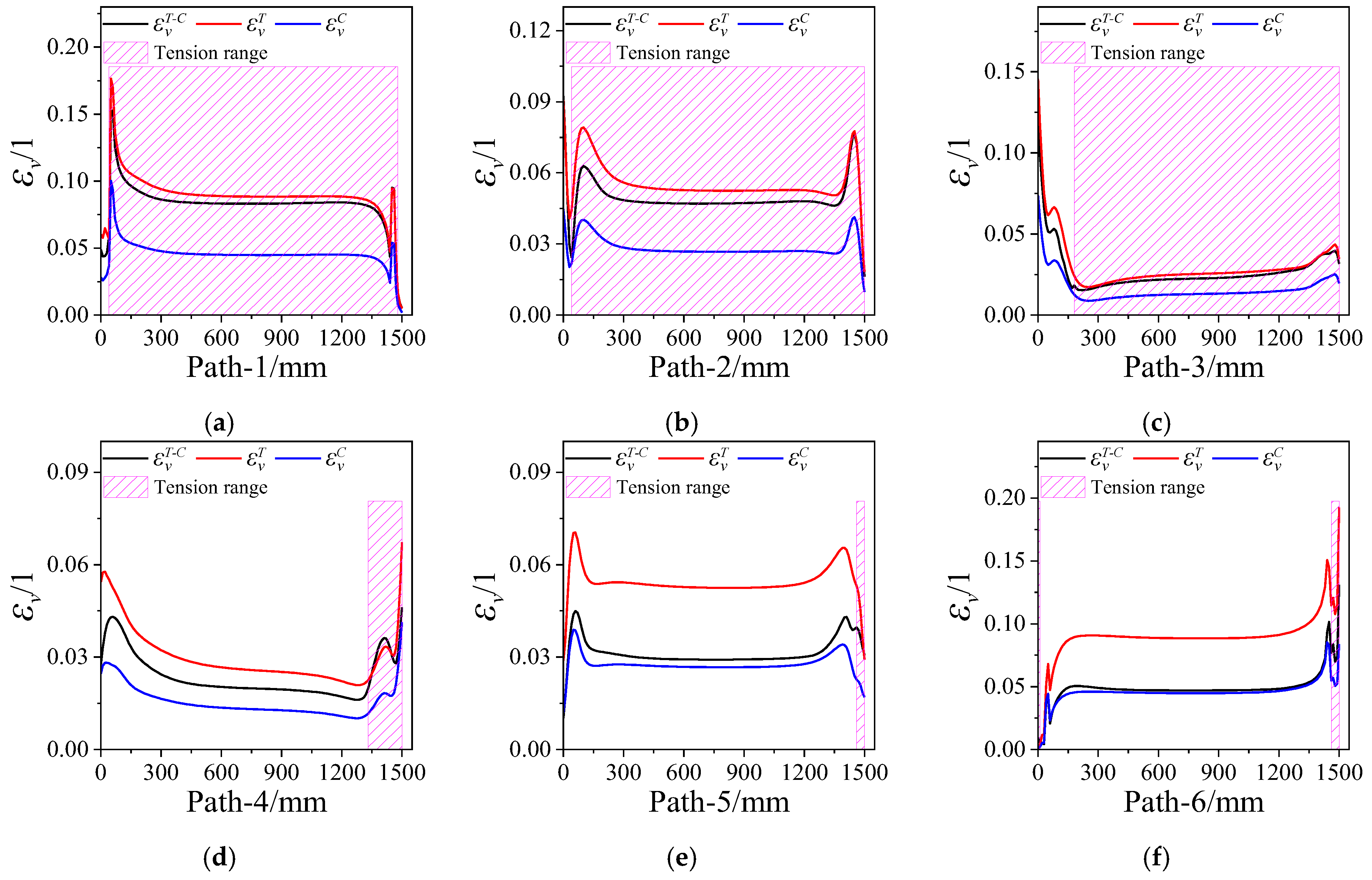
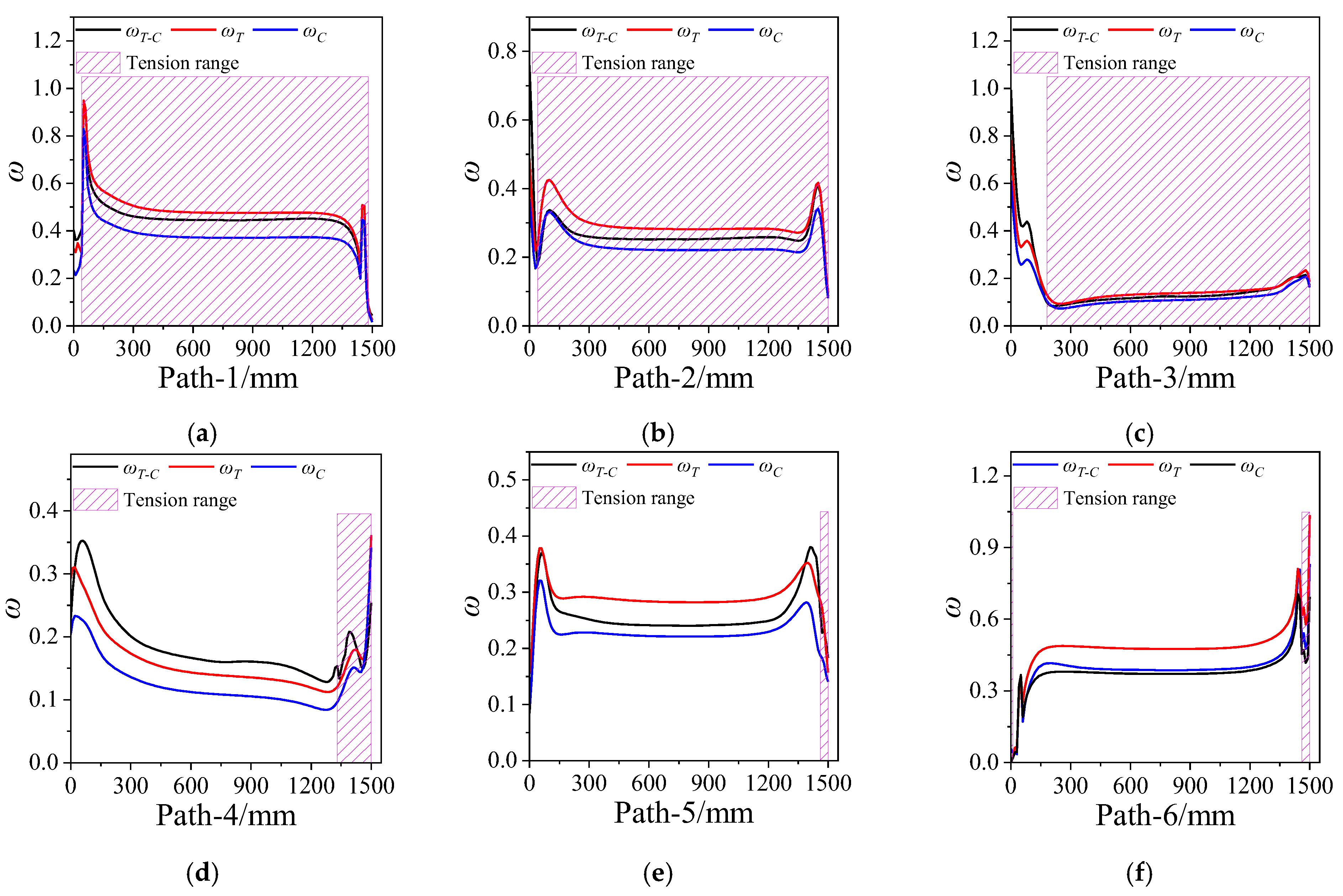
4.1. Mechanical Response
4.2. Structural Integrity Analysis
5. Conclusions
- (1)
- The mechanical state of the NEPE propellant grain is the coexistence of tension and compression under the combined axial and transverse overloads, and the tension and compression regions in the propellant grain is independent of the propellant constitutive behavior.
- (2)
- The tension–compression asymmetry of the propellant mechanical properties has a certain impact on its mechanical response. The maximum equivalent stress and strain considering the tension–compression asymmetry falls between that obtained with the tension and compression constitutive model, and is the same as damage coefficient.
- (3)
- The safety factor of the NEPE propellant grain considering the tension–compression asymmetry of its mechanical properties is larger than that non-considering, and the traditional method of structural integrity assessment is conservative.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Hufferd, W.L.; Fitzgerald, J.E. JANNAF Solid Propellant Structural Integrity Handbook; Chemical Propulsion Information Agency: Laurel, MD, USA, 1987. [Google Scholar]
- Shen, L.L.; Shen, Z.B.; Li, H.Y.; Zhang, Z.Y. A Voronoi Cell Finite Element Method for Estimating Effective Mechanical Properties of Composite Solid Propellants. J. Mech. Sci. Technol. 2017, 31, 5377–5385. [Google Scholar] [CrossRef]
- Wang, Z.J.; Qiang, H.F.; Wang, G.; Hang, Q.Z. Tensile Mechanical Properties and Constitutive Model for HTPB Propellant at Low Temperature and High Strain Rate. J. Appl. Polym. Sci. 2015, 132, 365–368. [Google Scholar] [CrossRef]
- Ramshorst, M.C.J.; Benedetto, G.L.; Duvalois, W.; Hooijmeijer, P.A.; Heijden, A.E.D.M. Investigation of the Failure Mechanism of HTPB/AP/Al Propellant by In-Situ Uniaxial Tensile Experimentation in SEM. Propellants Explos. Pyrotech. 2016, 41, 700–708. [Google Scholar] [CrossRef]
- Marimuthu, R.; Nageswara Rao, B. Development of Efficient Finite Elements for Structural Integrity Analysis of Solid Rocket Motor Propellant Grains. Int. J. Press. Vessel. Pip. 2013, 111–112, 131–145. [Google Scholar] [CrossRef]
- Tong, X.; Chen, X.; Xu, J.S.; Zheng, Y.; Zhi, S.J. The Heat Build-up of A Polymer Matrix Composite under Cyclic Loading: Experimental Assessment and Numerical Simulation. Int. J. Fatigue 2018, 116, 323–333. [Google Scholar] [CrossRef]
- Majerus, J.N.; Tamekuni, M. Effects of Material Nonlinearity and Failure Criteria upon Solid-Propellant Integrity. J. Spacecr. Rocket. 1966, 3, 393–399. [Google Scholar] [CrossRef]
- Ren, P.; Hou, X.; He, G.R.; Gao, J.; He, T.S. Comparative Research of Tensile and Compressive Modulus of Composite Solid Propellant for Solid Rocket Motor. J. Astronautic. 2010, 31, 2354–2359. [Google Scholar]
- Wang, Z.J.; Qiang, H.F.; Wang, G.; Geng, B. Strength Criterion of Composite Solid Propellants under Dynamic Loading. Def. Technol. 2018, 14, 457–462. [Google Scholar] [CrossRef]
- Wu, W.J.; Li, H.Y.; Shen, Z.B.; Cui, H.R. Research on Constant Speed Tension and Compression Mechanical Properties of Azide Polyether Propellant. Propellants Explos. Pyrotech. 2022, 7, e202200055. [Google Scholar] [CrossRef]
- Zhang, X.J.; Chang, X.L.; Lai, J.W.; Hu, K. Comparative Research of Tensile and Compressive Mechanical Properties of HTPB Propellant at Low Temperature. J. Solid Rocket. Technol. 2013, 36, 771–774. (In Chinese) [Google Scholar]
- Wang, H.L.; Xu, J.S.; Zhou, C.S.; Jin, Q.M. Research on the Asymmetrical Mechanical Properties in Tension and Compression of Modified Double base Propellant. J. Solid Rocket. Technol. 2017, 40, 341–346+352. (In Chinese) [Google Scholar]
- Betten, J.; Sklepus, S.; Zolochevsky, A. A Creep Damage Model for Initially Isotropic Materials with Different Properties in Tension and Compression. Eng. Fract. Mech. 1998, 59, 623–641. [Google Scholar] [CrossRef]
- Mahnken, R.; Shaban, A. Finite Elasto-Viscoplastic Modeling of Polymers Including Asymmetric Effects. Arch. Appl. Mech. 2013, 83, 53–71. [Google Scholar] [CrossRef]
- Ambartsumyan, C.A. Elasticity Theory of Different Moduli; Wu, R.F.; Zhang, Y.Z., Translators; China Railway Publishing House: Beijing, China, 1986. [Google Scholar]
- Latorre, M.; Montans, F.J. Bi-modulus Materials Consistent with A Stored Energy Function: Theory and Numerical Implementation. Comput. Struct. 2020, 229, 106176. [Google Scholar] [CrossRef]
- He, X.T.; Zheng, Z.L.; Sun, J.Y.; Li, Y.M.; Chen, S.L. Convergence Analysis of A Finite Element Method Based on Different Moduli in Tension and Compression. Int. J. Solids Struct. 2009, 46, 3734–3740. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Zhang, H.W.; Wu, J.; Yan, B. A Stabilized Complementarity Formulation for Nonlinear Analysis of 3D Bimodular Materials. Acta Mech. Sin. 2016, 32, 481–490. [Google Scholar] [CrossRef]
- Wang, L.L.; Dong, X.L.; Sun, Z.J. Dynamic Constitutive Behavior of Materials at High Strain Rate Taking Account of Damage Evolution. Explos. Shock. Waves 2006, 26, 193–198. (In Chinese) [Google Scholar]
- Sun, C.X.; Ju., Y.T.; Zheng., Y.; Wang., P.B.; Zhang., J.F. Mechanical Properties of Double-Base Propellant at High Strain Rates and its Damage-Modified ZWT Constitutive Model. Explos. Shock. Waves 2013, 33, 507–512. (In Chinese) [Google Scholar]
- Li, H.; Wang, S.X.; Li, M.; Xu, J.S.; Fan, X.G.; Chen, X. Experimental Research on Tensile Mechanical Properties of NEPE Propellant under Confining Pressure. Propellants Explos. Pyrotech. 2020, 45, 1769–1779. [Google Scholar] [CrossRef]
- Li, H.; Xu, J.S.; Chen, X.; Hou, Y.F.; Fan, X.G.; Li, M.; Li, H.W. Experimental Investigation and Modeling the Compressive Behavior of NEPE Propellant under Confining Pressure. Propellants Explos. Pyrotech. 2021, 46, 1023–1035. [Google Scholar] [CrossRef]
- Swanson, S.R.; Christensen, L.W. A Constitutive Formulation for High-Elongation Propellants. J. Spacecraft. Rocket. 2012, 20, 559–566. [Google Scholar] [CrossRef]
- Haj-Ali, R.M.; Muliana, A.H. A Micromechanical Constitutive Framework for the Nonlinear Viscoelastic Behavior of Pultruded Composite Materials. Int. J. Solids Struct. 2003, 40, 1037–1057. [Google Scholar] [CrossRef]
- Haj-Ali, R.M.; Muliana, A.H. Numerical Finite Element Formulation of the Schapery Non-linear Viscoelastic Material Model. Int. J. Numer. Methods Eng. 2004, 59, 25–45. [Google Scholar] [CrossRef]
- Sun, J.Y.; Zhu, H.Q.; Qin, S.H.; Yang, D.L.; He, X.T. A Review on the Research of Mechanical Problems with Different Moduli in Tension and Compression. J. Mech. Sci. Technol. 2010, 24, 1845–1854. [Google Scholar] [CrossRef]






| E−/E+ = 1 | E−/E+ = 2 | E−/E+ = 5 | E−/E+ = 10 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| z (m) | uz* (10−3 m) | uz (10−3 m) | error (%) | uz* (10−3 m) | uz (10−3 m) | error (%) | uz* (10−3 m) | uz (10−3 m) | error (%) | uz* (10−3 m) | uz (10−3 m) | error (%) |
| 2 | −4.80 | −4.80 | 0 | −4.80 | −4.80 | 0 | −4.80 | −4.80 | 0 | −4.80 | −4.80 | 0 |
| 4 | −8.00 | −8.00 | 0 | −8.00 | −8.00 | 0 | −8.00 | −8.00 | 0 | −8.00 | −8.00 | 0 |
| 5 | −9.00 | −9.00 | 0 | −9.00 | −9.00 | 0 | −9.00 | −9.00 | 0 | −9.00 | −9.00 | 0 |
| 7 | −9.80 | −9.80 | 0 | −9.80 | −9.80 | 0 | −9.80 | −9.80 | 0 | −9.80 | −9.80 | 0 |
| 8 | −9.60 | −9.60 | 0 | −9.40 | −9.41 | 0.11 | −8.80 | −8.81 | 0.14 | −7.80 | −7.81 | 0.13 |
| 9 | −9.00 | −9.00 | 0 | −8.20 | −8.21 | 0.12 | −5.80 | −5.81 | 0.17 | −1.80 | −1.82 | 1.11 |
| 10 | −8.00 | −8.00 | 0 | −6.20 | −6.21 | 0.16 | −0.80 | −0.81 | 1.25 | 8.20 | 8.17 | 0.37 |
| σm/MPa | α/MPa | E1/MPa | θ1/s | E2/MPa | θ2/s | m/1 | η/1 | εth/1 | |
|---|---|---|---|---|---|---|---|---|---|
| Tensile state | 6.771 | 0.2473 | 0.1334 | 0.1161 | 0.4527 | 1.259 | 1.798 | 1.502 | 0.186 |
| Compressive state | 20.002 | 0.1 | 1.909 | 19.476 | 0.15 | 228.437 | 0.989 | 0.512 | 0.101 |
| Parameter | Case | Insulation | Propellant |
|---|---|---|---|
| Density/(kg/m3) | 7850 | 1220 | 1735 |
| Modulus/MPa | 1.96 × 105 | 30 | / |
| Poisson’s ratio/1 | 0.28 | 0.498 | 0.498 |
| Safety Factor | Value |
|---|---|
| ST | 1.73 |
| SC | 4.98 |
| ST−C | 5.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Han, W.; Zhou, D.; Wu, H. Structural Integrity Assessment of an NEPE Propellant Grain Considering the Tension–Compression Asymmetry in Its Mechanical Property. Polymers 2023, 15, 3339. https://doi.org/10.3390/polym15163339
Zhang P, Han W, Zhou D, Wu H. Structural Integrity Assessment of an NEPE Propellant Grain Considering the Tension–Compression Asymmetry in Its Mechanical Property. Polymers. 2023; 15(16):3339. https://doi.org/10.3390/polym15163339
Chicago/Turabian StyleZhang, Pengjun, Wangshen Han, Dongmo Zhou, and Hanxu Wu. 2023. "Structural Integrity Assessment of an NEPE Propellant Grain Considering the Tension–Compression Asymmetry in Its Mechanical Property" Polymers 15, no. 16: 3339. https://doi.org/10.3390/polym15163339
APA StyleZhang, P., Han, W., Zhou, D., & Wu, H. (2023). Structural Integrity Assessment of an NEPE Propellant Grain Considering the Tension–Compression Asymmetry in Its Mechanical Property. Polymers, 15(16), 3339. https://doi.org/10.3390/polym15163339






