Abstract
Self-oscillating coupled machines are capable of absorbing energy from the external environment to maintain their own motion and have the advantages of autonomy and portability, which also contribute to the exploration of the field of synchronization and clustering. Based on a thermally responsive liquid crystal elastomer (LCE) spring self-oscillator in a linear temperature field, this paper constructs a coupling and synchronization model of two self-oscillators connected by springs. Based on the existing dynamic LCE model, this paper theoretically reveals the self-oscillation mechanism and synchronization mechanism of two self-oscillators. The results show that adjusting the initial conditions and system parameters causes the coupled system to exhibit two synchronization modes: in-phase mode and anti-phase mode. The work conducted by the driving force compensates for the damping dissipation of the system, thus maintaining self-oscillation. The phase diagrams of different system parameters are drawn to illuminate the self-oscillation and synchronization mechanism. For weak interaction, changing the initial conditions may obtain the modes of in-phase and anti-phase. Under conditions of strong interactions, the system consistently exhibits an in-phase mode. Furthermore, an investigation is conducted on the influence of system parameters, such as the LCE elastic coefficient and spring elastic coefficient, on the amplitudes and frequencies of the two synchronization modes. This study aims to enhance the understanding of self-oscillator synchronization and its potential applications in areas such as energy harvesting, power generation, detection, soft robotics, medical devices and micro/nanodevices.
1. Introduction
Self-oscillation refers to the phenomenon where a system generates sustained oscillations or periodic changes without external excitation, due to internal coupling and feedback mechanisms [1,2,3,4,5,6,7]. As a result, self-oscillating systems do not require a continuous energy supply from external sources, reducing energy consumption and system complexity. These systems can be adjusted and controlled by tuning internal parameters and coupling methods. Additionally, self-oscillating systems exhibit great flexibility capable of displaying various oscillatory behaviors such as periodic oscillations [8,9] and chaotic oscillations [10,11,12]. Various feedback mechanisms have been suggested to counteract energy loss attributed to damping dissipation, including the coupling of chemical reactions and large deformations [13,14,15], as well as the self-shading mechanism [16]. Currently, self-oscillation systems are widely used in various scientific and engineering fields, such as sensor technology [10,17,18,19,20,21,22], soft robots [23,24] and so on.
In recent years, the exploration of active materials has further expanded the possibilities of self-oscillating systems. Through ongoing research and development, scientists continue to discover new active materials with unique properties and enhanced performance, such as dielectric elastomers [25], hydrogels [26,27], ionic gels [13], thermal response polymers [28] and liquid crystal elastomer (LCE) [29,30,31]. These active substances produce different responses when stimulated by light [7], heat [9], electricity [32] and magnetism [33], and a variety of self-sustained motion modes have been established according to this property, for example, torsion [34,35], vibration [6,36,37], bending [38,39,40,41,42], swing [43], rolling [44], oscillating [45], jumping [46,47], rotation [48], buckling [49,50], twisting [51], stretching [52], eversion or inversion [53] and other movements. LCE, a unique material, possesses a hybrid nature that combines the characteristics of both liquid crystals and elastomers, which constitutes a polymer network structure resulting from the cross-linking of liquid crystal monomer molecules. It is capable of making reversible morphological changes when exposed to external stimuli, including light, electricity, heat and magnetism. Therefore, LCE as a driver and deformation structure has the advantages of fast feedback speed, simple control, low noise [54,55,56,57,58] and so on. At present, a lot of work has been carried out on the experimental and theoretical research of self-oscillation based on LCE.
Despite the extensive research conducted on individual self-oscillator, there is still much to explore regarding the interplay and collective effect of multiple self-oscillators. Synchronization is found everywhere in nature, from the cardiac pacemaker cells to the migration of species, from pendulums to musical instruments, power systems, and lasers, and has many practical applications in electrical and mechanical engineering [59,60,61,62,63]. The roots of synchronization research date back to the 17th-century observation and discovery by the Dutch scientist Huygens of the synchronous behavior of two coupled pendulums [64]. He found that when two coupled pendulums are located on the same beam, they oscillate synchronously in opposite directions. Finally, it is found that the anti-phase synchronization between two pendulums is achieved by the tiny vibrations propagated by the beam, that is, by beam coupling [65]. In recent years, there are more and more research projects on how to apply the synchronization phenomenon to various fields, such as nonlinear systems [66,67,68] and complex network synchronization behavior [69,70,71,72].
Currently, there are few research studies on the interaction and synchronization of self-oscillation systems with multiple responsive materials. Li et al. investigated the synchronization of two coupled light-driven self-oscillating LCE pendulums [7]. The collective motion of two joint LCE oscillators based on the self-shadowing effect was investigated by Du et al. [73]. To achieve more functions and applications, further investigation is warranted to explore the synchronization phenomenon and its underlying mechanisms. This paper is based on the study of thermally responsive LCE spring self-oscillators in a linear temperature field, focusing on the synchronization behavior of two identical self-oscillators connected by springs and their mechanism. Based on the well-established dynamic LCE model [74,75,76], the mechanisms of self-oscillation and synchronization are theoretically investigated. The revelation of the interaction and synchronization mechanism among multiple self-oscillators is helpful to enhance the understanding of self-oscillator synchronization and its potential applications in areas such as energy harvesting, power generation, detection, soft robotics, medical devices and micro/nanodevices. In addition, the research in this paper has the potential to be extended to large-scale synchronization systems containing a large number of coupled oscillators, which has a promising application in this field.
The structure of this document is as follows. In Section 2, the dynamic model of the LCE spring oscillator is developed in conjunction with a well-established LCE dynamic model, and the governing equations of the synchronized system under a linear temperature field are derived. In Section 3, two synchronization modes of self-oscillation are proposed and the mechanisms of self-oscillation and synchronization are elaborated. In Section 4, the effects of the LCE elastic coefficient, spring elastic coefficient, thermal expansion coefficient, temperature gradient, first damping coefficient, second damping coefficient and characteristic time on the amplitude and frequency of the synchronization system are studied in detail. Finally, the conclusions of this paper are summarized in Section 5.
2. Model and Theoretical Formulation
In the current section, a coupled self-oscillating system consisting of two LCE fibers and a linear spring under a linear temperature field is proposed. Meanwhile, the governing equations and solution methods of the system are given.
2.1. Dynamic Model of Two LCE Spring Oscillators
Figure 1 illustrates the coupled self-oscillating system within a linear temperature field, which consists of two identical LCE spring oscillators connected by two springs. In the non-stress state, the primary length of the LCE fiber is and the primary length of the spring is , as shown in Figure 1a. According to Yakacki et al. [28], LC monomer (RM257) and cross-linking agent (PETMP), etc., are used as raw materials, and LCE fibers can be made by a two-step cross-linking reaction. First, one end of the LCE fiber is fixed, while another end is connected with a spring. The lower end of the spring is connected with another spring through a fixed pulley so that the two LCE fibers can be connected in series. To ensure that the system is force stabilized, the LCE fiber and the spring should be pre-stretched, where the prestretch amount is , , respectively. In the state of equilibrium, the lengths of the LCE fibers and the springs are and , respectively, as shown in Figure 1b. Then, the equilibrium equation of the system in the non-stress state can be obtained:
where and are the initial elastic forces of the two springs, respectively; and are the initial elastic forces of two LCE fibers, respectively, where , . and are elastic coefficients of spring and LCE fiber, respectively.
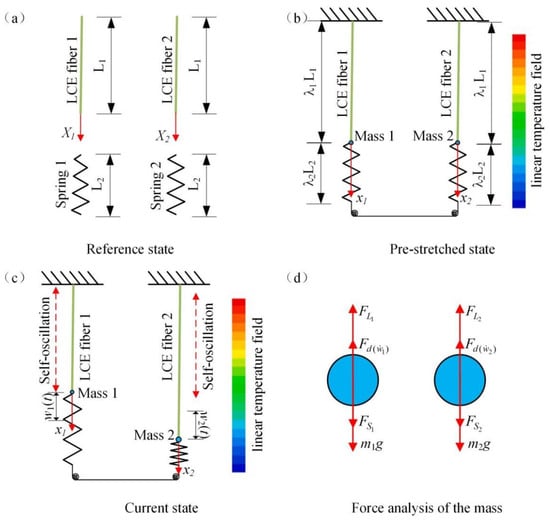
Figure 1.
Schematic diagram of two identical LCE fibers connected by two identical springs within the linear temperature field. (a) Reference state; (b) pre-stretched state; (c) current state; (d) force analysis of the mass. Two coupled LCE oscillators can vibrate synchronously within the linear temperature field.
In this case, we can obtain the relationship between λ1 and λ2, i.e.:
where , , , , , and .
When placed in the linear temperature field, LCE fibers begin to oscillate along the vertical direction, in which the displacements of particles 1 and 2 are and , respectively, as shown in Figure 1c. The force analysis diagram of the two particles is given in Figure 1d, where and are the elastic force of the two springs, respectively (referred to as spring force); and are the elastic force of two fibers (hereinafter referred to as the driving force); and and are the damping force in the process of vibration. To simplify the analysis, we make the assumption that the damping force is directly proportional to the particle’s velocity and always acts in the opposite direction to the particle’s motion. The dynamic governing equations of the system can then be obtained and can be applied at any time:
where , indicate the particle’s acceleration , , , is the particle’s velocity , , and the spring force is , .
Since the system can vibrate continuously without divergence, only nonlinear damping is studied, and it is assumed that:
where and represent the first and second damping coefficients, respectively.
2.2. Tension in the LCE Fibers
According to the non-uniform deformation of LCE fiber in a linear temperature field, the Lagrangian coordinate system , and Euler coordinate system , need to be established by taking the particle at the end of LCE fiber as the origin, as shown in Figure 1a,b. When LCE fiber vibrates, the instantaneous position and displacement of a particle can be used as , . The displacement of the particle is represented by and , respectively.
We assume that the driving force of LCE fiber is linearly dependent on strain:
where is the elastic coefficient of LCE fiber, and one-dimensional strain , is given by:
We assume that the heat-induced strain is linearly related to the temperature difference in LCE fiber:
where represents the coefficient of thermal expansion, represents thermal contraction, and represents thermal expansion.
Since the driving force is uniform and constant in the LCE fiber, it can be obtained by integrating both sides of Equation (5) from 0 to and combining with Equations (6) and (7); the driving force at the end of the LCE fiber can be written as:
Since the temperature field in LCE fiber is unevenly distributed and changes with time, heat exchange occurs between the fiber and its surroundings, resulting in a temperature distribution denoted by . For simplicity, there is an assumption that the radius R is much smaller than the length L so that the temperature field in the LCE fiber can be seen as uniform, i.e., . In this case, the temperature in the fiber can be obtained:
where indicates the characteristic time, is the heat capacity per unit length of the fiber, and is the heat transfer coefficient. Assume that the steady-state temperature field in the environment is linear:
where refers to the temperature at and represents the gradient of temperature.
By defining the following infinitesimal constants: , , , , , , , , , , , and ( is the temperature at ).
Thus, the elastic force of LCE fiber can be obtained
The solution of the temperature field is [77]:
By substituting Equation (12) into Equation (11), the elastic force of LCE fiber can be obtained:
2.3. Governing Equations
By defining , , , and combing with Equations (4) and (13), Equation (3) can be rewritten as:
Equation (14) is an ordinary differential equation with second-order variable coefficients, which is difficult to obtain its analytic solution. In this case, the classical fourth-order Runge–Kutta method is adopted to solve Equation (14) numerically, and the steady-state response of LCE fiber is obtained, meaning, the time-history curve of oscillation of the system.
3. Two Modes of Synchronization and Their Mechanisms
In the current section, two synchronization modes, namely in-phase mode and anti-phase mode, are proposed according to the dynamic Equation (14), and the self-oscillation mechanism and synchronization mechanism are elaborated in detail.
To better study the synchronization behaviors of two LCE spring oscillators, it is necessary to obtain the typical values of the dimensionless system parameters. According to the existing experiments [52,54,78,79], the actual values of system parameters are summarized in Table 1, and the dimensionless system parameters are calculated in Table 2.

Table 1.
Material properties and geometric parameters.

Table 2.
Dimensionless parameters.
3.1. Two Synchronization Modes
The time histories of mass displacements can be obtained by setting system parameters , , , , , , , . The calculation results show that there are two synchronous modes in the system, namely in-phase mode and anti-phase mode, as shown in Figure 2. In calculation, the system parameter is set to: , , , , , . When , , , the two LCE fibers with the same initial velocity first vibrate in the same direction within the linear temperature field. Then, under the influence of damping, the amplitude of self-oscillation gradually decreases and finally stops on the upper side, as shown in Figure 2a,b. Although fibers convert heat into kinetic energy when heated, the converted kinetic energy does not keep them oscillating. When , , , the fiber will continue to vibrate in the temperature field, and finally evolve into self-oscillation, as shown in Figure 2c,d. In this case, the energy obtained from the temperature field is greater than the damping dissipation, so the self-oscillation is guaranteed. When , , , the system can maintain the static mode of anti-phase mode, as shown in Figure 2e,f. As , , , Figure 2g,h plot the displacement-time diagram and phase trajectory diagram in the anti-phase mode. A similar experimental phenomenon was reported by Ghislaine et al. [69], where two liquid crystal network oscillators interacted with each other driven by light and underwent synchronized in-phase and anti-phase oscillations in the steady state.
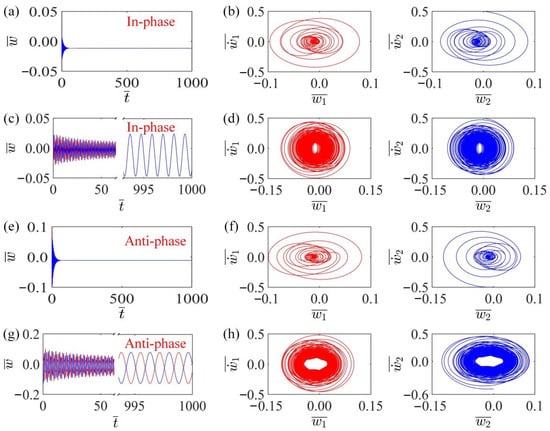
Figure 2.
Two synchronization modes and two motion states of the thermal response LCE self-excited oscillator. The parameters are , , , , , . (a,b) are stationary states in in-phase mode with parameters , , . (c,d) are the vibration states in in-phase mode with parameters , , . (e,f) are stationary states in anti-phase mode with parameters , , . (g,h) are the self-oscillation in anti-phase mode with , , . There exist two synchronous modes of the system, namely, in-phase mode and anti-phase mode.
3.2. Self-Oscillation Mechanism
To further investigate the mechanism of self-oscillation of LCE fiber within the linear temperature field, Figure 3a,b plot the time-history curves of LCE fiber for in-phase and anti-phase modes, indicating that two LCE fibers oscillate periodically within the temperature field in in-phase and anti-phase modes. Figure 3c,e plot the curve of the tension of LCE fiber and spring changing with time in in-phase mode, indicating that the tension of LCE fiber and spring change periodically. Figure 3d,f plot the time-varying curves of the driving force and spring force in anti-phase mode, which indicate that the tension of LCE fiber and spring also maintain periodic changes in anti-phase mode.
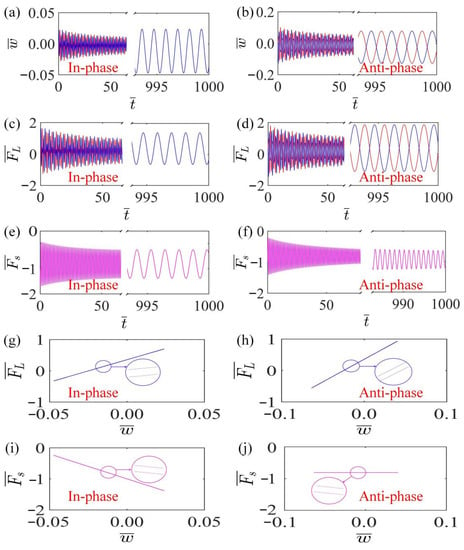
Figure 3.
Self-oscillation mechanism of thermally responsive coupled LCE self-oscillators. The parameters for the in-phase mode are , , , , , , , , ; the parameters for the anti-phase mode are , , , , , , , , . (a,b) Time-history curves for in-phase and anti-phase modes; (c,d) change curve of driving force with time in in-phase and anti-phase modes; (e,f) spring force versus time curves for in-phase and anti-phase modes; (g,h) curves of the work done by the driving force for in-phase and anti-phase modes; (i,j) curves of the work carried out by the spring force for in-phase and anti-phase modes. The energy absorbed by the system from the external environment compensates for the damping dissipation, thus maintaining the self-oscillation of the system.
Figure 3g,i show that in the in-phase mode, the LCE fiber and spring tension, along with the displacement, form hysteresis loops, and the region surrounded by the hysteresis loops represents the work done by the LCE fiber tension and spring force. The work done by the driving force of LCE fiber represents the energy input of the system, while the work done by the spring represents the work expended by the resistance. When the energy gain is equal to the resistance dissipation, the system will maintain self-oscillation. Figure 3h,j draw the hysteresis loops of the driving force of LCE fiber and spring force in anti-phase mode, which refers to the same energy compensation mechanism as the case of the in-phase mode.
3.3. Synchronization Mechanism
To better study the mechanism of synchronization between two LCE fibers after self-oscillation in a linear temperature field, we plot some key physical quantities in the process of self-oscillation. Figure 4a,b draw the time-history curves for in-phase and anti-phase modes. Figure 4c,d, respectively, draw the change curve of the phase difference between fiber 1 and fiber 2 for in-phase and anti-phase modes. Figure 4c,d show that in the in-phase mode, the phase difference gradually decreases until it reaches zero, while in the anti-phase mode, the phase difference finally reaches a fixed value which is equal to half a cycle.
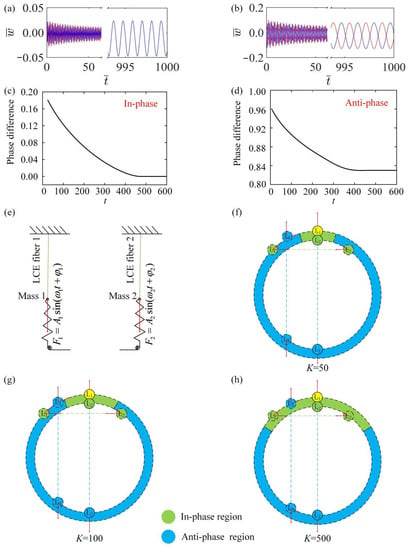
Figure 4.
Synchronization mechanism of LCE spring oscillator. The parameters for the in-phase mode are , , , , , , , , ; the parameters for the anti-phase mode are , , , , , , , , . (a,b) Time history curve for in-phase and anti-phase modes; (c,d) phase difference curve for in-phase and anti-phase modes; (e) model of additional periodic forces applied; (f–h) schematic diagram of the interaction between phase attraction (in-phase region) and phase repulsion (anti-phase region) of two coupled harmonic oscillators. Two coupled harmonic oscillators always produce in-phase mode under strong interaction, while they may produce in-phase and anti-phase modes by changing the initial conditions under weak interaction.
Through careful calculation, it is found that when the initial velocity directions of two self-oscillators are the same, the system will always develop into a synchronous mode. However, when the initial velocity direction is opposite, there is a critical LCE elastic coefficient that triggers a transition between in-phase and anti-phase modes. This result is similar to the existing experiment in that the elasticity coefficient can affect the synchronization mode of the system [69]. When the elastic coefficient of LCE is , the system can be affected by the initial velocity, where the anti-phase synchronization mode occurs. When , the system always leads to an in-phase synchronous mode. In the case of weak interaction, i.e., , the system can be likened to being acted on by external forces, as shown in Figure 4e. The system is divided into two LCE self-exciter separately for discussion. In the in-phase mode, each LCE oscillator is equivalent to applying an additional cycle force to another oscillator, which can be expressed as and . When the periodic force is consistent with the frequency of the harmonic oscillator, the synchronization phenomenon occurs. The same is true in the anti-phase mode.
Under the weak interaction, Figure 4f–h plots the changes in the system synchronization mode by changing the velocity of when the initial velocity of is fixed. As shown in Figure 4f–h, the ring represents the phase change in the process of movement. When the velocity of is unchanged, the position of does not change. When the velocity of is in the blue region, the system can achieve anti-phase mode, because the phases of the two repel each other. It can be seen from Figure 4f–h that an increase in the LCE elasticity coefficient leads to an increase in the synchronization region until, finally, the synchronization region covers all regions.
4. Parametric Analysis
In Equation (14), there are seven dimensionless parameters: , , , , , and , which will affect the motion process of the system. This section discusses the influence of these system parameters on the amplitude and frequency of self-oscillation in in-phase and anti-phase modes.
4.1. Effect of LCE Elasticity Coefficient
In Figure 5a,b, the amplitude and frequency of the system change with the change of LCE fiber elasticity coefficient in in-phase and anti-phase modes. Figure 5a,b show that when , no matter in which mode, the system always achieves a static state, because the driving force is less than the initial elastic force of the spring, and the LCE oscillator cannot vibrate, i.e., the amplitude and frequency are 0. When , the amplitude and frequency of the system gradually increase with the increase of . These results can be understood through the energy input and dissipation of damping. With the increase of , the driving force gradually increases, and the energy supply from the linear temperature field gradually increases, so the amplitude and frequency of the self-oscillation increase. Figure 5c,d draw the limit cycles of different in two modes. Figure 5c,d show that there is a limit value for the static state and self-excited state in the two synchronous modes, namely .
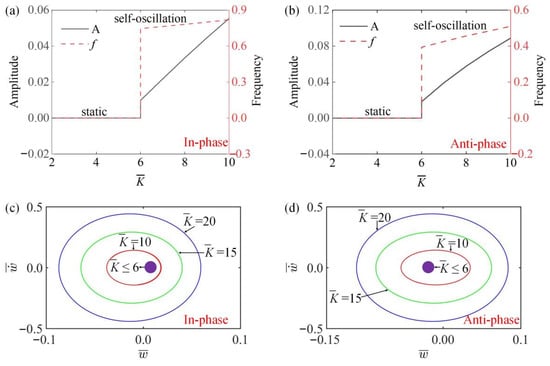
Figure 5.
The influence of LCE elastic coefficient on amplitude and frequency. The parameters for the in-phase mode are , , , , , , , ; the parameters for the anti-phase mode are , , , , , , , . (a,b) Time history curve of in-phase and anti-phase modes; (c,d) limit cycles of in-phase and anti-phase modes. The amplitude and frequency increase with the increase of .
4.2. Effect of Spring Elasticity Coefficient
Figure 6a,b, respectively, draw the curves of the amplitude and frequency changing with different spring elastic coefficients in the in-phase and the anti-phase modes. Figure 6a shows that in the in-phase mode, with the increase of spring elastic coefficient , the amplitude of the system gradually decreases and the frequency increases, because with the increase of , the damping dissipation increases, so the amplitude decreases gradually, while the increase of makes the spring stiffness increase, so the frequency increases gradually. Figure 6b shows that the amplitude and frequency of the system remain basically unchanged in the anti-phase mode. This is because in inverting mode, the two LCE fibers move in opposite directions and at equal distances, so the total length of the spring connected to the lower end remains the original length, and the amplitude and frequency of the system remain the same. Figure 6c,d show the different limit cycles with different spring elastic coefficients in two modes. The results show that the system is always in a vibration state in in-phase mode or anti-phase mode, and its motion mode is independent of .
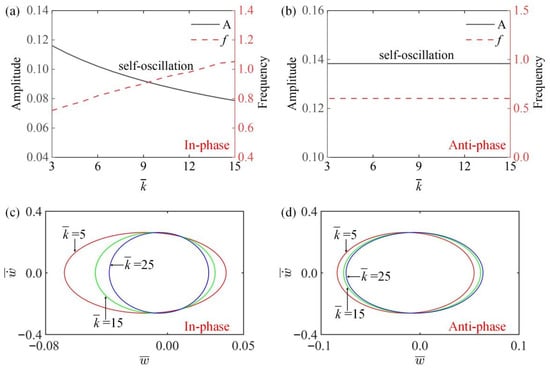
Figure 6.
The influence of spring elastic coefficient on amplitude and frequency. The parameters for the in-phase mode are , , , , , , , ; the parameters for the anti-phase mode are , , , , , , , . (a,b) Time history curve of in-phase and anti-phase modes; (c,d) limit cycles of in-phase and anti-phase modes. In the in-phase mode, the amplitude decreases and the frequency increases with the increase of spring elastic coefficient . In anti-phase mode, the amplitude and frequency are not affected by .
4.3. Effect of Thermal Expansion Coefficient
In Figure 7a,b, the amplitude and frequency of the system change with different thermal expansion coefficients in the in-phase and the anti-phase modes. It can be seen from Figure 7a,b that when , the system in two modes is in a static state, and the amplitude and frequency are zero. When , the amplitude increases with the increase of the absolute value of , and the frequency is unaffected, because the driving force gradually increases with the increase of , so the amplitude gradually increases. Figure 7c,d draw the images of limit cycles changing with different thermal expansion coefficients in the in-phase and the anti-phase modes. Figure 7 shows that there is a critical value for both static state and vibration state in two modes, namely .
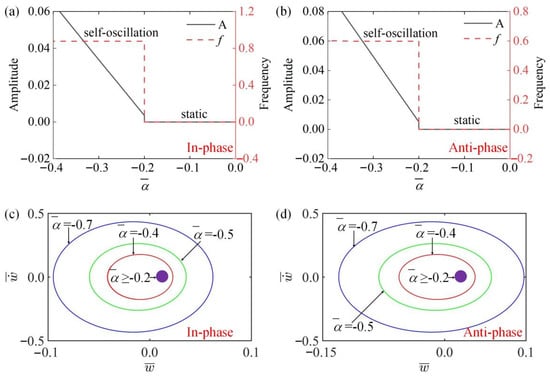
Figure 7.
The influence of thermal expansion coefficient on amplitude and frequency. The parameters for the in-phase mode are , , , , , , , ; the parameters for the anti-phase mode are , , , , , , , . (a,b) Time history curve of in-phase and anti-phase modes; (c,d) limit cycles of in-phase and anti-phase modes. The amplitudes in two modes increase as the absolute value of increases, while the frequencies remain constant.
4.4. Effect of Temperature Gradient
Figure 8a,b plot the variation curves of amplitude and frequency of the system along with temperature gradient in the in-phase and anti-phase modes. Figure 8a,b show that when , the system is in a static state, where the amplitude and frequency are 0. On the contrary, when , the amplitude of two modes increases with the increase of , while the frequency is unchanged, which can be understood through energy input and damping dissipation because with the increase of , the temperature of the temperature field gradually increases, and the driving force gradually increases, so the amplitude gradually increases. In Figure 8c,d, the limit cycles change with different temperature gradients in two modes. It can be seen that there is a critical value for both static state and self-oscillation state in in-phase and anti-phase modes.
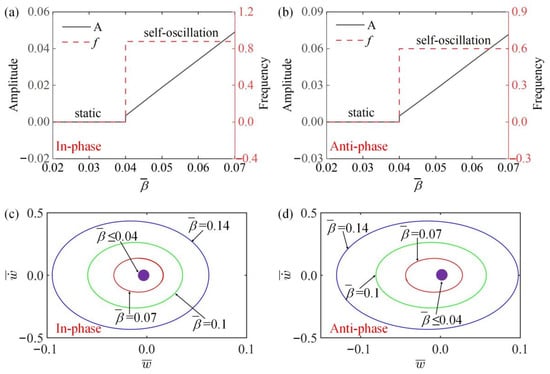
Figure 8.
The influence of temperature gradient on amplitude and frequency. The parameters for the in-phase mode are , , , , , , , ; the parameters for the anti-phase mode are , , , , , , , . (a,b) Time history curve of in-phase and anti-phase modes; (c,d) limit cycles of different modes. The amplitude of self-oscillation increases with the increase of , and the frequency remains unchanged.
4.5. Effect of the First Damping Coefficient
Figure 9a,b show the variation curves of the amplitude and frequency with the change of the first damping coefficient in the in-phase and anti-phase modes. It can be seen from Figure 9a,b that when , the system is in static states, and the amplitude and frequency are 0. When , the amplitude of both the in-phase and the anti-phase modes decreases with the increase of , while the frequency is unaffected, because with the increase of , the work carried out by damping increases and the energy dissipation of the system increases, so the amplitude gradually decreases. In Figure 9c,d, the limit cycles change with the change of the first damping coefficient in the two modes. The results show that the same limit value exists in the static state and vibration state of the in-phase and the anti-phase modes, namely, .
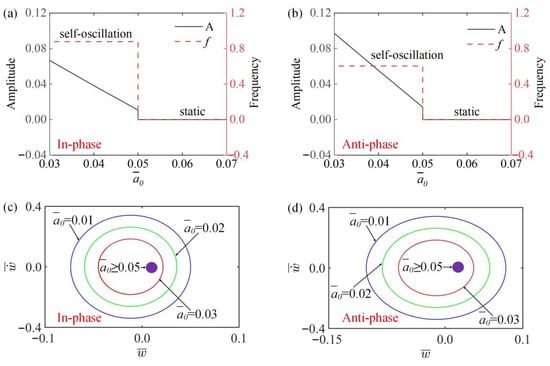
Figure 9.
The influence of first damping coefficient on amplitude and frequency. The parameters for the in-phase mode are , , , , , , , ; the parameters for the anti-phase mode are , , , , , , , . (a,b) Time history curve of in-phase and anti-phase modes; (c,d) limit cycles of two modes. The amplitude of self-oscillation decreases with the increase of , while the frequency remains unchanged.
4.6. Effect of the Second Damping Coefficient
Figure 10a,b show that the amplitude and frequency of the self-oscillation change with the change of the second damping coefficient in the in-phase and the anti-phase modes. It can be seen from Figure 10 that the amplitude of the system decreases gradually as the second damping coefficient increases in the in-phase and the anti-phase modes, while the frequency remains unchanged. This is because as increases, the damping dissipation increases and so the amplitude gradually decreases. Figure 10c,d draw the images of the change of limit cycles with different second damping coefficients in two modes. The results indicate that the system is always in a vibration state in in-phase and anti-phase modes, and its motion mode is independent of .
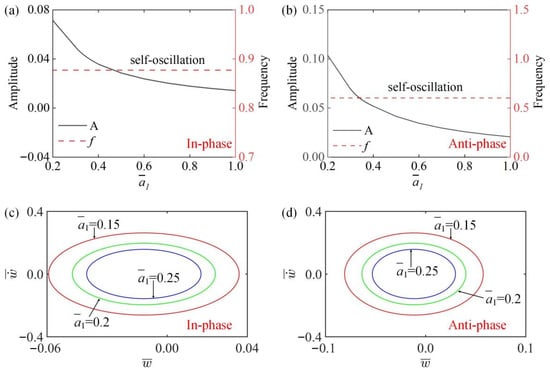
Figure 10.
The influence of second damping coefficient on amplitude and frequency. The parameters for the in-phase mode are , , , , , , , ; the parameters for the anti-phase mode are , , , , , , , . (a,b) Time history curve of in-phase and anti-phase modes; (c,d) limit cycles of in-phase mode and anti-phase mode. In both in-phase mode and anti-phase mode, the amplitude decreases as the second damping coefficient increases, while the frequency remains constant.
4.7. Effect of the Characteristic Time
In Figure 11a,b, the amplitude and frequency change with different characteristic times in the in-phase and the anti-phase modes. The results show that in both modes, when , the system is in a static state and the amplitude and frequency are 0. At , the amplitude of the self-oscillation increases as increases, and the frequency stays the same, because with the increase of , the heat transfer rate in LCE fiber increases, resulting in the gradual increase of driving force , so the amplitude gradually increases. Figure 11c,d draw the images of limit cycles changing with different temperature gradients in in-phase and anti-phase modes. It can be obtained that there is a critical value for triggering the self-oscillators in both modes.
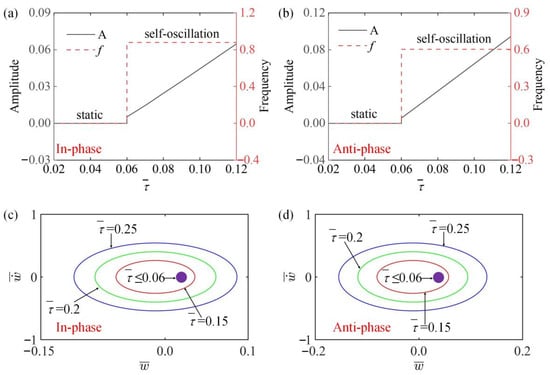
Figure 11.
The influence of characteristic time on amplitude and frequency. The parameters for the in-phase mode are , , , , , , , ; the parameters for the anti-phase mode are , , , , , , , . (a,b) Time history curve of in-phase and anti-phase modes; (c,d) limit cycles for different parameters. The amplitude of both modes increases with the increase of , while the frequency remains unchanged.
5. Conclusions
The prevalence of synchronization and collective behaviors among self-excited coupled oscillators in nature necessitates investigation due to their inherent benefits, such as efficient energy harvesting, autonomous operation, and enhanced equipment portability. In this paper, based on thermally responsive LCE spring self-oscillators under a linear temperature field, the synchronous behavior of two coupled self-oscillators connected by springs is theoretically investigated. The mechanisms of self-oscillation and synchronization are theoretically investigated, integrating the well-established dynamic LCE model. According to the numerical findings, the system exhibits two synchronization modes: the in-phase mode and the anti-phase mode. Self-oscillations are sustained through a dynamic balance between damped dissipation and work carried out by the driving force.
The numerical findings indicate that the synchronization mode primarily depends on the interaction between two LCE self-oscillators. In cases of strong interaction with the elastic coefficient of LCE, the system consistently develops into the in-phase synchronous mode. However, when the interaction is weak, altering the initial conditions can lead to the in-phase and anti-phase modes. When the initial velocity direction of the two self-oscillators is the same or the initial velocity direction is opposite but the value is small, the system achieves the in-phase synchronous mode. On the contrary, as the initial velocity direction of the two self-oscillators is opposite and the relative value is large, the system evolves into an anti-phase synchronization mode.
In addition, the influences of the LCE elastic coefficient, spring elastic coefficient, thermal expansion coefficient and other system parameters on the synchronous mode, amplitude and frequency of the self-oscillations are systematically studied. The self-oscillation amplitude demonstrates a positive correlation with the increase of LCE elastic coefficient, thermal expansion coefficient, temperature gradient and characteristic time, while demonstrates a negative correlation with the increase of spring elastic coefficient and damping coefficient. Unlike existing work about self-oscillating synchronization systems based on active materials [7,70], this paper elucidates in detail the mechanism of the synchronization phenomenon. This study is expected to advance the comprehension of self-oscillator synchronization and provide its potential applications in diverse fields, including energy harvesting, power generation, detection, soft robotics, medical devices and micro/nanodevices. In addition, the research in this paper has the potential to be extended to large-scale synchronization systems containing a large number of coupled oscillators, which has a promising application in this field.
Author Contributions
The contribution of the authors is as follows: Data Curation, Visualization, Validation, Methodology, Software, K.L.; Validation, Methodology, Software, Writing—Original Draft Preparation, H.W.; Methodology, Software, Writing—Original Draft Preparation, B.Z.; Validation, Writing—Reviewing and Editing, Y.D.; Conceptualization, Investigation, Supervision, Writing—Reviewing and Editing, Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the University Natural Science Research Project of Anhui Province under Grant Nos. 2022AH020029 and KJ2020A0453, the National Natural Science Foundation of China under Grant Nos. 12172001 and 12202002, and Anhui Provincial Natural Science Foundation under Grant Nos. 2208085Y01 and 2008085QA23.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.
References
- Ge, F.; Yang, R.; Tong, X.; Camerel, F.; Zhao, Y. A multifunctional dyedoped liquid crystal polymer actuator: Light-guided transportation, turning in locomotion, and autonomous motion. Angew. Chem. Int. Ed. 2018, 57, 11758–11763. [Google Scholar] [CrossRef]
- Preston, D.J.; Jiang, H.J.; Sanchez, V.; Rothemund, P.; Rawson, J.; Nemitz, M.P.; Lee, W.; Suo, Z.; Walsh, C.J.; Whitesides, G.M. A soft ring oscillator. Sci. Robot. 2019, 4, 5496. [Google Scholar] [CrossRef]
- Ding, W. Self-Excited Vibration; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Wang, X.; Tan, C.F.; Chan, K.H.; Lu, X.; Zhu, L.; Kim, S.; Ho, G.W. In-built thermo-mechanical cooperative feedback mechanism for self-propelled multimodal locomotion and electricity generation. Nat. Commun. 2018, 9, 3438. [Google Scholar] [CrossRef] [PubMed]
- Li, M.H.; Keller, P.; Li, B.; Wang, X.; Brunet, M. Light-driven side-on nematic elastomer actuators. Adv. Mater. 2003, 15, 569–572. [Google Scholar] [CrossRef]
- Zeng, H.; Lahikainen, M.; Liu, L.; Ahmed, Z.; Wani, O.M.; Wang, M.; Priimagi, A. Light-fuelled freestyle self-oscillators. Nat. Commun. 2019, 10, 5057. [Google Scholar] [CrossRef]
- Li, K.; Zhang, B.; Cheng, Q.; Dai, Y.; Yu, Y. Light-Fueled Synchronization of Two Coupled Liquid Crystal Elastomer Self-Oscillators. Polymers 2023, 15, 2886. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.; Cheng, W.; Dai, Y.; Li, K. Self-oscillating floating of a spherical liquid crystal elastomer balloon under steady illumination. Int. J. Mech. Sci. 2023, 241, 107985. [Google Scholar] [CrossRef]
- Yu, Y.; Du, C.; Li, K.; Cai, S. Controllable and versatile self-motivated motion of a fiber on a hot surface. Extreme Mech. Lett. 2022, 57, 101918. [Google Scholar] [CrossRef]
- Xu, P.; Wu, H.; Dai, Y.; Li, K. Self-sustained chaotic floating of a liquid crystal elastomer balloon under steady illumination. Heliyon 2023, 9, e14447. [Google Scholar] [CrossRef]
- Kumar, K.; Knie, C.; Bléger, D.; Peletier, M.A.; Friedrich, H.; Hecht, S.; Broer, D.; Debije, M.G.; Schening, A. A chaotic self-oscillating sunlight-driven polymer actuator. Nat. Commun. 2016, 7, 11975. [Google Scholar] [CrossRef]
- Grosso, M.; Keunings, R.; Crescitelli, S.; Maffettone, P.L. Prediction of chaotic dynamics in sheared liquid crystalline polymers. Phys. Rev. Lett. 2001, 86, 3184–3187. [Google Scholar] [CrossRef]
- Boissonade, J.; Kepper, P.D. Multiple types of spatio-temporal oscillations induced by differential diffusion in the Landolt reaction. Phys. Chem. Chem. Phys. 2011, 13, 4132–4137. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Wu, P.Y.; Cai, S.Q. Chemomechanical oscillations in a responsive gel induced by an autocatalytic reaction. J. Appl. Phys. 2014, 116, 043523. [Google Scholar] [CrossRef]
- Su, H.; Yan, H.; Zhong, Z. Deep neural networks for large deformation of photo-thermo-pH responsive cationic gels. Appl. Math. Model. 2021, 100, 549–563. [Google Scholar] [CrossRef]
- Cheng, Y.; Lu, H.; Lee, X.; Zeng, H.; Priimagi, A. Kirigami-based light-induced shape-morphing and locomotion. Adv. Mater. 2019, 32, 1906233. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Chang, L.; Hu, Y.; Huang, M.; Ji, Q.; Lu, P.; Liu, J.; Chen, W.; Wu, Y. An autonomous soft actuator with light-driven self-sustained wavelike oscillation for phototactic self-locomotion and power generation. Adv. Funct. Mater. 2020, 30, 1908842. [Google Scholar] [CrossRef]
- Chun, S.; Pang, C.; Cho, S.B. A micropillar-assisted versatile strategy for highly sensitive and efficient triboelectric energy generation under in-plane stimuli. Adv. Mater. 2020, 32, 1905539. [Google Scholar] [CrossRef] [PubMed]
- Kriegman, S.; Blackiston, D.; Levin, M.; Bongard, J. A scalable pipeline for designing reconfigurable organisms. Proc. Natl. Acad. Sci. USA 2020, 117, 1853–1859. [Google Scholar] [CrossRef]
- Hu, W.; Lum, G.Z.; Mastrangeli, M.; Sitti, M. Small-scale soft-bodied robot with multimodal locomotion. Nature 2018, 554, 81–85. [Google Scholar] [CrossRef]
- Shin, B.; Ha, J.; Lee, M.; Park, K.; Park, G.H.; Choi, T.H.; Cho, K.J.; Kim, H.Y. Hygrobot: A self-locomotive ratcheted actuator powered by environmental humidity. Sci. Robot. 2018, 3, 14. [Google Scholar] [CrossRef]
- Liao, B.; Zang, H.; Chen, M.; Wang, Y.; Lang, X.; Zhu, N.; Yang, Z.; Yi, Y. Soft Rod-Climbing Robot Inspired by Winding Locomotion of Snake. Soft Robot. 2020, 7, 500–511. [Google Scholar] [CrossRef] [PubMed]
- White, T.J.; Broer, D.J. Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers. Nat. Mater. 2015, 14, 1087–1098. [Google Scholar] [CrossRef]
- He, Q.; Yin, R.; Hua, Y.; Jiao, W.; Mo, C.; Shu, H.; Raney, J. A modular strategy for distributed, embodied control of electronics-free soft robots. Sci. Adv. 2023, 9, eade9247. [Google Scholar] [CrossRef]
- Wu, J.; Yao, S.; Zhang, H.; Man, W.; Bai, Z.; Zhang, F.; Wang, X.; Fang, D.; Zhang, Y. Liquid crystal elastomer metamaterials with giant biaxial thermal shrinkage for enhancing skin regeneration. Adv. Mater. 2021, 33, 2170356. [Google Scholar] [CrossRef]
- Yoshida, R. Self-oscillating gels driven by the Belousov-Zhabotinsky reaction as novel smart materials. Adv. Mater. 2010, 22, 3463–3483. [Google Scholar] [CrossRef]
- Hua, M.; Kim, C.; Du, Y.; Wu, D.; Bai, R.; He, X. Swaying gel: Chemo-mechanical self-oscillation based on dynamic buckling. Matter 2021, 4, 1029–1041. [Google Scholar] [CrossRef]
- Shen, Q.; Trabia, S.; Stalbaum, T.; Palmre, V.; Kim, K.; Oh, I. A multiple-shape memory polymer-metal composite actuator capable of programmable control, creating complex 3D motion of bending, twisting, and oscillation. Sci. Rep. 2016, 6, 24462. [Google Scholar] [CrossRef]
- Yakacki, C.M.; Saed, M.; Nair, D.P.; Gong, T.; Reed, S.M.; Bowman, C.N. Tailorable and programmable liquid-crystalline elastomers using a two-stage thiol-acrylate reaction. RSC Adv. 2015, 5, 18997–19001. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, R.; Jin, L.; Liu, M.; Gao, Y.; Raney, J.; Yang, S. 3D-Printed Photoresponsive Liquid Crystal Elastomer Composites for Free-Form Actuation. Adv. Funct. Mater. 2023, 33, 2210614. [Google Scholar] [CrossRef]
- Wang, Y.; Dang, A.; Zhang, Z.; Yin, R.; Gao, Y.; Feng, L.; Yang, S. Repeatable and Reprogrammable Shape Morphing from Photoresponsive Gold Nanorod/Liquid Crystal Elastomers. Adv. Mater. 2020, 32, 2004270. [Google Scholar] [CrossRef]
- Na, Y.H.; Aburaya, Y.; Orihara, H.; Hiraoka, K. Measurement of electrically induced shear strain in a chiral smectic liquid-crystal elastomer. Phys. Rev. E 2011, 83, 061709. [Google Scholar] [CrossRef] [PubMed]
- Haber, J.M.; Sanchez-Ferrer, A.; Mihut, A.M.; Dietsch, H.; Hirt, A.M.; Mezzenga, R. Liquid-crystalline elastomer-nanoparticle hybrids with reversible switch of magnetic memory. Adv. Mater. 2013, 25, 1787–1791. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Y.; Lv, J. Phototunable self-oscillating system driven by a self-winding fiber actuator. Nat. Commun. 2021, 12, 3211. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Chi, Y.; Hong, Y.; Li, Y.; Yang, S.; Yin, J. Twisting for soft intelligent autonomous robot in unstructured environments. Proc. Natl. Acad. Sci. USA 2022, 119, e2200265119. [Google Scholar] [CrossRef]
- Xu, T.; Pei, D.; Yu, S.; Zhang, X.; Yi, M.; Li, C. Design of MXene composites with biomimetic rapid and self-oscillating actuation under ambient circumstances. ACS Appl. Mater. Interfaces 2021, 13, 31978–31985. [Google Scholar] [CrossRef]
- Cunha, M.; Peeketi, A.R.; Ramgopal, A.; Annabattula, R.K.; Schenning, A. Light-driven continual oscillatory rocking of a polymer film. Open Chem. 2020, 9, 1149–1152. [Google Scholar]
- Hu, Y.; Ji, Q.; Huang, M.; Chang, L.; Zhang, C.; Wu, G.; Zi, B.; Bao, N.; Chen, W.; Wu, Y. Light-driven self-oscillating actuators with pototactic locomotion based on black phosphorus heterostructure. Angew. Chem. Int. Ed. 2021, 60, 20511–20517. [Google Scholar] [CrossRef]
- Sun, J.; Hu, W.; Zhang, L.; Lan, R.; Yang, H.; Yang, D. Light-driven self-oscillating behavior of liquid-crystalline networks triggered by dynamic isomerization of molecular motors. Adv. Funct. Mater. 2021, 31, 2103311. [Google Scholar] [CrossRef]
- Manna, R.K.; Shklyaev, O.E.; Balazs, A.C. Chemical pumps and flexible sheets spontaneously form self-regulating oscillators in solution. Proc. Natl. Acad. Sci. USA 2021, 118, e2022987118. [Google Scholar] [CrossRef]
- Li, Z.; Myung, N.V.; Yin, Y. Light-powered soft steam engines for self-adaptive oscillation and biomimetic swimming. Sci. Robot. 2021, 6, eabi4523. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, J.; Wu, H.; Dai, Y.; Li, K. Self-Oscillating Curling of a Liquid Crystal Elastomer Beam under Steady Light. Polymers 2023, 15, 344. [Google Scholar] [CrossRef] [PubMed]
- Serak, S.; Tabiryan, N.V.; Vergara, R.; White, T.; Vaia, R.; Bunning, T. Liquid crystalline polymer cantilever oscillators fueled by light. Soft Matter 2010, 6, 779–783. [Google Scholar] [CrossRef]
- Bazir, A.; Baumann, A.; Ziebert, F.; Kulić, I.M. Dynamics of fiberboids. Soft Matter 2020, 16, 5210–5223. [Google Scholar] [CrossRef]
- Zhou, L.; Dai, Y.; Fang, J.; Li, K. Light-powered self-oscillation in liquid crystal elastomer auxetic metamaterials with large volume change. Int. J. Mech. Sci. 2023, 254, 108423. [Google Scholar] [CrossRef]
- Kim, Y.; Berg, J.v.D.; Crosby, A.J. Autonomous snapping and jumping polymer gels. Nat. Mater. 2021, 20, 1695–1701. [Google Scholar] [CrossRef]
- Graeber, G.; Regulagadda, K.; Hodel, P.; Küttel, C.; Landolf, D.; Schutzius, T.M.; Poulikakos, D. Leidenfrost droplet trampolining. Nat. Commun. 2021, 12, 1727. [Google Scholar] [CrossRef]
- Baumann, A.; Sánchez-Ferrer, A.; Jacomine, L.; Martinoty, P.; Le Houerou, V.; Ziebert, F.; Kuli´c, I.M. Motorizing fibres with geometric zero-energy modes. Nat. Mater. 2018, 17, 523–527. [Google Scholar] [CrossRef] [PubMed]
- Kuenstler, A.S.; Chen, Y.; Bui, P.; Kim, H.; DeSimone, A.; Jin, L.; Hayward, R. Blueprinting photothermal shape-morphing of liquid crystal elastomers. Adv. Mater. 2020, 32, 2000609. [Google Scholar] [CrossRef]
- Ge, D.; Dai, Y.; Li, K. Self-Sustained Euler Buckling of an Optically Responsive Rod with Different Boundary Constraints. Polymers 2023, 15, 316. [Google Scholar] [CrossRef]
- Gelebart, A.; Mulder, D.; Varga, M.; Konya, A.; Vantomme, G.; Meijer, E.; Selinger, R. Making waves in a photoactive polymer film. Nature 2017, 546, 632–636. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Wang, Z.; Wang, Y.; Wang, Z.; Li, C.; Annapooranan, R.; Zeng, J.; Chen, R.; Cai, S. Electrospun liquid crystal elastomer microfiber actuator. Sci. Robot. 2021, 6, eabi9704. [Google Scholar] [CrossRef] [PubMed]
- Ge, D.; Dai, Y.; Li, K. Light-powered self-spinning of a button spinner. Int. J. Mech. Sci. 2023, 238, 107824. [Google Scholar] [CrossRef]
- Camacho, L.M.; Finkelmann, H.; Palffy, M.P.; Shelley, M. Fast liquid-crystal elastomer swims into the dark. Nat. Mater. 2004, 3, 307–310. [Google Scholar] [CrossRef]
- Lu, X.; Guo, S.; Tong, X.; Xia, H.; Zhao, Y. Tunable photo controlled motions using stored strain energy in malleable azobenzene liquid crystalline polymer actuators. Adv. Mater. 2017, 29, 1606467. [Google Scholar] [CrossRef] [PubMed]
- Rothemund, P.; Ainla, A.; Belding, L.; Preston, D.; Kurihara, S.; Suo, Z.; Whitesides, G. A soft bistable valve for autonomous control of soft actuators. Sci. Robot. 2018, 3, eaar7986. [Google Scholar] [CrossRef] [PubMed]
- Lan, R.; Sun, J.; Shen, C.; Huang, R.; Zhang, Z.; Zhang, L.; Wang, L.; Yang, H. Near-infrared photodriven self-sustained oscillation of liquid-crystalline network film with predesignated polydopamine coating. Adv. Mater. 2020, 32, 1906319. [Google Scholar] [CrossRef]
- Lan, R.; Sun, J.; Shen, C.; Huang, R.; Zhang, Z.; Ma, C.; Bao, J.; Zhang, L.; Wang, L.; Yang, D.; et al. Light-Driven Liquid Crystalline Networks and Soft Actuators with Degree-of-Freedom-Controlled Molecular Motors. Adv. Funct. Mater. 2020, 30, 2000252. [Google Scholar] [CrossRef]
- Strogatz, S. Synchronization: A Universal Concept in Nonlinear Science. Phys. Today 2003, 56, 47. [Google Scholar] [CrossRef]
- Vicsek, T.; Zafeiris, A. Collective motion. Phys. Rep. 2012, 517, 71–140. [Google Scholar] [CrossRef]
- Boccaletti, S. The Synchronized Dynamics of Complex Systems. Monograph 2008, 6, 1–239. [Google Scholar]
- O’Keeffe, K.P.; Hong, H.; Strogatz, S.H. Oscillators that sync and swarm. Nat. Commun. 2017, 8, 1504. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y. Synchronized dancing under light. Nat. Mater. 2021, 20, 1594–1595. [Google Scholar] [CrossRef]
- Bennett, M.; Schatz, M.F.; Rockwood, H. Huygens’s clocks. Proc. R. Soc. Math. Phys. 2002, 458, 563–579. [Google Scholar] [CrossRef]
- Ramirez, J.P.; Olvera, L.A.; Nijmeijer, H. The sympathy of two pendulum clocks: Beyond Huygens’ observations. Sci. Rep. 2016, 6, 23580. [Google Scholar] [CrossRef] [PubMed]
- Bayani, A.; Jafari, S.; Azarnoush, H.; Nazarimehr, F.; Boccaletti, S.; Perc, M. Explosive synchronization dependence on initial conditions: The minimal Kuramoto model. Chaos Solitons Fract. 2023, 169, 113243. [Google Scholar] [CrossRef]
- Wang, C. Dynamic Behavior Analysis and Robust Synchronization of a Novel Fractional-Order Chaotic System with Multiwing Attractors. J. Math. 2021, 2021, 6684906. [Google Scholar] [CrossRef]
- Yan, S.; Wang, J.; Wang, E.; Wang, Q.; Sun, X.; Li, L. A four-dimensional chaotic system with coexisting attractors and its backstepping control and synchronization. Integration 2023, 91, 67–78. [Google Scholar] [CrossRef]
- Parastesh, F.; Rajagopal, K.; Jafari, S.; Perc, M.; Schöll, E. Blinking coupling enhances network synchronization. Phys. Rev. E 2022, 105, 5. [Google Scholar] [CrossRef]
- Sar, G.K.; Chowdhury, S.N.; Perc, M.; Ghosh, D. Swarmalators under competitive time-varying phase interactions. New J. Phys. 2022, 24, 043004. [Google Scholar] [CrossRef]
- Levis, D.; Pagonabarraga, I.; Díaz-Guilera, A. Synchronization in Dynamical Networks of Locally Coupled Self-Propelled Oscillators. Phys. Rev. X 2017, 7, 1. [Google Scholar] [CrossRef]
- Ghislaine, V.; Lars, C.M.E.; Anne, H.G.; Meijer, E.W.; Alexander, Y.P.; Henk, N.; Dirk, J.B. Coupled liquid crystalline oscillators in Huygens’ synchrony. Nat. Mater. 2021, 12, 1702–1706. [Google Scholar]
- Du, C.; Cheng, Q.; Li, K.; Yu, Y. Self-Sustained Collective Motion of Two Joint Liquid Crystal Elastomer Spring Oscillator Powered by Steady Illumination. Micromachines 2022, 13, 271. [Google Scholar] [CrossRef]
- Warner, M.; Terentjev, E.M. Liquid Crystal Elastomers; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Nagele, T.; Hoche, R.; Zinth, W.; Wachtveitl, J. Femtosecond photoisomerization of cis-azobenzene. Chem. Phys. Lett. 1997, 272, 489–495. [Google Scholar] [CrossRef]
- Gregorc, M.; Zalar, B.; Domenici, V.; Ambrožič, G.; Drevenšek-Olenik, I.; Fally, M.; Čopič, M. Depth profile of optically recorded patterns in light-sensitive liquid-crystal elastomers. Phys. Rev. E 2011, 84, 3. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Du, C.; Wang, W.; Li, K. A thermally-responsive fiber engine in a linear temperature field. Int. J. Mech. Sci. 2022, 225, 107391. [Google Scholar] [CrossRef]
- Braun, L.B.; Hessberger, T.; Pütz, E.; Müller, C.; Giesselmann, F.; Serra, C.A.; Zentel, R. Actuating thermo- and photo-responsive tubes from liquid crystalline elastomers. J. Mater. Chem. C 2018, 6, 9093–9101. [Google Scholar] [CrossRef]
- Fung, Y.C.; Drucker, D.C. Foundation of Solid Mechanics. J. Appl. Mech. 1966, 33, 238. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).