Characterization and Modeling of Ply/Tool and Ply/Ply Slippage Phenomena of Unidirectional Polycarbonate CF Tapes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Used Materials
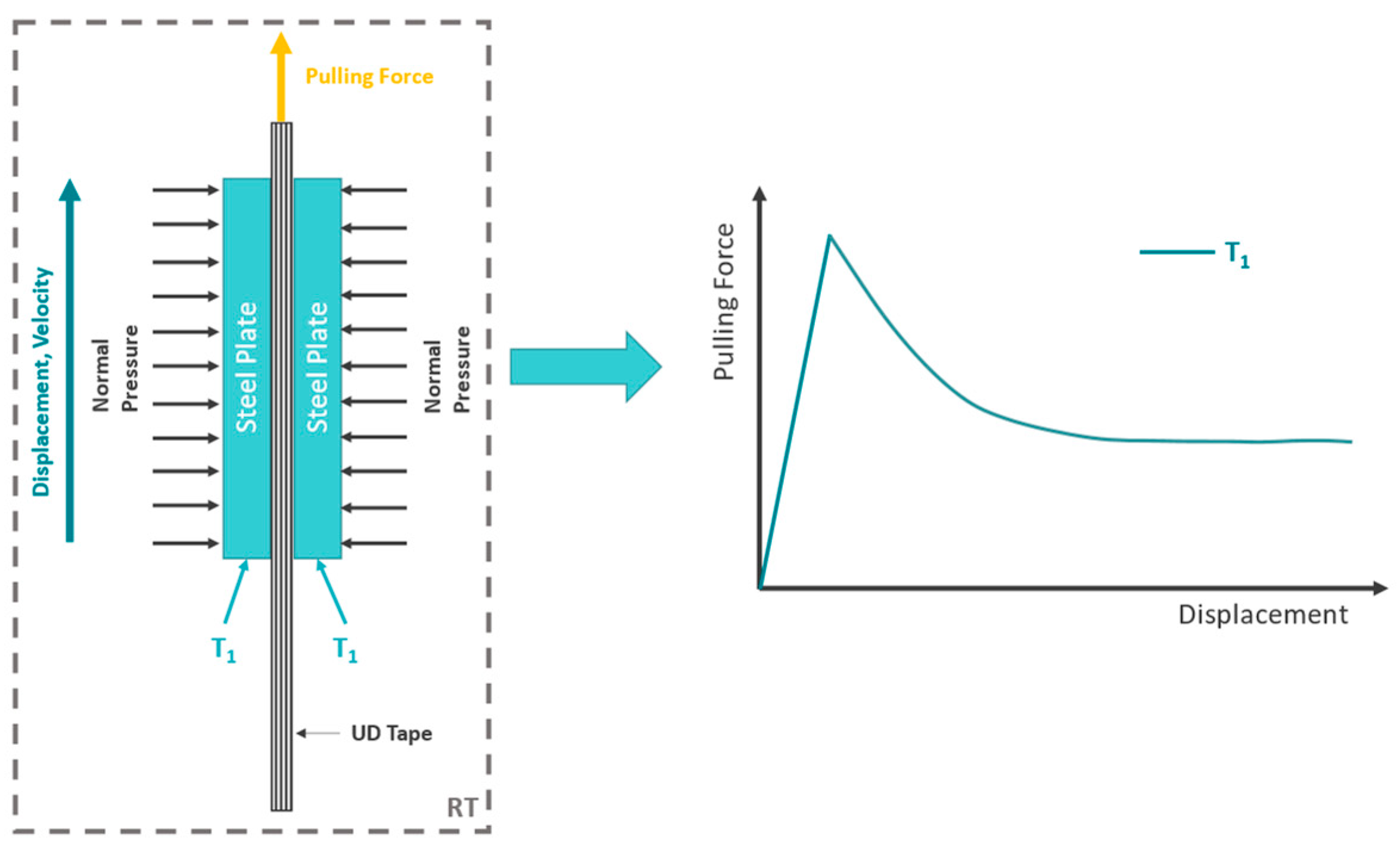
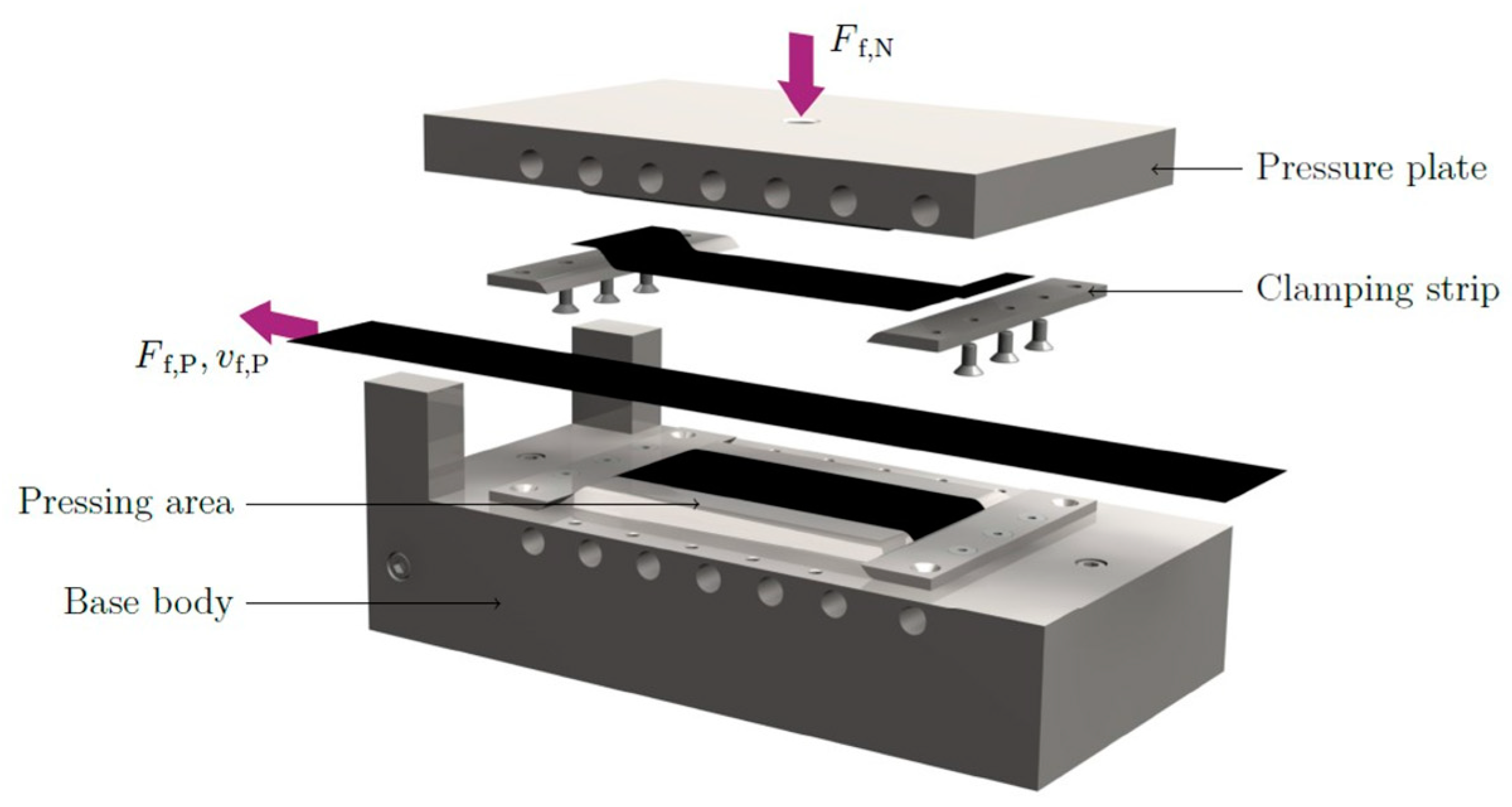
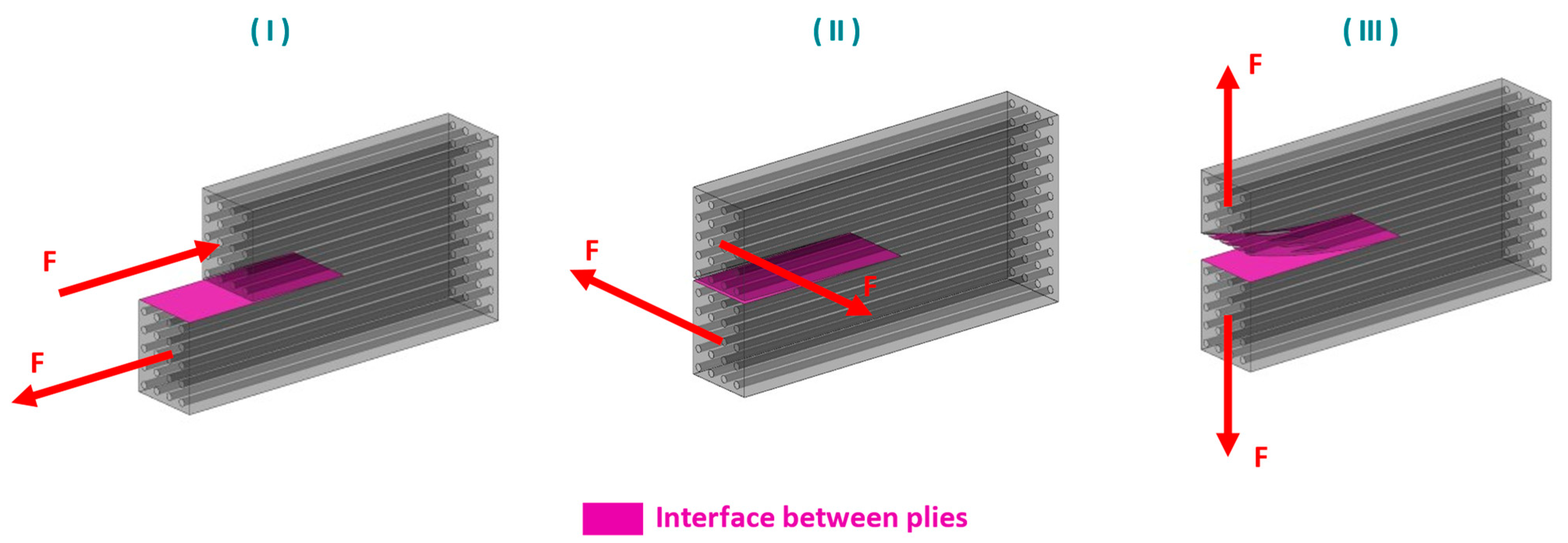
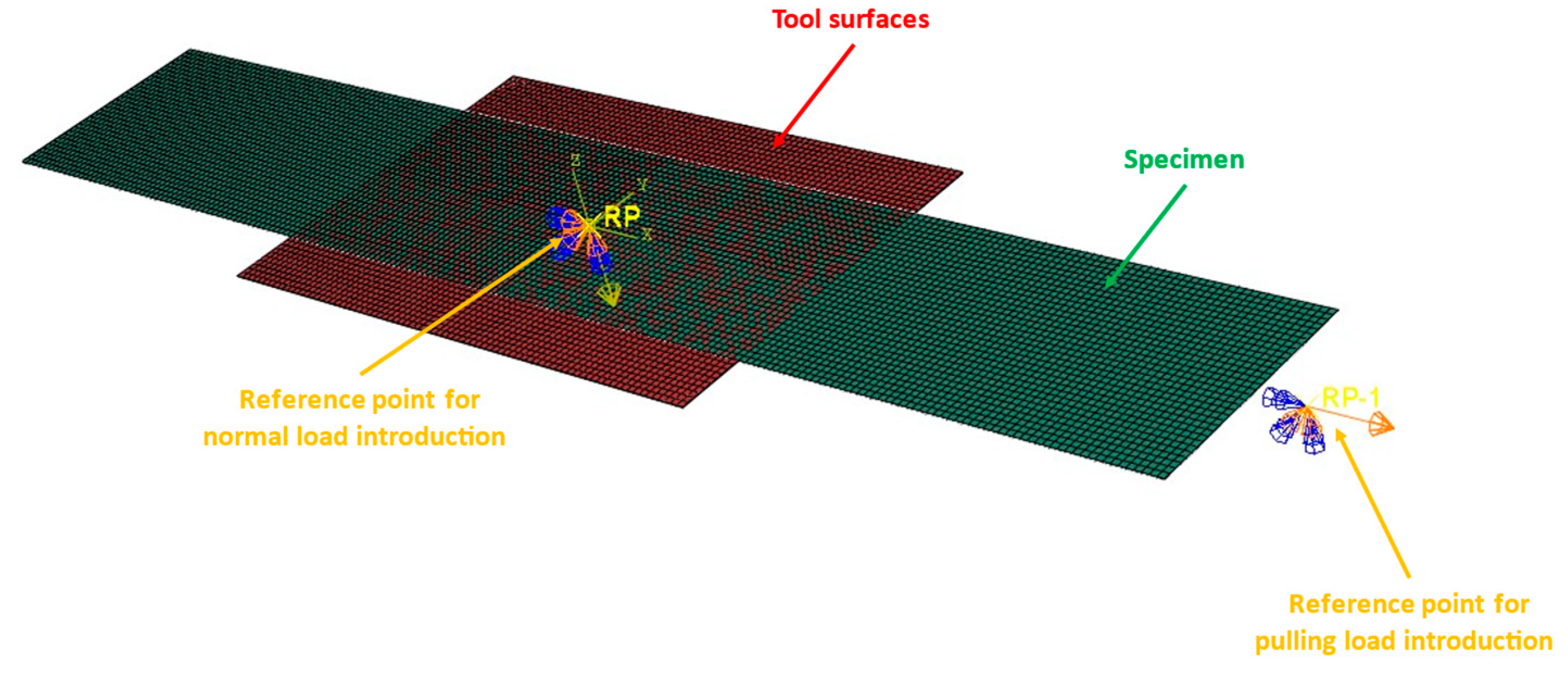
2.2. Experimental Setup and Testing Conditions
3. Numerical Modeling
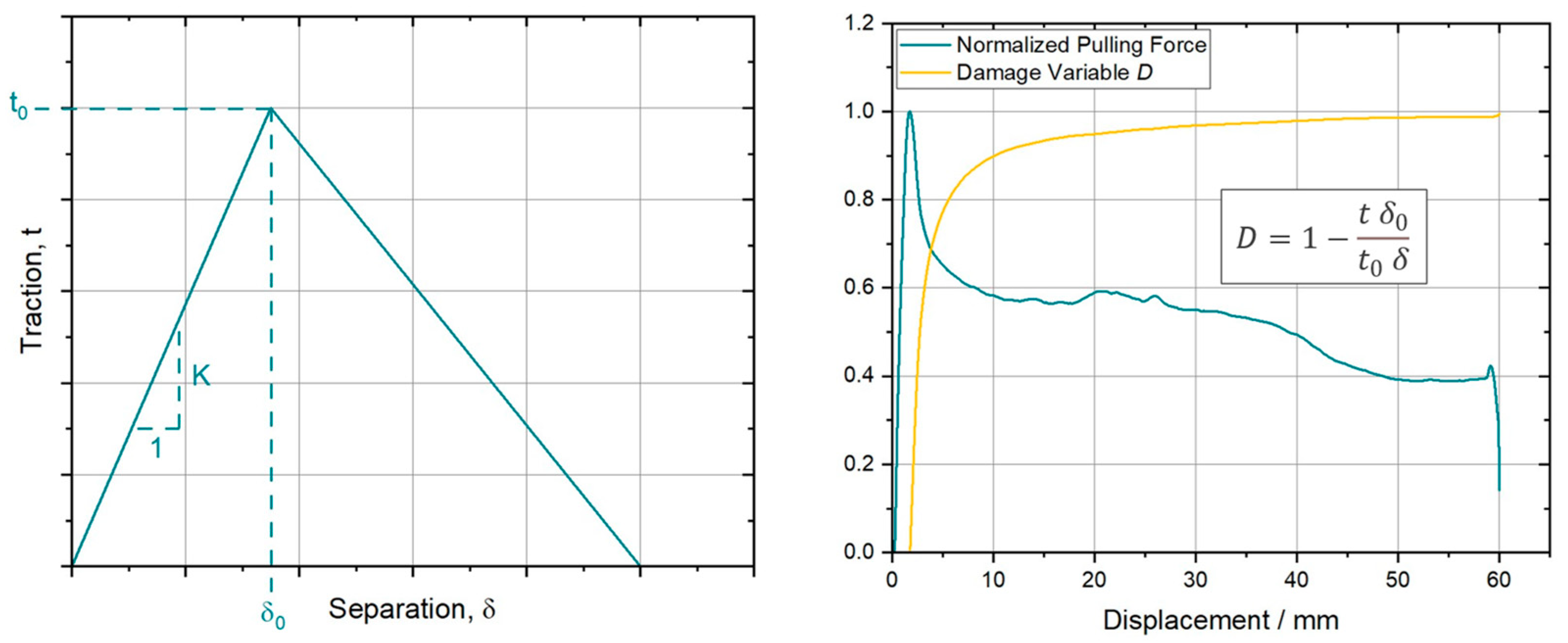
3.1. Cohesive Zone Modeling
4. Results and Discussion
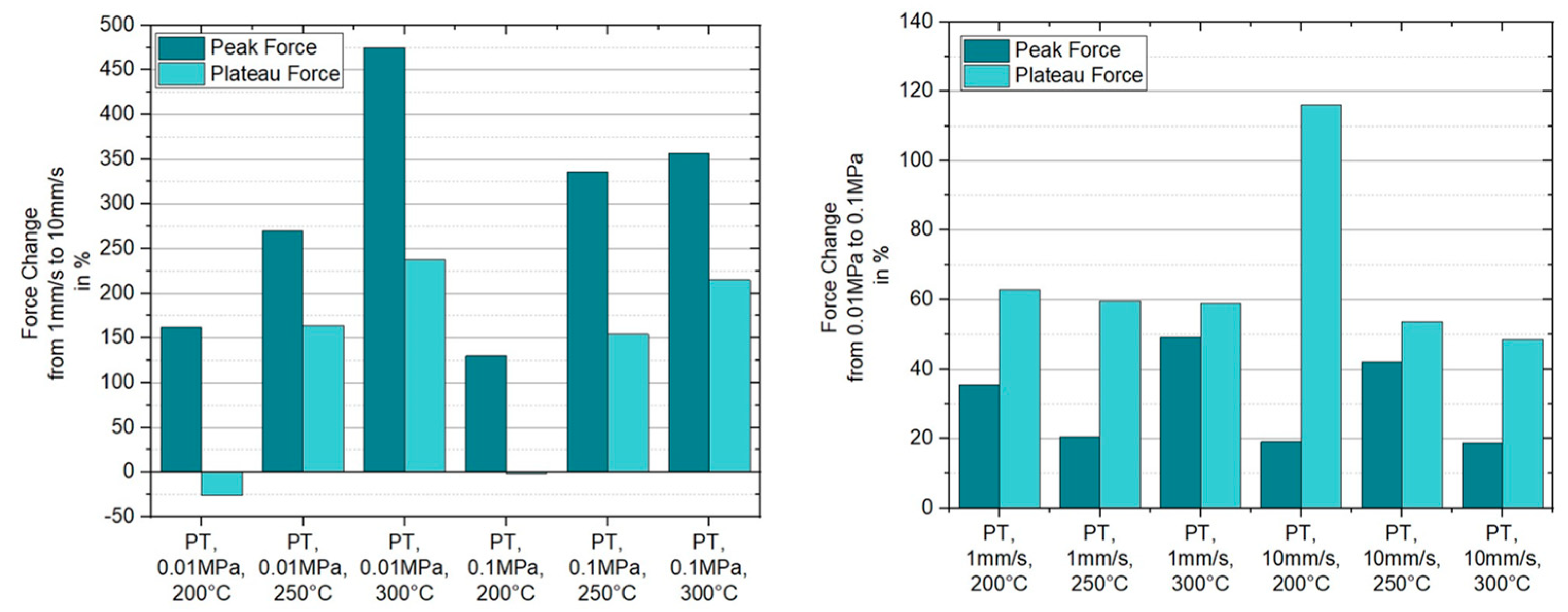
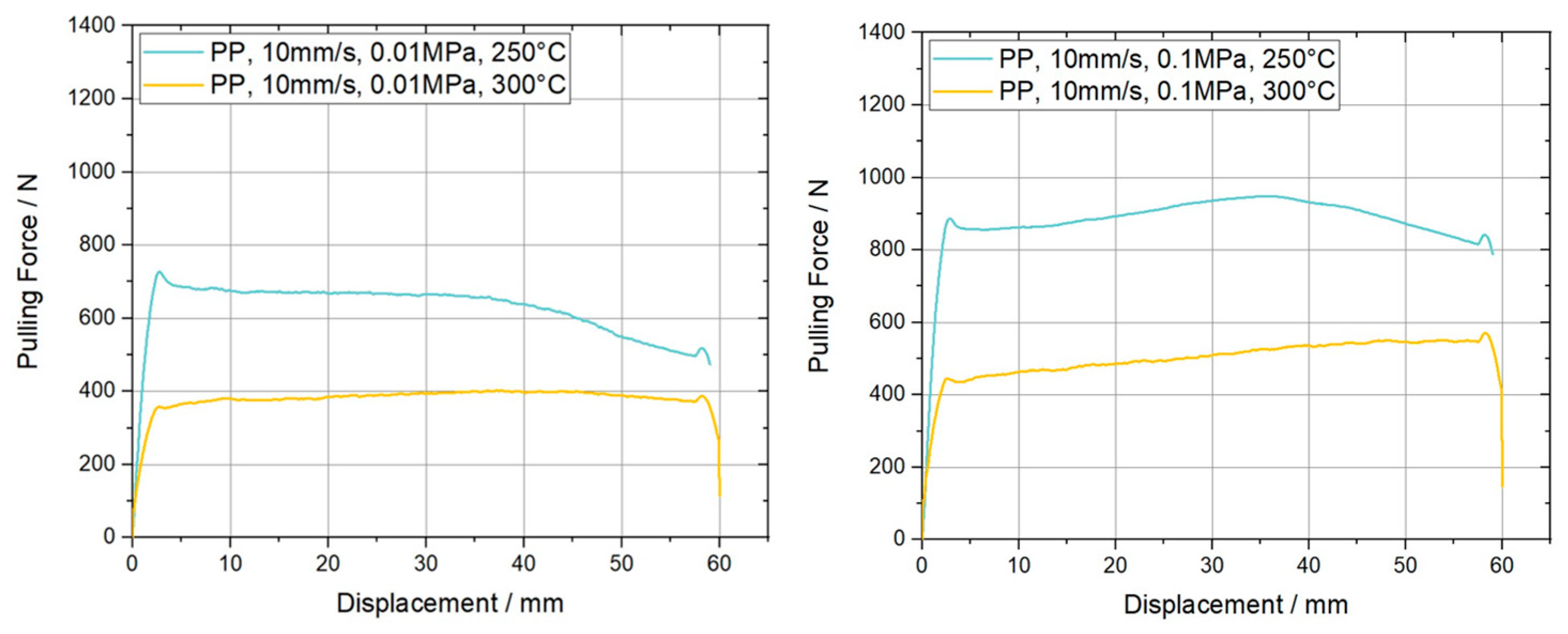
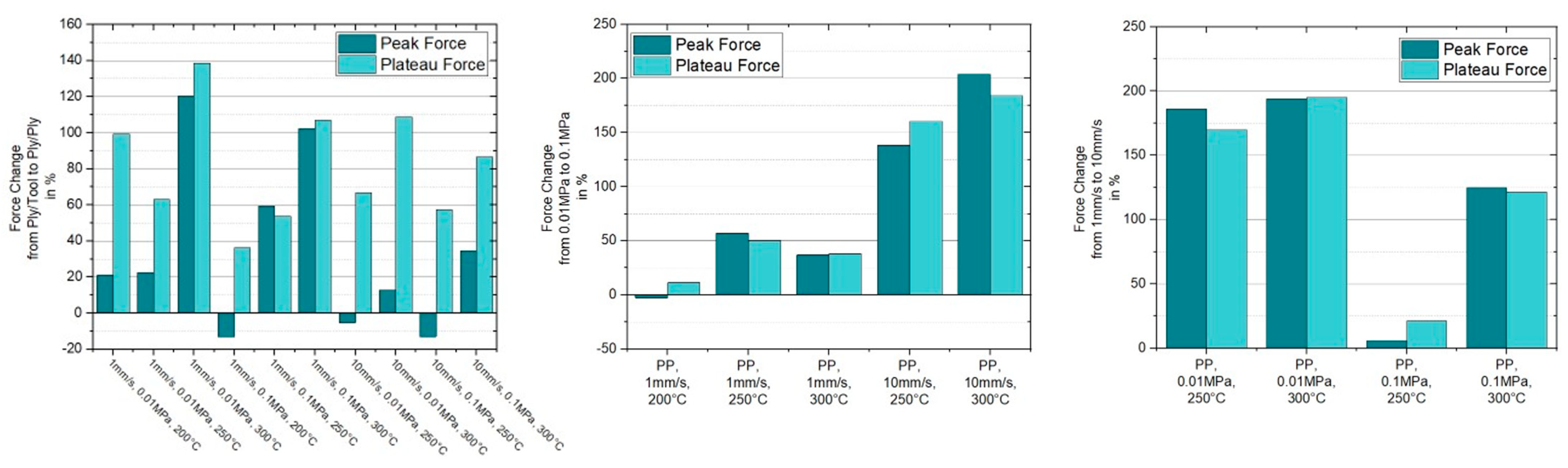
4.1. Experimental Results
4.1.1. Ply/Tool Experiments
4.1.2. Ply/Ply Experiments
4.2. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Federation of Reinforced Plastics. Handbook—Reinforced Plastics/Composites; Springer DE: Frankfurt am Main, Germany, 2014; Volume 4, ISBN 978-3-658-02755-1. [Google Scholar]
- Laresser, D. Investigation of the Forming Behavior of a Thermoplastic Unidirectional Tape Laminate: Forming Experiment, Modeling, Simulation; Johannes Kepler University Linz: Linz, Austria, 2020. [Google Scholar]
- Schürmann, H. Konstruieren mit Faser-Kunststoff-Verbund; Springer: Berlin/Heidelberg, Germany, 2007; Volume 2, ISBN 978-3-540-72189-5. [Google Scholar]
- Land, P.; Crossley, R.; Branson, D.; Ratchev, S. Technology Review of Thermal Forming Techniques for use in Composite Component Manufacture. SAE Int. J. Mater. Manf. 2016, 9, 81–89. [Google Scholar] [CrossRef]
- Kropka, M.; Muehlbacher, M.; Neumeyer, T.; Altstaedt, V. From UD-tape to final part—A comprehensive approach towards thermoplastic composites. Procedia CIRP 2017, 66, 96–100. [Google Scholar] [CrossRef]
- Machado, M.; Cakmak, U.D.; Kallai, I.; Major, Z. Thermomechananical viscoelastic analysis of woven-reinforced thermoplastic-matrix composites. Compos. Struct. 2016, 157, 256–264. [Google Scholar] [CrossRef]
- Stelzer, P.S.; Cakmak, U.D.; Eisner, L.; Doppelbauer, L.K.; Kallai, I.; Schweizer, G.; Prammer, H.R.; Major, Z. Experimental feasibility and environmental impacts of compression molded discontinuous carbon fiber composites with opportunities for circular economy. Compos. B Eng. 2022, 234, 109638. [Google Scholar] [CrossRef]
- Rettenwander, T.; Fischlschweiger, M.; Machado, M.; Steinbichler, G.; Major, Z. Tailored patch placement on a base load carrying laminate: A computational structural optimisation with experimental validation. Compos. Struct. 2014, 116, 48–54. [Google Scholar] [CrossRef]
- Sachs, U. Friction and Bending in Thermoplastic Composite Forming Processes; University of Twente: Enschede, The Netherlands, 2014; ISBN 978-94-6259-483-8. [Google Scholar]
- Vanclooster, K. Forming of Multilayered Fabric Reinforced Thermoplastic Composites; University Leuven: Leuven, Belgium, 2010; ISBN 978-94-6018-223-5. [Google Scholar]
- Pierik, R.; Grouve, W.; Wijskamp, S.; Akkerman, R. On the origin of start-up effects in ply-ply friction for UD fiber-reinforced thermoplastics in melt. In Proceedings of the 24th International Conference on Material Forming, Liege, Belgium, 14–16 April 2021. [Google Scholar] [CrossRef]
- Sachs, U.; Akkerman, R.; Haanappel, S.P.; Thije, R.H.W.T.; Rooij, M.B.D. Friction in Forming of UD Composites. AIP Conf. Proc. 2011, 1353, 984–989. [Google Scholar] [CrossRef]
- Haanappel, S.P. Forming of UD Fibre Reinforced Thermoplastics; University of Twente: Enschede, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Groves, D.J. A characterization of shear flow in continuous fibre thermoplastic laminates. Composites 1989, 20, 28–32. [Google Scholar] [CrossRef]
- Morris, S.R.; Sun, C.T. An investigation of interply slip behaviour in AS4 PEEK at forming temperatures. Compos. Manuf. 1994, 5, 217–224. [Google Scholar] [CrossRef]
- Murtagh, A.M.; Lennon, J.J.; Mallon, P.J. Surface friction effects related to pressforming of continuous fibre thermoplastic composites. Compos. Manuf. 1995, 6, 165–175. [Google Scholar] [CrossRef]
- Murtagh, A.M.; Monaghan, M.R.; Mallon, P.J. Development of a shear deformation apparatus to characterize the interply slip mechanism of advanced thermoplastic composites. Key Eng. Mater. 1993, 86–87, 123–130. [Google Scholar] [CrossRef]
- ten Thije, R.H.W.; Akkerman, R. Design of an experimental setup to measure tool-ply and ply-ply friction in thermoplastic laminates. Int. J. Mater. Form. 2009, 2, 197–200. [Google Scholar] [CrossRef]
- Wang, W.T.; Yu, H.; Potter, K.; Kim, B.C. Improvement of composite drape forming quality by enhancing interply slip. In Proceedings of the ECCM17, 17th European Conference on Composite Materials, Munich, Germany, 26–30 June 2016; ISBN 978-30-0053-387-7. [Google Scholar]
- Rashidi, A.; Crawford, B.; Olfatbakhsh, T.; Milani, A.S. A mixed lubrication model for inter-ply friction behaviour of uncured fabric prepregs. Compos. A Appl. Sci. Manuf. 2021, 149, 106571. [Google Scholar] [CrossRef]
- Harrison, P.; Thije, R.T.; Akkerman, R.; Long, A.C. Characterising and modelling tool-ply friciton of viscous textile composites. World J. Eng. 2010, 7, 5–22. [Google Scholar]
- Fetfatsidis, K.A.; Jauffres, D.; Sherwood, J.A.; Chen, J. Characterization of the tool/fabric and fabric/fabric friction for woven-fabric composites during the thermostamping process. Int. J. Mater. Form. 2011, 6, 209–211. [Google Scholar] [CrossRef]
- Grewal, H.S.; Hojjati, M. Inter-ply Friction of Unidirectional Tape and Woven Fabric Out-of-autoclave Prepregs. Int. J. Compos. Mater. 2017, 7, 161–170. [Google Scholar] [CrossRef]
- Hanna, E.G.; Poitou, A.; Casari, P. Modeling the interply slip during forming of thermoplastic laminates. Mater. Phys. Mech. 2018, 40, 22–36. [Google Scholar] [CrossRef]
- Ondarcuhu, R. Tack of a Polymer Melt: Adhesion Measurements and Fracture Profile Observations. J. Phys. II Fr. 1997, 7, 1893–1916. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, A. Universal scaling behavior of the tackiness of polymer melts. Rubber Chem. Technol. 2019, 92, 625–638. [Google Scholar] [CrossRef]
- Krämer, E.T.M.; Grouve, W.J.B.; Warnet, L.L.; Koussios, S.; Akkerman, R. Tool-ply interaction in the formation of waviness during C/PEEK consolidation. Compos. A Appl. Sci. Manuf. 2021, 144, 106327. [Google Scholar] [CrossRef]
- Lee, J.M.; Kim, B.M.; Lee, C.J.; Ko, D.C. A characterisation of tool-ply friction behaviors in thermoplastic composite. Procedia Eng. 2017, 90, 90–94. [Google Scholar] [CrossRef]
- White, K.D.; Sherwood, J.A. Effect of Thickness Changes and Friction in Thermoforming Process Simulations in LS-DYNA® for UHMWPE Unidirectional Cross-Plies. In Proceedings of the 16th International LS-DYNA Conference, Virtual, 10–11 July 2020. [Google Scholar]
- Bergström, J. Mechanics of Solid Polymers—Theory and Computational Modelling, 1st ed.; Elsevier Inc.: London, UK, 2015; ISBN 978-0-323-31150-2. [Google Scholar]
- Osswald, T.A. Understanding Polymer Processing, 2nd ed.; Hanser Publishers: Munich, Germany, 2017; ISBN 978-1-56990-648-4. [Google Scholar]
- Kazatchkov, I.B.; Hatzikiriakos, S.G. Relaxation effects of slip in shear flow of linear molten polymers. Rheol. Acta 2010, 49, 267–274. [Google Scholar] [CrossRef]
- Hatzikiriakos, S.G. Wall slip of molten polymers. Prog. Polym. Sci. 2012, 37, 624–643. [Google Scholar] [CrossRef]
- Sorba, G.; Binetruy, C.; Chinesta, F. In-plane shearing of a UD prepreg modeled as transversely isotropic fluid: Comparison between continuous and discontinuous fiber tension approaches. AIP Conf. Proc. 2016, 1769, 170008. [Google Scholar] [CrossRef]
- Abaqus Documentation. 2020. Available online: https://help.3ds.com/2020/english/dssimulia_established/SIMACAEELMRefMap/simaelm-c-cohesiveinit.htm?contextscope=all&id=64c2e6bdaf914ecc9dec22483da9150b (accessed on 5 July 2023).
- Gross, D.; Seelig, T. Fracture Mechanics: With an Introduction to Micromechanics, 3rd ed.; Springer Publishing: Karlsruhe, Germany, 2018; ISBN 978-3-319-71090-7. [Google Scholar]







| Ply-Tool Experiments | ||
|---|---|---|
| Temperature/°C | Pulling Velocity/(mm/s) | Normal Pressure/MPa |
| 100 | 1 | 0.01 |
| 100 | 1 | 0.1 |
| 100 | 10 | 0.01 |
| 100 | 10 | 0.1 |
| 200 | 1 | 0.01 |
| 200 | 1 | 0.1 |
| 200 | 10 | 0.01 |
| 200 | 10 | 0.1 |
| 250 | 1 | 0.01 |
| 250 | 1 | 0.1 |
| 250 | 10 | 0.01 |
| 250 | 10 | 0.1 |
| 300 | 1 | 0.01 |
| 300 | 1 | 0.1 |
| 300 | 10 | 0.01 |
| 300 | 10 | 0.1 |
| Ply-Ply Experiments | ||
| Temperature/°C | Pulling Velocity/(mm/s) | Normal Pressure/MPa |
| 200 | 1 | 0.01 |
| 200 | 1 | 0.1 |
| 200 | 10 | 0.01 |
| 200 | 10 | 0.1 |
| 250 | 1 | 0.01 |
| 250 | 1 | 0.1 |
| 250 | 10 | 0.01 |
| 250 | 10 | 0.1 |
| 300 | 1 | 0.01 |
| 300 | 1 | 0.1 |
| 300 | 10 | 0.01 |
| 300 | 10 | 0.1 |
| Stiffness—Traction-Separation (Uncoupled) | |||
|---|---|---|---|
| /(N/mm3) | /(N/mm3) | /(N/mm3) | Temperature/°C |
| 106 | 0.098 | 0.098 | 200 |
| 106 | 0.019 | 0.019 | 250 |
| 106 | 0.0061 | 0.0061 | 300 |
| Damage Initiation—Maximum Separation | |||
| /mm | /mm | /mm | Temperature/°C |
| 106 | 1.26 | 1.26 | 200 |
| 106 | 1.80 | 1.80 | 250 |
| 106 | 1.44 | 1.44 | 300 |
| Damage Evolution—Tabular | |||
| )/- | )/mm | Temperature/°C | |
| 0 | 0 | 200 | |
| … | … | … | |
| 0.94 | 20 | 250 | |
| … | … | … | |
| 0.98 | 60 | 300 | |
| Ply-Tool Experiments | |||
|---|---|---|---|
| Temperature/°C | Pulling Velocity/(mm/s) | Normal Pressure/MPa | R2—Value/- |
| 100 | 1 | 0.01 | 0.90 |
| 100 | 1 | 0.1 | 0.70 |
| 100 | 10 | 0.01 | 0.84 |
| 100 | 10 | 0.1 | 0.75 |
| 200 | 1 | 0.01 | 0.70 |
| 200 | 1 | 0.1 | 0.85 |
| 200 | 10 | 0.01 | 0.87 |
| 200 | 10 | 0.1 | 0.93 |
| 250 | 1 | 0.01 | 0.72 |
| 250 | 1 | 0.1 | 0.85 |
| 250 | 10 | 0.01 | 0.91 |
| 250 | 10 | 0.1 | 0.74 |
| 300 | 1 | 0.01 | 0.88 |
| 300 | 1 | 0.1 | 0.79 |
| 300 | 10 | 0.01 | 0.73 |
| 300 | 10 | 0.1 | 0.72 |
| Ply-Ply Experiments | |||
| Temperature/°C | Pulling Velocity/(mm/s) | Normal Pressure/MPa | R2—Value/- |
| 200 | 1 | 0.01 | 0.95 |
| 200 | 1 | 0.1 | 0.72 |
| 200 | 10 | 0.01 | 0.72 |
| 200 | 10 | 0.1 | 0.78 |
| 250 | 1 | 0.01 | 0.77 |
| 250 | 1 | 0.1 | 0.72 |
| 250 | 10 | 0.01 | 0.92 |
| 250 | 10 | 0.1 | 0.89 |
| 300 | 1 | 0.01 | 0.81 |
| 300 | 1 | 0.1 | 0.88 |
| 300 | 10 | 0.01 | 0.74 |
| 300 | 10 | 0.1 | 0.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapshammer, A.; Laresser, D.; Miron, M.C.; Baudach, F.; Major, Z. Characterization and Modeling of Ply/Tool and Ply/Ply Slippage Phenomena of Unidirectional Polycarbonate CF Tapes. Polymers 2023, 15, 3520. https://doi.org/10.3390/polym15173520
Kapshammer A, Laresser D, Miron MC, Baudach F, Major Z. Characterization and Modeling of Ply/Tool and Ply/Ply Slippage Phenomena of Unidirectional Polycarbonate CF Tapes. Polymers. 2023; 15(17):3520. https://doi.org/10.3390/polym15173520
Chicago/Turabian StyleKapshammer, Andreas, Daniel Laresser, Matei C. Miron, Felix Baudach, and Zoltan Major. 2023. "Characterization and Modeling of Ply/Tool and Ply/Ply Slippage Phenomena of Unidirectional Polycarbonate CF Tapes" Polymers 15, no. 17: 3520. https://doi.org/10.3390/polym15173520
APA StyleKapshammer, A., Laresser, D., Miron, M. C., Baudach, F., & Major, Z. (2023). Characterization and Modeling of Ply/Tool and Ply/Ply Slippage Phenomena of Unidirectional Polycarbonate CF Tapes. Polymers, 15(17), 3520. https://doi.org/10.3390/polym15173520





