On the Creation and Optical Microstructure Characterisation of Additively Manufactured Foam Structures (AMF) †
Abstract
:1. Introduction and Motivation
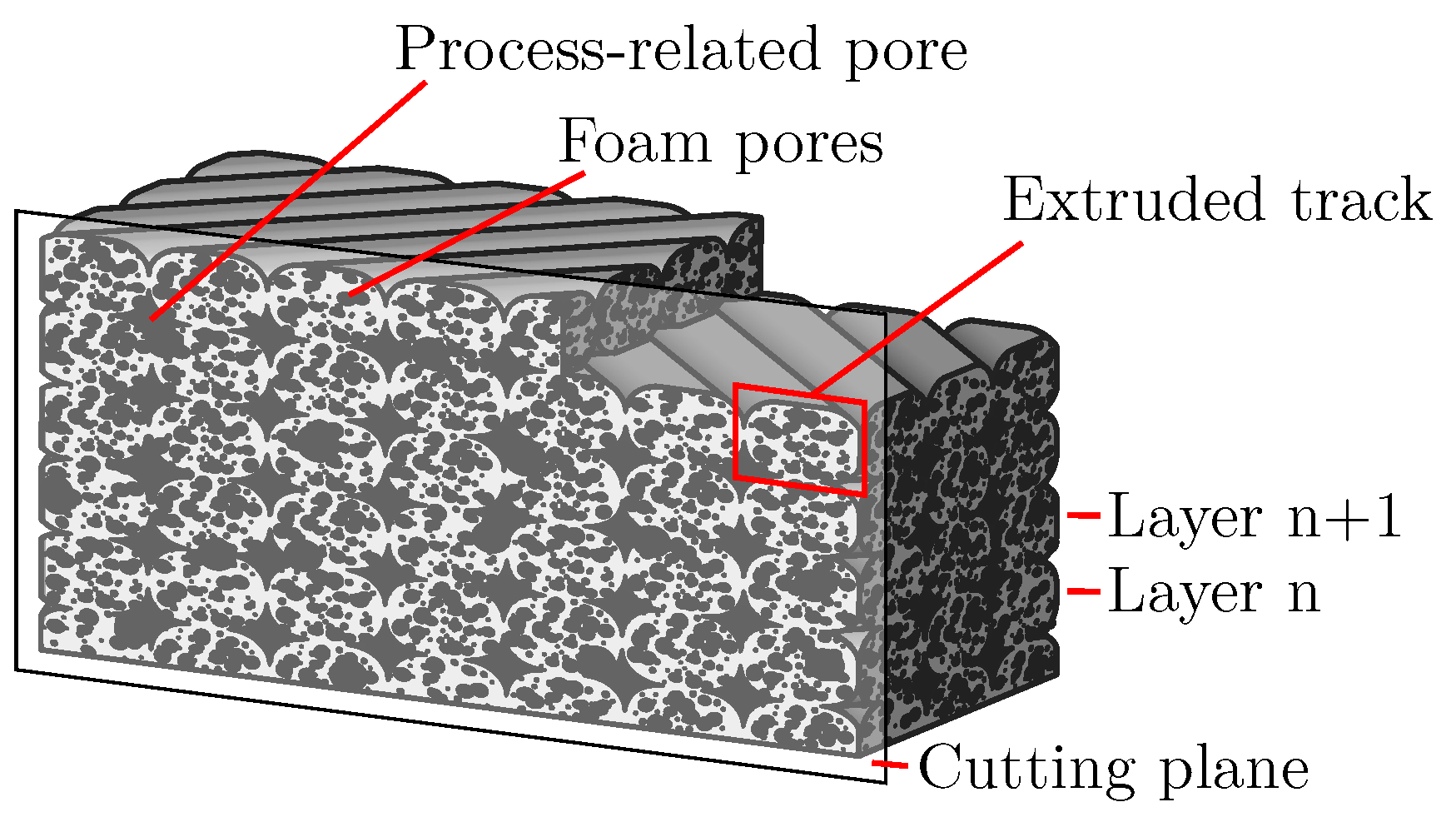
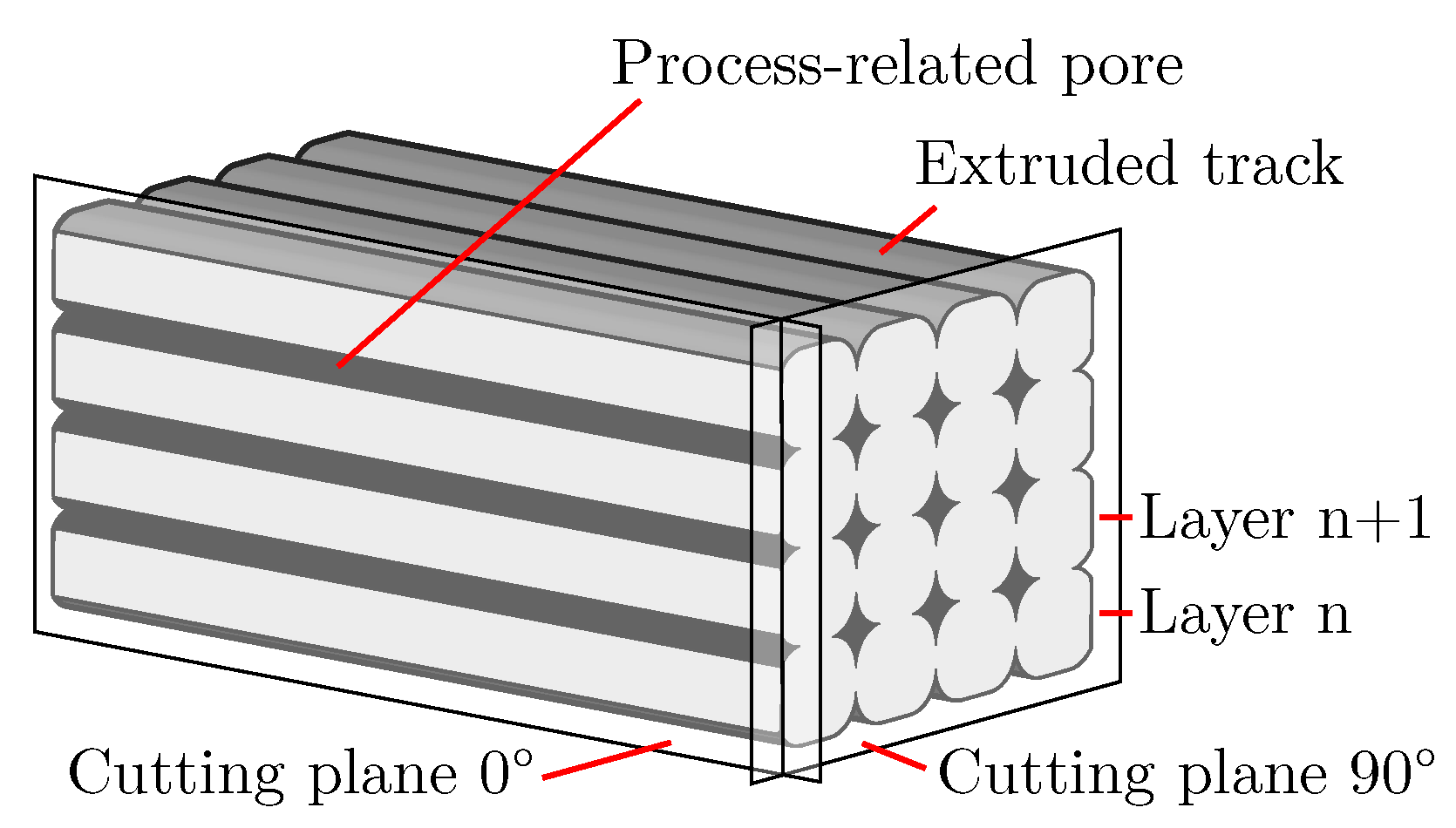
2. Nomenclature for AMF
- Foam pores
- Process-related pores
- Foam structure
- Additively manufactured structure
- Additively manufactured foam structure (AMF)
- Degree of foaming
- Fineness
- Porosity
3. Features for the Characterisation of Foam Structures
4. Material and Methods
4.1. Material and Machine Used
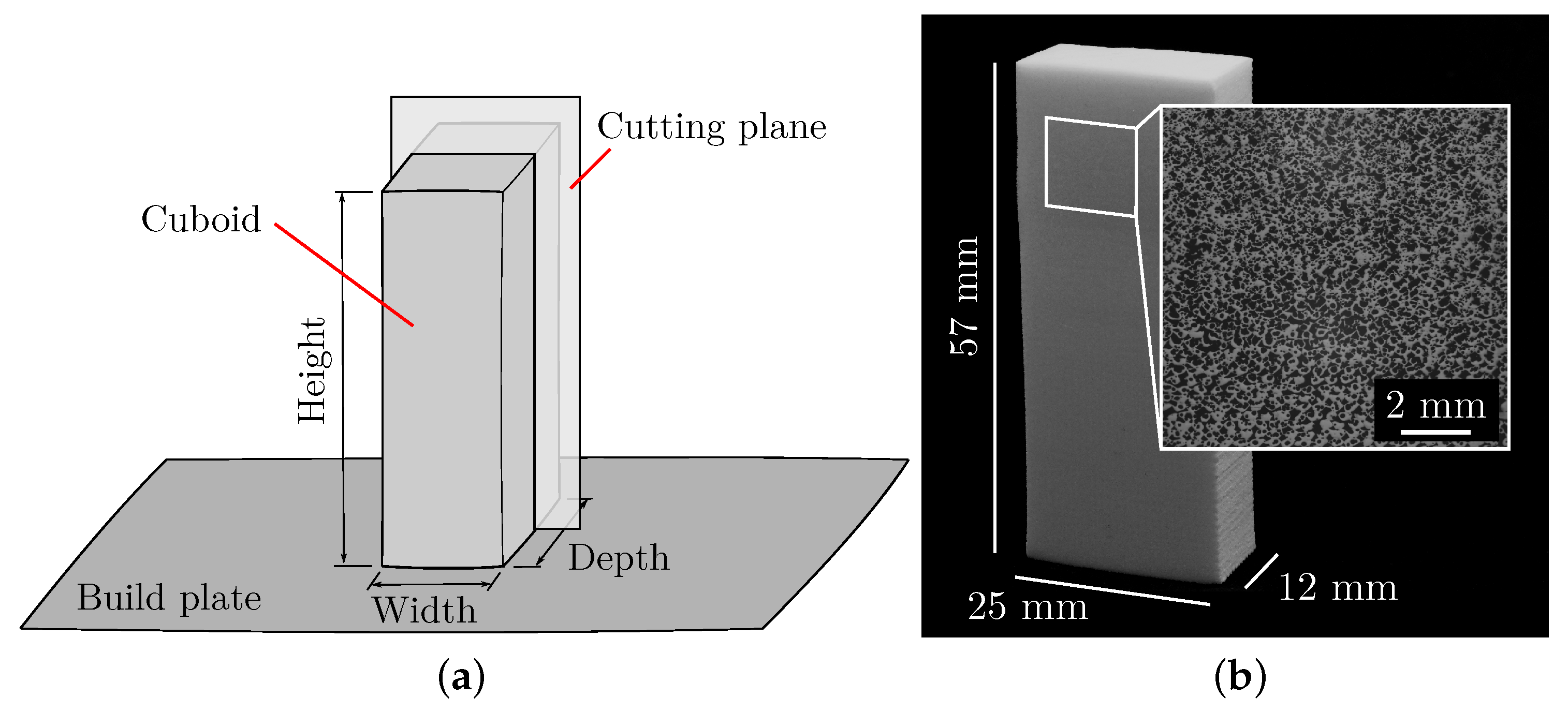
4.2. Specimen Manufacturing of AMF and Image Preparation
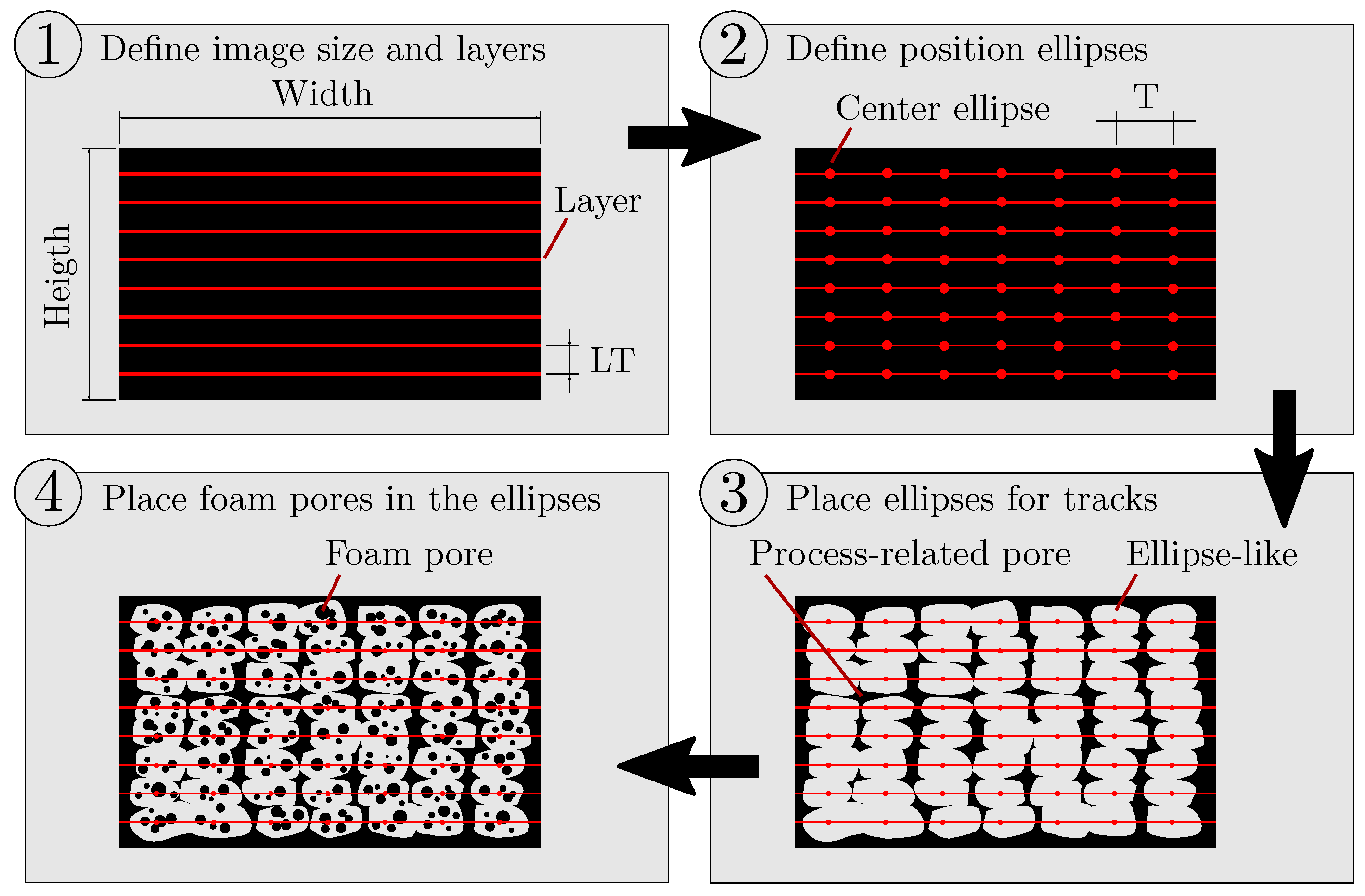
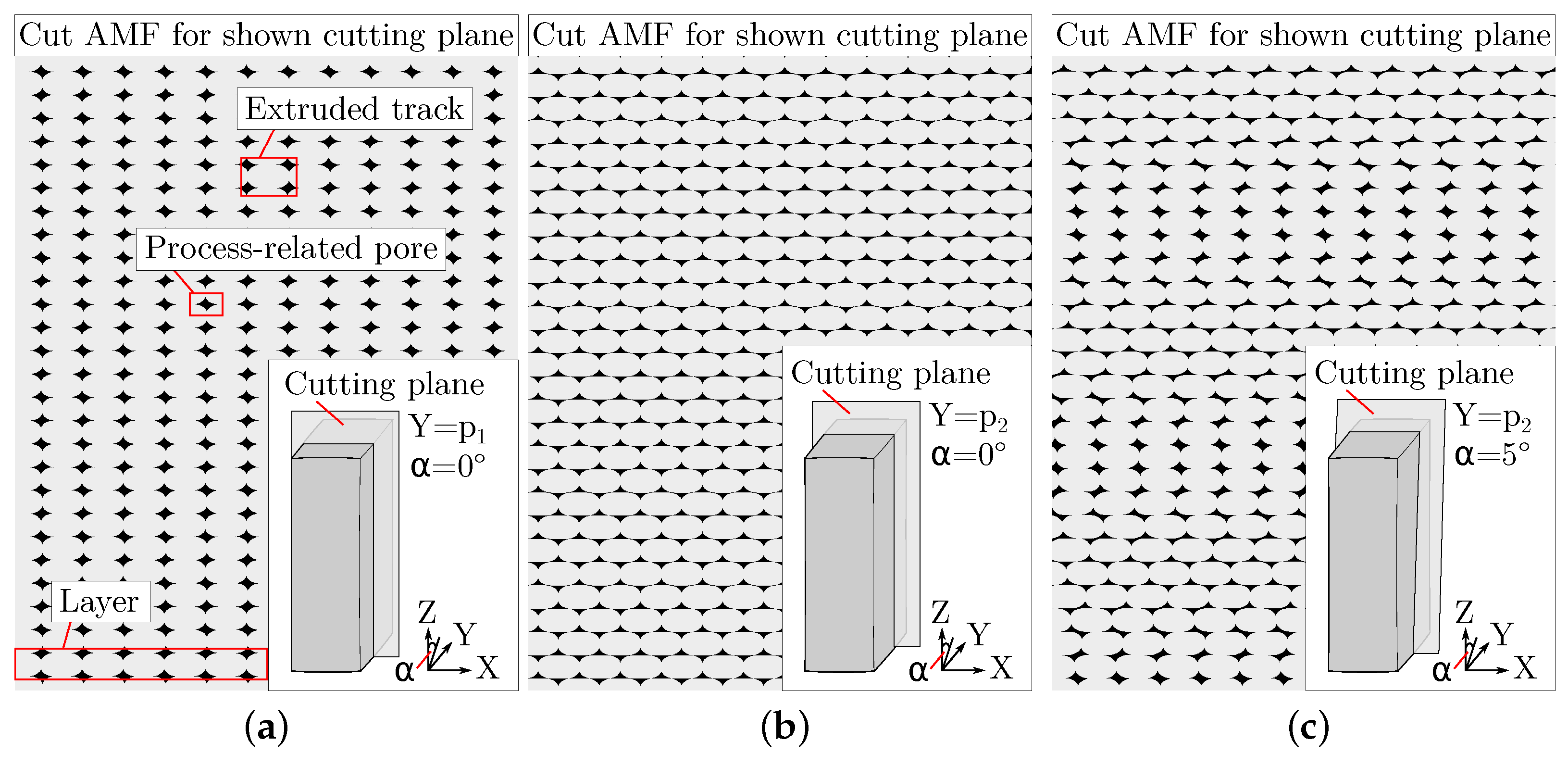
4.3. Creation of Artificial Images of AMF
- The image size and the layer thickness are specified in pixels. From this, horizontal lines result that determine the centre of the layers.
- The specified droplet aspect ratio (parameter of the APF process) and the layer thickness can be used to calculate the distance of the tracks T according to [22], which results in the positions of the tracks within the layers.
- Ellipses are placed at these positions, which are allowed to deviate randomly from these positions by a small value and are slightly deformed in their shape.
- Foam pores of a specified size and amount are randomly placed within the ellipses. The pore size and the pore amount are allowed to deviate by a small value.
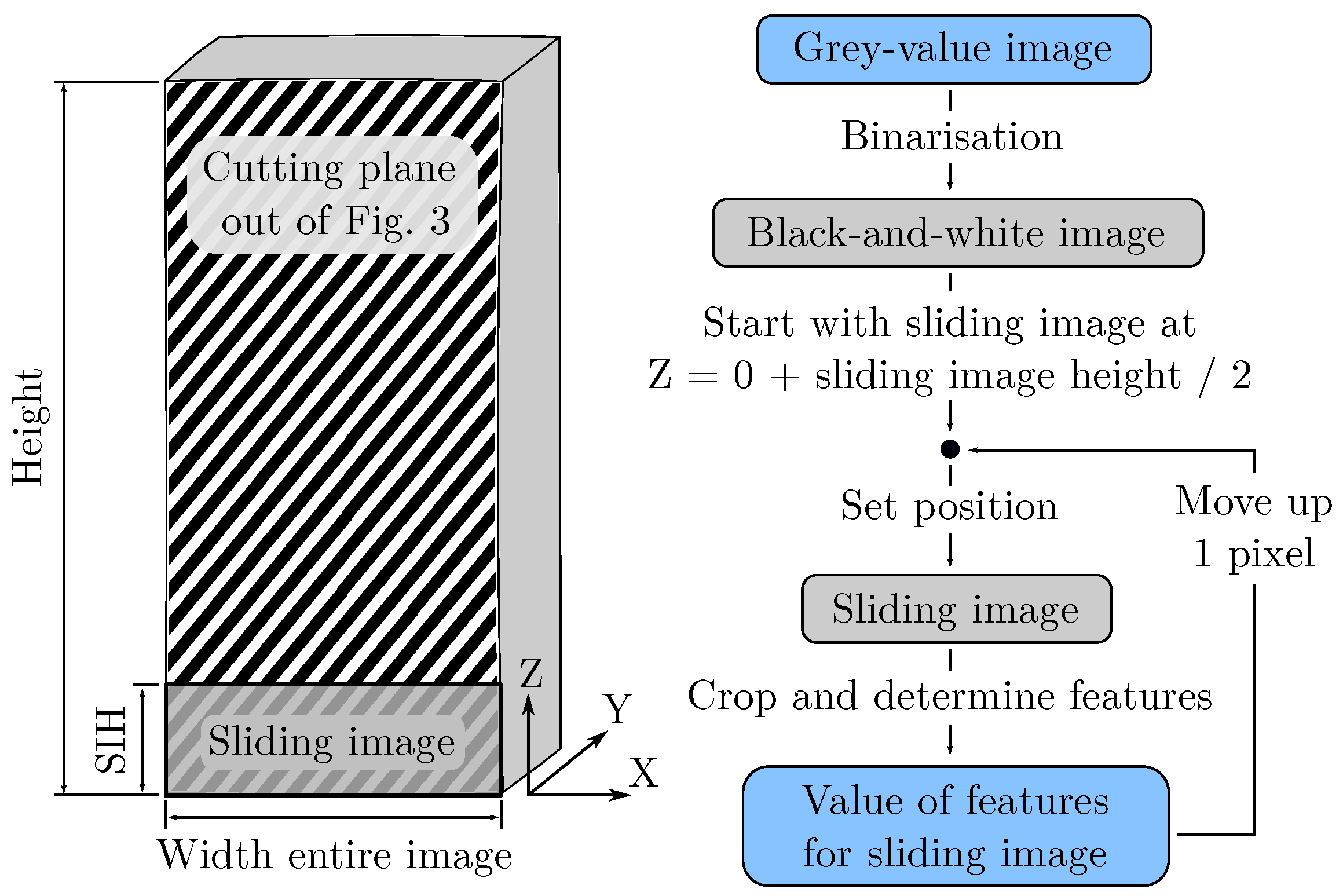
4.4. Determination of Image Features on AMF
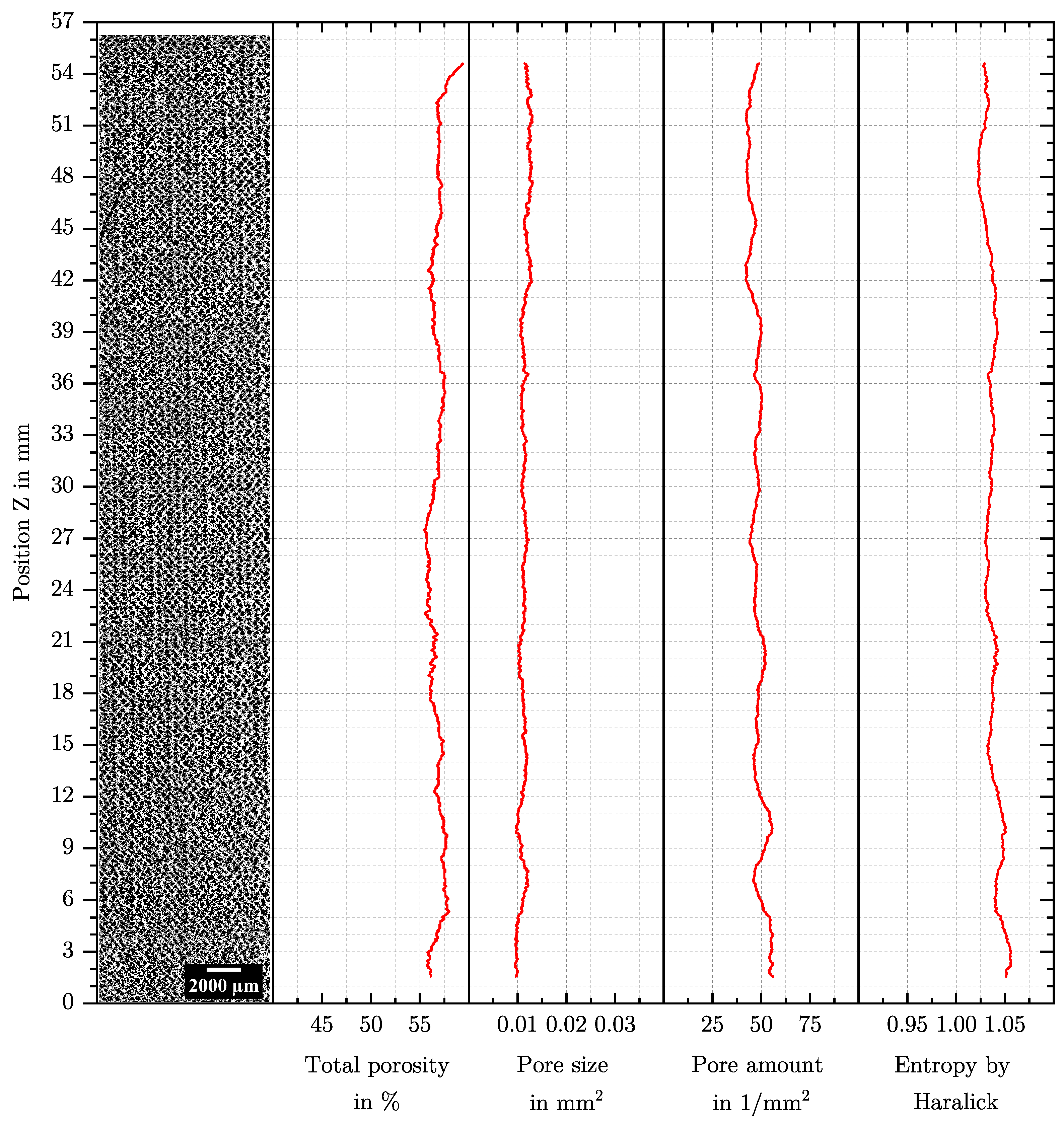
4.4.1. Determination of the Total Porosity
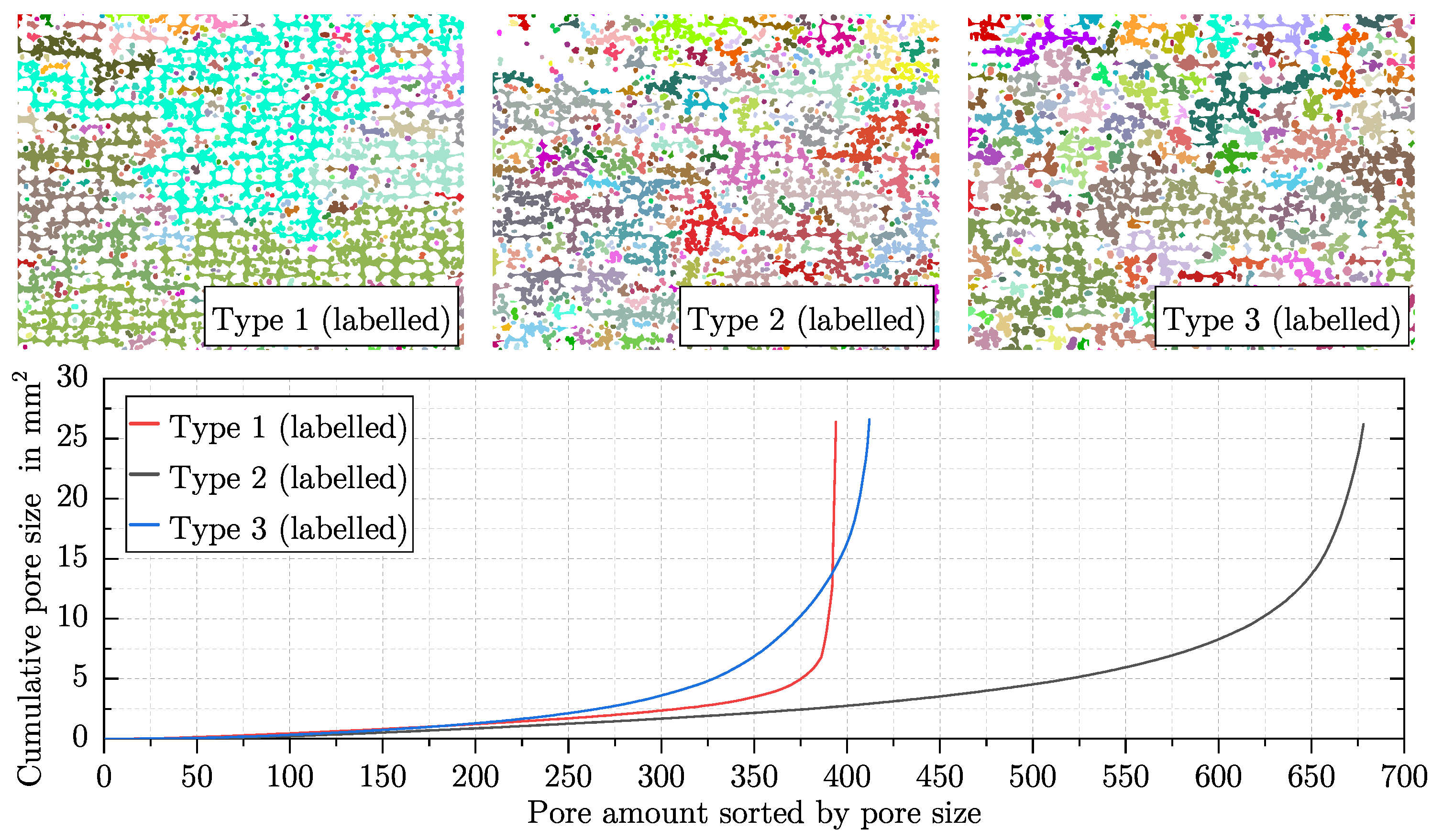
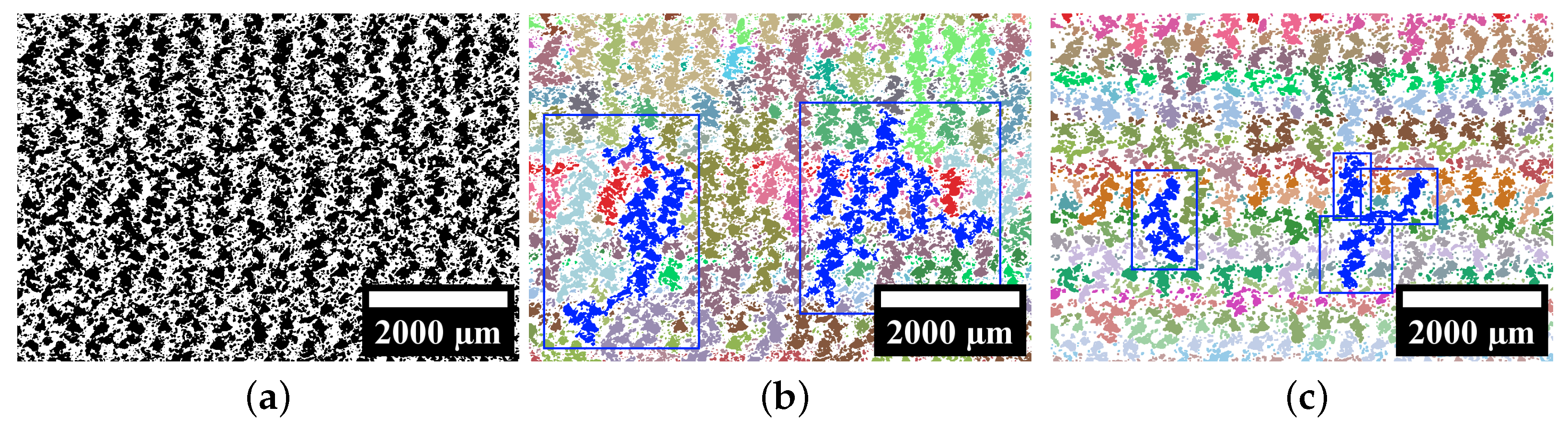
4.4.2. Determination of Pore Size and Pore Amount
4.4.3. Determination of the Entropy by Haralick
5. Results
5.1. Change of the Features for the Two Manufactured AMFs
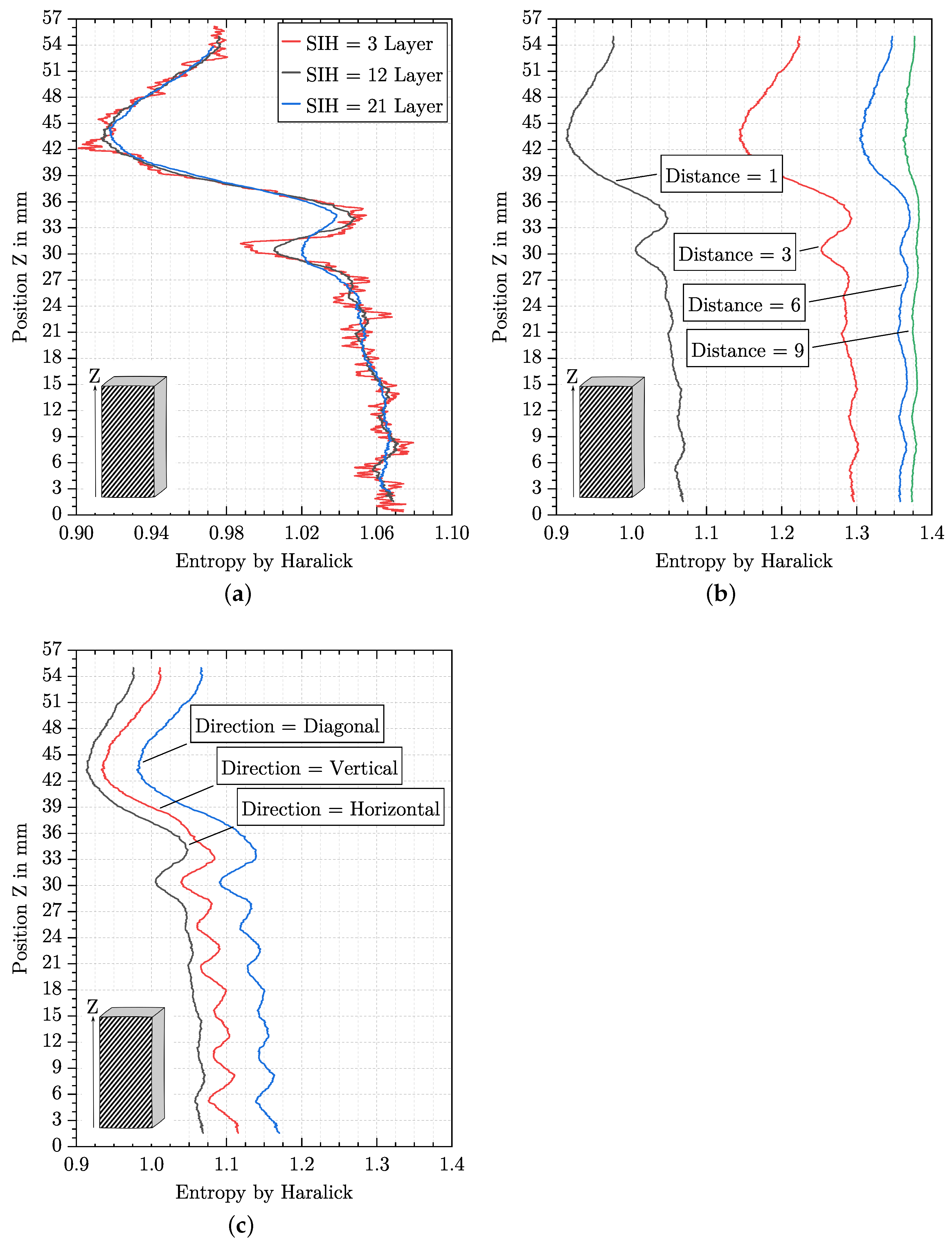
5.2. Influence of SIH, Distance and Direction on the Entropy by Haralick
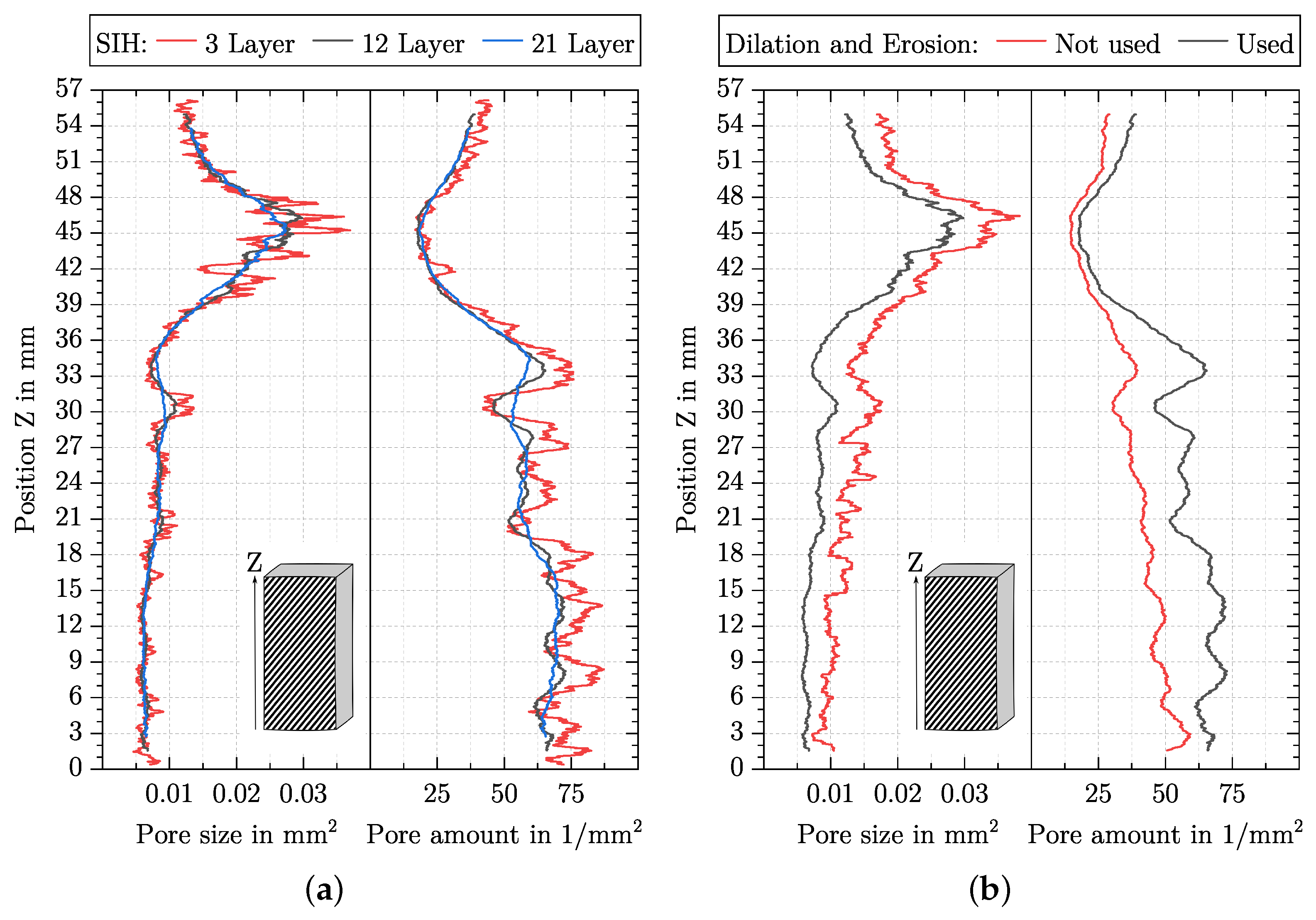
5.3. Influence of SIH and Dilation and Erosion on the Pore Size and Pore Amount
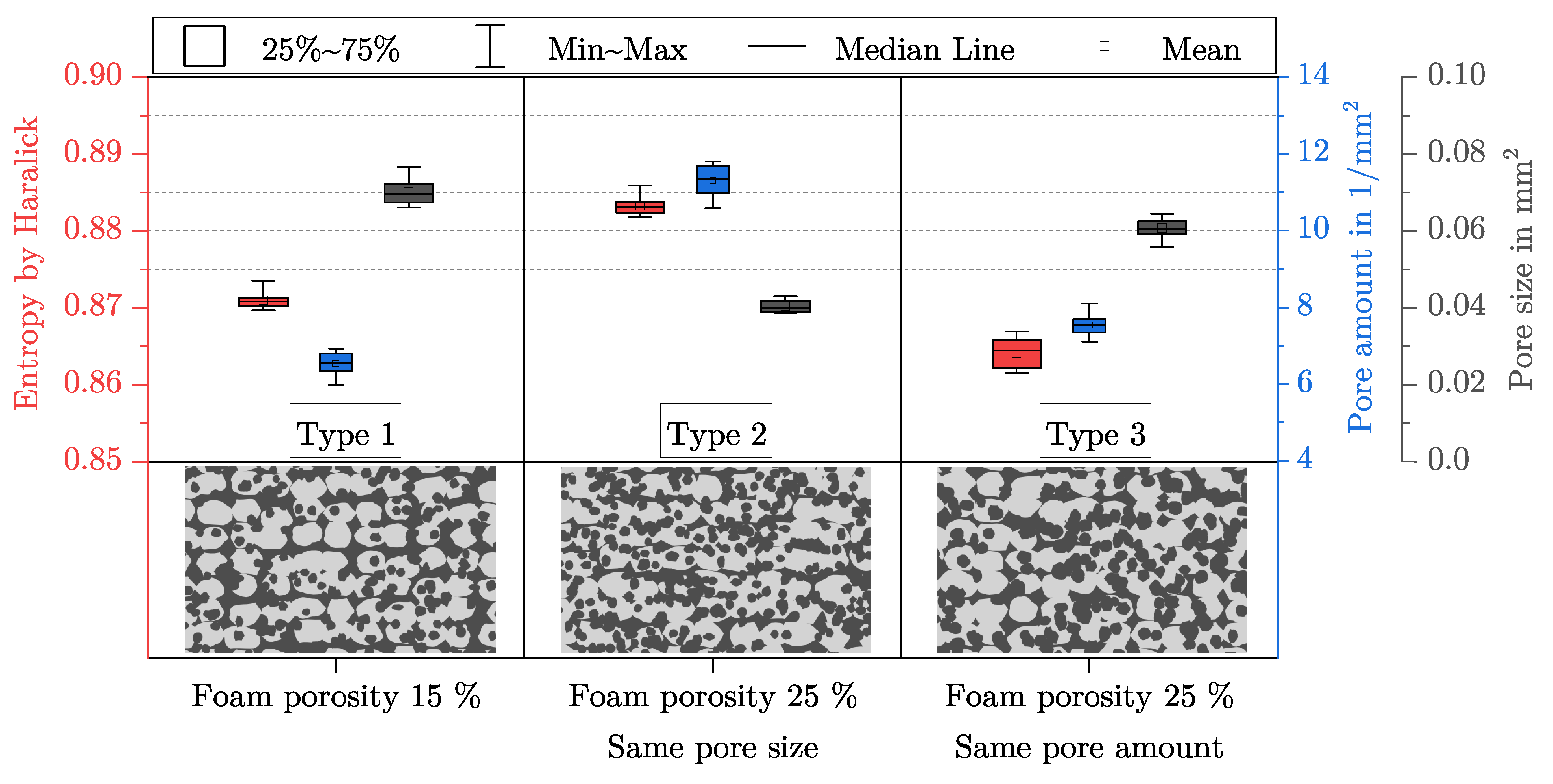
5.4. The Behaviour of the Features for Specific Artificial Images
6. Discussion
6.1. Influence of the Additively Manufactured Structure on the Characterisation of AMF
6.2. Characterisation of the Fineness of the Foam Structure
6.3. Interaction between the Additively Manufactured Structure and the Foam Structure
- The degree of foaming is a measure of the increase in volume of an initially non-foamed plastic mass. For foam structures, the porosity can be used to determine the degree of foaming.
- The fineness of a foam structure indicates how many pores the porosity is distributed over. The porosity remains constant—accordingly, so does the volume of a structure. For example, the pore amount or the pore size can be used as a measure (see Section 6.2).
6.4. An Optimal Determination of the Features for Characterisation of AMF
- Sliding image height (SIH)
- Direction and Distance
- Dilation and Erosion
7. Conclusions
- The feature total porosity is only suitable for the validation of whether the porosity specified in the slicing process has been achieved. It cannot be used to observe changes in the foaming behaviour of an additively manufactured foam structure.
- The features pore size and pore amount can be used to characterise the fineness of a foam structure. Furthermore, they can be used to identify networks of process-related pores. These are an indicator for a change in the degree of foaming.
- The feature entropy by Haralick is generally well suited for identifying changes within additively manufactured foam structures, and wrong estimations can be excluded. It can therefore be used to first identify factual changes and then investigate them with further features.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahn, S.H.; Montero, M.; Odell, D.; Roundy, S.; Wright, P.K. Anisotropic material properties of fused deposition modeling ABS. Rapid Prototyp. J. 2002, 8, 248–257. [Google Scholar] [CrossRef]
- Wu, W.; Geng, P.; Li, G.; Zhao, D.; Zhang, H.; Zhao, J. Influence of layer thickness and raster angle on the mechanical properties of 3D-printed PEEK and a comparative mechanical study between PEEK and ABS. Materials 2015, 8, 5834–5846. [Google Scholar] [CrossRef]
- Hirsch, A.; Hecker, F.; Moritzer, E. Process parameter optimization to improve the mechanical properties of Arburg Plastic Freeformed components. In Proceedings of the 30th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 12–14 August 2019; pp. 505–714. [Google Scholar]
- Pinter, P.; Baumann, S.; Lohr, C.; Heuer, A.; Englert, L.; Weidenmann, K.A. Mechanical properties of additively manufactured polymer samples using a Piezo controlled injection molding unit and fused filament fabrication compared with a conventional injection molding process. In Proceedings of the 2018 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 13–15 August 2018. [Google Scholar]
- Tao, Y.; Kong, F.; Li, Z.; Zhang, J.; Zhao, X.; Yin, Q.; Xing, D.; Li, P. A review on voids of 3D printed parts by fused filament fabrication. J. Mater. Res. Technol. 2021, 15, 4860–4879. [Google Scholar] [CrossRef]
- Charlon, S.; Soulestin, J. Thermal and geometry impacts on the structure and mechanical properties of part produced by polymer additive manufacturing. J. Appl. Polym. Sci. 2020, 137, 49038. [Google Scholar] [CrossRef]
- Nofar, M.; Utz, J.; Geis, N.; Altstädt, V.; Ruckdäschel, H. Foam 3D printing of thermoplastics: A symbiosis of additive manufacturing and foaming technology. Adv. Sci. 2022, 9, 2105701. [Google Scholar] [CrossRef]
- Coogan, T.J.; Kazmer, D.O. Bond and part strength in fused deposition modeling. Rapid Prototyp. J. 2017, 23, 414–422. [Google Scholar] [CrossRef]
- Heuer, A.; Huether, J.; Liebig, W.V.; Elsner, P. Fused filament fabrication: Comparison of methods for determining the interfacial strength of single welded tracks. Manuf. Rev. 2021, 8, 32. [Google Scholar] [CrossRef]
- Gibson, L.J. Cellular solids. Mrs Bull. 2003, 28, 270–274. [Google Scholar] [CrossRef]
- Bonthu, D.; Bharath, H.S.; Gururaja, S.; Prabhakar, P.; Doddamani, M. 3D printing of syntactic foam cored sandwich composite. Compos. Part C Open Access 2020, 3, 100068. [Google Scholar] [CrossRef]
- Bonthu, D.; Doddamani, M. Compressive response of 3D printed graded foams. Compos. Part C Open Access 2021, 6, 100181. [Google Scholar]
- Damanpack, A.R.; Sousa, A.; Bodaghi, M. Porous PLAs with Controllable Density by FDM 3D Printing and Chemical Foaming Agent. Micromachines 2021, 12, 866. [Google Scholar] [CrossRef]
- Kalia, K.; Ameli, A. Understanding the Process-Microstructure-Property Relationships in Material Extrusion Additive Manufacturing of Polylactic Acid Microcellular Foams. Addit. Manuf. 2023, 72, 103636. [Google Scholar] [CrossRef]
- Kalia, K.; Francoeur, B.; Amirkhizi, A.; Ameli, A. In situ foam 3D printing of microcellular structures using material extrusion additive manufacturing. ACS Appl. Mater. Interfaces 2022, 14, 22454–22465. [Google Scholar] [CrossRef] [PubMed]
- Pawar, A.; Ausias, G.; Corre, Y.-M.; Grohens, Y.; Férec, J. Mastering the density of 3D printed thermoplastic elastomer foam structures with controlled temperature. Addit. Manuf. 2022, 58, 103066. [Google Scholar] [CrossRef]
- Pang, Y.; Cao, Y.; Zheng, W.; Park, C.B. A comprehensive review of cell structure variation and general rules for polymer microcellular foams. Chem. Eng. J. 2022, 430, 132662. [Google Scholar] [CrossRef]
- Limper, A. Verfahrenstechnik der Thermoplastextrusion; Carl Hanser Verlag GmbH Co KG: Munchen, Germany, 2012. [Google Scholar]
- Altstädt, V.; Mantey, A. Thermoplast-Schaumspritzgießen; Munich Carl Hanser Verlag: Munich, Germany, 2011. [Google Scholar]
- Villamizar, A.C.; Han, D.C. Studies on structural foam processing II. Bubble dynamics in foam injection molding. Polym. Eng. Sci. 1978, 18, 699–710. [Google Scholar] [CrossRef]
- Okolieocha, C.; Raps, D.; Subramaniam, K.; Altstädt, V. Microcellular to nanocellular polymer foams: Progress (2004–2015) and future directions—A review. Eur. Polymer J. 2015, 73, 500–519. [Google Scholar] [CrossRef]
- Eisele, L.; Heuer, A.; Weidenmann, K.A.; Liebig, W.V. Can Different Parameter Sets Lead to Equivalent Optima between Geometric Accuracy and Mechanical Properties in Arburg Plastic Freeforming? Polymers 2023, 15, 1516. [Google Scholar] [CrossRef]
- Lee, S.T.; Park, C.B. Foam Extrusion: Principles and Practice; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Zdravkov, B.; Čermák, J.; Šefara, D.M.; Janků, J. Pore classification in the characterization of porous materials: A perspective. Open Chem. 2007, 5, 385–395. [Google Scholar] [CrossRef]
- Tronvoll, S.A.; Welo, T.; Elverum, C.W. The effects of voids on structural properties of fused deposition modelled parts: A probabilistic approach. Int. J. Adv. Manuf. Technol. 2018, 97, 3607–3618. [Google Scholar] [CrossRef]
- Chen, C.H. Handbook of Pattern Recognition and Computer Vision; World Scientific: Singapore, 2015. [Google Scholar]
- Armi, L.; Fekri-Ershad, S. Texture image analysis and texture classification methods—A review. arXiv 2019, arXiv:1904.06554. [Google Scholar]
- Sharma, M.; Singh, S. Evaluation of texture methods for image analysis. In Proceedings of the Seventh Australian and New Zealand Intelligent Information Systems Conference, Perth, WA, Australia, 18–21 November 2001; pp. 117–121. [Google Scholar]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Germain, J.C.; Aguilera, J.M. Identifying industrial food foam structures by 2D surface image analysis and pattern recognition. J. Food Eng. 2012, 111, 440–448. [Google Scholar] [CrossRef]
- INEOS Styrolution Europe GmbH. CAMPUS Datenblatt Terluran GP-35-ABS; CAMPUS GmbH: Frankfurt am Main, Germany, 2018. [Google Scholar]
- Polymer-Service PSG GmbH. Produktdatenblatt Clariant Hydrocerol ITP 815; Polymer-Service PSG GmbH: Beckedorf-Seevetal, Germany, 2017. [Google Scholar]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef]
- Preibisch, S.; Saalfeld, S.; Tomancak, P. Globally optimal stitching of tiled 3D microscopic image acquisitions. Bioinformatics 2009, 25, 1463–1465. [Google Scholar] [CrossRef] [PubMed]
- Legl, D.; Arganda-Carreras, I.; Andrey, P. MorphoLibJ: Integrated library and plugins for mathematical morphology with ImageJ. Bioinformatics 2016, 32, 3532–3534. [Google Scholar]
- Brynolfsson, P.; Nilsson, D.; Torheim, T.; Asklund, T.; Karlsson, C.T.; Trygg, J.; Nyholm, T.; Garpebring, A. Haralick texture features from apparent diffusion coefficient (ADC) MRI images depend on imaging and pre-processing parameters. Sci. Rep. 2017, 7, 4041. [Google Scholar] [CrossRef]
- Eaves, D. Handbook of Polymer Foams; iSmithers Rapra Publishing: Shrewsbury, UK, 2004. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heuer, A.; Rees, M.; Weidenmann, K.A.; Liebig, W.V. On the Creation and Optical Microstructure Characterisation of Additively Manufactured Foam Structures (AMF). Polymers 2023, 15, 3544. https://doi.org/10.3390/polym15173544
Heuer A, Rees M, Weidenmann KA, Liebig WV. On the Creation and Optical Microstructure Characterisation of Additively Manufactured Foam Structures (AMF). Polymers. 2023; 15(17):3544. https://doi.org/10.3390/polym15173544
Chicago/Turabian StyleHeuer, Anselm, Maike Rees, Kay A. Weidenmann, and Wilfried V. Liebig. 2023. "On the Creation and Optical Microstructure Characterisation of Additively Manufactured Foam Structures (AMF)" Polymers 15, no. 17: 3544. https://doi.org/10.3390/polym15173544
APA StyleHeuer, A., Rees, M., Weidenmann, K. A., & Liebig, W. V. (2023). On the Creation and Optical Microstructure Characterisation of Additively Manufactured Foam Structures (AMF). Polymers, 15(17), 3544. https://doi.org/10.3390/polym15173544






