Topology Optimization for Digital Light Projector Additive Manufacturing Addressing the In-Situ Structural Strength Issue
Abstract
:1. Introduction
2. Topology Optimization Considerations for DLP 3D Printing
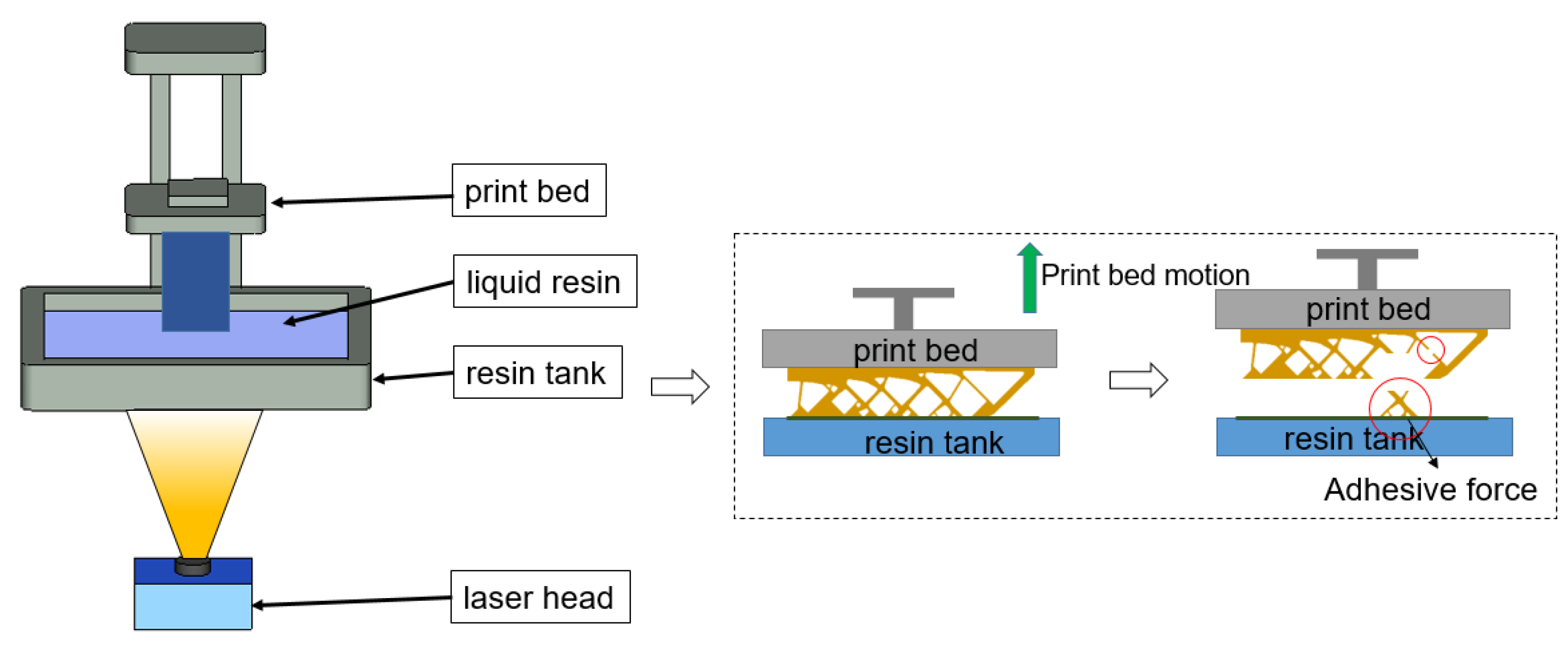
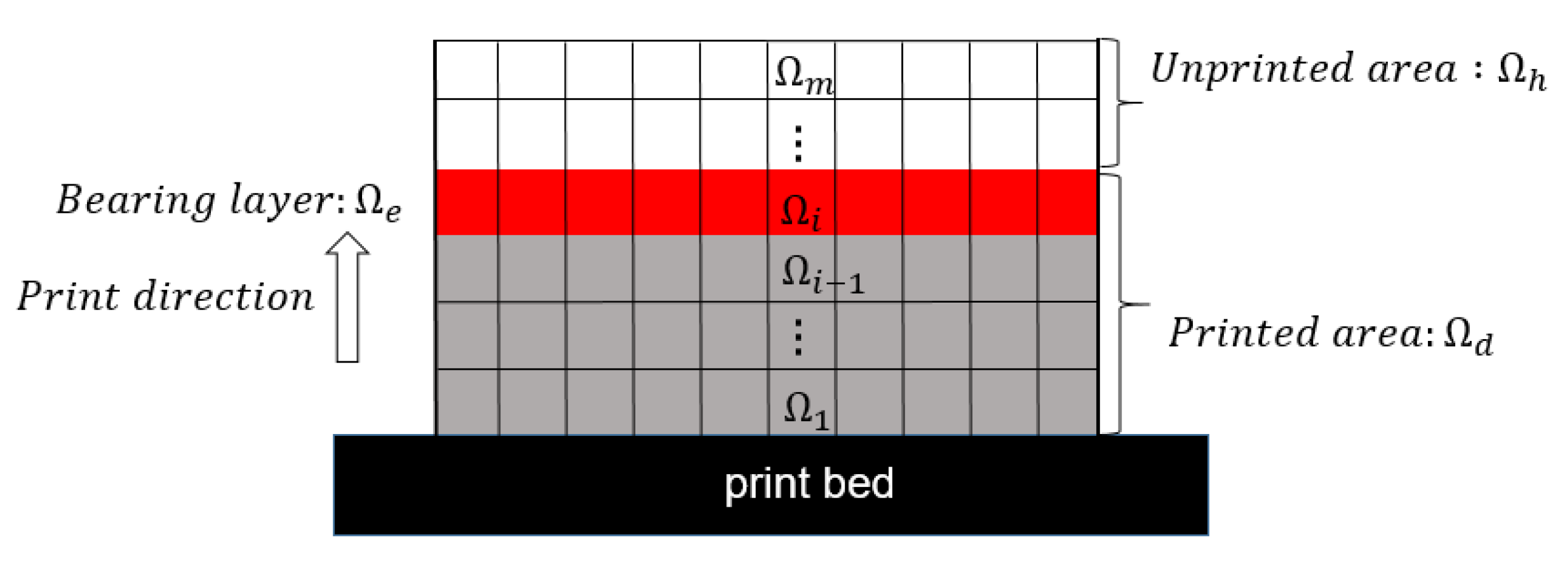
2.1. DLP Process Model
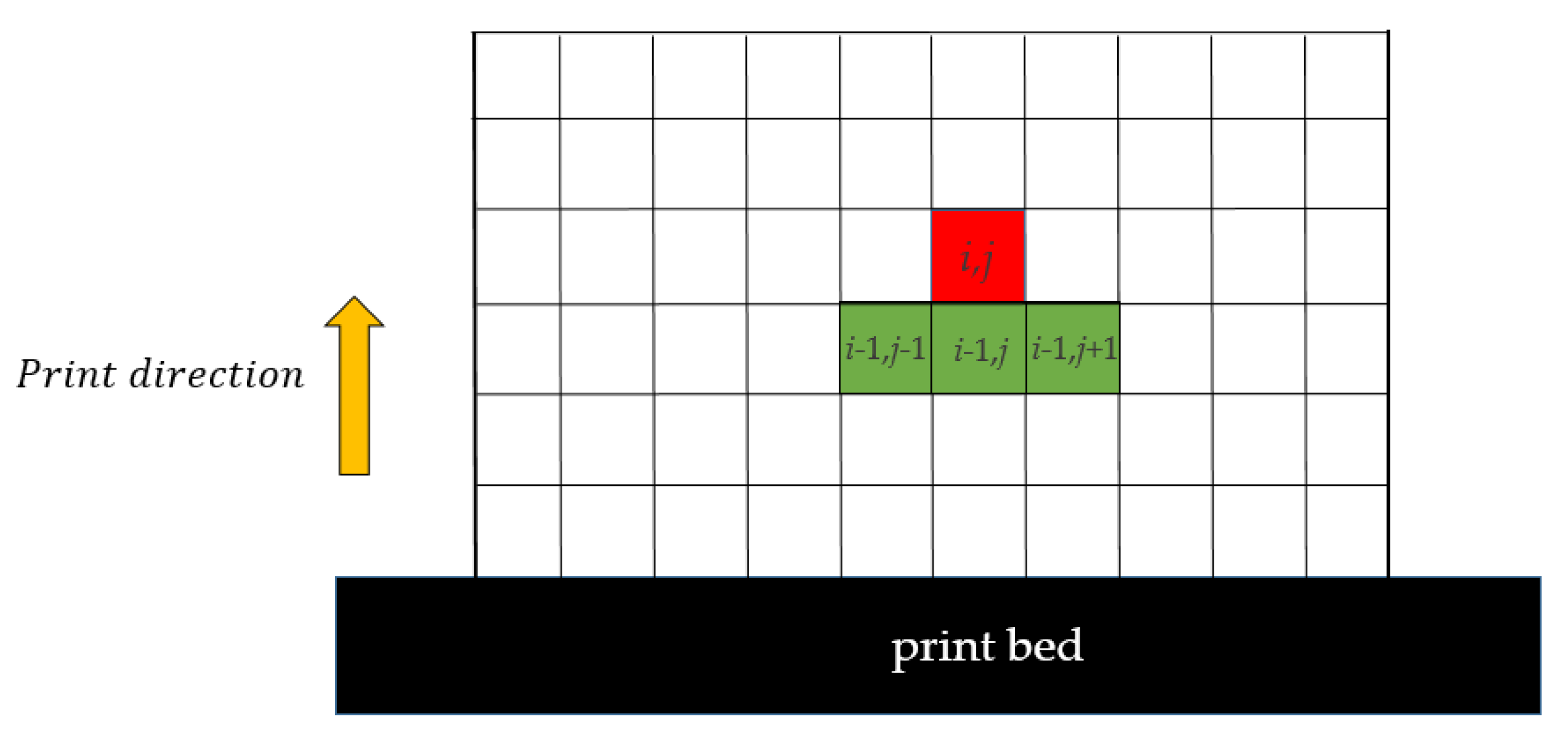
2.2. AM Filter for Fabricable Self-Support Structures
3. Interpolation Scheme and Total Stress Calculation
4. Formulation and Solution of Optimization Problems
4.1. Optimization Problem Formulation
4.2. Sensitivity Analysis
5. Numerical Examples
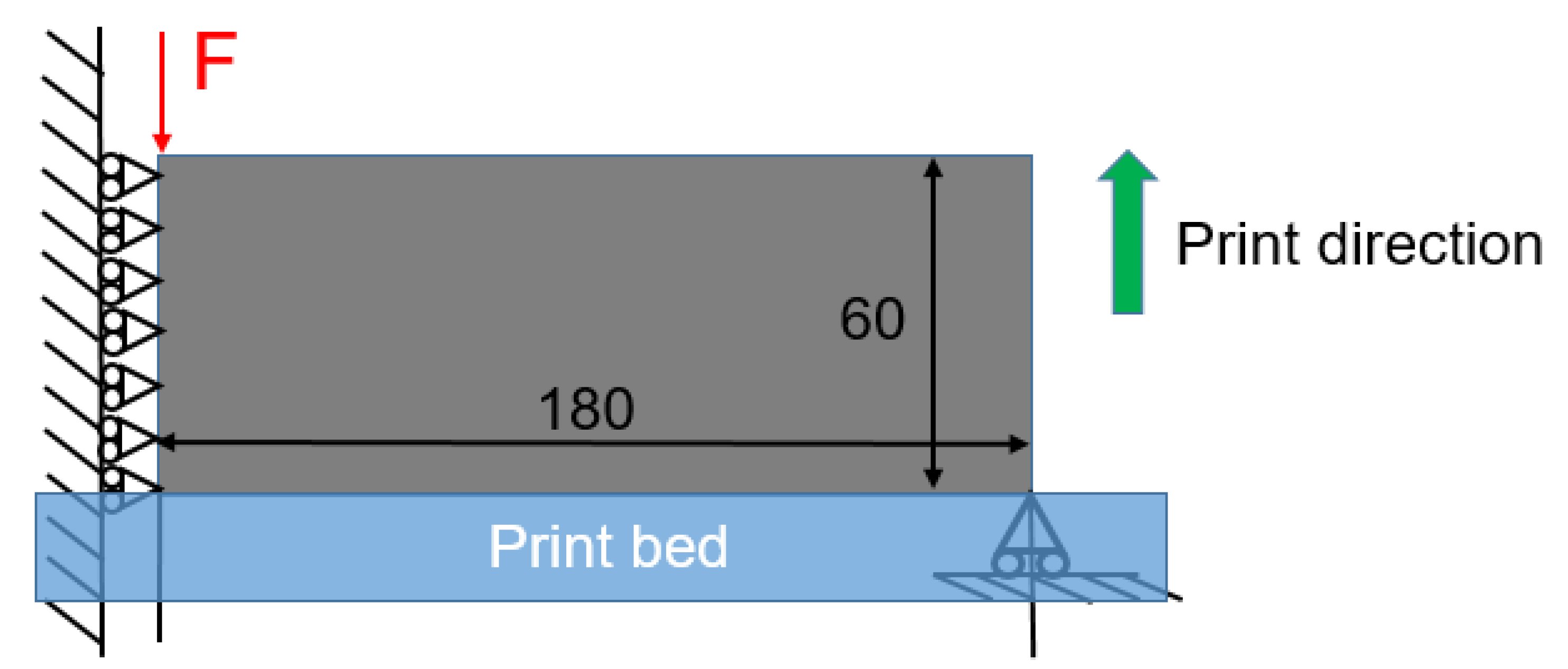
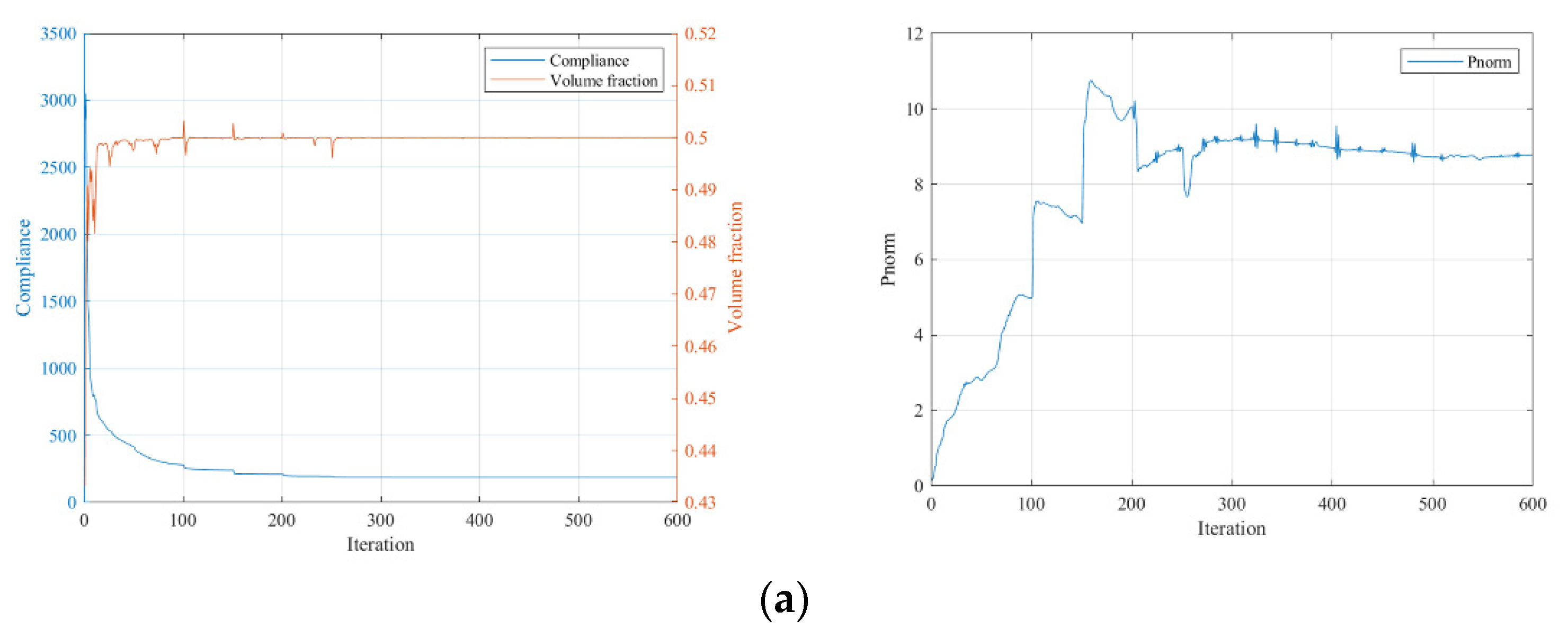
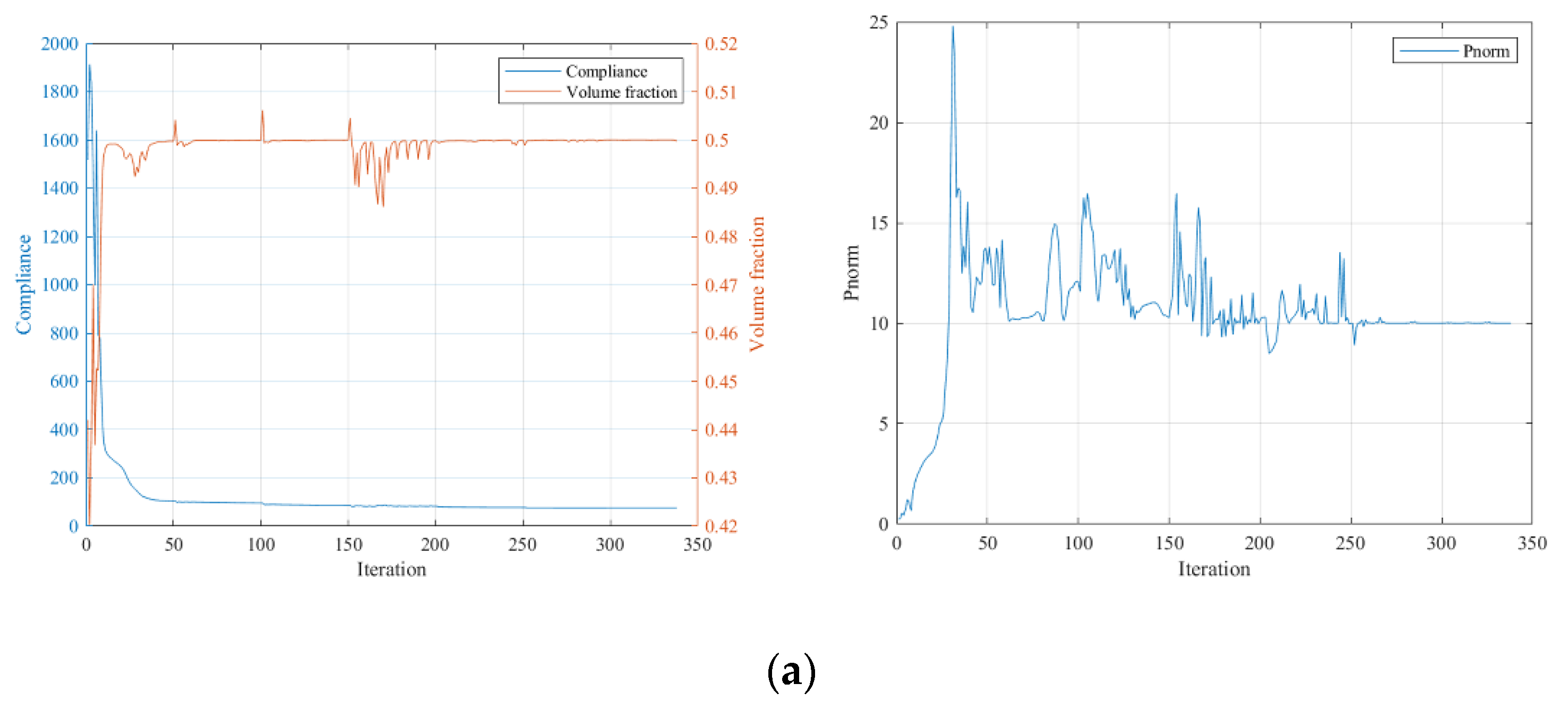
5.1. The MBB Beam Structure
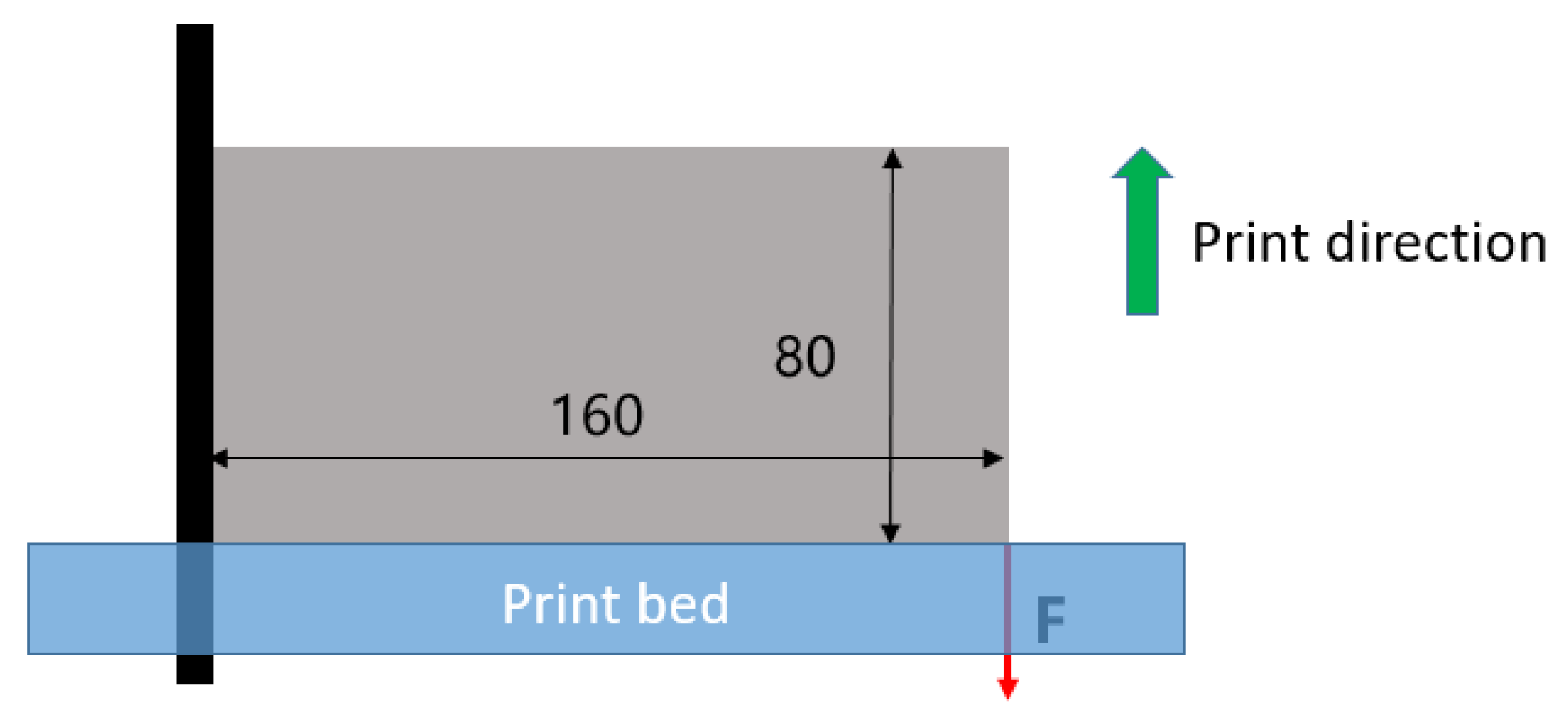
5.2. Cantilever Beam
- (1)
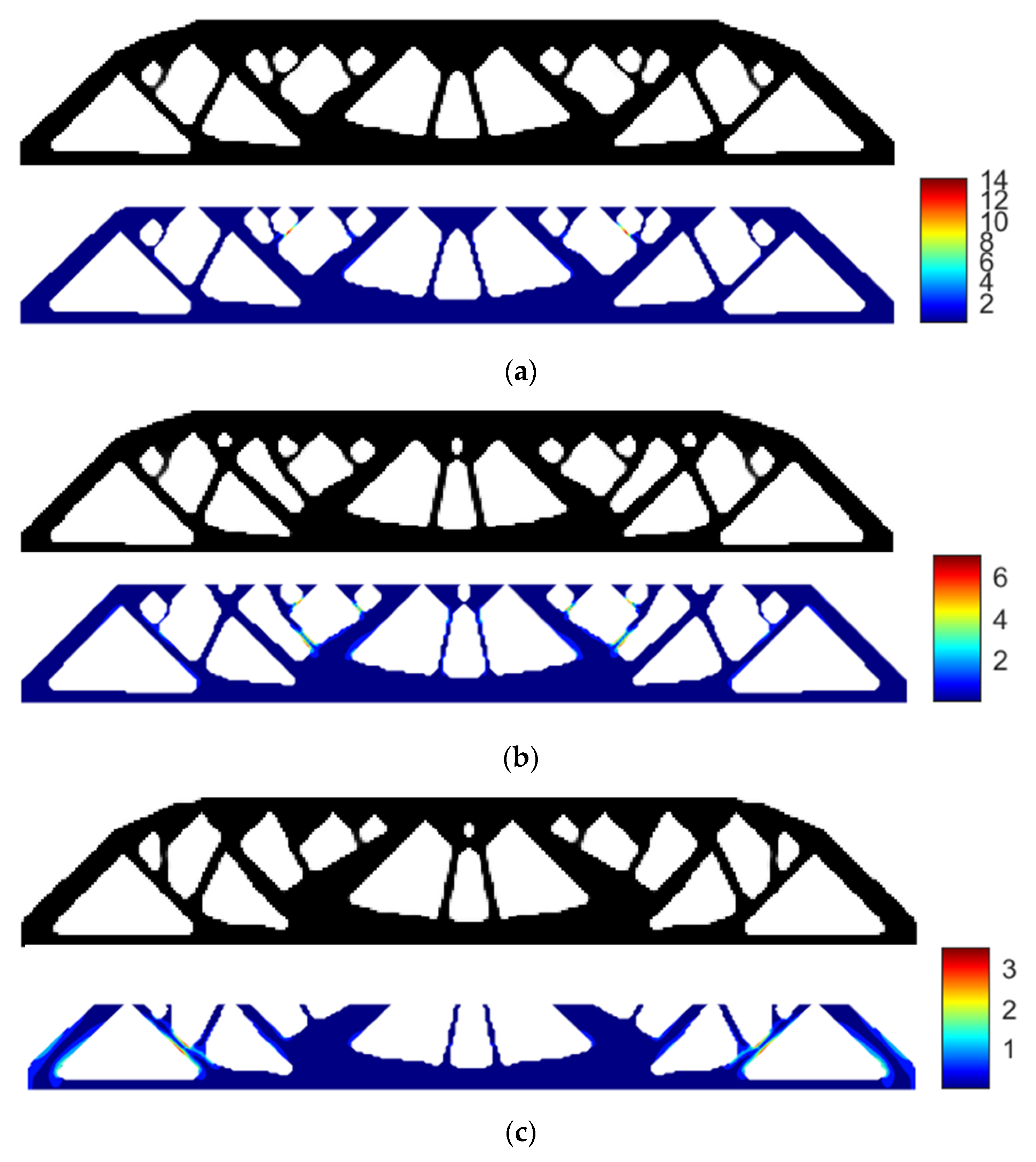
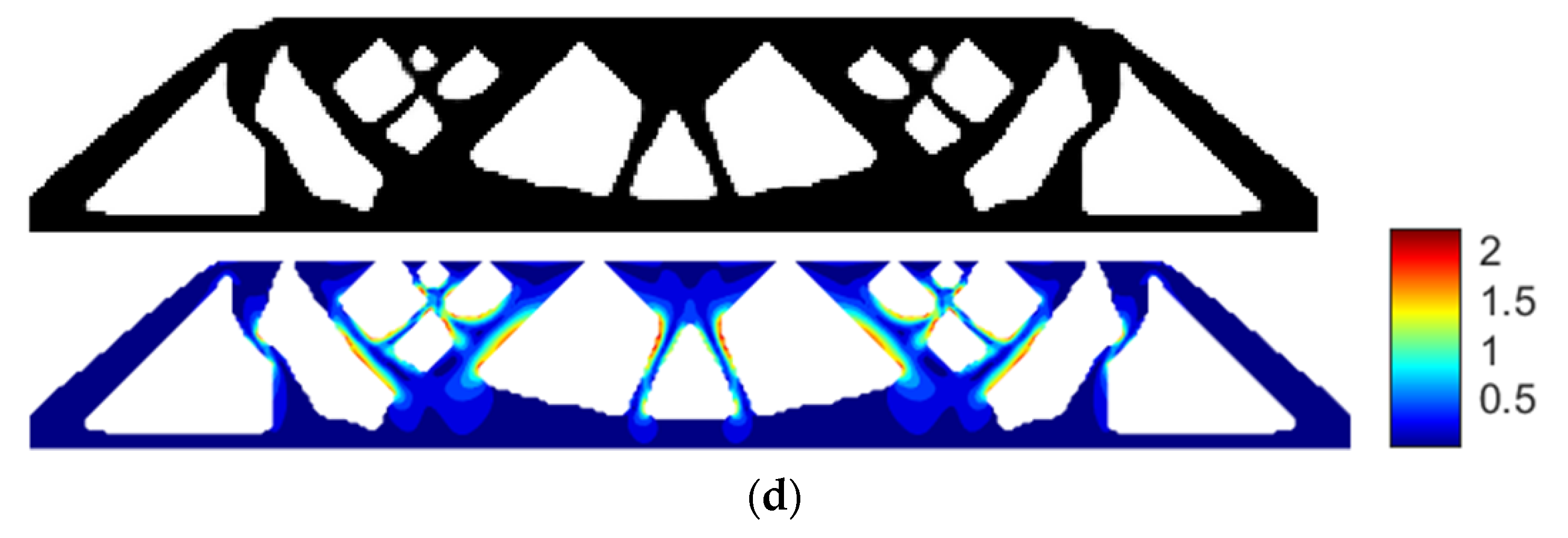
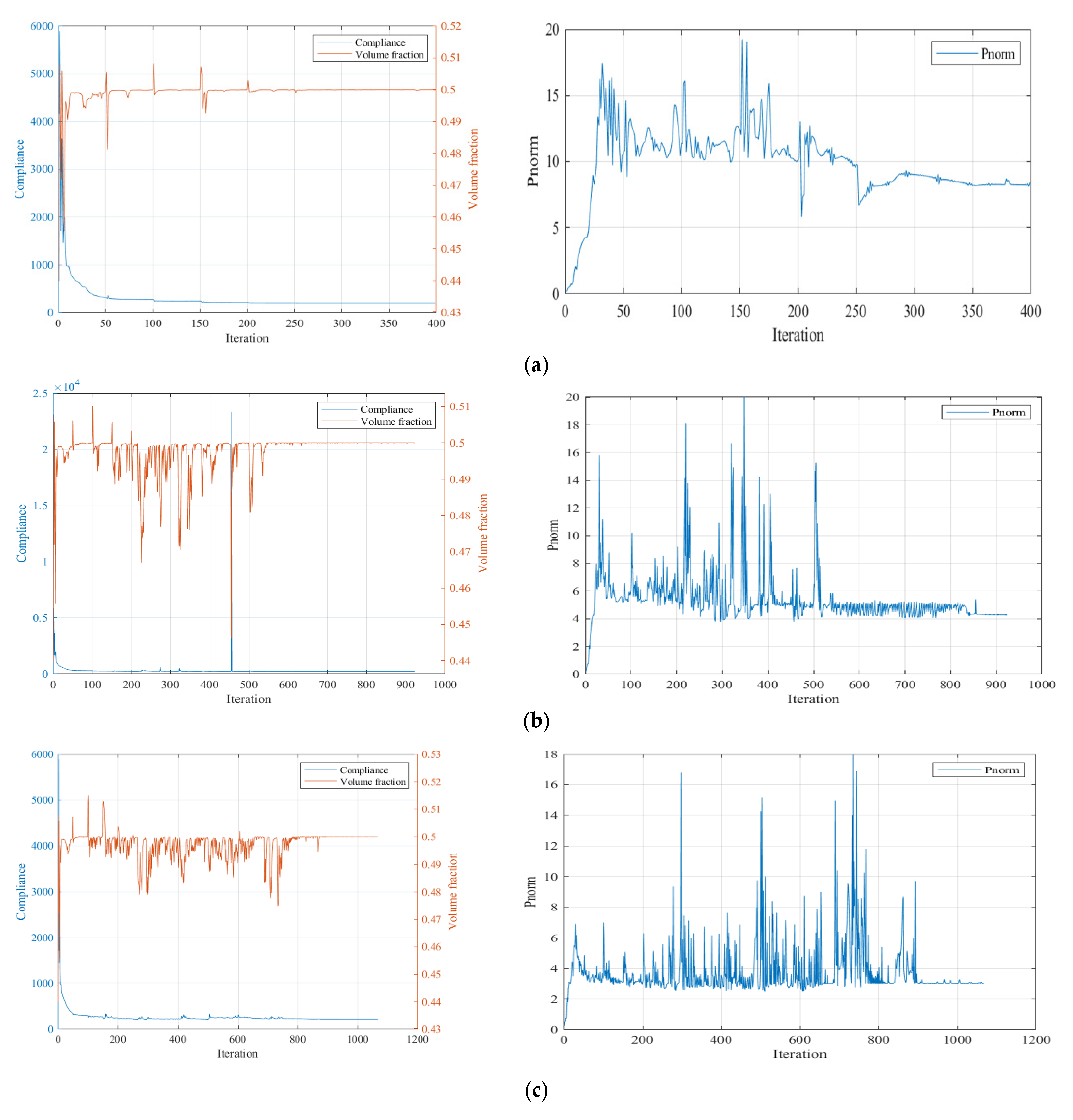
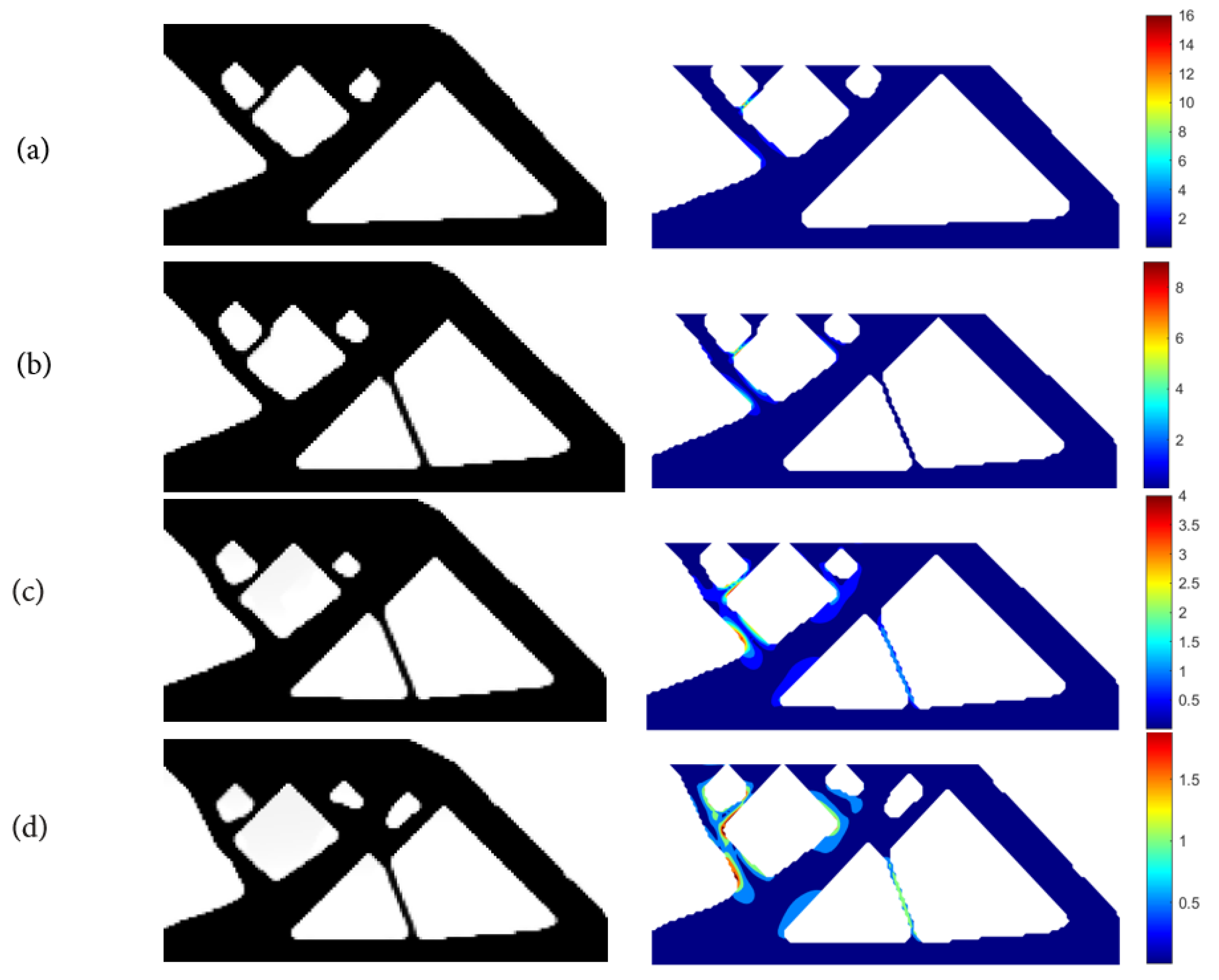
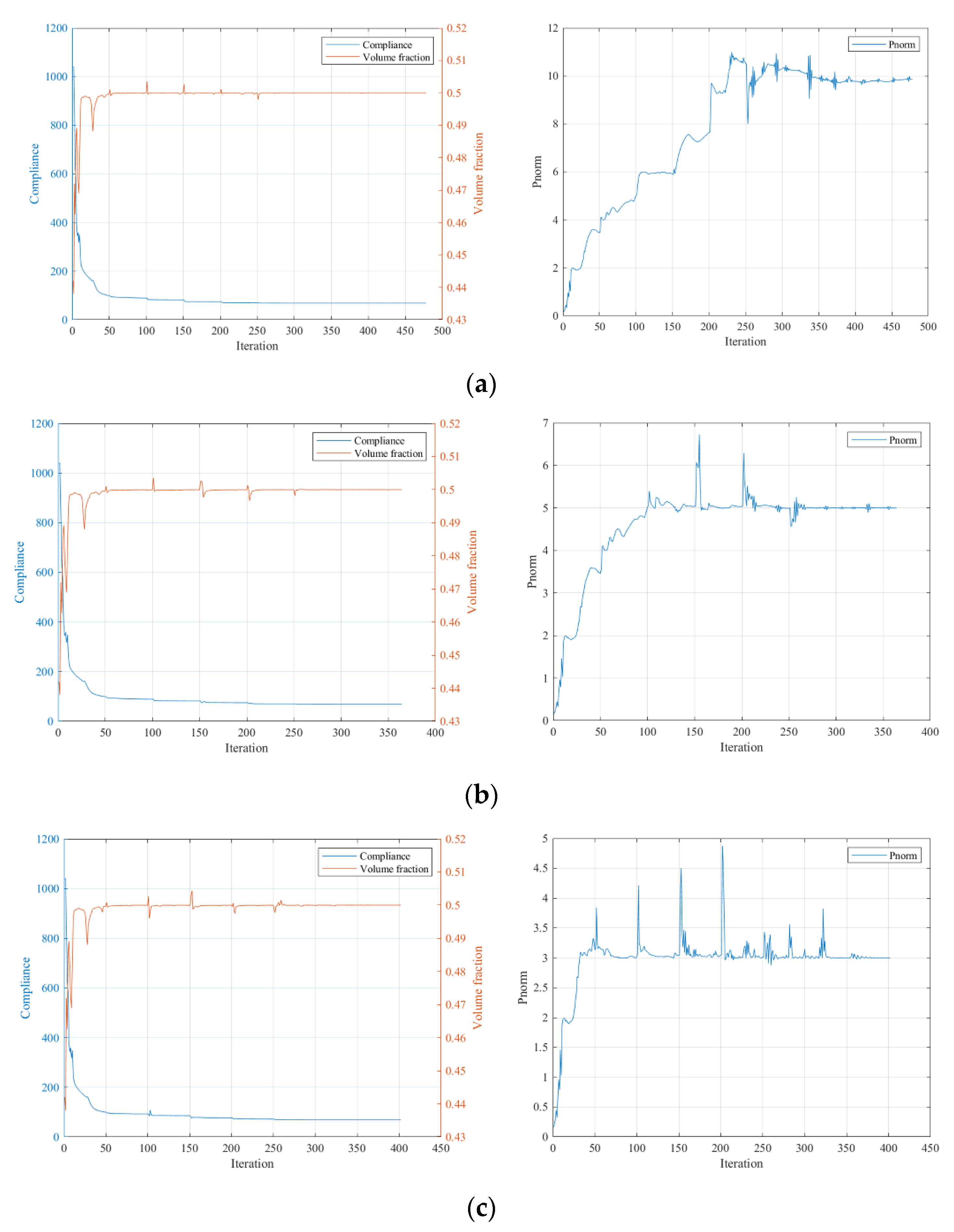
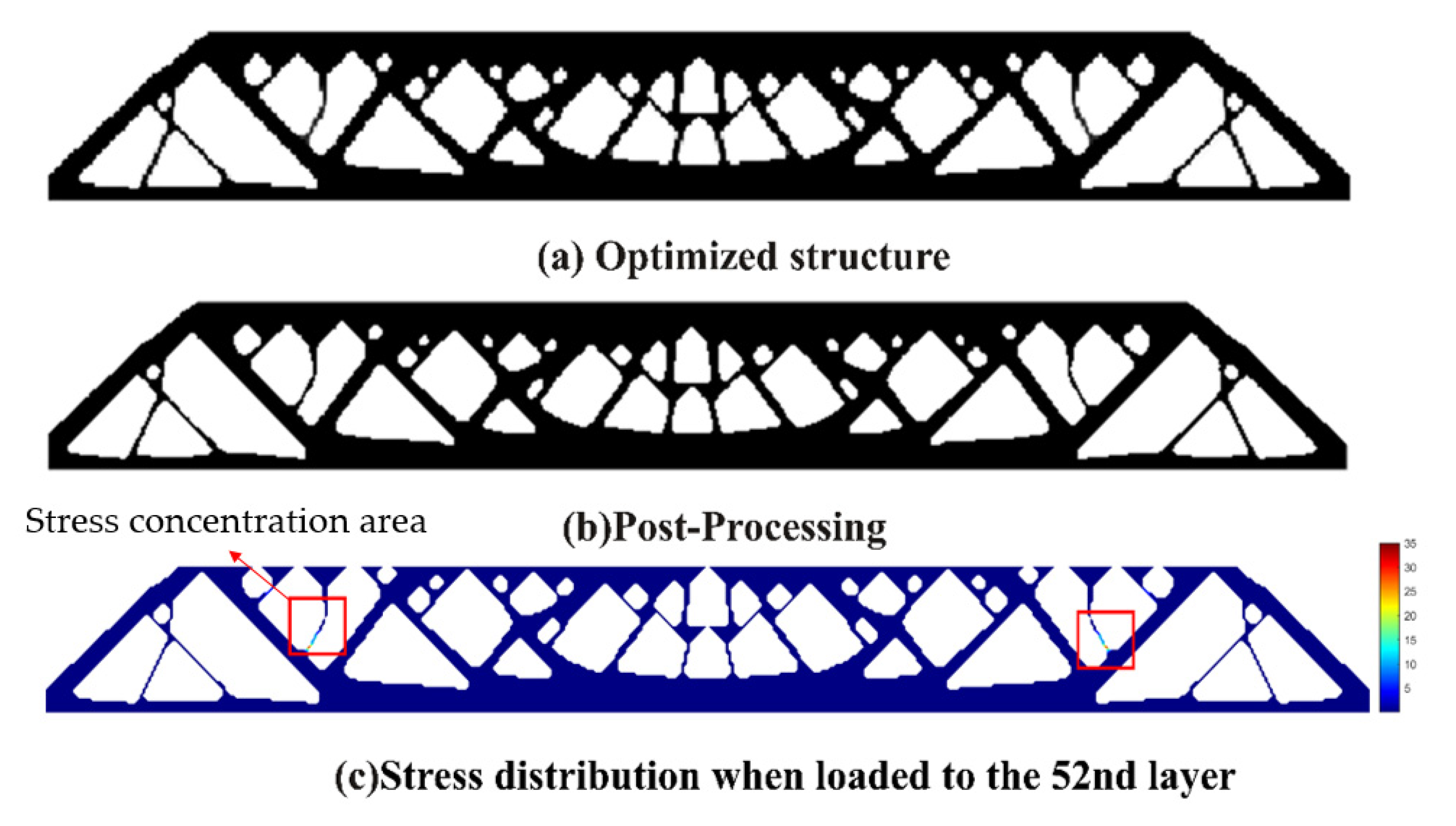
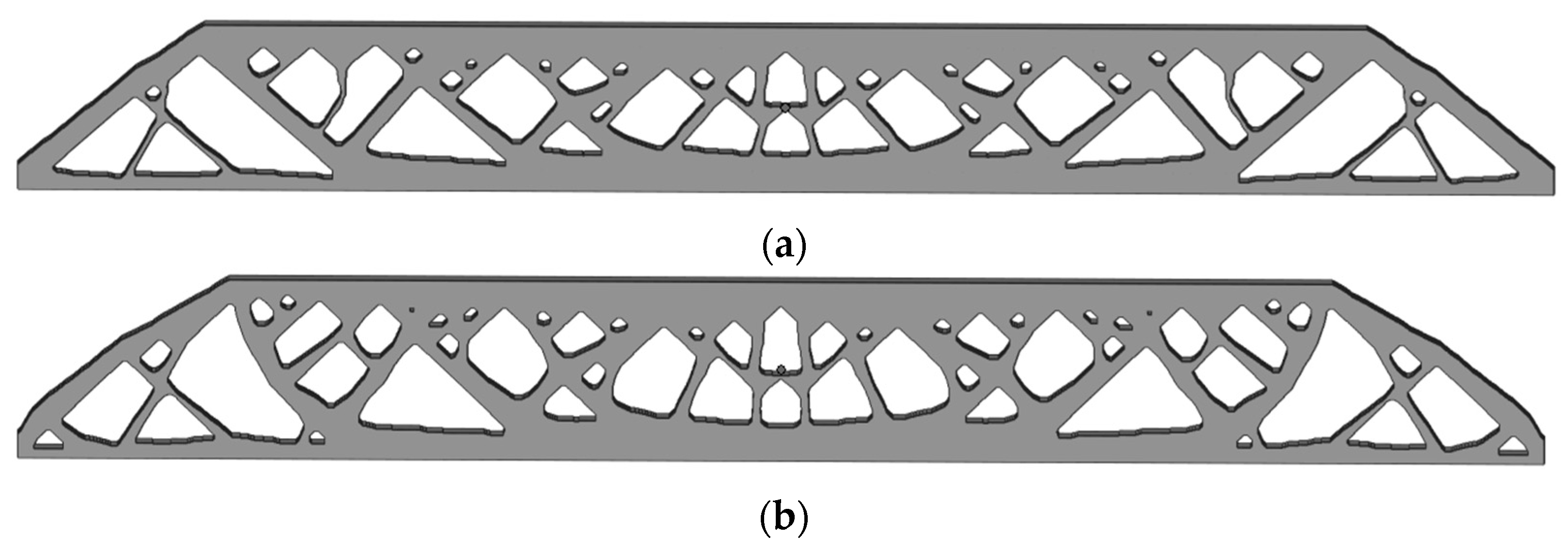
- Using SIMP interpolation, the minimum compliance of 81.5803 is first obtained without imposing the stress constraint, and if we apply the layer-based adhesion load to this result, the maximum P-norm stress occurs at the 59th layer’s adhesion load, reaching 17.906. Hence, to reduce the risk of failure, we take the stress limits of 10, 5, and 3, respectively, to perform the process of stress-constrained topology optimization, obtaining the optimized structures and corresponding stress profiles for the most stress-concentrated load steps, referring to Figure 11.
- (2)
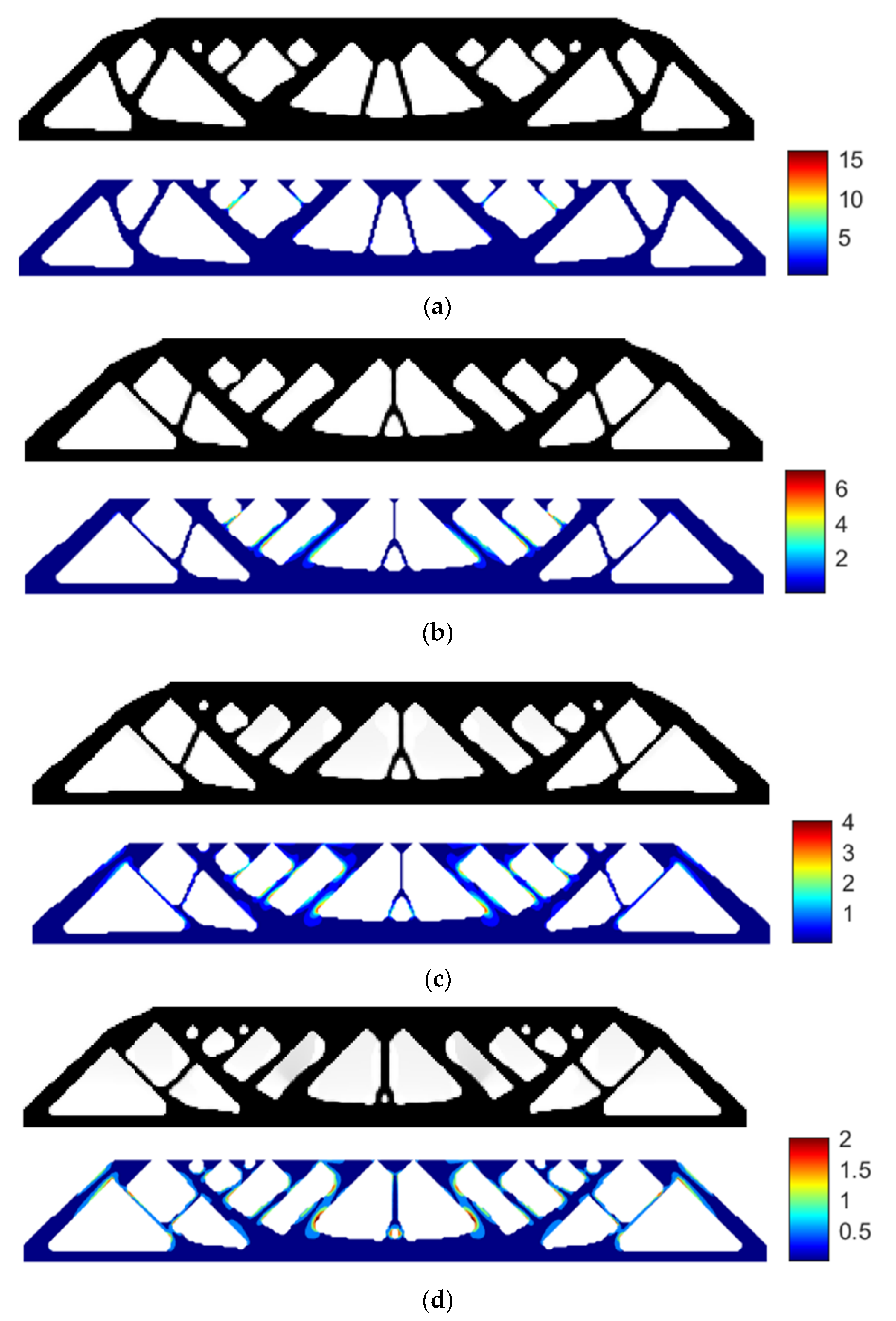
- Using RAMP interpolation, the minimum compliance of 68.2931 is obtained without the stress constraint, and if we apply the layer-based adhesion load, the maximum stress occurs at the 63rd layer’s adhesion load step, reaching 17.1274. Hence, to reduce the failure risk, we again take the stress limits of 10, 5, and 3, respectively, to perform the process of stress-constrained topology optimization, obtaining the optimized structures and corresponding stress profiles for the most stress-concentrated load steps, shown in Figure 13.
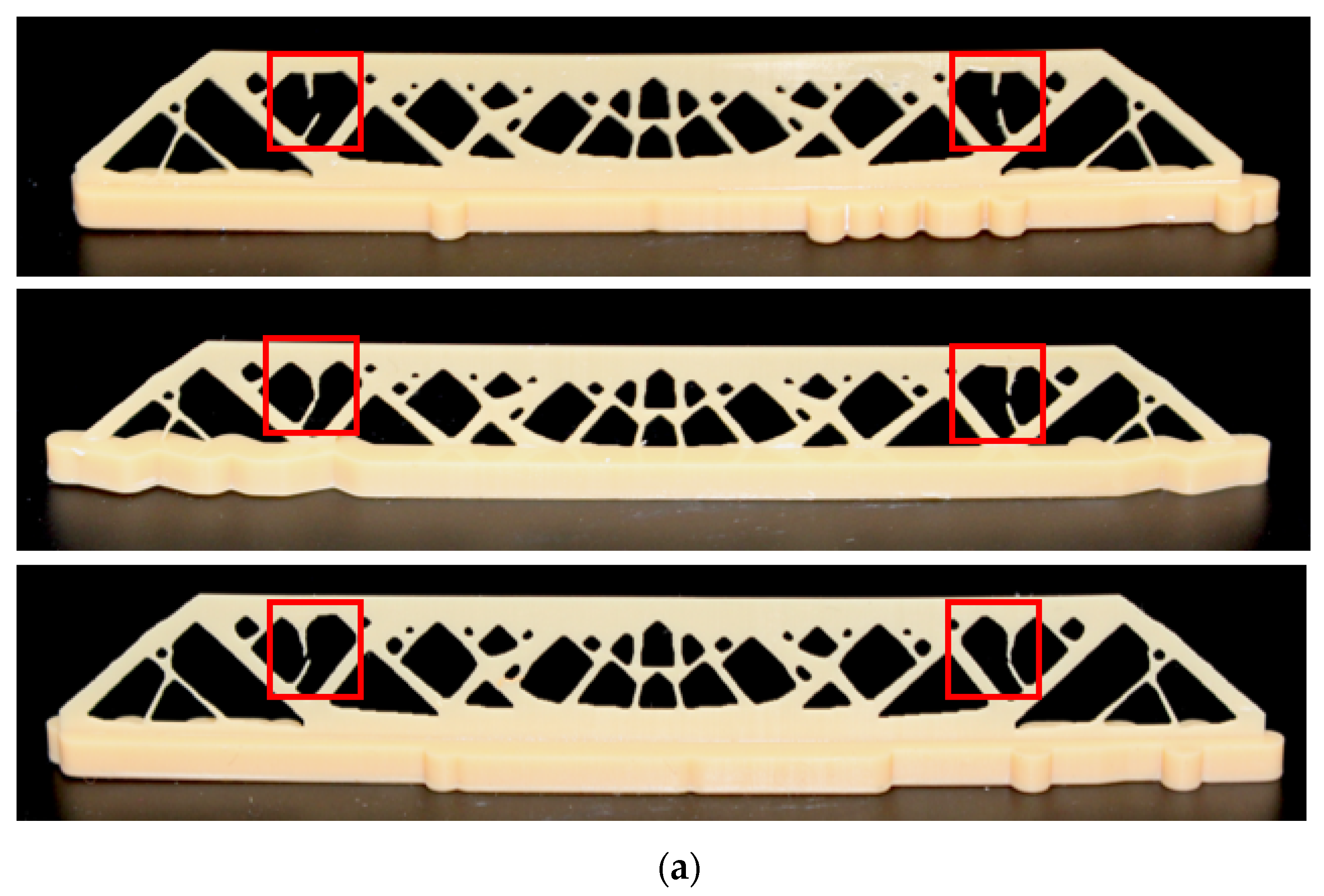
6. Experimental Validation
7. Conclusions
- (1)
- To mimic the in-process stress concentrations, an SIMP-like interpolation is proposed to simulate the adhesion forces between the workpiece and resin base for DLP additive manufacturing.
- (2)
- A greater than 1 penalization parameter is adopted for the stress term to prevent artificial high stresses at the boundary non-solid elements since the AM filter is applied after Heaviside projection and the approximated and operators unavoidably lead to non-solid elements.
- (3)
- Both the SIMP and RAMP interpolations allow us to achieve topology optimization designs considering the maximum volume fraction and P-norm stress constraints. SIMP interpolation exhibits more fluctuations in converging the optimization process. RAMP interpolation has a smoother convergence process, although some cases show a small amount of irremovable gray elements.
- (4)
- Experiments validate the necessity and effect of imposing the stress constraints. The stress-concentrated thin struts are replaced by thickened structural features through size and shape enhancement, and the overall stress field tends to distribute more evenly. Hence, failures are not encountered in the modified designs and, simultaneously, the local shaping accuracy is guaranteed as well.
- (5)
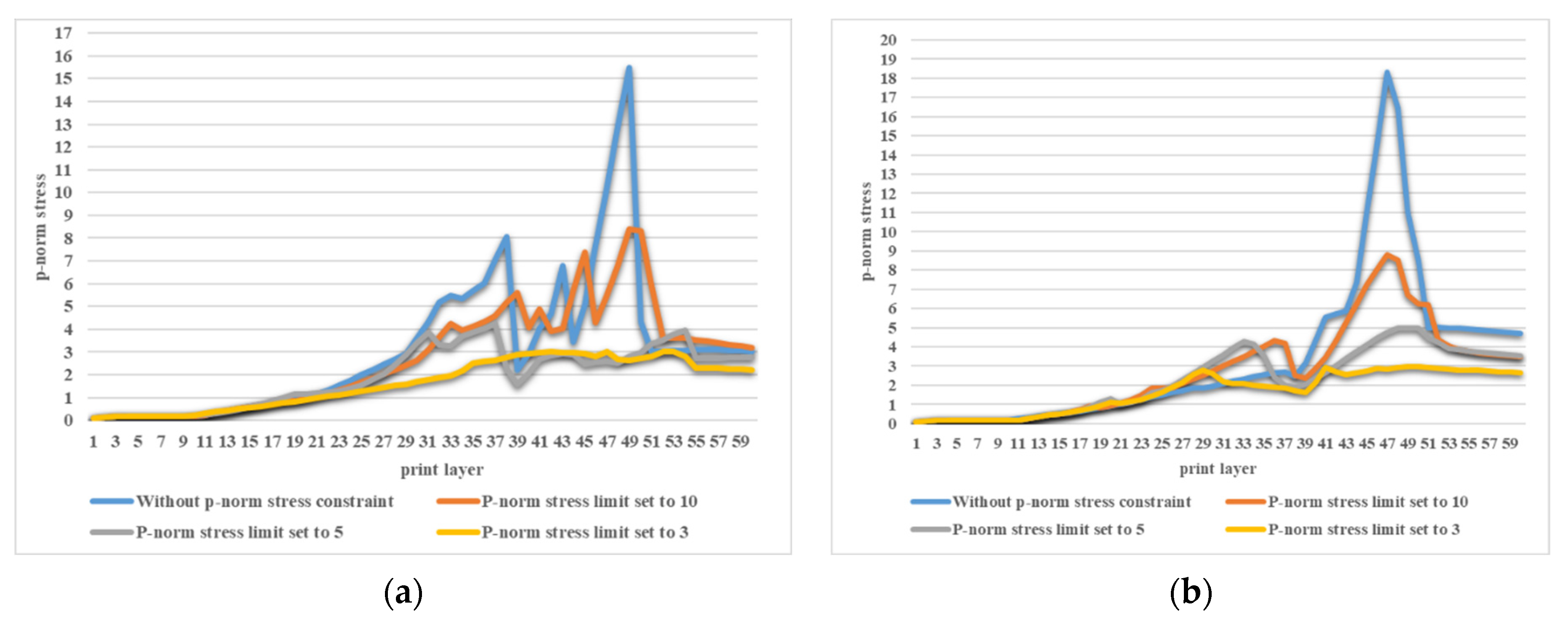
- The layerwise P-norm stresses are summarized in Figure 20 for both the SIMP and RAMP interpolations. Apparently, a stricter stress restriction leads to an overall reduction in P-norm stresses, indicating the effectiveness of the layerwise stress constraints.
- (6)
- A stricter stress restriction, i.e., lower P-norm stress upper limit, causes the decreased overall stiffness of the optimized structure for both the SIMP and RAMP interpolations.
- (7)
- Interestingly, topological optimization that considers the maximum volume fraction and stress constraints may yield better structural stiffness than topological optimization that only considers the volume constraints. This phenomenon deserves careful further investigation.
- (8)
- The build orientation plays an equally important role in topology optimization design considering the process stress constraints in additive manufacturing. Appropriate build directions may allow us to resolve the maximum P-norm stress constraints without significantly impacting the structural stiffness. This topic will be investigated in our forthcoming research.
- (9)
- Finally, considering the computational cost, the finite element analysis simulating the layer-based adhesion loading conditions and the stress term-related adjoint equations occupies the majority of the calculation time. Adopting parallel computing could greatly reduce the computing time, especially for larger-scale problems, and this scheme deserves further exploration as well.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, J.; Chen, Q.; Liang, X.; To, A.C. Manufacturing cost constrained topology optimization for additive manufacturing. Front. Mech. Eng. 2019, 14, 213–221. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, T.; Xu, S.; Liu, J. Multiscale topology optimization for solid–lattice–void hybrid structures through an ordered multi-phase interpolation. Comput. Aided Des. 2023, 154, 103424. [Google Scholar] [CrossRef]
- Chaudhary, R.; Fabbri, P.; Leoni, E.; Mazzanti, F.; Akbari, R.; Antonini, C. Additive manufacturing by digital light processing: A review. Prog. Addit. Manuf. 2023, 8, 331–351. [Google Scholar] [CrossRef]
- Liu, J.; Huang, J.; Zheng, Y.; Hou, S.; Xu, S.; Ma, Y.; Huang, C.; Zou, B.; Li, L. Challenges in topology optimization for hybrid additive–subtractive manufacturing: A review. Comput. Aided Des. 2023, 161, 103531. [Google Scholar] [CrossRef]
- Krishnamurthy, V.; Poudel, L.; Ebert, M.; Weber, D.H.; Wu, R.; Zhou, W.; Akleman, E.; Sha, Z. LayerLock: Layer-Wise Collision-Free Multi-Robot Additive Manufacturing Using Topologically Interlocked Space-Filling Shapes. Comput. Aided Des. 2022, 152, 103392. [Google Scholar] [CrossRef]
- Liu, J.; Gaynor, A.T.; Chen, S.; Kang, Z.; Suresh, K.; Takezawa, A.; Li, L.; Kato, J.; Tang, J.; Wang, C.C.L.; et al. Current and future trends in topology optimization for additive manufacturing. Struct. Multidiscip. Optim. 2018, 57, 2457–2483. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, W.; Quan, D.; Shi, G.; Tang, L.; Hou, Y.; Breitkopf, P.; Zhu, J.; Gao, T. From Topology Optimization Design to Additive Manufacturing: Today’s Success and Tomorrow’s Roadmap. Arch. Comput. Methods Eng. 2020, 27, 805–830. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Ma, Y. Residual stress constrained self-support topology optimization for metal additive manufacturing. Comput. Methods Appl. Mech. Eng. 2022, 389, 114380. [Google Scholar] [CrossRef]
- Boissier, M.; Allaire, G.; Tournier, C. Time Dependent Scanning Path Optimization for the Powder Bed Fusion Additive Manufacturing Process. Comput. Aided Des. 2022, 142, 103122. [Google Scholar] [CrossRef]
- Bihr, M.; Allaire, G.; Betbeder-Lauque, X.; Bogosel, B.; Bordeu, F.; Querois, J. Part and supports optimization in metal powder bed additive manufacturing using simplified process simulation. Comput. Methods Appl. Mech. Eng. 2022, 395, 114975. [Google Scholar] [CrossRef]
- Miki, T.; Yamada, T. Topology optimization considering the distortion in additive manufacturing. Finite Elem. Anal. Des. 2021, 193, 103558. [Google Scholar] [CrossRef]
- Liu, J.; Yu, H. Concurrent deposition path planning and structural topology optimization for additive manufacturing. Rapid Prototyp. J. 2017, 23, 930–942. [Google Scholar] [CrossRef]
- Dapogny, C.; Estevez, R.; Faure, A.; Michailidis, G. Shape and topology optimization considering anisotropic features induced by additive manufacturing processes. Comput. Methods Appl. Mech. Eng. 2019, 344, 626–665. [Google Scholar] [CrossRef]
- Liu, J.; Huang, J.; Yan, J.; Li, L.; Li, S. Full sensitivity-driven gap/overlap free design of carbon fiber-reinforced composites for 3D printing. Appl. Math. Model. 2022, 103, 308–326. [Google Scholar] [CrossRef]
- Zhang, P.; Liu, J.; To, A.C. Role of anisotropic properties on topology optimization of additive manufactured load bearing structures. Scr. Mater. 2017, 135, 148–152. [Google Scholar] [CrossRef]
- Gaynor, A.T.; Guest, J.K. Topology optimization considering overhang constraints: Eliminating sacrificial support material in additive manufacturing through design. Struct. Multidiscip. Optim. 2016, 54, 1157–1172. [Google Scholar] [CrossRef]
- Langelaar, M. An additive manufacturing filter for topology optimization of print-ready designs. Struct. Multidiscip. Optim. 2017, 55, 871–883. [Google Scholar] [CrossRef]
- Biedermann, M.; Beutler, P.; Meboldt, M. Automated design of additive manufactured flow components with consideration of overhang constraint. Addit. Manuf. 2021, 46, 102119. [Google Scholar] [CrossRef]
- Wu, Z.; Xiao, R. A topology optimization approach to structure design with self-supporting constraints in additive manufacturing. J. Comput. Des. Eng. 2022, 9, 364–379. [Google Scholar] [CrossRef]
- Bai, Y.; Cai, J.; Wang, Z.; Li, S. Incorporating additive manufacturing constraints into magneto-structural topology optimization. J. Comput. Des. Eng. 2022, 9, 1665–1679. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, T.; Liu, J.; Yu, H. Deposition path-dependent lightweight support design and its implication to self-support topology optimization. J. Comput. Des. Eng. 2022, 9, 2314–2331. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Wei, P.; Chen, S. Generating support structures for additive manufacturing with continuum topology optimization methods. Rapid Prototyp. J. 2018, 25, 232–246. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Huang, J.; Zou, B.; Ma, Y. Multi-scale topology optimization with shell and interface layers for additive manufacturing. Addit. Manuf. 2021, 37, 101698. [Google Scholar] [CrossRef]
- Xiao, M.; Liu, X.; Zhang, Y.; Gao, L.; Gao, J.; Chu, S. Design of graded lattice sandwich structures by multiscale topology optimization. Comput. Methods Appl. Mech. Eng. 2021, 384, 113949. [Google Scholar] [CrossRef]
- Zhou, Y.; Gao, L.; Li, H. Topology optimization design of graded infills for 3D curved volume by a conformal sweeping method. Comput. Methods Appl. Mech. Eng. 2023, 412, 116009. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, S.; Liu, J.; Ma, Y. Comprehensive clustering-based topology optimization for connectable multi-scale additive manufacturing structures. Addit. Manuf. 2022, 54, 102786. [Google Scholar] [CrossRef]
- Wu, S.; Luo, Z.; Li, Z.; Liu, S.; Zhang, L.-C. Topological design of pentamode metamaterials with additive manufacturing. Comput. Methods Appl. Mech. Eng. 2021, 377, 113708. [Google Scholar] [CrossRef]
- Langelaar, M. Topology optimization for multi-axis machining. Comput. Methods Appl. Mech. Eng. 2019, 351, 226–252. [Google Scholar] [CrossRef]
- Mirzendehdel, A.M.; Behandish, M.; Nelaturi, S. Topology Optimization for Manufacturing with Accessible Support Structures. Comput. Aided Des. 2022, 142, 103117. [Google Scholar] [CrossRef]
- Lee, H.Y.; Zhu, M.; Guest, J.K. Topology optimization considering multi-axis machining constraints using projection methods. Comput. Methods Appl. Mech. Eng. 2022, 390, 114464. [Google Scholar] [CrossRef]
- Mirzendehdel, A.M.; Rankouhi, B.; Suresh, K. Strength-based topology optimization for anisotropic parts. Addit. Manuf. 2018, 19, 104–113. [Google Scholar] [CrossRef]
- Yu, H.; Huang, J.; Zou, B.; Shao, W.; Liu, J. Stress-constrained shell-lattice infill structural optimization for additive manufacturing. Virtual Phys. Prototyp. 2020, 15, 35–48. [Google Scholar] [CrossRef]
- Bruggi, M. On an alternative approach to stress constraints relaxation in topology optimization. Struct. Multidiscip. Optim. 2008, 36, 125–141. [Google Scholar] [CrossRef]
- Bruggi, M.; Duysinx, P. Topology optimization for minimum weight with compliance and stress constraints. Struct. Multidiscip. Optim. 2012, 46, 369–384. [Google Scholar] [CrossRef]
- Le, C.; Norato, J.; Bruns, T.; Ha, C.; Tortorelli, D. Stress-based topology optimization for continua. Struct. Multidiscip. Optim. 2010, 41, 605–620. [Google Scholar] [CrossRef]
- Holmberg, E.; Torstenfelt, B.; Klarbring, A. Stress constrained topology optimization. Struct. Multidiscip. Optim. 2013, 48, 33–47. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Zou, B.; Li, Q.; Ma, Y. Stress constrained multi-material topology optimization with the ordered SIMP method. Comput. Methods Appl. Mech. Eng. 2021, 373, 113453. [Google Scholar] [CrossRef]
- Liu, J.; Yan, J.; Yu, H. Stress-constrained topology optimization for material extrusion polymer additive manufacturing. J. Comput. Des. Eng. 2021, 8, 979–993. [Google Scholar] [CrossRef]
- Yang, D.; Liu, H.; Zhang, W.; Li, S. Stress-constrained topology optimization based on maximum stress measures. Comput. Struct. 2018, 198, 23–39. [Google Scholar] [CrossRef]
- Emmendoerfer, H.; Fancello, E.A.; Silva, E.C.N. Stress-constrained level set topology optimization for compliant mechanisms. Comput. Methods Appl. Mech. Eng. 2020, 362, 112777. [Google Scholar] [CrossRef]
- Picelli, R.; Townsend, S.; Brampton, C.; Norato, J.; Kim, H.A. Stress-based shape and topology optimization with the level set method. Comput. Methods Appl. Mech. Eng. 2018, 329, 1–23. [Google Scholar] [CrossRef]
- Liu, P.; Shi, L.; Kang, Z. Multi-material structural topology optimization considering material interfacial stress constraints. Comput. Methods Appl. Mech. Eng. 2020, 363, 112887. [Google Scholar] [CrossRef]
- Xia, L.; Zhang, L.; Xia, Q.; Shi, T. Stress-based topology optimization using bi-directional evolutionary structural optimization method. Comput. Methods Appl. Mech. Eng. 2018, 333, 356–370. [Google Scholar] [CrossRef]
- Lee, E.; James, K.A.; Martins, J.R.R.A. Stress-constrained topology optimization with design-dependent loading. Struct. Multidiscip. Optim. 2012, 46, 647–661. [Google Scholar] [CrossRef]
- Emmendoerfer, H.; Silva, E.C.N.; Fancello, E.A. Stress-constrained level set topology optimization for design-dependent pressure load problems. Comput. Methods Appl. Mech. Eng. 2019, 344, 569–601. [Google Scholar] [CrossRef]
- Garcez, G.L.; Picelli, R.; Pavanello, R. Bi-directional evolutionary topology optimization based on stress minimization under design-dependent surface loads. Eng. Optim. 2023, 55, 1168–1188. [Google Scholar] [CrossRef]
- Stolpe, M.; Svanberg, K. An alternative interpolation scheme for minimum compliance topology optimization. Struct. Multidiscip. Optim. 2001, 22, 116–124. [Google Scholar] [CrossRef]
- Wang, S.; Daelemans, L.; Fiorio, R.; Gou, M.; D’hooge, D.R.; De Clerck, K.; Cardon, L. Improving Mechanical Properties for Extrusion-Based Additive Manufacturing of Poly(Lactic Acid) by Annealing and Blending with Poly(3-Hydroxybutyrate). Polymers 2019, 11, 1529. [Google Scholar] [CrossRef]
- Liravi, F.; Das, S.; Zhou, C. Separation force analysis and prediction based on cohesive element model for constrained-surface Stereolithography processes. Comput. Aided Des. 2015, 69, 134–142. [Google Scholar] [CrossRef]
- Ye, H.; Venketeswaran, A.; Das, S.; Zhou, C. Investigation of separation force for constrained-surface stereolithography process from mechanics perspective. Rapid Prototyp. J. 2017, 23, 696–710. [Google Scholar] [CrossRef]
- Svanberg, K. The method of moving asymptotes—A new method for structural optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Liu, J.; Li, L. Topology Optimization for Digital Light Projector Additive Manufacturing Addressing the In-Situ Structural Strength Issue. Polymers 2023, 15, 3573. https://doi.org/10.3390/polym15173573
Wang J, Liu J, Li L. Topology Optimization for Digital Light Projector Additive Manufacturing Addressing the In-Situ Structural Strength Issue. Polymers. 2023; 15(17):3573. https://doi.org/10.3390/polym15173573
Chicago/Turabian StyleWang, Jun, Jikai Liu, and Lei Li. 2023. "Topology Optimization for Digital Light Projector Additive Manufacturing Addressing the In-Situ Structural Strength Issue" Polymers 15, no. 17: 3573. https://doi.org/10.3390/polym15173573
APA StyleWang, J., Liu, J., & Li, L. (2023). Topology Optimization for Digital Light Projector Additive Manufacturing Addressing the In-Situ Structural Strength Issue. Polymers, 15(17), 3573. https://doi.org/10.3390/polym15173573






