Multi-Layer Fabric Composites Combined with Non-Newtonian Shear Thickening in Ballistic Protection—Hybrid Numerical Methods and Ballistic Tests
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Ballistic Tests
2.3. Numerical Analysis
3. Results
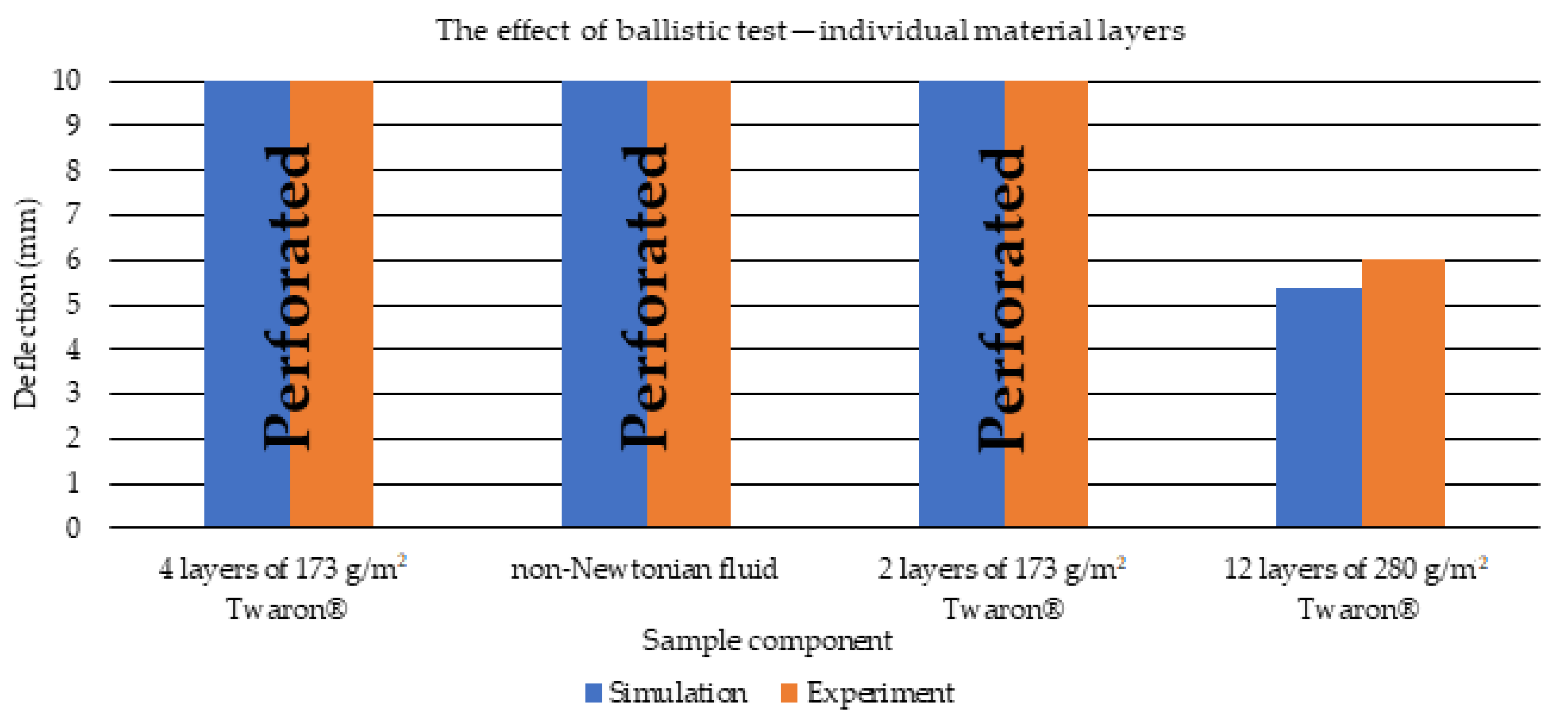
3.1. Ballistic Tests
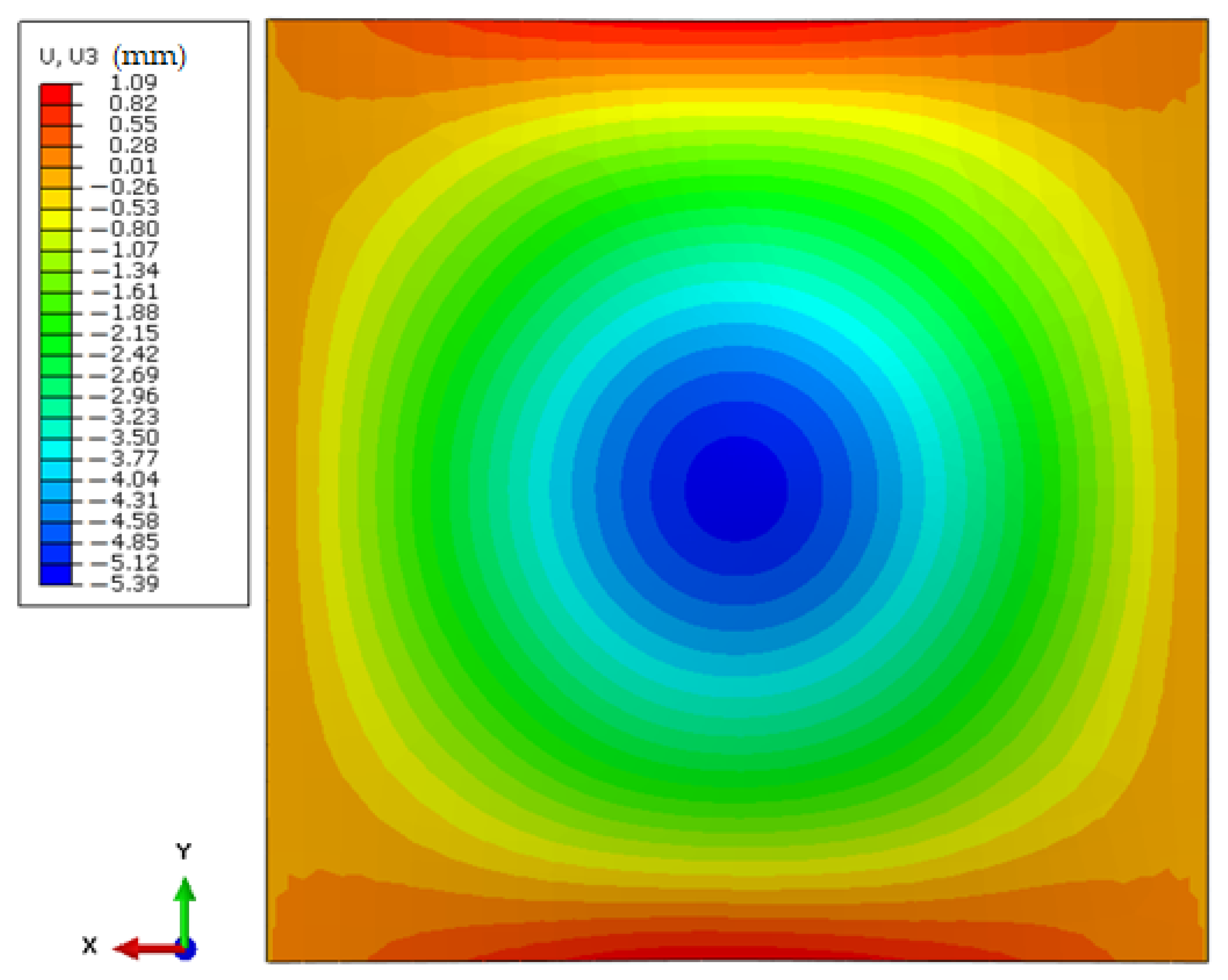
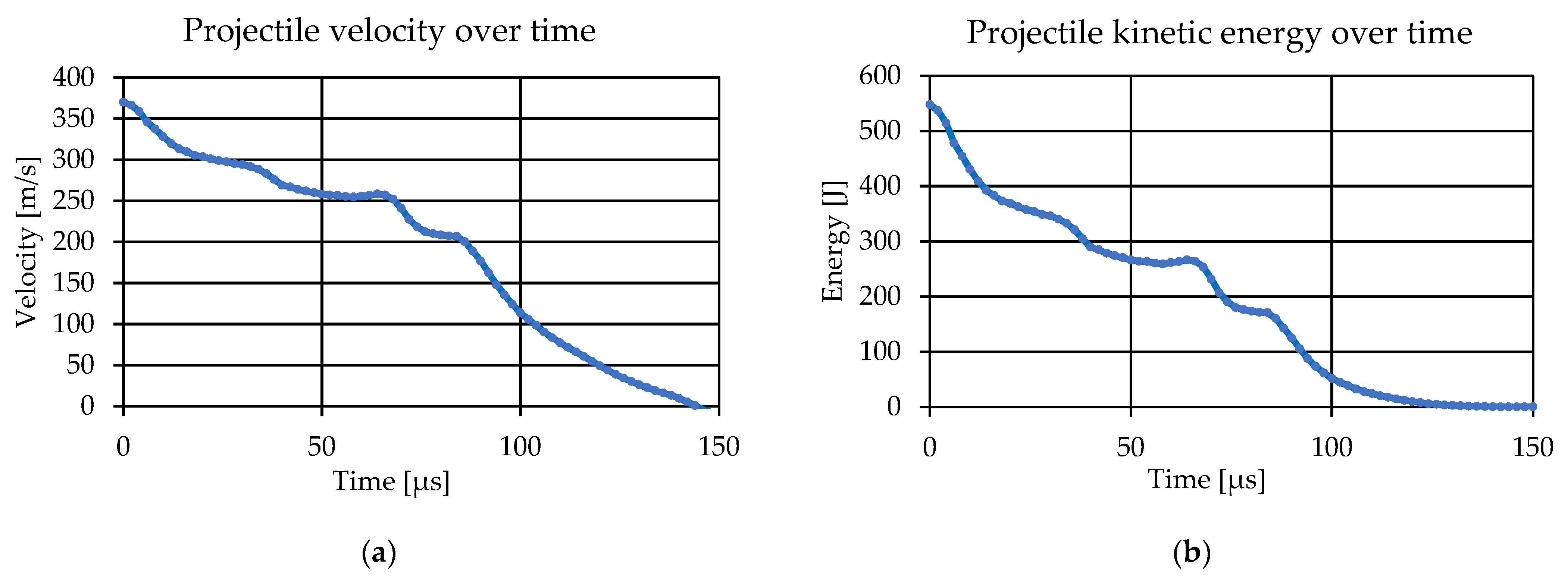
3.2. Numerical Simulations
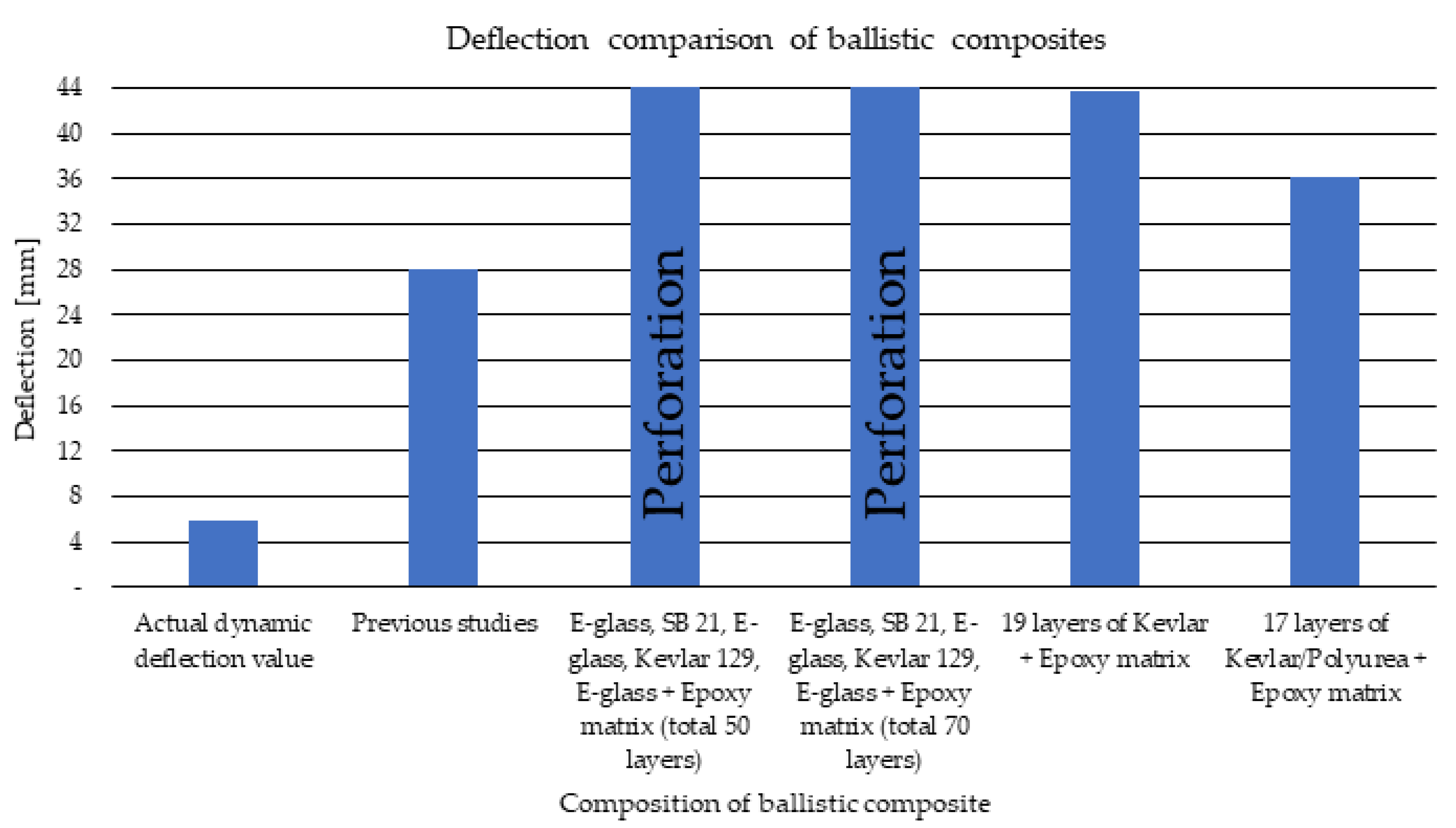
3.3. Comparison of the Obtained Deflection Values to Other Matrices Used in the Literature
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jamroziak, K. Identification of Material Properties in Terminal Ballistics; Publishing House of the Wrocław University of Technology: Wrocław, Poland, 2013; pp. 18–29. [Google Scholar]
- Sen, S.; Bin Jamal M, N.; Shaw, A.; Deb, A. Numerical Investigation of Ballistic Performance of Shear Thickening Fluid (STF)-Kevlar Composite. Int. J. Mech. Sci. 2019, 164, 105174. [Google Scholar] [CrossRef]
- Iannucci, L.; Dechaene, R.; Willows, M.; Degrieck, J. A Failure Model for the Analysis of Thin Woven Glass Composite Structures under Impact Loadings. Comput. Struct. 2001, 79, 785–799. [Google Scholar] [CrossRef]
- Zee, R.H.; Hsieh, C.Y. Energy Loss Partitioning during Ballistic Impact of Polymer Composites. Polym. Compos. 1993, 14, 265–271. [Google Scholar] [CrossRef]
- Li, S.; Sitnikova, E. Representative Volume Elements and Unit Cells; Woodhead Publishing: Duxford, UK, 2020. [Google Scholar]
- Pach, J.; Pyka, D.; Jamroziak, K.; Mayer, P. The Experimental and Numerical Analysis of the Ballistic Resistance of Polymer Composites. Compos. Part B Eng. 2017, 113, 24–30. [Google Scholar] [CrossRef]
- Tabiei, A.; Ivanov, I. Materially and Geometrically Non-Linear Woven Composite Micro-Mechanical Model with Failure for Finite Element Simulations. Int. J. Non Linear. Mech. 2004, 39, 175–188. [Google Scholar] [CrossRef]
- Soni, G.; Singh, R.; Mitra, M.; Falzon, B.G. Modelling Matrix Damage and Fibre–Matrix Interfacial Decohesion in Composite Laminates via a Multi-Fibre Multi-Layer Representative Volume Element (M2RVE). Int. J. Solids Struct. 2014, 51, 449–461. [Google Scholar] [CrossRef]
- Nunes, S.G.; Scazzosi, R.; Manes, A.; Amico, S.C.; de Amorim Júnior, W.F.; Giglio, M. Influence of Projectile and Thickness on the Ballistic Behavior of Aramid Composites: Experimental and Numerical Study. Int. J. Impact Eng. 2019, 132, 103307. [Google Scholar] [CrossRef]
- Scazzosi, R.; Manes, A.; Giglio, M. An Enhanced Material Model for the Simulation of High-Velocity Impact on Fiber-Reinforced Composites. Procedia Struct. Integr. 2019, 24, 53–65. [Google Scholar] [CrossRef]
- Bresciani, L.M.; Manes, A.; Ruggiero, A.; Iannitti, G.; Giglio, M. Experimental Tests and Numerical Modelling of Ballistic Impacts against Kevlar 29 Plain-Woven Fabrics with an Epoxy Matrix: Macro-Homogeneous and Meso-Heterogeneous Approaches. Compos. Part B Eng. 2016, 88, 114–130. [Google Scholar] [CrossRef]
- Briscoe, B.J.; Motamedi, F. The Ballistic Impact Characteristics of Aramid Fabrics: The Influence of Interface Friction. Wear 1992, 158, 229–247. [Google Scholar] [CrossRef]
- Kirkwood, J.E.; Kirkwood, K.M.; Lee, Y.S.; Ronald, G.; Egres, J.R.; Wagner, N.J.; Wetzel, E.D. Yarn Pull-Out as a Mechanism for Dissipating Ballistic Impact Energy in Kevlar® KM-2 Fabric: Part II: Predicting Ballistic Performance. Text. Res. J. 2004, 74, 939–948. [Google Scholar] [CrossRef]
- Duan, Y.; Keefe, M.; Bogetti, T.A.; Powers, B. Finite Element Modeling of Transverse Impact on a Ballistic Fabric. Int. J. Mech. Sci. 2006, 48, 33–43. [Google Scholar] [CrossRef]
- Chocron, S.; Figueroa, E.; King, N.; Kirchdoerfer, T.; Nicholls, A.E.; Sagebiel, E.; Weiss, C.; Freitas, C.J. Modeling and Validation of Full Fabric Targets under Ballistic Impact. Compos. Sci. Technol. 2010, 70, 2012–2022. [Google Scholar] [CrossRef]
- Roylance, D.; Wang, S.S. Penetration Mechanics of Textile Structures. Methods Phenom. 1980, 5, 273–292. [Google Scholar] [CrossRef]
- Das, S.; Jagan, S.; Shaw, A.; Pal, A. Determination of Inter-Yarn Friction and Its Effect on Ballistic Response of Para-Aramid Woven Fabric under Low Velocity Impact. Compos. Struct. 2015, 120, 129–140. [Google Scholar] [CrossRef]
- Tan, V.B.C.Ã.; Shim, V.P.W.; Zeng, X. Modelling Crimp in Woven Fabrics Subjected to Ballistic Impact. Int. J. Impact Eng. 2005, 32, 561–574. [Google Scholar] [CrossRef]
- Nilakantan, G.; Gillespie, J.W.G., Jr. Ballistic Impact Modeling of Woven Fabrics Considering Yarn Strength, Friction, Projectile Impact Location, and Fabric Boundary Condition Effects. Compos. Struct. 2012, 94, 3624–3634. [Google Scholar] [CrossRef]
- Yang, E.C.; Linforth, S.; Ngo, T.; Tran, P. International Journal of Mechanical Sciences Hybrid-Mesh Modelling & Validation of Woven Fabric Subjected to Medium Velocity Impact. Int. J. Mech. Sci. 2018, 144, 427–437. [Google Scholar] [CrossRef]
- Nilakantan, G.; Nutt, S. Effects of Fabric Target Shape and Size on the V 50 Ballistic Impact Response of Soft Body Armor. Compos. Struct. 2014, 116, 661–669. [Google Scholar] [CrossRef]
- Nilakantan, G.; Keefe, M.; Bogetti, T.A.; Adkinson, R.; Gillespie, J.W. On the Finite Element Analysis of Woven Fabric Impact Using Multiscale Modeling Techniques. Int. J. Solids Struct. 2010, 47, 2300–2315. [Google Scholar] [CrossRef]
- Grujicic, M.; Bell, W.C.; Arakere, G.; He, T.; Xie, X.; Cheeseman, B.A. Development of a Meso-Scale Material Model for Ballistic Fabric and Its Use in Flexible-Armor Protection Systems. J. Mater. Eng. Perform. 2010, 19, 22–39. [Google Scholar] [CrossRef]
- Barauskas, R.; Abraitiene, A. Computational Analysis of Impact of a Bullet against the Multilayer Fabrics in LS-DYNA. Int. J. Impact Eng. 2007, 34, 1286–1305. [Google Scholar] [CrossRef]
- Otero, F.; Oller, S.; Martinez, X.; Salomón, O. Numerical Homogenization for Composite Materials Analysis. Comparison with Other Micro Mechanical Formulations. Compos. Struct. 2015, 122, 405–416. [Google Scholar] [CrossRef]
- Andreassen, E.; Andreasen, C.S. How to Determine Composite Material Properties Using Numerical Homogenization. Comput. Mater. Sci. 2014, 83, 488–495. [Google Scholar] [CrossRef]
- Carvelli, V.; Poggi, C. A Homogenization Procedure for the Numerical Analysis of Woven Fabric Composites. Compos. Part A Appl. Sci. Manuf. 2001, 32, 1425–1432. [Google Scholar] [CrossRef]
- Szymczak, T.; Kowalewski, Z.L. Mechanical properties of selected composites and methods of assessing their failure. Transp. Samoch. 2014, 4, 33–54. [Google Scholar]
- Na, W.; Ahn, H.; Han, S.; Harrison, P.; Park, J.K.; Jeong, E.; Yu, W.R. Shear Behavior of a Shear Thickening Fluid-Impregnated Aramid Fabrics at High Shear Rate. Compos. Part B Eng. 2016, 97, 162–175. [Google Scholar] [CrossRef]
- He, Q.; Cao, S.; Wang, Y.; Xuan, S.; Wang, P.; Gong, X. Impact Resistance of Shear Thickening Fluid/Kevlar Composite Treated with Shear-Stiffening Gel. Compos. Part A Appl. Sci. Manuf. 2018, 106, 82–90. [Google Scholar] [CrossRef]
- Petel, O.E. Response of Shear Thickening Materials to Uniaxial Shock Compression. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 2011; p. 240. [Google Scholar]
- Park, Y.; Kim, Y.; Baluch, A.H.; Kim, C.G. Empirical Study of the High Velocity Impact Energy Absorption Characteristics of Shear Thickening Fluid (STF) Impregnated Kevlar Fabric. Int. J. Impact Eng. 2014, 72, 67–74. [Google Scholar] [CrossRef]
- Asija, N.; Chouhan, H.; Gebremeskel, S.A.; Bhatnagar, N. Impact Response of Shear Thickening Fluid (STF) Treated High Strength Polymer Composites—Effect of STF Intercalation Method. Procedia Eng. 2017, 173, 655–662. [Google Scholar] [CrossRef]
- Gürgen, S.; Kuşhan, M.C. The Stab Resistance of Fabrics Impregnated with Shear Thickening Fluids Including Various Particle Size of Additives. Compos. Part A Appl. Sci. Manuf. 2017, 94, 50–60. [Google Scholar] [CrossRef]
- Hasanzadeh, M.; Mottaghitalab, V. The Role of Shear-Thickening Fluids (STFs) in Ballistic and Stab-Resistance Improvement of Flexible Armor. J. Mater. Eng. Perform. 2014, 23, 1182–1196. [Google Scholar] [CrossRef]
- Egres, R.G., Jr.; Lee, Y.S.; Kirkwood, J.E.; Kirkwood, K.M.; Wetzel, E.D.; Wagner, N.J. “Liquid Armor”: Protective Fabrics Utilizing Shear Thickening Fluids. In Proceedings of the 4th International Conference of Safety and Protective Fabrics, Pittsburgh, PA, USA, 26–27 September 2004; pp. 1–8. [Google Scholar]
- Wetzel, E.D.; Lee, Y.S.; Egres, R.G.; Kirkwood, K.M.; Kirkwood, J.E.; Wagner, N.J. The Effect of Rheological Parameters on the Ballistic Properties of Shear Thickening Fluid (STF)-Kevlar Composites. AIP Conf. Proc. 2004, 712, 288–293. [Google Scholar] [CrossRef]
- Majumdar, A.; Butola, B.S.; Srivastava, A. An Analysis of Deformation and Energy Absorption Modes of Shear Thickening Fluid Treated Kevlar Fabrics as Soft Body Armour Materials. Mater. Des. 2013, 51, 148–153. [Google Scholar] [CrossRef]
- Cwalina, C.D.; McCutcheon, C.M.; Dombrowski, R.D.; Wagner, N.J. Engineering Enhanced Cut and Puncture Resistance into the Thermal Micrometeoroid Garment (TMG) Using Shear Thickening Fluid (STF)—Armor™ Absorber Layers. Compos. Sci. Technol. 2016, 131, 61–66. [Google Scholar] [CrossRef]
- Manukonda, B.H.; Chatterjee, V.A.; Verma, S.K.; Bhattacharjee, D.; Biswas, I.; Neogi, S. Rheology Based Design of Shear Thickening Fluid for Soft Body Armor Applications. Period. Polytech. Chem. Eng. 2020, 64, 75–84. [Google Scholar] [CrossRef]
- Pyka, D.; Pach, J.; Jamroziak, K. Numerical Modeling of Ballistic Resistance of Thermoplastic Laminate Under 9 × 19 Mm Parabellum Ammunition. Eng. Mech. 2019, 2019, 307–310. [Google Scholar] [CrossRef]
- Jamroziak, K.; Pyka, D.; Pach, J.; Bocian, M.; Kurzawa, A.; Kurowski, J. Dissipative Properties of Non-Newtonian Fluid under Impact Load. Eng. Mech. 2018, 2018, 321–324. [Google Scholar] [CrossRef][Green Version]
- Fürstner, A.; Ackermann, L.; Gabor, B.; Goddard, R.; Lehmann, C.W.; Mynott, R.; Stelzer, F.; Thiel, O.R. Comparative Investigation of Ruthenium-Based Metathesis Catalysts Bearing N-Heterocyclic Carbene (NHC) Ligands. Chem. Eur. J. 2001, 7, 3236–3253. [Google Scholar] [CrossRef]
- Wisniewski, A.; Gmitrzuk, M. Validation of Numerical Model of the Twaron CT709 Ballistic Fabric. In Proceedings of the 27th International Symposium on Ballistics, Freiburg, Germany, 22–26 April 2013; Volume 2, pp. 1535–1544. [Google Scholar]
- ABAQUS; Version 6.6; Analysis User’s Manual Documentation; Washington University in St. Louis: St. Louis, MO, USA, 2009.
- Shrot, A.; Bäker, M. Determination of Johnson–Cook Parameters from Machining Simulations. Comput. Mater. Sci. 2012, 52, 298–304. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture Characteristics of Three Metals Subjected to Various Strains, Strain Rates, Temperatures and Pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Ziółkowski, G.; Pach, J.; Pyka, D.; Kurzynowski, T.; Jamroziak, K. X-ray Computed Tomography for the Development of Ballistic Composite. Materials 2020, 13, 5566. [Google Scholar] [CrossRef]
- Talebi, H.; Wong, S.V.; Hamouda, A.M.S. Finite Element Evaluation of Projectile Nose Angle Effects in Ballistic Perforation of High Strength Fabric. Compos. Struct. 2009, 87, 314–320. [Google Scholar] [CrossRef]
- Pyka, D.; Jamroziak, K.; Ziolkowski, G.; Pach, J.; Bocian, M. Research on Ballistic Resistance of DCPD Laminate under Pistol Ammunition Fire. Eng. Mech. 2018, 2018, 701–704. [Google Scholar] [CrossRef]
- Zhu, L.; Zhu, G.; Feng, J.; Jin, L.; Ma, P. Impact Tensile Behavior Analysis of Twaron Fiber Tows from Fast Fourier Transform. Text. Res. J. 2019, 89, 1363–1370. [Google Scholar] [CrossRef]
- Małachowski, J. Effect of blast wave on chosen structure—Numerical and experimental study. Int. J. Math. Comput. Simulat. 2008, 2, 228–237. [Google Scholar]
- Małachowski, J.; Gieleta, R. Security improvement for oil and gas pipeline infrastructure. J. KONES Powertrain Transp. 2008, 15, 2. [Google Scholar]
- Bocian, M.; Pach, J.; Jamroziak, K.; Kosobudzki, M.; Polak, S.; Pyka, D.; Kurzawa, A.; Kurowski, J. Experimental and Numerical Analysis of Aramid Fiber Laminates with DCPD Resin Matrix Subjected to Impact Tests. MATEC Web Conf. 2017, 112, 04013. [Google Scholar] [CrossRef]
- Moćko, W.; Kowalewski, W. Application of selected constitutive equations to describe the mechanical properties of high-nitrogen steel type VP159. Eng. Model. 2012, 43, 203–210. [Google Scholar]
- Stopel, M. Design of Mechanical Structures Subjected to Loads Increasing at High Speed. Ph.D. Thesis, University of Technology and Life Sciences in Bydgoszcz, Bydgoszcz, Poland, 2018. [Google Scholar]
- Yilmaz, H.; Bedir, F.; Elmas, U. Experimentally Investigating the Ballistic Properties of the Polymer-Matrixed Layered and Fiber reinforced Composite Materials. Int. Conf. Appl. Mech. Mech. Eng. 2014, 16, 1–12. [Google Scholar] [CrossRef]
- Shih, C.H.; You, J.L.; Lee, Y.L.; Cheng, A.Y.; Chang, C.P.; Liu, Y.M.; Der Ger, M. Design and Ballistic Performance of Hybrid Plates Manufactured from Aramid Composites for Developing Multilayered Armor Systems. Polymers 2022, 14, 5026. [Google Scholar] [CrossRef] [PubMed]




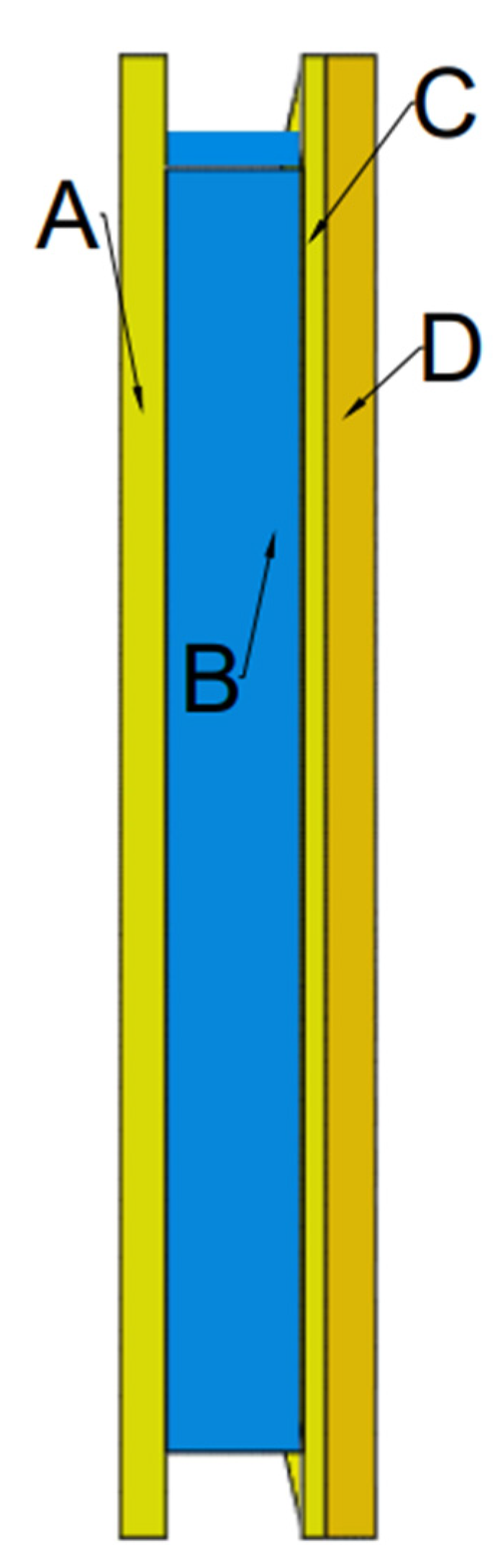





| Material | MW (g/mol) | ρ (g/cm3) | TM (°C) | TB (°C) | λ (W/mK) | η (Pa·s) |
|---|---|---|---|---|---|---|
| Propylene glycol | 76.10 | 1.036 | −59 | 188 | 0.34 | 0.042 |
| Silica | 60.08 | 2.648 (α) 2.196 (amorphous) | 1713 | 2230 | - | - |
| Material | E (GPa) | v (-) | ρ (kg/m3) | A (MPa) | B (MPa) | n (-) | c (s−1) |
|---|---|---|---|---|---|---|---|
| Lead | 13 | 0.42 | 11,300 | 35 | 46 | 0.48 | 0.01 |
| Brass | 130 | 0.38 | 8941 | 112 | 505 | 0.42 | 0.01 |
| Material | E (GPa) | v (-) | ρ (kg/m3) | Re (MPa) | G (GPa) | FS (-) |
|---|---|---|---|---|---|---|
| DCPD (dicyclopentadiene) | 3.1 | 0.20 | 98 | - | 0.70 | 0.02 |
| Twaron® 280 g/m2 | 115.0 | 0.30 | 1440 | 3600 | 3.60 | 0.10 |
| Twaron® 173 g/m2 | 71.0 | 0.36 | 1440 | 3200 | 31.00 for G12 0.16 for G23 = G13 | 0.10 |
| Material | E1 = E2 (MPa) | E3 (Mpa) | ρ (kg/m3) | v (-) | G (Gpa) | Re = Rm (Mpa) | FS (-) |
|---|---|---|---|---|---|---|---|
| Orthotropic layer for Twaron® 280 g/m2 | 90,735 | 10,122 | 1150 | 0.28 | 2.99 | 2840 | 0.10 |
| Orthotropic layer for Twaron® 173 g/m2 | 56,673 | 3883 | 1150 | 0.33 | 24.61 for G12 and G13 0.28 for G23 | 2525 | 0.10 |
| Material | ρ (kg/m3) | C0 (km/s) | s (-) | Γ0 (-) |
|---|---|---|---|---|
| Silica + Polypropylene glycol | 2722 | 2.1 | 3.75 | 0.8 |
| Shield Component | Type | Size (mm) |
|---|---|---|
| Layers of 173 g/m2 Twaron® | Hex | 0.5 |
| Non-Newtonian fluid in honeycomb cells | Hex | 0.5 |
| Layers of 280 g/m2 Twaron® | Hex | 0.5 |
| Layer | 4 Layers of 173 g/m2 Twaron® | Non-Newtonian Fluid | 2 Layers of 173 g/m2 Twaron® | 12 Layers of 280 g/m2 Twaron® |
|---|---|---|---|---|
| Mises stress value (MPa) | 1300 | 0 | 1300 | 2700 |
| Projectile | D (mm) | L (mm) |
|---|---|---|
| Ballistic test | 14.25 | 8.33 |
| Numerical | 14.49 | 8.53 |
| Relative error | 1.70% | 2.40% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roszak, M.; Pyka, D.; Bocian, M.; Barsan, N.; Dragašius, E.; Jamroziak, K. Multi-Layer Fabric Composites Combined with Non-Newtonian Shear Thickening in Ballistic Protection—Hybrid Numerical Methods and Ballistic Tests. Polymers 2023, 15, 3584. https://doi.org/10.3390/polym15173584
Roszak M, Pyka D, Bocian M, Barsan N, Dragašius E, Jamroziak K. Multi-Layer Fabric Composites Combined with Non-Newtonian Shear Thickening in Ballistic Protection—Hybrid Numerical Methods and Ballistic Tests. Polymers. 2023; 15(17):3584. https://doi.org/10.3390/polym15173584
Chicago/Turabian StyleRoszak, Maciej, Dariusz Pyka, Mirosław Bocian, Narcis Barsan, Egidijus Dragašius, and Krzysztof Jamroziak. 2023. "Multi-Layer Fabric Composites Combined with Non-Newtonian Shear Thickening in Ballistic Protection—Hybrid Numerical Methods and Ballistic Tests" Polymers 15, no. 17: 3584. https://doi.org/10.3390/polym15173584
APA StyleRoszak, M., Pyka, D., Bocian, M., Barsan, N., Dragašius, E., & Jamroziak, K. (2023). Multi-Layer Fabric Composites Combined with Non-Newtonian Shear Thickening in Ballistic Protection—Hybrid Numerical Methods and Ballistic Tests. Polymers, 15(17), 3584. https://doi.org/10.3390/polym15173584









