Influence of Three-Dimensional Printing Parameters on Compressive Properties and Surface Smoothness of Polylactic Acid Specimens
Abstract
:1. Introduction
| Influence on Mechanical and Surface Properties | |||
|---|---|---|---|
| Compressive Properties | Surface Quality | ||
| Nozzle temperature |
|
| |
| 3D printing parameters | Raster angle |
| |
| Infill pattern |
|
| |
| Infill density |
| ||
| Layer height |
| ||
| Printing speed |
| ||
| Build orientation | |||
| Air gap |
| ||
| Extrusion width |
| ||
2. Materials and Methods
2.1. Sample Preparation
2.2. Design of Experiments
2.3. Density Measurement
2.4. Surface Roughness
2.5. Compression and Hysteresis Compression
2.6. Scanning Electron Microscopy (SEM)
3. Results and Discussion
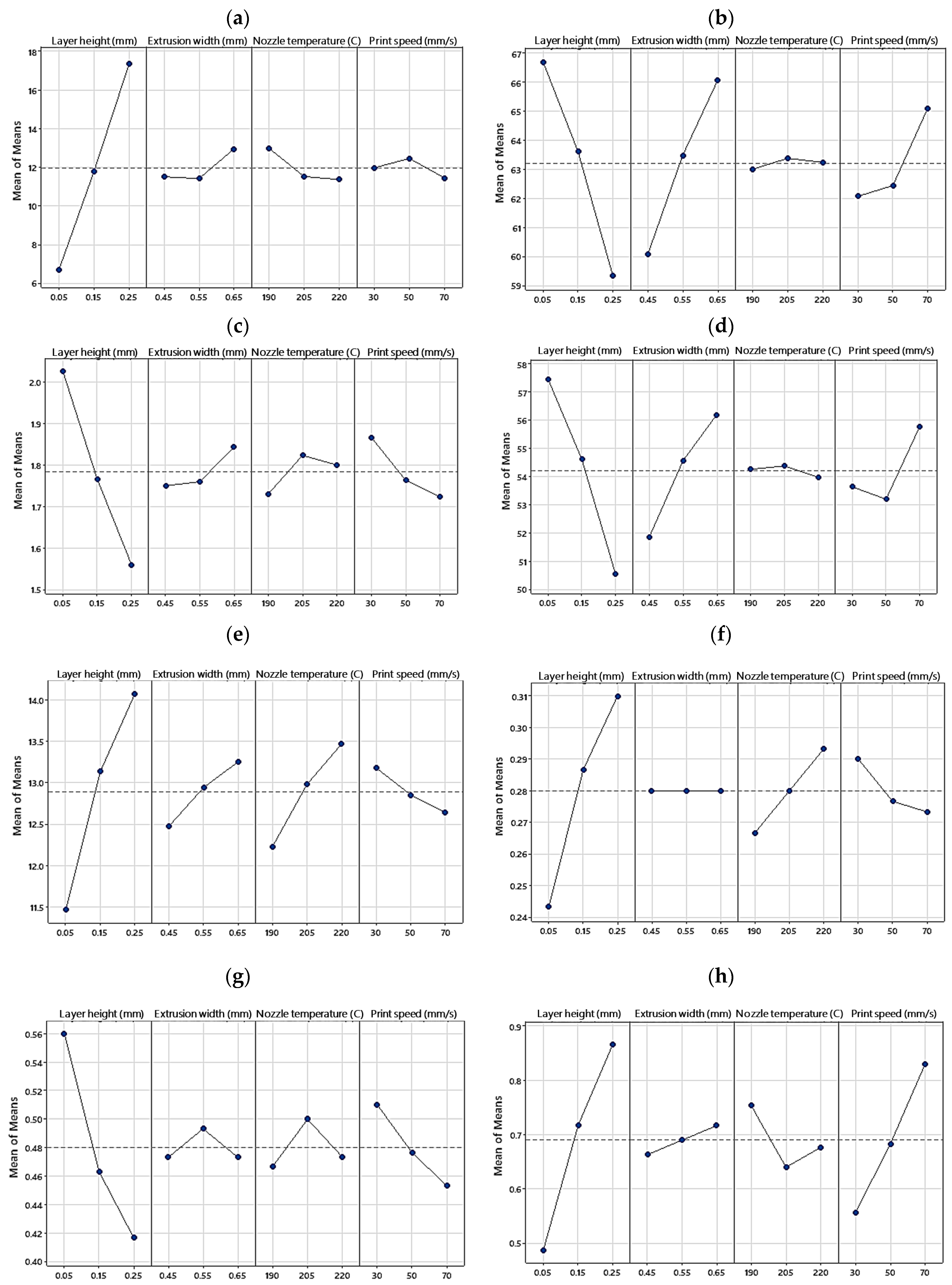
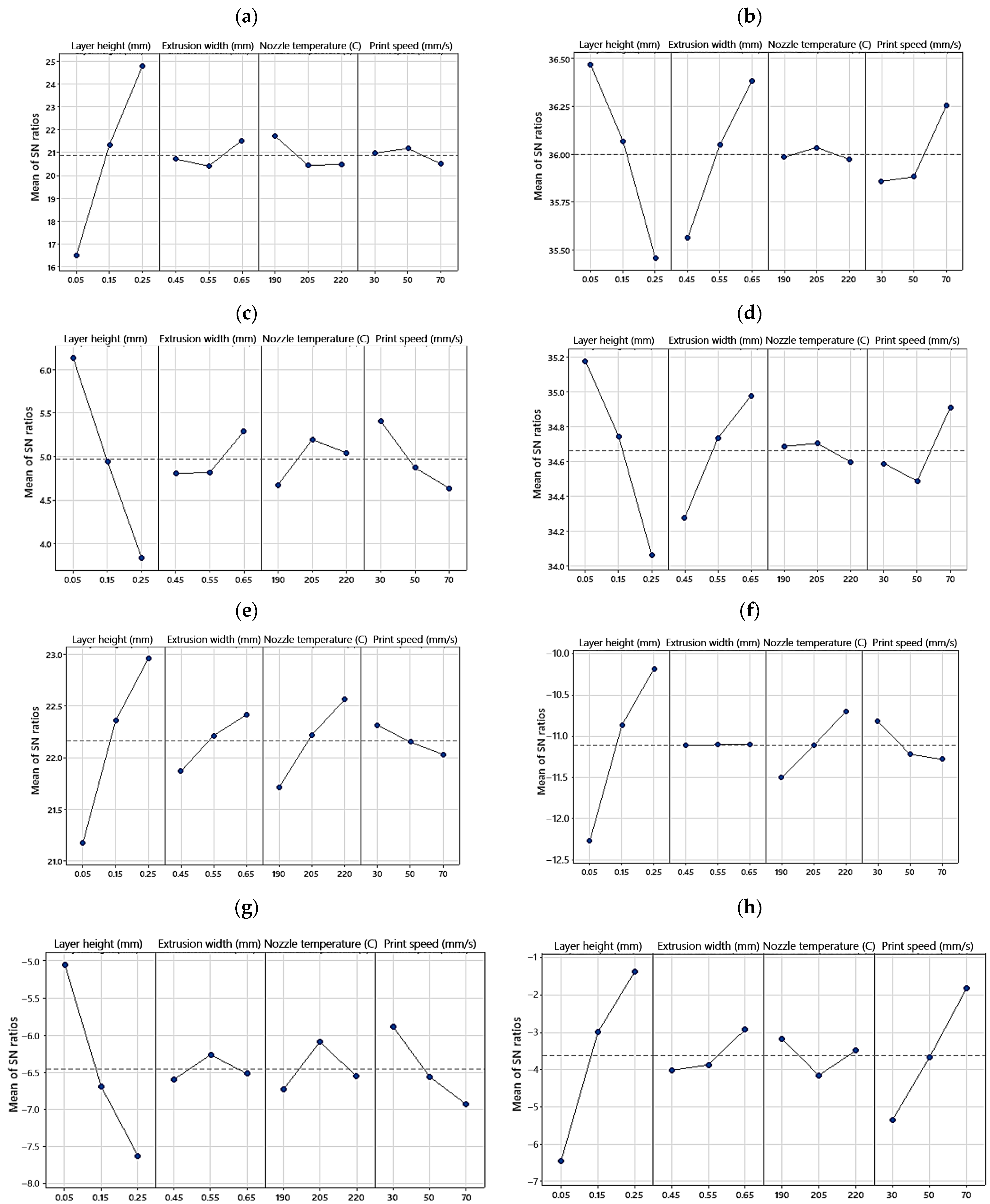
3.1. Analysis of Variance (ANOVA)
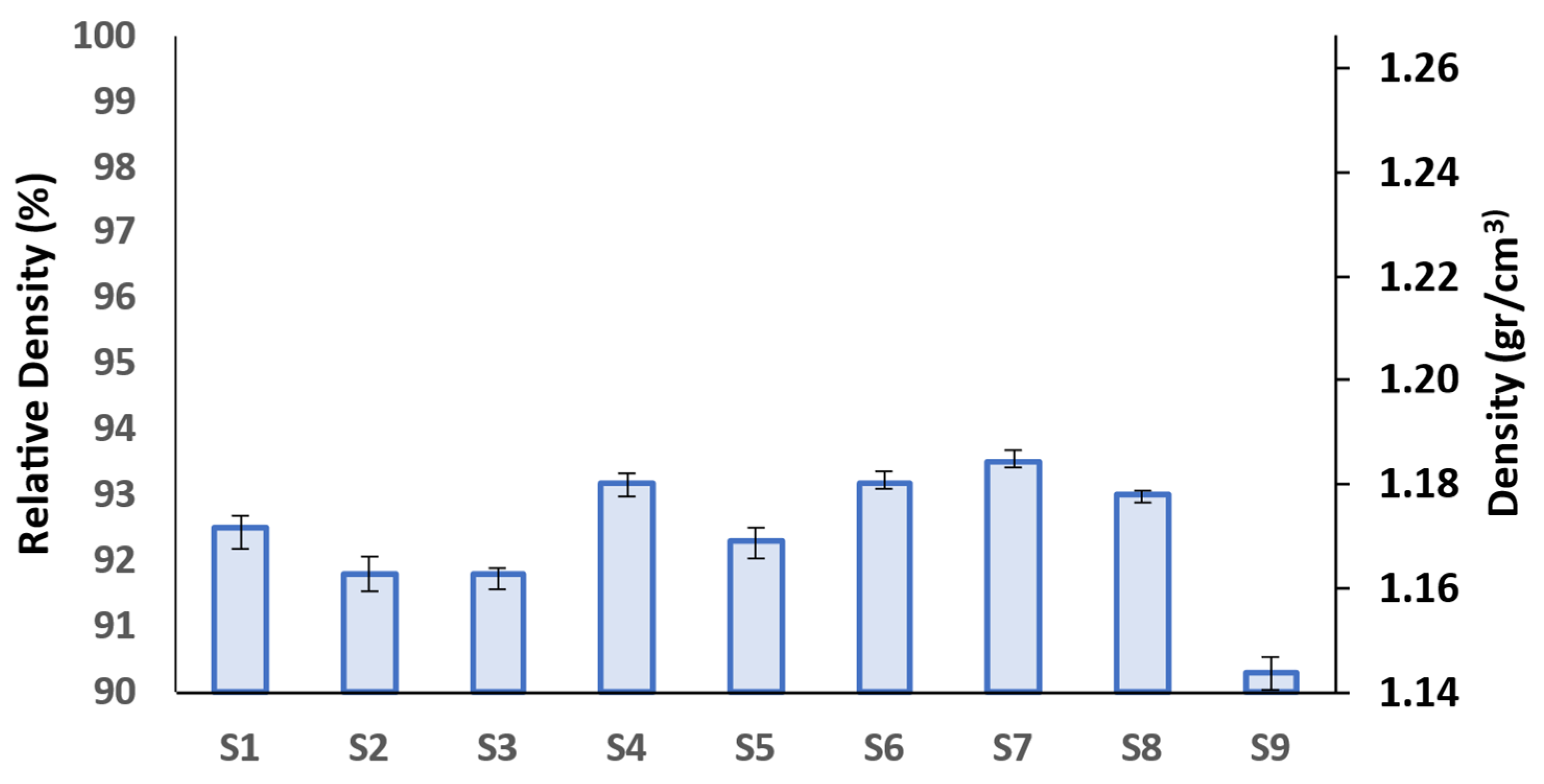
3.2. Relative Density
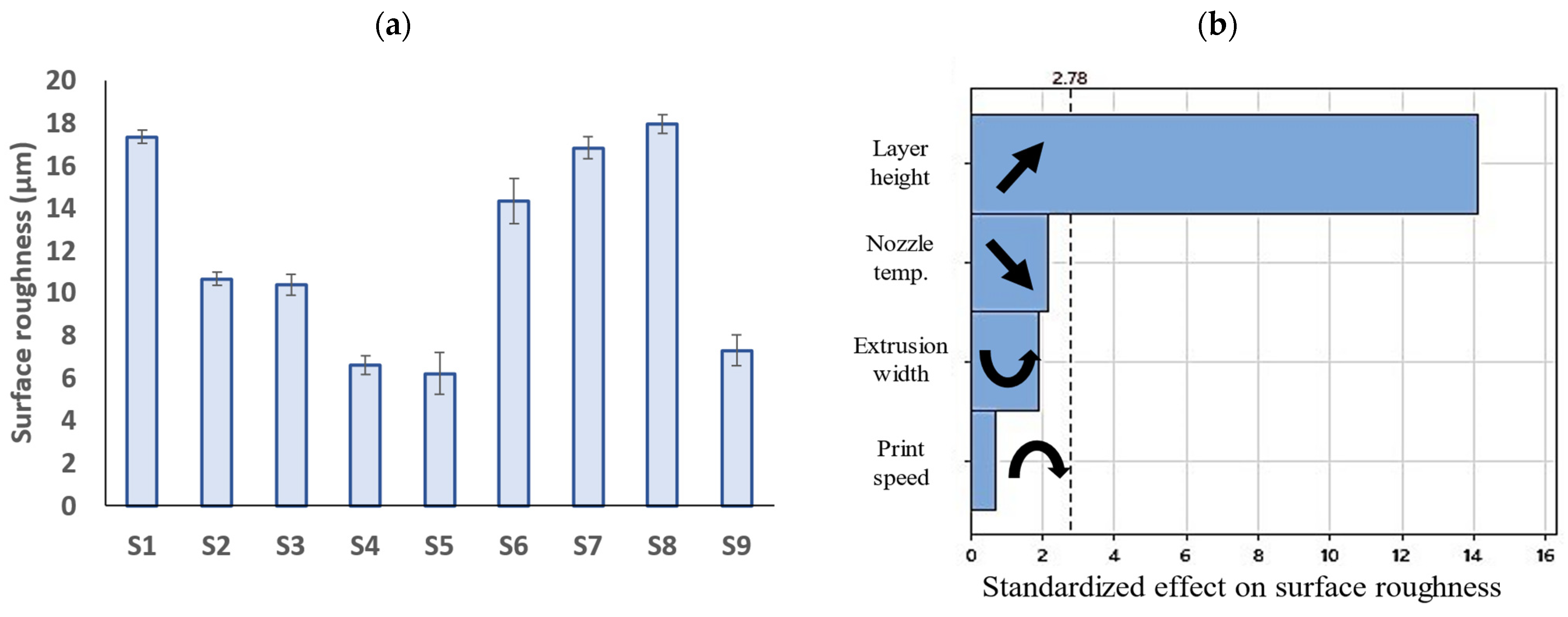
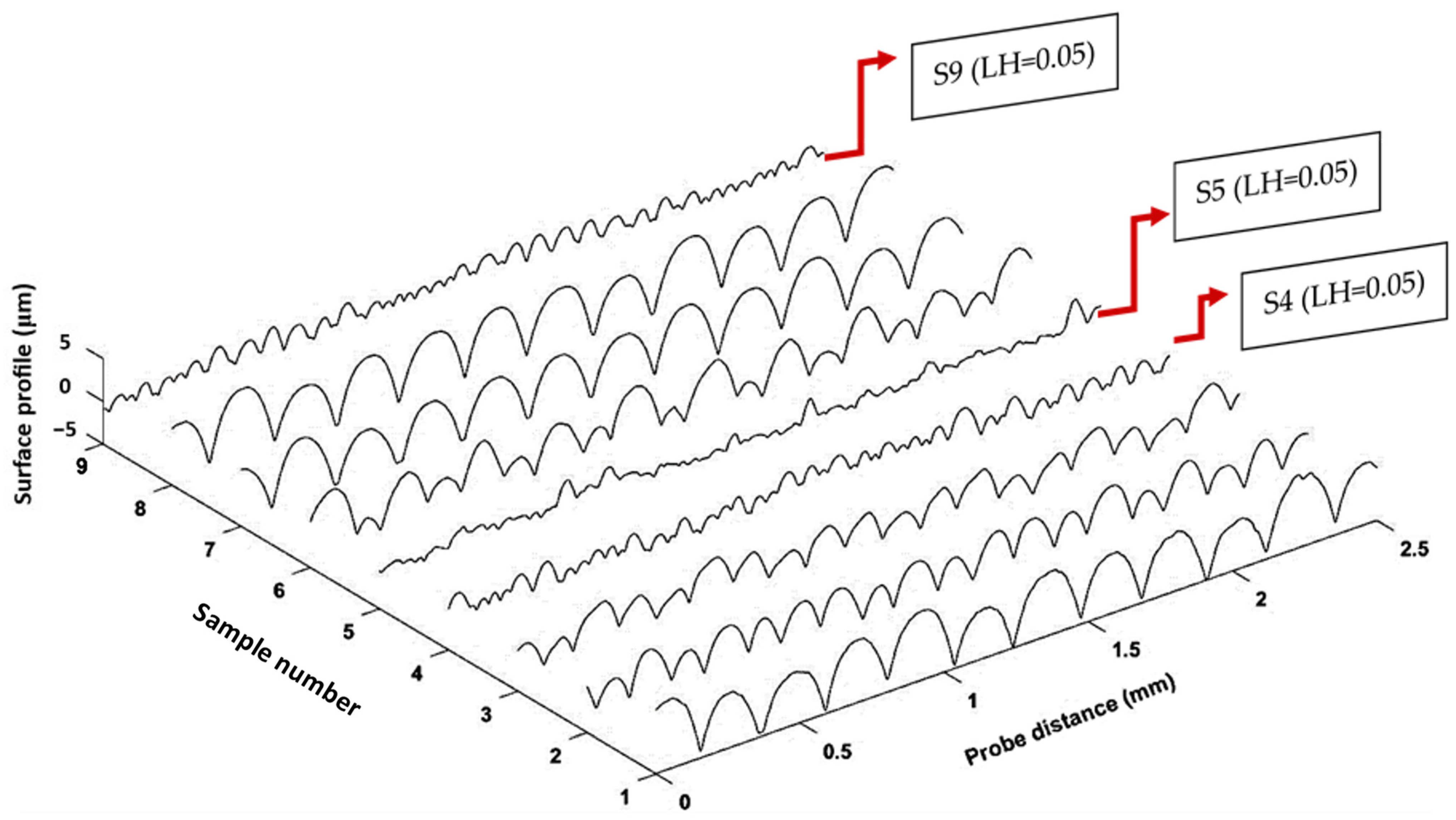
3.3. Surface Roughness
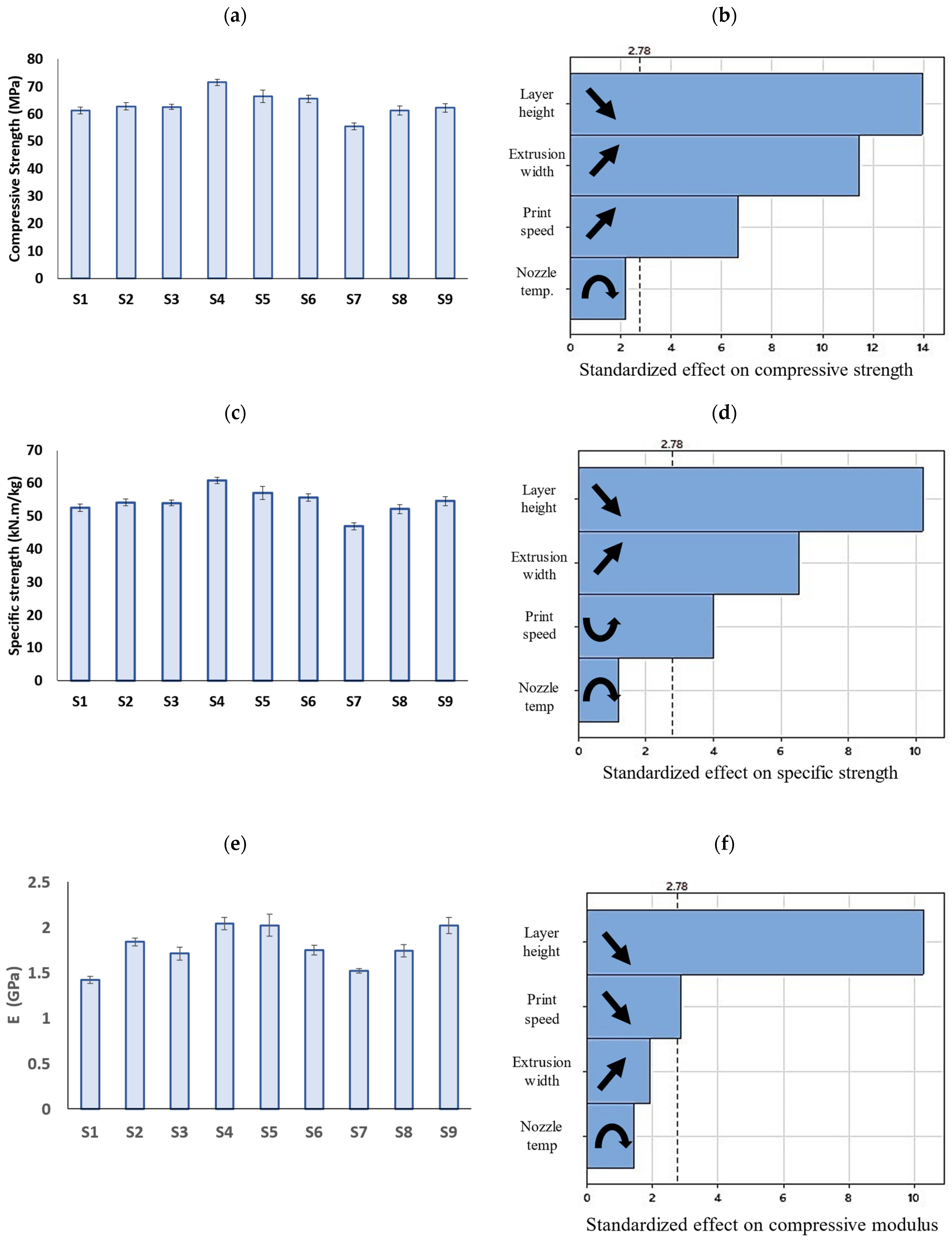
3.4. Compressive Properties
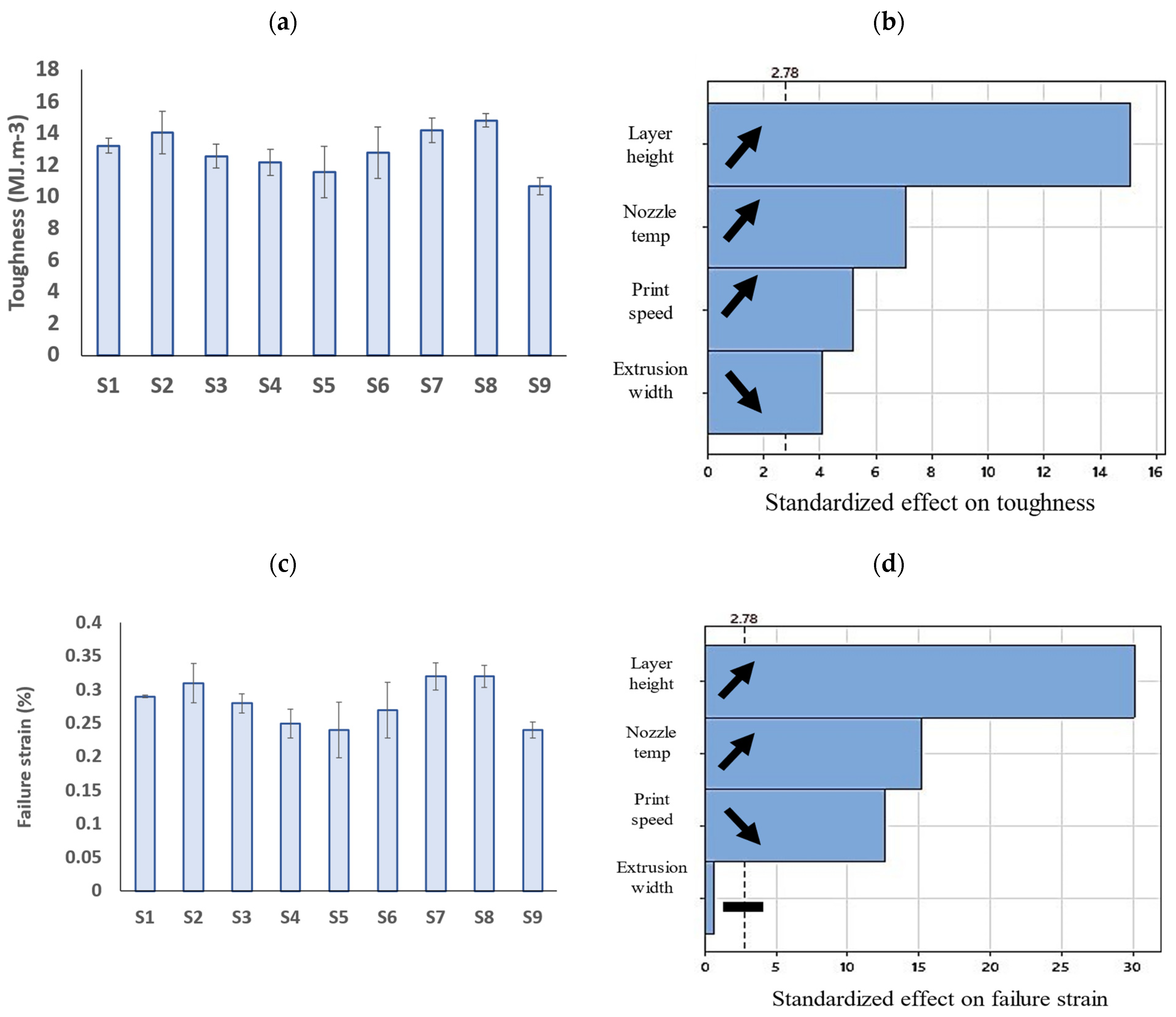
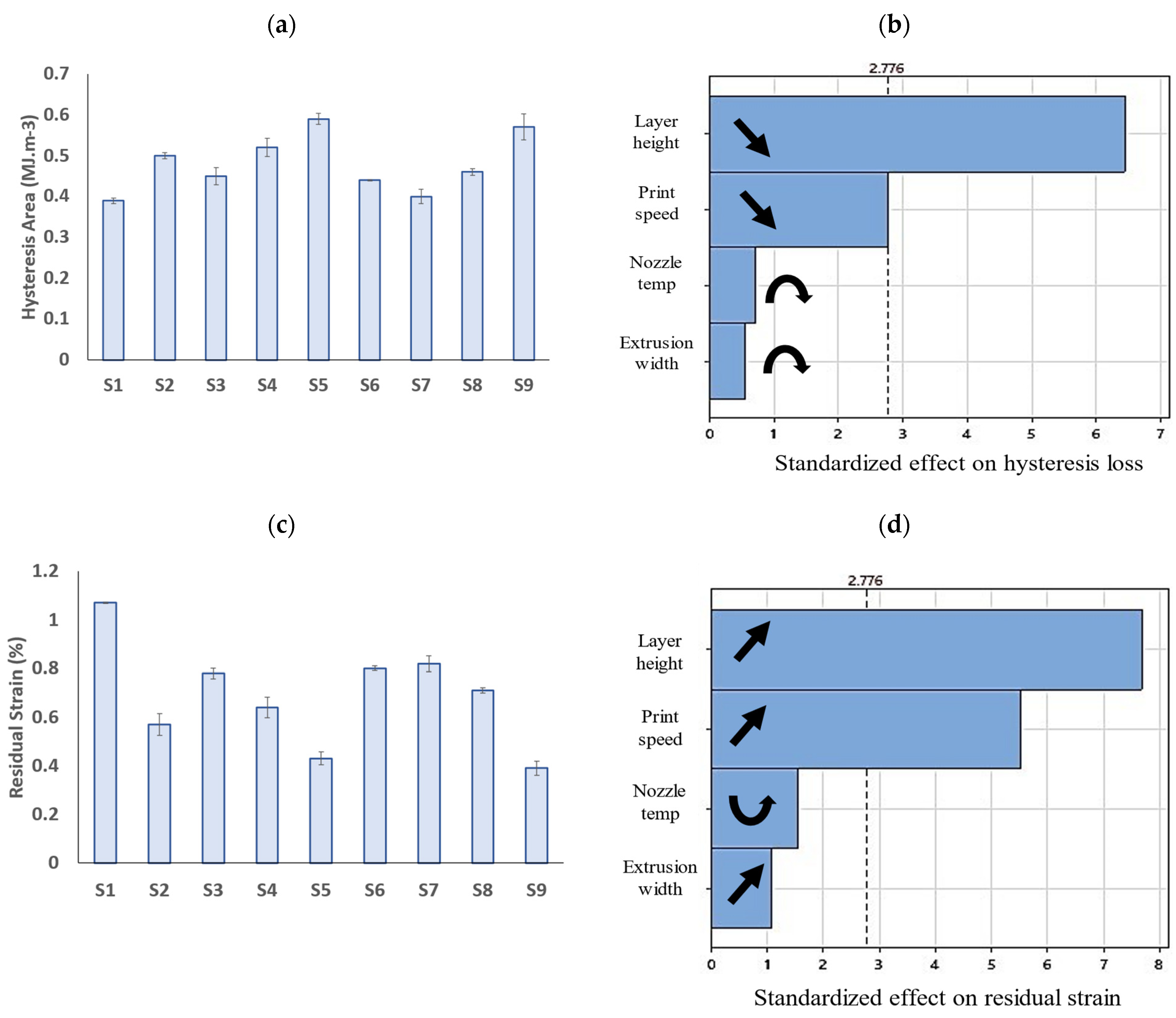
3.5. Hysteresis Properties
3.6. Optimization
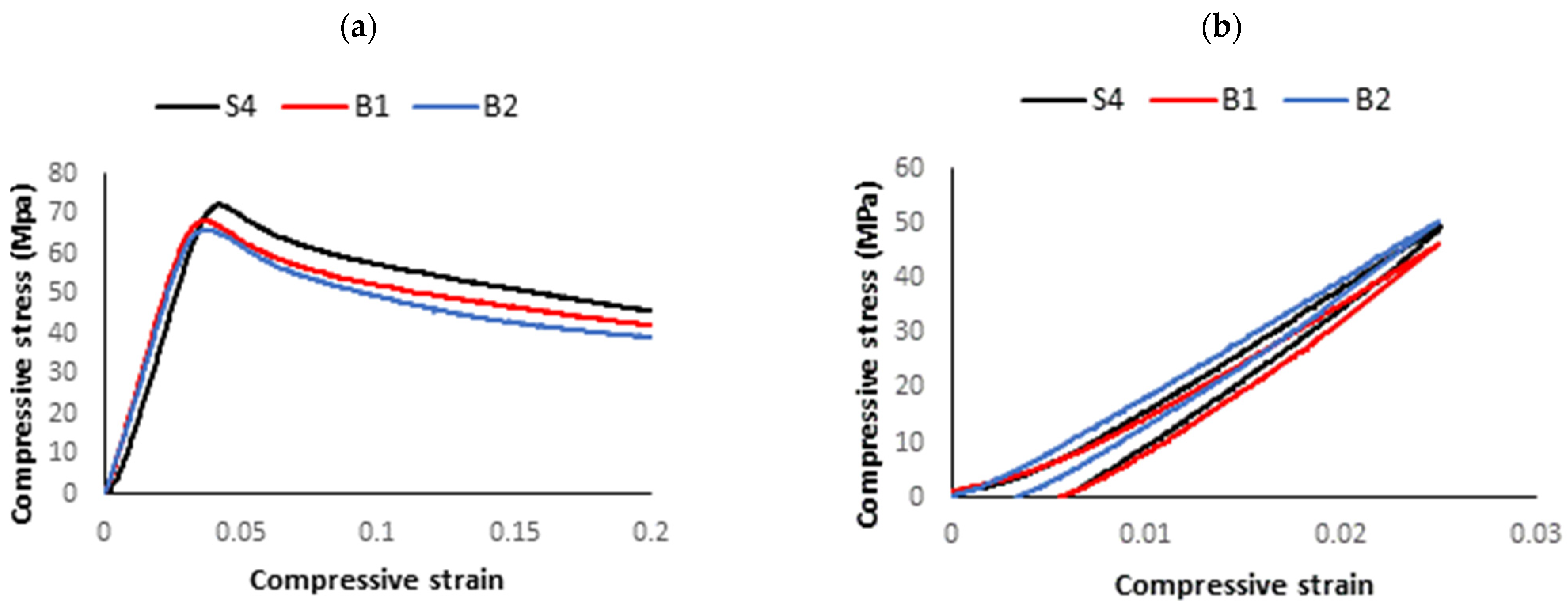
3.7. Failure Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| LH | Layer height | E | Compressive modulus |
| EW | Extrusion width | σ/ρ | Specific strength |
| T | Nozzle temperature | Toughness | |
| V | Print speed | Failure strain | |
| Relative density | Hysteresis area (hysteresis loss) | ||
| Ra | Surface roughness | Residual strain | |
| Compressive strength | DI | Desirability index | |
| PLA | Polylactic Acid | FFF | Fused filament fabrication |
| ANOVA | Analysis of variance | FDM | Fused Deposition Modeling |
| PEEK | Polyether ether ketone | ABS | Acrylonitrile butadiene styrene |
References
- Altıparmak, S.C.; Yardley, V.A.; Shi, Z.; Lin, J. Extrusion-Based Additive Manufacturing Technologies: State of the Art and Future Perspectives. J. Manuf. Process. 2022, 83, 607–636. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, J.; Zhi, P.; Liu, L.; Liu, C.; Fang, A.; Zhang, Q. 3d Printing Method for Bone Tissue Engineering Scaffold. Med. Nov. Technol. Devices 2023, 17, 100205. [Google Scholar] [CrossRef]
- Soleyman, E.; Aberoumand, M.; Soltanmohammadi, K.; Rahmatabadi, D.; Ghasemi, I.; Baniassadi, M.; Abrinia, K.; Baghani, M. 4d Printing of Pet-G Via Fdm Including Tailormade Excess Third Shape. Manuf. Lett. 2022, 33, 1–4. [Google Scholar] [CrossRef]
- Sun, Z.P.; Guo, Y.B.; Shim, V.P. Characterisation and Modeling of Additively-Manufactured Polymeric Hybrid Lattice Structures for Energy Absorption. Int. J. Mech. Sci. 2021, 191, 106101. [Google Scholar] [CrossRef]
- Liang, X.; Gao, J.; Xu, W.; Wang, X.; Shen, Y.; Tang, J.; Cui, S.; Yang, X.; Liu, Q.; Yu, L. Structural Mechanics of 3d-Printed Poly (Lactic Acid) Scaffolds with Tetragonal, Hexagonal and Wheel-Like Designs. Biofabrication 2019, 11, 035009. [Google Scholar] [CrossRef]
- Palmić, T.B.; Slavič, J. Single-Process 3d-Printed Stacked Dielectric Actuator. Int. J. Mech. Sci. 2022, 230, 107555. [Google Scholar] [CrossRef]
- Mwema, F.M.; Akinlabi, E.T.; Mwema, F.M.; Akinlabi, E.T. Basics of Fused Deposition Modelling (Fdm). In Fused Deposition Modeling: Strategies for Quality Enhancement; Springer International Publishing: Cham, Switzerland, 2020; pp. 1–15. [Google Scholar]
- Giorleo, L.; Ceretti, E. Deep Drawing Punches Produced Using Fused Filament Fabrication Technology: Performance Evaluation. J. Manuf. Process. 2022, 84, 1–9. [Google Scholar] [CrossRef]
- Strano, M.; Rane, K.; Farid, M.A.; Mussi, V.; Zaragoza, V.; Monno, M. Extrusion-Based Additive Manufacturing of Forming and Molding Tools. Int. J. Adv. Manuf. Technol. 2021, 117, 2059–2071. [Google Scholar] [CrossRef]
- Schuh, G.; Bergweiler, G.; Fiedler, F.; Bickendorf, P.; Schumacher, P. Small Series Production and Geometric Analysis of Sheet Metal Car Body Parts Using Forming Tools Made of Fused Filament Fabricated Pla. In Proceedings of the 2020 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, Singapore, 14–17 December 2020. [Google Scholar]
- Kampker, A.; Bergweiler, G.; Hollah, A.; Lichtenthäler, K.; Leimbrink, S. Design and Testing of the Different Interfaces in a 3d Printed Welding Jig. Procedia CIRP 2019, 81, 45–50. [Google Scholar] [CrossRef]
- Krznar, N.; Pilipović, A.; Šercer, M. Additive Manufacturing of Fixture for Automated 3d Scanning–Case Study. Procedia Eng. 2016, 149, 197–202. [Google Scholar] [CrossRef]
- Post, B.; Richardson, B.; Lloyd, P.; Love, L.; Nolet, S.; Hannan, J. Additive Manufacturing of Wind Turbine Molds; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 2017. [Google Scholar]
- Sánchez-Belenguer, C.; Vendrell-Vidal, E.; Sánchez-López, M.; Díaz-Marín, C.; Aura-Castro, E. Automatic Production of Tailored Packaging for Fragile Archaeological Artifacts. J. Comput. Cult. Heritage 2015, 8, 1–11. [Google Scholar] [CrossRef]
- Pal, A.K.; Mohanty, A.K.; Misra, M. Additive Manufacturing Technology of Polymeric Materials for Customized Products: Recent Developments and Future Prospective. RSC Adv. 2021, 11, 36398–36438. [Google Scholar] [CrossRef] [PubMed]
- Nadagouda, M.N.; Rastogi, V.; Ginn, M. A Review on 3d Printing Techniques for Medical Applications. Curr. Opin. Chem. Eng. 2020, 28, 152–157. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Optimization of Fused Deposition Modeling Process Parameters: A Review of Current Research and Future Prospects. Adv. Manuf. 2015, 3, 42–53. [Google Scholar] [CrossRef]
- Bian, Y.-H.; Yu, G.; Zhao, X.; Li, S.-X.; He, X.-L.; Tian, C.-X.; Li, Z.-Y. Exit Morphology and Mechanical Property of Fdm Printed Pla: Influence of Hot Melt Extrusion Process. Adv. Manuf. 2023, 11, 56–74. [Google Scholar] [CrossRef]
- Cojocaru, V.; Frunzaverde, D.; Miclosina, C.-O.; Marginean, G. The Influence of the Process Parameters on the Mechanical Properties of Pla Specimens Produced by Fused Filament Fabrication—A Review. Polymers 2022, 14, 886. [Google Scholar] [CrossRef]
- Vanaei, H.R.; Raissi, K.; Deligant, M.; Shirinbayan, M.; Fitoussi, J.; Khelladi, S.; Tcharkhtchi, A. Toward the Understanding of Temperature Effect on Bonding Strength, Dimensions and Geometry of 3d-Printed Parts. J. Mater. Sci. 2020, 55, 14677–14689. [Google Scholar] [CrossRef]
- Kuznetsov, V.E.; Solonin, A.N.; Tavitov, A.; Urzhumtsev, O.; Vakulik, A. Increasing Strength of Fff Three-Dimensional Printed Parts by Influencing on Temperature-Related Parameters of the Process. Rapid Prototyp. J. 2020, 26, 107–121. [Google Scholar] [CrossRef]
- Gurrala, P.K.; Regalla, S.P. Part Strength Evolution with Bonding between Filaments in Fused Deposition Modelling: This Paper Studies How Coalescence of Filaments Contributes to the Strength of Final Fdm Part. Virtual Phys. Prototyp. 2014, 9, 141–149. [Google Scholar] [CrossRef]
- Gray, R.W.; Baird, D.G.; Bøhn, J.H. Effects of Processing Conditions on Short Tlcp Fiber Reinforced Fdm Parts. Rapid Prototyp. J. 1998, 4, 14–25. [Google Scholar] [CrossRef]
- Zhong, W.; Li, F.; Zhang, Z.; Song, L.; Li, Z. Short Fiber Reinforced Composites for Fused Deposition Modeling. Mater. Sci. Eng. A 2001, 301, 125–130. [Google Scholar] [CrossRef]
- Rahmatabadi, D.; Soltanmohammadi, K.; Aberoumand, M.; Soleyman, E.; Ghasemi, I.; Baniassadi, M.; Abrinia, K.; Bodaghi, M.; Baghani, M. Development of Pure Poly Vinyl Chloride (Pvc) with Excellent 3d Printability and Macro-and Micro-Structural Properties. Macromol. Mater. Eng. 2023, 308, 2200568. [Google Scholar] [CrossRef]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Parametric Appraisal of Mechanical Property of Fused Deposition Modelling Processed Parts. Mater. Des. 2010, 31, 287–295. [Google Scholar] [CrossRef]
- Bakhtiari, H.; Aamir, M.; Tolouei-Rad, M. Effect of 3d Printing Parameters on the Fatigue Properties of Parts Manufactured by Fused Filament Fabrication: A Review. Appl. Sci. 2023, 13, 904. [Google Scholar] [CrossRef]
- Gordelier, T.J.; Thies, P.R.; Turner, L.; Johanning, L. Optimising the Fdm Additive Manufacturing Process to Achieve Maximum Tensile Strength: A State-of-the-Art Review. Rapid Prototyp. J. 2019, 25, 953–971. [Google Scholar] [CrossRef]
- Gabor, C.; Pop, M.A.; Magli, D.; Bedo, T.; Munteanu, S.I.; Munteanu, D. The Optimization of the Production Procedure in Relation to the Mechanical Properties of Additively Manufactured Parts. Mater. Today Proc. 2019, 19, 1008–1013. [Google Scholar] [CrossRef]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Experimental Investigation and Empirical Modelling of Fdm Process for Compressive Strength Improvement. J. Adv. Res. 2012, 3, 81–90. [Google Scholar] [CrossRef]
- Dave, H.K.; Rajpurohit, S.R.; Patadiya, N.H.; Dave, S.J.; Sharma, K.S.; Thambad, S.S.; Srinivasn, V.P.; Sheth, K.V. Compressive Strength of Pla Based Scaffolds: Effect of Layer Height, Infill Density and Print Speed. Int. J. Mod. Manuf. Technol. 2019, 11, 21–27. [Google Scholar]
- Prajapati, A.R.; Rajpurohit, S.R.; Patadiya, N.H.; Dave, H.K. Analysis of Compressive Strength of 3d Printed Pla Part. In Advances in Manufacturing Processes: Select Proceedings of RAM 2020; Springer Singapore: Singapore, 2021. [Google Scholar]
- Aloyaydi, B.; Sivasankaran, S.; Mustafa, A. Investigation of Infill-Patterns on Mechanical Response of 3d Printed Poly-Lactic-Acid. Polym. Test. 2020, 87, 106557. [Google Scholar] [CrossRef]
- Yadav, P.; Sahai, A.; Sharma, R.S. Strength and Surface Characteristics of Fdm-Based 3d Printed Pla Parts for Multiple Infill Design Patterns. J. Inst. Eng. (India) Ser. C 2021, 102, 197–207. [Google Scholar] [CrossRef]
- Nomani, J.; Wilson, D.; Paulino, M.; Mohammed, M.I. Effect of Layer Thickness and Cross-Section Geometry on the Tensile and Compression Properties of 3d Printed Abs. Mater. Today Commun. 2020, 22, 100626. [Google Scholar] [CrossRef]
- Moradi, M.; Aminzadeh, A.; Rahmatabadi, D.; Rasouli, S.A. Statistical and Experimental Analysis of Process Parameters of 3d Nylon Printed Parts by Fused Deposition Modeling: Response Surface Modeling and Optimization. J. Mater. Eng. Perform. 2021, 30, 5441–5454. [Google Scholar] [CrossRef]
- Shaqour, B.; Abuabiah, M.; Abdel-Fattah, S.; Juaidi, A.; Abdallah, R.; Abuzaina, W.; Qarout, M.; Verleije, B.; Cos, P. Gaining a Better Understanding of the Extrusion Process in Fused Filament Fabrication 3d Printing: A Review. Int. J. Adv. Manuf. Technol. 2021, 114, 1279–1291. [Google Scholar] [CrossRef]
- Khan, M.M.K.; Liang, R.F.; Gupta, R.K.; Agarwal, S. Rheological and Mechanical Properties of Abs/Pc Blends. Korea-Aust. Rheol. J. 2005, 17, 1–7. [Google Scholar]
- Hu, G.-S.; Wang, B.-B.; Gao, F.-Z. Investigation on the Rheological Behavior of Nylon 6/11. Mater. Sci. Eng. A 2006, 426, 263–265. [Google Scholar] [CrossRef]
- Wu, W.; Geng, P.; Li, G.; Zhao, D.; Zhang, H.; Zhao, J. Influence of Layer Thickness and Raster Angle on the Mechanical Properties of 3d-Printed Peek and a Comparative Mechanical Study between Peek and Abs. Materials 2015, 8, 5834–5846. [Google Scholar] [CrossRef]
- Basgul, C.; Yu, T.; MacDonald, D.W.; Siskey, R.; Marcolongo, M.; Kurtz, S.M. Does Annealing Improve the Interlayer Adhesion and Structural Integrity of Fff 3d Printed Peek Lumbar Spinal Cages? J. Mech. Behav. Biomed. Mater. 2020, 102, 103455. [Google Scholar] [CrossRef]
- Nancharaiah, T.R.D.R.V.; Raju, D.R.; Raju, V.R. An Experimental Investigation on Surface Quality and Dimensional Accuracy of Fdm Components. Int. J. Emerg. Technol. 2010, 1, 106–111. [Google Scholar]
- Vasudevarao, B.; Natarajan, D.P.; Henderson, M.; Razdan, A. Sensitivity of Rp Surface Finish to Process Parameter Variation 251. In Proceedings of the 2000 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2000. [Google Scholar]
- Vijay, P.; Danaiah, P.; Rajesh, K.V.D. Critical Parameters Effecting the Rapid Prototyping Surface Finish. J. Mech. Eng. Autom. 2011, 1, 17–20. [Google Scholar] [CrossRef]
- Peng, A.H. Methods of Improving Part Accuracy During Rapid Prototyping. Adv. Mater. Res. 2012, 430–432, 760–763. [Google Scholar] [CrossRef]
- Lužanin, O.; Movrin, D.; Plančak, M. Experimental Investigation of Extrusion Speed and Temperature Effects on Arithmetic Mean Surface Roughness in Fdm-Built Specimens. J. Technol. Plast. 2013, 38, 179–190. [Google Scholar]
- Patel, D.M. Effects of Infill Patterns on Time, Surface Roughness and Tensile Strength in 3d Printing. Int. J. Eng. Dev. Res. 2017, 5, 566–569. [Google Scholar]
- Sood, A.K. Study on Parametric Optimization of Fused Deposition Modelling (FDM) Process. Ph.D. Thesis, National Institute of Technology, Rourkela, India, 2011. [Google Scholar]
- Wang, P.; Zou, B.; Ding, S. Modeling of Surface Roughness Based on Heat Transfer Considering Diffusion among Deposition Filaments for Fdm 3d Printing Heat-Resistant Resin. Appl. Therm. Eng. 2019, 161, 114064. [Google Scholar] [CrossRef]
- Baig, A.M.; Moeed, K.M.; Haque, M.S. A Study on the Effect of Infill Percentage and Infill Pattern on the Compressive Behaviour of the Fdm Printed Polylactic Acid (Pla) Polymer. GRD J. Glob. Res. Dev. J. Eng. 2019, 9, 5–8. [Google Scholar]
- Motaparti, K.P.; Taylor, G.; Leu, M.-C.; Chandrashekhara, K.; Castle, J.; Matlack, M. Effects of Build Parameters on Compression Properties for Ultem 9085 Parts by Fused Deposition Modeling. In Proceedings of the 27th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2016. [Google Scholar]
- Abbas, T.; Othman, F.M.; Ali, H.B. Effect of Infill Parameter on Compression Property in Fdm Process. Int. J. Eng. Res. Appl. 2017, 7, 16–19. [Google Scholar]
- Ahn, S.-H.; Montero, M.; Odell, D.; Roundy, S.; Wright, P.K. Anisotropic Material Properties of Fused Deposition Modeling Abs. Rapid Prototyp. J. 2002, 8, 248–257. [Google Scholar] [CrossRef]
- ASTM D792-20; Standard Test Methods for Density and Specific Gravity (Relative Density) of Plastics by Displacement. American Standard Methods. The American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2008.
- Forster, A.M. Materials Testing Standards for Additive Manufacturing of Polymer Materials: State of the Art and Standards Applicability; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2015. [Google Scholar]
- Gaweł, A.; Kuciel, S. The Study of Physico-Mechanical Properties of Polylactide Composites with Different Level of Infill Produced by the Fdm Method. Polymers 2020, 12, 3056. [Google Scholar] [CrossRef]
- Neter, J.; Kutner, M.H.; Nachtsheim, C.J.; Wasserman, W. Applied Linear Statistical Models; Marshall University: Huntington, WV, USA, 1996. [Google Scholar]
- He, F.; Khan, M. Effects of Printing Parameters on the Fatigue Behaviour of 3d-Printed Abs under Dynamic Thermo-Mechanical Loads. Polymers 2021, 13, 2362. [Google Scholar] [CrossRef]
- Kuznetsov, V.E.; Solonin, A.N.; Urzhumtsev, O.D.; Schilling, R.; Tavitov, A.G. Strength of Pla Components Fabricated with Fused Deposition Technology Using a Desktop 3d Printer as a Function of Geometrical Parameters of the Process. Polymers 2018, 10, 313. [Google Scholar] [CrossRef]
- Ding, S.; Zou, B.; Wang, P.; Ding, H. Effects of Nozzle Temperature and Building Orientation on Mechanical Properties and Microstructure of Peek and Pei Printed by 3d-Fdm. Polym. Test. 2019, 78, 105948. [Google Scholar] [CrossRef]
- Basgul, C.; Yu, T.; MacDonald, D.W.; Siskey, R.; Marcolongo, M.; Kurtz, S.M. Structure–Property Relationships for 3d-Printed Peek Intervertebral Lumbar Cages Produced Using Fused Filament Fabrication. J. Mater. Res. 2018, 33, 2040–2051. [Google Scholar] [CrossRef] [PubMed]
- Hashmi, A.W.; Mali, H.S.; Meena, A. The Surface Quality Improvement Methods for Fdm Printed Parts: A Review. In Fused Deposition Modeling Based 3D Printing; Springer: Cham, Switzerland, 2021; pp. 167–194. [Google Scholar]
- Guessasma, S.; Belhabib, S.; Nouri, H.; Ben Hassana, O. Anisotropic Damage Inferred to 3d Printed Polymers Using Fused Deposition Modelling and Subject to Severe Compression. Eur. Polym. J. 2016, 85, 324–340. [Google Scholar] [CrossRef]
- Garzon-Hernandez, S.; Garcia-Gonzalez, D.; Jérusalem, A.; Arias, A. Design of Fdm 3d Printed Polymers: An Experimental-Modelling Methodology for the Prediction of Mechanical Properties. Mater. Des. 2020, 188, 108414. [Google Scholar] [CrossRef]
- Calafel, I.; Aguirresarobe, R.H.; Peñas, M.I.; Santamaria, A.; Tierno, M.; Conde, J.I.; Pascual, B. Searching for Rheological Conditions for Fff 3d Printing with Pvc Based Flexible Compounds. Materials 2020, 13, 178. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wang, X.Z.; Yu, W.W.; Deng, Y.H. Numerical Investigation of the Influence of Process Conditions on the Temperature Variation in Fused Deposition Modeling. Mater. Des. 2017, 130, 59–68. [Google Scholar] [CrossRef]
- Samykano, M.; Selvamani, S.K.; Kadirgama, K.; Ngui, W.K.; Kanagaraj, G.; Sudhakar, K. Mechanical Property of Fdm Printed Abs: Influence of Printing Parameters. Int. J. Adv. Manuf. Technol. 2019, 102, 2779–2796. [Google Scholar] [CrossRef]
- Alzoubi, M.F.; Tanbour, E.Y.; Al-Waked, R. Compression and Hysteresis Curves of Nonlinear Polyurethane Foams under Different Densities, Strain Rates and Different Environmental Conditions. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Denver, CO, USA, 11–17 November 2011. [Google Scholar]
- Singh, L.; Khan, R.A.; Aggarwal, M.L. Relationship between Damping Factor and Compressive Residual Stress for Shot-Peened Austenitic Stainless Steel. Int. Sch. Res. Not. 2011, 2011, 867484. [Google Scholar] [CrossRef]
- Prasadh, S.; Wong, R.C.W. Unraveling the Mechanical Strength of Biomaterials Used as a Bone Scaffold in Oral and Maxillofacial Defects. Oral Sci. Int. 2018, 15, 48–55. [Google Scholar] [CrossRef]
- Ravandi, M.R.M.; Dezianian, S.; Ahmad, M.T.; Ghoddosian, A.; Azadi, M. Compressive Strength of Metamaterial Bones Fabricated by 3d Printing with Different Porosities in Cubic Cells. Mater. Chem. Phys. 2023, 299, 127515. [Google Scholar] [CrossRef]

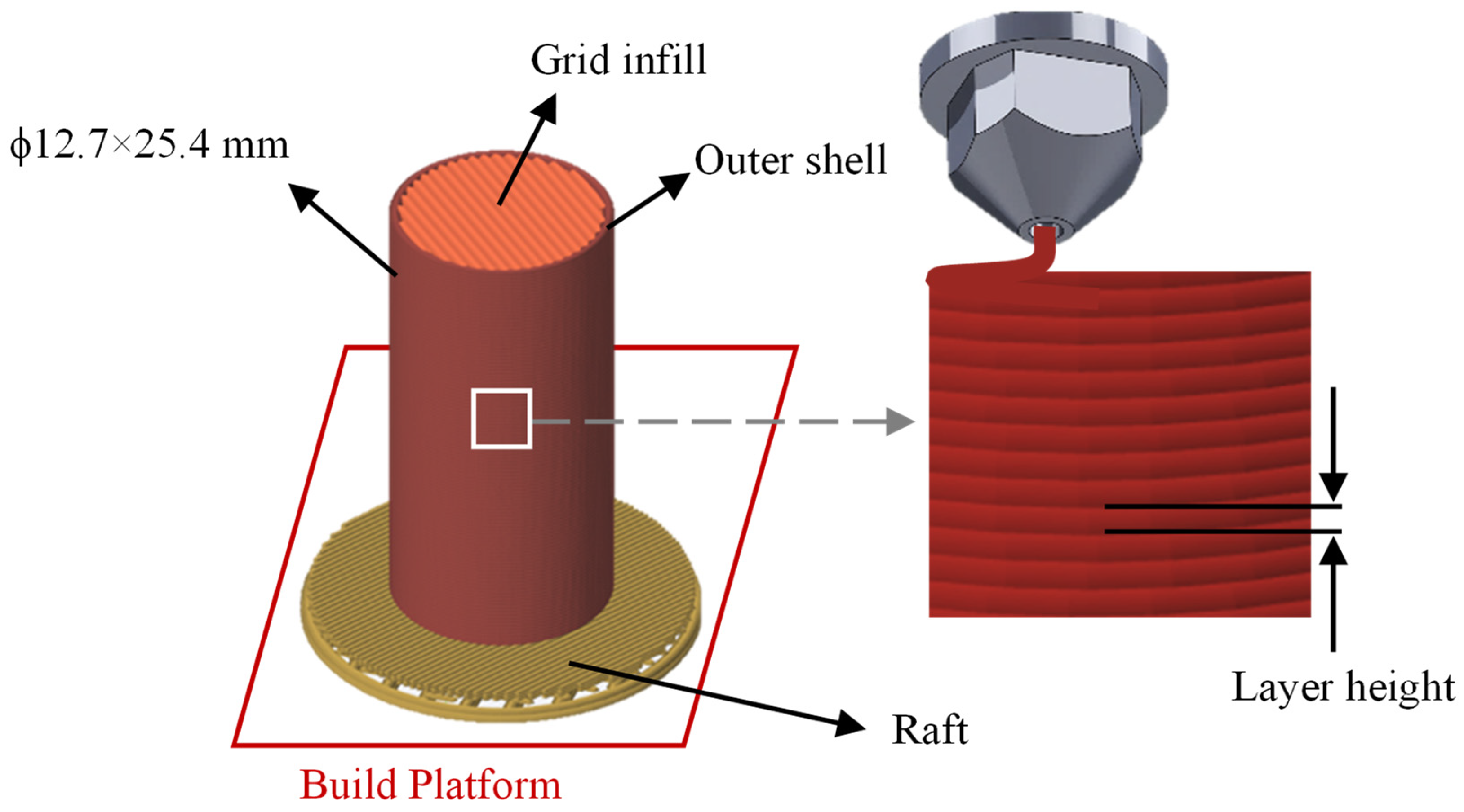


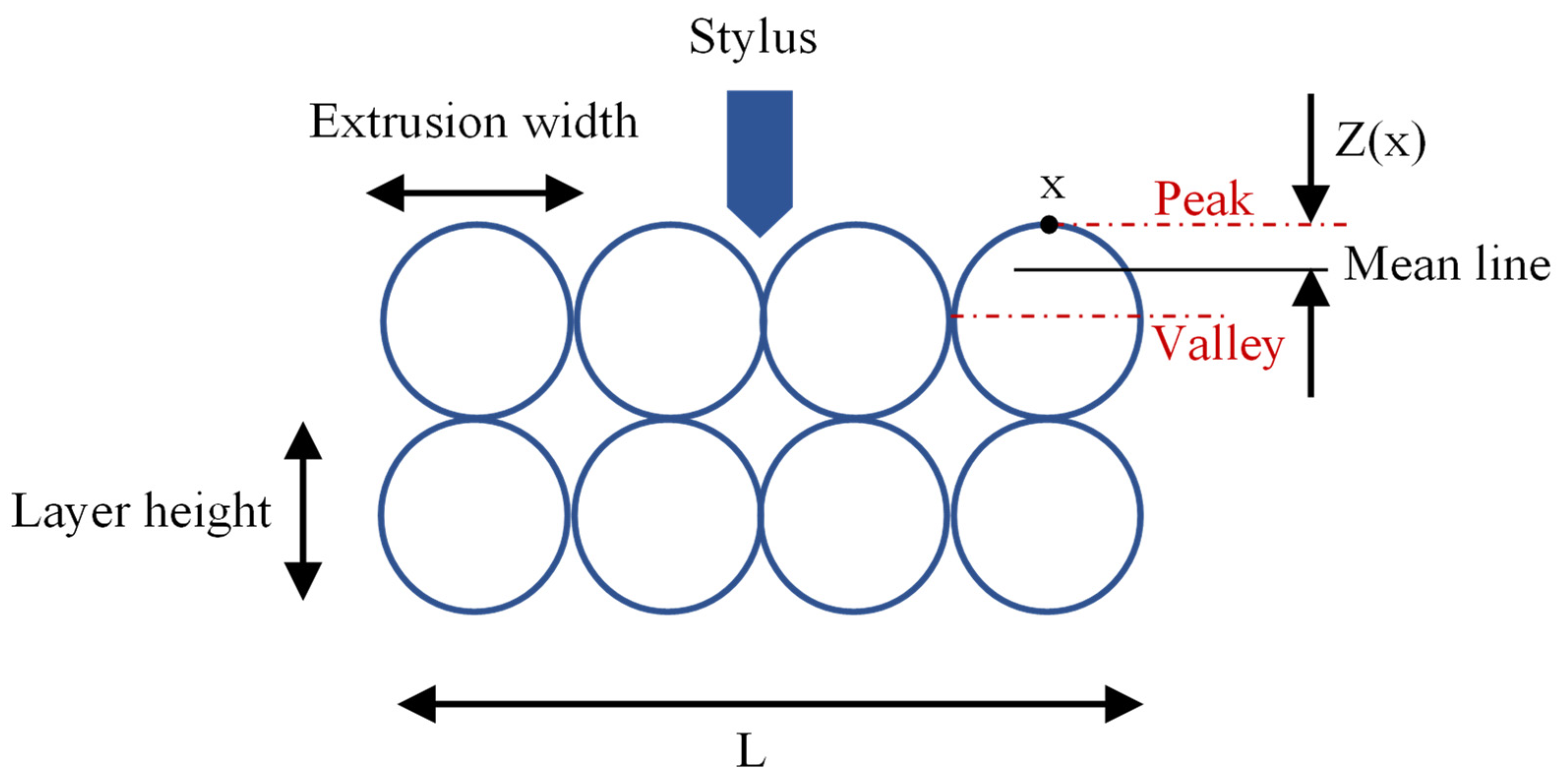





| Variables | Unit | Low (−1) | Medium (0) | High (+1) |
|---|---|---|---|---|
| Layer height (LH) | mm | 0.05 | 0.15 | 0.25 |
| Extrusion width (EW) | mm | 0.45 | 0.55 | 0.65 |
| Nozzle temperature (T) | °C | 190 | 205 | 220 |
| Print speed (V) | mm/s | 30 | 50 | 70 |
| Responses | ||||
| Relative density | ||||
| Surface roughness | ||||
| Compressive strength | ||||
| Compressive modulus | ||||
| Specific strength | ||||
| Failure strain | ||||
| Hysteresis loss (Area) | ||||
| Residual strain | ||||
| Sample No. | Layer Height (mm) | Extrusion Width (mm) | Nozzle Temperature (°C) | Print Speed (mm/s) |
|---|---|---|---|---|
| S1 | 0.25 | 0.55 | 190 | 70 |
| S2 | 0.15 | 0.55 | 220 | 30 |
| S3 | 0.15 | 0.45 | 205 | 70 |
| S4 | 0.05 | 0.65 | 220 | 70 |
| S5 | 0.05 | 0.55 | 205 | 50 |
| S6 | 0.15 | 0.65 | 190 | 50 |
| S7 | 0.25 | 0.45 | 220 | 50 |
| S8 | 0.25 | 0.65 | 205 | 30 |
| S9 | 0.05 | 0.45 | 190 | 30 |
| No. | T (min) | (%) | Ra (µm) | (MPa) | E (GPa) | σ/ρ (kN.m/kg) | (%) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| S1 | 14 | 92.50 | 17.35 | 61.30 | 1.42 | 52.53 | 13.21 | 0.29 | 0.39 | 1.07 |
| S2 | 32 | 91.80 | 10.67 | 62.78 | 1.84 | 54.17 | 14.05 | 0.31 | 0.50 | 0.57 |
| S3 | 25 | 91.80 | 10.40 | 62.55 | 1.71 | 54.01 | 12.56 | 0.28 | 0.45 | 0.78 |
| S4 | 60 | 93.20 | 6.59 | 71.49 | 2.04 | 60.79 | 12.15 | 0.25 | 0.52 | 0.64 |
| S5 | 70 | 92.30 | 6.22 | 66.38 | 2.02 | 56.98 | 11.57 | 0.24 | 0.59 | 0.43 |
| S6 | 23 | 93.20 | 14.32 | 65.50 | 1.75 | 55.65 | 12.79 | 0.27 | 0.44 | 0.80 |
| S7 | 17 | 93.50 | 16.83 | 55.46 | 1.52 | 46.96 | 14.20 | 0.32 | 0.40 | 0.82 |
| S8 | 18 | 93.00 | 17.95 | 61.22 | 1.74 | 52.15 | 14.81 | 0.32 | 0.46 | 0.71 |
| S9 | 106 | 90.30 | 7.30 | 62.23 | 2.02 | 54.59 | 10.68 | 0.24 | 0.57 | 0.39 |
| DF | Adj SS | Adj MS | F-Value | p-Value | Remarks | |
|---|---|---|---|---|---|---|
| Surface roughness | ||||||
| Regression | 4.000 | 178.390 | 44.598 | 52.060 | 0.001 | Significant |
| Layer height (mm) | 1.000 | 170.880 | 170.880 | 199.480 | <0.001 | Significant |
| Extrusion width (mm) | 1.000 | 3.125 | 3.125 | 3.650 | 0.129 | Insignificant |
| Nozzle temperature (C) | 1.000 | 3.969 | 3.969 | 4.630 | 0.098 | Insignificant |
| Print speed (mm/s) | 1.000 | 0.416 | 0.416 | 0.490 | 0.524 | Insignificant |
| Error | 4.000 | 3.426 | 0.857 | |||
| Total | 8.000 | 181.816 | ||||
| Compressive strength | ||||||
| Regression | 4.000 | 167.300 | 41.825 | 94.000 | <0.001 | Significant |
| Layer height (mm) | 1.000 | 86.762 | 86.762 | 195.000 | <0.001 | Significant |
| Extrusion width (mm) | 1.000 | 58.500 | 58.500 | 131.480 | <0.001 | Significant |
| Nozzle temperature (C) | 1.000 | 2.134 | 2.134 | 4.800 | 0.094 | Insignificant |
| Print speed (mm/s) | 1.000 | 19.904 | 19.904 | 44.730 | 0.003 | Significant |
| Error | 4.000 | 1.780 | 0.445 | |||
| Total | 8.000 | 169.079 | ||||
| Compressive modulus | ||||||
| Regression | 4.000 | 4.664 | 1.166 | 29.950 | 0.003 | Significant |
| Layer height (mm) | 1.000 | 4.114 | 4.114 | 105.650 | 0.001 | Significant |
| Extrusion width (mm) | 1.000 | 0.146 | 0.146 | 3.760 | 0.125 | Insignificant |
| Nozzle temperature (C) | 1.000 | 0.081 | 0.081 | 2.090 | 0.222 | Insignificant |
| Print speed (mm/s) | 1.000 | 0.323 | 0.323 | 8.290 | 0.045 | Significant |
| Error | 4.000 | 0.156 | 0.039 | |||
| Total | 8.000 | 4.819 | ||||
| Specific strength | ||||||
| Regression | 4.000 | 116.649 | 29.162 | 41.060 | 0.002 | Significant |
| Layer height (mm) | 1.000 | 73.994 | 73.994 | 104.170 | 0.001 | Significant |
| Extrusion width (mm) | 1.000 | 30.294 | 30.294 | 42.650 | 0.003 | Significant |
| Nozzle temperature (C) | 1.000 | 1.032 | 1.032 | 1.450 | 0.295 | Insignificant |
| Print speed (mm/s) | 1.000 | 11.330 | 11.330 | 15.950 | 0.016 | Significant |
| Error | 4.000 | 2.841 | 0.710 | |||
| Total | 8.000 | 119.491 | ||||
| Toughness | ||||||
| Regression | 4.000 | 14.602 | 3.651 | 80.440 | <0.001 | Significant |
| Layer height (mm) | 1.000 | 10.331 | 10.331 | 227.640 | <0.001 | Significant |
| Extrusion width (mm) | 1.000 | 0.766 | 0.766 | 16.880 | 0.015 | Significant |
| Nozzle temperature (C) | 1.000 | 2.274 | 2.274 | 50.100 | 0.002 | Significant |
| Print speed (mm/s) | 1.000 | 1.231 | 1.231 | 27.130 | 0.006 | Significant |
| Error | 4.000 | 0.182 | 0.045 | |||
| Total | 8.000 | 14.784 | ||||
| Failure strain | ||||||
| Regression | 4.000 | 0.011 | 0.003 | 325.020 | <0.001 | Significant |
| Layer height (mm) | 1.000 | 0.008 | 0.008 | 908.720 | <0.001 | Significant |
| Extrusion width (mm) | 1.000 | 0.000 | 0.000 | 0.420 | 0.553 | Insignificant |
| Nozzle temperature (C) | 1.000 | 0.002 | 0.002 | 231.480 | <0.001 | Significant |
| Print speed (mm/s) | 1.000 | 0.001 | 0.001 | 159.450 | <0.001 | Significant |
| Error | 4.000 | 0.000 | 0.000 | |||
| Total | 8.000 | 0.011 | ||||
| Hysteresis loss | ||||||
| Regression | 4.000 | 12.544 | 3.136 | 12.540 | 0.016 | Significant |
| Layer height (mm) | 1.000 | 10.406 | 10.406 | 41.610 | 0.003 | Significant |
| Extrusion width (mm) | 1.000 | 0.076 | 0.076 | 0.310 | 0.610 | Insignificant |
| Nozzle temperature (C) | 1.000 | 0.126 | 0.126 | 0.500 | 0.517 | Insignificant |
| Print speed (mm/s) | 1.000 | 1.935 | 1.935 | 7.740 | 0.050 | Significant |
| Error | 4.000 | 1.001 | 0.250 | |||
| Total | 8.000 | 13.544 | ||||
| Residual strain | ||||||
| Regression | 4.000 | 0.342 | 0.085 | 23.330 | 0.005 | Significant |
| Layer height (mm) | 1.000 | 0.217 | 0.217 | 59.140 | 0.002 | Significant |
| Extrusion width (mm) | 1.000 | 0.004 | 0.004 | 1.160 | 0.341 | Insignificant |
| Nozzle temperature (C) | 1.000 | 0.009 | 0.009 | 2.410 | 0.196 | Insignificant |
| Print speed (mm/s) | 1.000 | 0.112 | 0.112 | 30.600 | 0.005 | Significant |
| Error | 4.000 | 0.015 | 0.004 | |||
| Total | 8.000 | 0.356 | ||||
| Predicted R-sq (%) (Full Model) | Predicted R-sq (%) (Reduced Model) | Improvement (%) | |
|---|---|---|---|
| Surface roughness | 89.28 | 92.15 | 3.21 |
| Compressive strength | 93.53 | 94.5 | 1.04 |
| Compressive modulus | 82.25 | 83.24 | 1.2 |
| Specific strength | 84.87 | 91.54 | 7.86 |
| Failure strain | 98.53 | 99.05 | 0.53 |
| Hysteresis loss | 64.48 | 81.53 | 26.44 |
| Residual strain | 82.71 | 87.66 | 5.98 |
| No. | LH | EW | T | V | Ra | E | DI | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.05 | 0.65 | 220 | 70 | 92.47 | 6.77 | 71.46 | 2.02 | 61.02 | 12.28 | 0.25 | 0.52 | 0.61 | 1.00 |
| A2 | 0.05 | 0.65 | 205 | 70 | 92.01 | 6.66 | 71.46 | 2.02 | 61.02 | 11.82 | 0.24 | 0.55 | 0.58 | 1.00 |
| A3 | 0.05 | 0.65 | 190 | 70 | 91.63 | 7.45 | 71.46 | 2.02 | 61.02 | 11.20 | 0.22 | 0.51 | 0.69 | 0.97 |
| A4 | 0.05 | 0.55 | 190 | 70 | 91.63 | 6.86 | 68.88 | 1.98 | 59.38 | 10.98 | 0.22 | 0.51 | 0.69 | 0.84 |
| A5 | 0.05 | 0.55 | 220 | 70 | 92.47 | 6.28 | 68.88 | 1.98 | 59.38 | 12.02 | 0.25 | 0.52 | 0.61 | 0.84 |
| B1 | 0.05 | 0.65 | 205 | 70 | 92.01 | 6.66 | 71.46 | 2.02 | 61.02 | 11.82 | 0.24 | 0.55 | 0.58 | 0.85 |
| B2 | 0.05 | 0.65 | 220 | 30 | 91.66 | 6.77 | 68.42 | 2.11 | 58.87 | 12.28 | 0.26 | 0.60 | 0.34 | 0.84 |
| B3 | 0.05 | 0.65 | 220 | 70 | 92.47 | 6.77 | 71.46 | 2.02 | 61.02 | 12.28 | 0.25 | 0.52 | 0.61 | 0.84 |
| B4 | 0.05 | 0.65 | 205 | 30 | 91.21 | 6.66 | 68.42 | 2.11 | 58.87 | 11.82 | 0.25 | 0.63 | 0.30 | 0.82 |
| B5 | 0.05 | 0.65 | 205 | 50 | 92.51 | 6.66 | 68.79 | 2.05 | 58.44 | 11.82 | 0.24 | 0.58 | 0.43 | 0.81 |
| E | σ/ρ | T | Ra | |||||
|---|---|---|---|---|---|---|---|---|
| A1 (Experimental) | 93.2 | 71.49 | 2.04 | 60.79 | 0.52 | 12.15 | 6.59 | 0.25 |
| A1 (Predicted) | 92.47 | 71.46 | 2.02 | 61.02 | 0.52 | 12.28 | 6.77 | 0.25 |
| A2 (=B1) (Experimental) | 93.6 | 67.79 | 2.29 | 56.36 | 0.56 | 12.38 | 4.92 | 0.26 |
| A2 (=B1) (Predicted) | 92 | 71.46 | 2.02 | 61.02 | 0.55 | 11.82 | 6.66 | 0.24 |
| B2 (Experimental) | 93.7 | 67.15 | 2.26 | 56.77 | 0.65 | 9.82 | 5.86 | 0.21 |
| B2 (Predicted) | 91.66 | 68.42 | 2.11 | 58.87 | 0.6 | 12.28 | 6.77 | 0.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakhtiari, H.; Nikzad, M.; Tolouei-Rad, M. Influence of Three-Dimensional Printing Parameters on Compressive Properties and Surface Smoothness of Polylactic Acid Specimens. Polymers 2023, 15, 3827. https://doi.org/10.3390/polym15183827
Bakhtiari H, Nikzad M, Tolouei-Rad M. Influence of Three-Dimensional Printing Parameters on Compressive Properties and Surface Smoothness of Polylactic Acid Specimens. Polymers. 2023; 15(18):3827. https://doi.org/10.3390/polym15183827
Chicago/Turabian StyleBakhtiari, Hamed, Mostafa Nikzad, and Majid Tolouei-Rad. 2023. "Influence of Three-Dimensional Printing Parameters on Compressive Properties and Surface Smoothness of Polylactic Acid Specimens" Polymers 15, no. 18: 3827. https://doi.org/10.3390/polym15183827
APA StyleBakhtiari, H., Nikzad, M., & Tolouei-Rad, M. (2023). Influence of Three-Dimensional Printing Parameters on Compressive Properties and Surface Smoothness of Polylactic Acid Specimens. Polymers, 15(18), 3827. https://doi.org/10.3390/polym15183827








